Интерференция света
Закон независимости световых пучков геометрической оптики означает, что световые пучки встречаясь, не воздействуют друг на друга. В явлениях, в которых проявляется волновая природа света, этот закон утрачивает силу. При наложении световые волн в общем случае выполняется принцип суперпозиции
: результирующий световой вектор является суммой световых векторов отдельных волн. При этом может получиться волна, интенсивность которой не будет равна сумме интенсивностей складывающихся волн.
Интерференция свойственна не только световым волнам, являющимися по своей природе электромагнитными волнами, но и волнам любого другого типа. Поскольку волны любого вида удовлетворяют одним и тем же волновым уравнениям, то при описании интерференции любых видов волн применяется один и тот же математический аппарат. Поэтому, сущность интерференции рассмотрим на примере сложения двух одномерных гармонических волн (волн вида 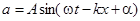 ) одинаковой частоты. Накладываясь друг на друга, они возбуждают в некоторой точке пространства гармонические колебания ) одинаковой частоты. Накладываясь друг на друга, они возбуждают в некоторой точке пространства гармонические колебания
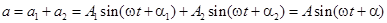 , ,
амплитуда которых определяется выражением
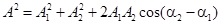 . .
Интенсивность волны пропорциональна квадрату амплитуды 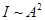 . Поэтому, наблюдаемая при наложении волн интенсивность . Поэтому, наблюдаемая при наложении волн интенсивность
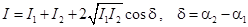 . (1) . (1)
Результат сложения зависит от разности фаз d (меняющейся при переходе к другой пространственной точке). В тех точках пространства, для которых 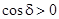 , , 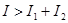 ; в точках, для которых ; в точках, для которых 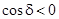 , , 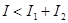 . .
Таким образом, при наложении гармонических (в общем случае когерентных) световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией
волн.
Рассмотрим точечный источник света S
, который излучает монохроматический свет (свет фиксированной частоты) (рис.). До точки P
первый луч проходит в среде с показателем преломления 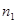 путь путь 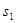 , второй луч проходит в среде с показателем преломления , второй луч проходит в среде с показателем преломления 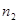 путь путь 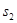 . Если в точке S
фаза колебаний равна . Если в точке S
фаза колебаний равна 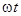 , то первый луч возбудит в точке P
колебание , то первый луч возбудит в точке P
колебание 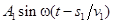 , а второй луч – колебание , а второй луч – колебание 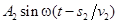 ( (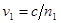 и и 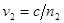 – фазовые скорости волн). Следовательно, разность фаз колебаний, возбуждаемых лучами в точке P
, будет равна – фазовые скорости волн). Следовательно, разность фаз колебаний, возбуждаемых лучами в точке P
, будет равна
Реклама

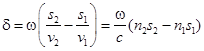 . .
Множитель 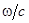 равен равен 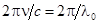 ( (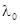 – длина волны в вакууме) и выражению для разности фаз можно придать вид – длина волны в вакууме) и выражению для разности фаз можно придать вид
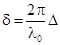 , (2) , (2)
где 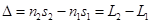 (3) (3)
есть величина, называемая оптической разностью хода
.
Из формулы (2) видно, что если оптическая разность хода равна целому числу длин волн в вакууме
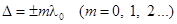 , (4) , (4)
то разность фаз 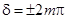 и колебания будут происходить с одинаковой фазой. Следовательно, условие (4) есть условие интерференционного максимума. и колебания будут происходить с одинаковой фазой. Следовательно, условие (4) есть условие интерференционного максимума.
Если D равна полуцелому числу длин волн в вакууме,
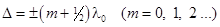 , (5) , (5)
то 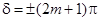 , так что колебания в точке P
находятся в противофазе. Условие (5) есть условие интерференционного минимума. , так что колебания в точке P
находятся в противофазе. Условие (5) есть условие интерференционного минимума.
Когерентность.
В реальности монохроматических
волн (неограниченных во времени волн фиксированной частоты) не существует. Для реальных световых волн необходимым условием интерференции является их когерентность
. Так называется согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.
Некогерентность естественных источников света обусловлена тем, что излучение светящегося тела складывается из волн, испускаемых многими атомами. Отдельные атомы излучают цуги волн длительностью ~10-8
с и протяженностью около 3 м независимо друг от друга. Начальные фазы этих волновых цугов никак не связаны между собой. Помимо этого, даже для одного и того же атома начальные фазы цугов при следующих актах излучения меняются случайным образом.
Временной подход к анализу интерференции.
Рассмотрим следующую простую модель излучения: точечный источник испускает последовательность гармонических цугов с равными длительностями t, равными амплитудами A
и независимыми друг от друга случайными начальными фазами. При сложении двух таких волн интенсивность колебаний в некоторой точке будет равна
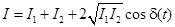 , (6) , (6)
где разность фаз 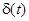 претерпевает скачкообразные изменения. Если оптическая разность хода D больше длины цуга, то складываются колебания заведомо разных цугов, поэтому претерпевает скачкообразные изменения. Если оптическая разность хода D больше длины цуга, то складываются колебания заведомо разных цугов, поэтому 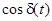 имеет случайные значения. Всякий прибор, с помощью которого можно наблюдать интерференционную картину (глаз, фотопластинка и т.п.), обладает некоторой инерционностью. В связи с этим он регистрирует картину, усредненную по некоторому промежутку имеет случайные значения. Всякий прибор, с помощью которого можно наблюдать интерференционную картину (глаз, фотопластинка и т.п.), обладает некоторой инерционностью. В связи с этим он регистрирует картину, усредненную по некоторому промежутку 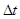 . На практике . На практике 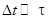 и поэтому, множитель и поэтому, множитель 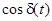 принимает случайным образом все значения от –1 до +1 и имеет среднее значение равное нулю. Таким образом, средняя интенсивность принимает случайным образом все значения от –1 до +1 и имеет среднее значение равное нулю. Таким образом, средняя интенсивность 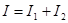 и интерференция отсутствует. Если же D меньше длины цуга, то в точке наблюдения частично перекрываются разные участки одного и того же цуга и поэтому некоторую часть времени и интерференция отсутствует. Если же D меньше длины цуга, то в точке наблюдения частично перекрываются разные участки одного и того же цуга и поэтому некоторую часть времени 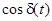 имеет вполне определенное значение (случайное в остальное время). В силу этого имеет вполне определенное значение (случайное в остальное время). В силу этого 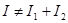 и в меру перекрытия будет наблюдаться более или менее контрастная интерференционная картина. и в меру перекрытия будет наблюдаться более или менее контрастная интерференционная картина.
Реклама

Продолжительность одного цуга t естественно отождествить со временем когерентности
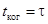 . За это время волна распространится в вакууме на расстояние . За это время волна распространится в вакууме на расстояние 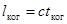 , называемое длиной когерентности
. По своему определению длина когерентности есть расстояние, при прохождении которого волна утрачивает когерентность. Это значит, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для данного источника. , называемое длиной когерентности
. По своему определению длина когерентности есть расстояние, при прохождении которого волна утрачивает когерентность. Это значит, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для данного источника.
Рассмотренная модель излучения является идеализированной, так как в ней принималось, что свет состоит из последовательности цугов, имеющих одинаковую частоту w, длительность t и случайные начальные фазы. В более правдоподобных моделях излучения света атомами, включая реальное излучение, при рассмотрении интерференции также возникает временной параметр 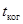 . Если временная разность хода двух лучей меньше . Если временная разность хода двух лучей меньше 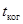 , то наблюдается более или менее контрастная интерференционная картина, в противном случае интерференция практически не наблюдается. , то наблюдается более или менее контрастная интерференционная картина, в противном случае интерференция практически не наблюдается.
Рассмотренный подход к анализу интерференции использует временные характеристики световых волн (время когерентности). Анализ можно провести и иным (спектральным) способом, в котором немонохроматический свет представляется в виде суперпозиции монохроматических пучков с различными частотами. Спектральный и временной подходы к анализу интерференции являются разными способами рассуждений о степени когерентности колебаний. Они приводят к идентичным выводам относительно интерференционной картины.
Спектральный подход к анализу интерференции.
Пусть интервал длин волн ограничен и заключен между l и 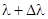 . Интерференция не будет наблюдаться, если максимум m
-го порядка для . Интерференция не будет наблюдаться, если максимум m
-го порядка для 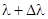 совпадет с максимумом (m
+1)-го порядка для l. В этих условиях весь провал между соседними максимумами для l будет заполнен максимумами неразличимых длин волн нашего интервала (рис.). Условие неразличимости интерференционной картины: совпадет с максимумом (m
+1)-го порядка для l. В этих условиях весь провал между соседними максимумами для l будет заполнен максимумами неразличимых длин волн нашего интервала (рис.). Условие неразличимости интерференционной картины: 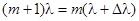 , т.е. , т.е. 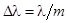 , где m
– целое число. , где m
– целое число.
Порядок интерференции m
определяется разностью хода световых пучков и длиной волны соотношением 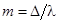 . Отсюда следует, что разность хода, при которой исчезает интерференционная картина, т.е. длина когерентности, равна . Отсюда следует, что разность хода, при которой исчезает интерференционная картина, т.е. длина когерентности, равна
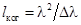 . (7) . (7)
Она определяется свойствами источника света (либо применяемого монохроматора – устройства, пропускающего свет узкого диапазона длин волн). Пространственная когерентность и время когерентности связаны между собой соотношением 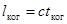 . Используя соотношения . Используя соотношения 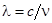 и и 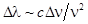 , где n – частота, Dn – интервал частот немонохроматического пучка, находим связь между временем когерентности и интервалом частот , где n – частота, Dn – интервал частот немонохроматического пучка, находим связь между временем когерентности и интервалом частот
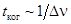 . (8) . (8)
Эта связь имеет общий характер.
Расчет интерференционной картины от двух источников.
Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников 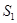 и и 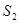 , имеющих вид параллельных, тонких светящихся нитей либо узких щелей. Если в области, в которой волны перекрываются, внести экран, то на нем будет видна интерференционная картина, которая имеет вид чередующихся светлых и темных полос. Рассчитаем положение полос и их ширину. Экран поместим параллельно обеим щелям на одинаковом расстоянии l
. Начало отсчета выберем в точке O
, относительно которой , имеющих вид параллельных, тонких светящихся нитей либо узких щелей. Если в области, в которой волны перекрываются, внести экран, то на нем будет видна интерференционная картина, которая имеет вид чередующихся светлых и темных полос. Рассчитаем положение полос и их ширину. Экран поместим параллельно обеим щелям на одинаковом расстоянии l
. Начало отсчета выберем в точке O
, относительно которой 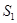 и и 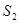 расположены симметрично. Источники будем считать испускающими свет в одинаковой фазе. Из рисунка видно, что расположены симметрично. Источники будем считать испускающими свет в одинаковой фазе. Из рисунка видно, что
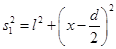 , , 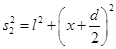 . .
Следовательно
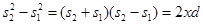
и оптическая разность хода равна
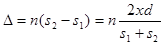 . .
Разность хода 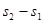 составляет несколько длин волн и всегда значительно меньше составляет несколько длин волн и всегда значительно меньше 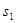 и и 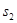 ( (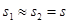 ). Поэтому можно положить ). Поэтому можно положить 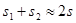 и и
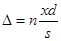 . (9) . (9)
В большинстве случаев 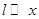 , поэтому , поэтому 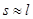 , т.е. , т.е.
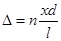 (10) (10)
Подстановка значения D в условие (4) дает, что максимумы интенсивности будут наблюдаться при значениях
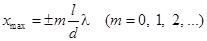 . (11) . (11)
Здесь 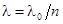 – длина волны в среде. – длина волны в среде.
Подставив (10) в условие (5), получим координаты минимумов интенсивности
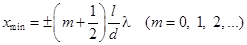 . (12) . (12)
Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами
, а расстояние между соседними минимумами –шириной интерференционной полосы
. Из (11) и (12) следует, что эти расстояния имеют одинаковое значение
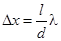 . (13) . (13)
Интерференция двух плоских волн. Пусть происходит наложение двух плоских волн, амплитуды которых одинаковы, а направления их распространения образуют угол 2j (рис.). Направления колебаний светового вектора будем считать перпендикулярными к плоскости рисунка. Волновые векторы 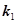 и и 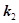 лежат в плоскости рисунка и имеют одинаковый модуль, равный лежат в плоскости рисунка и имеют одинаковый модуль, равный 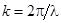 . Уравнения волн имеют вид . Уравнения волн имеют вид
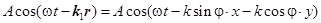 , ,
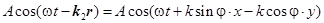 , ,
а результирующие колебания –
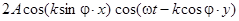 . .
Из последнего выражения следует, что в точках, где 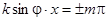 ( (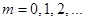 ), амплитуда колебаний равна 2A
; в точках, где ), амплитуда колебаний равна 2A
; в точках, где 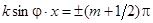 , амплитуда колебаний равна нулю. Где бы ни располагался экран, перпендикулярный к оси y
, на нем будет наблюдаться система чередующихся светлых и темных полос, параллельных оси z
. Координаты максимумов интенсивности , амплитуда колебаний равна нулю. Где бы ни располагался экран, перпендикулярный к оси y
, на нем будет наблюдаться система чередующихся светлых и темных полос, параллельных оси z
. Координаты максимумов интенсивности
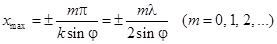 . (14) . (14)
Пространственная когерентность.
Во всех практических интерференционных схемах большое значение имеют размеры источника света. Если размеры источника значительно меньше длины световой волны то, конечно, всегда получается резкая интерференционная картина (при выполнении условия временной когерентности), ибо оптическая разность пути до какой-либо точки интерференционного поля для всего источника будет одна и та же. Однако на практике размеры источников света обычно значительно превосходят длину световой волны. Каждая точка источника создает свою интерференционную картину. Результирующая картина получается наложением картин всех элементов протяженного источника, излучение которых считаем некогерентными между собой. Эти картины не совпадают друг с другом так, что результирующая картина окажется более или менее размытой и при значительной ширине источника перестанет наблюдаться.
Влияние размеров источника на резкость интерференционной картины можно выразить количественно, исходя из общей интерференционной схемы (рис.). Пусть AB
– протяженный источник ширины b
. Рассмотрим результирующую интерференционную картину в окрестности некоторой точки экрана. Максимумы, получаемые от разных точек источника, будут смещены относительно друг друга. Если максимумы от точки B
совпадают с максимумами от точки A
так, что их порядок интерференции отличается на единицу то, результирующая интерференционная картина будет смазанной и интерференция не наблюдается (рис.). Для того чтобы интерференция была возможна, размер источника света не должен превышать некоторой величины. Эту величину определим из условия совпадения максимума (m
+1)–го порядка, получаемого от точки A
, с максимумом m
–го порядка, получаемым от точки B
. Отличие оптических разностей хода точек A
и B
составляет, очевидно, 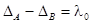 . Используя (10), получаем соотношение . Используя (10), получаем соотношение
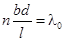 , ,
где l
– расстояние между источником света и щелями. Определяя угловой размер источника 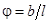 и используя связь длин волн в вакууме и среде и используя связь длин волн в вакууме и среде 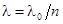 , получаем условие , получаем условие
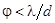 . (15) . (15)
Формула (15) определяет угловые размеры источника, при которых наблюдается интерференция. Пусть теперь зафиксированы угловые размеры источника света. Тогда расстояние между щелями, при котором можно еще наблюдать интерференцию от источника с угловым размером j должно удовлетворять, согласно (15), условию
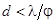 . (16) . (16)
В соответствии с принципом Гюйгенса, реальный источник света в данной схеме можно заменить псевдоисточниками, расположенными на месте щелей. Отсутствие интерференционной картины означает, что волновые колебания этих источников некогерентны. Введем расстояние 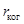 , при смещении на которое в направлении, поперечном распространению света, волновые колебания становятся некогерентными. Колебания в двух точках, отстоящих друг от друга на расстояние , при смещении на которое в направлении, поперечном распространению света, волновые колебания становятся некогерентными. Колебания в двух точках, отстоящих друг от друга на расстояние 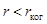 , будут частично когерентными. Расстояние , будут частично когерентными. Расстояние 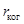 называется радиусом когерентности
. Из (16) следует называется радиусом когерентности
. Из (16) следует
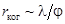 . .
Угловой размер Солнца составляет около 0,01 рад, длина световых волн ~0,5 мкм. Следовательно, радиус когерентности приходящих от Солнца световых волн имеет значение 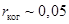 мм. При использовании Солнца в качестве источника света щели следует располагать на расстоянии, меньшем 0,05 мм, а для наблюдения отчетливых интерференционных полос нужно брать d
~ 0,02 мм. Юнг получил интерференцию в 1802 г. от двух щелей, увеличив пространственную когерентность падающего на щели света. Такое увеличение Юнг осуществил, пропустив предварительно свет через небольшое отверстие в непрозрачном экране. мм. При использовании Солнца в качестве источника света щели следует располагать на расстоянии, меньшем 0,05 мм, а для наблюдения отчетливых интерференционных полос нужно брать d
~ 0,02 мм. Юнг получил интерференцию в 1802 г. от двух щелей, увеличив пространственную когерентность падающего на щели света. Такое увеличение Юнг осуществил, пропустив предварительно свет через небольшое отверстие в непрозрачном экране.
Излучение лазера, по сравнению с естественным светом, обладает огромной временной и пространственной когерентностью. Временная когерентность имеет значение порядка 10–5
с (гелий-неоновый лазер) а пространственная когерентность наблюдается во всем поперечном сечении светового пучка.
Методы наблюдения интерференции света.
1. Метод Юнга.
Источником сета служит ярко освещенная щель S
(рис), от которой световая волна падает на две узкие равноудаленные щели 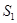 и и 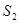 , параллельные щели S
. Таким образом, щели играют роль когерентных источников. Интерференционная картина наблюдается на экране (Э
), расположенном на некотором расстоянии от щелей , параллельные щели S
. Таким образом, щели играют роль когерентных источников. Интерференционная картина наблюдается на экране (Э
), расположенном на некотором расстоянии от щелей 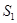 и и 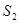 . В такой постановке Юнг осуществил первое наблюдение интерференции. . В такой постановке Юнг осуществил первое наблюдение интерференции.
2. Зеркала Френеля.
Два плоских зеркала (рис.), расположены относительно друг друга под небольшим углом (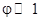 ). На расстоянии r
от линии пересечения зеркал параллельно ей находится прямолинейный источник света S
. Световые пучки, отразившись от зеркал, являются мнимыми изображениями S
в зеркалах. Мнимые источники ). На расстоянии r
от линии пересечения зеркал параллельно ей находится прямолинейный источник света S
. Световые пучки, отразившись от зеркал, являются мнимыми изображениями S
в зеркалах. Мнимые источники 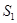 и и 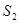 взаимно когерентны, и их световые пучки интерферируют в области взаимного перекрытия. От прямого попадания света на экран предохраняет заслонка. взаимно когерентны, и их световые пучки интерферируют в области взаимного перекрытия. От прямого попадания света на экран предохраняет заслонка.
Бипризма Френеля.
Она состоит из двух одинаковых с общей гранью призм с малыми преломляющими углами (рис.). Свет от прямолинейного источника S
преломляется в обеих призмах, в результате чего образуются две когерентные цилиндрические волны, исходящих из мнимых источников 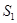 и и 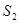 . На поверхности экрана в некоторой его части происходит наложение этих волн и наблюдается интерференция. . На поверхности экрана в некоторой его части происходит наложение этих волн и наблюдается интерференция.
|