| Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Вятский государственный гуманитарный университет»
Физико-математический факультет
Кафедра дидактики физики и математики
Выпускная квалификационная работа
Использование элементов ТРИЗ-педагогики в обучении школьников математике
Выполнил
студент V курса физико-математического факультета
(специальность 050201.65 Математика) Утёмов Вячеслав Викторович
Научный руководитель:
канд. пед. наук, ст. преп. кафедры
дидактики физики и математики
Горев Павел Михайлович
Рецензент:
канд. пед. наук, ст. преп. кафедры
дидактики физики и математики
Малых Елена Владимировна
Работа допущена к защите в государственной аттестационной комиссии
«___»__________2008 г. Зам. зав. Кафедрой М.В. Крутихина
«___»__________2008 г. Декан факультета Е.В. Кантор
Киров, 2008
Содержание
Введение
Глава 1. «Прикладная диалектика» и ее применение в педагогике
1.1. Теория решения изобретательских задач (ТРИЗ)
1.2. Развитие творческой личности и ТРИЗ
1.3. ТРИЗ – рабочий инструмент диалектики
1.4. Образование на основе логики и диалектики
1.5. Культура мышления
1.6. Принципы дидактики в ТРИЗ-педагогике
1.7. ТРИЗ и образовательная сфера
1.8. Этапы развития ТРИЗ-педагогики
1.9. Теория решения изобретательских задач
как метод исследования педагогических систем
1.10. Термин «ТРИЗ-педагогика»
Глава 2. Использование инструментов ТРИЗ
в обучении школьников математике
2.1. Ситуация как средство развития творческих способностей
2.2. Мета-алгоритм изобретения ТРИЗ
и решение учебных математических задач
2.3. Вепольный анализ при решении учебных математических задач
2.4. Метод переизобретения знаний
2.5. Методы технического творчества
при обучении школьников математике
2.6. Принципы решения математических задач
2.7. ТРИЗ-педагогика на уроках математики
Глава 3. Описание и анализ опытно-экспериментальной работы
3.1. Психологические аспекты сущности креативности
3.2. Ключевые психологические идеи тренинга
3.3. Тренинг креативного мышления
3.4. Анализ результатов опытно-экспериментальной работы
Заключение
Библиографический список
Приложения
Введение
Анализ участия в программе по оценке образовательных достижений учащихся PISA (Programme for International Student Assessment: Monitoring Knowledge and Skills in the New Millennium) в исследованиях 2006 года [11], российских школьников показали, что учащиеся испытывают затруднения, среди прочих, при работе:
Реклама

· с заданиями, составленными на материале из разных предметных областей, для правильного выполнения которых надо интегрировать разнообразные знания, использовать общеучебные умения, отбирать и использовать адекватные описываемой ситуации способы размышления, анализа;
· с заданиями, в которых неясно, к какой области знаний надо обратиться, чтобы определить способ действия или информацию, необходимые для выявления и решения проблемы;
· с заданиями, где нужно привлекать дополнительную информацию (в том числе выходящую за рамки описанной в задании ситуации), или, напротив, с заданиями, содержащими избыточную информацию и «лишние» данные;
· с комплексными или структурированными заданиями, состоящими из нескольких взаимосвязанных вопросов.
Среди целей, предъявляемых к современному школьному образованию, выделяется формирование личности, способной решать поставленные перед ней задачи в условиях рыночной экономики, в частности, быстро находить наиболее оптимальное и эффективное решение преодолеваемой проблемы. Такая цель направлена на реализацию внутреннего потенциала школьника, развитие его творческого начала, продуктивности мышления, которые как раз и должны способствовать развитию умения справляется с выше перечисленными заданиями. Это с одной стороны.
С другой стороны, в методике преподавания математики существуют три ключевых вопроса: «Что преподавать?», «Как преподавать?» и «Зачем преподавать?». Последний из них наиболее трудный. Сегодня главное в образовании – развитие, формирование общей культуры человека, способного в частности, самостоятельно добывать и перерабатывать информацию или, другими словами, на уроках математики разумней не учить математике, а учить математикой
[48]. Это вызывает затруднения на практике. Необходимо внедрение на уроки математики в школе таких общих для всех дисциплин элементов, которые позволили бы интегрировать математику с другими образовательными областями.
В последнее время с высоким темпом адаптируется применение ТРИЗ (теории решения изобретательских задач Г. С. Альтшуллера) в образовании, которая получило название ТРИЗ-педагогика. Это отражается в ряде диссертаций на соискание ученых степеней: проектирование образовательных технологий на основе ТРИЗ [47], развитие системно-логического мышления учащихся в процессе изучения теории решения изобретательских задач (ТРИЗ) [84] и др. Внедрение инструментов ТРИЗ в образование способствует продуктивности мышления [68], а также играет роль «общего» языка для интеграции различных образовательных областей [34]. Все это определяет актуальность
темы выпускной квалификационной работы.
Реклама

Эффективность отдельных приемов ТРИЗ убедительно была доказана в ходе экспериментальной работы по применению ТРИЗ в педагогике [57, 58, 77, 78, 79] (по физике – А. Гин, литературе – Ю. Мурашковский, О. Алешина, по биологии – И. Андржеевская, по информатике [36], естествознанию [31,37] и др.). Однако применение ТРИЗ-педагогики на уроках математики в литературе не встречается, что и обуславливает противоречие
и научную новизну
настоящего исследования: применение ТРИЗ-педагогики на уроках дает положительные результаты, а ее применение на уроках математики не разработано.
Цель выпускной квалификационной работы
– разработать и апробировать на практике механизмы применения инструментов ТРИЗ-педагогики в обучении школьников математике.
Объектом исследования
выступает развивающий учебно-воспитательный процесс в условиях общеобразовательного учреждения. Предметом исследования
является развитие продуктивности мышления учащихся на уроках математики через использование инструментов ТРИЗ-педагогики.
В основе исследования лежат следующие гипотетические положения
:
· включение в образовательный процесс инструментов ТРИЗ-педагогики, способствует развитию креативности
мышления;
· включение в образовательный процесс инструментов ТРИЗ-педагогики, способствует развитию системности
мышления;
· обучение на уроках математики в средней школе будет проходить эффективней благодаря овладению учащимися практическим опытом работы с методами активизации мышления, основанных на ТРИЗ;
· эффективность принципов разработанного курса не зависит от уровня сложности программного материала в экспериментальном классе.
Для достижения цели и доказательства изложенных гипотетических положений были определены следующие задачи
работы:
· рассмотреть механизмы применения ТРИЗ в образовательной сфере;
· уточнить термин ТРИЗ-педагогика с позиции педагогической технологии;
· разработать механизмы использования инструментов ТРИЗ-педагогики в обучении школьников математике;
· разработать курс на основе внеклассных занятий по математике с применением ТРИЗ-педагогики;
· проверить данные и разработанные механизмы в ходе опытно-экспериментального преподавания, определив истинность гипотетических положений.
Содержание выпускной квалификационной работы представлено во ведении, трех главах, заключении и приложениях. Библиографический список насчитывает 89 источников.
В первой главе ««Прикладная диалектика» и ее применение в педагогике»
рассматривается место, сущность и роль в применении инструментов ТРИЗ в образовании. Рассматривается история развития ТРИЗ, этапы становления ТРИЗ-педагогики, и уточняется термин «ТРИЗ-педагогика».
Во второй главе «Использование инструментов ТРИЗ при обучении школьников математике»
предлагаются механизмы применения инструментов ТРИЗ-педагогики при обучении школьников математике в общеобразовательной школе. Среди предложенных механизмов, рассматриваются методы, которые могут быть использованы на факультативных занятиях по математике (мета-алгоритм изобретения ТРИЗ, вепольный анализ), методы, которые могут быть использованы непосредственно на уроках математики (ситуация, метод «переизобретения» знаний, принципы решения математических задач), а так же универсальные методы технического творчества.
В третьей главе «Описание и анализ опытно-экспериментальной работы
» рассматривается курс «Тренинг креативного мышления», разработанный в рамках опытного преподавания и анализируются результаты опытно-экспериментальной работы.
В приложениях
представлены материалы опытного преподавания, материалы занятий с учениками, бланки для тестирования результатов Гилфорда и Торенса, использованные при анализе опытной работы.
Глава 1. «Прикладная диалектика» и ее применение в педагогике
И бог создал все живые существа, какие до сих пор
двигаются по земле, и одно из них было человеком. И только этот ком глины, ставший человеком, умел говорить. И бог наклонился поближе, когда созданный из глины человек привстал, оглянулся и заговорил. Человек подмигнул и вежливо спросил:– А в чем смысл всего этого? – Разве у всего должен быть смысл? – спросил бог. – Конечно, – сказал человек. – Тогда предоставляю тебе найти этот смысл! – сказал бог и удалился.
Боконон, персонаж книги Курта Воннегута «Колыбель для кошки».
1.1. Теория решения изобретательских задач (ТРИЗ)
В 1946 году в СССР началась работа над созданием научной технологии творчества. Новая технология получила название ТРИЗ – теория решения изобретательских задач. Первая публикация по ТРИЗ относится к 1956 году [8]. Разработка ТРИЗ принадлежит советскому ученому Генриху Альтшуллеру [3, 4, 5, 7] и дальнейшее развитие получила в работах [52, 65, 88] и в материалах, регулярно публиковавшихся журналом «Техника и наука» в 1979-1983 годах.
Отечественная теория решения изобретательских задач принципиально отличается от метода проб и ошибок и всех его модификаций. Основная идея ТРИЗ: технические системы возникают и развиваются не «как попало», а по определенным законам. Эти законы можно познать и использовать для сознательного – без множества «пустых» проб – решения изобретательских задач. ТРИЗ превращает производство новых технических идей в точную науку. Решение изобретательских задач – вместо поисков вслепую – строится на системе логических операций.
Теоретической основой ТРИЗ являются законы развития технических систем. Прежде всего, это законы материалистической диалектики. Используются также некоторые аналоги биологических законов, ряд законов выявлен изучением исторических тенденций развития техники, широко применяются общие законы развития систем.
Законы проверены, уточнены, детализированы, а иногда и выявлены путем анализа больших массивов патентной информации по сильным решениям (десятки и сотни тысяч отобранных патентов и авторских свидетельств). Весь инструментарий ТРИЗ, включая фонды физических, химических, геометрических эффектов, также выявлялся и развивался на основе изучения больших массивов патентной информации. В этом смысле ТРИЗ можно считать обобщением сильных сторон творческого опыта многих поколений изобретателей
[63]: отбираются и исследуются сильные решения, критически изучаются решения слабые и ошибочные.
Главный закон развития технических систем – стремление к увеличению степени идеальности: идеальная техническая система
(ТС) возникает тогда, когда системы нет, а ее функция выполняется. Пытаясь обычными (уже известными) путями повысить идеальность технической системы, мы улучшаем один показатель (например, уменьшаем вес транспортного средства) за счет ухудшения других показателей (например, снижается прочность). Конструктор ищет компромиссное решение в каждом конкретном случае. Изобретатель должен сломать компромисс: улучшить один показатель, не ухудшая других. Поэтому в наиболее распространенном случае процесс решения изобретательских задач можно рассматривать как выявление, анализ и разрешение технического противоречия.
Основным рабочим механизмом совершенствования ТС и синтеза новых ТС в ТРИЗ служат алгоритм решения изобретательских задач (АРИЗ)
и система изобретательских стандартов.
Решение задач по АРИЗ идет без множества «пустых» проб, планомерно, шаг за шагом по четким правилам корректируют первоначальную формулировку задачи, строят модель задачи, определяют имеющиеся вещественно-полевые ресурсы (ВПР), составляют идеальный конечный результат (ИКР), выявляют и анализируют физические противоречия, прилагают к задаче операторы необычных, смелых, дерзких преобразований, специальными приемами гасят психологическую инерцию и форсируют воображение.
Сходные противоречия разрешают однотипными приемами, наиболее сильные приемы – комплексные (сочетания нескольких приемов, часто – сочетания приемов с физ-, хим-, геомэффектами). Самые сильные комплексные приемы образуют систему стандартов
– аппарат ТРИЗ для решения типовых изобретательских задач. Следует подчеркнуть, что стандартные задачи стандартны только с позиций ТРИЗ; изобретатель, незнакомый с ТРИЗ, воспринимает такие задачи как нетипичные, сложные. Стандарты могут быть использованы для решения задач, сложных даже с позиций ТРИЗ; такие задачи решаются сочетанием нескольких стандартов.
Важное значение имеет в ТРИЗ упорядоченный и постоянно пополняемый информационный фонд:
указатели применения физических, химических и геометрических эффектов, банк типовых приемов устранения технических и физических противоречий. Этот фонд – операционная основа всех инструментов ТРИЗ.
Особый раздел ТРИЗ – курс развития творческого воображения
(РТВ). В этом курсе, в основном, на нетехнических примерах отрабатывается умение применять операторы ТРИЗ. Курс РТВ расшатывает привычные представления об объектах, ломает жесткие стереотипы.
Знание законов развития ТС позволяет решать не только имеющиеся изобретательские задачи, но и прогнозировать появление новых задач. Результаты такого прогнозирования значительно точнее, чем полученные с помощью субъективных методов, например, экспертными оценками. ТРИЗ стремится к планомерной эволюции ТС. Таким образом, современная ТРИЗ превращается в ТРТС – теорию развития технических систем.
ТРИЗ возникла в технике, потому что здесь был мощный патентный фонд, послуживший фундаментом теории. Но, помимо технических, существуют и другие системы: научные, художественные, социальные и т. д. Развитие всех систем подчинено сходным закономерностям, поэтому многие идеи и механизмы ТРИЗ могут быть использованы при построении теорий решения нетехнических творческих задач [72]. В частности, с помощью механизмов, используемых в ТРИЗ, была открыта ветроэнергетика растений и объяснены парадоксы, связанные с эффектом Рассела [46].
Аппарат теории решения изобретательских задач постоянно проверяется, корректируется и совершенствуется в ходе практического применения. Ежегодно в сотнях школ и курсов ТРИЗ слушатели решают множество учебных и неучебных (новых производственных) задач. Анализ письменных работ позволяет объективно определять причины ошибок: совершены ли они по вине преподавателя, по вине слушателя или имеет место сбой того или иного инструмента ТРИЗ. Накопленная информация тщательно изучается, это позволяет быстро развивать методику обучения ТРИЗ и саму теорию.
До 70-х годов обучение ТРИЗ велось преимущественно на экспериментальных семинарах, с 1970 года обучение сосредоточивается в постоянно действующих учебных центрах: народных университетах научно-технического творчества (Ленинград, Днепропетровск, Петрозаводск), общественных институтах и школах изобретательского творчества (Кишинев, Минск, Новосибирск, Ангарск, Владивосток), учебу организуют также центры НТТМ, различные министерства, ведомства, предприятия. Занятия ведутся в институтах патентоведения, в ряде отраслевых институтов повышения квалификации (ИПК). В 1980 году в ИПК Минэлектротехпрома впервые начата подготовка специалистов по ТРИЗ для постоянной работы в подразделениях функционально-стоимостного анализа (ФСА).
За 1972-1981 годы через школы ТРИЗ прошло примерно 7000 слушателей, подано почти 11 000 заявок, получено свыше 4000 авторских свидетельств (более половины заявок еще на рассмотрении), экономия от внедрения составляет миллионы рублей, общие расходы на обучение не превышают ста тысяч.
ТРИЗ – новая отрасль знания, быстро формирующаяся в отдельную науку. У ТРИЗ своя область изучения (законы развития технических систем, законы развития творческой личности), свой метод (анализ больших массивов патентной, историко-технической и историко-биографической информации), свой язык (вепольный анализ: технические «реакции» можно записывать так, как реакции химические), свой информационный фонд (принципы, методы и приемы разрешения противоречий, указатели применения эффектов).
1.2. Развитие творческой личности и ТРИЗ
Каждый инструмент оказывает обратное действие на человека, использующего этот инструмент. ТРИЗ-инструмент предназначен для тонких, дерзких, высокоорганизованных мысленных операций. Решение одной задачи еще не меняет стиля мышления, но в ходе занятий решаются десятки, сотни задач, постепенно мышление перестраивается, становится более гибким и управляемым.
ТРИЗ обеспечивает выход на решение, близкое к идеальному, но творческий процесс не сводится к одному лишь поиску решения.
Для формирования активной творческой позиции нужны как минимум шесть качеств личности [17]:
1) наличие достойной цели – новой (или недостигнутой), значительной, общественно полезной;
2) умение программировать достижение поставленной цели;
3) большая работоспособность по выполнению намеченных планов;
4) умение решать творческие задачи в выбранной области, владение техникой преодоления противоречий на пути к цели;
5) готовность «держать удар»: отстаивать свои идеи, выносить непризнание, непонимание;
6) результативность: на пути к конечной цели должны регулярно вырабатываться промежуточные результаты.
Воспитание комплекса творческих качеств – главная цель жизненной стратегии творческой личности
(ЖСТЛ). Метод построения ЖСТЛ обычный для всех исследований в ТРИЗ: анализ больших информационных массивов (с целью выявления общих закономерностей). Изучено свыше тысячи биографий творческих личностей [6].
Удалось проследить становление и развитие творческой личности на протяжении всей жизни. На историко-биографических примерах убедительно доказано: творческий образ жизни доступен каждому, для этого не нужны особые прирожденные способности или сверхблагоприятные условия. В силах любого человека выбрать достойную цель и начать планомерную борьбу за ее достижение [5].
Подробно рассматривая путь к цели, ЖСТЛ дает человеку суммированный жизненный опыт поколений творцов: предупреждает о типичных опасностях, рекомендует конкретные методы их преодоления, предсказывает наиболее сильные ходы. Систематические исследования по ЖСТЛ постепенно формируют новую область знания – теорию развития творческой личности (ТРТЛ).
1.3. ТРИЗ – рабочий инструмент диалектики
ТРИЗ использует законы материалистической диалектики [5] для организации творческой деятельности. Механизмы ТРИЗ позволяют инструментализировать эти глобальные законы развития в применении к частным задачам изобретательского творчества.
Методологический анализ этих разработок должен способствовать реализации инструментальной функции естествознания и его сближению с массовым изобретательством. ТРИЗ формализует наиболее ответственную стадию научно-технических разработок, на которой происходит диалектическое взаимодействие фундаментальных и прикладных исследований. Если раньше вычленение практически полезных фрагментов естественнонаучного знания осуществлялось в каждом конкретном случае стихийно, то ТРИЗ программирует ряд мыслительных и информационно-знаковых операций, гарантирующих внедрение науки в конструкторскую практику [70].
1.4. Образование на основе логики и диалектики
Мировое сообщество (ЮНЕСКО) признает губительность действия современной системы образования на общество. Попытки реформирования предпринимаются. Среди них можно указать более или менее целостно спроектированную в 70-х годах систему дистанционного обучения Открытого университета Великобритании. Разработчики положили в основу системы принципы гуманистического образования американского психотерапевта К. Роджерса. Однако, несмотря на широкое распространение этой системы в мире, она не приводит к изменениям в системе образования. Попытки гумманизации образования делаются и в нашей стране, но устойчивость системы настолько велика, что всякие попытки изменений она успешно поглощает [18].
Традиционные методы обучения развивают логическое мышление. Современные требования к системе обучения выходят за пределы традиционной логики, ставя задачей формировать навыки творческой личности, умеющей решать проблемные ситуации, в основе которых лежит диалектическое противоречие. Творческое мышление предполагает осознание стратегии мыследеятельности и проявляется в виде стиля мышления. Для формирования навыков организованного системного мышления предлагаются системы упражнений, выполняемых на базе алгоритма решения проблемных ситуаций [43,71].
Существующая же система образования ориентирована в основном на подготовку исполнителей, у которых готовность к творческой деятельности не сформирована. Необходимость формировать качества творческой личности только провозглашается задачей системы образования, но методы реализации этой задачи в педагогике практически отсутствуют. В то же время для выработки навыков творческого мышления можно применить алгоритмические приемы на основе ТРИЗ, разработанные в техническом творчестве для решения проблем. Требуется адаптация этой методики для системы образования. В большинстве новейших теорий, где разрабатываются проблемы интеллекта, мышление рассматривается как система интеллектуальных операций, связанных с практическими действиями. Решающее значение в процессе мышления играет субъективный фактор, так как носителем мышления является реальный человек, для деятельности которого характерно единство эмоционального, волевого и интеллектуального начал. Сама мысль рождается не из другой мысли, а из мотивирующей сферы сознания, которая охватывает влечения и потребности, интересы и побуждения, чувства [43]. При всем многообразии проблем, связанных с мышлением, авторы сознательно ограничивают круг рассматриваемых вопросов только теми, которые имеют отношение к практическим методам формирования культуры мышления.
1.5. Культура мышления
Культура мышления – это результат целенаправленного воздействия на процесс выполнения субъектом мыслительных операций с целью получить эффективные решения проблемных ситуаций [43]. Воздействие на субъект выполняет система образования. Образование должно стать обучением искусству пользоваться знаниями, вырабатывать стиль мышления, позволяющий анализировать проблемы в любой области жизни. Обучение мышлению, или формирование культуры мышления непосредственно в учебном процессе будет происходить тогда, когда учебный материал будет вводиться не как описательный, а как содержащий реальную проблему, но при этом необходима методология решения проблем. Важнейшим моментом такого учебного процесса станет переход от преимущественно нерефлексивного к осознанному овладению и владению мыслительными приемами и операциями. Подобные теоретические концепции были заложены в основу проблемного обучения, предложенного в конце 60-х – начале 70-х годов. Однако практическое внедрение проблемного обучения в учебный процесс затормозилось из-за отсутствия банка проблемных ситуаций и неподготовленности педагогов к переконструированию учебного материала. Современная эпоха создала потребность в новом типе личности, способной самостоятельно принимать решения, осознанно осуществлять свой выбор, умеющей гибко реагировать на изменения обстоятельств и самой творить новые обстоятельства. Этим потребностям удовлетворяют качества личности, которые психология определяет как творческие. Таким образом, современные социально-экономические условия функционирования общества побуждают систему образования уделять всё больше внимания проблемам творчества и формированию качеств творческой личности в процессе обучения и воспитания [43, 44, 85].
Исследования в области природы творчества выявили ряд качеств творческой личности, особенностей её мышления и условий, способствующих её развитию. Однако, как отмечают исследователи, накопленный материал не реализуется в практической педагогике для развития творческого потенциала личности [85, 86]. Разработка программ, ориентированных на активизацию и развитие творческого потенциала личности, тормозится отсутствием методического инструментария, с помощью которого можно было бы создавать творческие задания, и, самое главное, формировать навыки творческого мышления непосредственно в учебном процессе. В пособии [85] на конкретных упражнениях, которые являются учебными моделями, даются определения и характеристики компонентов мышления, способствующих протеканию творческих реакций, создавая предпосылки для их формирования.
Потребность понять природу творчества возникла как следствие необходимости воздействовать на творческую деятельность с целью повышения её эффективности. Ещё древнегреческие философы стремились в своих системах обучения применять методы, которые развивали бы в учениках творческое мышление. В дальнейшем начались поиски более активных форм воздействия на человеческую психику, которые позволяли бы управлять творческой деятельностью. Исследуя проблему творчества, учитывают следующее [85]:
1) в ходе исторического развития изменялись не только средства и формы творчества, но и его субъективный фактор, то есть сам человек;
2) в творческой деятельности кульминируются не только типичные черты жизни общества, но и порождённые общественным развитием проявления психологических особенностей различных членов общества.
Психология творчества как наука начала складываться на рубеже 19-го и 20-го столетий. Творчество в ней рассматривалось как психологический процесс созидания нового и как совокупность свойств личности, обеспечивающих её включённость в этот процесс.
С позиций психологии основной причиной задержки обучения культуре мышления считается недостаточное внимание к тому, каким образом рефлексируются ситуации организованного и организуемого мышления. Считается, что внедрение методов формирования культуры мышления сдерживалось из-за отсутствия методологии, без которой все технологии сводятся к рекомендациям типа «для эффективного решения проблемы ее необходимо глубоко и всесторонне проанализировать» (при этом ни методы анализа проблемы, ни критерии для оценок не даются), и предлагают практическую методологию формирования культуры мышления на основе теории решения изобретательских задач (ТРИЗ) разработанной Г. С. Альтшуллером [43].
1.6. Принципы дидактики в ТРИЗ-педагогике
Люди постепенно осознают, что запомнить всю информацию, которая обрушивается ежедневно на человека, невозможно, да и не нужно. Поэтому нужно менять приоритет в образовании [13]. Знания должны уступить способам деятельности и творчества. Процессом педагогического творчества можно управлять на основе законов, лежащих в основе ТРИЗ. Анализ педагогической практики позволяет выделить три модели обучения: информационную, информационно-творческую и сотворчества (учителя и учащихся). «Важнейшая задача цивилизации, – писал Т. Эдисон, – научить человека мыслить» (цит. по [41]).
В последние 10 лет накапливаются опыт и разработки приемов педагогической техники [23]. Приемы педагогической техники – это сеть. Они поддерживают друг друга, складываясь в единое целое, в систему. Их пять. Это немного, но каждый из них реализуется с помощью гаммы конкретных приемов [25,56].
1. Принцип свободы выбора.
В любом обучающем или управляющем действии, где только возможно, необходимо предоставлять право выбора. С одним важным условием – право выбора всегда уравновешивается осознанной ответственностью за свой выбор. Это можно сделать в рамках современной системы обучения. Вот некоторые примеры свободного выбора: В. Ф. Шаталов задает ученикам много задач, и они сами выбирают для решения любые из них; у С. Н. Лысенковой дети сами выбирают, какие трудные слова учительница должна написать на доске; И. П. Волков дает ученикам только тему, а учащиеся сами определяют, какой предмет изготовить и из какого материала [56].
2. Принцип открытости.
Необходимо не только давать знания, но еще и показывать их границы. Сталкивать ученика с проблемами, решения которых лежат за пределами изучаемого курса.
3. Принцип деятельности.
Нужно организовать освоение учениками знаний, умений, навыков, смыслов преимущественно в форме деятельности. Чтобы знание становилось инструментом, ученик должен с ним работать. Пока проверкой знаний считается бойкий ответ-пересказ в режиме фонографа, пока изучение и повторение осуществляются в режиме заучивания, школа работает процентов на девяносто в холостом режиме.
4. Принцип обратной связи.
Регулярно контролировать процесс обучения с помощью развитой системы приемов обратной связи. Чем более развита система – техническая, экономическая, социальная или педагогическая, – тем больше в ней механизмов обратной связи. Летчик в полете отслеживает по приборам ряд параметров: от температуры за бортом до количества горючего в баках. Без этого успешный полет не представим.
5. Принцип идеальности.
Идеальность – одно из ключевых понятий ТРИЗ [5]. Психоаналитикам знаком принцип удовольствия, экономистам –принцип рентабельности, инженерам – принцип повышения коэффициента полезного действия (КПД). Суть всех этих принципов едина. Любое наше действие характеризуется не только получаемой от него пользой, но и затратами сил, нервов, времени и средств. Необходимо максимально использовать возможности, знания, интересы самих учащихся с целью повышения результативности и уменьшения затрат в процессе образования.
1.7. ТРИЗ и образовательная сфера
Темпы развития современной цивилизации, в отличие от древних времен и средневековья, очень высоки. Человечеству приходится за единицу времени решать гораздо больше проблемных задач, чем раньше. А вслед за каждой решенной проблемной задачей появляются новые, которые также нужно решать. Решение проблемных задач есть творчество, потому что при решении проблемных задач создаются новые материальные и духовные ценности.
Таким образом, обществу нужно все больше творческих личностей [69]. Эта социальная и экономическая потребность нашла свое выражение в Законе Российской Федерации «Об образовании», в Федеральной программе развития образования, в Концепции модернизации образования и других документах. Творческие личности особенно необходимы в связи с принятыми Президентом и Правительством Российской Федерации решениями о формировании Национальной инновационной системы, провозглашенным инновационным путем развития России.
Таким образом, можно говорить о необходимости формирование творческих личностей учащихся. В начале 20 века было принять считать [12], что творчество – удел немногих людей, которые наделены творческими способностями от природы. А как сказано выше, таких людей обществу не хватает. Вывод один: необходимо учить творчеству, но как это делать? О методах положительного применения инструментов ТРИЗ в педагогике для обучения творчеству написано разнообразная литература [34, 66].
Тогда возникает вопрос: чему учить в условиях быстрого старения знаний? Ответ на этот вопрос известен, он сформулирован во многих педагогических публикациях: нужно переходить от преимущественного обучения знаниям к преимущественному обучению методам деятельности [53], или, еще уже, учить методам творческой деятельности [34].
А инструментарий ТРИЗ, как было сказано выше, прививает творческую деятельность.
ТРИЗ-педагогика – это педагогическая система, направленная на решение с помощью ТРИЗ актуальных проблем современного и будущего образования [63].
1.8. Этапы развития ТРИЗ-педагогики
ТРИЗ-педагогика оформилась как самостоятельное педагогическое направление в конце 80-хх гг. XX века. Основы TPИЗ педагогики заложил Г. С. Альтшуллер, который увидел, что созданная им наука не только помогает решать проблемные задач, но и формирует творческие личности. Он высказал идею создания теории развития творческой личности (ТРТЛ) и внес большой вклад в ее становление. ТРИЗ-педагогика является развитием ТРИЗ в ее применении в образовании. В развитие ТРИЗ-педагогики внесли вклад многие ученики и последователи Г.С. Альтшуллера: Е. Злотин, А. В. Зусман, Ю. П. Саламатов, И. Л. Викентьев, И. К. Каиков, В. А. Бухвалов, М. М. Зиновкина, Ю. С. Мурашковский, И. Н. Мурашковская, В. И. Тимохов, С. Модестов, М. И. Меерович, Л. П. Шрагина, Г. И. Иванов, А. А. Гин, С. Гин, М. Н. Шустерман, З. Г. Шустерман, М. С. Гафитулин, И. Г. Тамберг, А. А. Нестеренко, Т. А. Сидорчук, В. Г. Березина, Т. В. Клеймихина, С. Крейнина, А. В. Лимаренко, С. В. Сычев, О. И. Сычева и др.
Историю развития ТРИЗ-педагогики можно разделить следующие этапы [34].
1-й этап:
ТРИЗ в клубах и кружках технического творчества.
Это применение ТРИЗ в образовании еще не являлось собственно ТРИЗ-педагогикой. Хотя оно дало импульс дальнейшего вхождению ТРИЗ в образование в виде системы ТРИЗ-педагогики. Уже несколько десятков лет инженеры, изучавшие ТРИЗ на курсах, предназначенных специально для них, приходят в школы и учреждения дополнительного образования, для того, чтобы проводить внеклассные занятия по техническому творчеству. На таких занятиях дети создают идеи новых, еще не существующих, самолетов, космических кораблей, судов, автомобилей, машин и механизмов, а затем изготавливают их модели. Такие модели часто побеждают на различных конкурсах и выставках, в том числе российских и международных. По этим идеям подаются заявки на изобретения и выдаются патенты.
2-й этап:
ТРИЗ как предмет в школах, лицеях, гимназиях.
С 90-х гг. в стране стали создаваться лицеи и гимназии; увеличивалось количество специализированных классов, ориентированных на поступление их выпускников в вузы, при этом во все большем количестве вузов преподавалась ТРИЗ. Поэтому в ряде таких специализированных классов лицеев, гимназий, школ ТРИЗ стала преподаваться как предмет за счет школьного компонента базисного учебного плана, а в некоторых случаях как платная дополнительная образовательная услуга.
В то же время, такое применение ТРИЗ в школе не может полностью решить задачу формирования творческих личностей учащихся, поставленную в Законе РФ об образовании.
В тех учебных заведениях, где преподавалась ТРИЗ, выявился эффект, который «подсказывал» пути дальнейшего распространения этой науки в школе. На этом этапе, перед учителями других предметов встала задача преподавать так, чтобы, изучая их предметы, ученики одновременно учились творчеству на основе ТРИЗ.
3-й этап:
ТРИЗ в решении творческих задач на уроках.
ТРИЗ не могла войти в другие предметы в качестве содержания. Но она вошла в них в качестве метода обучения. ТРИЗ-педагогика, в полном смысле этого слова, началась с решения на уроках творческих задач. Это локально проблемные задачи (т.е. решение их известно человечеству, но неизвестно ученикам), требующие для своего решения применения ТРИЗ и тех знаний, которые изучаются по программе соответствующего предмета. Постановка задачи может выходить за пределы изучаемого предмета, но решение состоит в применении тех знаний, которые предусмотрены программой этого предмета. Работа по составлению наборов таких задач требует времени и создания коллективов разработчиков. К настоящему времени больше всего в этом направлении сделано в области биологии, опубликованы два сборника [26].
Метод творческих задач непосредственно направлен на формирование творческих способностей учащихся. Этот метод охватывал не весь урок Использование изучаемого нового материала только как «фонда эффектов» для решения творческих задач во многом сохраняет репродуктивный характер усвоения знаний, предусмотренных программой.
4-й этап:
ТРИЗ в изучении нового материала.
Ряд идей, положивших начало этому этапу, был высказан и изложен В.А. Бухваловым и Ю.С. Мурашковским в их книге «Изобретаем черепаху» [14], авторами некоторых задач, содержащихся в [26].
Каждое изучаемое в школе понятие, в любом предмете, есть развивающаяся система, имеющая своих предшественников. У систем-предшественников были свои противоречия развития. Эти противоречия были преодолены, в результате чего и появилась система, которую сейчас ученики изучают согласно программе. При изучении нового материала нужно вскрыть эти противоречия и найти те методы ТРИЗ, которыми они были преодолены. Таким образом, ТРИЗ используется для лучшего понимания и усвоения содержания предмета.
Изучение материала школьных предметов на основе ТРИЗ позволяет учащимся видеть единство нашего мира, глубже разбираться в его закономерностях, формирует у них стиль мышления, помогающий усваивать новые знания не только на уроках, ведущихся на основе ТРИЗ-педагогики, но и при самостоятельном изучении [61].
5-й этап:
ТРИЗ в решении актуальных задач развития образования.
Педагогические системы – это часть антропогенного мира. В своем развитии они также преодолевают противоречия, и преодолевают их теми же методами, пусть и найденными стихийно или по интуиции, которые содержатся в ТРИЗ.
Следовательно, если применять методы ТРИЗ при развитии педагогических систем не стихийно, а осознанно, то это позволит быстрее и эффективнее решать проблемы развития образования.
Каждый педагог имеет свою систему воспитывающего обучения, состоящую из разных инструментов – приемов, методов и форм работы. Эти педагогические инструменты постоянно развиваются – педагоги испытывают потребность в новых приемах, методах и формах работы, соответствующих изменяющимся условиям жизни. Как же появляются новые педагогические инструменты, существуют ли закономерности в их создании? Именно здесь нам может помочь теория решения изобретательских задач, которая позволяет разрешать противоречия, возникающие в любой области человеческой деятельности. В результате преодоления противоречий и рождаются, в частности, новые педагогические формы, методы и приемы работы [13].
Основные элементы теории решения изобретательских задач разрабатывались Г. С. Альтшуллером для технических систем, поэтому мы рассмотрим ниже лишь их общую логику, используя для этого педагогические примеры.
Система
Система – это целое, состоящее из взаимосвязанных элементов (подсистем), обладающее системным эффектом. Мы живем в системном мире: все объекты, окружающие нас, являются системами. Педагогические объекты и процессы не составляют исключения. Например, урок – система, состоящая из подсистем-звеньев. Каждое звено имеет свою структуру и выполняет определенные функции: проверка знаний, изучение нового материала, закрепление, инструктаж по домашнему заданию. Урок как система имеет системный эффект – развивает и воспитывает учащихся посредством деятельности на конкретном предметном содержании. Ни одно из звеньев урока не дает системного эффекта всего урока в целом.
Системный оператор
Минимально он представляет собой девятиэкранную схему (рис. 1). Левый ряд – прошлое, центральный – настоящее, правый – будущее. Нижние три экрана – подсистемы, средние – системы, верхние – надсистемы.

Рис. 1. Системный оператор
Системный оператор способствует развитию системного видения педагогических объектов и процессов и, самое важное, связей между ними. Допустим, традиционный урок – это система. Поместим его в настоящее. Он состоит из подсистем-звеньев и вместе с тем входит в надсистему – систему уроков по теме. Эту иерархию можно продолжать вниз (каждое звено состоит из определенной последовательности действий, каждое действие – отдельных операций) и вверх (система уроков по теме входит в систему уроков по разделу, которые входят в систему уроков по курсу и так далее). Теперь рассмотрим прошлое традиционного урока. Четырехзвенная структура урока появилась в начале XIX века, до этого были занятия, на которых преимущество отдавалось одному – двум видам деятельности учащихся. Эти два вида и были звеньями занятий, последние входили в систему занятий по определенному курсу. Что будет после традиционного урока?
Ресурсы
Ресурсы – это структурные, функциональные и временные возможности в дидактической системе или ее элементах для дальнейшего развития. Рассмотрим основные виды ресурсов урока.
Внутрисистемные
(ресурсы внутри урока) – это возможности включения дополнительных звеньев в урок: самостоятельных практических работ, фрагментов лабораторных работ, элементов активных форм проведения урока (микровикторин, конкурсов и т. д.). Внешнесистемные
(ресурсы, расположенные рядом с нашим уроком) – это предыдущий и последующий уроки по теме. Используя внешнесистемные ресурсы урока, можно комбинировать содержание изучаемого материала, изучение взаимосвязей, творческие задания. Надсистемные
– ресурсы следующей общей системы, к которой относится наша система. Урок относится к системе уроков по теме, поэтому они и являются надсистемными ресурсами. Используя надсистемные ресурсы, можно достаточно широко комбинировать теоретическое содержание изучаемого предмета и практические задания.
Ресурсы информации
– возможности изменения объема содержания, изучаемого на одном (нескольких) уроках (дидактической единицы). Возможно укрепление или уменьшение объема дидактической единицы в зависимости от поставленной цели. Ресурсы времени
– возможности увеличения или уменьшения продолжительности отдельных звеньев урока для определенных целей. Функциональные ресурсы
– возможности для увеличения функций отдельных звеньев или всего урока. На практике достигаются за счет внесения дополнительных заданий в отдельные звенья урока. Системный ресурс
– новые полезные свойства, которые могут быть получены при изменении связей между отдельными звеньями урока или новым сочетанием уроков по теме, новым сочетанием тем, разделов.
При решении педагогических задач очень важно сделать предварительный анализ ресурсов, что часто упускается из виду. Например, при планировании деятельности учащихся на этапе изучения нового материала можно внести элементы пройденного, если они логически связаны, тем самым, увеличив функциональные возможности данного этапа и сохранив время для дополнительного решения задач вместо повторения теории на обобщающих уроках.
Рассмотрим, как инструменты ТРИЗ могут входить при использовании различных педагогических систем.
Развивающее обучение (Эльконина-Давыдова)
представляет ученикам мир, различные его объекты в развертке колонки по вертикали системного оператора (надсистема – система – подсистема), тогда как мыслительный инструмент ТРИЗ – системный оператор – предусматривает как минимум 9 экранов восприятия, включая аналогичные вертикальные колонки для прошлого и будущее системы. Дополнение до полного системного оператора плюс включение инструментов ТРИЗ в уроки-исследования, позволяют повысить успешность переоткрытия знаний, эффективнее используя систему развивающего обучения.
Коллективный способ обучения (КСО)
усовершенствовал организацию учебного процесса, пока оставив без изменения прежнюю репродуктивную методику. По второму закону существования систем – закону согласования – новой организации учебного процесса должна соответствовать и новая творческая методика, например, ТРИЗ-педагогика. Совместное применение ТРИЗ-педагогики и КСО позволяет реализовать принцип непрерывной и безотлагательной передачи знаний, поскольку новые структурированные знания, создаваемые учащимися на уроках, будут безотлагательно сообщаться ими друг другу, системно воспринимаясь ими.
Индивидуально-ориентированный способ обучения (ИОСО)
в настоящее время предусматривает траектории обучения, различающиеся уровнем усвоения знаний по различным предметам. ТРИЗ-педагогика позволит конструктивно добавить в ИОСО образовательные траектории, включающие выполнение учащимися творческих научных работ и изобретений, благодаря применению инструментов ТРИЗ.
Система диалектического обучения (СДО)
,
ранее известная под названием «словесно-логический метод обучения», ставит учащихся в режим частичного (под руководством учителя) переоткрытия знаний на основе диалектики Гегеля. Это хорошо соответствует задаче формирования когнитивной (познавательной) сферы деятельности личности. В то же время, ускоряющиеся темпы развития цивилизации требуют от общества большего количества людей с развитой креативной (творческой) сферой деятельности. Здесь также – путь взаимодействия СДО и ТРИЗ-педагогики.
Система «Экология и диалектика»
формирует представление у учащихся о мире, как во многом случайном, неопределенном, имеющем статистические закономерности. Это, несомненно, серьезный шаг по сравнению с прежде формировавшимся представлением о мире, как о детерминированном, жестко определенном. В то же время, задача развития креативного мышления требует формирования представления о мире, как развивающемся по определенным законам, которые можно познавать и использовать для ускорения его развития, во избежание застоев в развитии, которые могут иметь и часто имеют серьезные отрицательные последствия. Это можно сделать во взаимодействии системы «Экология и диалектика» и ТРИЗ-педагогики.
Проектный метод обучения
нацеливает учащихся на решение проблемных задач при особой организации этого процесса. Применение ТРИЗ в проектном методе позволяет существенно повысить эффективность выполнения проектов, чаще и эффективнее представлять результаты проектов на научные конференции и выставки школьников, патентовать и внедрять их.
1.10. Термин «ТРИЗ-педагогика»
Куда лучше совсем не думать о постижении истины, чем пытаться делать это, не имея метода.
Рене Декарт
В последние годы в российской педагогике активно разрабатывается подход, получивший название «личностно-ориентированное обучение», в котором обосновывается необходимость признания и учета уникальности личного (субъектного) опыта каждого ученика [89]. При таком подходе ученику предоставляется свобода выбора учебного содержания, поощряется индивидуальная избирательность по отношению к форме обучения, признается существование индивидуально-специфических способов усвоения материала [53, 54].
Однако при этом нельзя полностью отрицать потребности общества. Общество нуждается в личностях, обладающих определенной интеллектуальной и нравственной культурой. В этом заключаются гарантии дальнейшего развития человечества [70].
Известно выражение М. Монтеня: «Мозг хорошо устроенный стоит больше, чем мозг хорошо наполненный». Тем самым подчеркивается различие между образованностью (кругом знаний, получаемых в школе) и интеллектуальной воспитанностью (степенью умственного развития личности), между которыми никак нельзя ставить знак равенства.
Это означает, что целью образовательного процесса является не просто усвоение содержания отдельных учебных дисциплин, но, в первую очередь, развитие и обогащение интеллектуальных ресурсов личности средствами этих дисциплин.
Наряду с передачей ученику системы научных знаний об окружающей действительности, а также вооружением его методами научного познания необходимо создавать условия для его личностного роста, формирования у него психологической готовности к дальнейшей деятельности с учетом своеобразия и ценности его внутреннего мира.
В ТРИЗ целевые установки педагогики предлагается решать на основе так называемой теории развития творческой личности (ТРТЛ).
Отвечая на вопрос «Способна ли сегодняшняя ТРТЛ стать идеологическим стержнем образовательной системы?», многие авторы однозначно склонны к ответу «нет» [1, 70].
Термины «ТРИЗ-педагогика» и «ТРИЗ + педагогика», в которых усматриваются необоснованные претензии на решение основных задач воспитания и обучения исключительно средствами ТРИЗ, назвать общепринятыми нельзя.
Поэтому логичней употреблять термин «педагогика + элементы ТРИЗ».
Из наиболее распространенных в отечественной педагогической практике можно выделить следующие образовательные технологии [70]:
· педагогические технологии на основе личностной ориентации педагогического процесса (гуманно-личностная технология Ш. А. Амонашвили, педагогика сотрудничества);
· педагогические технологии на основе активизации и интенсификации деятельности учащихся (игровые технологии, проблемное обучение, обучение на основе опорных сигналов В. Ф. Шаталова);
· педагогические технологии на основе дидактического усовершенствования и реконструирования учебного материала (реализация теории поэтапного формирования умственных действий, использование укрупненных дидактических единиц П. М. Эрдниева, «диалог культур» В. С. Библера и С. Ю. Курганова);
· технологии развивающего обучения (система развивающего обучения Л. В. Занкова, развивающее обучение Д. Б. Эльконина и В. В. Давыдова);
· частнопредметные педагогические технологии (технология раннего и интенсивного обучения грамоте Н. А. Зайцева, технология обучения математике на основе решения задач Р. Г. Хазанкина и др.).
Ни к одной из перечисленных педагогических технологий отнести применение ТРИЗ в педагогике на данный момент нельзя.
Педагогическая технология должна обладать признаками системы. В структуру педагогической технологии обязательно должны входить:
· концептуальная основа;
· содержательная часть (цели обучения, содержание учебного материала);
· описание технологического процесса (процессуальная часть): организация учебного процесса; деятельность учителя по управлению процессом усвоения материала; методы и формы работы учителя; диагностика учебного процесса.
В ТРИЗ определена [55] (небесспорно) содержательная часть, а также делаются попытки определить часть процессуальную (ведется апробация отдельных форм и методов обучения). Концептуальная часть (а здесь под концепцией понимаются не основы «железной» ТРИЗ, а концепция усвоения опыта, научное обоснование процесса достижения образовательных целей) не определена совершенно [51].
Все вышесказанное не позволяет считать на сегодняшний день использование элементов ТРИЗ в учебном процессе ни педагогической технологией, ни, тем более, новой отдельной педагогикой.
В пособиях по ТРИЗ говорится о мышлении (его «системности», «функциональности», «диалектичности» и даже «синергетичности», т. е. о том, что связано с понятиями ТРИЗ: система, функция, противоречие и т. д.), а также о воображении (поскольку традиционная «железная» ТРИЗ имеет разработанный курс РТВ – развитие творческого воображения). Однако возрастные закономерности развития того же мышления отражены слабо, несмотря на декларируемые в пособиях требования учета возрастных и других психологических особенностей детей. Хотя методы развития мышления с учетом психологических особенностей можно встретить в работах П. Я. Гальперина, М. И. Махмутова, А. М. Матюшкина, И. С. Якиманской и т. д.
На сегодняшний день отрицательными сторонами применения ТРИЗ в педагогике можно также назвать следующие:
· в школах насаждается неразработанная методика преподавания ТРИЗ, основанная на поверхностном знании самих основ ТРИЗ;
· наблюдающаяся «порча» самой школы ТРИЗ, большое количество дилетантов в рядах ТРИЗ, выдающих себя за экспертов или разработчиков;
· внедрение ТРИЗ в учебный процесс без какого-либо учета возрастных и психологических закономерностей.
Можно с большой эффективностью использовать элементы ТРИЗ в учебном процессе, но выборочно. Эффективность отдельных приемов убедительно была доказана в ходе экспериментальной работы по применению ТРИЗ в педагогике [57, 58, 77, 78, 79]: по физике (А. Гин), литературе (Ю. Мурашковский, О. Алешина), по биологии (И. Андржеевская), по информатике [36] и естествознанию [31, 37].
Внедрение отдельных элементов ТРИЗ в учебный процесс способствует развития системности мышления, благодаря разработанному инструментарию самого ТРИЗ [27, 50]. Наиболее ценным положительным результатам внедрения в преподавании общеобразовательных предметов в школе элементов ТРИЗ может стать укрепления единства теоретико-методологической (концептуальной) трактовки образования и ее реализации в конкретных учебных технологиях, благодаря созданию преемственности материала основанного на инструментарии ТРИЗ. Например:
· на уроке математики учитель вводить дробные числа как бисистему из числителя и знаменателя, формируя противоречие и применяя для его разрешения закон перехода в бисистему;
· на уроке биологии материал о фасеточных органах зрения подается как проявление в живой природе закона перехода в полисистему и закономерностей, соответствующих принципу дробления.
· на уроке русского языка, когда речь идет о возникновении приставки, ее появление связывается с стихийным применением законна перехода в бисистему.
Таким образом, появляется некая комфортность усвоения различного (на первый взгляд) материала, информация, которую получает ученик, уже не кажется «взятой с потолка», формируется фундаментальность приобретенных знаний и в этом положительный эффект применения ТРИЗ в педагогике.
Но ТРИЗ-педагогика – это не преподавание ТРИЗ и не развитие системы образования методами ТРИЗ. Под термином «ТРИЗ-педагогика» мы будем понимать подготовку мышления для решения творческих задач. Эта подготовка подразумевает и особую дидактику, и предметную сферу. Предмет – творческие задачи и правила их решения. Дидактика – особые упражнения, подготавливающие к решению задач, и особая деятельность по решению этих задач.
При этом ТРИЗ-педагогика может использовать в своих дидактических целях методы, никак не относящиеся к собственно ТРИЗ. Так, мозговой штурм или морфологический анализ имеют ряд своих дидактических преимуществ, которые целесообразно использовать. Методологической основой для ТРИЗ-педагогики является ТРИЗ [24].
Таким образом, внедрение отдельных элементов ТРИЗ в школьные предметы дает положительный результат, но о методике внедрения в школьный курс математики на данный момент говорят всего несколько работ [9, 10] одного автора, ориентированных на младших школьников. Поэтому вопрос о внедрение элементов ТРИЗ в преподавание школьного курса математики остается открытым.
Глава 2. Использование инструментов ТРИЗ
в обучении школьников математике
2.1. Ситуация как средство развития творческих способностей
Математика, особенно в школе, воспринимается как «нетворческий» предмет. О развитии творческих математических способностей на уроках математики можно прочитать в книгах Д. Пойа [64], Н. Тучнина [73] и др. Однако разговор в них идет именно о математическом творчестве, а сегодняшний социальный заказ общества предъявляет к личности, среди прочих качеств, умение действовать в нестандартных ситуациях [53], причем далеких от применения «явной» математики. Таким образом, речь идет о формировании такого качества личности как креативность, а не математическая креативность.
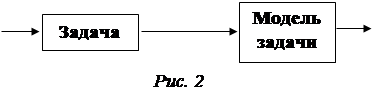 |
При решении текстовых задач рекомендуется от задачи переходить к модели задачи (алгебраической и аналитической), таким образом, дальнейшее решение заключается в решении модели [39] (рис. 2). С точки зрения ТРИЗ это система (антропогенная) и к ней предъявляется требование: способствовать развитию креативности в процессе ее реализации. Опыт преподавания показывает сложность выполнения этого требования на практике. Кардинально преобразовывать данную систему не рационально (ее применения эффективно для достижения других дидактических целей математики, методика ее использования хорошо отработана) с одной стороны, а с другой преобразование необходимо для выполнения указанного требования к системе.
Сформулируем ИКР: система осталось неизменной, но требование стало выполняться. Используем инструмент ТРИЗ – вепольный анализ, который позволяет добавить в систему новое «вещество» Х, которое создает поле, отвечающее предлагаемому требованию (рис. 3).

Тогда, используя общий алгоритм решения задачи в ТРИЗ [5], элемент Х – это некоторая ситуация (рис. 4). Именно переход от ситуации к задаче должен помочь развивать на уроках математики креативность, причем при использовании данной схемы отработанная методика по использованию модели перехода от задачи просто необходима для сохранения других дидактических целей.
Задача отличается от ситуации наличием четкой формулировки, условие содержит все необходимые данные в явном виде, метод решения зачастую известен и представляет собой цепочку формальных операций, правильный ответ определен однозначно. Ситуация[1]
в свою очередь имеет неопределенное условие, разные подходы к решению, множества решений, благодаря чему она ближе к проблемным ситуациям, возникающим в жизни.
Основная цель практико-ориентированных (прикладных и практических) задач в школе на уроках математики (А. Азевич, Е. В. Величко, М. В. Крутихина, В. А. Петров, В. В. Пикан, Н. А. Терешин, А. Н. Тихонов, Ю. Ф. Фоминых, И. М. Шапиро и др.) заключается в осуществлении содержательной и методологической связи школьного курса математики с профессиональной составляющей образования, то есть способствуют развитию профессиональных умений, входящих в состав учебной и познавательной деятельности в процессе изучения математики, а не развитию креативности учащегося. Поэтому практико-ориентированные задачи нельзя в полной мере назвать ситуацией.
Пример 1.
Окно имеет форму прямоугольника, завершенного сверху полукругом. Укажите такие размеры окна, чтобы при данном периметре Р
оно пропускало больше света.
Данный пример – практико-ориентированная задача, и её решение заключается в применении производной (задача на максимум и минимум). Четкое формулировка условия задачи, все необходимые данные в явном виде, метод решения представляет собой цепочку формальных операций. Поэтому это задача, а не ситуация.
Пример 2.
Как можно, не переплывая реки, измерить ее ширину [59, 60].
Данный пример – ситуация. Из условия не совсем ясно, чем можно пользоваться, какая река. Она имеет разные подходы к решению, причем в каждом подходе мы переходим к формулировке новой задачи (модели задачи).
1-ый способ
. Используем прибор с тремя булавками на вершинах равнобедренного прямоугольного треугольника. Пусть требуется определить ширину АВ
реки (рис. 5), стоя на том берегу, где точка В,
и не перебираясь на противоположный.

Встав где-нибудь у точки С
, держите булавочный прибор близ глаз так, чтобы, смотря одним глазом вдоль двух булавок, вы видели, как обе они покрывают точки В
и А.
Понятно, что, когда это вам удастся, вы будете находиться как раз на продолжении прямой АВ.
Теперь, не двигая дощечки прибора, смотрите вдоль других двух булавок (перпендикулярно к прежнему направлению) и заметьте какую-нибудь точку D,
покрываемую этими булавками, т.е. лежащую на прямой, перпендикулярной к АС.
После этого воткните в точку С
веху, покиньте это место и идите с вашим инструментом вдоль прямой CD,
пока не найдете на ней такую точку Е
(рис. 6), откуда можно одновременно покрыть для глаза булавкой b
шест точки С
, а булавкой а –
точку А.
Это будет значить, что вы отыскали на берегу третью вершину треугольника АСЕ,
в котором угол С
– прямой, а угол Е
равен острому углу булавочного прибора, т.е. половине прямого. Очевидно, и угол А
равен половине прямого, т.е. АС
= СЕ.
Если вы измерите расстояние СЕ,
например, шагами, вы узнаете расстояние АС,
а отняв ВС,
которое легко измерить, определите искомую ширину реки.
2-ой способ
. Здесь также находят точку С
на продолжении АВ
и намечают при помощи булавочного прибора прямую CD
под прямым углом к СА
(рис. 7).
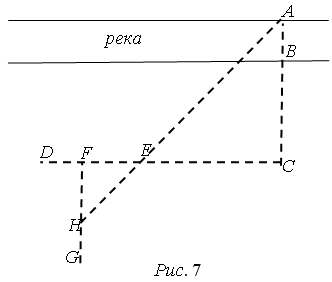
На прямой CD
отмеряют равные расстояния СЕ
и EF
произвольной длины и втыкают в точки E
и F
вехи. Став затем в точке F
с булавочным прибором, намечают направление FG,
перпендикулярное к FC.
Теперь, идя вдоль FG,
отыскивают на этой линии такую точку H
, из которой веха Е
кажется покрывающей точку А.
Это будет означать, что точки Н, Е
и А
лежат на одной прямой. Задача решена: расстояние FH
равно расстоянию АС,
от которого достаточно лишь отнять ВС,
чтобы узнать, искомую ширину реки.
Другие способы разрешения ситуации, использующие признаки подобия треугольников, прямоугольный треугольник с углом в 30° можно посмотреть у Я. И. Перельмана [60].
При разрешении данной ситуации мы сначала переходили к задаче (модели задачи), формулировали ее на математическом языке, и только после чего ее решали. В первом способе мы ставили перед собой задачу: используя известный равнобедренный прямоугольный треугольник измерить длину отрезка АВ.
Во втором способе: использовать признаки равенства треугольников для нахождения длины отрезка АВ.
Рассмотрим другой пример.
Пример 3. Задача древних индусов
(перевод В.К. Лебедева).
Над озером тихим,
С полфута размером, высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Воле цветка над водой,
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода
Здесь глубока?
Обозначим (рис. 8) искомую глубину CD
пруда через 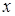 . Тогда, по теореме Пифагора легко найди искомую глубину. . Тогда, по теореме Пифагора легко найди искомую глубину.

Это задача, у неё четкое формулировка условия, все необходимые данные в явном виде, метод решения представляет собой цепочку формальных операций. Попробуем превратить данную задачу в ситуацию.
Пример 4.
Как можно измерить глубину реки с берега
Контрольное решение: рассмотрим ресурсы с точки зрения ТРИЗ, которыми мы располагаем. Текущая вода, берег, дно, человек. Упростим задачу. Как измерить с берега глубину водоема с неподвижной водой? Например, с берега озера. Тоже непросто, упростим еще. Как измерить глубину неподвижной воды у самого берега. А это равносильно измерению глубины колодца. Надо привязать к камню веревку или леску с поплавками, разнесенными, скажем, на 1 метр и бросить камень в колодец, или может помочь метод из примера 3. А как измерить глубину озера с берега? Во-первых, надо чтобы веревка была перпендикулярна поверхности воды. Как это сделать? На веревку с камнем навесим поплавки и бросим камень в нужное место озера, тогда будет видно, сколько поплавков утонуло, а сколько лежит на поверхности.
Введем следующее усложнение задачи – течение. Отметим место на берегу реки и перпендикулярно берегу бросим камень с веревкой и с поплавками на середину реки. Течение отнесет веревку с поплавками на расстояние В.
Определим число погруженных поплавков K
и рассчитаем по теореме Пифагора глубину реки 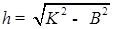 . .
В данном примере мы снова переходили от ситуации к формулировке задачи (модели задачи), уточняли ее, рассматривали используемые ресурсы. Вариантов решения у данного примера скорее очень много, они опираются на использование каких-либо свойств, причем некоторые решения нематематические.
Переход от задачи к ее модели для решения достаточно хорошо применяется в основной школе, а переход от ситуации к задаче применятся редко, «неосознанно», но как показывает первый опыт использования данного перехода [80], именно он может стать опорой для развития творческих способностей у учащихся на уроках математики в школе.
2.2. Мета-алгоритм изобретения ТРИЗ и решение учебных математических задач
ТРИЗ является качественной теорией. Строгое соответствие моделей качественных теорий концепциям конструктивной математики очень упрощенно; можно сказать, что конструктивная математика имеет дело с качественными моделями, определяемыми следующим конструктивным способом [19]: 1) фиксируются исходные конструктивные объекты, определяемые, в частности, в виде примеров или образцов; 2) фиксируются правила (не обязательно аксиоматические), по которым строятся новые объекты из уже имеющихся; 3) фиксируются условия, налагаемые на исходные и построенные объекты и определяющие их конструктивность (например, осуществимость, полезность и эффективность).
Совокупность правил, определяющих построение новых конструктивных образов, называется алгоритмом. Обобщенные алгоритмы, на основе которых могут быть построены специализированные (ориентированные на определенное приложение, на определенный класс моделей) или детализированные (более точные) алгоритмы в ТРИЗ называются мета-алгоритмами [55].
Поэтому логично рассмотреть применение мета-алгоритма ТРИЗ в преподавании математики. Хотя школьная математика отлична от математики [48], но преемственность построения рассуждений сохраняется.
Рассмотрим обобщенную схему мета-алгоритма изобретения (рис. 9, Prof. Dr. Dr. Sc. techn. M. Orloff, Modern TRIZ Academy International, Berlin), а также упрощенный мета-алгоритм для решения некоторого класса учебных математических задач (рис. 10).
Тогда ход решения задачи можно уложить в 4 крупных этапа:
· диагностика (исследование задачи),
· редукция (построение модели задачи (алгебраической, аналитической и др.)),
· трансформация (выбор метода решения (вычисления) модели),
· верификация (проверка решения).
При этом данная схема совпадает с методикой организации решения учебной математической задачи соблюдением формально-логической схемы рассуждения «анализ – построение – доказательство – исследование» при решении геометрических задач на построение и т.п. [39, 82].
Переходы 1 и 3 требуют знания теории моделей и прикладных областей ее применения. Переход 2 требует умения строить и решать модели теории.
Пример 5.
В двух цехах завода стоят станки двух типов. Первого типа 2 и 1 соответственно в первом и втором цехе, второго – 6 и 2. Определите среднею мощность, потребляемой станком каждого типа, если первый цех потребляет 340 киловатт-часов, второй – 130.
Решение представим в виде мета-алгоритма (рис. 11).


Пусть в двух цехах завода работает разное количество станков двух типов. Для точного определения средней мощности, потребляемой станком определенного типа, было решено воспользоваться имеющимися измерениями расхода электроэнергии по каждому цеху за сутки. На этапе диагностики проблемы было установлено количество станков каждого типа и данные по потреблению электроэнергии. На этапе редукции была построена система из двух линейных уравнений с двумя неизвестными. На этапе трансформации из двух простейших подходящих методов (метод исключения переменных и метод замены и подстановки переменных) выбрали последний. На этапе верификации путем прямой подстановки полученных значений искомых переменных в исходные уравнения убедились в правильности решения задачи.
Этот пример служит практической иллюстрацией абстрактной схемы, приведенной на рис. 10.
Пример 6.
Что больше 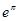 или или 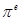 ? ?
Решение представлено на рис. 12. Необходимо сравнить два числа. На этапе диагностики проблемы было установлено что непосредственное сравнение затруднительно. На этапе редукции была построена функция (обобщение по двум ее значениям) . На этапе трансформации из методов доказательства монотонности функции выбрали наиболее подходящий с использованием производной . На этапе верификации доказали монотонность.
На этапе верификации путем исследования полученного решения убедились в правильности решения задачи.

Таким образом, при использовании мета-алгоритма для решения учебных математических задач появляется возможность наглядней представлять ход решения задачи.
Причем на этапах диагностики
и редукции
преимущественно используется анализ (проблемы решения), на этапах трансформации
и верификации
– синтез (идеи решения). Тем самым, используя при решении задачи мета-алгоритм, ребенок на уроках математики осознано учиться использовать разные способы мышления.
Обучение – это замена удивления пониманием …
Виктор Кротов
Известно, что ни одно событие в материальном мире не происходит без видоизменения вещества и энергии (поля). Взаимодействие этих двух составляющих и определяет все многообразие мира.
При решении задач зачастую трудно сразу найти решение, требуются тактические шаги, конкретизирующие наши действия. Для этого нужен точный анализ взаимодействия веществ и энергии в оперативной зоне задачи, с точки зрения ТРИЗ.
Выйти из этого положения в изобретательской деятельности позволяет так называемый вепольный анализ. Слово «веполь» образовано от слов «вещество» и «поле». Вепольный анализ проводится в оперативной зоне возникновения задачи, т. е. там, где выявлено физическое противоречие. В этом месте обязательно должны быть два вещества 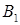 и и 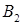 , полезно или вредно взаимодействующие между собой, и поле П
, которое связывает эти два вещества (рис. 12). , полезно или вредно взаимодействующие между собой, и поле П
, которое связывает эти два вещества (рис. 12).
В нашей работе будем придерживаться упрощенной схемой вепольного анализа [2, 35], основанного на двух правилах:
1) если одно вещество вредно воздействует на другое, то между ними вводят третье вещество;
2) если поле вредно воздействует на вещество, то между ними водят второе поле, нейтрализующее действие первого, или его вредное действие оттягивает третье вещество.
При решении учебных математических задач в роли «веществ» выступают объекты математики (геометрические фигуры, числа), а в качестве поля свойства объектов, их движение и т.п.
Пример 7.
Может ли пятизначное число равняться произведению своих цифр [49]?
Решение. Применим вепольный анализ ТРИЗ, для этого необходимо определить как минимум два вещества и поле, воздействующее на них.
Пусть есть число 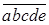 . Произведение цифр числа равняется . Произведение цифр числа равняется 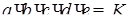 . Рассмотрим два вещества . Рассмотрим два вещества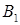 – – 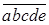 , , 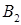 – К
и поле – П,
действующее на вещества «вредно» (вещества между собой связаны, изменение одного вещества ведет к изменению другого, что затрудняет нахождения такого вещества, что бы – К
и поле – П,
действующее на вещества «вредно» (вещества между собой связаны, изменение одного вещества ведет к изменению другого, что затрудняет нахождения такого вещества, что бы 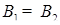 ), (рис. 12). ), (рис. 12).

Используем первое правило вепольного анализа, введем новое вещество 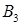 , оттягивающие на себя вредное воздействие поля П.
(рис. 13). Решение задачи на вепольном языке составлено. Теперь надо определить, что же такое третье вещество оттягивающие на себя вредное действие поля. Это вещество должно взаимодействовать с , оттягивающие на себя вредное воздействие поля П.
(рис. 13). Решение задачи на вепольном языке составлено. Теперь надо определить, что же такое третье вещество оттягивающие на себя вредное действие поля. Это вещество должно взаимодействовать с 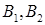 , если учесть, что отношение двух чисел – это их сравнение, получим, вспомнив условие задачи, что надо найти такое число, которое легко сравниваться с числами , если учесть, что отношение двух чисел – это их сравнение, получим, вспомнив условие задачи, что надо найти такое число, которое легко сравниваться с числами 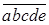 и К.
Тогда в качестве такого вещества можно взять и К.
Тогда в качестве такого вещества можно взять 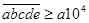 , а , а 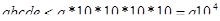 , получим , получим 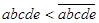 . Равенства нет, а значит, таких чисел нет. . Равенства нет, а значит, таких чисел нет.
Пример 8.
Как нужно у квадрата срезать 4 угла, чтобы получился правильный восьмиугольник?

На вепольном языке получаем, что есть одно вещество 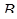 и на него «вредно» действует некоторое поле П
(рис. 14), (первоначально трудно увидеть положительные стороны действия поля П
). Второе правило гласит, что необходимо внести новое поля и на него «вредно» действует некоторое поле П
(рис. 14), (первоначально трудно увидеть положительные стороны действия поля П
). Второе правило гласит, что необходимо внести новое поля 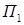 (рис. 15). Новое поле создает некое действие применительно к геометрическим объектам, можно сказать, что это движение. Тогда решение задачи свелось к нахождению какого-либо движения для ответа на поставленный вопрос задачи. В книге «Математическая шкатулка» [49] предлагается движение, заключающееся в повороте квадрата, тогда общая часть двух квадратов будет правильным восьмиугольником. (рис. 15). Новое поле создает некое действие применительно к геометрическим объектам, можно сказать, что это движение. Тогда решение задачи свелось к нахождению какого-либо движения для ответа на поставленный вопрос задачи. В книге «Математическая шкатулка» [49] предлагается движение, заключающееся в повороте квадрата, тогда общая часть двух квадратов будет правильным восьмиугольником.
При использовании элементов вепольного анализа решение задачи сводиться к нахождению третьего вещества или нового поля, что значительно легче решения первоначальной задачи. Начальные рассуждения на вепольном языке кажутся слишком «затянутыми» и затруднительными, но, как показывает практика, при хорошей отработке элементов вепольного анализа их использование при решении задач происходит уже «подсознательно».
2.4. Метод переизобретения знаний[2]
ТРИЗ является продолжением диалектики Аристотеля и Гегеля и дополняет их конкретными инструментальными методами преодоления противоречий. Поэтому ТРИЗ позволяет более описывать, а главное – проектировать процессы развития различных систем [30]. Таким образом, изучая любую систему, можно более глубоко понять эту систему и одновременно формировать творческое мышление, если рассматривать ее как результат развития системы-предшественницы, преодоления в ней противоречий в соответствии с теми закономерностями, которые теперь известны, как законы, принципы, приемы, стандарты ТРИЗ [40]. Один из вариантов такого рассмотрения – переизобретение знаний с помощью ТРИЗ.
Объектами изучения в математике являются глубинные закономерности нашего мира, выраженные в математических понятиях и правилах. И те, и другие, согласно ТРИЗ, а также философским наукам системологии и диалектике, являются развивающимися системами. Рассмотрим возможности их переизобретения в учебном процессе.
При использовании элементов ТРИЗ-педагогики при изучении школьной математики путем переизобретения знаний вполне возможно, если переизобретать не закономерности, а описывающие их понятия
и правила
.
Пример 9.
Рассмотрим совокупность равенств типа 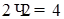 , , 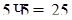 и т. д., т. е. таблицу умножения. Из истории арифметики известно, что раньше людям было известно сложение, а уже затем умножение. У операции сложения была проблема, связанная, например, с определением площадей. Необходимо было многократно складывать одинаковые слагаемые. Переизобрести с учащимися операцию умножения можно, применяя к сложению закон развертывания-свертывания
(в части свертывания) и принцип объединения
. Многократные операции сложения одинаковых слагаемых можно объединить, свернуть в операции умножения. и т. д., т. е. таблицу умножения. Из истории арифметики известно, что раньше людям было известно сложение, а уже затем умножение. У операции сложения была проблема, связанная, например, с определением площадей. Необходимо было многократно складывать одинаковые слагаемые. Переизобрести с учащимися операцию умножения можно, применяя к сложению закон развертывания-свертывания
(в части свертывания) и принцип объединения
. Многократные операции сложения одинаковых слагаемых можно объединить, свернуть в операции умножения.
Пример 10.
Когда-то людям были известны только целые числа. Но их оказывалось недостаточно, когда было необходимо измерять доли каких-либо объектов. В результате стихийного применения принципа дробления
люди создали идею дробей. Развитие дробных чисел можно рассматривать и дальше. Первые дроби у древних (унция и т. п.) были очень неудобны, особенно при арифметических операциях. Проблема была решена с использованием для записи дробных чисел их предшественников – целых чисел – стихийным применением закона перехода в бисистему
. Современная простая дробь – это бисистема
из числителя и знаменателя. Смешанные числа – это полисистемы
из целой части, числителя и знаменателя. Проблема сложения и вычитания простых дробей с разными знаменателями была решена путем стихийного применения принципа эквипотенциальности
(приведение к общему знаменателю). Все же у простых дробей правила выполнения арифметических операций, хотя и достаточно понятны, но не совсем просты, отличаются от правил операций с целыми числами. Проблема была решена стихийным применением к целым числам принципа инверсии
. В десятичных дробях вес разрядов справа от запятой (по степеням 10) – отрицательный, в противоположность положительному весу разрядов слева от запятой.
Пример 11.
Отрицательные числа получаются из положительных применением принципа инверсии.
Пример 12.
Иррациональные числа получаются из рациональных применением принципа непрерывности полезного действия
: числа занимают непрерывно всю числовую ось.
Пример 13.
Комплексные числа получаются из вещественных применением принципа перехода в другое измерение
: от числовой прямой к числовой комплексной плоскости.
Пример 14.
Переменные получаются из постоянных применением принципа динамичности.
Пример 15.
Функции одной переменной получаются из одиночных переменных по закону перехода в бисистему.
Пример 16.
Функции нескольких переменных получаются из одиночных переменных по закону перехода в полисистему
.
Пример 17.
Создание Ньютоном и Лейбницем интегрального исчисления – классический пример перехода на микроуровень
.
Таким образом, можно аналогично рассуждать в отношении других математических объектов, используя метод переизобретения знаний. Использовать данный метод можно на факультативных занятиях. Учащаемся наглядно показывается, как их уровень знакомства с математикой соответствует общим законам развития систем.
2.5. Методы технического творчества при обучении школьников математике
В конце первой главы в инструменты ТРИЗ-педагогики мы включили методы мышления, не относящиеся собственно к ТРИЗ. По сравнению классическими инструментами ТРИЗ методы технического творчества лучше отработаны при использовании их в учебном процессе [22, 42, 67, 68, 70] начиная с начальной школы [20, 28, 29, 87], но об использовании данных методов при обучении школьников математике литературы не встречается, хотя они являются ценным дидактическим материалом.
К основным методам научного творчества можно отнести: метод проб и ошибок; метод морфологического анализа; мозговой штурм; синергетику.
Данные методы достаточно легко можно применять при решении учебных математических задач.
Пример 18.
В каком случае произведение двух натуральных чисел дает четное число?
Используем метод проб и ошибок, переберем все возможные варианты четности двух чисел. И сделаем соответствующий вывод. В альтернативу можно показать применение идеального конечно результата ТРИЗ, сформулировав, что произведение данных чисел дало четной число 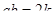 , тогда вывод о необходимости четности хотя бы одного из них достаточно логичен. , тогда вывод о необходимости четности хотя бы одного из них достаточно логичен.
При решении многих математических задач при использовании метода проб и ошибок другого математического аппарата рассуждений, учащиеся осознанно усваивают ценность математики.
Пример 19.
Укажите способы определения высоты здания без сложных приборов.
Коллективное (групповое) решение этой задачи методом мозгового штурма приводит к разнообразным выводам. Наиболее оптимальное и эффективное из них, как правило, попутно подводит к изучению темы «Подобные треугольники» [76].
Рассмотрим два из возможных вариантов решения. Первый вариант предполагает, что человек AB
стоит и смотрит на здание ED
(рис. 16). Измерив расстояния AD
и AO
, зная свою высоту AB
, можно рассмотреть подобные треугольники BEC
и ОВА
, из соотношения сторон которых можно
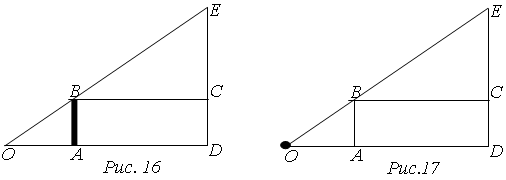
узнать искомое.
Второй вариант решения предполагает, что человек смотрит из точки О
на некоторый предмет AB
, высоту которого мы можем измерить, например, палку (рис. 17). Тогда из подобия тех же треугольников, что и в первом варианте с легкостью находится искомое.
Другие контрольные ответы заключается с применением тени, зеркала и построение высотомеров [59].
Пример 20.
В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что один из нас имеет белые, один черные и один рыжие волосы, но ни у одного из нас нет волос того цвета, на который указывает его фамилия», – заметил черноволосый. «Ты прав», – сказал Белов. Какой цвет волос у художника?
Для решения этой задачи можно воспользоваться морфологическим анализом и составить морфологический ящик, используя который решение становиться более наглядным.
Морфологический ящик
| Друзья
|
Цвет волос
|
| Белые
|
Рыжие
|
Черные
|
| Белов
|
-
|
+
|
-
|
| Рыжов
|
-
|
-
|
+
|
| Чернов
|
+
|
-
|
-
|
Морфологический анализ хорошо применим для решения логических задач, где морфологический ящик применяется в другой интерпретации и уже давно используется при решении задач.
Аналогичным образом использование других методов научного творчества в математике делает разнообразным способы подачи материала, и разработки по использованию их представляются возможными т.к. научное творчество отчасти схоже с математическим [73].
2.6. Принципы решения математических задач[3]
На основе ТРИЗ можно сформулировать советы – принципы решения математических задач, которые могут помочь избежать многих ошибок и подсказать, как найти решение.
Принцип отсроченного действия.
После прочтения задачи первое желание, которое возникает – это не решать ее. Пойди на поводу у этого желания, повремени с преобразованиями и другими действиями. Возможно, именно в этот момент ты подметишь полезную закономерность. Если данный этап не принес плодов, то попытайся найти область определения или хотя бы некоторое множество ее содержащее.
Пример 21.
Решите уравнение: 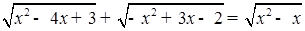 . .
Не будем спешить возводить обе части уравнения в квадрат, а найдем область определения:
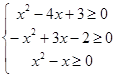 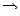 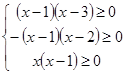 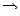 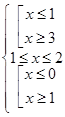  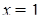
Подставляя х
= 1, убеждаемся, что это единственный корень.
Принцип максимума локальной информации.
На каждом шагу процесса поиска решения необходимо стремиться к получению максимальной информации из структуры полученной ситуации. Данный принцип мы использовали при решении предыдущей задачи.
Принцип правильности решения.
Некоторые описки и ошибки совершаются человеком на подсознательном уровне (порой достаточно при решении задачи один раз заменить знак «плюс» на «минус» и дальше можно уже никуда не спешить, ибо все последующие правильные действия приведут к неправильному результату) и поэтому обнаружить их самому очень трудно. Отсюда вытекает необходимость как локального контроля (каждый шаг в решении проверять дважды), так и глобальной проверки (проверка результата решения, хотя бы частично, на правильность и реальность).
Пример 22.
Решите уравнение: 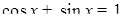 . .
Возведем обе части уравнения в квадрат. Имеем:
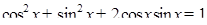 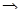 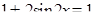 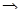  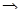 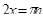 , , 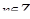 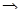 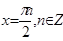 . .
На этом решение не окончено, было использовано возведение в квадрат, которое может привести к посторонним корням. Поэтому использовать принцип правильности решения обязательно. Тем самым после проверки получим 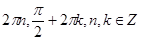 . .
Принцип отсечения ложных гипотез.
В процессе решения задачи часто приходиться различного рода предположения (выдвигать гипотезы). Главное, чего здесь следует опасаться – это не пойди на поводу у ложной гипотезы.
Пример 23.
Основанием пирамиды является трапеция с основаниями a
, b
и высотой h.
Грань пирамиды, проходящая через меньшее основание трапеции, перпендикулярна плоскости основания. Противоположная грань является равнобедренным треугольником с углом  при вершине пирамиды. Через точку пересечения диагоналей трапеции параллельно ее основаниям и вершину пирамиды проведена плоскость. Найти площадь треугольника, получившегося в сечении. при вершине пирамиды. Через точку пересечения диагоналей трапеции параллельно ее основаниям и вершину пирамиды проведена плоскость. Найти площадь треугольника, получившегося в сечении.
Гипотезой зачастую принимается, что прямая, по которой плоскость пересекает основание пирамиды, является средней линией трапеции. После этого предположения уже можно не суетиться, задача будет решена неверно.
Отсечение ложных гипотез осуществляется через метод вариации параметров.
Так,
если в нашей задаче изменить длины боковых сторон и основание трапеции, то станет очевидно, что наша гипотеза ложна. Для отсечения ложных гипотез может пригодиться и метод от противного.
Предполагаем, что гипотеза верна, и смотрим, к каким последствиям это приведет.
Принцип наихудшего случая.
С задачей надо обращать нежно, не навязывать ей своей воли. Так если в задаче речь идет о пирамиде, то совсем не обязательно, что бы она была правильной; центр вписанного в пирамиду шара не обязан лежать на высоте пирамиды и т.д.
Принцип непрерывности логических цепочек.
Нельзя использовать недоказанные утверждения в процессе решения, ибо недоказанное утверждение может оказаться неверным, а из неверного утверждения можно вывести и истину и ложь с помощью правил рассуждения. Поэтому в логической цепочке 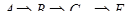 в идеале все составляющие звенья должны присутствовать в явном виде. в идеале все составляющие звенья должны присутствовать в явном виде.
Пример 24.
Решите неравенство: 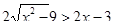 . .
Найдем область решения: 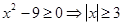 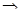 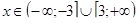 . .
Рассмотрим исходное неравенство на интервалах:
· 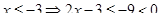 . Значит, в правой части исходного неравенства на данном интервале стоит отрицательное выражение. Но . Значит, в правой части исходного неравенства на данном интервале стоит отрицательное выражение. Но 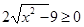 в виду не отрицательности квадратного корня. Следовательно, все х
из данного интервала являются решениями исходного неравенства. в виду не отрицательности квадратного корня. Следовательно, все х
из данного интервала являются решениями исходного неравенства.
· 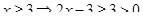 . Итак, на данном интервале обе части неравенства неотрицательные и допустимо возведение в квадрат. Имеем: . Итак, на данном интервале обе части неравенства неотрицательные и допустимо возведение в квадрат. Имеем: 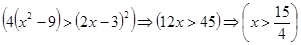 . И далее: . И далее: 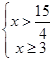 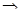 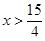 . .
Объединяя решения из интервалов, получим ответ: 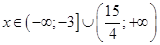 . .
Принцип полноты пространств альтернатив.
Принцип утверждает необходимость исчерпывающего учета всех необходимых составных частей основания. Или все возможные случаи должны быть рассмотрены.
Пример 25.
Доказать, что произведение трех последовательных целых чисел делиться на 6.
Пусть 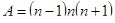 произведение трех последовательных целых чисел. Так как НОД(2;3)=1
то достаточно доказать, что А
делиться на 2 и на 3. произведение трех последовательных целых чисел. Так как НОД(2;3)=1
то достаточно доказать, что А
делиться на 2 и на 3.
При делении целого числа на 2 возможно два остатка 0 или 1. В соответствии с этим имеем две альтернативы:
· 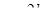 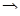 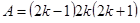
· 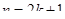 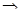 
Очевидно, что в обоих случаях А
делиться на 2.
При делении целого числа на 3 возможны три остатка: 0, 1 и 2. Получаем три альтернативы:
· 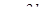 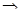 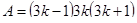
· 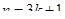 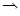 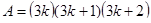
· 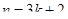  
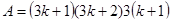
Очевидно, что в каждом из рассмотренных случаев А
делится на 3. Что и требовалось доказать.
Принцип простоты.
Выбранное решение поставленной задачи должны быть достаточно простым. На своем пути к познанию истины человечество стремилось к простым оригинальным и ярким решениям и ценило их. С другой стороны, лишние выкладки решения, которые присутствуют в нерациональных решениях, могут послужить источником дополнительных ошибок.
Пример 26.
Решите уравнение: 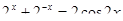 . .
Первый способ. Умножим обе части уравнения на 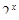 (по свойству показательной функции (по свойству показательной функции 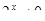 ) получим: ) получим: 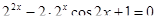 . Решая это уравнение, считая его квадратным, получим: . Решая это уравнение, считая его квадратным, получим: 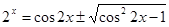 . Откуда . Откуда 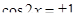 , и равенство принимает вид: , и равенство принимает вид: 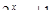 . Но . Но 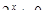 . Значит . Значит 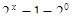 и и 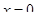 есть единственно решение уравнения. есть единственно решение уравнения.
Второй способ. Используя неравенство 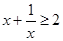 при при 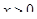 . Можно получить, что . Можно получить, что 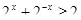 , но с другой стороны , но с другой стороны 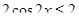 . Тогда можно сразу сделать вывод о том, что единственный корень при . Тогда можно сразу сделать вывод о том, что единственный корень при 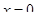 . .
Принцип системности решения.
Решая задачу, после того как решение нами осмыслено, мы своеобразно обращаемся к надсистеме (с точки зрения ТРИЗ) и ее базе данных, стараясь набросить на задачу некую информационную сеть. Затем мы приступаем к анализу составных частей и структуры задачи, привлекая для этого соответствующие подсистемы и информационное обеспечение (в ТРИЗ это называется переход в подсистему). Если эта деятельность не принесли результата, то опять обращаемся к надсистеме исходной задачи, пытаясь наиболее полно детерминировать поведение задачи, а затем снова возвращаемся к подсистеме. Этот системный подход
может повторяться многократно, причем на разных уровнях. Отсюда однозначно вытекает заключение: необходимое условие решение задачи – это знание соответствующей теории, без которой информационная сеть будет с просветами.
Пример 27.
Решите уравнение: 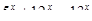 . .
Начнем с «экспериментальной стадии», пытаясь попросту угадать корень (переход в подсистему). Очевидно, один корень 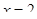 . .
Если бы нам удалось показать, что других корней нет, то задача была бы решена. Перейдем в надсистему: есть две функции, причем строго возрастающие. Тогда накидываем информационную сеть (сумма двух строго возрастающих функций, функция, строго возрастающая на их общей области определения). Тем самым доказываем единственность корня.
В процесс решения задачи учащемуся приходиться преодолевать не только психологические барьеры, но вызванные ими отрицательные эмоции. Может быть, рассмотренные советы помогут преодолеть и то, и другое.
С необходимостью использования данных советов человек сталкивается во многих видах интеллектуальной деятельности, в частности, в процессе принятия решения. Поэтому навыки, приобретенные им при использовании данных задач на уроках математики, могут оказаться полезным и в очень отдаленных от нее областях, несмотря на имеющиеся различия принципиального характера.
2.7. ТРИЗ-педагогика на уроках математики
Интеграция в общеобразовательные дисциплины методологии творчества, базирующейся на ТРИЗ и других методах поиска нестандартных решений, ставящих своей целью развитие творческого воображения и фантазии, формирование творческого системного мышления, выявление и развитие творческих способностей школьников, овладение способами, необходимыми для творческой деятельности, позволит повысить движущую силу развития творческого потенциала – интерес школьников к учебной работе, обеспечит самостоятельный поиск необходимой дополнительной учебной информации.
В этой главе мы адаптировали некоторые инструменты ТРИЗ для использования их на уроках математики. Приемы мышления, используемые в математике [38]: абстрагирование и конкретизация, обобщение и специализация, аналогии, можно сравнить с аналогичными принципами используемыми в ТРИЗ: принципом перехода в надсистему, принципом перехода в подсистему и принципом копирования.
Рассмотренные в этой главе способы по применению ТРИЗ-педагогики на уроках математики могут помочь решить проблему по формированию продуктивного мышления (креативность + системность) [83] у учащихся в школе на уроках математики.
Рассмотренные способы учат как надо действовать для того, чтобы получить желаемый продукт, результат, какие нормы надо соблюдать, чтобы получить продукт гарантированного качества. Кроме того, они дают возможность интегрировать часть полученной учебной информацию на уроках математики с гуманитарными и естественными наукам в единую систему знаний.
Глава 3. Описание и анализ опытно-экспериментальной работы
В рамках выпускной квалификационной работы был разработан и апробирован курс «Тренинг креативного мышления» на основе внеклассных занятий по математике в средней школе, базирующийся на инструментах ТРИЗ-педагогики.
3.1. Психологические аспекты сущности креативности
Чтобы перейти от репродуктивного обучения к творческому, деятельность … должна организовываться таким образом, что бы она приводила к получению учеником качественно новых результатов, как в обучении, так и в его развитии.
А. В. Хуторской
Понимание сущности творчества и лежащих в его основе способностей – вопрос, по которому существует множество разноречивых психологических, педагогических и философских теорий мнений и концепций [33, 42, 81].
Рассмотрим некоторые психологические аспекты, которые важны для понимания сущности предлагаемого тренинга развития креативности (от анг. create – творить, создавать).
Творчество в широком смысле рассматривается как деятельность в ситуации неопределенности, направленная на получение результатов, обладающей объективной или субъективной новизной. В этом плане она не обязательно связанна с такими видами деятельности, традиционно относимыми к «творческим», как рисование, сочинение музыки и стихов, и т.п. Оно проявляется, когда приходиться действовать в ситуациях неопределенности, отсутствия четких алгоритмов, неизвестности сути и способов решения, встающих перед человеком проблем, непредсказуемо меняющихся условий.
Креативность как система творческих способностей рассматривается в психологии в нескольких ракурсах. Под ней понимают:
· систему личностных качеств;
· характеристику интеллектуальной сферы (Айзенк, 2004);
· самостоятельное качество мышления, не сводимое к интеллекту в его традиционном понимании (Гилфорд, 1967; Пономарев, 1988).
Существуют различные определения креативности, в которых акцент может делаться на:
· продукты, создаваемые благодаря ей: креативность как способность порождать нечто новое, необычное, оригинальное;
· процессы: креативность как особая разновидность творческого мышления, высокоразвитое воображение, эстетическое мировосприятие и т.п.
· личностные качества: креативность как открытость новому жизненному опыту, независимость, гибкость, динамичность, оригинальность, самобытность личности;
· внешние условия: креативность как способность продуктивно действовать в ситуациях с высокой степенью неопределенности, где отсутствует заранее известные алгоритмы, гарантированно ведущие к успеху.
Так или иначе, под креативностью понимается некая противоположность обыденности, стандартности, комфортности (податливости внешнему влиянию), а также восприятие человеком себя как «субъекта» действительности [45].
Под творческими способностями мы будем понимать характеристики, которые позволяют продуктивно осваивать деятельность, направленную на получение результатов, обладающих новизной.
Таким образом, креативность включает:
1) интеллектуальные предпосылки творческой деятельности, позволяющие создавать нечто новое, ранее не известное (творческие способности в узком смысле этого понятия), а также предварительный набор знаний и умений, необходимых для того, чтобы это новое создавать;
2) личностные качества, позволяющие продуктивно действовать в ситуациях неопределенности, выходить за рамки предсказуемого, проявлять спонтанность;
3) «метатворчество» – жизненную позицию человека, подразумевающую отказ от шаблонности, стереотипности в суждениях и действиях, желание воспринимать и создавать нечто новое, изменяться самому и изменять мир вокруг себя, высокую ценность свободы, активности и развития.
Согласно концепции Дж. Гилфорда и Э. Торренса, креативность рассматривается как самобытная разновидность мышления – так называемое дивергентное («расходящееся, идущее в разных направлениях») мышление (рис. 18), которое опускает варьирование путей решения проблемы, приводит к неожиданным выводам и результатам [12]. Такое мышление противопоставляет конвергентному («сходящемуся»), (рис. 19), направленному на поиск единственно правильного решения на основе анализа множества предварительных условий (Дружинин, 1999). Дивергентное мышление не ориентируется на известное или подходящие решение проблемы, а проявляется в том случае, кода проблема еще не раскрыта и неизвестен путь ее решения.
Приведем обобщенную сравнительную характеристику разновидностей мышления, соответствующих традиционному, академическому интеллекту и ориентированных на творческий поиск [32].
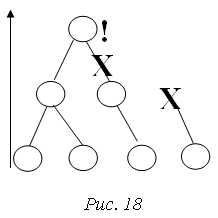
Завершающая стадия
– выбор верного варианта решения проблемы, отсечение всех остальных.
Стадия сбора информации
– варианты анализируются, критически оцениваются, ошибочные отсекаются, число альтернатив сокращается.
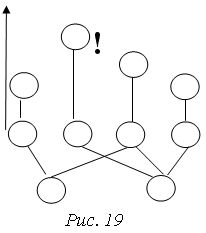
Начальная стадия
– предполагаются различные варианты способов решения проблемы.
Завершающая стадия
– критическая оценка предложенных вариантов, выбор наиболее приемлемых.
Стадия сбора информации
– максимальное расширение видения проблемного поля, генерирование идей о других возможных способах решения проблемы (без критической оценки этих идей)
Начальная стадия
– число видимых способов решения проблемы относительно не велико. Задача – собрать дополнительную информацию, позволяющую расширить представления об этих способа.
3.2. Ключевые психологические идеи тренинга
Современный мир стремительно меняется. И на учебе, и на работе, и в быту человек раз за разом сталкивается с новыми ситуациями, в которых велика степень неопределенности, нет заранее известных способов действий, гарантированно ведущих к успеху. В рамках выпускной квалификационной работы разработан курс «Тренинг креативного мышления», на основе внеклассных занятий по математике, призванный помочь научить справляться с такими ситуациями, опираясь на свои творческие способности.
При разработке курса были использованы положение о развитии креативности учащихся (Дж. Гилфорд, Е. Торренс, Е. Е. Туник) и о возрастной динамике креативности (Д. Б. Богоявленская, В. Н. Дружинин, Е. Торренс, В. С. Юркевич).
Главных проявлений креативности всего два:
1) возможность продуктивно действовать в ситуациях новизны и неопределенности, при недостатке информации, когда нет заранее известных способов действий, гарантированно ведущих к положительному результату;
2) возможность создавать какой-либо продукт, обладающий новизной (субъективной или объективной) и оригинальностью.
Отметим ключевые идеи, на которых базируется программа тренинга.
· Поле для развития креативности – это не только виды деятельности, традиционно относимые к творческим (рисование, игра на гитаре и т.п.), но и любые жизненные ситуации, в которых присутствуют новизна и неопределенность.
· Креативность – это не единичная способность, а комплекс особенностей интеллекта и качеств личности, а также общая жизненная позиция человека. Она не сводится ни к какому-то единичному психологическому качеству, ни к специальным творческим способностям (художественным, музыкальным и т.п.).
· Креативности не специфична, она не связана жестко с конкретными видами деятельности и может активизироваться в самых разных ситуациях. Ее тренировка в каком-то одном виде деятельности ведет к тому, что она начинает ярче проявляться и в других видах.
· Креативность в той или иной степени свойственна всем людям, а не является уникальным психологическим качеством, «печатью гения». Конечно, степень ее вырожденности существенно различается, однако у большинства людей она вполне достаточна, чтобы творчески подходить к решению жизненных проблем. Если этого не случится, то проблема обычно не в отсутствии творческих способностей, а в их недостаточной «настройке», неумении им пользоваться.
· Креативность управляема и развиваема – ее можно активизировать и тренировать, в том числе и посредством специально разработанного материала на основе общеобразовательных дисциплин. Предлагаемый тренинг как раз и выступает способом тренировки креативности на основе кружковых занятий по математике.
3.3. Тренинг креативного мышления
Среди целей, предъявляемых к современному школьному образованию, выделяется формирование личности, способной решать поставленные перед ней задачи в условиях рыночной экономики, в частности, быстро находить наиболее оптимальное и эффективное решение преодолеваемой проблемы. Такая цель направлена на реализацию внутреннего потенциала школьника, развитие творческого начала, его креативности. А также, все более остро обозначаются проблемы интеграции в образовании, раскрывающиеся в фундаментальном изучении дисциплин и, в то же время, межпредметных связях с другими образовательными областями. Однако вопросы организации учебно-воспитательного процесса, в котором на основе интегрированного подхода подготавливается выпускник школы, обученный основным практикам жизнедеятельности общества, затрагиваются мало, с позиции его необходимости, а не конкретной реализации [75], что подчеркивает актуальность
тренинга.
В разработанном курсе «Тренинг креативного мышления» предлагается одна из возможных реализаций обозначенных тенденций, при которых учебно-воспитательный процесс направлен на развитие креативности ученика в интегративной связи математики с другими образовательными областями [76].
Целью
курса является содействие развитию креативной мыслительной деятельности средствами математики.
Концепция
обучения базируется на использование инструментов ТРИЗ-педагогики. Тренинг разбит на девять взаимосвязанных занятий
: метод проб и ошибок; мозговой штурм; обратный мозговой штурм; морфологический анализ; идеальный конечный результат; отрицание или взгляд со стороны; принцип перехода в другое измерение; переход в надсистему; переход в подсистему (см. Приложение 1).
Каждое занятие направлено на усвоение того или иного метода активизации знаний или принципы разрешения противоречий через систему математических задач.
Новизна
курса заключается в применении указанных выше методов и приемов для решения конкретных математических задач, и их использование при разрешении жизненных проблемных ситуаций.
Каждое из занятий состоит из трех взаимосвязанных этапов:
· на первом этапе деятельность учителя была направлена на формирование у школьников понимания идеи нового приема;
· второй этап направлен на осознание учащимися применения выделенного приема в бытовых ситуациях;
· на третьем этапе школьники учились использовать прием при решении конкретных математических задач.
Кроме того, в начале каждого занятия ученикам предлагается проблемная ситуация, попытки разрешения которой зачастую приводят к неэффективному решению, в основном из-за использования только раннее изученных методов или жизненного опыта. В такой работе происходит актуализация знаний, после чего ученики «подталкиваются» педагогом к наиболее оптимальному и эффективному решению, обобщение которого приводит к новому приему активизации мышления.
Данный курс образует комплексную методику развития креативности на основе кружковых занятий по математике в средней школе, благодаря включению в образовательный процесс инструментов ТРИЗ-педагогики.
Таким образом, разработанный курс призван подтвердить гипотетические положения выпускной квалификационной работы.
Опытно-экспериментальная работа осуществлялась в МОУ СОШ с УИОП № 21 г. Кирова и МОУ СОШ № 57 г. Кирова.
В МОУ СОШ с УИОП № 21 г. Кирова был проведен полностью курс «Тренинг креативного мышления» (9 занятий):
· в 7-б и 8-б классах с углубленным изучением математики (июнь 2007 г.);
· в общеобразовательном 8-в классе (декабрь 2007 г.).
В МОУ СОШ № 57 г. Кирова был проведен краткий курс «Тренинг креативного мышления» (2 занятия) в 10-б классе с профильным уровнем изучения математики (февраль 2008 г.).
Для проверки гипотетических положений был использован комплексный метод, который включает в себя теоретический анализ психологической, педагогической литературы по изучаемой проблеме, включая наблюдение, беседы, формирующий эксперимент, тестирование с применением теста креативности Е. П. Торренса (для 8-в класса), теста Дж. Гилфорда (для 7-б и 8-б классов), статистические методы обработки материалов (статистику Хотеллинга, критерий Уилкоксона).
3.4. Анализ результатов опытно-экспериментальной работы
3.4.1 Анализ результатов опытно-экспериментальной работы в 7-б и 8-б классах МОУ СОШ с УИОП №21 г. Кирова
1. Сравним средние результаты изучаемых параметров (беглость, гибкость, оригинальность) в начале и конце эксперимента отдельно. Для этого наглядно представим результаты опытно-экспериментальной работы (диаграмма 1), рассмотрев в прямом сравнении (слева), и относительный рост уровня креативности по исследуемым параметрам (справа).
В экспериментальной группе по всем трем параметрам наблюдается рост показателей от 4% до 14%.
2. Используя многомерные методы статистического анализа (статистику Хотеллинга), заключаем, что есть основания на указание существенного различия общей креативности школьников экспериментальной группы до и после эксперимента (см. Приложение 2).
Диаграмма 1
Результаты оценки исследуемых параметров
в начале (тест 1) и конце эксперимента (тест 2)
у экспериментальной группы

3. Определим характер изменения показателей экспериментальной группы, применив критерий Уилкоксона. Сформулируем нулевую гипотезу  : «предлагаемая методика не способствует улучшению параметров креативности (соответственно беглости, гибкости и оригинальности)». Тогда конкурирующая гипотеза : «предлагаемая методика не способствует улучшению параметров креативности (соответственно беглости, гибкости и оригинальности)». Тогда конкурирующая гипотеза  будет определяться следующим образом: «предлагаемая методика способствует улучшению параметров креативности (соответственно беглости, гибкости и оригинальности)». будет определяться следующим образом: «предлагаемая методика способствует улучшению параметров креативности (соответственно беглости, гибкости и оригинальности)».
По данным таблицы для параметра «беглость» получаем меньшее сумма рангов 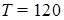 относиться к положительным разностям. При уровне значимости относиться к положительным разностям. При уровне значимости 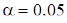 критическое значение статистики критическое значение статистики 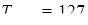 . Таким образом, . Таким образом, 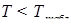 и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза  : «предлагаемая методика приобщения школьников к опыту творческой деятельности способствует улучшению беглости мышления». : «предлагаемая методика приобщения школьников к опыту творческой деятельности способствует улучшению беглости мышления».
Аналогично для параметра «гибкость» получаем меньшее сумма рангов 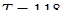 относиться к положительным разностям. При уровне значимости относиться к положительным разностям. При уровне значимости 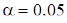 критическое значение статистики критическое значение статистики 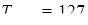 . Таким образом, . Таким образом, 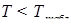 и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза  : «предлагаемая методика приобщения школьников к опыту творческой деятельности способствует улучшению гибкости мышления». : «предлагаемая методика приобщения школьников к опыту творческой деятельности способствует улучшению гибкости мышления».
Результаты оценки параметров «беглость», «гибкость», «оригинальность» в начале (тест 1) и конце эксперимента (тест 2)
| №
|
Беглость
|
Гибкость
|
Оригинальность
|
| Тест 1
|
Тест 2
|
Разность
|
Ранг
|
Тест 1
|
Тест 2
|
Разность
|
Ранг
|
Тест 1
|
Тест 2
|
Разность
|
Ранг
|
| 1
|
26,8
|
30,5
|
3,7
|
9
|
65
|
72
|
7
|
14
|
10
|
20
|
10
|
15
|
| 2
|
24,1
|
40,1
|
16
|
2
|
71
|
101
|
30
|
6
|
25
|
58
|
33
|
1
|
| 3
|
43
|
43,9
|
0,9
|
14
|
80
|
117
|
37
|
4
|
0
|
28
|
28
|
5
|
| 4
|
31,4
|
45,4
|
14
|
4
|
74
|
112
|
38
|
3
|
20
|
42
|
22
|
12
|
| 5
|
34,8
|
32,9
|
-1,9
|
19
|
91
|
70
|
-21
|
28
|
15
|
38
|
23
|
9
|
| 6
|
32
|
26,3
|
-5,7
|
27
|
72
|
57
|
-15
|
27
|
40
|
10
|
-30
|
28
|
| 7
|
40,7
|
61
|
20,3
|
1
|
77
|
121
|
44
|
2
|
28
|
30
|
2
|
16
|
| 8
|
35,2
|
36,8
|
1,6
|
13
|
82
|
88
|
6
|
17
|
30
|
58
|
28
|
5
|
| 9
|
32,7
|
38,9
|
6,2
|
7
|
90
|
102
|
12
|
13
|
25
|
43
|
18
|
13
|
| 10
|
37
|
45
|
8
|
5
|
87
|
116
|
29
|
7
|
30
|
63
|
33
|
1
|
| 11
|
35,8
|
38
|
2,2
|
12
|
79
|
86
|
7
|
14
|
40
|
35
|
-5
|
20
|
| 12
|
36,3
|
36,1
|
-0,2
|
16
|
98
|
84
|
-14
|
26
|
25
|
23
|
-2
|
18
|
| 13
|
42,6
|
49,6
|
7
|
6
|
97
|
110
|
13
|
12
|
25
|
55
|
30
|
4
|
| 14
|
40,6
|
38,8
|
-1,8
|
18
|
97
|
102
|
5
|
18
|
30
|
53
|
23
|
9
|
| 15
|
36,2
|
38,5
|
2,3
|
11
|
89
|
81
|
-8
|
23
|
45
|
38
|
-7
|
22
|
| 16
|
45,8
|
43,3
|
-2,5
|
23
|
100
|
119
|
19
|
9
|
30
|
43
|
13
|
14
|
| 17
|
42,4
|
39,1
|
-3,3
|
24
|
97
|
104
|
7
|
14
|
45
|
43
|
-2
|
18
|
| 18
|
56
|
55
|
-1
|
17
|
86
|
138
|
52
|
1
|
58
|
85
|
27
|
7
|
| 19
|
53,8
|
68,7
|
14,9
|
3
|
107
|
124
|
17
|
11
|
40
|
30
|
-10
|
24
|
| 20
|
38,3
|
31
|
-7,3
|
28
|
99
|
86
|
-13
|
25
|
65
|
33
|
-32
|
29
|
| 21
|
49
|
49
|
99
|
99
|
65
|
65
|
| 22
|
52,3
|
48,5
|
-3,8
|
26
|
123
|
126
|
3
|
19
|
45
|
76
|
31
|
3
|
| 23
|
56,6
|
54,3
|
-2,3
|
22
|
111
|
102
|
-9
|
24
|
55
|
50
|
-5
|
20
|
| 24
|
50,8
|
56,4
|
5,6
|
8
|
128
|
147
|
19
|
9
|
45
|
70
|
25
|
8
|
| 25
|
57,2
|
57,2
|
104
|
104
|
65
|
65
|
| 26
|
59,5
|
45,5
|
-14
|
29
|
108
|
104
|
-4
|
21
|
60
|
51
|
-9
|
23
|
| 27
|
45,7
|
43,7
|
-2
|
20
|
99
|
100
|
1
|
20
|
83
|
85
|
2
|
16
|
| 28
|
50,2
|
53,9
|
3,7
|
10
|
107
|
134
|
27
|
8
|
71
|
50
|
-21
|
27
|
| 29
|
46,5
|
46,5
|
91
|
91
|
105
|
105
|
| 30
|
36,2
|
32,7
|
-3,5
|
25
|
113
|
92
|
-21
|
28
|
98
|
80
|
-18
|
26
|
| 31
|
52,5
|
53,3
|
0,8
|
15
|
116
|
152
|
36
|
5
|
103
|
126
|
23
|
9
|
| 32
|
66,8
|
64,6
|
-2,2
|
21
|
144
|
139
|
-5
|
22
|
121
|
110
|
-11
|
25
|
Для параметра «оригинальность» получаем меньшее сумма рангов 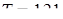 относиться к положительным разностям. При уровне значимости относиться к положительным разностям. При уровне значимости 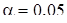 критическое значение статистики критическое значение статистики 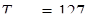 . Таким образом, . Таким образом, 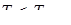 и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза  : «предлагаемая методика способствует улучшению оригинальности мышления». : «предлагаемая методика способствует улучшению оригинальности мышления».
Таким образом, анализ результатов исследования с помощью критерия Уилкокосона, определяет обоснованные многомерными статистическими методами различия в сторону повышения результатов общей креативности учащихся экспериментальной группы после эксперимента.
3.4.2 Анализ результатов опытно-экспериментальной работы
в 8-в классе МОУ СОШ с УИОП № 21 г. Кирова
Обработку и анализ результатов опытно-экспериментальной работы проведем по следующей схеме.
1. Сравним средние результаты изучаемых параметров (беглость, гибкость, оригинальность, разработанность) в начале и конце эксперимента у экспериментальной группы. Для этого наглядно представим результаты опытно-экспериментальной работы (диаграмма 2): прямое сравнение, относительный рост, сравнение с нормой.
Диаграмма 2
Результаты оценки изучаемых параметров в начале (тест 1) и в конце эксперимента (тест 2)
В прямом сравнении

Относительное сравнение
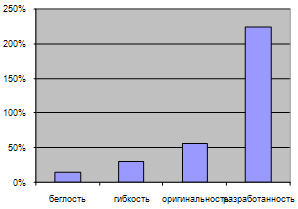
Сравнение с нормой

Диаграммы дают наглядную иллюстрацию того, что рост изучаемых параметров в разной степени присутствует довольно ощутимо (от 14% до 224%) . Наибольший рост достигает параметр разработанность, по большей степени это обосновывается тем, что дети при проведении теста 1 не были готовы и привычны к такому роду деятельности, сдерживая свои внутренние возможности, своеобразно «комплексуя», при проведение же теста 2 дети адаптировались к данной деятельности и полностью использовали свой творческий потенциал. До эксперимента отклонение средних показателей от средних показатели КТГМ 8 классов в пределах нормы, хотя и ниже их. После эксперимента показатели так же остались в пределах нормы, но уже выше их.
2. Используя многомерные методы статистического анализа, заключаем, что есть основания на указание существенного различия общей креативности школьников экспериментальной группы до и после эксперимента (см. Приложение 3).
3. Определим характер изменения показателей экспериментальной группы, применив критерий знаков и проанализировав суммарный балл по каждому из параметров. Сформулируем нулевую гипотезу  : «предлагаемая методика не способствует улучшению параметров креативности (соответственно беглости, гибкости, оригинальности, разработанности)». Тогда конкурирующая гипотеза : «предлагаемая методика не способствует улучшению параметров креативности (соответственно беглости, гибкости, оригинальности, разработанности)». Тогда конкурирующая гипотеза  будет определяться следующим образом: «предлагаемая методика способствует улучшению параметров креативности (соответственно беглости, гибкости, оригинальности и разработанности)». будет определяться следующим образом: «предлагаемая методика способствует улучшению параметров креативности (соответственно беглости, гибкости, оригинальности и разработанности)».
Результаты оценки параметров «беглость», «гибкость», «оригинальность», «разработанность» в начале (тест 1) и конце эксперимента (тест 2)
| №
|
беглость
|
гибкость
|
оригинальность
|
разработанность
|
| Тест 1
|
Тест 2
|
Знак
|
Тест 1
|
Тест 2
|
Знак
|
Тест 1
|
Тест 2
|
Знак
|
Тест 1
|
Тест 2
|
Знак
|
| 1
|
6
|
6
|
0
|
6
|
6
|
0
|
5
|
11
|
+
|
6
|
11
|
+
|
| 2
|
10
|
10
|
0
|
8
|
8
|
0
|
10
|
24
|
+
|
11
|
24
|
+
|
| 3
|
10
|
10
|
0
|
5
|
8
|
+
|
10
|
41
|
+
|
17
|
41
|
+
|
| 4
|
7
|
10
|
+
|
7
|
8
|
+
|
7
|
68
|
+
|
18
|
68
|
+
|
| 5
|
10
|
10
|
0
|
6
|
8
|
+
|
5
|
32
|
+
|
12
|
32
|
+
|
| 6
|
9
|
8
|
-
|
7
|
8
|
+
|
9
|
30
|
+
|
15
|
30
|
+
|
| 7
|
9
|
10
|
+
|
5
|
9
|
+
|
7
|
50
|
+
|
14
|
50
|
+
|
| 8
|
10
|
10
|
0
|
9
|
7
|
-
|
10
|
48
|
+
|
8
|
48
|
+
|
| 9
|
5
|
6
|
+
|
3
|
6
|
+
|
6
|
35
|
+
|
7
|
35
|
+
|
| 10
|
10
|
10
|
0
|
10
|
9
|
-
|
8
|
57
|
+
|
23
|
57
|
+
|
| 11
|
10
|
10
|
0
|
7
|
8
|
+
|
12
|
46
|
+
|
16
|
46
|
+
|
| 12
|
10
|
10
|
0
|
8
|
8
|
0
|
9
|
60
|
+
|
13
|
60
|
+
|
| 13
|
9
|
10
|
+
|
6
|
8
|
+
|
7
|
30
|
+
|
9
|
30
|
+
|
| 14
|
10
|
10
|
0
|
10
|
9
|
-
|
12
|
25
|
+
|
13
|
25
|
+
|
| 15
|
10
|
10
|
0
|
7
|
9
|
+
|
8
|
26
|
+
|
15
|
26
|
+
|
| 16
|
6
|
8
|
+
|
2
|
6
|
+
|
0
|
22
|
+
|
6
|
22
|
+
|
| 17
|
6
|
9
|
+
|
5
|
9
|
+
|
4
|
38
|
+
|
7
|
38
|
+
|
| 18
|
5
|
10
|
+
|
4
|
9
|
+
|
5
|
28
|
+
|
4
|
28
|
+
|
| 19
|
6
|
10
|
+
|
6
|
9
|
+
|
11
|
53
|
+
|
10
|
53
|
+
|
| 20
|
10
|
10
|
0
|
8
|
9
|
+
|
14
|
35
|
+
|
19
|
35
|
+
|
| 21
|
10
|
10
|
0
|
4
|
8
|
+
|
14
|
63
|
+
|
15
|
63
|
+
|
| 22
|
5
|
9
|
+
|
5
|
9
|
+
|
7
|
30
|
+
|
7
|
30
|
+
|
| 23
|
4
|
8
|
+
|
4
|
7
|
+
|
5
|
14
|
+
|
3
|
14
|
+
|
| Всего
|
11
|
20
|
15
|
23
|
17
|
23
|
| +
|
10
|
10
|
17
|
23
|
23
|
| -
|
1
|
3
|
0
|
0
|
По данным таблицы для параметра «беглость» получаем общее количество ненулевых разностей  , значение экспериментальной статистики , значение экспериментальной статистики  (число знаков «+»). При уровне значимости (число знаков «+»). При уровне значимости 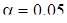 критическое значение статистики критическое значение статистики 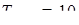 . Таким образом, . Таким образом, 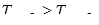 и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза 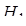 : «предлагаемая методика способствует улучшению беглости мышления». : «предлагаемая методика способствует улучшению беглости мышления».
Аналогично для параметра «гибкость» получаем общее количество ненулевых разностей 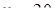 , значение экспериментальной статистики , значение экспериментальной статистики  (число знаков «+»). При уровне значимости (число знаков «+»). При уровне значимости 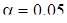 критическое значение статистики критическое значение статистики 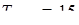 . .
Таким образом, 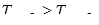 и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза  : «предлагаемая методика способствует улучшению гибкости мышления». : «предлагаемая методика способствует улучшению гибкости мышления».
Для параметра «оригинальность» получаем общее количество ненулевых разностей  , значение экспериментальной статистики , значение экспериментальной статистики  (число знаков «+»). При уровне значимости (число знаков «+»). При уровне значимости  критическое значение статистики критическое значение статистики 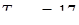 . Таким образом, . Таким образом, 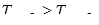 и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза 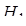 : «предлагаемая методика способствует улучшению оригинальности мышления». : «предлагаемая методика способствует улучшению оригинальности мышления».
Для параметра «разработанность» получаем общее количество ненулевых разностей  , значение экспериментальной статистики , значение экспериментальной статистики  (число знаков «+»). При уровне значимости (число знаков «+»). При уровне значимости  критическое значение статистики критическое значение статистики 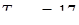 . Таким образом, . Таким образом, 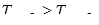 и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза 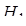 : «предлагаемая методика способствует улучшению разработанности мышления». : «предлагаемая методика способствует улучшению разработанности мышления».
Таким образом, анализ результатов исследования с помощью критерия знаков, определяет обоснованные многомерными статистическими методами различия в сторону повышения результатов общей креативности учащихся экспериментальной группы после эксперимента.
Заключение
Математические сведения могут применяться умело и с пользой только в том случае, если они усвоены творчески, так что учащийся видит сам, как можно было бы прийти к ним самостоятельно.
А.Н. Колмогоров
Основная задача школьных программ – сделать школьное образование междисциплинарным, сформулировать междисциплинарное видение творчества, которое сегодня занимает доминирующие место в решении проблемы развития компетенций школьников [11]. Такая постановка задачи удачно сворачивает обе поставленных во введении проблемы.
В выпускной квалификационной работе возможным вариантом решения данной задачи предлагается воспользоваться инструментами ТРИЗ-педагогики. Теоретические и прикладные основы которой, изложенные в многочисленных работах, мы рассмотрели. При этом мы уточнили термин «ТРИЗ-педагогика» как подготовку мышления для решения творческих задач, причем используя не только методы ТРИЗ, но и методы научного технического творчества. Однако методологическая основа базируется на ТРИЗ. Тем самым решены первые две поставленные задачи работы.
В рамках работы разработаны возможные механизмы использования инструментов ТРИЗ-педагогики при преподавании математики в общеобразовательной школе, а также апробирован курс на основе внеклассных занятий по математике с применением ТРИЗ-педагогики, анализ которого на основе тестов Гилфорда и Торенса, анкет и бесед с учителями работающих с классом позволяет говорить не только о решении третьей и четвертой задачи исследования, но о подтверждении гипотетических положений.
Таким образом, можно говорить о достижении поставленной цели.
Кроме того, основные положения выпускной квалификационной работы подтверждены апробацией в ходе выступлений на международной научно-практической конференции «Образование и межнациональные отношения: теория и социальная практика» (Ижевск, 14-16 ноября 2007 г., [76]), международной научно-практической конференции «IX Сибирская школа молодого ученого: проблемы повышения качества и эффективности профессионального образования» (Томск, 23-25 октября 2007 г., [74]); Восьмой международной научной конференции преподавателей, аспирантов и студентов (Новосибирск, 28-29 февраля 2008 г., [75]). На статью, предложенную на последней конференции, в которой раскрывается основное содержание исследования выпускной квалификационной работы, получены два отзыва, подтверждающих значимость и актуальность предпринятых нам исследований, а также необходимость дальнейшего развития исследования.
Все выше сказанное и потвержденные гипотезы дают нам право говорить о необходимости и возможности дальнейшего исследования по применению инструментов ТРИЗ-педагогики в преподавании математики.
Библиографический список
1. Авдевич, В. И. Несколько общих мыслей о творчестве и педагогике [Электронный ресурс] / В. И. Авдевич // Проблемы ТРТЛ. Проблемы творческой педагогики. [Режим доступа: http://www.trizminsk.org].
2. Альтов, Г. С. И тут появился изобретатель [Текст] / Г. С. Альтов. – М.: Детская литература, 1984. – 124 с.
3. Альтшуллер, Г. С. Алгоритм изобретения [Текст] / Г. С. Альтшуллер. – М.: Московский рабочий, 1973. – 232 с.
4. Альтшуллер, Г. С. Найти идею введение в теорию решения изобретательских задач [Текст] / Г. С. Альтшуллер. – Новосибирск: Наука, 1991. – 225 с.
5. Альтшуллер, Г. С. Творчество как точная наука [Текст] / Г. С. Альтшуллер. – Петрозаводск: Скандинавия, 2004. – 208 с.
6. Альтшуллер, Г. С. Как стать Еретиком [Текст] / Г. С. Альтшуллер, И. М. Верткин // Как стать Еретиком. Техника – Молодежь – Творчество; сост. А.Б. Селюцкий. – Петрозаводск: Карелия, 1991. – 365 с.
7. Альтшуллер, Г. С. Крылья для Икара [Текст] / Г. С. Альтшуллер, А. Б. Селюцкий. – Петрозаводск: Карелия, 1991. – 214 с.
8. Альтшуллер, Г. С. Психология изобретательского творчества [Текст] / Г. С. Альтшуллер, Р. Б. Шапиро //Вопросы психологии. – 1956. – № 3. – С. 5-11.
9. Белова, Г. В. Система работы с математическими определениями [Текст] / Г.В. Белова // Проблемы теории развития творческой личности: сборник научных трудов. Челябинск: Изд-во ЧГПУ «Факел». – 1998. – Вып. №1. – 60 с.
10. Белова, Г. В. Творческие копилки на уроках математики [Текст] / Г. В. Белова // Научно-практическая конференция «Творчество во имя достойной жизни», 16-17 августа 2000 г. Тезисы докладов. Петрозаводск, 2000 – 320 с.
11. Беркалиев, Т. Н. Инновации и качество школьного образования [Текст]: научно-метод. пособие для педагогов инновационных школ / Т. Н. Беркалиев, Е. С. Заир-Бек, А. П. Тряпицына. – СПб.: КАРО, 2007. –144 с.
12. Богоявленская, Д. Б. Психология творческих способностей [Текст] / Д. Б. Богоявленская. – М.: Академия, 2002. – 320 с.
13. Бухвалов, В. А. Алгоритмы педагогического творчества [Текст]: кн. для учителя / В. А. Бухвалов. – М.: Просвещение, 1993. – 96 с.
14. Бухвалов, В. А. Изобретаем черепаху: как применять ТРИЗ в школьном курсе биологии [Текст]: кн. для учителей и учащихся / В. А. Бухвалов, Ю. С. Мурашковский. – Рига, 1993. – 168 с.
15. Великович, Л. Л. Подготовка к экзаменам по математике [Текст]: учеб. пособие для абитуриентов и учащихся 9-11 кл. Ч. I / Л. Л. Великович; под ред. А. А. Гина, Л. Д. Корсун. – М.: Народное образование, 2006. – 304 с.
16. Великович, Л. Л. Подготовка к экзаменам по математике [Текст]: учеб. пособие для абитуриентов и учащихся 9-11 кл. Ч. II / Л. Л. Великович; под ред. А. А. Гина, Л. Д. Корсун. – М.: Народное образование, 2006. – 308 с.
17. Верткин, И. М. Бороться и искать. О качествах творческой личности / И. М. Верткин // Нить в лабиринте. Техника – молодежь – творчество. Сост. А. Б. Селюцкий. – Петрозаводск: Карелия, 1988. – 277 с.
18. Гальетов, В. П. Роль ТРИЗ в реформе системы образования / В. П. Гальетов // Творческие технологии. – Челябинск: ЮУГУ, 2001. – С.19-25.
19. Вейль, Г. О философии математики [Текст] / Г. Вейль. – М.: КомКнига, 2005. – 128 с.
20. Гин, А. А. Задачи-сказки от кота Потряскина [Текст]: для детей младшего школьного возраста / А. А. Гин. – М.: Вита-Пресс, 2002 – 80 с.
21. Гин, А. А. ТРИЗ-педагогика [Электронный ресурс] / А. А. Гин. – [Режим доступа: http://www.trizway.com].
22. Гин, А. А. Бескровная Атака. Технологии проведения учебного мозгового штурма [Текст] / А.А. Гин // Педагогика + ТРИЗ. – № 3. – Мн.: ПолиБиг, 1997. – 64 с.
23. Гин, А. А. Приемы педагогической техники [Текст] / А. А. Гин. – М.: Вита-Пресс, 2007. – 112 с.
24. Гин, А. А. Цели и задачи ТРИЗ-педагогики [Электронный ресурс] / А. А. Гин; доклад на 9-й научно-практической конференции «Развитие творческих способностей в процессе обучения и воспитания на основе ТРИЗ», июнь 2006 г. – [Режим доступа: http://www.trizway.com].
25. Гин, А. А. Школа-фабрика умрет. Что дальше? [Текст] / А. А. Гин // Педагогика+ТРИЗ. – № 6. – М.: Вита-Пресс, 2001. – С. 5-18.
26. Гин, А. А. 150 творческих задач для сельской школы [Текст]: учеб.-методич. пособие / А. А. Гин, И. Ю. Андржевская. – М.: Народное образование, 2007. – 234 с.
27. Гин, С. И. Учить по-тризовски. Как? [Текст] / С. И. Гин // Школьные технологии. – 2006. – № 3. – С. 110-112.
28. Гин, С. И. Занятия по ТРИЗ в детском саду [Текст]: пособие для педагогов дошк. учреждений / С. И. Гин. – Мн: ИВЦ Минфина, 2007. – 112 с.
29. Гин, С. И. Мир фантазии [Текст]: метод. пособие для учителей начальной школы / С.И. Гин. – М: Вита-Пресс, 2007. – 128 с.
30. Гитин, А. В. Методы сильного мышления [Текст] / А. В. Гитин // Учителям о ТРИЗ. – № 4. – СПб.: Союз писателей Санкт-Петербурга, 2001. – С. 11-39.
31. Глазунова, М. А. Интегрированный курс на основе ТРИЗ-педагогики [Текст] / М. А. Глазунова, М. И. Меерович, Л. И. Шрагина // Педагогика. – 2002. – № 6 – С. 40-43.
32. Грецов, А. Г. Тренинг креативности для старшеклассников и студентов [Текст] / А. Г. Грецов. – СПб.: Питер, 2007. – 208 с.
33. Грецов, А. Г. Психологические тренинги с подростками [Текст] / А. Г. Грецов. – СПб.: Питер, 2008. – 386 с.
34. Джеус, А. В. Молодежные интенсивные школы инновационной эпохи. Современное научное творчество и изобретательство учащихся [Текст] / А. В. Джеус, И. В. Романец, Т. В. Погребная, А. В. Козлов, О. В. Сидоркина. – Красноярск: ИПЦ КГТУ, 2006. – 300 с.
35. Иванов, Г. И. Формулы творчества, или Как научиться изобретать [Текст]: кн. для учащихся ст. классов / Г. И. Иванов. – М.: Просвещение, 1994. – 208 с.
36. Иванова, Н. Г. Материалы конкурса «ТРИЗформашка-2006» [Текст] / Н. Г. Иванова, М. А. Плаксина, О. Л. Русакова // Информатика. – 2006. – №23. – С. 29-36.
37. Камин, А. Л. Тропою следопыта. Естественные мысли о школьном курсе естествознания [Текст] / А. Л. Кимин // Школьные технологии. – 2001. – № 5 – С. 221-228.
38. Канин, Е. С. Изучение начал математического анализа в средней школе [Текст] / Е. С. Канин. – Киров: Изд-во ВятГГУ, 2006. – 170 с.
39. Канин, Е. С. Учебные математические задачи [Текст] / Е. С. Канин. – Киров: Изд-во ВятГГУ, 2004. – 154 с.
40. Козлов, А. В. ТРИЗ для учителей математики [Текст] / А. В. Козлов, Т. В. Погребная // Технологии творчества.– Челябинск, 1999. – № 1. – С. 15-18.
41. Лихолетов, В. В. О роли творческих технологий в обеспечении конкурентоспособности специалистов [Текст] / В. В. Лихолетов, В. Н. Борщенюк // Творческие технологии. – Челябинск, 2001. – С. 118-123.
42. Матюшкин, А. М. Мышление, обучение, творчество [Текст] / А. М. Матюшкин. – М.: Изд-во МПСИ, 2003. – 720 с.
43. Меерович, М. И. Основы культуры мышления [Текст] / М. И. Меерович, Л. И. Шрагина // Школьные технологии. – 1997. – № 5. – С. 34-38.
44. Меерович, М. И. От методов решения технических проблем до технологии формирования культуры мышления. Концепция применения ТРИЗ в педагогике [Текст] // М. И. Меерович, Л. И. Шрагина. – Одесса: УЛП ТРИЗ, 1998. – 226 с.
45. Микалко, М. Игры разума. Тренинг креативного мышления [Текст] / М. Микалко. – СПб.: Питер, 2008 – 448 с.
46. Митрофанов, В. В. О природе эффекта Рассела [Текст] / В. В. Митрофанов, В. И. Соколов // Физика твердого тела. – 1974. – Т. 16. – № 8. – С. 12-28.
47. Модестов, С. Ю. Проектирование образовательных технологий на основе ТРИЗ [Текст]: автореф. дис. канд. пед. наук: 13.00.01 / С. Ю. Модестов; СПб: РГПУ им. А.И. Герцена, 2001. – 18 с.
48. Мордкович, А. Г. Беседы с учителями математики [Текст]: учеб.-метод. пособие / А. Г. Мордкович. – М.: Оникс 21 век, 2005. – 336 с.
49. Нагибин, Ф. Ф. Математическая шкатулка [Текст] / Ф. Ф. Нагибин, Е. С. Канин. – М.: Дрофа, 2006. – 270 с.
50. Нестеренко, А. А. Детское научное творчество – подлинник или копия? [Электронный ресурс] / А.А. Нестеренко // Проблемы ТРТЛ. Проблемы творческой педагогики. [Режим доступа: www.trizminsk.org].
51. Нестеренко, А. А. Несколько мыслей о ТРИЗ-педагогике [Текст] / А. А. Нестеренко. – Технология творчества. – 1999. – № 3. – С. 12-16.
52. Нить в лабиринте. Техника – молодежь – творчество [Текст] / Сост. А. Б. Селюцкий. – Петрозаводск: Карелия, 1988. – 277 с.
53. Образовательная система «Школа 2100». Педагогика здравого смысла [Текст]: сборник материалов / Под ред. А. А. Леонтьева. – М.: Баласс, 2003. – 368 с.
54. Образовательная система «Школа 2100». Сборник программ. Дошкольная подготовка. Начальная школа. Основная и старшая школа [Текст] / Под ред. А. А. Леонтьева. – М.: «Баласс», 2004. – 528 с.
55. Орлов, М. А. Основы классической ТРИЗ. Практическое руководство для изобретательного мышления [Текст] / М. А. Орлов. – М.: СОЛОН-ПРЕСС, 2006. – 432 с.
56. Основы педагогического мастерства [Текст] / Под ред. И. А. Зязюна. – М.: Просвещение, 1989. –211 с.
57. Педагогика + ТРИЗ [Текст]: сборник статей для учителей, воспитателей и менеджеров образования. №3. – Мн.: ПолиБиг, 1997. – 64 с.
58. Педагогика + ТРИЗ [Текст]: сборник статей для учителей, воспитателей и менеджеров образования. №4. – Гомель: ПолиБиг, 1998. – 64 с.
59. Перельман, Я. И. Геометрия на вольном воздухе [Текст] / Я. И. Перельман; А. Л. Бондаренко. – М.: АСТ, 2008. – 94 с.
60. Перельман, Я. И. Занимательная геометрия [Текст] / Я. И. Перельман. – М.: Астрель, 2007. – 350 с.
61. Погребная, Т. В. ТРИЗ-педагогика и модернизация образования [Электронный ресурс] / Т. В. Погребная, А. В. Козлов, О. В. Сидоркина // «ТРИЗ-Конференция – 2007». – [Режим доступа: http://www.metodolog.ru].
62. Погребная, Т. В. ТРИЗ-педагогика в преподавании математики [Рукопись] / Т. В. Погребная, А. В. Козлов. – Красноярский государственный технический университет, Красноярский краевой Институт повышения квалификации работников образования, 2008.
63. Погребная, Т. В. Современная ТРИЗ-педагогика в системе непрерывного образования педагогов [Текст]: пособие для самоопределения / Т. В. Погребная, А. В. Козлов, О. В. Сидоркина. – Красноярск: ККИПКРО, 2005. – 42 с.
64. Пойа, Д. Как решить задачу [Текст] / Д. Пойа. – М.: Учпедгиз, 1961. – 220 с.
65. Правила игры без правил. Техника – молодежь – творчество [Текст] / Сост. А. Б. Селюцкий. – Петрозаводск: Карелия, 1989. – 280 с.
66. Применение ТРИЗ в преподавании школьных предметов [Текст]: аналитический обзор рукописных работ из фонда материалов по ТРИЗ / ЧОУНБ // Технологии творчества. – 2000. – № 1. – С. 38-54.
67. Сборник задач для изучающих ТРИЗ [Текст] / Сост. А. В. Кислов, Е. Л. Пчелкина. – СПБ.: РА ТРИЗ, 2007. – 56 с.
68. Терехова, Г. В. Творческие задания как средство развития креативных способностей школьников в учебном процессе [Текст]: автореф. дис. канд. пед. наук: 13.00.01 / Г. В. Терехова. – Челябинск, 2002.
69. Толмачев, А. А. Диагноз ТРИЗ [Текст] / А. А. Толмачев. – СПб.: КОСТА, 2004. – 496 с.
70. Толмачев, А. А. Об одном из подходов к обучению ТРИЗ [Текст] / А. А. Толмачев. // Журнал ТРИЗ. – 1996. – №1 (11). – С. 93-94.
71. Три поколения ТРИЗ [Текст] // Материалы конференции 20 октября 2007 г. – СПб: ТРИЗ-Петербург, 2007. – 112 с.
72. Тучнин, Н. П. Как задать вопрос? О мат. творчестве школьников [Текст]: кн. для учащихся / Н. П. Тучин. – М.: Просвещение, 1993. – 192 с.
73. Утёмов, В. В. О некоторых аспектах реализации идей самообразовательного пространства / В. В. Утёмов // Проблемы повышения качества и эффективности профессионального образования. Материалы Международной научно-практической конференции. IX Сибирская школа молодого ученого. 23-25 октября 2007 г. Под общ. Ред. В. А. Дмитриенко. – Томск: STT, 2007. – С. 86-87.
74. Утёмов, В. В. О некоторых интегративных подходах в обучении школьников / В. В. Утёмов // Наука. Университет. 2008. Материалы восьмой международной научной конференции преподавателей, аспирантов и студентов. 28-29 февраля 2008 г. АНО ВПО «НСИ», Новосибирск, 2008. – С.
75. Утёмов, В. В. Об опыте использования принципов ТРИЗ-педагогики в обучении школьников математике /В. В. Утёмов // Образование и межнациональные отношения: теория и социальная практика. Материалы Международной научно-практической конференции. 14-16 ноября 2007 г. Под ред. А. А. Баранова, Э. Р. Хакимова, Я. С. Сунцовой. ГОУ ВПО «УдГУ». – Ижевск, 2007. – С. 458-460.
76. Учителям о ТРИЗ. Выпуск 2 [Текст]: сборник методических материалов по преподаванию ТРИЗ в начальной школе. – Спб.: Атос, 1997. – 180 с.
77. Учителям о ТРИЗ. Выпуск 4 [Текст]: сборник методических материалов по преподаванию ТРИЗ. – Спб.: Союз писателей Санкт Петербурга, 2001. – 200 с.
78. Учителям о ТРИЗ. Выпуск 5 [Текст]: сборник методических материалов по преподаванию ТРИЗ. – Спб.: Союз писателей Санкт Петербурга, 2004. – 240 с.
79. Фищенко, Н. В. Факультативный курс по системе развивающего обучения «Союз математики и ТРИЗ в начальной школе» [Электронный ресурс] / Н. В. Фищенко. – [Режим доступа: http://www.trizland.ru].
80. Халифаева, О. А. Психологические условия развития креативности подростков в учебно-воспитательном процессе [Текст]: автореф. дис. канд. псих. наук / О. А. Халифаева. – Астрахань, ГОУ ВПО АГУ, 2007 – 18 с.
81. Хинчин, А. Я. О воспитательном эффекте уроков математики [Текст] / А. Я. Хинчин // Повышение эффективности обучения математике в школе; сост. Г. Д. Глейзер. – М.: Просвещение, 1989. – С. 18-37.
82. Хуторской, А. В. Развитие одаренности школьников. Методика продуктивного обучения [Текст] / А. В. Хуторской. – М.: ВЛАДОС, 2000. – 320 с.
83. Ширяева, В. А. Развитие системно-логического мышления учащихся в процессе изучения теории решения изобретательских задач (ТРИЗ) [Текст]: автореф. дис. канд. пед. наук / В. А. Ширяева. – Саратов: СГУ им. Н. Г. Чернышевского, 2000. – 18 с.
84. Шрагина, Л. И. Логика воображения [Текст] / Л. И. Шрагина. – Одесса: Черноморье, 1995. – 111 с.
85. Шумилин, А. Т. Проблемы теории творчества [Текст] / А. Т. Шумилин. – М.: Высшая школа, 1989. – 143 с.
86. Шустерман, З. Г. Новые приключения Колобка, или Наука думать для больших и маленьких [Текст] / З. Г. Шустерман. – М.: Педагогика–Пресс, 1993. – 256 с.
87. Электронная книга «Введение в ТРИЗ. Основные понятия и подходы». Официальное издание Фонда Г. С. Альтшуллера, версия 3.0. [Электронный ресурс]. [Режим доступа http://www.altshuller.ru/e-books/download/triz1.zip].
88. Якиманская, И. С. Личностно-ориентированное обучение в современной школе [Текст] / И. С. Якиманская. – М: Просвещение, 1996. – 286 с.
Приложение 1
Тренинг креативного мышления
Занятие № 1. Метод проб и ошибок
Цель занятия:
познакомить учащихся с понятием креативности и методом проб и ошибок.
1.
Вводное тестирование экспериментальной группы.
2.
Беседа с учащимися.
Занятия, которые у нас с вами сегодня начинаются, называются «Тренинг креативного мышления». Каждый день мы слышим либо по телевизору, либо в школе, либо на улице слово креативность. Нам говорят вот это креативно, а вот это нет. Вот это креативный подход, а вот этот обычный. Так что же такое креативность? Как вы считаете, что скрывается под словом тренинг креативного мышления?
Да, каждый из вас абсолютно в чем-то прав, под креативность мы будем понимать способность человека к творчеству, способность создавать, что-то оригинальное, казалось бы, из стандартной ситуации.
Нам с вами приходится ежедневно решать очень много всевозможных, разнообразных проблем. Задачи бывают не только, как наверно зачастую вы считаете, математические, но и жизненные (бытовые, семейные, политические).
Каждый день современному человеку приходится преодолевать всевозможные трудности, и при том, как более эффективно. А знать решение всех проблем, которые с нами могут приключится невозможно.
Давайте попробуем посчитать хотя бы сколько математических задач мы с вами решаем во время обучения в школе. Итак, допустим, что на уроке вы решаете 5 задач, а дома еще 3. На каждом году обучения в школе вы посещаете около 200 уроков математики, тогда получаем, что в год мы решаем около 1600 задач. За первые 8 лет обучения в школе мы с вами решим 12 800 задач. Отбросим 800, имея ввиду праздники или случаи когда вам не удалось решить задачи, получим 12 000. Можно даже вычесть еще 2 000 которые решили не самостоятельно. Итак, получаем что вы решили 10 000 задач, т.е вы умеете решать около 10 000 задач.
Казалось бы, вон как много, зачем нам уметь решать какие то другие задачи и этого хватит. А нет. Ученые посчитали, что за свою жизнь человек решает порядка миллиона проблемных ситуаций. Так что, скажите вы, теперь что бы комфортно жить в будущем нам в школе придется научиться все их решать, так на это уйдет как раз вся жизнь даже больше.
На самом деле как хорошо бы их уметь решать с помощью одного алгоритма или универсального механизма. Загрузил все данные нашей проблемы, и она выдает нам сразу решение. Такого алгоритма, конечно же, нет. А вот приемы и методы, которые нам зачастую помогают придти к решению какой-либо проблемы, есть. И наша задача научится ими пользоваться в рамках нашего тренинга.
3.
Прикладное упражнение.
Упражнение 1.
Сейчас на парту будет выдано изображение чего-либо попробуйте в парах придумать название этой картинке, как можно точнее отражающее сюжет картинки. Потом мы с вами посмотрим, у какого наиболее оригинально получится. (Плавно подводит к переборному методу при придумывании названии картинки). (Пример фото «Микромир»)

4.
Метод проб и ошибок.
Зачастую когда мы с вами решаем, какую либо задачу, мы выбираем самый легкий способ решения, просто перебираем все возможные варианты. Из всех вариантов оставляем только те, которые нам подходят. Такой метод решения, задач, когда происходит перебор всех вариантов решения, носит название – метод проб и ошибок. От начальных условий задачи мы двигаемся в «всевозможные» стороны, своеобразно пытаясь найди решение, и лишь часть из направлений поиска оказываются успешными.

5.
Упражнения математического характера.
Упражнение 2.
В каком случае произведение двух натуральных чисел дает четное число.
Решение.
Рассмотрим произведение двух натуральных чисел 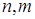 , и если учесть то, что , и если учесть то, что 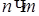 должно равняться четному числу, то должно равняться четному числу, то 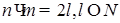 . Значит достаточно рассмотреть три случая, когда числа оба четные, оба нечетные и одно четное второе нет. Тогда ответом будет любая пара натуральных чисел одно, из которых четное. . Значит достаточно рассмотреть три случая, когда числа оба четные, оба нечетные и одно четное второе нет. Тогда ответом будет любая пара натуральных чисел одно, из которых четное.
Упражнение 3.
Сумма каких двух натуральных чисел равна их произведению?
Упражнение 4.
Сумма каких двух натуральных чисел больше чем их произведение?
Упражнение 5.
Могут ли числа 458, 523, 652 быт квадратами или кубами целого числа?
6.
Подведение итогов.
Занятие № 2. Идеальный конечный результат
Цель занятия:
познакомить учащихся с принципом идеального конечного результата как инструмента для продуктивного решения задачи.
1.
Повторение. Метод проб и ошибок.
Представьте, что девочка Света собралась на дискотеку и думает, что ей одеть. Начинает подбирать себе платье. Первое – не то, второе –не то, третье, четвертое…шестое – вот это то. И в итоге нашла себе платье. Все хорошо, она просто взяла и стала перебирать все возможные варианты, все имеющиеся у нее платья и в итоге «натолкнулась» на нужное.
Такой метод, когда перед нами стоит проблема, мы называли на прошлом занятии Метод проб и ошибок. А теперь представьте, что у Светы не 10 платьев, а 100 или даже 1000 или и того больше. То тогда сколь ей понадобиться время, что бы найди нужное платье. Час, два, неделю, а потом и дискотека закончится. Точно также при решении каких-либо задач очень не эффективно бывает перебирать все варианты, на это может, уйди уйма времени.
Так, например, решая какое-либо уравнение нам легче его именно «решать», а не перебирать все варианты.
Поэтому наверно нам нужны какие-то способы, которые более эффективно решают поставленные перед нами задачи. Один из них мы сегодня разберем.
2.
Что такое ИКР?
– Приходилось ли вам когда-либо стрелять из спортивного лука? Смогли ли вы с первого раза попасть в мишень на расстоянии 50 метров?
– Наверно нет. Вряд ли.
– Не уверены? Да, для этого надо тренироваться. Предположим, что вы хорошо натренированы. Тогда смоги ли бы попасть в мишень?
– Да, несомненно.
– А если предположить, что вам завязали глаза? Вы бы смогли попасть?
– Нет. Мы же не видим цели!
– Но ведь цель перед вами. А если вас еще покрутить вокруг себя перед выстрелом? Вы будете стрелять наугад. И каковы будут ваши шансы попасть?
– Да кто же так стреляет, непонятно в какую сторону, да притом не видя цели.
– А как же тогда можно решить задачу, если решать ее, не видя цели?
Принцип идеально конечно результата (ИКР) – ожидаемый конечный результат осуществляется в идеальных условиях, то есть требуемая функция системы выполняется при отсутствии ее самой. При этом под системой понимается любая совокупность рассматриваемых взаимосвязанных компонентов.
Школьные задачки для возможности самоконтроля часта, снабжены ответами на решение задачи. И многие ученики не удерживаются от соблазна сначала посмотреть правильный ответ, а потом решать задачу, получив своеобразный мысленный ориентир. Одним из таких ориентиров при решении проблем, и не только математических, служит ИКР.
3.
Разбор прикладных упражнений.
Ситуация 1.
Приехал школьник - житель Севера на каникулы к дедушке. Пригласил его дед охотиться на медведя. Не хотел школьник показаться трусом. Согласился. Пошли они. Нашли берлогу. Разбудили медведя. Выскочил медведь из берлоги, бросился на них. Они - бежать. Бежит школьник и думает: «У меня же ружье. И я - не трус». Разворачивается и стреляет в медведя. Подходит тут к нему старый охотник и говорит: «Однако, плохой ты охотник. Зачем стрелял? Теперь бери его и тащи. Добежал бы до дома - там бы и убили».
Данный пример заслуживает более детального разбора. Все дело в различном понимании главной функции. Для старого охотника главная функция - доставить добычу в дом. Для школьника - проявить свою храбрость на охоте. И по всей вероятности, старый охотник уже умел применять наш принцип, поскольку очень четко формулирует идеальный способ доставки добычи в дом - добыча САМА себя доставляет.
В природе также встречаются аналогичные примеры идеальности.
Ситуация 2. Рыбка-антенна.
Обитающая в морских глубинах, обычно лежит на дне и приманивает кусочком мясистой кожице, которая болтается на кончике шипа, выступающего из верхней челюсти хищницы. Прежде чем наивная жертва осознает ошибку, она уже окажется в желудке охотницы.
Ситуация 3. Растение росянка.
Это небольшое растение можно найти на торфяных болотах. Его листья, собранные в розетку, покрыты красноватыми ловчими волосками-щупальцами с красной головкой наверху. Она выделяет липкую жидкость и поэтому покрыта росой. В центре листа волоски короткие, по краям - более длинные. Мухи, муравьи, привлеченные блеском капелек, попадают на лист и прилипают к нему. Жертва мечется, бьется и при этом задевает соседние волоски, сама себя все более запутывая. Край листа начинает медленно загибаться и накрывает свою добычу, которая здесь же и переваривается.
Ситуация 4. Волшебная лампа Лавегрова.
Вам потребуется очень много времени, чтобы найти выключатель у настольной лампы Адапсоп, созданной дизайнером Россом Лавегровом. Его просто нет. Чувствительный к прикосновению алюминиевый ободок плафона соединен с реостатом внутри - лампы, что позволяет одним движением руки не только включать или выключать свет, но и менять его интенсивность от совсем приглушенного до максимально яркого.
Но все же это не совсем идеальный способ включения. А что если бы лампа сама себя включала в нужный момент?
Идеальный выключатель - выключателя нет, а его функция выполняется. Специальный датчик сам включает ночник при наступлении темноты, Когда темнеет, а света нет, лампочка сама зажигается, а когда встает солнце - гаснет.
Ситуация 5. Плеер без плеера.
Плеер от компании Evoltion Technologies имеет такой размер, что он просто помещается в ухо, по форме он похож на простой наушник.
Вернемся к девочке Свете, которая собирается на дискотеку, для более быстро выбора ей достаточно вспомнить, что она собирается именно на дискотеку, тогда например спортивные варианты одежды уже сразу не подойдут и не стоит тратить на них время.
Упражнение 1. Дорожные знаки.
Ночью дорожные знаки не видны, поскольку не освещаются. Только при достаточном близком приближении к ним, когда они освещены светом фар, можно разглядеть знак.
Противоречие
. Знаки должны быть освещены, что бы их было видно, и не должны быть освещены, поскольку неэкономно расходовать электроэнергию на их постоянное освещение.
ИКР
. Когда знаки сами себя освещают в нужный момент при приближении автомобиля.
Решение
. Дорожные знаки покрыты специальным люминофорной краской, которая начинает светиться при освещении ее даже слабым светом. Такие знаки видно издалека.
Упражнение 2. ИКР вокруг вас.
Попробуйте привести свои примеры из живой природы или окружающей вас техники.
4.
Математические упражнения.
Упражнение 3.
Сумма, каких двух натуральных чисел равна их произведению.
ИКР:
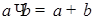 . .
Решение
: 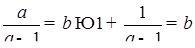 , а значит , а значит 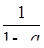 целое. Но это число может быть целым только при целое. Но это число может быть целым только при 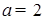 . Ответ: . Ответ: 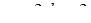 . .
Упражнение 4.
Сумма, каких двух натуральных чисел больше чем их произведение.
ИКР:
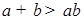 . .
Решение
: 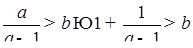 . Т.к. . Т.к. 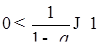  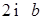 . .
Тогда если 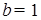 тогда тогда 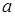 любое ( любое (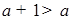 ). ).
Если 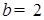 тогда тогда 
Ответ
: Только в том случаи, если одно из чисел есть 1.
Упражнение 5.
По разные стороны от прямого шоссе расположены две деревни. В каком месте на шоссе нужно построить автобусную остановку, чтобы расстояние от каждой деревни до нее было одинаковым? Шириной шоссе пренебречь.
ИКР.
Для решения воспользуемся принципом ИКР: соединим отрезком k
(дорога) две точки A
и B
(две деревни). Если середина M
в точности попадает на дорогу (l
), то задача решена (рис. 1).
Решение.
Рассмотрение случая, когда центр отрезка k
не лежит на прямой l,
подталкивает на мысль, что двигая прямую k
, точка М
помогает легко найти требуемую точку С,
восстановив к ней перпендикуляр и рассмотрев равнобедренные треугольники 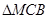 и и 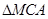 (рис. 2). (рис. 2).
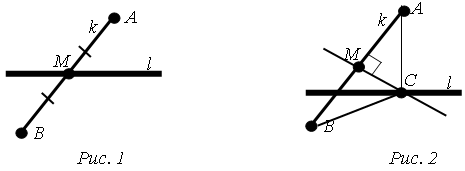
Конечно, стоит сделать вывод о том, что задача не будет иметь решения, если отрезок k
будет перпендикуляром к прямой l
.
Упражнение 6.
Задачи для самостоятельно решения.
1. А где нужно строить автобусную остановку, если деревни расположены по одну сторону от шоссе?
2. Какое натуральное число больше его единиц в семь раз?
3. Какую последнею цифру может иметь квадрат натурального числа?
4. Какую последнею цифру может иметь куб натурального числа?
5. Найдите число, одна треть с одной четвертью которого составляет 21
6. Полтрети – число 100. Что это за число?
7. Докажите, что если произведение 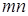 нечетно, то и число m
нечетно, и число n
нечетно. нечетно, то и число m
нечетно, и число n
нечетно.
8. Докажите, что всякое нечетное число, не равное единице, есть разность квадратов двух каких-то чисел.
9. В комнате находятся 5 человек. Докажите, что найдутся 2 человека, сделавшие одинаковое число рукопожатий.
10. Сколько существует четырехзначных чисел с суммой цифр 34?
11. Петя решал пример 47+48+49+…+58 и у него получился ответ 1266. Покажите, что Петя где-то ошибся.
12. Сколько чисел от 1 до 100 ни делится, ни на 2, ни на 3?
5.
Подведение итогов. Домашнее задание.

Занятие № 3. Метод Мозгового Штурма (ММШ)
Цель занятия:
познакомить учащихся с ММШ как инструментом для активизации мышления.
1.
Повторение: ИКР.
 Игра «Муха».
Рисуется таблица размером Игра «Муха».
Рисуется таблица размером 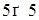 на доске. Учащимся говорится, что в точке М
находится муха, которая умеет передвигаться по шагам (вверх, вниз, влево, вправо). Задача ребят внимательно мысленно следить за движением «мухи», движение которой задает учитель. на доске. Учащимся говорится, что в точке М
находится муха, которая умеет передвигаться по шагам (вверх, вниз, влево, вправо). Задача ребят внимательно мысленно следить за движением «мухи», движение которой задает учитель.
Затем предлагается муху поместить в таблицу большим размером. И попробовать поиграть снова.
А теперь давай посмотрим на эту игру немножко с другой стороны. Нам были даны начальные условия (муха находится в точке М,
перемещается по шагам) и поставлена задача (определить, где будет находиться «муха» после команд, которые будут зачитываться). Для решения этой проблемы достаточно было мысленно перемещать после каждой команды «муху», в итоге после последней команды мы получали ответ на поставленную задачу. Т.е. у нас были начальные условия, от которых мы двигались к требуемому результату, который на прошлом занятии мы формулировали как ИКР, а он в свою очередь способствовал решению наших задач.
А если поставлена какая-нибудь проблема и нам ей требуется решить. Дамы знаем начальные условия, да мы можем сформулировать ИКР, но как приблизится к решению, здесь нам не кто не говорит, куда надо двигаться, а хотелось бы.
Один из таких методов, который помогает приблизиться к решению задачи, мы сегодня разберем. Метод мозгового штурма, метод коллективного придумывания идей, который активно использовался во второй половине 20 века на многих крупных зарубежных компаний: Samsung, LG, General Motors и многие другие.
2.
Что такое МШ?
Никому не пожелаешь побывать в переделке типа той, в которую попал американец Алекс Осборн. Представьте себе: вторая мировая война, в открытом океане караван грузовых судов. И так уж случилось, что в какой-то момент они остались без охраны. И вдруг радиотелеграмма: будьте внимательны - в вашем районе действует немецкая подводная лодка. Алекс - он был капитаном одного из этих кораблей - живо себе представил: вот показывается перископ подлодки, а вот и торпеда, оставляя за собой мелкие буруны, мчится прямо в борт. Что делать? Задача, казалось бы, неразрешимая.
И тогда капитан вспомнил практику, к которой в затруднительных положениях прибегали еще средневековые пираты. Выстроилась на палубе вся команда, и все, начиная с младших матросов, отвечали только на один вопрос: как спастись в ситуации торпедной атаки? Можно говорить все, что только придет в голову! - а вдруг чья-то «дикая» идея послужит ключиком к решению проблемы... Например, повар подал такую идею: давайте все выбежим на борт и одновременно подуем на торпеду. Глядишь, и сдуем ее с курса - мимо пройдет...
Им повезло. Подлодка не появилась. Но после войны Осборн вспомнил этот случай и однажды в компании друзей решил проанализировать ситуацию. Вспомнил и предложение повара. И спокойный анализ показал, что абсурдная идея кока привела к настоящему решению! Конечно, «мощным дувом» торпеду не повернешь, как щеки ни напрягай. Но зато ее можно немного притормозить и сбить с курса струей корабельной помпы, которая есть на каждом судне. Конечно, успех не гарантирован - но когда на карту поставлена жизнь, стоит попытаться...
Почему бы не использовать такой способ поиска новых идей в мирной жизни? В 1953 году бывший капитан Алекс Осборн выпускает книгу «Управляемое воображение». С нее-то и началась популяризация мозгового штурма в Америке, а затем и в других странах.
Наверное, вы замечали за собой, когда у вас появляется какая-нибудь, по вашему мнению, хорошая идея решения и в этот момент кто-нибудь начнет критиковать вас, то вы мгновенно «скисаете», резко снижается желание придумывать решение дальше.
С другой стороны, ряд людей не доверяют и собственным идеям. Самокритика – нормальное и здоровое свойство личности, но порой именинно она закрывает дорогу дальнейшей творческой деятельности.
Пример:
о том, что звук можно искусственно передавать на расстоянии (телефон), физики задумывались еще в 60-х годах XIX века. Над проблемой работал англичанин Чарльз Уитстоун и немец Йоханн Рейс, а американский ученый впоследствии со слезами на глазах говорил, что идея множество раз приходила ему в голову, но он множество раз откидывал её как нелепую.
Учитывая все замечания, предлагается разбить весь процесс принятие решений на стадии.
3.
Правила проведения «мозгового штурма».
Обычно штурм проводится в группах численностью 7-9 учащихся.
Группу перед штурмом инструктируют. Основное правило на первом этапе штурма - НИКАКОЙ КРИТИКИ!
Первый этап. СОЗДАНИЕ БАНКА ИДЕЙ
Главная цель - наработать как можно больше возможных решений. В том числе тех, которые на первый взгляд кажутся «дикими». Иногда имеет смысл прервать этап раньше, если идеи явно иссякли и ведущий не может исправить положение.
Второй этап. АНАЛИЗ ИДЕЙ
Все высказанные идеи группа рассматривает критически. При этом придерживается основного правила: в каждой идее желательно найти что-то полезное, рациональное зерно, возможность усовершенствовать эту идею или хотя бы применить в других условиях.
Третий этап. ОБРАБОТКА РЕЗУЛЬТАТОВ
Группа отбирает от 2 до 5 самых интересных решений и выбирает спикера, который рассказывает о них классу и учителю. (Возможны варианты: например, группа отбирает самое практичное предложение и самое «дикое».) В некоторых случаях целью группы является найти как можно больше решений, и тогда спикер может огласить все идеи.
4.
Прикладные упражнения
Упражнение 1.
Несколько лет мировая пресса писала о загадочных кругах, которые таинственно возникали на пшеничных полях графства Уилтшир в Англии. В пределах такого круга стебли злаков почему-то согнуты и уложены на землю по часовой стрелке. Причем если сначала появились просто круги, то потом они стали переплетаться, составляя замысловатые фигуры. Предложите гипотезы, объясняющие это явление. Какие из гипотез кажутся вам наиболее правдивыми?
Решение.
Список предполагаемых идей: неравномерности в строении почвы; неравномерное распределение удобрений; в почву попал яд; болезнь растений в результате заражения микроорганизмами; стаи птиц высаживаются кольцами; какие-то животные, например олени, вытаптывают посевы в брачных играх; особые метеорологические явления типа мини-торнадо или шаровых молний; шуточки студентов; сами крестьяне потихоньку вытаптывают круги для привлечения зевак, с которых можно брать деньги, и др.
Упражнение 2.
Сейчас попробуйте самостоятельно по парам придумать идеи решения задачи. Для этого выберите, кто из вас будет фиксировать все идеи на бумаге. И так, после того как, я озвучу задачу, у вас будет 5 минут, что бы в паре придумать идеи решения, один из вас, их все должен записывать, после того как я скажу второй этап, вы приступаете к реализации второго этапа ММШ, т.е. анализ идей, пытаетесь в каждой идее найти рационально зерно, развить её в итоге оставить две, три наиболее подходящих идеи решения.
Предложите способ проверки (не экзамен, не контрольная работа, не опрос) и оценивание знаний (без отметок) учеников вашей школы.
5.
Математические упражнения.
Упражнение 3.
Предложите способы определения высоты высотного здания простыми средствами, то есть без сложных приборов. (Подобные треугольники).
Решение.
Рассмотрим две возможных варианта решения.
Первый (рис. 1) случай, когда человек AB
стоит и смотрит на здание ED.
Измерив, расстояние AD
, зная свою высоту AB,
а также измерив, расстояние AO
(вычислив 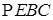 , соответственно найдя , соответственно найдя 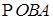 ) рассматривая подобные треугольники ) рассматривая подобные треугольники 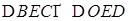 находим искомое. находим искомое.
Второй (рис. 2) случай, когда человек смотрит из точки О
, а AB
любой предмет, высоту которого мы можем измерить (например: палка). Тогда из подобия этих же треугольников мы с легкостью находим искомое.

Упражнение 4.
Задумайте натуральное число от 22 до 77. Прибавьте к нему 81. Вычеркните первую цифру вашего числа. Прибавьте 4. Скажите, что получилось. Ответ: 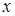 +15. +15.
Упражнение 5.
Известно, что 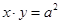 . Найди наименьшую сумму . Найди наименьшую сумму 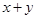 . .
Решение.
- Пусть 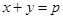 , рассмотрим , рассмотрим 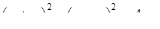 , то , то  , ,  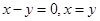
- Тогда 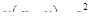 , т.е. , т.е. 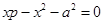 , или , или 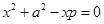 : :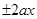 , получаем , получаем  , последнее равенство возможно , последнее равенство возможно 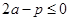 , т.е. очевидно наименьшее значение равно , т.е. очевидно наименьшее значение равно 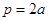
- Увеличим одно число на 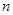 , а другое увеличится соответственно на , а другое увеличится соответственно на 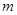 , тогда , тогда  , производя вычисления получим , производя вычисления получим 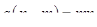  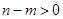 , тогда , тогда 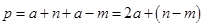 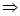 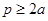 . Наименьше значение очевидно. . Наименьше значение очевидно.
- 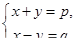 решая систему получим решая систему получим 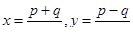 . . 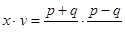 , отсюда , отсюда  и и 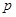 будет наименьшим , когда будет наименьшим , когда 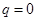 . .
- Установить в каком случае 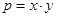 , будет наибольшей. Как должны соотноситься числа , будет наибольшей. Как должны соотноситься числа 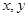 . .
- Найди числа 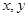 , если , если 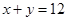 , а , а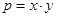 наибольшее. наибольшее.
- Найди наименьше значение суммы 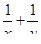 , если , если 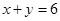 и и 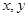 положительные числа. Достаточно рассмотреть положительные числа. Достаточно рассмотреть 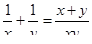 . .
6.
Подведение итогов. Домашнее задание.
Памятки участникам ММШ
Памятка генератору идей:
· Ты участвуешь в коллективном поиске, поэтому всячески поддерживай своих товарищей
· Теоретически не существует не разрешимых проблем
· Ваша общая цель: выдвижение как можно большего числа идей. Чем больше идей, тем больше шансов на решение задачи.
· Категорически запрещена прямая и косвенная критика выдвигаемых идей, и их промежуточная оценка.
· Любая высказанная идея полезна не Толька сама по себе, она является катализатором процесса «генерации».
· Чем необычней, невероятней, неожиданней идея, тем вероятнее успех. Поэтому не бойся выдвигать фантастические, нелепые, абсурдные, сомнительные идеи.
· Для твоей фантазии не существует каких-либо ограничений, рамок, условий
· Относись к каждой высказанной идее доброжелательно, поддержи, постарайся развить ее.
Памятка аналитику.
Исходя из того, что идея-это та, которая анализируется в данный момент. Помни:
· Каждая из идей содержит рациональное зерно. Найди его, попытайся развить данный принцип.
· Оценивая идею, помни о специфике проблемы
· Попытайтесь скомбинировать несколько идей для постарения нового принципа, который может быть реализован.
Занятие № 4. Обратный мозговой штурм (ОМШ)
Цель занятия:
познакомить учащихся с ОМШ как инструментом для активизации мышления.
1.
Разбор творческого задания № 2 «Друдлы».
2.
Работа с друдлами изображенными на доске.

Когда дома самостоятельно или сейчас в классе вы пытались найти, что же скрывает тот или иной друдл сначала, большинство из вас, генерировали идею, а потом анализировали её (критиковали). Этот прием, напоминает коллективный метод активизации мышления - «мозговой штурм», когда весь процесс делится на стадии: генерирования идей, критики, анализ. Мы с ним познакомились на предыдущем занятии.
3.
Что такое ОМШ?
Процесс решение задачи методом мозгового штурма разбивается, по сути, на две стадии на первой мы генерируем идеи, на втором критикуем. А что будет, если мы поступим на оборот, т.е. сначала по критикуем условие либо решение задачи, только потом будем генерировать. Такой метод называется обратный мозговой штурм.
Упражнение «Мерчандайзер».
Есть такая работа – Мерчандайзер, слово происходит от английского merchandise – товары. Эти работники отвечают за размещение товаров в торговом пространстве. Иногда они работают в крупных супермаркетах, но чаще им приходится обслуживать сразу несколько торговых точек. Представьте себе, что вы мерчандайзер. Вам нужно за один день успеть обойти 8 торговых точек. Транспорта между ними нет, приходится ходить пешком. Попробуйте спланировать свой маршрут таким образом, что бы посетив все торговые точки, в общей сложности пройди наименьшее расстояние.
Работа ведется по партам, та пара, чей путь окажется короче – победят.
4.
Прикладные задания.
Упражнение 1.
Предложено затыкать пробоину в борту судна эластичной оболочкой. Оболочку раздувают, и течь останавливается. Найдите недостатки такого метода.
5.
Математические задания.
Упражнение 2.
Решение задачи совместно методом ОМШ (в начале идет этап критика, а потом генерирование идей): «…И сказал Кощей Ивану Царевичу: Жить тебе до завтрашнего дня. Утром явишься перед до мной, задумаю я 3 цифры - 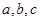 , назовешь ты мне 3 числа , назовешь ты мне 3 числа  . Выслушаю я тебя и скажу, чему равна сумма . Выслушаю я тебя и скажу, чему равна сумма 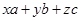 . Тогда отгадай, какие цифры . Тогда отгадай, какие цифры 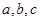 я задумал, иначе – голова с плеч. Опечалил Иван царевич, пошел думать думу. Надо ему помочь. я задумал, иначе – голова с плеч. Опечалил Иван царевич, пошел думать думу. Надо ему помочь.
Явные трудности:
- Уравнение с тремя неизвестными решать не умеем. Изменим условие задачи пусть 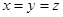 , тогда , тогда 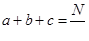 . Тогда если . Тогда если 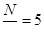 , то 5=2+3+0, 5=1+2+2, 5=1+1+3, 5=5+0+0…. , то 5=2+3+0, 5=1+2+2, 5=1+1+3, 5=5+0+0….
- Даже маленькие числа могут быть представлены в виде суммы трех слагаемых не единственным образом. Попробую получить уравнение с 2 неизвестными при 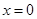 . Тогда . Тогда 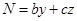 , отсюда , отсюда 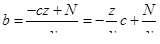 . Увы! . Увы!
- Уравнение с 2 неизвестными имеет бесконечно много решений.
Цифры! Тогда 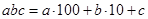 . .
Упражнение 3.
Привели нового заключенного в тюрьму и сказали, что в комнате в которую будут водить всех без исключения заключенных есть лампа (первоначально она выключена). Её можно включить или выключить. Вводить будут в неизвестном порядке и по несколько раз. Так вот если он точно скажет, сколько заключенных сидит в тюрьме, причем все заключенные сидеть в одиночных камерах, то его отпустят иначе всех убьют. И отпустили его на общее собрание заключенных, что бы он сними о чем-нибудь смог договориться, так что посчитать их не хватит времени. О чем он должен договориться?
6.
Подведение итогов.
Занятие № 5. Морфологический анализ
Цель занятия:
познакомить учащихся с МА и морфологическим ящиком как инструментом для продуктивного перебора возможных вариантов.
1.
Игра «Что за число?»
Придумать в парах, список вопрос на которые можно отвечать только да или нет. Так что бы можно было точно определить число, задуманное вашим другом от 1 до 1024. Какое наименьшее число вопросов можно придумать.
Решение. Каждый раз, когда мы, с вами получаем ответ на наш вопрос о числе, область, где может находиться число, в лучшем случае должна уменьшаться в два раза, т. е мы должны пополам разбивать область решения. Иначе, если мы задали вопрос, который разбивает область решения не неравные части, то узнав, что число находится в большой части, мы получили бы в итоге не эффективное уменьшение области решения. Тогда достаточно задавать вопрос: «больше ли загаданное число середины области решения» (на каждом шаге, область решения уменьшается в два раза).
Например: Загадано число 2.
| Список вопросов:
|
Ответ
|
Область решения
|
| Больше 512
|
Нет
|
(0,512]
|
| Больше 256
|
Нет
|
(0,256]
|
| Больше 128
|
Нет
|
(0,128]
|
| Больше 64
|
Нет
|
(0,64]
|
| Больше 32
|
Нет
|
(0,32]
|
| Больше 16
|
Нет
|
(0,16]
|
| Больше 8
|
Нет
|
(0,8]
|
| Больше 4
|
Нет
|
(0,4]
|
| Больше 2
|
Нет
|
(0,2]
|
| Это число 1
|
Нет
|
2
|
Ответ: 2.
Сможет ли кто-нибудь из вас сказать, как вы мыслили при решении данной задачи? Скорее вы думали так: «Раз мы должны найди число, тогда подойдут только те вопросы, после ответа которых, область предполагаемых решений будет уменьшаться…». Таким образом, сначала мы анализировали условия и возможные варианты решения, только после этого, выдвигали идеи решения. Этот прием коллективного мышления, схож с методом обратного мозгового штурма, который мы узнали на последнем занятии.
Сегодня мы с вами познакомимся еще с одним методом активизации мышления «Морфологический анализ».
2.
Что такое «Морфологический анализ»?
При переборе вариантов наугад значительная часть вариантов обычно пропускается. Метод МА позволяет осуществить поиск новых идеи путем систематического перебора возможных вариантов. Метод заключается в следующем:
- Выбирается объект изменения (процесс, явление)
- Для него выбираются основные характеристики
- Для каждой характеристики выбираются все его возможные значения
- Полученные данные заносятся в таблицу, в которой ось основных осей играют выбранные характеристики
- Составляются различные комбинации выделенных значений параметров и проводятся исследование каждой комбинации, как возможное решение проблемы.
Такая таблица называется морфологическим ящиком.
3.
Прикладные упражнения.
Упражнение 1.
Построение морфологического ящика для объектов: парта, гвоздь, холодильник.
Пример составления морфологического ящика. Объект – автомобиль.
Список характеристик: двигатель, движитель, кабина, горючее, управление, дорога.
Двигатель. Внутреннего сгорания, реактивный, электрический, атомный, плазменный.
Движитель. Колесо, гусеницы, винт, ноги.
Кабина (расположение относительно двигателя). Спереди, сзади, сверху, снизу, по бокам, вне объекта.
Горючее. Горение, батарее, электричество.
Управление. Ручное, автоматичное, полуавтоматическое, дистанционное.
Дорога. С твердым покрытием, грунтовая, жидкая, отсутствует.
4.
Математические упражнения.
Упражнение 2.
В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. "Замечательно, что один из нас имеет белые, один черные и один рыжие волосы, но ни у одного из нас нет волос того цвета, на который указывает его фамилия", - заметил черноволосый. "Ты прав", - сказал Белов.
Какой цвет волос у художника?
Составим морфологический ящик для этой задачи.
Морфологический ящик
| Друзья
|
Цвет волос
|
| Белые
|
Рыжие
|
Черные
|
| Белов
|
-
|
+
|
-
|
| Рыжов
|
-
|
-
|
+
|
| Чернов
|
+
|
-
|
-
|
Упражнение 3.
Три гнома Эй, Ай и Ой вышли на прогулку в красной, зеленой и синей рубашках. Туфли на них были таких же цветов. У Эя цвет рубашки и туфель совпадал. У Оя ни туфли, ни рубашка не были красными. Ай был в зеленых туфлях, а в рубашке другого цвета. Как были одеты гномы? Ответ: Эй – красная рубашка и туфли, Ой – в синей рубашке, Ай – в зеленой рубашке и синих туфлях.
Упражнение 4.
В очереди за билетами в кино стоят друзья – Юра, Миша, Володя, Саша и Олег. Известно, что Юра купит билет раньше, чем Миша, но позже Олега; Володя и Олег не стоят рядом, а Саша не находится рядом ни с Олегом, ни с Юрой, ни с Володей. Кто за кем стоит? (Олег–Юра–Володя–Миша–Саша)
Упражнение 5.
Трое учителей: физик, математик и физрук работают в одной сельской школе. Их фамилии: Борисов, Иванов и Семенов. У физика нет любимчиков среди учеников, и он живет дальше всех от школы. На прошлой неделе Семенов поставил любимой ученице Борисова двойку! Известно, что математик добирается до школы дольше, чем Семенов. Назовите фамилии физика, математика и физрука.
Упражнение 6.
Шесть шахматистов под именами А, Б, В, Г, Д, Е сыграли между собой в турнире по одной партии. А сыграл все партии вничью, Б не проиграл ни одной партии, В выиграл у победителя соревнований и сыграл вничью с Д, Г обогнал Д, и не отстал от Е. Сколько очков набрал и какое место занял каждый из шахматистов?
Упражнение 7. Упражнение для самостоятельно решения.
Считается, что А. Эйнштейн придумал эту загадку в прошлом веке, и он полагал, будто 98% жителей Земли будет не в состоянии ее решить.
Задача:
- Есть пять домов, каждый разного цвета.
- В каждом доме живет один человек отличающийся от соседнего по национальности: немец, англичанин, швед, датчанин, норвежец.
- Каждый пьет только один напиток, курит определенную марку сигарет и держит определенное животное.
- Никто из 5 человек не пьет одинаковые с другими напитки, не курит одинаковые сигареты и не держит одинаковое животное.
Подсказки:
- Англичанин живет в красном доме
- Швед держит собаку
- Датчанин пьет чай
- Зеленый дом стоит слева от белого
- Жилец зеленого дома пьет кофе
- Человек, который курит «Pall Mall» держит птицу
- Жилец из среднего дома пьет молоко
- Жилец из желтого дома курит «Dunhill»
- Норвежец живет в первом доме
- Курильщик «Marlboro» живет около, того, кто держит кошку
- Человек, который содержит лошадь, живет около того, кто курит «Dunhill»
- Курильщик сигарет «Winfiedld» пьет пиво
- Норвежец живет около голубого дома
- Немец курит «Rothmans»
- Курильщик «Marlboro» живет по соседству с человеком, который пьет воду.
Вопрос
: Кому принадлежит рыба? (немцу, живущему в зеленом доме)
| №
|
1
|
2
|
3
|
4
|
5
|
| Национальность
|
Норвежец
|
Датчанин
|
Англичанин
|
Немец
|
Швед
|
| Цвет
|
Желтый
|
Голубой
|
Красный
|
Зеленый
|
Белый
|
| Сигареты
|
Dunhill
|
Marlboro
|
Pall Mall
|
Rothmans
|
Winfiedld
|
| Напиток
|
Вода
|
Чай
|
Молоко
|
Кофе
|
Пиво
|
| Животное
|
Кошка
|
Лошадь
|
Птица
|
Рыба
|
Собака
|
5.
Подведение итогов. Домашние задание.

Занятие № 6. Принцип перехода в другое измерение
Цель занятия:
познакомить учащихся с инструментом ТРИЗа принципом перехода в другое измерение как приема разрешения противоречия.
1.
Разбор творческого задания № 4.
2.
Ситуация.
Пришел нанаец к своему другу эскимосу. Видит на полу лежит шкура белого медведя с раздвинутой пастью. Спрашивает эскимоса:
- Ты сколько раз в него стрелял?
- Десять.
- А сколько раз попал?
- Ни одного.
- А от чего же он умер?
- От смеха…
Да, нам бы впору тоже посмеяться. Да только смеются приходиться над собой, ведь если вдуматься, от неэффективности моделей поведения страдаем не только мы с вами, от них страдает все человечество.
Все больше и больше говорят о неэффективности моделях поведения, понимая под этим шаблоны, стереотипы, привычки. Проблема состоит в том, что большинство людей, зачастую находится в плену своих стереотипов. Которые порой мешают адекватно выходить из проблемных ситуаций.
Человек предрасполагается к какому-либо конкретному методу и образу мышления при решении задачи, игнорируя все другие методы, кроме единственной встречающей в самом начале.
Так это же привычка, скажете вы. И будите правы. Очень многое в жизни человек делает по привычке. Встает рано утром, умывается, чистит зубы, обувается, идет на работу. По привычке. Привычка полагает нам, но только в обыденной жизни. А вот «мыслить по привычке» уже не всегда является наилучшим способом действия.
Известный ученый и Филисов древности Аристотель написал в одном из своих трактатов, что у мухи восемь ног. И это не становилось под сомнение почти две тысячи лет, пока кому-то не пришло в голову пересчитать ноги у мухи. Оказалось шесть! И таких пример много, когда «мыслить по привычке» дает отрицательный эффект.
Сегодня мы рассмотрим один из принципов помогающих уходить от мысли по привычке. Принцип перехода в другое измерение.
3.
Что такое «Принцип перехода в другое измерение»?
Принцип перехода в другое измерение
1.а. Если трудно разместить что-то на прямой линии, можно попытаться разместить это на кривой (что-то же: на площади). 1.б. Если при перемещении по прямой линии возникают трудности, можно перемещаться по кривой
2. Если тесно на линии, можно занять площадь
3. Если нахватает площади, можно занять объем
4. Объект можно наклонить или положить на бок
5. Можно использовать обратную сторону плоского предмета
6. Можно использовать свет, падающий на соседнюю плоскость.
4.
Практические упражнения.
Упражнение 1.
Как по пересечённой местности пробежать, если весь путь перегорожен заборами от полуметра до метра высотой ? Бег с прыжками.
Упражнение 2.
А как съехать с горы, если впереди большое дерево? Объехать - это и значит - заменить перемещение по прямой на перемещение по кривой.
Упражнение 3.
Семеро молодых японских семей решили в складчину приобрести участок земли для постройки дома. Но их средств хватило только на площадь, на которой можно разместить одну квартиру. Придётся ли им отказаться от намерения иметь отдельные квартиры? Или есть выход? Выход есть - семиэтажный дом. Можно и заработать. Построить более высокий дом, а лишние квартиры продать.
Упражнение 4.
Однажды Карлсон взял с собой банку с вареньем. Он обычно сначала съедал половину, а когда проголодается ещё половину. На банке нет делений. Как отмерить из этой банки ровно половину с одной попытки? Если ёмкость цилиндрическая, наклонить, так, чтобы верхняя часть донышка оказалась на одной горизонтали с нижней точкой горлышка.
Упражнение 5.
Как изобретатель применил тот же принцип? Задача. При исследовании чистоты воды для полного осаждения мути на дно пробирки требуется несколько часов. Для ускорения этого процесса используют центрифуги или специальные активаторы, например, химическое осаждение, но это требует дорогой и сложной аппаратуры. Изобретатель показал фокус: взял пробирку с жидкостью в руки, отвернулся, недолго поколдовал над ней и показал всем осевшую муть. Что он сделал? Он изменил длину пути частиц, положив пробирку на бок. Подержав её так некоторое время, изобретатель осторожно вернул её в вертикальное положение. При этом осевшая муть сползла на дно.
Упражнение 6.
Эксперт по тиграм Питер Джонсон предложил изобретение, ставшее постоянным спасением для многих жителей Индии. Эксперт знал, что тигр предпочитает нападать на жертву со спины. Какую идею защиты от тигров он предложил? На затылке должно быть лицо, и его там нет и не может быть. Тигр тоже это знает. Предлагается сделать ещё одно лицо - двуликого Януса - маску на затылке.
Упражнение 7.
Свеча стоит перед зеркалом - свет как от двух свечей. В зеркальном зале больше света. Это явление использовал II.П. Кулибин для освещения внутреннего коридора царско-сельского дворца. Он вёл на кухню, в нем не было ни одного окна, и он освещался множеством масляных коптилок, которых шёл нестерпимый чад, из-за копоти ничего не было видно. Половые сталкивались на бегу и повреждали царские угощения. Кулибин осветил коридор с помощью системы зеркал. Свет из боковых освещенных залов проникал и коридор по цепочке отражений в зеркалах.
5.
Математические упражнения.
Упражнение 8.
На листе школьной тетради разместить (построить линию) из 6 спичек.
Упражнение 9.
На листе школьной тетради разместить (построить линию) из 10 спичек.
Упражнение 10.
Провести через четыре точки треугольник.
Упражнение 11.
Провести через три точки четырехугольник.
Упражнение 12.
Серия задач:
· Построить из 3 спичек один треугольник
· Построить из 9 спичек 4 треугольника
· Построить из 9 спичек 5 треугольника. Один большой и 4 маленьких.
· Построить из 12 спичек, 6 треугольников. Шестиугольник.
· Построить из 11 спичек, 6 треугольников. Из 3 задания пристроить еще 2 спички, образовав треугольник.
· Составить из 6 спичек, 4 треугольника.
· Составить из 9 спичек, 7 треугольников.
6.
Подведение итогов. Домашнее задание.

Занятие № 7. Отрицание или взгляд со стороны
Цель занятия:
познакомить учащихся с термином отрицание как методом для активизации мышления.
1.
Упражнение «Дома и колодца».
На листе бумаги вам выдана карта деревни «Х
», в деревни 4 дома все они пронумерованы, для каждого дома администрация деревни построили определенный колодец, и разрешали им пользоваться, если дорожки от колодца к дому не будут пересекаться. Необходимо помочь жителям деревни и соединить дома и колодцы так, что бы дорожки не пересекались.
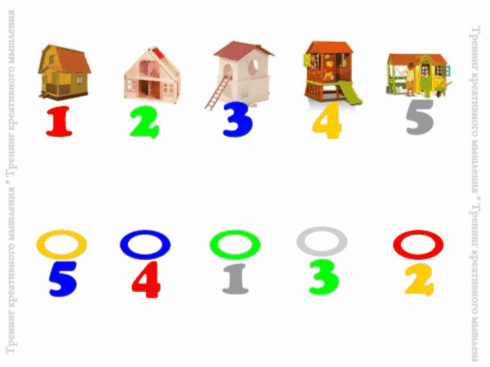
Для решения этой задачи, достаточно было уйди от стереотипов, что любая дорожка прямая, воспользоваться принципом перехода в другое измерение, и изменить прямую траекторию - на криволинейную. Попытки построить дорожки – прямыми, признак стереотипного мышления, и в данной задачи нам не друг. Подобных ситуаций в жизни - бесчисленное множество. И в эффективности их решения и заключается основная проблема. Поэтому рассмотренный нами принцип на предыдущем занятии не стоит откладывать в дальний ящик памяти, а использовать в повседневной жизни.
2.
Что такое «Отрицание»?
История развития велосипеда
Велосипед удивительное изобретение. Это транспортное средство сочетает в себе простоту и эффективность. Популярное выражение «изобретать велосипед» дошло до наших дней в значение изобретать уже изобретенное. На различные конструкции и усовершенствование велосипеда в 19 веке, был выдано несколько десятков патентов, а в некоторых европейских странах почти половина изобретений того времени было связано с велосипедом. Действительно создается впечатление того, что каждый уважающий себя изобретатель того времени считал своим долгом попробовать свои силы в изобретении велосипеда. Но самое интересное, что реальное изобретения велосипеда продолжается до сих пор.
О конструкции с колесами, предназначенные для самостоятельно перемещения их человеком, упоминаются уже в 15 веке. Однако по настоящему велосипед начал совершенствоваться с начала 19 века.
«Быстроного» - именно так окрестил свое изобретение немецкий барон фон Драйвз. Машину, на которой летним утром 1817 года барон в присутствии многих зрителей обогнал почтовую карету, можно назвать прообразом велосипеда. Он напоминает самокат, который состоит из двух деревянных колес, расположенных друг за другом, рамы седла и упора, что бы упираться руками и грудью при движении. При езде нужно было отталкиваться от земли, что бы повернуть обязательно остановиться.
Свое изобретение фон Драйвз решил назвать на латинский манер, соединив два слова «velocie» (быстрый) и «pedis» (нога), так появился на свет «быстроного» или велосипед.
Возникло противоречие между потребностью быстро двигаться и необходимость поворачивать.
Противоречие был разрешено введение новшества – управляемое переднее колесо. Вилка переднего колеса соединялась через шарнир, обеспечивая вращение переднего колеса вокруг вертикальной оси с помощью руля.
В момент соприкосновения ног перед отталкиванием возникало торможение. На долгих подъемах приходилось слезать.
Появилось новое противоречие, скорость самоката зависела от силы отталкивания, а сильное отталкивание приводило к износу обуви.
Пытались даже сделать стальные башмаки, но они были тяжелыми и неудобными. Необходимо было придать самокату свойство, исключающее отталкивание ногами от земли. В 1860 году Пьер Мишо, ремонтируя старый самокат установил на передние колесо две педали, с помощью которых ноги вращали колесо.
Уже через два года такие самокаты стали выпускать серийно под название велосипед.
Теперь скорость движения зависела от скорости вращения педалей. Дальнейшее увеличение скорости достигали увеличением диаметра переднего колеса. Велосипед достигал большую скорость по сравнению со своими предшественниками, стал опасен для окружающих и для самого ездока. Останавливать ногами стало очень проблематично.
Возникло новое противоречие, повышение скорости вело к повышению опасности, из-за отсутствия тормозов.
В следующих велосипедах появилась тормоза.
Новое противоречие было связано с тем, что при езде по неровной поверхности человека сильно трясло.
В России велосипеды нарекли в ту эпоху «костотрясами» - до того было на них мучительно кататься.
Так в велосипеде появились амортизирующая пластина.
При движении на больших скоростях по неровной поверхности, деревянные рамы и вилки часто ломались.
Возникло новое противоречие. Необходимо было достичь прочности рам и вилок. Начали появляться велосипеды, у которых рамы и вилки были стальными.
В 1885 году англичанин Старлей изготовил велосипед с цепным приводом «Ровер».
Летним днем 1887 году 10 летний Джонни, сын ветеринара из Белфаста, шотландца Джона Бойда Денлопа, пришел домой в крайне не довольном состоянии и заявил отцу, что завтра в их школе состоятся велосипедные гонки, и что от езды на велосипеде будут опять болеть кости.
Новое противоречии заключалось придании велосипеду более мягкую езду, а добавление новых элементов вело к увеличению веса конструкции.
После разговора отец Джонни сидел в саду, размышляя как бы помочь сыну. В задумчивости взглянул на старый садовый шланг, валявшийся на земле, затем взял его разрезал по полам наполнил каждую половинку водой, обвязал ободы колес и накрепко подогнал все швы. Джонни выиграл соревнования.
Слава о чудо шланге разлетелась по округе, после чего велосипеды с покрышками наполненные водой стали производить серийно.
Новое противоречие если на ободе тонкий слой резины, то сильно трясет, а при сильных ударах обод деформируется.
Так отцу Джонни пришла новое идея в 1888 году наполнят покрышки не водой, а воздухом.
И велосипед стал уже похож на современный.
До сих пор такое удивительно изобретение как велосипед, претерпевает изменения, совершенствуется.
История развития велосипеда хорошо нам показывает, что появление велосипеда, да и большинство изобретений, не было случайным, а было постепенно решение появившихся проблем, которые мы формулировали как противоречия.
Так почему для решении какой-либо ситуации не попытаться найди противоречие которое заложено в проблеме либо искусственно создать его и разрешить его.
Тема сегодняшнего занятия «Отрицание или взгляд со стороны»
3.
Практические упражнения.
Даже природа использует для своих «изобретений» подобные приемы взгляда со стороны.
Ситуация 1.
Зубы должны быть острые, чтобы ими можно было кусать, и не должны быть острыми, чтобы ими можно было жевать. Разделение противоречивых свойств в пространстве. Передние зубы - острые, задние - тупые, предназначенные для пережевывания пищи.
Ситуация 2.
Шкурка зайца должна быть белой, чтобы он мог легко прятаться зимой, и не должна быть белой, чтобы он мог легко маскироваться летом.
Такой прием на практике называют прием разделения противоречий.
Разделение противоречивых свойств во времени. Зимой - белая шкурка, летом - серая.
Ситуация 3.
Примеры противоречий можно найти и в изобразительном искусстве, и в литературе. Конфликт, его развитие и разрешение обязательно присутствует в драматических произведениях. Герою, как правило, противопоставляется антигерой, добру - зло, любви - ненависть, добрым волшебникам в сказках - злые, темные силы.
Упражнение 1.
«Отдавать не отдавая». Один французский банкир был жаден. Даже после смерти. Умирая, он оставил наследнику большую сумму денег, но в завещании потребовал вложить ему в гроб 20 тысяч фунтов стерлингов. Деньги нужно положить - ведь это записано в завещании, но этого не хочется делать наследнику. Тем более, что из-за такой суммы любители легкой наживы могут и вскрыть могилу. Как быть?
Решение. Наследник вложил покойнику в гроб именной чек на 20 тыс. ф. ст. На чеке крупными буквами было выведено имя и фамилия покойного.
Упражнение 2.
«Видеть не смотря». Давным-давно в Греции жил царь, у которого был сын Персей. Боги предсказали царю, что он погибнет от руки своего сына. Испугался царь и решил избавиться от Персея. Приказал отец юноше принести во дворец голову Медузы-Горгоны. Она была страшным чудовищем. Вместо рук у нее были крылья, вместо ног - лапы со страшными когтями, голова была человеческая, но вместо волос на ней вились ядовитые змеи. Прекрасно было лицо Медузы, но тот, кто смотрел на него, превращался в камень.
Богиня Афина дала Персею сверкающий, как зеркало, щит, который должен был помочь Персею справиться с Медузой. Но каким образом?
Противоречие: Персей должен видеть Медузу-Горгону, чтобы ее убить, и не должен видеть, чтобы не превратиться в камень. Как видеть не смотря?
Решение. Герой решил использовать зеркальный щит, чтобы смотреть на отражение Медузы в нем. Таким образом, Персей видел Медузу-Горгону не смотря на нее.
Упражнение 3.
«Угощать не угощая». Жили-были в лесу журавль и лиса. Пришла раз лиса к журавлю и говорит: «Приходи, сосед, в гости». На следующий день пришел журавль к лисе. Поставила она похлебку на стол. Налила журавлю мелкую миску. Тыкал тот в миску клювом, тыкал - ничего не смог съесть. А за это время лиса всю похлебку и вылакала. Обиделся журавль и решил отомстить лисе. Пригласил он ее к себе в гости.
Пришла лиса в гости. Поставил журавль перед лисой кувшин с узким горлом и говорит: «Угощайся, соседка!». Как ни крутилась лиса - не смогла поесть. А у журавля шея тонкая, длинная, он и из кувшина может достать. Так понемногу все клювом и склевал.
4.
Математические упражнения.
Упражнение 4.
Составьте отрицание к следующим высказываниям.
· Лошади едят овес и сено.
· Число 21 – простое.
· Инопланетяне существуют.
· 2  2. 2.
· Слон это насекомое.
· Жизнь прекрасна!
· x > 0.
· 7 – счастливое число.
· Вы обедали сегодня?
· Все люди негры.
Упражнение 5.
Докажите, что не существует треугольника с углами 40°, 60°, 70°. Доказательство
. Предположим обратное: пусть существует треугольник с такими углами. Тогда сумма углов этого треугольника равна 40°+60°+70°=170°. Но таких треугольников не существует. Получили противоречие!!!
Упражнение 6.
Докажите, что при любом натуральном n
неверно равенство: m
(m
+1)=19991999.
· Можно ли разменять 25 долларов десятью купюрами достоинством в 1, 3, 5 долларов?
· Можно ли в прямоугольной таблице 5*10 так расставить произвольные числа, чтобы сумма чисел любой строки равнялась бы 30, а сумма чисел любого столбца равнялась бы 10?
· а) Можно ли расставить числа в клетках таблицы 7 Ч 7 так, чтобы сумма чисел в каждой строке была бы равна 5, а в каждом столбце была бы равна 4? б) Тот же вопрос для таблицы 5 Ч 6 (5 строк и 6 столбцов). в) Тот же вопрос для таблицы 8 Ч 10.
· Можно ли расставить числа в клетках таблицы 7 Ч 7 так, чтобы сумма чисел в каждой строке была бы равна 5, а в каждом столбце была бы равна 4?
· Тот же вопрос для таблицы 5 Ч 6 (5 строк и 6 столбцов).
· Тот же вопрос для таблицы 8 Ч 10.
5.
Подведение итогов.
Известна история, о том, как к мудрому человеку подошли двое с просьбой рассудить. Мудрец выслушал одного и сказал – ты прав. Выслушал другого, который привел аргументы в защиты противоположной точки зрения, и опять сказал – ты прав. Присутствующий при этом третий возмутился: «Это не правильно - не могут быть правы двое утверждающее противоположное». И ты прав – сказал мудрец.
Когда нам приходится решать какие-либо задачи, мы обязательно сможем ее решить достаточно посмотреть вокруг.
Занятие № 8. Переход в надсистему
Цель занятия:
познакомить учащихся с «принципом перехода в надсистему» как методом для активизации мышления.
1.
Что такое надсистема?
2.
Прикладные упражнения.
При развитии техника исчерпав возможности своего развития, в надсистему (закон перехода в надсистему) в качестве одной из ее частей: при этом дальнейшее ее развитие идет на уровне надсистемы. Переход в надсистему может осуществляться по трем основным путям:
· создание надсистем из однородных (одинаковых) элементов (например, объединение электростанций в единое энергетическое кольцо идр.),
· создание надсистем из конкурирующих (альтернативных) систем (например, парусно-паровые корабли и др.),
· создание надсистем из антагонистических систем (например, кондиционер, как объединение холодильника с нагревателем и т. д.).
3.
Математические упражнения.
Упражнение 1.
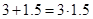 . Найди другие числа удовлетворяющие этим условиям. . Найди другие числа удовлетворяющие этим условиям.
Упражнение 2.
Найди корни: 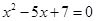 , легче , легче 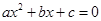
Упражнение 3.
Доказать, что 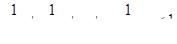 , при любых , при любых 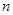
Упражнение 4.
Какое число равно обратному себе?
Упражнение 5.
Произведение, каких чисел меньше 0 (больше 0).
Упражнение 6.
Сумма каких чисел равна одному из слагаемых?
Упражнение 7.
Докажите, что все числа последовательности делятся на 13: 257 257, 123 123.. (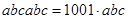 ) )
Упражнение 8.
Доказать, что всякое нечетное число, неравное единице есть разность двух квадратов.
4.
Подведение итогов.
Занятие № 9. Переход в подсистему
Цель занятия:
познакомить учащихся с «принципом перехода в подсистему» как методом для активизации мышления.
1.
Что такое подсистема?
2.
Прикладные упражнения.
Если трудно решить проблему в явном виде или в той форме как она сейчас, то порой помогает метод рассмотрение из того из чего состоит проблема. Например, полезно совершенствовать не сами составляющие компьютера вместе, а по частям, совершенствуя их, не зависимо друг от друга.
3.
Математические упражнения.
Упражнение 1.
Докажите, что уравнение 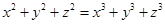 имеет бесконечно много решений. имеет бесконечно много решений.
Решение: разбор в частном случаи 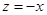 , , 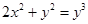 . . 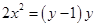 . .
Упражнение 2.
На плоскости дано 100 прямых. Сколько может точек пересечения.
Упражнение 3.
Найди частное 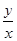 , если , если 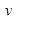 , , 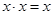
Упражнение 4.
Сколько различных квадратов изображено на рисунке:
Упражнение 5.
Давайте рассмотрим преобразование:
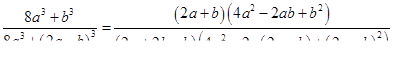 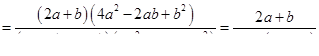 . .
А значит 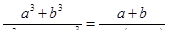 . Верно? . Верно?
Упражнение 6.
Можно ли доску размером 5х5 заполнить доминошками размером 1х2?
4.
Итоговое т тестирование.
5.
Подведение итогов. Работа на последействие.
Рекомендации позволяющие делать свою жизнь креативнее
1. Регулярно выполняйте физические упражнения.
2. Следите за тем, чтобы ваша диета была разнообразной и сбалансированной.
3. Овладейте техникой релаксации и медитации.
4. Совершенствуйте уверенность в себе.
5. Ведите дневник, делайте зарисовки, пишите стихи, короткие рассказы и песни.
6. Читайте художественную литературу, развивающую воображение.
7. Задумывайтесь об альтернативных способах использования предметов, с которыми вы сталкиваетесь в повседневности.
8. Задумывайтесь о сходстве непохожих друг на друга вещей.
9. Займитесь живописью или скульптурой.
10. Посещайте вдохновляющие места.
11. Займитесь делами, о которых вы обычно не помышляли.
12. Старайтесь быть более спонтанными и общительными.
13. Смотрите комедии и старайтесь сформировать свой собственный юмористический стиль. Слушайте классическую музыку.
14. Регулярно ищите способы вырваться из вашей «зоны комфорта».
15. Старайтесь выполнять свои ежедневные рутинные обязанности разными способами.
16. Заводите новых друзей и расширяйте свой круг общения.
17. Думайте о себе как о творческой личности.
18. Думайте о креативности, как о способе существования.
19. Подражайте той известной творческой личности, которой вы восхищаетесь.
20. Развивайте бунтарские черты характера.
21. Приучитесь задавать себе вопрос: «А что, если…».
22. Не засиживайтесь перед телевизором.
23. Позвольте себе мечтать.
24. Не бойтесь оказаться неправым или совершить ошибку.
25. Не выносите поспешных суждений.
26. Интересуйтесь абсолютно всем.
[1]
Под ситуацией мы будем понимать задачи «открытого» типа, внедрением в школу которых занимается ТРИЗ-педагогика (см. [21,26])
[2]
Пазработка осуществлена на основе статьи [62]
[3]
Разработка осуществлена на основе книг [15, 16].
|