| Государственное образовательное учреждение высшего профессионального образования
ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Гидромеханика и транспортные машины»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе по дисциплине
«Теплотехника»
Тема:
«Термодинамический расчет, анализ и оптимизация
идеализированного цикла поршневого ДВС»
Выполнил: студент Д.С Кураш,
Группы: МГ-317
подпись, дата
Шифр курсовой работы __________
Проверил: А.Х. Шамутдинов
Оценка подпись, дата
г. Омск, 2010
СОДЕРЖАНИЕ (пример)
1.1 Содержание задачи №1 3
1.2 Краткое описание цикла поршневого ДВС 3
1.3 Расчет цикла ДВС 5
1.3.1 Определение параметров характерных точек цикла 5
1.3.2 Расчет термодинамических процессов 7
1.3.3 Расчет характеристик цикла 12
1.3.4 Построение Т-s диаграммы цикла 15
1.4 Оптимизация цикла варьированием заданного параметра 20
Задача № 1
1.1 Содержание задачи (вариант 14)
Для цикла поршневого ДВС, заданного параметрами р1
=0.14 МПа; Т1
= 300 К; ε
= 18; λ
= 1,3; ρ
= 1,48 кг/м3
; n
1
= 1,34; n
2
= 1,28, определить параметры всех характерных точек цикла, термодинамические характеристики каждого процесса и цикла в целом. Исследовать влияние параметра n1
на величину термического КПД η
t
и максимальной температуры Т
max
при варьировании указанного параметра в пределах 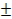 20 %. По результатам расчетов построить графики зависимостей η
t
и Т
ma
x
от варьируемого параметра, на основании которых сделать заключение об его оптимальном значении, принимая за предельно допустимое значение Т
ma
x
величину Тпр
= 1600 К. В качестве рабочего тела принимать сухой воздух. 20 %. По результатам расчетов построить графики зависимостей η
t
и Т
ma
x
от варьируемого параметра, на основании которых сделать заключение об его оптимальном значении, принимая за предельно допустимое значение Т
ma
x
величину Тпр
= 1600 К. В качестве рабочего тела принимать сухой воздух.
1.2 Краткое описание цикла
Для анализа задан цикл поршневого ДВС со смешанным подводом теплоты, который реализуется в современных быстроходных дизельных двигателях. Подробное описание такого цикла приведено в учебниках [1,3] и др., ниже приведено краткое описание.
На рис. 1 приведена идеализированная p-v
диаграмма, наглядно отображающая основные процессы такого цикла. Во время хода впуска (на диаграмме не показан) атмосферный воздух, проходя через систему фильтров и открытый впускной клапан, поступает в цилиндр двигателя. В конце впуска (точка 1 на диаграмме) впускной клапан закрывается, и по мере перемещения поршня к верхней мертвой точке (ВМТ) происходит политропное сжатие воздуха (процесс 1-2). Ввиду быстротечности этого процесса характер его близок к адиабатному, температура воздуха к концу сжатия (точка 2) сильно увеличивается, в этот момент под большим давлением производят впрыск топлива, в мелкодисперсном виде. Топливо при высокой температуре воздуха, в который оно попадает, очень быстро испаряется и самовоспламеняется. Первые порции при этом сгорают практически мгновенно (процесс 3-4).
Реклама

Для интенсификации процессов топливо часто впрыскивают в специальную предкамеру из жаростойкой стали, имеющую очень высокую температуру. Последующие порции топлива сгорают по мере их попадания в цилиндр во время перемещения поршня от ВМТ к НМТ (нижней мертвой точке). При этом давление в цилиндре практически не изменяется (процесс 3-4). Далее совершается политропное расширение продуктов сгорания (процесс 4-5), по окончании которого, когда поршень приходит в НМТ, открывается выпускной клапан (точка 5) и во время хода выталкивания продукты сгорания выбрасывается в атмосферу. Поскольку суммарная работа процессов всасывания и выталкивания практически равна нулю, идеализируя картину, их заменяют одним изохорным процессом отвода теплоты (процесс 5-1).
1.3 Расчет цикла ДВС
*
1.3.1 Определение параметров характерных точек цикла
Точка 1.
По формуле (5) из расчёта ДВС находим:
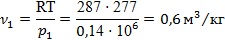
Точка 2
. Из формулы (6) находим 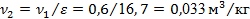 . Используя уравнение (6), давление p2
найдем по формуле (8): . Используя уравнение (6), давление p2
найдем по формуле (8):
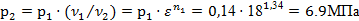 . .
Величину Т2
находим из уравнения (4):
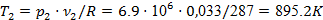 . .
Точка 3
. Из формулы (9) находим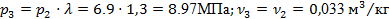
Температуру Т3
находим из уравнения (4):
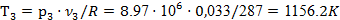 . .
Используя соотношения (12) находим Т3
:
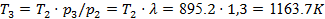 . .
Практическое совпадение результатов (невязка около 0,1 % возникает из-за округлений) служит подтверждением безошибочности проведенных вычислений.
Точка 4.
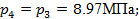 Из выражения (10) Из выражения (10)
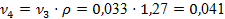 . .
Температуру Т4
найдем по выражению (13): 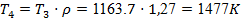 . .
Точка 5.
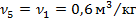 . Давление в точке 5 найдем так же, как находили его для точки 2: . Давление в точке 5 найдем так же, как находили его для точки 2:
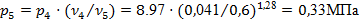 . .
Температуру Т5
находим из формулы (4):
 . .
Полученные результаты заносим в сводную таблицу (табл. 1).
1.3.2 Расчет термодинамических процессов
Рассчитываем теперь процесс 1-2.
Это политропный процесс с показателем политропы n1
= 1,34. Чтобы реализовать формулы (14) – (18), сначала по формулам (19) и (20) рассчитываем значения средних теплоемкостей, предварительно рассчитав t1
и t2
:
Реклама

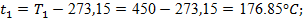
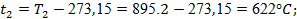
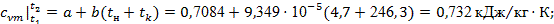
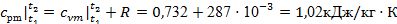 . .
Теплоту процесса 1-2
находим по формуле (14):
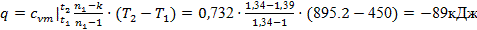 , ,
Работу процесса 1-2
находим по формуле (15):
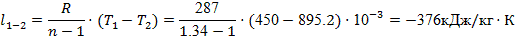
Изменения внутренней энергии и энтальпии рассчитываем по формулам (16) и (17):
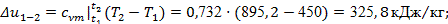
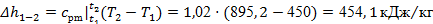 . .
По формуле (18) находим величину Δ
s
1-2
:
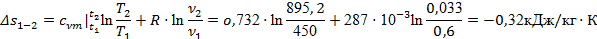
Далее по формуле (21) находим:
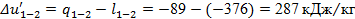
Погрешность расчёта (22):
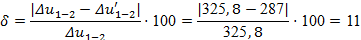
Расчет процесса 2-3
начинаем также с определения величин
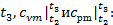
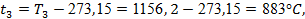
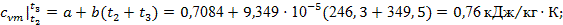
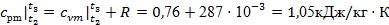
Поскольку процесс 2-3
изохорный (у таких процессов значение n
= ±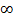 ), формулы (14), (16), (17) и (18) существенно упрощаются, позволяя рассчитывать значения соответствующих величин: ), формулы (14), (16), (17) и (18) существенно упрощаются, позволяя рассчитывать значения соответствующих величин:
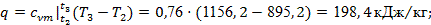
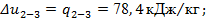
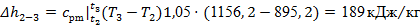
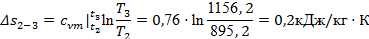
Для самопроверки воспользуемся соотношением (24):
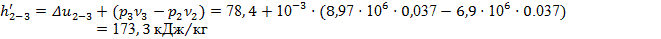
Погрешность расчёта (24) составляет незначительную величину:
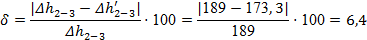
Процесс 3-4
изобарный и для него показатель политропы n
= 0. Это тоже упрощает формулы (14) – (16). Расчеты начинаем с определения температуры t
4
и теплоемкостей:
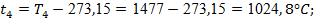
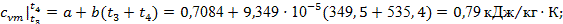
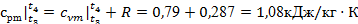 . .
Определяем теперь характеристики процесса 3-4
:
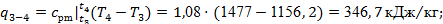

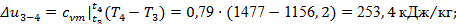

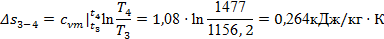
Проверку проведем обоими способами, воспользовавшись формулами (21 ‑ 22):
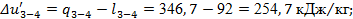
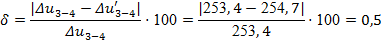
По выражению (23):
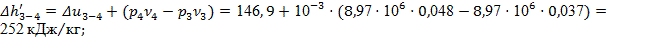 и по формуле(24): и по формуле(24):
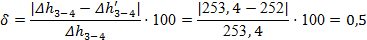
Чтобы рассчитать процесс 4-5
, определим температуру t
5
, cν
m
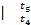 и c
pm и c
pm
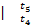 по формулам (19) и (20): по формулам (19) и (20):
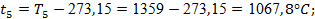
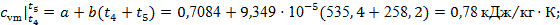
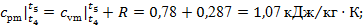
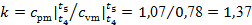 . .
Далее рассчитываем характеристики процесса 4-5
по формулам (14 – 18):
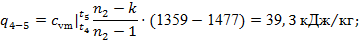
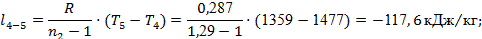
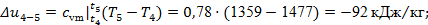
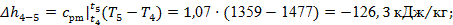
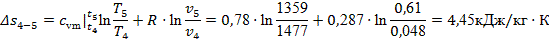
Проверка:
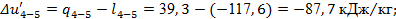
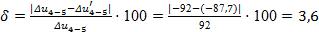 . .
Производим расчет последнего процесса 5-1
. Это процесс изохорный и расчет его аналогичен расчету процесса 2-3
. Начинаем, как обычно, с расчета теплоемкостей:
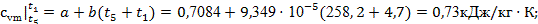
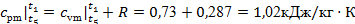
Основные характеристики процесса:
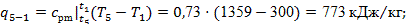
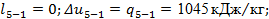
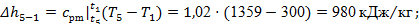
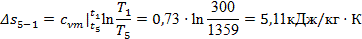
Проверку проведем по формуле (23):
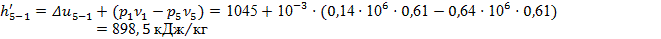
Погрешность расчета определим по формуле (24):
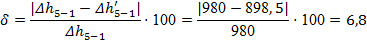
Прежде чем перейти к расчетам характеристик цикла, рассчитываем сначала значения энтропии в каждой характерной точке цикла. Для точки 1 можно записать
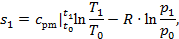
где t0
= 0 °C (T0
= 273,15 К); p0
= 0,1013 МПа – параметры воздуха при нормальных условиях; при таком состоянии считается, что S = 0.
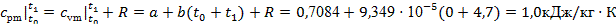
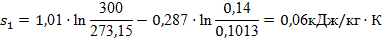
Далее находим
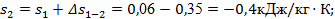
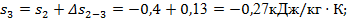
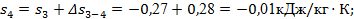
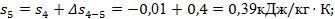
или
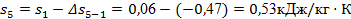 . .
Практическое совпадение значений s5
, рассчитанных двумя способами, свидетельствует об отсутствии заметных погрешностей при расчетах величин .s. Все результаты заносим в табл. 1.
1.3.3 Расчет характеристик цикла
Теплоту за цикл, рассчитываем по выражению (25):
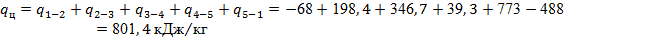
Работу за цикл определим по выражению (26):
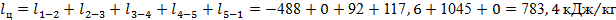 . .
Известно, что за цикл q
ц
= l
ц
. В наших расчетах несовпадение незначительно. Невязка объясняется округлениями в промежуточных расчетах (27):
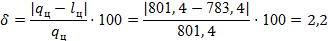
Количество подведенной теплоты
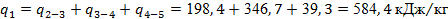
Найдем изменения внутренней энергии, энтальпии и энтропии за цикл. Теоретически эти изменения должны быть равными нулю.
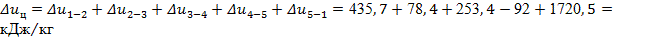 ; ;
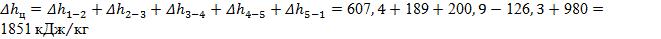 ; ;
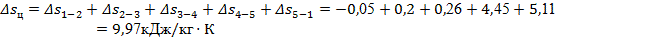
Некоторые отличия рассчитанных величин от нуля объясняются округлениями при расчетах. Естественно, что сопоставлять невязку, например, нужно не с нулем, а с любым слагаемым, входящим в сумму. И тогда видно, что невязка и здесь составляет доли процента.
Рассчитаем термический КПД цикла по формуле (28):
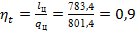 . .
Рассчитаем термический КПД идеализированного цикла с адиабатными процессами сжатия и расширения по формуле (1), приведенной в [4] и принимая в среднем k
= 1,39:
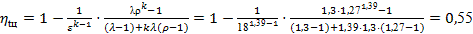 . .
Термический КПД цикла Карно для того же интервала температур, в котором реализуется реальный цикл по формуле (29), будет:
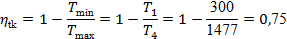
Результаты расчетов заносим в сводные: табл. 1 и табл. 2:
Таблица 1
Сводная таблица исходных данных и результатов расчета
| Наименование
|
Значения параметров
|
| р
, МПа
|
ν
, м3
/кг
|
Т
, К
|
S
, кДж/кг·К
|
| Параметры точек
|
1
2
3
4
5
|
0,14
6,9
8,97
8,97
0,64
|
0,61
0,037
0,037
0,048
0,61
|
300
895,2
1156,2
1477
1359
|
0,05
-0,2
-0,26
2,45
3,11
|
| Наименование
|
Значения параметров
|
| q
, кДж/кг
|
l
, кДж/кг
|
Δ
u
, кДж/кг
|
Δ
h
, кДж/кг
|
Δ
S
, кДж/кг
|
| Характеристики процессов
|
1-2
2-3
3-4
4-5
5-1
|
-68
198,4
346,7
77,3
39,3
|
-400
0
92
1045
-,117,6
|
435,7
78,4
253.4
-92
-127,6
|
246,5
108,3
200,9
-296,7
-258,6
|
-0,35
0,13
0,28
0,4
-0,47
|
| Суммы
|
593,7
|
415,4
|
496,5
|
8,4
|
0,01
|
Таблица 2
Результаты расчета
| Термический КПД
|
ηt
|
0,9
|
| Термический КПД идеализированного цикла Карно
|
ηt
ц
|
0,55
|
| Термический КПД цикла Карно
|
ηtk
|
0,75
|
| Коэффициент заполнения цикла
|
k
|
0,51
|
1.3.4 Построение T-s диаграммы цикла
Чтобы построить T-s
диаграмму, выбираем масштабы по осям координат: T
t
= 10 К/мм; s
s
= 0,01 кДж/(кг·К) / мм. Изображаем оси T
и s
, наносим координатную сетку, а затем и характерные точки цикла. Точки 2 и 3, 3 и 4, 5 и 1 соединяем по лекалу кривыми, по характеру близкими к экспонентам, а политропные процессы 1-2 и 4-5 с достаточной точностью можно изображать прямыми линиями (рис. 1П). Чтобы определить коэффициент заполнения цикла, найдем площадь цикла 1-2-3-4-5-1 непосредственно на диаграмме, пересчитывая квадратные сантиметры (на рисунке пронумерованы): Fц
= 25,4 см2
.
Площадь описанного цикла Карно рассчитываем, измерив, размеры прямоугольника в сантиметрах: Fк = 8,5·5,9 = 50,2 см2
. Тогда коэффициент заполнения цикла будет
k = Fц / Fк
= 25,4/ 50,2 = 0,51
| Рис. 1П. Т-
s
- диаграмма цикла
ных слоев многослойной стенки
|
|
1.4 Оптимизация цикла варьированием параметра n1
Используя данные таблицы, строим графики зависимостей: Т
max
= f
(n
1
)
| Рис. 2П. Зависимость Т
max
от n
1
ных слоев многослойной стенки
|
|
и η
t
=
f
(
n
1
):
| Рис. 3П. Зависимость η
t
от n
1
ных слоев многослойной стенки
|
|
Из рисунков видно, что наибольшую эффективность имеет цикл с n
1
= 1,37. Это и понятно, поскольку при n
1
= k
процесс сжатия протекает адиабатно, а адиабатные процессы самые "экономичные". Вывод: оптимальным является значение n
1
= 1,37. При этом T
4
< T
пр
.
Задача № 2
2.1 Содержание задачи № 2 (вариант 42)
Цикл Ренкина задан параметрами р
1
= 10 МПа; t
1
= 450°С; р
2
= 0,07 МПа. Исследовать влияние параметра t
1
на величину термического КПД цикла ηt
и удельный расход теплоты q
, рассчитав эти величины при варьировании заданного параметра в пределах 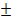 20 %. Построить графики зависимостей η
t
и q
от варьируемого параметра, на основании которых сделать заключение об оптимальном его значении. Краткое описание цикла см. на стр. 13-15. 20 %. Построить графики зависимостей η
t
и q
от варьируемого параметра, на основании которых сделать заключение об оптимальном его значении. Краткое описание цикла см. на стр. 13-15.
2.2 Расчет цикла
*
Для определения параметров p, v
, t
, h
и s
каждой из характерных точек цикла воспользуемся таблицами состояний [5] и известной h-s
диаграммой воды и пара.
Точка 1
. Давление и температура здесь заданы: р
1
= 3,494 МПа; t
1
= 273°С. Тогда на пересечении изобары: р
= 34,9 бар и изотермы t
1
= 273 °С на h-s
диаграмме находим положение точки 1 и по соответствующим изолиниям определяем значения остальных параметров: v
1
= 0,0636 м3
/кг; h
1
= 2900,2 кДж/кг; s
1
= 6,321 кДж/(кг·К). Эти же значения можно определить и по таблицам состояний перегретого пара, применяя двунаправленное линейное интерполирование, подробно описанное в [3] и [4].
Точка 2
. Поскольку процесс 1-2
принимается адиабатным, положение точки 2 находим, проводя вертикальную линию вниз (s
= const
) до пересечения с изобарой р
= р
2
= 0,27 бар.
_ * В настоящем расчете все исходные параметры умножены на 0,91, чтобы вариант 42 оставался доступным для работы.
По соответствующим изолиниям находим: t
2
= t
нас
= 66,9 °С, ν
2
= 4,5157 м3
/кг; h
2
= 2117,6 кДж/кг; s2
= s1
= 6,321 кДж/(кг К); x
2
= 0,78. Эти же значения можно рассчитать, пользуясь таблицами насыщенных состояний и определив сначала значение x
2
:
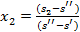 , ,
после чего и значения других параметров, например:
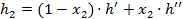
Параметры остальных точек находим по таблицам насыщенных состояний (по давлениям).
Точка 3
. Давление р
3
= р
2
= 0,27 бар, остальные параметры – это параметры воды на линии насыщения при этом давлении. Из таблицы находим:
t
3
= t
нас
= 66,9 °С; ν
3
= 0,0010 м3
/кг; h
3
= 280,0 кДж/кг; s
3
= 0,917 кДж/(кг К).
Точка 4
. Давление р
4
= р
1
= 3,494 бар, температура: t
4
= t
3
= 242,4 °С. По этим значениям с помощью таблицы состояний воды следовало бы найти остальные параметры. Однако, учитывая, что величина параметров воды очень мало зависит от ее давления, обычно принимают ν
4
= ν
3
= 0,001 м3
/кг; h
4
= h
3
= 280,0 кДж/кг; s
4
= s
3
= 0,917 кДж/(кг·К).
Точка 5
. Здесь р
5
= р
1
= 3,494 бара, а остальные параметры этой точки – это параметры воды на линии насыщения при этом давлении: t
5
= t
нас
= 242,4 °С; v
5
= v
'= 0,0012 м3
/кг; h
5
= h
' = 1049,3 кДж/кг; s
5
= s
' = 2,724 кДж/(кг·К).
Точка 6
. Давление р
6
= р
1
= 3,494 бар, все же остальные параметры определяются как параметры сухого насыщенного пара при этом давлении. Из таблицы насыщенных состояний воды находим: t
6
= t
нас
= 242,4 °С; v
6
= v
''= 0,0572 м3
/кг; h
6
= h
'' = 2802,5 кДж/кг; s
6
= s
'' = 6,126 кДж/(кг·К).
2.3.1 Расчет термического КПД и других параметров цикла
Рассчитываем теперь основные характеристики цикла. Термический КПД цикла по формуле (30):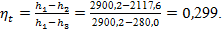
Удельный расход пара по формуле(31):
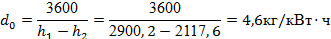
Удельный расход теплоты по формуле(32):
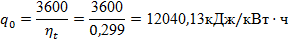
Результаты расчетов сводим в итоговую таблицу 1
Таблица 1
Итоговая таблица расчетов
| Точка
|
р
, МПа
|
t
, 0
С
|
ν
, м3
/кг
|
h
, кДж/кг
|
s
, кДж/(кг·К)
|
х
|
| 1
|
3,494
|
273,0
|
0,0636
|
2900,2
|
6,321
|
| 2
|
0,027
|
66,9
|
4,5157
|
2117,6
|
6,321
|
0,78
|
| 3
|
0,027
|
66,9
|
0,0010
|
280,0
|
0,917
|
| 4
|
3,494
|
242,2
|
0,0010
|
280,0
|
0,917
|
| 5
|
3,494
|
242,2
|
0,0012
|
1049,3
|
2,724
|
| 6
|
3,494
|
242,2
|
0,0572
|
2802,5
|
6,126
|
2.4 Результаты варьирования и их анализ
Таблица 2
Результаты расчета основных параметров цикла
| Значение варьируемого параметра t
1,
 С С
|
Процент изменения параметра
|
d
, кг/кВт ч
|
q
, кДж/кВт·ч
|
η
t
|
| 218,4
|
-20
|
5,079
|
12353
|
0,291
|
| 245,7
|
-10
|
4,807
|
12183
|
0,295
|
| 273,0
|
0
|
4,600
|
12053
|
0,299
|
| 300,3
|
+10
|
4,425
|
11930
|
0,302
|
| 327,6
|
+20
|
4,267
|
11804
|
0,305
|
Ниже на рис. 4П – 6П полученные результаты отражены графически в виде соответствующих зависимостей.
Рис. 4П. Зависимость q
= f(t1
)
| Рис. 6П. Зависимость η
t
=f
(t
1
)
|
|
Из рисунков видно, что с увеличением температуры t
1
эффективность цикла увеличивается практически по линейному закону. При этом удельные расходы пара и теплоты уменьшаются примерно на 12 %, а термический коэффициент полезного действия примерно на столько же увеличивается.
Задача №3
Определить потерю теплоты через 1м2
кирпичной обмуровки котла толщиной 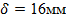 и температуры стенки и температуры стенки  и и 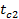 , если температура газов , если температура газов 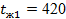 °C температура воздуха °C температура воздуха 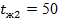 °C коэффициент теплоотдачи со стороны газов °C коэффициент теплоотдачи со стороны газов 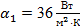 , коэффициент теплоотдачи со стороны воздуха , коэффициент теплоотдачи со стороны воздуха 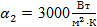 и коэффициент теплопроводности обмуровки и коэффициент теплопроводности обмуровки 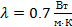
Дано:
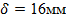 , ,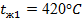 , ,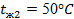 ; ;
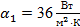 ; ; 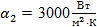 ; ; 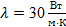
Найти:
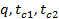
Решение:
1). Согласно уравнению (40) коэффициент теплопередачи 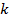 равен: равен:
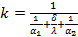 ; ; 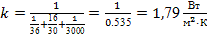
Подставляя это значение в формулу (41), определим плотность теплового потока:
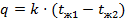 ; ;
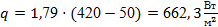
Для определения температур стенок  и и 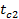 составим уравнения для плотности теплового потока (в данном примере – 3 уравнения). Так как тепловой поток один и тот же во всех 3-х процессах, то получим следующие выражения: составим уравнения для плотности теплового потока (в данном примере – 3 уравнения). Так как тепловой поток один и тот же во всех 3-х процессах, то получим следующие выражения:
1. плотность теплового потока от горячего газа к стенке по формуле Ньютона – Рихмана:
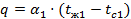
2. плотность теплового потока, обусловленная теплопроводностью через твердую стенку: 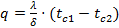
3. плотность теплового потока от второй поверхности стенки к воздуху:
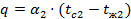
Отсюда необходимые значения температур, по формулам (42), равны:
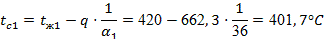
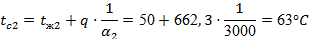
2). Построение температурного графика 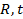 позволит убедиться в правильности нашего решения, т.е. значения температур стенки позволит убедиться в правильности нашего решения, т.е. значения температур стенки 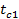 и и 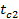 можно определить графическим способом. Всё построение подробно описано на стр.22 в настоящих МУ. можно определить графическим способом. Всё построение подробно описано на стр.22 в настоящих МУ.
3). Построение температурного графика в 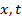 – координатах. Построение графика аналогично вышеизложенному, но по оси абсцисс откладываются в масштабе толщины слоев – координатах. Построение графика аналогично вышеизложенному, но по оси абсцисс откладываются в масштабе толщины слоев 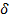 . .
| Рис. 8П. Теплопередача через кирпичную обмуровку котла
|
|
Задача №4
Паропровод диаметром 200/216 мм покрыт слоем совелитовой изоляции толщиной 110 мм, коэффициент теплопроводности которой 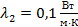 . .
Температура пара 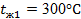 и окружающего воздуха и окружающего воздуха 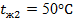 . Коэффициент теплопроводности стенки . Коэффициент теплопроводности стенки 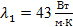 ; ;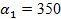 и и 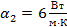 . Необходимо определить линейный коэффициент теплопередачи, линейную плотность теплового потока и температуру на поверхности соприкосновения паропровода с изоляцией. . Необходимо определить линейный коэффициент теплопередачи, линейную плотность теплового потока и температуру на поверхности соприкосновения паропровода с изоляцией.
Дано: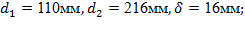 , ,
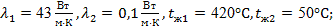
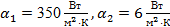
Найти: 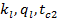 . .
Решение: Согласно условию задачи: 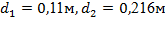 и и 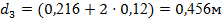
Линейный коэффициент теплопередачи определим по формуле (48): 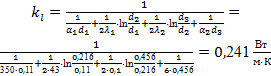
На основании формулы (47) найдем линейную плотность теплового потока
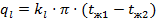
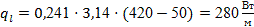 / /
Температуру поверхности соприкосновения паропровода с изоляцией найдем по формулам (46) и (49):
1).от пара к внутренней поверхности паропровода: 
2).от внутренней к наружной поверхности паропровода (обусловленная теплопроводностью): 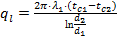
Отсюда 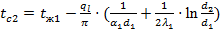
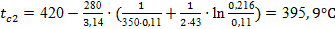 . .
|