| Содержание
Введение. 3
§1.Определения и примеры.. 5
§2. Пространства зависимости. 12
§3. Транзитивность. 16
§4. Связь транзитивных отношений зависимости с операторами замыкания 23
§5. Матроиды.. 27
Список библиографии. 32
Введение
Целью квалификационной работы является изучение понятия отношения зависимости, рассмотрение отношения зависимости на различных множествах.
Поставленная цель предполагает решение следующих задач:
1. Изучить и дать определение понятию отношение зависимости.
2. Рассмотреть некоторые примеры отношения зависимости.
3. Сформулировать и доказать свойства и теоремы как для произвольных, так и для транзитивных пространств зависимости.
4. Рассмотреть теорему о связи транзитивного отношения зависимости и алгебраического оператора замыкания.
5. Изучить понятие матроида, привести примеры матроидов.
6. Рассмотреть жадный алгоритм и его связь с матроидами.
На основании поставленных целей и задач квалификационная работа разбивается на 5 параграфов.
В первом параграфе приведены основные определения и рассмотрены некоторые примеры отношения зависимости.
Во втором – рассматриваются произвольные пространства зависимости, их свойства и некоторые теоремы.
Третий – посвящен транзитивным и конечномерным пространствам зависимости. Здесь рассмотрены свойства транзитивных пространств зависимости и доказаны теоремы, которые подтверждают существования базиса и инвариантность размерности в любом конечномерном транзитивном пространстве зависимости.
В четвертом параграфе формулируются основные определения касающиеся оператора замыкания и рассмотрена теорема о представлении транзитивного отношения зависимости с помощью алгебраического оператора замыкания.
Пятый параграф посвящен матроидам, примерам матроидов и их применению при изучении теоретической основой анализа «жадных» алгоритмов.
Основной литературой при написании квалификационной работы стали монографии: Кона П. «Универсальная алгебра» [2] и Куроша А. Г. «Курс высшей алгебры» [3].
§1.Определения и примеры
Определение 1.
Множество
Z подмножеств множества
A
назовем отношением зависимости на
A
, если выполняются следующие аксиомы:
Z
1
: 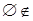 Z
;
Z
;
Реклама

Z
2
: 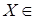 Z
Z
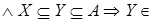 Z
;
Z
;
Z
3
: 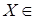 Z
Z
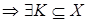 (
(
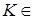 Z
Z
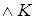 - конечно).
- конечно).
Подмножество множества
A
называется зависимым
, если оно принадлежит
Z
,
и независимым
в противном случае.
Легко убедиться в независимости аксиом Z
1
-
Z
3
..
Модель 1
: 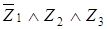 . Полагаем Z
=
B (А)
для любого множества . Полагаем Z
=
B (А)
для любого множества 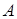 . .
Модель 2
: 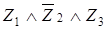 . Пусть Z
= . Пусть Z
=
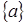 при при 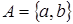 . .
Модель 3
: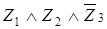 . Пусть Z
= . Пусть Z
=
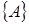 для бесконечного множества для бесконечного множества 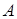 . .
Определение 2.
Пространством зависимости
назовем пару 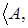 Z
Z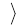 , где
Z
– отношение зависимости на
A
.
, где
Z
– отношение зависимости на
A
.
Определение 3.
Элемент 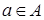 называется зависимым от множества называется зависимым от множества
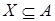 , если а
Î
X
или существует такое независимое подмножество
Y
множества
X
,
что , если а
Î
X
или существует такое независимое подмножество
Y
множества
X
,
что 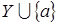 зависимо, т.е. зависимо, т.е. 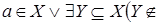 Z
Z
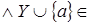 Z
). Z
).
Из определения 1 вытекает, что если элемент 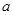 зависит от множества зависит от множества 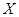 , то он зависит от некоторого конечного подмножества , то он зависит от некоторого конечного подмножества 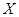 . .
Определение 4.
Множество всех элементов, зависящих от
X
,
называется оболочкой
множества
X
и обозначается через 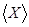 . .
Ясно, что 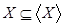 и включение и включение 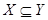 влечет включение их оболочек: влечет включение их оболочек: 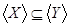 . .
Определение 5.
Если 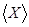 = A, то
X
называется порождающим множеством
множества
A
. = A, то
X
называется порождающим множеством
множества
A
.
Определение 6.
Н
езависимое порождающее подмножество множества A называется базисом
множества
A
.
Определение 7.
Множество 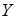 зависит
от зависит
от 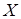 , если любой элемент из , если любой элемент из 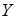 зависит от зависит от 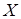 , то есть , то есть 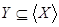 . .
Определение 8.
Отношение зависимости
Z
на
A
будем называть транзитивным
отношением зависимости
, если 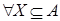
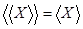 . .
Определение 9.
Транзитивным пространством зависимости
назовем пространство зависимости, в котором отношение зависимости обладает свойством транзитивности.
В качестве теоретико-множественного постулата будем использовать следующий принцип, эквивалентный известной аксиоме выбора.
Лемма Цорна
.
Непустое упорядоченное множество, в котором каждое линейно упорядоченное подмножество
обладает верхней гранью, имеет максимальный элемент.
Далее целесообразно рассмотреть некоторые примеры отношения зависимости:
Пример 1.
Понятие линейной зависимости в векторном пространстве V
над полем 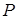 . Система векторов векторного пространства
V
называется линейно зависимой
, если существует конечная линейно зависимая ее подсистема, в противном случае – линейно независимой
. . Система векторов векторного пространства
V
называется линейно зависимой
, если существует конечная линейно зависимая ее подсистема, в противном случае – линейно независимой
.
Понятие линейной зависимости в конечномерных векторных пространствах дается в курсе алгебры. Конечная система векторов 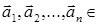 V
называется линейно зависимой
, если существуют элементы поля
V
называется линейно зависимой
, если существуют элементы поля 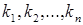 одновременно не равные нулю и такие, что линейная комбинация одновременно не равные нулю и такие, что линейная комбинация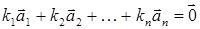 . Множество линейных комбинаций множества . Множество линейных комбинаций множества 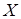 векторов векторного пространства
V
с коэффициентами из поля
P
называется линейной оболочкой
этих векторов и обозначается векторов векторного пространства
V
с коэффициентами из поля
P
называется линейной оболочкой
этих векторов и обозначается 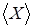 .
При этом .
При этом 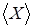 - является подпространством в пространстве V
, порожденным
- является подпространством в пространстве V
, порожденным 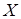 . Получаем транзитивное отношение зависимости. . Получаем транзитивное отношение зависимости.
Реклама

Пример 2.
Пусть поле 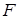 является расширением основного поля Р,
а является расширением основного поля Р,
а 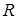 минимальное подкольцо содержащее элементы минимальное подкольцо содержащее элементы 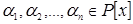 и поле Р
. Подкольцо и поле Р
. Подкольцо 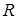 состоит из всех элементов поля состоит из всех элементов поля 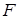 , которые выражаются через элементы , которые выражаются через элементы 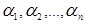 и элементы поля Р
при помощи сложения, вычитания и умножения: это будут всевозможные многочлены от и элементы поля Р
при помощи сложения, вычитания и умножения: это будут всевозможные многочлены от 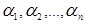 с коэффициентами из поля Р
. Тогда, если для всякого элемента с коэффициентами из поля Р
. Тогда, если для всякого элемента 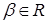 существует единственная запись в виде многочлена от существует единственная запись в виде многочлена от 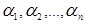 как неизвестных с коэффициентами из поля Р,
то есть если различные многочлены от как неизвестных с коэффициентами из поля Р,
то есть если различные многочлены от 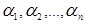 будут различными элементами подкольца будут различными элементами подкольца 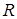 , то система элементов , то система элементов 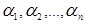 , будет называться алгебраически независимой
над полем
Р, в противном случае алгебраически зависимой
. Произвольное множество элементов поля Р называется зависимым
, если оно содержит конечное зависимое подмножество.
В первом случае кольцо , будет называться алгебраически независимой
над полем
Р, в противном случае алгебраически зависимой
. Произвольное множество элементов поля Р называется зависимым
, если оно содержит конечное зависимое подмножество.
В первом случае кольцо 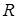 изоморфно кольцу многочленов изоморфно кольцу многочленов 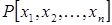 . Отношение алгебраической зависимости над полем Р
является транзитивным отношением зависимости. . Отношение алгебраической зависимости над полем Р
является транзитивным отношением зависимости.
Пример 3.
Пусть на множестве A
задано рефлексивное и симметричное бинарное отношение 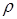 (называемое отношением сходства). Подмножество
X
множества
A
будем считать зависимым
, если оно содержит два различных элемента, находящихся в отношении (называемое отношением сходства). Подмножество
X
множества
A
будем считать зависимым
, если оно содержит два различных элемента, находящихся в отношении
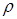 . .
Оболочкой множества 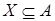 служит множество служит множество
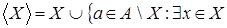 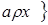
В этом случае можно усилить аксиому 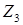 отношения зависимости следующим образом: отношения зависимости следующим образом:
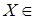 Z
Z
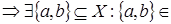 Z
.
Z
.
Тогда оболочкой множества 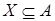 будет множество всех элементов, находящихся в отношении сходства хотя бы с одним элементом из множества будет множество всех элементов, находящихся в отношении сходства хотя бы с одним элементом из множества 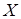 . .
Введенное отношение зависимости будет транзитивным тогда и только тогда, когда соответствующее бинарное отношение 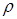 будет транзитивно, то есть является отношением эквивалентности на будет транзитивно, то есть является отношением эквивалентности на 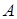 . .
В случае, когда 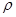 - отношение эквивалентности - отношение эквивалентности 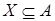 будет независимым
тогда и только тогда, когда будет независимым
тогда и только тогда, когда 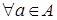 множество множество 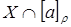 содержит не более одного элемента. Любое максимальное независимое подмножество будет содержать ровно по одному элементу из каждого класса эквивалентности содержит не более одного элемента. Любое максимальное независимое подмножество будет содержать ровно по одному элементу из каждого класса эквивалентности 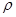 . .
Пример 4.
Рассмотрим четырехэлементное множество 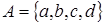 . .
Назовем подмножество 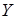 множества множества 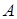 зависимым
тогда и только тогда, когда зависимым
тогда и только тогда, когда 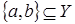 или или 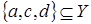 . .
Z
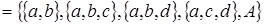 .
.
Рассмотрим подмножество 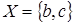 множества множества 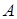 , по введенному определению оно будет независимо. Рассмотрим оболочку множества
, по введенному определению оно будет независимо. Рассмотрим оболочку множества 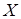  и найдем оболочку оболочки нашего множества и найдем оболочку оболочки нашего множества 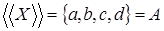 . Таким образом, мы получили . Таким образом, мы получили 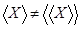 , то есть рассмотренное нами отношение зависимости не является транзитивным. , то есть рассмотренное нами отношение зависимости не является транзитивным.
Пример 5.
Рассмотрим произвольное множество 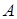 и
и 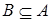 . Множество . Множество 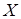 будем считать зависимым
, если будем считать зависимым
, если 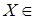 B (А)\ B (В), то есть
B (А)\ B (В), то есть 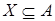 , но , но 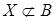 .
Таким образом, получили следующее транзитивное пространство зависимости: .
Таким образом, получили следующее транзитивное пространство зависимости: 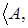 B (А)\ B (В B (А)\ B (В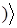 .
Оболочкой .
Оболочкой 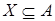 будет множество будет множество 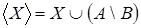 . .
В частности можно рассмотреть 2 случая:
1. 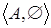 , то есть все множества независимы, тогда , то есть все множества независимы, тогда 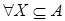 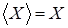 . .
2. 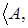 B (А) B (А)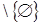 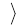 ,
то есть все множества, кроме пустого, будут зависимыми, в этом случае ,
то есть все множества, кроме пустого, будут зависимыми, в этом случае 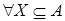 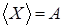 . .
Пример 6.
Рассмотрим произвольное множество 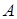 и его непустое конечное подмножество
и его непустое конечное подмножество 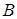 . Введем на множестве А
следующее отношение зависимости . Введем на множестве А
следующее отношение зависимости
Z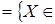 B (А)
B (А)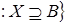 . .
Таким образом, зависимыми будут все надмножества множества 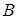 . .
Если 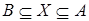 , то , то 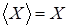 . .
Если 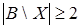 , то , то 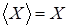 . .
Если 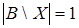 , то , то 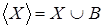 . .
Получаем транзитивное пространство зависимости.
Пример 7.
Подпространство пространства зависимости 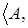 Z
Z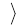 .
Рассмотрим
.
Рассмотрим 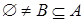 , где действует то же отношение зависимости Z
.
Тогда получим индуцированное пространство зависимости , где действует то же отношение зависимости Z
.
Тогда получим индуцированное пространство зависимости 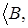 Z Z
 B
B 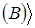 .
В этом случае зависимыми будут только те подмножества множества .
В этом случае зависимыми будут только те подмножества множества 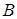 , которые были зависимы в пространстве , которые были зависимы в пространстве 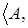 Z
Z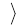 .
И если пространство
.
И если пространство 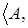 Z
Z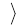 транзитивно, то транзитивным будет и подпространство
транзитивно, то транзитивным будет и подпространство 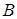 . .
Пример 8.
Пусть 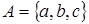 и Z
= и Z
=
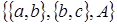 . Такое пространство зависимости . Такое пространство зависимости 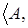 Z
Z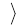 не транзитивно, так как
не транзитивно, так как 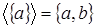 и и 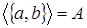 . Пространство А имеет два базиса . Пространство А имеет два базиса 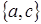 и и 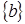 , которые являются и единственными минимальными порождающими множествами в , которые являются и единственными минимальными порождающими множествами в 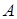 . .
Этот пример показывает, что существуют не транзитивные пространства зависимости, в которых минимальные порождающие множества независимы, то есть являются базисами.
Пример 9.
Зададим на множестве N
натуральных чисел следующее отношение зависимости:
Z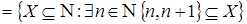 .
.
Получаем бесконечную строго возрастающую цепочку оболочек в 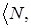 Z
Z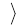 . При
. При 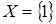 получаем получаем
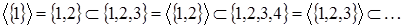 . .
Таким образом, имеем 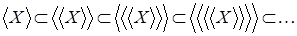 . .
Замечание.
Понятие пространства зависимости можно и удобно определять через базу зависимости. Именно, множество
B
всех минимальных зависимых множеств пространства зависимости
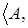 Z
Z назовем его базой
.
Ясно, что множества из B
непусты, конечны и не содержатся друг в друге. Кроме того, любое независимое множество содержит некоторое множество базы B
.
Пространство
назовем его базой
.
Ясно, что множества из B
непусты, конечны и не содержатся друг в друге. Кроме того, любое независимое множество содержит некоторое множество базы B
.
Пространство  Z
Z имеет единственную базу и однозначно определяется ей. Поэтому пространства зависимости можно задавать базами.
имеет единственную базу и однозначно определяется ей. Поэтому пространства зависимости можно задавать базами.
Легко видеть, что верно следующее утверждение:
Непустое множество
B
подмножеств множества
 задает на задает на 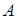 отношение зависимости тогда и только тогда, когда множества из
B
непусты, конечны и не включены друг в друга. отношение зависимости тогда и только тогда, когда множества из
B
непусты, конечны и не включены друг в друга.
В терминах базы B
можно сформулировать условие транзитивности соответствующего пространства зависимости.
§2. Пространства зависимости
Теорема
1.
Пусть
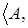 Z
Z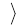 - произвольное пространство зависимости. Рассмотрим следующие три утверждения:
- произвольное пространство зависимости. Рассмотрим следующие три утверждения:
(i) X
— базис в
A
;
(ii) X
— максимальное независимое подмножество в
A
;
(iii) X
— минимальное порождающее множество в
A
.
Тогда  и и 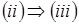 . .
Доказательство:
(
i
)
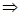 (
ii
)
Если X
– базис, то по определению 6 X
– независимое порождающее подмножество. Докажем от противного, что оно максимальное. Пусть существует независимые множества
(
ii
)
Если X
– базис, то по определению 6 X
– независимое порождающее подмножество. Докажем от противного, что оно максимальное. Пусть существует независимые множества 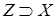 . Возьмем . Возьмем 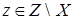 , тогда , тогда 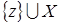 независимо, так как любое подмножество независимого множества независимо. Поэтому по определениям 3 и 5 независимо, так как любое подмножество независимого множества независимо. Поэтому по определениям 3 и 5 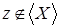 , откуда , откуда 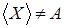 , получили противоречие с условием. Поэтому X
является максимальным независимым подмножеством в A
. , получили противоречие с условием. Поэтому X
является максимальным независимым подмножеством в A
.
(
ii
)
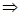 (
i
)
Докажем от противного, пусть
(
i
)
Докажем от противного, пусть 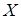 не базис в не базис в 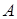 , то есть , то есть 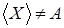 . Тогда . Тогда 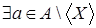 такое, что такое, что 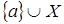 независимо и лежит в независимо и лежит в 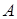 , получили противоречие с максимальностью , получили противоречие с максимальностью 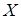 . .
(ii) 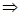 (iii)
Если X
— максимальное независимое множество в A
, то всякий элемент у (iii)
Если X
— максимальное независимое множество в A
, то всякий элемент у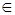 A
либо принадлежит X
,
либо таков, что
A
либо принадлежит X
,
либо таков, что 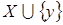 зависимо, а поэтому зависимо, а поэтому 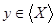 в том и другом случае, то есть в том и другом случае, то есть 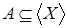 Поскольку Поскольку 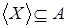 , то X
-
порождающее множество.
Значит, , то X
-
порождающее множество.
Значит, 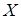 - базис пространства - базис пространства 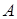 . .
Докажем теперь, что оно минимально. Пусть множество 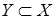 . Докажем, что оно не является порождающим для A
. Возьмем . Докажем, что оно не является порождающим для A
. Возьмем 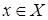 , но , но 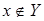 . Тогда . Тогда 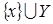 независимо, как подмножество множества X
. Поэтому по определениям 3 и 5 независимо, как подмножество множества X
. Поэтому по определениям 3 и 5 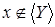 и и 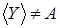 , а это значит, что Y
не является порождающим множеством. Вывод: X
– минимальное порождающее множество в A
. , а это значит, что Y
не является порождающим множеством. Вывод: X
– минимальное порождающее множество в A
.
(i) 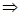 (iii) С
праведливо, по доказанным выше утверждениям (i) (iii) С
праведливо, по доказанным выше утверждениям (i)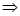 (ii) и (ii) (ii) и (ii) 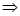 (iii). ■ (iii). ■
Определение - обозначение 10.
Для произвольного множества 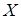 пространства зависимости пространства зависимости 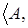 Z
Z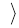 обозначим
обозначим
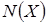 множество всех максимальных независимых подмножеств, а через множество всех максимальных независимых подмножеств, а через  - множество всех минимальных порождающих подмножеств этого множества. - множество всех минимальных порождающих подмножеств этого множества.
Из теоремы 1 вытекает, что 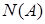 совпадает с множеством всевозможных базисов пространства совпадает с множеством всевозможных базисов пространства 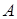 и
и 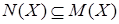 для любого для любого 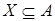 . .
Следующий пример показывает, что обратное включение 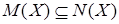 верно не всегда. верно не всегда.
Пример 10.
Рассмотрим девятиэлементное множество 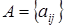 , которое записано в виде матрицы , которое записано в виде матрицы  . Зависимыми
будем считать подмножества множества . Зависимыми
будем считать подмножества множества 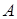 , содержащие «прямые линии»: столбцы, строки или диагонали матрицы , содержащие «прямые линии»: столбцы, строки или диагонали матрицы 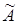 . .
Рассмотрим множества 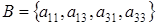 и и 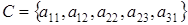 , они будет максимальными независимыми, так как не содержат прямых и при добавлении любого элемента из , они будет максимальными независимыми, так как не содержат прямых и при добавлении любого элемента из 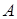 , не лежащего в них, становятся зависимыми. Здесь максимальные независимые множества содержат разное количество элементов. , не лежащего в них, становятся зависимыми. Здесь максимальные независимые множества содержат разное количество элементов.
Рассмотрим еще одно множество 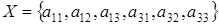 , оно является минимальным порождающим, так как если исключить из него хотя бы один элемент, то оно уже не будет порождающим множеством. Легко заметить, что , оно является минимальным порождающим, так как если исключить из него хотя бы один элемент, то оно уже не будет порождающим множеством. Легко заметить, что 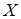 зависимо, поэтому не является базисом. Данный пример иллюстрирует, что (iii) зависимо, поэтому не является базисом. Данный пример иллюстрирует, что (iii)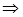 (i) не верно в общем случае, то есть для произвольных пространств зависимости. (i) не верно в общем случае, то есть для произвольных пространств зависимости.
Для любого пространства зависимости 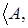 Z
Z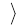 выполняются следующие свойства:
выполняются следующие свойства:
Замещение.
Если 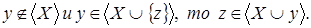
Доказательство:
Пусть 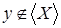 , , 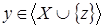 . Так как . Так как 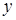 зависит от зависит от 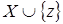 , то , то 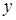 зависит от независимого подмножества зависит от независимого подмножества 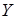 множества множества 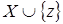 , то есть , то есть 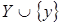 зависимо. Теперь, если бы зависимо. Теперь, если бы 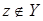 , то , то 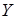 было бы подмножеством множества было бы подмножеством множества 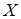 и поэтому и поэтому 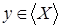 , что противоречило бы нашему предположению. Поэтому , что противоречило бы нашему предположению. Поэтому 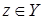 . Возьмем . Возьмем 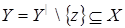 . Тогда . Тогда 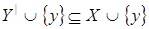 независимо, так как независимо, так как 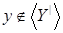 . Но . Но 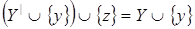 зависимо. Откуда зависимо. Откуда 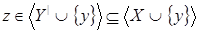 . .
Вложенность.
Объединение любой системы вложенных друг в друга независимых множеств является независимым множеством, то есть  - независимо, где - независимо, где 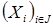 также независимы и также независимы и 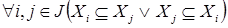
Доказательство:
Докажем от противного. Предположим, что 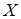 зависимо, тогда в нем найдется конечное зависимое подмножество зависимо, тогда в нем найдется конечное зависимое подмножество 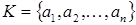 : :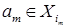 . Имеем . Имеем 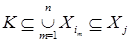 , получили противоречие с независимостью , получили противоречие с независимостью 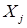 . .
Максимальность.
Любое независимое множество содержится в максимальном независимом множестве.
Доказательство:
Пусть 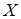 - произвольное независимое множество в - произвольное независимое множество в 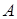 . Образуем множество . Образуем множество 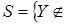 Z
: Z
: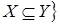 всех независимых множеств, содержащих
всех независимых множеств, содержащих 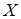 . Относительно . Относительно 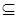 множество множество 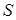 является упорядоченным множеством, удовлетворяющим по свойству вложенности, условию леммы Цорна. Тогда по лемме Цорна в является упорядоченным множеством, удовлетворяющим по свойству вложенности, условию леммы Цорна. Тогда по лемме Цорна в 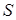 существует максимальный элемен существует максимальный элемен 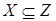 . .
Теорема
2.
Любое пространство зависимости обладает базисом.
Доказательство:
Возьмем пустое множество, оно независимо. По свойству максимальности оно должно содержаться в некотором максимальном независимом множестве, которое по теореме 1 является базисом.
§3. Транзитивность
Особый интерес представляют транзитивные пространства зависимости. Важным результатом является доказательство инвариантности размерности любого транзитивного пространства зависимости.
Докажем некоторые свойства
, справедливые для транзитивных пространств зависимости 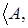 Z
Z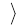 .
.
Свойство 1:
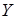 зависит от зависит от 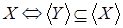 .
.
Доказательство:
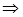
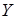 зависит от зависит от 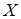 , то есть , то есть 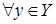 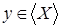 , и , и 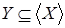 . Рассмотрим . Рассмотрим 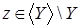 , тогда , тогда 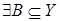 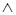 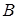 - независимо и - независимо и 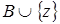 - зависимо, а - зависимо, а 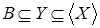 , получаем, что , получаем, что 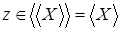 , поэтому , поэтому 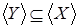 . Имеем . Имеем 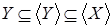 . .
 По определению 8 любое подмножество По определению 8 любое подмножество 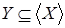 зависит от зависит от 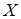
Свойство 2:
Если 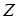 зависит от зависит от 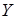 , а , а 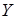 зависит от зависит от 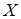 , то , то 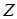 зависит от зависит от 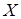 . .
Доказательство:
Запишем условие, используя свойство 1  , а , а 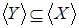 , тогда очевидно, что , тогда очевидно, что 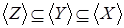 .■ .■
Свойство 3:
Если
X
— минимальное порождающее множество в
A
, то
X
— базис в
A
.
Доказательство:
Пусть X
— минимальное порождающее множество в A
. Покажем, что оно не может быть зависимым, так как в этом случае его можно было бы заменить собственным подмножеством, все еще порождающим A
. Действительно, в силу транзитивности отношения зависимости, любое множество, порождающее множество X,
будет так же порождать и множество A
. Следовательно, X
- независимое порождающее множество, которое по определению 6 является базисом.
Свойство 4: 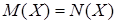 для любого
для любого 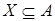 . .
Доказательство:
Следует из свойства 3.
Свойство 5 (о замене.)
:
Если
X
— независимое множество и
Y
— порождающее множество в
A
, то существует такое подмножество 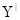 множества
Y
, что множества
Y
, что 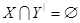 и и
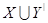 — базис для
A
.
— базис для
A
.
Доказательство:
Рассмотрим систему J таких независимых подмножеств Z множества A
,
что 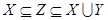 . .
Так как X
независимо, то такие множества существуют; кроме того, если 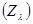 — некоторое линейно упорядоченное множество множеств из J,
то его объединение — некоторое линейно упорядоченное множество множеств из J,
то его объединение 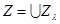 снова принадлежит J,
поскольку Z удовлетворяет условию снова принадлежит J,
поскольку Z удовлетворяет условию 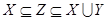 , и если Z зависимо, то некоторое конечное подмножество множества Z должно было бы быть зависимым; это подмножество содержалось бы в некотором множестве
, и если Z зависимо, то некоторое конечное подмножество множества Z должно было бы быть зависимым; это подмножество содержалось бы в некотором множестве 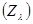 в противоречии с тем фактом, что все в противоречии с тем фактом, что все 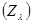 независимы. независимы.
По лемме Цорна J имеет максимальный элемент М;
в силу максимальности каждый элемент множества Y
либо принадлежит М,
либо зависит от М,
откуда 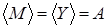 . Этим доказано, что М — базис в A
.
Так как . Этим доказано, что М — базис в A
.
Так как 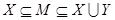 , то М имеет вид , то М имеет вид 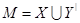 , где , где 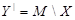 удовлетворяет условиям удовлетворяет условиям 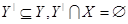 .■ .■
Определение 11.
Пространство зависимости
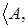 Z
Z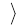 называется конечномерным, если любое его независимое множество конечно.
называется конечномерным, если любое его независимое множество конечно.
Теорема 3
.
Пусть
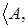 Z
Z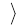 - транзитивное пространство зависимости. Тогда любые два базиса в этом пространстве равномощны.
- транзитивное пространство зависимости. Тогда любые два базиса в этом пространстве равномощны.
Доказательство:
Рассмотрим сначала случай конечномерного пространства 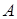 . .
Пусть В, С
— любые два базиса в А
, их существование обеспечивается теоремой 2, и 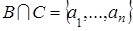 , , 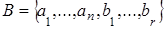 , , 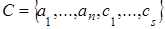 , где различные элементы обозначены различными буквами или снабжены различными индексами. Применим индукцию по max
(
r
,
s
). , где различные элементы обозначены различными буквами или снабжены различными индексами. Применим индукцию по max
(
r
,
s
).
Если r = 0
или s = 0
, то 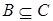 или или 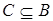 , и , и 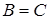 . Поэтому можно предполагать, что r ≥ 1, s ≥ 1
, без ограничения общности будем считать, что r > s
, так что на самом деле r > 1
. . Поэтому можно предполагать, что r ≥ 1, s ≥ 1
, без ограничения общности будем считать, что r > s
, так что на самом деле r > 1
.
Предположим, что базисы будут равномощными для любого t < r
По лемме о замене множество 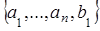 можно дополнить до базиса D
элементами базиса С
, скажем можно дополнить до базиса D
элементами базиса С
, скажем
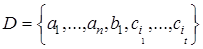 , t ≤ s < r. , t ≤ s < r.
Теперь пересечение D
c В
состоит из n + 1
элемента, и D
содержит, кроме того, еще t (< r) элементов, тогда как В
содержит, кроме этого пересечения, еще r - 1 элементов, так что по предположению индукции 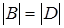 , то есть , то есть 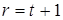 . .
Поскольку r > 1
, отсюда вытекает, что t ≥ 1
, и поэтому пересечение D
с С содержит не меньше чем n+1
элементов. Используя еще раз предположение индукции, находим, что 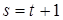 и, следовательно, r = s
и базисы В
и С
равномощны. и, следовательно, r = s
и базисы В
и С
равномощны.
Далее, пусть В
- конечный базис в 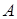 . Тогда и любой другой базис С
пространства
. Тогда и любой другой базис С
пространства 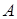 будет конечным. Действительно, В
выражается через конечное множество элементов
будет конечным. Действительно, В
выражается через конечное множество элементов 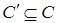 в силу транзитивности в силу транзитивности 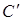 будет порождающим и независимым множеством в будет порождающим и независимым множеством в 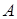 , то есть
, то есть 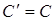 . .
Наконец, если базисы В
и С
бесконечны. Каждый элемент из В
зависит от некоторого конечного подмножества базиса С
, и наоборот. Мощность множества всех конечных подмножеств всякого бесконечного множества равна мощности самого множества. Поэтому мощности В
и С
совпадают.■
Теорема 4
.
Пусть
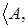 Z
Z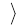 - произвольное пространство зависимости, тогда следующие условия эквивалентны
- произвольное пространство зависимости, тогда следующие условия эквивалентны
(i) Z
транзитивно;
(ii) для любого конечного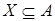 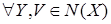 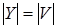 ; ;
(iii) 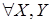 конечных и конечных и 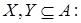 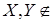 Z Z
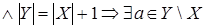
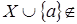 Z
; Z
;
(iv) для любого конечного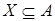 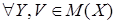 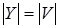 . .
Доказательство:
(
i
)
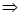 (
ii
)
Справедливо по теореме 3 и примеру 7.
(
ii
)
Справедливо по теореме 3 и примеру 7.
(
ii
)
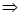 (
iii
)
Возьмем
(
iii
)
Возьмем 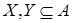 , так что , так что 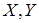 - независимы и - независимы и 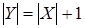 . Допустим, что утверждение . Допустим, что утверждение 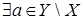 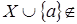 Z
неверно. Тогда Z
неверно. Тогда 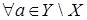 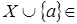 Z
.
Рассмотрим Z
.
Рассмотрим 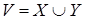 . Имеем . Имеем 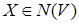 . Но . Но 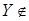 Z
, поэтому Z
, поэтому 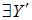 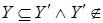 Z Z
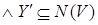 . По (ii) имеем . По (ii) имеем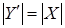 . Но . Но 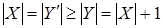 - противоречие. - противоречие.
(
iii
)
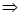 (
ii
)
Докажем от противного. Пусть
(
ii
)
Докажем от противного. Пусть 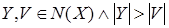 . Можно считать, что . Можно считать, что 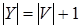 . Тогда по (iii) . Тогда по (iii) 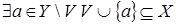 независимо. Получили противоречие с максимальностью независимо. Получили противоречие с максимальностью 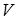
(
iii
)
 (
i
)
Нужно доказать равенство
(
i
)
Нужно доказать равенство 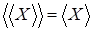 для произвольного для произвольного 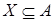 . .
Возьмем 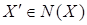 и покажем, что и покажем, что 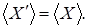 Так как Так как 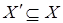 , то , то 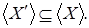 Пусть существует Пусть существует 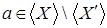 , тогда , тогда 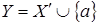 независимо и существует независимо и существует 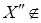 Z
и Z
и 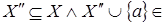 Z
. Расширяя Z
. Расширяя  в в 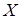 можно предположить, что можно предположить, что 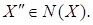 По (ii) По (ii) 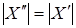 , то есть , то есть 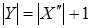 . Поэтому по (iii) . Поэтому по (iii) 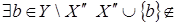 Z
. видим, что Z
. видим, что 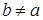 . Значит, . Значит, 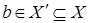 . Получаем противоречие с тем, что . Получаем противоречие с тем, что 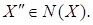 Следовательно, Следовательно, 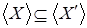 , то сеть , то сеть 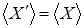 . .
Теперь достаточно показать, что 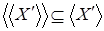 . Пусть . Пусть 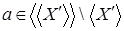 , тогда , тогда 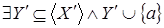 зависимо, расширяя зависимо, расширяя 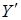 в в 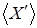 можно предположить, что можно предположить, что 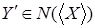 , кроме того , кроме того 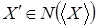 , тогда по (ii) , тогда по (ii) 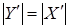 . . 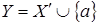 независимо, поэтому независимо, поэтому 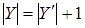 . По (iii) . По (iii) 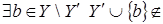 Z
. видим, что Z
. видим, что 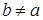 . Значит, . Значит, 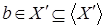 , получили противоречие с максимальностью , получили противоречие с максимальностью 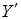 . Следовательно, . Следовательно, 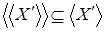 , обратное включение очевидно, поэтому , обратное включение очевидно, поэтому 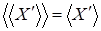 . .
(
iv
) 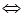 (
ii
)
В силу теорем 1 и 3 и доказанной эквивалентности (
ii
)
В силу теорем 1 и 3 и доказанной эквивалентности
(
i
) 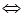 (
ii
)
.■ (
ii
)
.■
Далее будем рассматривать произвольное конечномерное транзитивное пространство зависимости 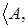 Z
Z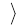 .
.
Определение 12.
Мощность максимального независимого подмножества данного множества 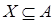 называется рангом
этого множества: называется рангом
этого множества:  . .
Будем рассматривать конечные подмножества 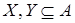 . .
Имеют место следующие свойства.
Свойство 1о
: 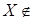 Z
Z 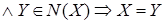 . .
Доказательство:
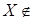 Z Z 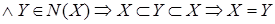 . .
Свойство 2о
:
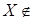 Z Z 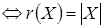 . .
Доказательство:
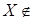 Z, возьмем
Z, возьмем 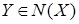 ,
тогда по свойству 1о ,
тогда по свойству 1о
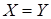 и и 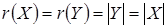 . Обратное утверждение следует из определения 13. . Обратное утверждение следует из определения 13.
Свойства 3о
– 7о
сформулированы для 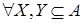 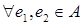 . .
Свойство 3о
:
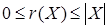 . .
Доказательство:
Ясно, что 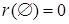 , и так как число элементов любого подмножества не больше числа элементов самого множества, то данное свойство выполняется. , и так как число элементов любого подмножества не больше числа элементов самого множества, то данное свойство выполняется.
Свойство 4о
:
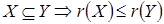 . .
Доказательство:
следует из того, что любое независимое подмножество в 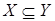 можно продолжить до максимального независимого подмножества в можно продолжить до максимального независимого подмножества в 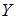 ; ;
Свойство 5о
:
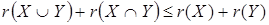 . .
Доказательство:
Пусть 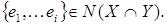 Тогда Тогда 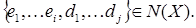 И затем И затем  . Имеем . Имеем 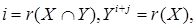 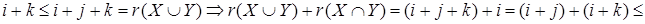 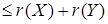 . .
Свойство 6о
:
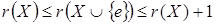 . .
Доказательство:
вытекает из свойства 40
;
Свойство 7о
:
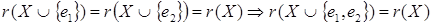 . .
Доказательство:
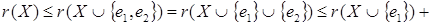
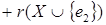 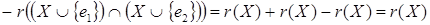 . .
§4. Связь транзитивных отношений зависимости с операторами замыкания
Транзитивное отношение зависимости также может быть описано с помощью алгебраического оператора замыкания некоторого типа. Для начала сформулируем определения используемых понятий.
Определение 13.
Множество E подмножеств множества A называется системой замыканий
, если 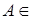 E и система E замкнута относительно пересечений, т. е. ∩
D E и система E замкнута относительно пересечений, т. е. ∩
D
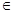 E для любой непустого подмножества
D E для любой непустого подмножества
D
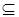 E E
Определение 14.
Оператором замыкания
на множестве A называется отображение J множества B (A) в себя, обладающее следующими свойствами:
J. 1. Если 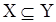 , то J(X) , то J(X)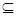 J(Y); J(Y);
J. 2. X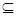 J(X); J(X);
J. 3. JJ(X) = J(X), для всех X, Y 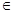 B (A). B (A).
Определение 15.
Оператор замыкания J на множестве A называется алгебраическим
, если для любых 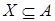 и и 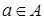 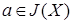 влечет влечет 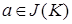 для некоторого конечного подмножества для некоторого конечного подмножества 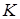 множества множества 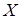 . .
Определение 16.
Система замыканий называется алгебраической
, если только соответствующий оператор замыкания является алгебраическим
Следует отметить теорему о взаимосвязи между системами замыканий и операторами замыканий.
Теорема 5.
Каждая система замыканий E на множестве
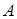 определяет оператор замыкания J на определяет оператор замыкания J на
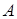 по правилу J(X) = ∩{Y по правилу J(X) = ∩{Y 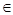 E | Y E | Y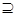 X}. Обратно, каждый оператор замыкания J на X}. Обратно, каждый оператор замыкания J на
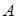 определяет систему замыканий E определяет систему замыканий E 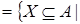 J J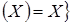 . .
Следующая теорема показывает связь транзитивного отношения зависимости и алгебраического оператора замыкания.
Теорема 6.
Для любого транзитивного отношения зависимости 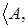 Z
Z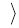 отображение
отображение 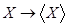 является алгебраическим оператором замыкания на
А
со свойством замещения. является алгебраическим оператором замыкания на
А
со свойством замещения.
Обратно, любой алгебраический оператор замыкания на А со свойством замещения получается таким способом из некоторого транзитивного отношения зависимости
Z
на
А.
Доказательство:
I.
Будем называть подмножество Т множества
A
замкнутым,
если 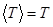 . .
Покажем сначала, что замкнутые подмножества образуют систему замыканий. Если 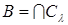 , где , где 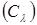 - семейство замкнутых множеств, то пусть - семейство замкнутых множеств, то пусть 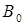 - такое независимое подмножество множества B, что
- такое независимое подмножество множества B, что 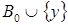 зависимо; поскольку зависимо; поскольку 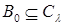 для всех для всех 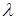 , имеем , имеем 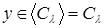 , откуда , откуда 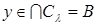 , то есть В замкнуто. , то есть В замкнуто.
Пусть 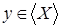 , то по определению 3 , то по определению 3 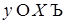 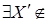 Z Z
 конечное, такое что конечное, такое что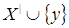 зависимо. В первом случае зависимо. В первом случае 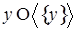 , а во втором , а во втором 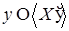 . И поскольку . И поскольку 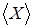 замкнуто в силу транзитивности, получаем алгебраический оператор замыкания. замкнуто в силу транзитивности, получаем алгебраический оператор замыкания.
Этим доказано, что замкнутые подмножества образуют алгебраическую систему замыканий.
Выполнение свойства замещения следует из соответствующего свойства пространств зависимости.
II.
Обратно, пусть 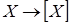 - алгебраический оператор замыкания со свойством замещения. - алгебраический оператор замыкания со свойством замещения.
Будем считать 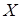 зависимым
, если зависимым
, если 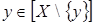 для некоторого для некоторого 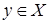 , и независимым
в противном случае. , и независимым
в противном случае.
Так как оператор алгебраический, то отсюда вытекает, что всякое зависимое множество обладает конечным зависимым подмножеством, и поскольку очевидно, что всякое множество, содержащее зависимое подмножество, само зависимо, таким образом получаем отношение зависимости. Условие транзитивности выполняется по определению, и это показывает, что мы имеем транзитивное отношение зависимости.
Теперь для любых 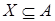 , , 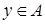 имеем имеем 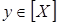 тогда и только тогда, когда тогда и только тогда, когда 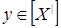 для некоторого конечного подмножества для некоторого конечного подмножества 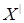 множества множества 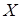 . Выбирая . Выбирая 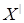 минимальным, можем предполагать, что минимальным, можем предполагать, что 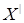 независимо. Отсюда вытекает, что независимо. Отсюда вытекает, что  и, следовательно, и, следовательно, 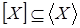 . .
Обратно, если 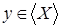 , то снова , то снова 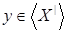 для некоторого конечного независимого подмножества для некоторого конечного независимого подмножества 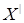 множества множества 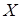 . Это означает, что . Это означает, что 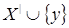 зависимо, т.е. зависимо, т.е. 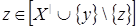 для некоторого для некоторого 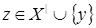 . .
В силу свойства замещения получаем, что 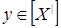 и и 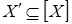 , поэтому , поэтому 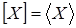 . .
Замечание.
Существуют алгебраические операторы замыкания, не обладающие свойством замещения. Для примера возьмем бесконечную циклическую полугруппу 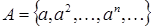 . .
Пусть 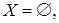 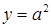 и и 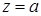 . Тогда . Тогда 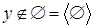 , , 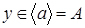 , но , но 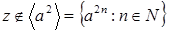 . .
§5. Матроиды
Понятие матроида тесно связано с понятием отношения зависимости, поэтому эта тема рассматривается в данной квалификационной работе. Однако с другой стороны оно является теоретической основой для изучения и анализа «жадных» алгоритмов.
Определение 17.
Матроидом 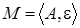 называется конечное множество и семейство его подмножеств
называется конечное множество и семейство его подмножеств 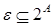 , такое что выполняется три аксиомы: , такое что выполняется три аксиомы:
М1
: 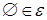 ; ;
М2
: 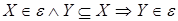 ; ;
М3
: 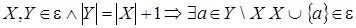
Определение 18.
Элементы множества 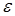 называются независимыми
, а остальные подмножества называются независимыми
, а остальные подмножества 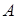 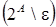 - зависимыми
множествами. - зависимыми
множествами.
В соответствии с введенными ранее аксиомами пространства зависимости видим, что матроиды - это в точности конечные транзитивное пространства зависимости.
Рассмотрим следующие примеры матроидов:
Пример 1.
Семейство всех линейно независимых подмножеств любого конечного множества векторов произвольного непустого векторного пространства является матроидом.
Действительно, по определению можно считать, что пустое множество линейно независимо. Всякое подмножество линейно независимого подмножества векторов линейно независимо. Пусть 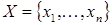 и и 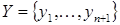 - линейно независимые множества. Если бы все векторы из множества - линейно независимые множества. Если бы все векторы из множества 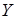 выражались в виде линейной комбинации векторов из множества выражались в виде линейной комбинации векторов из множества 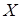 , то множество , то множество 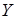 было бы линейно зависимым. Поэтому, среди векторов множества было бы линейно зависимым. Поэтому, среди векторов множества 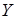 есть по крайней мере один вектор есть по крайней мере один вектор 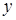 , который не входит в множество , который не входит в множество 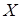 и не выражается в виде линейной комбинации векторов из множества и не выражается в виде линейной комбинации векторов из множества 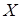 . Добавление вектора . Добавление вектора 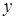 к множеству к множеству 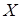 образует линейно независимое множество. образует линейно независимое множество.
Пример 2.
Свободные матроиды. Если 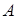 - произвольное конечное множество, то - произвольное конечное множество, то 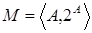 - матроид. Такой матроид называется свободным
. В свободном матроиде каждое множество независимо, А
является базисом и - матроид. Такой матроид называется свободным
. В свободном матроиде каждое множество независимо, А
является базисом и 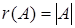 . .
Пример 3.
Матроид трансверсалей. Пусть 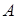 - некоторое конечное множество, и - некоторое конечное множество, и 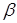 - некоторое семейство подмножеств этого множества. Подмножество - некоторое семейство подмножеств этого множества. Подмножество 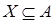 называется частичной трансверсалью семейства называется частичной трансверсалью семейства 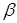 , если , если 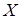 содержит не более чем по одному элементу каждого подмножества из семейства содержит не более чем по одному элементу каждого подмножества из семейства 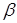 . Частичные трансверсали над . Частичные трансверсали над 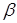 образуют матроид на А
. образуют матроид на А
.
Перейдем к рассмотрению жадного алгоритма. Для начала нужно сформулировать задачу, которую будем решать с его использованием.
Пусть имеются конечное множество 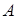 , , 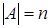 , весовая функция , весовая функция 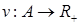 и семейство и семейство 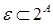 . .
Рассмотрим следующую задачу: найти 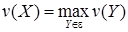 , где , где 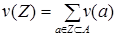 . Другими словами, необходимо выбрать в указанном семействе подмножество наибольшего веса. . Другими словами, необходимо выбрать в указанном семействе подмножество наибольшего веса.
Не ограничивая общности, можно считать, что 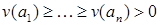
Рассмотрим такой алгоритм, который исходными данными имеет множество 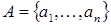 , семейство его подмножеств , семейство его подмножеств 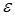 и весовую функцию и весовую функцию 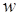 , причем множество , причем множество 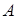 упорядочено в порядке убывания весов элементов. После выполнения этого алгоритма мы получим подмножество упорядочено в порядке убывания весов элементов. После выполнения этого алгоритма мы получим подмножество 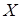 . .
Изначально искомое множество 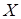 пусто, далее просматриваем по очереди все элементы из множества пусто, далее просматриваем по очереди все элементы из множества 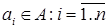 и проверяем зависимость множества и проверяем зависимость множества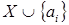 , если , если 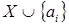 - независимо, то элемент - независимо, то элемент 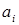 добавляем в множество добавляем в множество 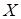 , если же , если же 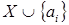 - зависимо, то переходим к элементу - зависимо, то переходим к элементу 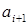 , пока все элементы из множества , пока все элементы из множества 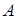 не будут проверены. не будут проверены.
Алгоритм такого типа называется «жадным». Совершенно очевидно, что по построению окончательное множество 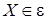 , то есть независимо. Также очевидно, что жадный алгоритм является чрезвычайно эффективным: количество шагов составляет , то есть независимо. Также очевидно, что жадный алгоритм является чрезвычайно эффективным: количество шагов составляет 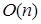 , то есть жадный алгоритм является линейным. (Не считая затрат на сортировку множества , то есть жадный алгоритм является линейным. (Не считая затрат на сортировку множества 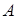 и проверку независимости и проверку независимости 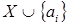 .) .)
Пример 4.
Пусть дана матрица 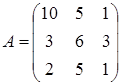 . Рассмотрим следующие задачи. . Рассмотрим следующие задачи.
Задача 1.
Выбрать по одному элементу из каждого столбца
, так чтобы их сумма была максимальна.
Здесь весовая функция 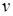 ставит в соответствие элементу матрицы ставит в соответствие элементу матрицы 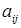 его значение. Например, его значение. Например, 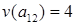 . .
Множество 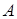 упорядоченно следующим образом: упорядоченно следующим образом: 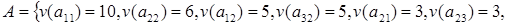
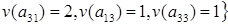 . .
Семейство независимых подмножеств 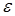 будут образовывать такие множества, в которых все элементы из разных столбцов и пустое множество. будут образовывать такие множества, в которых все элементы из разных столбцов и пустое множество.
Наш алгоритм будет работать следующим образом:
0 шаг (нач. усл.): 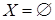 ; ;
1 шаг: поверяем для элемента 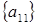 , , 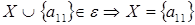 ; ;
2 шаг: для 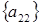 , ,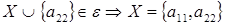 ; ;
3 шаг: для 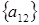 , ,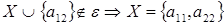 ; ;
4 шаг: для 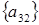 , ,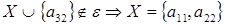 ; ;
5 шаг: для 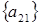 , ,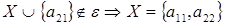 ; ;
6 шаг: для 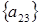 , ,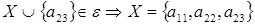 ; ;
7 шаг: для 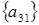 , ,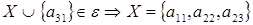 ; ;
8 шаг: для 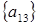 , , ; ;
9 шаг: для 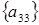 , ,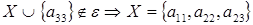 ; ;
В результате получили множество 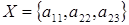 , , 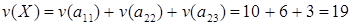 ., полученный результат действительно является решением задачи. ., полученный результат действительно является решением задачи.
Задача 2.
Выбрать по одному элементу из каждой строки
, так чтобы их сумма была максимальна.
Здесь функция 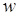 и множество и множество 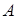 такие же как и в предыдущей задаче, а семейство независимых подмножеств такие же как и в предыдущей задаче, а семейство независимых подмножеств 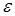 будут образовывать такие множества, в которых все элементы из разных строк и пустое множество. будут образовывать такие множества, в которых все элементы из разных строк и пустое множество.
Используя наш алгоритм получим следующее решение: множество 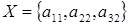 и и 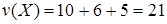 , которое так же является верным. , которое так же является верным.
Задача 3.
Выбрать по одному элементу из каждого столбца и из каждой строки
, так чтобы их сумма была максимальной.
В этой задаче функция 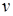 и множество и множество 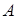 остаются прежними, а семейство независимых подмножеств остаются прежними, а семейство независимых подмножеств 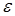 будут образовывать такие множества, в которых все элементы из разных столбцов и различных строк и пустое множество. будут образовывать такие множества, в которых все элементы из разных столбцов и различных строк и пустое множество.
Нетрудно видеть, что жадный алгоритм выберет следующие элементы:
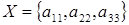 и и 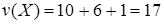 , которые не являются решением задачи, поскольку существует лучшее решение - , которые не являются решением задачи, поскольку существует лучшее решение - 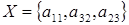 и и 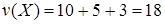 . .
Возникает вопрос, в каких же случаях жадный алгоритм действительно решает поставленную задачу? На поставленный вопрос поможет ответить теорема, сформулированная и доказанная в [4, с.75-76].
Теорема 7.
Для любой функции
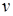 жадный алгоритм находит независимое множество жадный алгоритм находит независимое множество 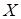 с наибольшим весом, тогда и только тогда, когда с наибольшим весом, тогда и только тогда, когда 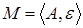 является матроидом. является матроидом.
Действительно, в нашем примере в задачах 1 и 2 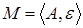 - матроид, а в задаче 3 таковым не является, так как не выполняется аксиома М3
. Если рассмотреть
- матроид, а в задаче 3 таковым не является, так как не выполняется аксиома М3
. Если рассмотреть 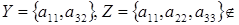 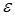 ,
тогда ,
тогда 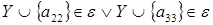 получили противоречие с независимостью хотя бы одного из множеств. получили противоречие с независимостью хотя бы одного из множеств.
Список библиографии
1. Ван дер Варден Б.Л. Алгебра. – М.: Наука, 1976. – 648 с.
2. Кон П. Универсальная алгебра. – М.: Мир, 1968. – 352 с.
3. Курош А. Г. Курс высшей алгебры. – СПб: Лань, 2006. – 432 с.
4. Новиков Ф. А. Дискретная математика для программистов. – Спб: Питер, 2001. – 304 с.
5. Фрид Э. Элементарное введение в абстрактную алгебру. – М.: Мир, 1974. – 260 с.
|