| Министерство образования и науки Украины
Севастопольский национальный технический университет
Кафедра ТК
Пояснительная записка
к курсовому проекту
«Разработка следящей системы промышленного робота»
по дисциплине
«Теория автоматического управления»
Исполнитель: ст.гр. А-44д.
Анищенко А.А.
Руководитель: Грушун Т.А.
Севастополь
2004
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1
КРАТКОЕ ОПИСАНИЕ САУ
Цель работы
Вариант задания
1.1 Краткое описание целей и принципов работы исследуемой САУ
1.2 Функциональная схема следящей системы промышленного робота
2
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОТДЕЛЬНЫХ ЗВЕНЬЕВ СИСТЕМЫ
3
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ КОРРЕКТИРУЮЩЕГО ЗВЕНА
4
Д – РАЗБИЕНИЕ
5
АНАЛИЗ ВЛИЯНИЯ НЕЛИНЕЙНОСТИ НА СВОЙСТВА САУ
6
АНАЛИЗ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
ЗАКЛЮЧЕНИЕ
БИБЛИОГРАФИЯ
Приложение А
Приложение Б
Приложение В
ВВЕДЕНИЕ
При проектировании САУ обычно задаются необходимые для нормальной работы показатели качества регулирования при некотором типовом воздействии. При этом решается как задача анализа, так и задача синтеза. Задача синтеза противоположна задаче анализа. Если при анализе структура и параметры заданы, а ищут или рассматривают поведение системы в заданных условиях, то в задаче синтеза задание и цель меняются местами.
Характер задания может быть различным. Существуют методы синтеза, при которых задается кривая переходного процесса. Однако реализация систем с переходным процессом, заданным чрезмерно жестко, как правило, оказывается весьма трудной: система получается неоправданно сложной и зачастую нереализуемой, в то время как небольшое отступление от заданной кривой может привести к существенному упрощению структуры. Поэтому более распространен метод задания более грубых качественных оценок, таких, как перерегулирование и время регулирования или же показатель колебательности, при которых сохраняется большая свобода в выборе детальной формы кривой переходного процесса. Задание кривой переходного процесса не исключено: им обычно пользуются при синтезе систем сложной структуры, когда требуется регулирование нескольких координат.
Задача синтеза обычно имеет множество решений, и выбор из этого множества наиболее рационального решения не может быть сделан только на основании математических расчетов. Это больше инженерная, чем математическая задача. Чаще всего задается ряд элементов системы управления (объект регулирования, двигатели, усилители и т. п., поскольку при построении систем разумно максимально использовать широкую номенклатуру элементов автоматики, выпускаемых промышленностью). Нередко выбор основных типовых звеньев предопределяет и основные черты структуры системы. Назовем совокупность заданных элементов неизменяемой частью системы, а ту часть, которую надо найти в процессе синтеза, — изменяемой частью системы или корректирующим устройством.
Реклама

При инженерном синтезе САУ необходимо обеспечить, во-первых, требуемую точность и, во-вторых, желаемый характер переходных процессов.
Решение первой задачи в большинстве случаев сводится к определению требуемого общего коэффициента усиления системы и, в случае необходимости,— вида корректирующих средств, повышающих точность системы. Эта задача может решаться при помощи определения ошибок в типовых режимах на основе критериев точности. Решение этой задачи, как правило, не сопряжено с трудностями принципиального или вычислительного характера, так как критерии точности достаточно просты для их практического использования. В сложных случаях можно прибегать к помощи моделирования. Решение оказывается сравнительно простым вследствие необходимости установления значений относительно небольшого числа параметров. В простейшем случае необходимо найти только общий коэффициент усиления системы.
Решение второй задачи — обеспечение приемлемых переходных процессов — оказывается почти всегда более трудным вследствие большого числа варьируемых параметров и многозначности решения задачи демпфирования системы. Поэтому существующие инженерные методы часто ограничиваются решением только второй задачи, так как их авторы считают, что обеспечение требуемой точности может быть достаточно просто сделано на основании использования существующих критериев точности и совершенствования их практически не требуется.
В настоящее время для целей анализа и синтеза систем САУ широко используются ПЭВМ, позволяющие производить полное или частичное моделирование системы. При таком моделировании становится возможным наиболее полно исследовать влияние различных факторов нелинейности, зависимость параметров от времени и т. п.
Однако моделирование на ЭВМ не может заменить расчетных методов проектирования, которые во многих случаях позволяют исследовать вопрос в общем виде и среди многих решений найти оптимальное. Поэтому, несмотря на развитие и распространение машинных методов синтеза, теория должна располагать собственными методами, которые дополняли бы моделирование и являлись бы теоретической базой при отыскании оптимального решения.
Реклама

В курсовом проекте будем рассматривать синтез последовательных корректирующих устройств (элементов) одноконтурных систем управления.
Основными вопросами, изучаемыми в курсовом проекте являются следующие:
- изучение целей и принципов работы САУ, основных алгоритмов их функционирования;
- построение различных видов математических моделей систем управления и их преобразование;
- анализ устойчивости и точности систем управления, построение временных и частотных динамических характеристик;
- синтез систем управления, выбор структуры и расчет параметров корректирующих устройств по заданным показателям точности управления и качества динамических характеристик.
При выполнении курсового проекта мы умело сочетали теоретические и численные методы, при расчетах широко использовались средства вычислительной техники. Выбор ЭВМ осуществляется на основе анализа эффективности их применения для решения конкретных задач исследования систем управления. При использовании ЭВМ мы самостоятельно выбирали пакеты прикладных программ, необходимых для анализа и расчета современных САУ.
1. КРАТКОЕ ОПИСАНИЕ САУ
Цель работы
Приобретение навыков анализа и синтеза систем автоматического управления (САУ) с применением ЭВМ.
Вариант задания
Вариант №10
Параметры передаточной функции:
W3
= КП
= 4;
W4
= КЯ
/ ТЯ
S+1 = 3.0 / 0,03S +1;
W5
= КМ
/ JS = 0.04 / 0.005S;
W6
= Kω
= 0.3 ;
W7
= 1 / iS = 1 / 60s;
W8
= KТГ
= 0,07;
W9
= КОС
= 1;
Показатели качества:
Время регулирования tp
=0,1с;
Перерегулирования σ = 2.9%;
Показатель колебательности μ = 1,5;
Напиши про С
Параметры нелинейности:
А =0.2;
1.1 Краткое описание целей функционирования и принципов работы САУ
Роботы обеспечивают автоматическую работу комплексов технологического оборудования, координированное функционирования большого числа локальных систем управления. Необходимость в групповом управлении вызвана потребностями комплексной автоматизации многофункциональных участков технологического оборудования или сложных многосвязных технологических циклов промышленного производства.
В теории регулирования под управлением понимается автоматическое осуществление совокупности воздействий, направленных на поддержания управляемого объекта в соответствии с целью управления.
Робот как объект управления представляет собой сложную электромеханическую систему, состоящую из многозвенной механической конструкции (рабочего механизма), исполнительного устройства и электронной системы управления. Рабочий механизм непосредственно воздействует на объект или среду. Исполнительное устройство включает совокупность приводов с соответствующими датчиками обратной связи, усилительными, преобразующими и корректирующими элементами.
Задача управления роботом заключается в формировании управляющих воздействий для исполнительных двигателей, обработка которых гарантировала бы прохождение захватным устройством манипулятора заданной пространственной траектории с заданной точностью.
Многообразие систем управления роботами можно группировать по разным признакам, например: по составу и типу входящих устройств, показателям качества управления, вид траектории движения и т.п. Однако имеются достаточно общие признаки, которые принципиально характеризуют процесс управления роботом. Прежде всего это способ управления
, определяемый в зависимости от степени участия оператора в управлении роботом. Другим столь же важным признаком является метод управления
, который можно применить для дальнейшей классификации выделенных классов.
С появлением промышленных роботов проблемы группового управления приобрели ещё большее значение. Возникла необходимость обеспечения совместной работы оборудования с роботами или роботов с роботами. Наибольшая потребность в таком управлении выявилась при автоматизации сборочных процессов. Главная особенность систем автоматического управления роботами – отсутствие непосредственного участия человека в процессе управления. Функция оператора состоит лишь в обучении, запуске и последующем периодическом наблюдении за работой робота.
Развивая систему программного управления, удаётся преодолеть ограниченность роботов первого поколения, повысить гибкость управления и в значительной мере исключить необходимость приспосабливания технологической среды к роботу. Последующие поколения роботов имеют более широкие возможности благодаря разнообразным средствам очувствления, адаптации и технической имитации отдельных интеллектуальных функций, присущих человеку.
1.2 Функциональная схема следящей системы промышленного робота
В соответствии с требуемыми условиями производственного процесса кинематические звенья и захватное устройство промышленного робота (ПР) должны перемещаться в пространстве по заданным траекториям. Такое перемещение в автоматическом режиме осуществляется в современных роботах с помощью системы управления, которая представляет собой сложный взаимосвязанный комплекс следящих систем управления положением звеньев манипулятора – следящих приводов. Каждый привод управляется определенной степенью подвижности манипулятора.
В общем случае, структура отдельной следящей системы промышленного робота (ССПР) может быть представлена функциональной схемой, изображённой на рисунке 1.1.
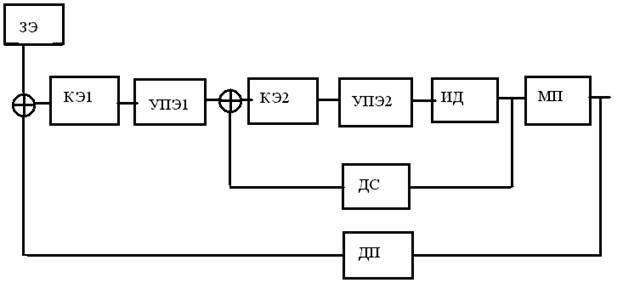
Рисунок 1.1 –Функциональная схема электрической ССПР.
На рисунке приняты такие обозначения:
ЗЭ – задающий элемент, формирующий задающие воздействие по угловому положению;
КЭ1, КЭ2 – корректирующие элементы;
УПЭ1, УПЭ2 – усилительно-преобразующие элементы;
ИД – исполнительный двигатель;
СЭ1, СЭ2 – сравнивающие элементы;
МВН
(t) – момент внешних сил;
q(t) – реальное угловое положение звена.
Задающий элемент ЗЭ формирует информацию о требуемых траекториях перемещения звеньев манипулятора и захватного устройства. Корректирующий элемент КЭ1 и усилительно-преобразующий УПЭ1 совместно выполняют функцию регулятора положения, характеристика которого может перестраиваться с целью достижения требуемых динамических качеств. Усилительно-преобразующий элемент УПЭ2 является усилителем мощности, совместно УПЭ2 и корректирующий элемент КЭ2 выполняют функцию регулятора скорости, от их выбора существенно зависят динамические характеристики ССПР. Остальные элементы следящей системы: электродвигатель ИД, датчик скорости ДС, датчик положения ДП, редуктор МП конструктивно входят в состав исполнительного органа манипулятора и являются неизменяемой частью системы, поскольку не могут быть изменены в процессе настройки ССПР. Как видно из рисунка, функциональная схема содержит два контура регулирования: подчинённый контур регулирования скорости двигателя (сервопривод) и контур регулирования углового или линейного положения (следящий привод).
Следящие системы ПР определяют важнейшие технические характеристики работы, в частности, его точность и быстродействие. В комплексе работы всех следящих систем ПР должна обеспечивать минимальное значение погрешности позиционирования захватного устройства манипулятора при максимально возможном быстродействии. При этом также необходимо обеспечить апериодичность процессов управления, т.к. перерегулирование в следящих системах, приводящее к «перебегу» заданных траекторий, могут привести к аварийным ситуациям. Будем рассматривать следящую систему промышленного робота, в которой в качестве исполнительного двигателя используется двигатель постоянного тока с независимым возбуждением. В качестве функциональных элементов ССПР используются следующие устройства: усилителем мощности является тиристорный преобразователь, измерителем скорости – тахогенератор постоянного тока, измеритель углового положения – потенциометрический датчик, корректирующие устройства регуляторов скорости и положения выбираются в процессе расчёта следящей системы.
2 МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОТДЕЛЬНЫХ ЗВЕНЬЕВ СИСТЕМЫ
В данном пункте курсовой работы стоит задача получить математическое описание двигателя постоянного тока. Структурная схема двигателя постоянного тока представлена на рисунке 3.1.
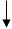  Мс(s) Мс(s)
Рисунок 2.1 - Структурная схема двигателя постоянного тока
С учетом обозначения сигналов на функциональной схеме, во временной области математические модели можно записать следующим образом:
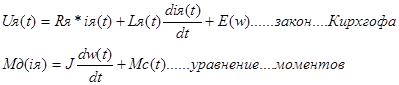
где ω – угловая скорость вращения вала двигателя;
J
– момент инерции всех вращающихся частей;
E
(
w
) – ЭДС;
M
с - момент сопротивления на валу двигателя
M
д – вращающий момент (динамический момент сил)
Разрешим каждое из уравнений относительно производных: выражаем производные и получаем систему дифференциальных уравнений:
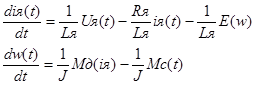
Так как Мд и E(w) являются нелинейными, то необходимо выполнить линеаризацию. Принимая i=iя0
; U=Uяo ; w=wo ; Mc=Mco ;
Раскладываем в ряд Тейлора и получаем:
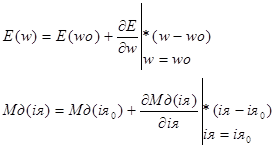
Получаем:
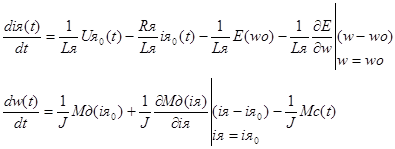 (1) (1)
Так как в установившемся режиме все производные равны нулю, то можем переписать систему в следующем виде:
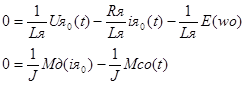 (2) (2)
Обозначим, что :
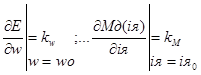
Теперь, чтоб получить линеаризованную модель, почленно вычитаем из (1) (2):
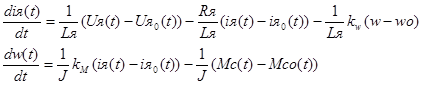
Считая отклонения Δ
U
я, Δ
i
я, Δ
w
малыми величинами, можно записать:
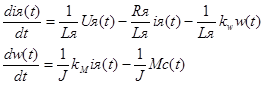
Применяя преобразование Лапласа, можно получить данную систему уравнений в операторной форме:
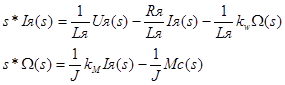 (3) (3)
Теперь получим выражения для передаточных функций W4, W5, W6 в операторной форме. Введем обозначения:
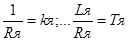
Тогда получаем выражение для передаточной функции W4(s) и в соответствии с вариантом задания записываем её вид:
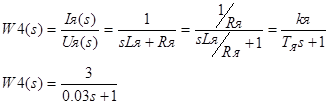
Передаточная функция W5(s) получается из второго уравнения (3):
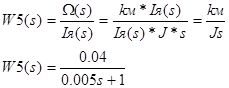
Передаточная функция W6(s):
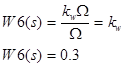
Теперь, принимая во внимание момент Mc.
Найдем передаточную функцию Wc c помощью второго уравнения (3): принимая ток якоря =0
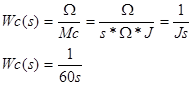
Теперь можно получить выражение для передаточной функции двигателя по управлению.
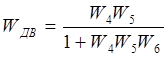
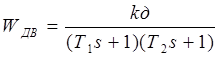
Приводим к виду:
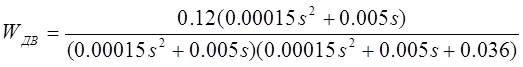
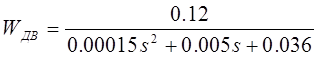
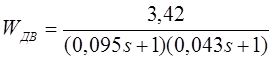
Находим корни характеристического полинома: S1
=-10,5 S2
=-22,8
Можно сделать вывод, что т.к. корни оба левые, то полином устойчив.
Структурная схема системы в целом будет иметь вид, представленный на рисунке 4.1:
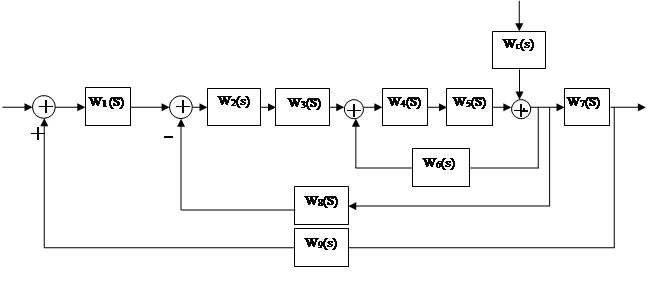
Рисунок 2.2 – Структурная схема всей системы в целом
Здесь на схеме указаны следующие передаточные функции:
W1
(s) = k – коэффициент усиления по параметру положения;
W2
(s) - передаточная функция корректирующего звена;
W3
(s) - передаточная функция усилителя-преобразователя (блок УПЭ2 на рисунке 2.1);
W4
(s), W5
(s), W6
(s) - передаточная функция двигателя постоянного тока (блок ИД);
W7
(s) – передаточная функция механической передачи (блок МП);
W8
(s) - передаточная функция измерителя скорости (блок ДС);
W9
(s) - передаточная функция датчика углового положения (блок ДП).
W3
(s) = Кп = 4
W7
(s) = 1/ (60*s)
W8
(s) = Ктг = 0,07
W9
(s) = Кос = 1
Формулы для остальных передаточных функций, фигурирующих в данной схеме, записаны выше.
3.ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ КОРРЕКТИРУЮЩЕГО ЗВЕНА
Для нормальной отработки в сервоприводе сигналов управления и установления на выходе требуемого параметра на заданном уровне необходимо решить задачу точности. Точность в системах автоматического управления определяется коэффициентами установившихся ошибок. Общее значение ошибки в установившемся режиме может быть записано в виде суммы:
e(t®¥) = e0
+ e1
+ e2
+ ¼
где e0
– статическая ошибка, e1
– скоростная ошибка, e2
– ошибка по ускорению. Сервопривод должен быть астатичен, т.е. основываясь на этом мы можем записать такую формулу:
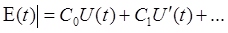
где C0
– коэффициент статической ошибки, С1
– коэффициент скоростной ошибки. Количество Сi
обеспечивает порядок астатизма.
Решим задачу синтеза корректирующего звена в сервоприводе, исходя из условия выполнения требований по точности и качеству, то есть общую задачу синтеза мы разделим на две задачи:
1. Задача точности
2. Задача качества
Исходными данными для синтеза являются показатели качества, согласно варианту задания, и коэффициенты скоростной и статической ошибок.
Решаем задачу точности
Здесь передаточная функция W2
= W21
*W22
, в которой W21
решает задачу точности, W22
решает задачу качества, т.к. мы решаем задачу точности нам надо определить W21
. Чтобы С0
было равно 0 нам надо ввести интегрирующие звено
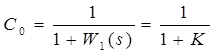
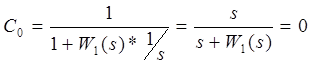
Так как статическая ошибка по задающему воздействию равна нулю (С0
= 0),то система имеет астатизм первого порядка по управлению. И тогда мы можем записать, что 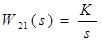 . .
Так как в системе имеется астатизм первого порядка, то статическая ошибка равна нулю, а скоростная ошибка будет определяться соотношением:
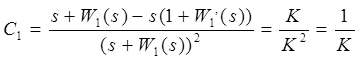
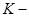 общий коэффициент усиления системы в сервоприводе. общий коэффициент усиления системы в сервоприводе.
Очевидно, что требования по статической ошибке мы выполнили. В свою очередь общий коэффициент усиления - К определяется произведением:
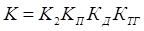
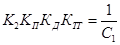
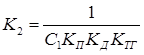
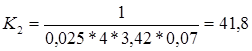
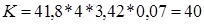
Таким образом, мы получили К такое, что удовлетворяются условия заданной точности и полностью решили требуемую задачу, т.е.

Передаточная функция сервопривода примет следующий вид:
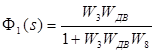
, где 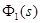 сервопривод безкоррекции. сервопривод безкоррекции.
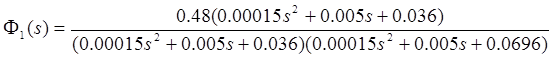
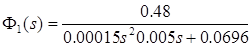
Проверяем на устойчивость по алгебраическому критерию – критерию Гурвица. Строим матрицу Гурвица
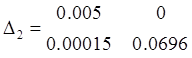
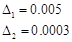 для того чтобы система была устойчива необходимо и достаточно, чтобы все главные миноры (диагональ) матрицы Гурвица были положительны (>0) определители больше нуля следовательно система устойчива. Строим переходный процесс в сервоприводе для того чтобы система была устойчива необходимо и достаточно, чтобы все главные миноры (диагональ) матрицы Гурвица были положительны (>0) определители больше нуля следовательно система устойчива. Строим переходный процесс в сервоприводе
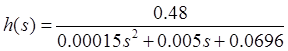
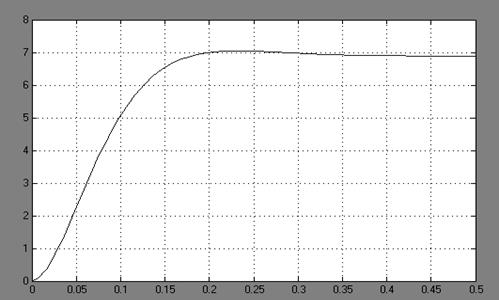
Рисунок 3.1 - Переходный процесс в сервоприводе и по нему определяем прямые показатели качества:
- время регулирования tP
= 0.15c
- перерегулирование σ =2,9%
Решение задачи обеспечения прямых показателей качества
При невозможности решить задачу повышения запасов устойчивости в рамках имеющейся системы приходится идти на изменение структуры, т.е. вводят корректирующие звенья в систему. Для решения этой задачи будем использовать метод академика Солодовникова. С помощью этого метода мы синтезируем новое звено в сервоприводе. При этом структура корректирующего звена неизвестна, необходимо с помощью метода ЛАЧХ Солодовникова выбрать звено таким образом, чтобы прямые показатели качества были бы не хуже заданным по ВЗ.
Структурная схема САУ сводится к виду
Такое приведение схемы может быть сделано, так как передаточная функция обратной связи W8
является безинерционным звеном. Обозначим произведение передаточных функций прямой цепи, как передаточную функцию неизменяемой части системы
:
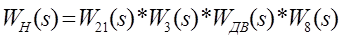
Структурную схему можно представить в следующем виде:

Рисунок 3.3 - Структурная схема САУ
В соответствии с этой схемой желаемая передаточная функция системы будет иметь вид:
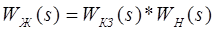
Если перейти от передаточной функции к логарифмическим амплитудно-частотным характеристикам, то справедлива следующая запись:
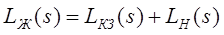
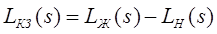
ЛАЧХ неизменяемой части системы Lн не представляет сложности при построении, так как мы имеем передаточную функцию неизменной части системы. Метод Солодовникова позволяет определить желаемую ЛАЧХ.
Неизменная часть будет иметь вид:
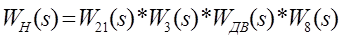
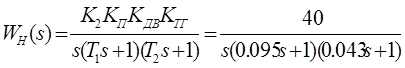
Желаемая ЛАЧХ состоит из 3-х частей:
1. низкочастотная – отвечает за точность системы;
2. среднечастотная – отвечает за качество системы;
3. высокочастотная – строится для удобства.
Для определения вида среднечастотной части ЛАЧХ Wж
используется прямой критерий качества. Перерегулирование взятое из ВЗ, s =5. По номограмме Солодовникова определяются частота положительности wп
и Рmax
и определяют частоту среза. Зная значение перерегулирования, мы из точки равной s =5 проводим перпендикуляр до пересечения с прямой и от этой точки опускаем перпендикуляр вниз и определяем значение Рmax
=1.0. Затем из этой точки поднимаем перпендикуляр до пересечения с другой прямой и под прямым углом опускаем прямую и определяем 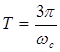 , откуда мы определяем, что К=3, т.к. , откуда мы определяем, что К=3, т.к.
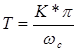 . .
Теперь мы определяем 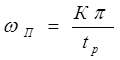
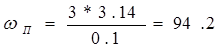
Частота среза: 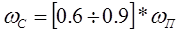
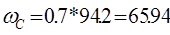
Используя значения Рmax
по номограммам определяем коридор ограничения средней части ЛАЧХ. Lз = ± 15 дБ. После построения желаемой ЛАЧХ, графически определяем вид корректирующего звена.
В приложении А
приведены построения, которые выполняются следующим образом:
· Используя значения Рmax по номограммам определяем коридор ограничения средней части ЛАЧХ.
· На ЛАЧХ выделяем частоту среза. Через точку, соответствующую частоте среза, под наклоном -20 дБ, до пересечения с коридором проводим линию средне частотной желаемой ЛАЧХ, обеспечивающую запас устойчивости по амплитуде.
· Построение низкочастотной ЛАЧХ
выполняется следующим образом:
Требования к точности системы были уже учтены в неизменяемой части системы за счет изменения коэффициента К, следовательно, в низкочастотной части желаемая и неизменяемая части должны совпадать. При этом их сопряжение производится за счет достройки фрагментов ЛАЧХ желаемой системы с наклоном кратным 20 дБ/дек.
· Построение высокочастотной желаемой ЛАЧХ.
Предполагается из удобства построения корректирующего звена задавать формой, совпадающей с формой высокочастотной ЛАЧХ неизменяемой части. Добавляется ω4, ω5, ω6.
· После построения желаемой ЛАЧХ, графически определяем вид корректирующего звена. График ЛАЧХ приведён в приложении А.
· Переходим от ЛАЧХ корректирующего звена к передаточной функции корректирующего звена. Для этого надо перейти от частот к постоянным времени – T4
, Т5
, Т6
.
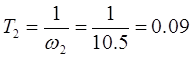
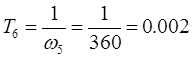
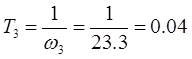
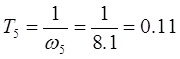
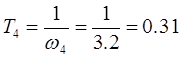
Передаточная функция корректирующего звена имеет следующий вид:
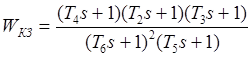
Тогда корректирующее звено будет иметь вид, если подставить значения Тn
:
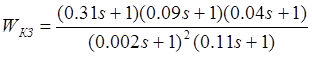
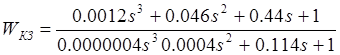
Проверка правильности выбора корректирующего звена.
Необходимо получить передаточную функцию замкнутого скорректированного контура сервопривода, она имеет следующий вид:
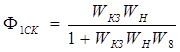
Подставив значения передаточных функций, получим следующее выражение:
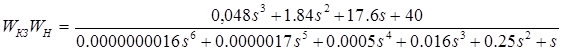
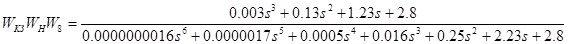
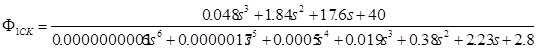
По передаточной функции замкнутого скорректированного контура строим переходный процесс, по которому определяем прямые показатели качества, которые должны совпадать или быть не больше заданных показателей качества.
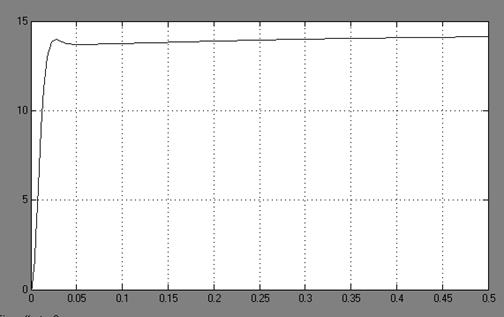
Рисунок 3.4 - График переходного процесса для скорректированного замкнутого контура
Из переходного процесса определим показатели качества:
1. время регулирования tр = 0,02 (с)
2. перерегулирование 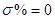
Показатели удовлетворяют начальным показателям качества:
- время регулирования tP
= 0.15c
- перерегулирование σ =2,9%
Определение параметров корректирующего звена.
Так как корректирующее звено имеет сложную передаточную функцию, и нет такого элементарного звена, основываясь на котором можно было бы реализовать звено коррекции, то будем составлять его из нескольких составляющих. Так как передаточные функции последовательно соединённых звеньев перемножаются, а ЛАЧХ складываются, то составим необходимое звено из трёх дифференцирующих звеньев с включением между ними согласующего операционного усилителя.
Для того, чтобы получить электрическую схему корректирующего устройства, необходимо ЛАЧХ корректирующего звена разбить на несколько простейших ЛАЧХ. Это разбиение представлено в приложении Б
. Схемы корректирующих устройств, соответствующих ЛАЧХ, приведены в [2] том 2.
Дифференцирующее звено:
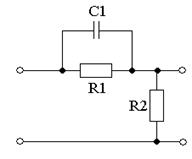
Рисунок 3.5 – Схема корректирующего устройства
T1 = R1×C1 T2 = R1×T1/(R1+R2)
Lо
= R1 /(R1+R2)
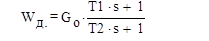
Усилительное звено:
Так как в дифференцирующем звене присутствует ослабление необходимо согласующий усилитель представить как усилитель сигнала
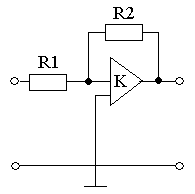
Рисунок 3.6 – Усилительное звено
Структурная схема реализации корректирующего звена будет иметь следующий вид:
Найдём коэффициент К усилителя
G = 20lgK
K = 10G
/20
К =
4. Д-РАЗБИЕНИЕ
После получения и исследования скорректированного сервопривода, можно исследовать следящие систему, но нам ещё не известен параметр К – регулятор положения. Исходя из требований устойчивости исследуемой САУ, проводим Д – разбиение по одному параметру и определяем диапазон изменения К, при которых система будет асимптотически устойчивой (неустойчивой).
Рассмотрим следующую систему:
К – регулятор положения;
Φ1 ск
– скорректированный сервопривод;
W7
(s) – передаточная функция механической передачи
Найдем все интервалы изменения параметра К, при которых заданная следящая система промышленного робота будет оставаться устойчивой, поэтому необходимо определить области устойчивости САУ в пространстве параметра К. Построим область
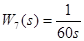
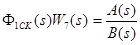
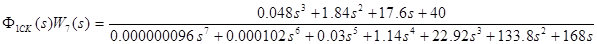
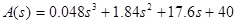
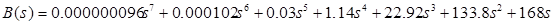
замкнутая система следящего сервопривода будет выглядеть следующим образом
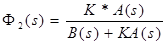
приравняем характеристический многочлен к нулю, откуда найдем коэффициент усиления по параметру положения.
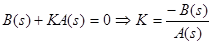
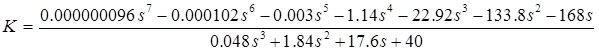
заменяем s = jω и получаем действительную и мнимую части
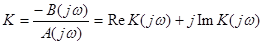
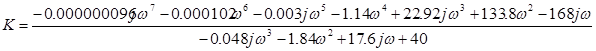
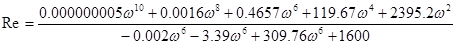
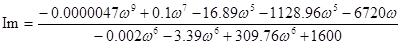
Теперь строим годограф Д – разбиения по параметру К
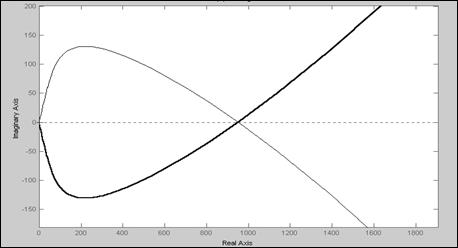
Рисунок 4.2 - График годографа Д –разбиения по параметру К
Заштрихуем области слева по ходу движения частоты w. Из графика видно, что область I [0 .. 950] является областью – претендентом на устойчивость
.
Проведём исследование характеристического многочлена Q(s) по критерию Рауса. Для этого необходимо взять только одно значение из отрезка [0 .. 950], так как в заштрихованной области количество левых и правых корней характеристического полинома Q(s) остается постоянным. Возьмем К=600, тогда:
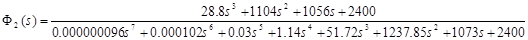 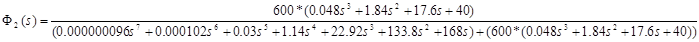
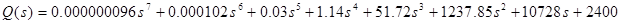
По критерию Рауса составляем таблицу чисел по полученному многочлену Q(s).
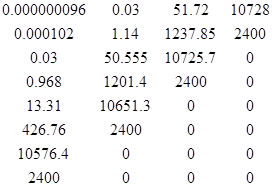
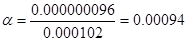
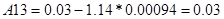
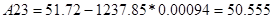

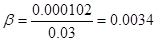
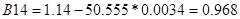
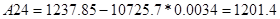
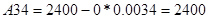
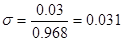
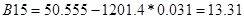
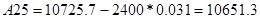
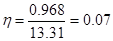
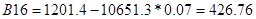
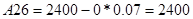
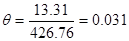
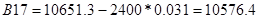
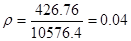
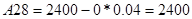
Для того, чтобы многочлен был устойчив, необходимо и достаточно, чтобы алгоритм построения таблицы Рауса был регулярным, и все числа в первом столбце были одного знака. Все числа первого столбца должны быть положительными.
В нашем случае все условия критерия выполняются, т. е. алгоритм построения таблицы Рауса регулярен, и все числа в первом столбце – одного знака и положительны, то можно сделать вывод, что система устойчива. Поэтому интервал [0 .. 950] можно считать устойчивым.
Подберем такое К при котором прямой показатель качества – колебательность – не превышает заданного придела μ =1,5. К=165
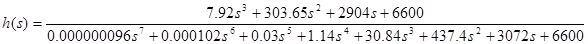
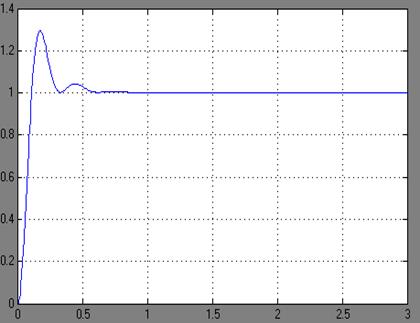
Рисунок 4.3 - График переходного процесса при К=165
Возьмем пять значений параметра К из этого интервала[0 .. 950]. Это делается для анализа показателей качества.К=100
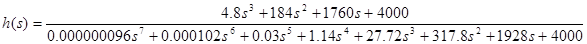
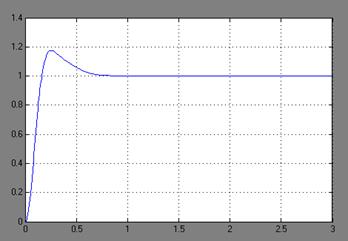
Рисунок 4.4 - График переходного процесса при К = 100 tP
= 0.5, σ = 1,19 К = 150
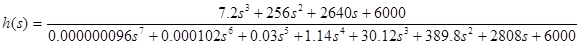
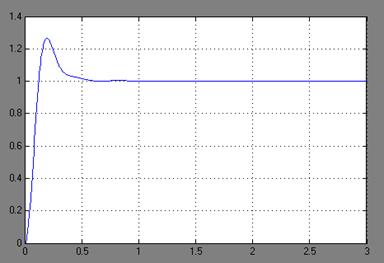
Рисунок 4.5 -
График переходного процесса при К = 150, tP
= 0.30, σ = 1,25 К = 180
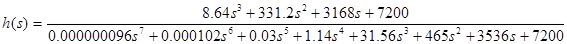
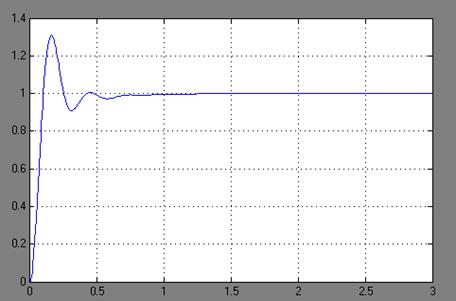
Рисунок 4.6 -
График переходного процесса при К = 180
К=200
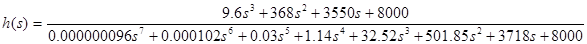
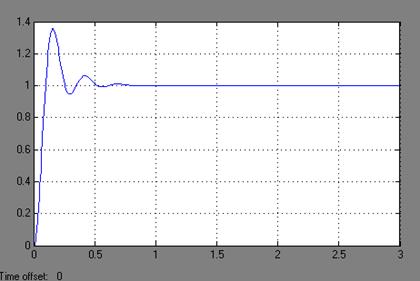
Рисунок 4.7 -
График переходного процесса при К = 200, tP
= 0.25, σ = 1,35
К=400
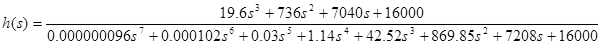
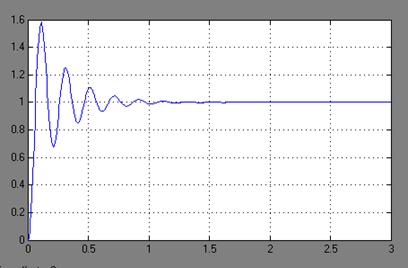
Рисунок 4.8 -
График переходного процесса при К = 400, tP
= 0.52, σ = 1,6
В результате построений переходных процессов при различных К можно сделать вывод, что при увеличении К перерегулирование будет увеличиваться; время регулирования при К = 100, К =150, К = 180 будет уменьшатся до К = 200, а после при К = 400 оно снова будет возрастать.
5 АНАЛИЗ ВЛИЯНИЯ НЕ ЛИНЕЙНОСТИ
Для анализа влияния нелинейности характеристик элементов следящей системы на её динамические свойства необходимо предварительно ввести в структурную схему системы нелинейные элементы.
Необходимо ввести в сервопривод нелинейный элемент (НЭ). Нелинейность можно задать функцией, отображаемой графиком, представленным на рисунке 5.1:
Рисунок 5.1 – Функция нелинейности
Нелинейный элемент имеет характеристику с насыщением, без зоны нечувствительности. Угол наклона характеристики должен быть 45°, т.к. нелинейный элемент повторяет входной сигнал до достижения значения выхода dр.огр
= А = 0,2°. Рассмотрим схему, представленную на рисунке 5.2:
Необходимо установить, возможно ли возникновение автоколебаний в такой системе. Данную задачу можно решить с помощью метода гармонического баланса, однако для этого исходную схему необходимо привести к виду, представленному на рисунке 5.3:
Рисунок 5.3 – Структурная схема
По нелинейному элементу, для применения метода гармонического баланса, получают его эквивалентную передаточную функцию, которая получается с помощью метода гармонической линеаризации с учетом гипотезы фильтрации низких частот, то есть получим схему, представленную на рисунке 5.4:
Рисунок 5.4 – Структурная схема с эквивалентной передаточной функцией
На рисунке 5.4 W
лч
(
s
) =
W
2
(
s
)*
W
3
(
s
)*
W
ДВ
(
s
)* (
W
8
(
s
)+
W
1
(
s
)*
W
7
(
s
))
, а W
экв
(
s
)
– эквивалентная передаточная функция. Для нахождения этой передаточной функции воспользуемся методом гармонического баланса. Суть этого метода заключается в том, что нелинейное выражение y
=
F
(
x
)
, в данном случае рассматривается кривая не имеющая гистерезис, заменяется выражением, которое с точностью до высших гармоник аналогично линейному:
у=
q
(А)
x
+ высшие гармоники
(40)
То есть криволинейная или ломанная характеристика y
=
F
(
x
)
с точностью до высших гармоник заменяется прямолинейной, тангенс угла наклона которой q
зависит от размера амплитуды колебаний А
.
Для рассматриваемого случая:
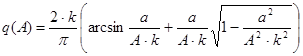 , (41) , (41)
где А
– амплитуда сигнала, причем А > а/
k
;
k
– тангенс угла наклона нелинейности, в рассматриваемом случае k
=1.
Передаточная функция замкнутой системы, изображенной на рисунке 5.4, имеет следующий вид:
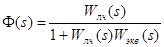 (42) (42)
Отсюда, приравняв знаменатель к нулю, получим:
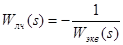 (43) (43)
Произведя замену s
на jω
, получим уравнение Гольдфарба:
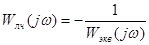 (43’) (43’)
Данное уравнение решается графически и его решение позволяет определить наличие в системе автоколебаний.
Передаточная функция линейной части:
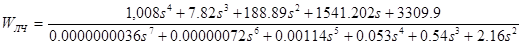
Заменив s
на jω
и выделив мнимую и реальную части, построим в одной координатной плоскости годограф линейной части системы и обратную характеристику нелинейного звена
Так как не существует пересечение годографа с обратной характеристикой нелинейного звена, описываемой уравнением (- 1/q(A)), то можно утверждать, что автоколебания в системе нет. Значит определять частоту и амплитуду автоколебаний не имеет смысла.
6 АНАЛИЗ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
В исследовании САУ ставится задача определить устойчивость по критерию Попова. Критерий Попова является достаточным
: для абсолютной устойчивости нелинейной САУ достаточно, чтобы линейная часть системы была асимптотически устойчивой, и для любых частот выполнялось неравенство Попова:
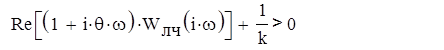 (24) (24)
q - любое действительное число,
k – значение k-сектора – тангенс угла наклона прямой задающей нелинейность. k = tg 45° = 1
Достаточно, чтобы существовало такое конечное действительное число q, что для всех частот w³0, выполнялось бы это неравенство.
Критерий Попова решается геометрически:
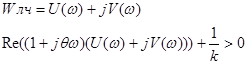
Для этого вводим понятие модифицированного годографа W*
(jw)= U*
(w)+j V*
(w), у которого действительная часть U*
(w)=U(w), а мнимая часть V*
(w)=wV(w), тогда условие Попова примет вид:
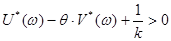
Очевидно, что равенство
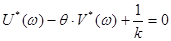
представляет собой уравнение прямой на плоскости W*
(jw)
Графическая интерпретация критерия Попова: для установления устойчивости нелинейной системы достаточно подобрать такую прямую на плоскости W*
(jw), проходящую через точку 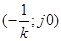 , что вся кривая W*
(jw) лежала справа от этой прямой. , что вся кривая W*
(jw) лежала справа от этой прямой.
Рассмотрим передаточную функцию линейной части:
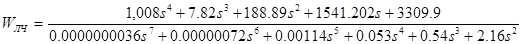
В данном случае линейная часть не является асимптотически устойчивой, то есть имеет нулевые корни, а следовательно в классической интерпретации критерий Попова применить нельзя. И поэтому в данном случае необходимо применить обобщение критерия Попова, а именно мы должны посмотреть выполняются ли условия при нулевых полюсах. Для астатизма 2 порядка, в этом случае абсолютная устойчивость определяется если выполняются придельная устойчивость. У нас два нулевых полюса, это видно из многочлена записанного в знаменателе, поэтому проверяем такие условия:
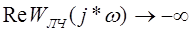
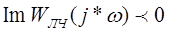 , при малых ω. , при малых ω.
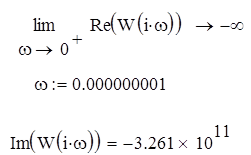
Эти условия выполняются, как видно из решения, следовательно можно сделать вывод, что система абсолютно устойчива.
Построим модифицированный годограф, т.е. выделим мнимую и реальную часть, заменив s = jw , и для получения модифицированного годографа мнимую часть умножим на w.
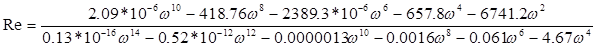
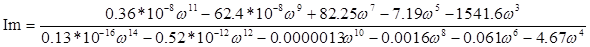 . .
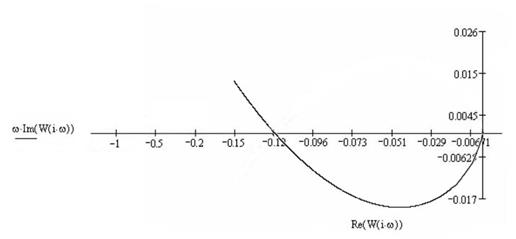
Рисунок 6.1 - Модифицированный годограф
Так как можно провести прямую через точку 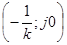 слева от характеристики, то нелинейная система абсолютно устойчива. слева от характеристики, то нелинейная система абсолютно устойчива.
В данной курсовой работе произведен расчет и анализ САУ следящей системы промышленного робота. Получена математическая модель исполнительного двигателя, произведена линеаризация этой модели, математические модели остальных звеньев изначально известны. Составлена структурная схема САУ. Для улучшения динамических характеристик была введена и рассчитана коррекция в сервоприводе. Разработана электрическая схема корректирующего устройства.
Произведен анализ влияния нелинейности на динамические свойства САУ. В ходе анализа системы была введена нелинейность в сервоприводе. Исходя из метода гармонического баланса выяснили, что в системе не могут присутствовать автоколебания. Также был проведен анализ влияния нелинейного элемента на абсолютную устойчивость системы. Проведя анализ САУ по критерию Попова, получили результат, что система абсолютно устойчива.
В данной курсовой работе произведено описание и анализ системы автоматического управления следящей системы промышленного робота. Выведена математическая модель и получена структурная схема САУ. Для улучшения динамических характеристик была введена коррекция в сервоприводе. Исходя из метода гармонического баланса выяснили, что в системе не могут присутствовать автоколебания. Необходимо было повести анализ влияния нелинейного элемента на абсолютную устойчивость системы. Проведя анализ САУ по критерию Попова, получили результат, что система абсолютно устойчивая.
БИБЛИОГРАФИЯ
1. Методические указания к выполнению курсового проекта по дисциплине «Теория автоматического управления»/Сост. Т.А.Грушун. – Севастополь: Издательство СевНТУ, 2003. -16с.
2. В.А. Бесекерский «Теория систем автоматического регулирования», Наука, М.: 1979г.-450с
3. В. В. Солодовников «Теория автоматического управления», книга вторая, М.: 1967г.-586с.
4. А.А.Воронов «Теория автоматического управления» - М., «Высшая школа»,1977г. - 303с.
5. И.М.Макаров «Управление робототехническими системами и гибкими автоматизированными производствами» -М., Высшая школа, 1986г. -159с.
|