Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет им. Ф. Скорины»
Математический факультет
Кафедра ТВ и матстатистики
Курсовая работа
КОНЕЧНЫЕ ГРУППЫ С ЗАДАННЫМИ СИСТЕМАМИ СЛАБО НОРМАЛЬНЫХ ПОДГРУПП
Исполнитель:
Студент группы М-32 Макарченко А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент Малинковский М.Т.
Гомель 2007
Содержание
ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ
ВВЕДЕНИЕ
1. Определение и общие свойства слабо нормальных подгрупп
2. Конечные группы со слабо нормальными подгруппами
ЗАКЛЮЧЕНИЕ
ЛИТЕРАТУРА
Перечень условных обозначений
В работе все рассматриваемые группы предполагаются конечными.
Будем различать знак включения множеств 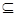 и знак строгого включения и знак строгого включения 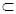 ; ;
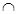 и и 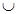 - соответственно знаки пересечения и объединения множеств; - соответственно знаки пересечения и объединения множеств;
 - пустое множество; - пустое множество;
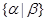 - множество всех - множество всех 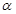 для которых выполняется условие для которых выполняется условие 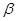 ; ;
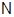 - множество всех натуральных чисел; - множество всех натуральных чисел;
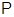 - множество всех простых чисел; - множество всех простых чисел;
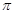 - некоторое множество простых чисел, т.е. - некоторое множество простых чисел, т.е. 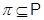 ; ;
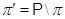 - дополнение к - дополнение к 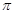 во множестве всех простых чисел; в частности, во множестве всех простых чисел; в частности, 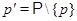 ; ;
примарное число - любое число вида 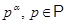 ; ;
Пусть  - группа. Тогда: - группа. Тогда:
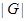 - порядок группы - порядок группы  ; ;
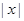 - порядок элемента - порядок элемента 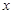 группы группы  ; ;
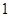 - единичный элемент и единичная подгруппа группы - единичный элемент и единичная подгруппа группы  ; ;
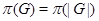 - множество всех простых делителей порядка группы - множество всех простых делителей порядка группы  ; ;
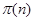 - множество всех различных простых делителей натурального числа - множество всех различных простых делителей натурального числа 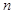 ; ;
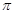 -группа - группа -группа - группа  , для которой , для которой 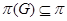 ; ;
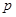 -группа - группа -группа - группа  , для которой , для которой 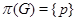 ; ;
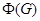 - подгруппа Фраттини группы - подгруппа Фраттини группы  , т.е. пересечение всех максимальных подгрупп группы , т.е. пересечение всех максимальных подгрупп группы  ; ;
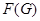 - подгруппа Фиттинга группы - подгруппа Фиттинга группы  , т.е. произведение всех нормальных нильпотентных подгрупп группы , т.е. произведение всех нормальных нильпотентных подгрупп группы  ; ;
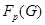 - наибольшая нормальная - наибольшая нормальная 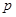 -нильпотентная подгруппа группы -нильпотентная подгруппа группы  ; ;
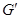 - коммутант группы - коммутант группы  , т.е. подгруппа, порожденная коммутаторами всех элементов группы , т.е. подгруппа, порожденная коммутаторами всех элементов группы  ; ;
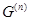 - - 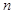 -ый коммутант группы -ый коммутант группы  ; ;
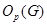 - наибольшая нормальная - наибольшая нормальная 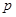 -подгруппа группы -подгруппа группы  ; ;
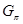 - - 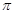 -холловская подгруппа группы -холловская подгруппа группы  ; ;
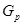 - силовская - силовская 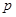 -подгруппа группы -подгруппа группы  ; ;
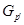 - дополнение к силовской - дополнение к силовской 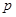 -подгруппе в группе -подгруппе в группе  , т.е. , т.е. 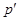 -холловская подгруппа группы -холловская подгруппа группы  ; ;
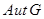 - группа всех автоморфизмов группы - группа всех автоморфизмов группы  ; ;
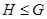 - - 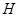 является подгруппой группы является подгруппой группы  ; ;
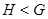 - - 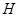 является собственной подгруппой группы является собственной подгруппой группы  ; ;
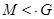 - - 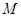 является максимальной подгруппой группы является максимальной подгруппой группы  ; ;
нетривиальная подгруппа - неединичная собственная подгруппа;
 - - 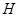 является нормальной подгруппой группы является нормальной подгруппой группы  ; ;
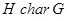 - подгруппа - подгруппа 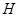 характеристична в группе характеристична в группе  , т.е. , т.е. 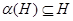 для любого автоморфизма для любого автоморфизма 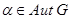 ; ;
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
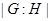 - индекс подгруппы - индекс подгруппы 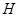 в группе в группе  ; ;
 ; ;
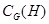 - централизатор подгруппы - централизатор подгруппы 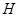 в группе в группе  ; ;
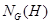 - нормализатор подгруппы - нормализатор подгруппы 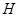 в группе в группе  ; ;
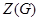 - центр группы - центр группы  ; ;
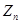 - циклическая группа порядка - циклическая группа порядка 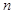 ; ;
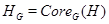 - ядро подгруппы - ядро подгруппы 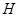 в группе в группе  , т.е. пересечение всех подгрупп, сопряжённых с , т.е. пересечение всех подгрупп, сопряжённых с 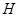 в в  . .
Если 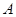 и и 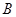 - подгруппы группы - подгруппы группы  , то: , то:
 - прямое произведение подгрупп - прямое произведение подгрупп 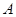 и и 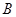 ; ;
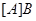 - полупрямое произведение нормальной подгруппы - полупрямое произведение нормальной подгруппы 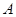 и подгруппы и подгруппы 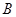 ; ;
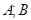 - - 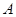 и и 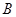 изоморфны. изоморфны.
Группа  называется: называется:
примарной, если  ; ;
бипримарной, если 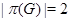 . .
Скобки 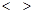 применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп. применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
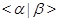 - подгруппа, порожденная всеми - подгруппа, порожденная всеми 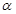 , для которых выполняется , для которых выполняется 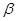 . .
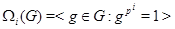 , где , где 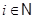 . .
Группу  называют: называют:
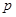 -замкнутой, если силовская -замкнутой, если силовская 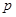 -подгруппа группы -подгруппа группы  нормальна в нормальна в  ; ;
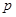 -нильпотентной, если -нильпотентной, если 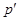 -холловская подгруппа группы -холловская подгруппа группы  нормальна в нормальна в  ; ;
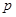 -разрешимой, если существует нормальный ряд, факторы которого либо -разрешимой, если существует нормальный ряд, факторы которого либо 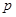 -группы, либо -группы, либо 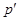 -группы; -группы;
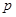 -сверхразрешимой, если каждый ее главный фактор является либо -сверхразрешимой, если каждый ее главный фактор является либо 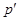 -группой, либо циклической группой; -группой, либо циклической группой;
нильпотентной, если все ее силовские подгруппы нормальны;
метанильпотентной, если существует нормальная нильпотентная подгруппа 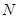 группы группы  такая, что такая, что 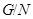 нильпотентна. нильпотентна.
разрешимой, если существует номер 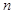 такой, что такой, что 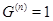 ; ;
сверхразрешимой, если она обладает главным рядом, все индексы которого являются простыми числами.
Группа Шмидта - это конечная ненильпотентная группа, все собственные группы которой нильпотентны.
Добавлением к подгруппе 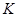 группы группы  называется такая подгруппа называется такая подгруппа 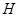 из из  , что , что 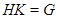 . .
Минимальная нормальная подгруппа группы 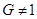 - неединичная нормальная подгруппа группы - неединичная нормальная подгруппа группы  , не содержащая собственных неединичных нормальных подгрупп группы , не содержащая собственных неединичных нормальных подгрупп группы  . .
Цоколь группы  - произведение всех минимальных нормальных подгрупп группы - произведение всех минимальных нормальных подгрупп группы  . .
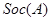 - цоколь группы - цоколь группы 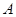 . .
Классы групп, т.е. совокупности групп, замкнутые относительно изоморфизмов, обозначаются прописными готическими буквами. Также обозначаются формации, т.е. классы групп, замкнутые относительно факторгрупп и подпрямых произведений. За некоторыми классами закреплены стандартные обозначения:
 - класс всех групп; - класс всех групп;
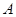 - класс всех абелевых групп; - класс всех абелевых групп;
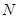 - класс всех нильпотентных групп; - класс всех нильпотентных групп;
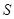 - класс всех разрешимых групп; - класс всех разрешимых групп;
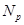 - класс всех - класс всех 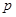 -групп; -групп;
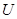 - класс всех сверхразрешимых групп; - класс всех сверхразрешимых групп;
Формации - это классы конечных групп, замкнутые относительно взятия гомоморфных образов и конечных подпрямых произведений.
Пусть 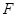 - некоторый класс групп и - некоторый класс групп и  - группа, тогда: - группа, тогда:
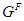 - - 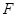 -корадикал группы -корадикал группы  , т.е. пересечение всех тех нормальных подгрупп , т.е. пересечение всех тех нормальных подгрупп 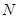 из из  , для которых , для которых 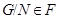 . Если . Если 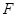 - формация, то - формация, то 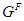 является наименьшей нормальной подгруппой группы является наименьшей нормальной подгруппой группы  , факторгруппа по которой принадлежит , факторгруппа по которой принадлежит 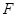 . Если . Если 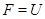 - формация всех сверхразрешимых групп, то - формация всех сверхразрешимых групп, то 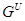 называется сверхразрешимым корадикалом группы называется сверхразрешимым корадикалом группы  . .
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Формация 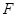 называется насыщенной, если всегда из называется насыщенной, если всегда из 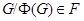 следует, что и следует, что и 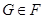 . .
Класс групп 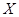 называется наследственным или замкнутым относительно подгрупп, если из того, что называется наследственным или замкнутым относительно подгрупп, если из того, что 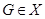 следует, что и каждая подгруппа группы следует, что и каждая подгруппа группы  также принадлежит также принадлежит 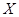 . .
Произведение формаций 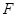 и и 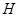 состоит из всех групп состоит из всех групп  , для которых , для которых 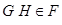 , т.е. , т.е. 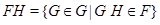 . .
Пусть 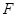 - некоторая непустая формация. Максимальная подгруппа - некоторая непустая формация. Максимальная подгруппа 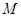 группы группы  называется называется 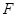 -абнормальной, если -абнормальной, если 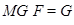 . .
Подгруппы 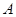 и и 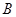 группы группы  называются перестановочными, если называются перестановочными, если 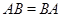 . .
Пусть 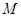 - максимальная подгруппа группы - максимальная подгруппа группы  . Нормальным индексом подгруппы . Нормальным индексом подгруппы 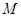 называют порядок главного фактора называют порядок главного фактора 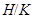 , где , где 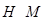 и и 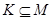 , и обозначают символом , и обозначают символом 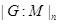 . .
Пусть  - группа и - группа и 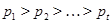 - различные простые делители порядка группы - различные простые делители порядка группы  . Тогда группа . Тогда группа  называется дисперсивной по Оре, если существуют подгруппы называется дисперсивной по Оре, если существуют подгруппы 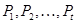 , такие что , такие что 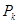 - силовская - силовская 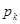 -подгруппа группы -подгруппа группы  и подгруппа и подгруппа 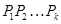 нормальна в нормальна в  для всех для всех 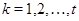 . .
Введение
В своей работе Оре рассмотрел два обобщения нормальности, оба из которых вызывают неослабевающий интерес у исследователей и в наши дни. Во-первых, в работе были впервые введены в математическую практику квазинормальные подгруппы: следуя, мы говорим, что подгруппа 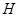 группы группы  квазинормальна в квазинормальна в  , если , если 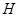 перестановочна с любой подгруппой из перестановочна с любой подгруппой из  (т.е. (т.е. 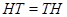 для всех подгрупп для всех подгрупп 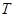 из из  ). Оказалось, что квазинормальные подгруппы обладают рядом интересных свойств и что фактически они мало отличаются от нормальных подгрупп. Отметим, в частности, что согласно, для любой квазинормальной подгруппы ). Оказалось, что квазинормальные подгруппы обладают рядом интересных свойств и что фактически они мало отличаются от нормальных подгрупп. Отметим, в частности, что согласно, для любой квазинормальной подгруппы 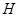 имеет место имеет место 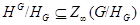 , а согласно, квазинормальные подгруппы - это в точности те субнормальные подгруппы группы , а согласно, квазинормальные подгруппы - это в точности те субнормальные подгруппы группы  , которые являются модулярными элементами в решетке всех подгрупп группы , которые являются модулярными элементами в решетке всех подгрупп группы  . .
Понятно, что если подгруппа 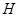 группы группы  нормальна в нормальна в  , то в , то в  всегда найдется такая подгруппа всегда найдется такая подгруппа 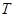 , что выполнено следующее условие: , что выполнено следующее условие:
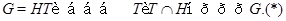
Таким образом, условие 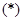 является еще одним обобщением нормальности. Такая идея также была впервые рассмотрена в работе, где в частности, было доказано, что: Группа является еще одним обобщением нормальности. Такая идея также была впервые рассмотрена в работе, где в частности, было доказано, что: Группа  является разрешимой тогда и только тогда, когда все ее максимальные подгруппы удовлетворяют условию является разрешимой тогда и только тогда, когда все ее максимальные подгруппы удовлетворяют условию 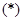 . В дальнейшем, в работе подгруппы, удовлетворяющие условию
. В дальнейшем, в работе подгруппы, удовлетворяющие условию 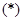 были названы были названы 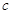 -нормальными. В этой же работе была построена красивая теория -нормальными. В этой же работе была построена красивая теория 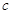 -нормальных подгрупп и даны некоторые ее приложения в вопросах классификации групп с заданными системами подгрупп. -нормальных подгрупп и даны некоторые ее приложения в вопросах классификации групп с заданными системами подгрупп.
В данной диссертационной работе мы анализируем следующее понятие, которое одновременно обобщает как условие квазинормальности, так и условие 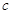 -нормальности для подгрупп. -нормальности для подгрупп.
Определение. Подгруппа 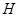 группы группы  называется слабо квазинормальной в называется слабо квазинормальной в  подгруппой, если существует такая подгруппа подгруппой, если существует такая подгруппа 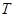 группы группы  , что , что 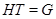 и и 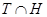 , , 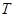 - квазинормальные в - квазинормальные в  подгруппы. подгруппы.
Следующий простой пример показывает, что в общем случае слабо квазинормальная подгруппа не является ни квазинормальной, ни 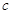 -нормальной. -нормальной.
Пример. Пусть
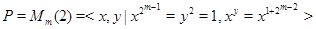 , ,
где 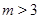 . И пусть . И пусть 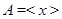 , , 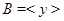 . Тогда . Тогда 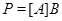 и и 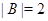 . Пусть . Пусть 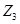 - группа простого порядка 3 и - группа простого порядка 3 и 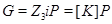 , где , где 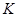 - база регулярного сплетения - база регулярного сплетения  . Поскольку . Поскольку 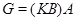 , , 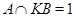 и и 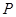 - модулярная группа, то - модулярная группа, то  квазинормальна в квазинормальна в  и поэтому подгруппа и поэтому подгруппа 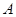 слабо квазинормальна в слабо квазинормальна в  . Значит, подгруппа . Значит, подгруппа 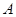 является слабо квазинормальной в является слабо квазинормальной в  , но не квазинормальной и не , но не квазинормальной и не 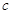 -нормальной в -нормальной в  . .
В последние годы значительно возрос интерес к квазинормальным и 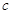 -нормальным подгруппам, что говорит о несомненной актуальности данного направления. Следует отметить, что многими авторами (Асаад, Бакли, Баллестер-Болинше, Ванг, Вей, Ли, Педра-Агуэла, Рамадан, А.Н. Скиба, Сринивазан и др.) получено большое число теорем связанных с изучением групп, те или иные выделенные системы подгрупп которых -нормальным подгруппам, что говорит о несомненной актуальности данного направления. Следует отметить, что многими авторами (Асаад, Бакли, Баллестер-Болинше, Ванг, Вей, Ли, Педра-Агуэла, Рамадан, А.Н. Скиба, Сринивазан и др.) получено большое число теорем связанных с изучением групп, те или иные выделенные системы подгрупп которых 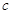 -нормальны или квазинормальны. Не смотря на тот факт, что квазинормальность и -нормальны или квазинормальны. Не смотря на тот факт, что квазинормальность и 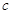 -нормальность являются вполне различными обобщениями нормальности, в настоящее время получено много аналогичных результатов независимо для квазинормальных и -нормальность являются вполне различными обобщениями нормальности, в настоящее время получено много аналогичных результатов независимо для квазинормальных и 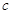 -нормальных подгрупп. В данной работе такой параллелизм устраняется на основе введенного выше понятия слабой квазинормальности. -нормальных подгрупп. В данной работе такой параллелизм устраняется на основе введенного выше понятия слабой квазинормальности.
Таким образом, задача изучения групп с заданной системой слабо квазинормальных подгрупп вполне актуальна, ее реализации посвящена данная работа.
Определение. Подгруппа 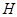 группы группы  называется слабо нормальной в называется слабо нормальной в  подгруппой, если существует такая квазинормальная подгруппа подгруппой, если существует такая квазинормальная подгруппа 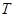 группы группы  , что , что 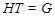 и и 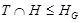 . .
Докажем ряд общих свойств слабо нормальных подгрупп.
Пусть  - группа и - группа и 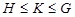 . Тогда справедливы следующие утверждения: . Тогда справедливы следующие утверждения:
(1) Пусть 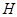 - нормальная в - нормальная в  подгруппа. Тогда подгруппа. Тогда 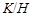 слабо нормальная подгруппа в группе слабо нормальная подгруппа в группе 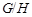 тогда и только тогда, когда тогда и только тогда, когда 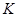 - слабо нормальная подгруппа в группе - слабо нормальная подгруппа в группе  . .
(2) Если 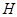 - слабо нормальная в - слабо нормальная в  подгруппа, то подгруппа, то 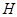 - слабо нормальная в - слабо нормальная в 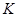 подгруппа. подгруппа.
(3) Пусть 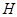 - нормальная в - нормальная в  подгруппа. Тогда для всех слабо нормальных в подгруппа. Тогда для всех слабо нормальных в  подгрупп подгрупп 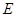 таких, что таких, что 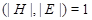 , , 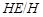 - слабо нормальная подгруппа в группе - слабо нормальная подгруппа в группе 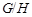 . .
Доказательство.
(1) Пусть 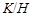 - слабо нормальная в - слабо нормальная в 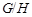 подгруппа и подгруппа и 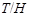 - такая квазинормальная в - такая квазинормальная в 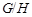 подгруппа, что подгруппа, что
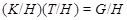
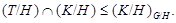
Тогда 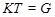 , , 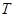 - квазинормальная в - квазинормальная в  подгруппа и подгруппа и 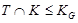 . Значит, . Значит, 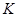 - слабо нормальная в - слабо нормальная в  подгруппа. подгруппа.
Пусть теперь, для некоторой квазинормальной в  подгруппы подгруппы 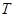 мы имеем мы имеем 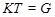 и и
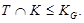
Ясно, что
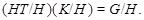
Поскольку
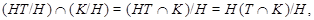
то
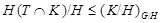
и 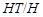 - квазинормальные в - квазинормальные в 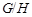 подгруппы. Следовательно, подгруппы. Следовательно, 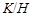 - слабо нормальная в - слабо нормальная в 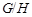 подгруппа. подгруппа.
Утверждение (2) очевидно.
(3) Пусть 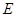 - слабо нормальная подгруппа в группе - слабо нормальная подгруппа в группе  и и 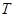 - квазинормальная в - квазинормальная в  подгруппа такая, что подгруппа такая, что 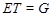 и и 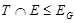 . Ясно, что . Ясно, что 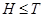 и и
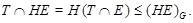
Значит, 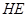 слабо нормальна в слабо нормальна в  и ввиду (1), и ввиду (1), 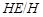 - слабо нормальная в - слабо нормальная в 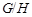 подгруппа. подгруппа.
В данном разделе мы докажем некоторые критерии разрешимых, метанильпотентных, дисперсивных по Оре и сверхразрешимых групп в терминах слабо нормальных подгрупп.
Следующая теорема доказывается аналогично теореме 3.5.1.
Группа  разрешима тогда и только тогда, когда разрешима тогда и только тогда, когда 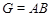 , где , где  , , 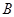 - подгруппы группы - подгруппы группы  такие, что каждая максимальная подгруппа из такие, что каждая максимальная подгруппа из  и каждая максимальная подгруппа из и каждая максимальная подгруппа из 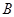 слабо нормальны в слабо нормальны в  . .
Пусть  - группа тогда следующие утверждения эквивалентны: - группа тогда следующие утверждения эквивалентны:
(1)  - разрешима; - разрешима;
(2) 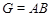 , где , где  , , 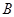 - подгруппы группы - подгруппы группы  такие, что каждая максимальная подгруппа из такие, что каждая максимальная подгруппа из  и каждая максимальная подгруппа из и каждая максимальная подгруппа из 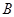 слабо квазинормальны в слабо квазинормальны в  ; ;
(3) 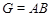 , где , где  , , 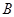 - подгруппы группы - подгруппы группы  такие, что каждая максимальная подгруппа из такие, что каждая максимальная подгруппа из  и каждая максимальная подгруппа из и каждая максимальная подгруппа из 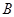 слабо нормальны в слабо нормальны в  . .
Группа  метанильпотентна тогда и только тогда, когда метанильпотентна тогда и только тогда, когда 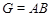 , где подгруппа , где подгруппа  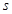 -квазинормальна в -квазинормальна в  , , 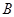 - нильпотентна и каждая силовская подгруппа из - нильпотентна и каждая силовская подгруппа из  слабо нормальна в слабо нормальна в  . .
Доказательство.
Допустим, что 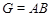 , где , где  - - 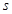 -квазинормальна в -квазинормальна в  , , 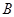 - нильпотентна и каждая силовская подгруппа из - нильпотентна и каждая силовская подгруппа из  слабо нормальна в слабо нормальна в  . Покажем, что группа . Покажем, что группа  метанильпотентна. Предположим, что это не верно и пусть метанильпотентна. Предположим, что это не верно и пусть  - контрпример минимального порядка. Тогда справедливы следующие утверждения. - контрпример минимального порядка. Тогда справедливы следующие утверждения.
(1)  не является нильпотентной группой
. не является нильпотентной группой
.
Предположим, что  нильпотентна. Так как ввиду леммы (3), нильпотентна. Так как ввиду леммы (3),  субнормальна, то субнормальна, то  содержится в некоторой нильпотентной нормальной подгруппе содержится в некоторой нильпотентной нормальной подгруппе 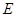 из из  по лемме (2). Тогда по лемме (2). Тогда

нильпотентна и поэтому  метанильпотентна. Полученное противоречие с выбором группы метанильпотентна. Полученное противоречие с выбором группы  доказывает (1). доказывает (1).
(2) 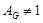 . .
Допустим, что 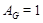 . Тогда ввиду леммы , . Тогда ввиду леммы ,  нильпотентна, что противоречит (1). Значит, мы имеем (2). нильпотентна, что противоречит (1). Значит, мы имеем (2).
(3) Если 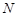 - абелева минимальная нормальная подгруппа группы - абелева минимальная нормальная подгруппа группы  , содержащаяся в , содержащаяся в  , то , то 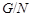 метанильпотентна
. метанильпотентна
.
Пусть 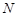 - - 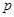 -группа и -группа и 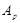 - силовская - силовская 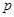 -подгруппа в -подгруппа в  . Тогда . Тогда 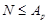 и поэтому по лемме каждая силовская подгруппа из и поэтому по лемме каждая силовская подгруппа из 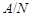 слабо нормальна в слабо нормальна в 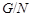 . Поскольку по лемме , . Поскольку по лемме , 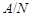 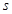 -квазинормальна в -квазинормальна в 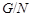 , ,
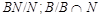
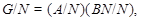
то условия теоремы справедливы для 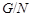 . Так как . Так как 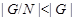 , то ввиду выбора группы , то ввиду выбора группы  , , 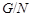 метанильпотентна. метанильпотентна.
(4) Условия теоремы справедливы для  (это проямо следует из леммы ).
(это проямо следует из леммы ).
(5)  разрешима
. разрешима
.
Если 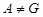 , то , то  метанильпотентна по (4)и выбору группы метанильпотентна по (4)и выбору группы  . Пусть теперь . Пусть теперь 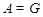 . Предположим, что для некоторой силовской подгруппы . Предположим, что для некоторой силовской подгруппы 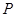 из из  мы имеем мы имеем 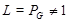 . Тогда ввиду (3), . Тогда ввиду (3),  разрешима. Пусть теперь разрешима. Пусть теперь 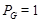 для каждой силовской подгруппы для каждой силовской подгруппы 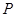 группы группы  . Тогда по условию каждая силовская подгруппа из . Тогда по условию каждая силовская подгруппа из  имеет квазинормальной дополнение в имеет квазинормальной дополнение в  и поэтому и поэтому  нильпотентна. Полученное противоречие в выбором группы нильпотентна. Полученное противоречие в выбором группы  доказывает (5). доказывает (5).
(6) В группе  имеется в точности одна минимальная нормальная подгруппа имеется в точности одна минимальная нормальная подгруппа 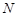 , содержащаяся в , содержащаяся в  .
.
Пусть 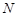 - минимальная нормальная подгруппа группы - минимальная нормальная подгруппа группы  , содержащаяся в , содержащаяся в  . Тогда . Тогда 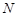 абелева согласно (5), и поэтому ввиду (3), абелева согласно (5), и поэтому ввиду (3), 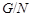 метанильпотентна. Так как класс всех метанильпотентных групп. Кроме того, так как класс всех метанильпотентных групп является насыщенной формацией (см. ), то метанильпотентна. Так как класс всех метанильпотентных групп. Кроме того, так как класс всех метанильпотентных групп является насыщенной формацией (см. ), то 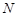 - единственная минимальная нормальная подгруппа группы - единственная минимальная нормальная подгруппа группы  , содержащаяся в , содержащаяся в  . .
(7) Если 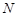 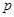 -группа, то каждая силовская -группа, то каждая силовская 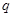 -подгруппа из -подгруппа из  , где , где 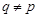 , имеет квазинормальное дополнение в , имеет квазинормальное дополнение в  . .
Пусть 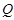 - силовская - силовская 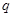 -подгруппа в -подгруппа в  , где , где 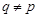 . Тогда ввиду (6), . Тогда ввиду (6), 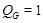 . По условию, . По условию, 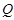 слабо нормальна в слабо нормальна в  и поэтому и поэтому  имеет квазинормальную подгруппу имеет квазинормальную подгруппу 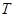 , такую что , такую что 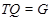 и и
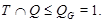
Заключительное противоречие
.
Пусть 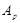 - силовская - силовская 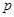 -подгруппа в -подгруппа в  и и 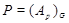 . Тогда . Тогда
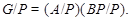
По условию  имеет квазинормальную подгруппу имеет квазинормальную подгруппу 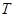 , такую что , такую что 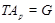 и и
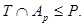
Тогда
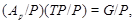
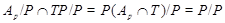
и поэтому 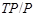 - дополнение для - дополнение для 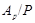 в в 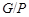 , которое является квазинормальной в , которое является квазинормальной в 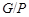 подгруппой. Если подгруппой. Если 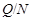 - - 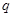 -подгруппа из -подгруппа из 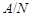 , где , где 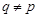 , то ввиду (7), , то ввиду (7), 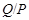 имеет дополнение в имеет дополнение в 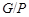 , которое является квазинормальной подгруппой (см. доказательство утверждения (3) леммы ). Тогда по лемме , , которое является квазинормальной подгруппой (см. доказательство утверждения (3) леммы ). Тогда по лемме , 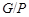 нильпотентна и поэтому нильпотентна и поэтому  метанильпотентна. Полученное противоречие доказывает метанильпотентность группы метанильпотентна. Полученное противоречие доказывает метанильпотентность группы  . .
Обратно, предположим, что  метанильпотентна. Покажем, что каждая силовская подгруппа из метанильпотентна. Покажем, что каждая силовская подгруппа из  слабо нормальна в слабо нормальна в  . Предположим, что это не верно и пусть . Предположим, что это не верно и пусть  - контрпример минимального порядка. Тогда - контрпример минимального порядка. Тогда  имеет силовскую подгруппу имеет силовскую подгруппу 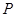 , которая не является слабо нормальной в , которая не является слабо нормальной в  . Пусть . Пусть 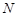 - произвольная минимальная нормальная подгруппа в - произвольная минимальная нормальная подгруппа в  и и 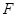 - подгруппа Фиттинга группы - подгруппа Фиттинга группы  . Предположим, что . Предположим, что 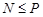 . Тогда . Тогда 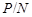 слабо нормальна в слабо нормальна в 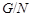 и поэтому по лемме (1), и поэтому по лемме (1), 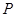 слабо нормальна в слабо нормальна в  , противоречие. Значит, , противоречие. Значит, 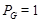 и поэтому и поэтому
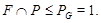
Так как по условию  метанильпотентна и метанильпотентна и 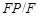 - силовская подгруппа в - силовская подгруппа в  , то , то 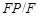 имеет нормальное дополнение имеет нормальное дополнение 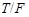 в в 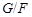 . Но поскольку . Но поскольку 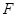 и и 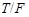 - - 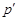 -группы, то -группы, то 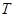 - нормальное дополнение для - нормальное дополнение для 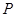 в в  . Следовательно, . Следовательно, 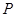 слабо нормальна в слабо нормальна в  . Полученное противоречие показывает, что каждая силовская подгруппа из . Полученное противоречие показывает, что каждая силовская подгруппа из  слабо нормальна в слабо нормальна в  . .
Пусть  - группа тогда следующие утверждения эквивалентны: - группа тогда следующие утверждения эквивалентны:
(1)  - метанильпотентна; - метанильпотентна;
(2) 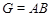 , где подгруппа , где подгруппа  субнормальна в субнормальна в  , , 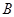 - абелева холлова подгруппа в - абелева холлова подгруппа в  и каждая силовская подгруппа из и каждая силовская подгруппа из  слабо квазинормальна в слабо квазинормальна в  ; ;
(3) 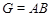 , где подгруппа , где подгруппа  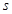 -квазинормальна в -квазинормальна в  , , 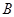 - нильпотентна и каждая силовская подгруппа из - нильпотентна и каждая силовская подгруппа из  слабо нормальна в слабо нормальна в  . .
Пусть 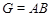 , где подгруппа , где подгруппа  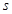 -квазинормальна в -квазинормальна в  , , 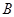 нильпотентна. Предположим, что любая максимальная подгруппа каждой нециклической подгруппы из нильпотентна. Предположим, что любая максимальная подгруппа каждой нециклической подгруппы из  слабо нормальна в слабо нормальна в  . Тогда . Тогда  сверхразрешима. сверхразрешима.
Доказательство.
Предположим, что эта теорема не верна и пусть  - контрпример минимального порядка. Тогда: - контрпример минимального порядка. Тогда:
(1) Каждая собственная подгруппа 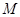 группы группы  , содержащая , содержащая  , сверхразрешима
. , сверхразрешима
.
Пусть 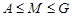 , где , где  . Тогда . Тогда
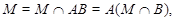
где 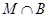 нильпотентна и нильпотентна и  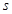 -квазинормальна в -квазинормальна в 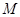 . Так как по лемме (2), любая максимальная подгруппа каждой нециклической силовской подгруппы из . Так как по лемме (2), любая максимальная подгруппа каждой нециклической силовской подгруппы из  слабо нормальна в слабо нормальна в 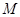 и и 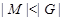 , то по выбору группы , то по выбору группы  мы имеем (1). мы имеем (1).
(2) Пусть 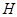 - неединичная нормальная подгруппа в - неединичная нормальная подгруппа в  . Предположим, что . Предположим, что 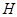 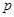 -группа. Допустим, что -группа. Допустим, что 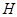 содержит силовскую содержит силовскую 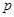 -подгруппу -подгруппу 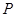 из из  , или , или 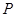 циклична, или циклична, или 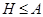 . Тогда . Тогда 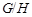 сверхразрешима. сверхразрешима.
Если 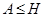 , то , то
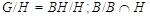
нильпотентна. Пусть теперь 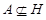 . Так как . Так как 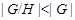 , то нам только нужно показать, что условия теоремы справедливы для , то нам только нужно показать, что условия теоремы справедливы для 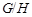 . Ясно, что . Ясно, что
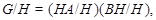
где 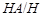 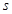 -квазинормальна в -квазинормальна в 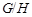 и и 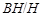 нильпотентна. Пусть нильпотентна. Пусть 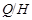 силовская силовская 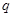 -подгруппа из -подгруппа из  и и 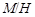 - произвольная максимальная подгруппа в - произвольная максимальная подгруппа в 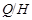 . Пусть . Пусть 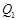 - силовская - силовская 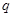 -подгруппа из -подгруппа из 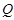 , такая что , такая что 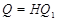 . Ясно, что . Ясно, что 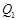 - силовская - силовская 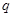 -подгруппа группы -подгруппа группы 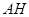 . Значит, . Значит, 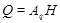 для некоторой силовской для некоторой силовской 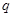 -подгруппы -подгруппы 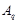 из из  . Предположим, что . Предположим, что 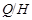 не является циклической подгруппой. Тогда не является циклической подгруппой. Тогда 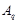 не циклична. Покажем, что не циклична. Покажем, что 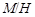 слабо нормальна в слабо нормальна в 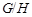 . Если . Если 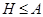 , то это прямо следует из леммы . Допустим, что либо силовская , то это прямо следует из леммы . Допустим, что либо силовская 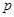 -подгруппа -подгруппа 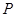 из из  циклическая, либо циклическая, либо 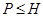 . Тогда . Тогда 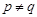 . Покажем, что . Покажем, что 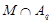 - максимальная в - максимальная в 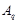 подгруппа. Так как подгруппа. Так как 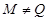 и и 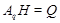 , то , то
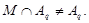
Предположим, что для некоторой подгруппы 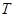 из из  мы имеем мы имеем
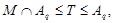
где
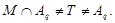
Тогда
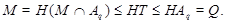
Так как 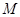 - максимальная в - максимальная в 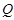 подгруппа, то либо подгруппа, то либо 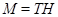 , либо , либо 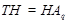 . Если . Если 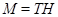 , то , то
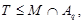
что противоречит выбору подгруппы 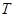 . Значит, . Значит, 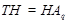 и поэтому мы имеем и поэтому мы имеем
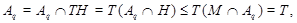
противоречие. Следовательно, 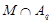 - максимальная в - максимальная в 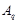 подгруппа и по условию подгруппа и по условию 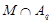 слабо нормальна в слабо нормальна в  . Значит, . Значит,
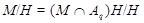
слабо нормальна в 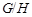 . Следовательно, условия теоремы справедливы для . Следовательно, условия теоремы справедливы для 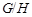 . .
(3) 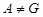 и и  сверхразрешима
. сверхразрешима
.
По выбору группы  , , 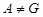 и поэтому и поэтому  сверхразрешима согласно (1). сверхразрешима согласно (1).
(4)  - разрешимая группа
. - разрешимая группа
.
По условию  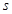 -квазинормальна в -квазинормальна в  и поэтому по лемме (3), и поэтому по лемме (3),  содержится в некоторой разрешимой нормальной подгруппе содержится в некоторой разрешимой нормальной подгруппе 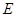 группы группы  . Так как группа . Так как группа  нильпотентна, то нильпотентна, то  разрешима. разрешима.
(5) Если 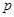 - простое число и - простое число и 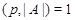 , то , то 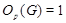 . .
Пусть 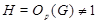 . Тогда ввиду (2), . Тогда ввиду (2), 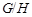 сверхразрешима. Если сверхразрешима. Если 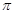 - множество всех простых делителей порядка группы - множество всех простых делителей порядка группы  , то по лемме (1), , то по лемме (1), 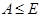 , где , где 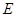 - нормальная - нормальная 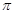 -подгруппа группы -подгруппа группы  и поэтому и поэтому

сверхразрешима. Но тогда
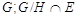
сверхразрешима. Полученное противоречие с выбором группы  доказывает (5). доказывает (5).
(6) 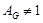 . .
Допустим, что 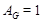 . Тогда по лемме , . Тогда по лемме ,  нильпотентна. Пусть нильпотентна. Пусть 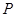 - силовская - силовская 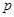 -подгруппа из -подгруппа из  . Так как ввиду леммы (3) . Так как ввиду леммы (3)  субнормальна в субнормальна в  , то , то 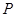 субнормальна в субнормальна в  . Тогда . Тогда 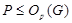 , согласно лемме (1). Но тогда ввиду (2), , согласно лемме (1). Но тогда ввиду (2), 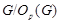 сверхразершима и поэтому сверхразершима и поэтому 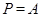 , по выбору группы , по выбору группы  . Так как . Так как 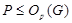 и и
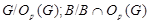
нильпотентно, то 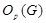 - силовская - силовская 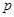 -подгруппа из -подгруппа из  . Пусть . Пусть 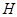 - холлова - холлова 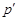 -подгруппа из -подгруппа из 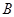 и и 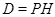 . По лемме , . По лемме , 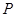 нормальна в нормальна в 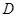 и поэтому и поэтому 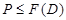 . Допустим, что для некоторого простого делителя порядка . Допустим, что для некоторого простого делителя порядка 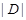 , отличного от , отличного от 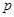 , мы имеем , мы имеем 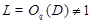 . Тогда . Тогда 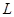 нормальна в нормальна в 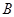 и поэтому и поэтому 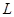 - нормальная подгруппа в - нормальная подгруппа в  , поскольку , поскольку 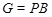 . Но тогда . Но тогда 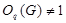 , что противоречит (5). Следовательно, , что противоречит (5). Следовательно, 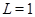 и поэтому и поэтому 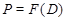 . Согласно теореме , . Согласно теореме , 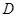 сверхразрешима и поэтому сверхразрешима и поэтому 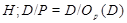 - абелева группа, экспонента которой делит - абелева группа, экспонента которой делит 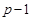 , согласно леммы . Но тогда , согласно леммы . Но тогда 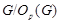 - абелева группа экспоненты, делящей - абелева группа экспоненты, делящей 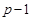 и поэтому и поэтому  сверхразрешима, согласно леммы . Полученное противоречие с выбором группы сверхразрешима, согласно леммы . Полученное противоречие с выбором группы  доказывает (6). доказывает (6).
Заключительное противоречие
.
Пусть 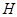 - минимальная нормальная подгруппа в - минимальная нормальная подгруппа в  , содержащаяся в , содержащаяся в  . Пусть . Пусть 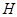 - - 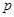 -группа и -группа и 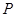 - силовская - силовская 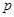 -подгруппа группы -подгруппа группы  . В силу (2), . В силу (2), 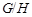 сверхразрешима и поэтому сверхразрешима и поэтому 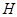 - единственная минимальная нормальная подгруппа группы - единственная минимальная нормальная подгруппа группы  , содержащаяся в , содержащаяся в  . Ясно, что . Ясно, что 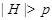 и и 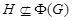 . Значит, по лемме для некоторой максимальной подгруппы . Значит, по лемме для некоторой максимальной подгруппы 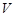 из из 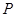 мы имеем мы имеем 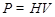 . Ясно, что . Ясно, что 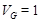 и поэтому по условию и поэтому по условию 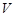 имеет дополнение имеет дополнение 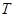 в в  , которое является квазинормальной в , которое является квазинормальной в  подгруппой. Тогда подгруппой. Тогда
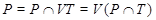
и поэтому 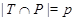 . Но тогда . Но тогда
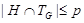
и поэтому, ввиду минимальности 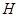 , , 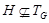 . Ввиду (5), . Ввиду (5),  имеет холлову имеет холлову  -подгруппу. Так как в силу леммы (3), -подгруппу. Так как в силу леммы (3), 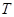 субнормальна в субнормальна в  , то каждая холлова , то каждая холлова  -подгруппа группы -подгруппа группы  содержится в содержится в 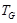 . Следовательно, . Следовательно, 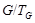 - - 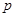 -группа. Отсюда следует, что -группа. Отсюда следует, что
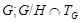
сверхразрешима. Полученное противоречие завершает доказательство теоремы.
Группа  дисперсивна по Оре тогда и только тогда, когда дисперсивна по Оре тогда и только тогда, когда 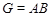 , где подгруппа , где подгруппа 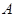 квазинормальна в квазинормальна в  , , 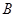 дисперсивна по Оре и каждая максимальная подгруппа любой нециклической силовской подгруппы группы дисперсивна по Оре и каждая максимальная подгруппа любой нециклической силовской подгруппы группы 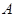 слабо нормальна в слабо нормальна в  . .
Доказательство.
Пусть 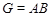 , где подгруппа , где подгруппа 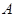 квазинормальна в квазинормальна в  , , 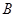 дисперсивна по Оре и каждая максимальная подгруппа любой нециклической силовской подгруппы группы дисперсивна по Оре и каждая максимальная подгруппа любой нециклической силовской подгруппы группы 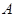 слабо нормальна в слабо нормальна в  . Покажем, что группа . Покажем, что группа  дисперсивна по Оре. Предположим, что это не верно и пусть дисперсивна по Оре. Предположим, что это не верно и пусть  - контрпример минимального порядка. Тогда: - контрпример минимального порядка. Тогда:
(1) Каждая собственная подгруппа 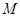 группы группы  , содержащая , содержащая 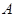 , дисперсивна по Оре
. , дисперсивна по Оре
.
Пусть 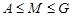 , где , где  . Тогда . Тогда
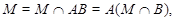
где 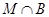 дисперсивна по Оре и дисперсивна по Оре и 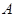 квазинормальна в квазинормальна в 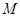 . Так как по лемме (2) любая максимальная подгруппа каждой нециклической силовской подгруппы из . Так как по лемме (2) любая максимальная подгруппа каждой нециклической силовской подгруппы из 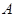 слабо нормальна в слабо нормальна в 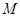 и и 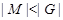 , то по выбору группы , то по выбору группы  мы имеем (1). мы имеем (1).
(2) Пусть 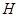 - неединичная нормальная подгруппа в - неединичная нормальная подгруппа в  , являющаяся , являющаяся 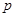 -группа для некоторого простого числа -группа для некоторого простого числа 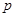 . Допустим, что либо . Допустим, что либо 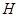 содержит силовскую содержит силовскую 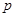 -подгруппу -подгруппу 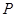 из из 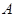 , либо , либо 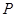 циклична, либо циклична, либо 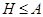 . Тогда . Тогда 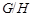 дисперсивна по Оре. дисперсивна по Оре.
Если 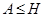 , то , то
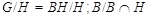
дисперсивна по Оре. Пусть теперь 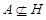 . Так как . Так как 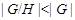 , то нам лишь нужно показать, что условия теоремы справедливы для , то нам лишь нужно показать, что условия теоремы справедливы для 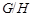 . Ясно, что . Ясно, что
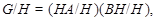
где 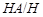 квазинормальна в квазинормальна в 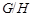 и и 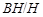 дисперсивна по Оре. Пусть дисперсивна по Оре. Пусть 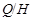 силовская силовская 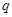 -подгруппа из -подгруппа из 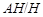 и и 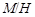 - произвольная максимальная подгруппа в - произвольная максимальная подгруппа в 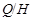 . Пусть . Пусть 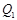 - силовская - силовская 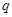 -подгруппа из -подгруппа из 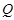 , такая что , такая что 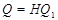 . Ясно, что . Ясно, что 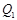 - силовская - силовская 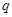 -подгруппа группы -подгруппа группы  . Значит, . Значит, 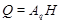 для некоторой силовской для некоторой силовской 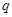 -подгруппы -подгруппы 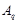 из из 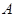 . Предположим, что . Предположим, что 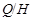 не является циклической подгруппой. Тогда не является циклической подгруппой. Тогда 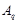 не циклична. Покажем, что не циклична. Покажем, что 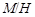 слабо нормальна в слабо нормальна в 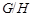 . Если . Если 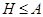 , то это прямо следует из леммы . Допустим, что либо силовская , то это прямо следует из леммы . Допустим, что либо силовская 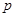 -подгруппа -подгруппа 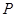 из из 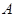 циклическая, либо циклическая, либо 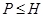 . Тогда . Тогда 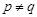 . Покажем, что . Покажем, что 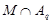 - максимальная в - максимальная в 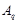 подгруппа. Так как подгруппа. Так как 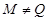 и и 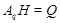 , то , то
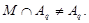
Предположим, что для некоторой подгруппы 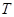 из из  мы имеем мы имеем
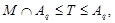
где
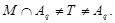
Тогда
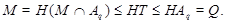
Так как 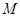 - максимальная в - максимальная в 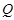 подгруппа, то либо подгруппа, то либо 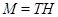 , либо , либо 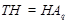 . Если . Если 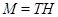 , то , то 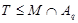 , что противоречит выбору подгруппы , что противоречит выбору подгруппы 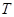 . Значит, . Значит, 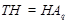 и поэтому мы имеем и поэтому мы имеем
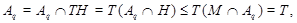
противоречие. Следовательно, 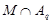 - максимальная в - максимальная в 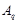 подгруппа и по условию подгруппа и по условию 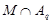 слабо нормальна в слабо нормальна в  . Значит, . Значит,
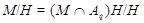
слабо нормальна в 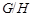 . Следовательно, условия теоремы справедливы для . Следовательно, условия теоремы справедливы для 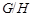 . .
(3) Если 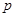 - простое число и - простое число и 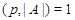 , то , то 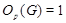 . .
Пусть
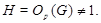
Тогда ввиду (2), 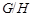 дисперсивна по Оре. С другой стороны, если дисперсивна по Оре. С другой стороны, если 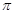 - множество всех простых делителей - множество всех простых делителей 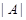 , то ввиду леммы (3) и леммы , , то ввиду леммы (3) и леммы , 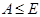 , где , где 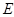 - нормальная - нормальная 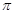 -подгруппа в -подгруппа в  и поэтому и поэтому

дисперсивна по Оре. Но тогда
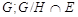
дисперсивна по Оре, противоречие. Значит, справедливо (3).
(4)  разрешима. разрешима.
По условию 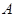 квазинормальна в квазинормальна в  и поэтому ввиду леммы (3) и леммы , и поэтому ввиду леммы (3) и леммы , 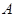 содержится в некоторой разрешимой нормальной подгруппе содержится в некоторой разрешимой нормальной подгруппе 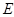 группы группы  . Так как . Так как

дисперсивна по Оре, то  разрешима. разрешима.
(5) 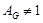 . .
Предположим, что 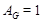 . Тогда согласно лемме , . Тогда согласно лемме , 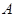 нильпотентна. Пусть нильпотентна. Пусть 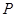 - силовская - силовская 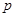 -подгруппа группы -подгруппа группы 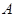 . Поскольку . Поскольку 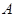 субнормальна в субнормальна в  , то , то 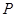 субнормальна в субнормальна в  . Значит, по лемме , . Значит, по лемме , 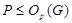 . Но ввиду (2), . Но ввиду (2), 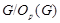 дисперсивна по Оре и поэтому по выбору группы дисперсивна по Оре и поэтому по выбору группы  , , 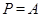 . Пусть . Пусть 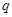 - наименьший простой делитель - наименьший простой делитель 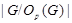 . Тогда . Тогда  имеет нормальную максимальную подгруппу имеет нормальную максимальную подгруппу 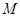 , такую что , такую что 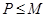 и и 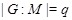 . Пусть . Пусть 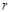 - наибольший простой делитель - наибольший простой делитель 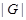 , , 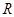 - силовская - силовская 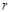 -подгруппа группы -подгруппа группы 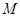 . Тогда ввиду (1), . Тогда ввиду (1), 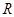 нормальна в нормальна в 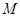 и поэтому и поэтому 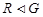 . Если . Если 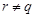 , то , то 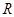 - силовская - силовская 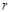 -подгруппа группы -подгруппа группы  и поэтому и поэтому 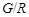 дисперсивна по Оре. Отсюда следует, что дисперсивна по Оре. Отсюда следует, что  дисперсивна по Оре, противоречие. Следовательно, дисперсивна по Оре, противоречие. Следовательно, 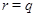 . Но тогда . Но тогда 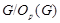 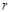 -группа. Пусть -группа. Пусть 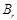 - силовская - силовская 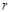 -подгруппа в -подгруппа в 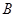 . Тогда . Тогда 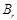 - силовская - силовская 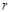 -подгруппа в -подгруппа в  . Поскольку . Поскольку 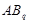 - подгруппа группы - подгруппа группы  и ввиду (1), и ввиду (1), 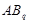 дисперсивна по Оре, то дисперсивна по Оре, то 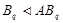 . Так как . Так как 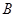 дисперсивна по Оре, то дисперсивна по Оре, то 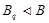 и поэтому и поэтому 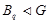 . Следовательно, группа . Следовательно, группа  дисперсивна по Оре. Полученное противоречие доказывает (5). дисперсивна по Оре. Полученное противоречие доказывает (5).
Заключительное противоречие
.
Пусть 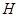 - минимальная нормальная подгруппа группы - минимальная нормальная подгруппа группы  , содержащаяся в , содержащаяся в 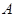 . Пусть . Пусть 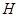 - - 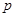 -группа и -группа и 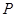 - силовская - силовская 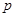 -подгруппа группы -подгруппа группы 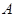 . Ввиду (2), . Ввиду (2), 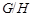 дисперсивна по Оре. Пусть дисперсивна по Оре. Пусть 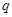 - наименьший простой делитель - наименьший простой делитель 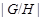 . Тогда . Тогда  имеет нормальную максимальную подгруппу имеет нормальную максимальную подгруппу 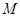 , такую что , такую что 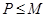 и и 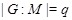 . Пусть . Пусть 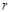 - наибольший простой делитель - наибольший простой делитель 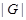 , , 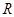 - силовская - силовская 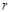 -подгруппа группы -подгруппа группы 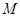 . Тогда ввиду (1), . Тогда ввиду (1), 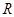 нормальна в нормальна в 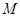 и поэтому и поэтому 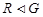 . Рассуждая как выше видим, что . Рассуждая как выше видим, что 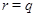 . Но тогда . Но тогда 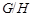 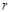 -группа. Значит, -группа. Значит, 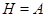 и поэтому и поэтому  дисперсивна по Оре. Полученное противоречие завершает доказательство теоремы. дисперсивна по Оре. Полученное противоречие завершает доказательство теоремы.
Заключение
В последние годы значительно возрос интерес к квазинормальным и 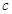 -нормальным подгруппам. Следует отметить, что получено большое число теорем связанных с изучением групп, те или иные выделенные системы подгрупп которых -нормальным подгруппам. Следует отметить, что получено большое число теорем связанных с изучением групп, те или иные выделенные системы подгрупп которых 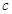 -нормальны или квазинормальны в группе -нормальны или квазинормальны в группе 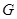 . Не смотря на тот факт, что квазинормальность и . Не смотря на тот факт, что квазинормальность и 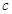 -нормальность являются вполне различными обобщениями нормальности, в настоящее время получено много аналогичных результатов не зависимо для квазинормальных и -нормальность являются вполне различными обобщениями нормальности, в настоящее время получено много аналогичных результатов не зависимо для квазинормальных и 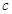 -нормальных подгрупп. В данной работе мы устраняем такой параллелизм на основе введенного понятия слабой квазинормальности. -нормальных подгрупп. В данной работе мы устраняем такой параллелизм на основе введенного понятия слабой квазинормальности.
Основные результаты данной работы:
- доказаны новые критерии принадлежности группы насыщенной формации;
- найдены описания разрешимых и метанильпотентных групп по свойствам их максимальных и силовских подгрупп;
- получены описания дисперсивных по Оре и сверхразрешимых групп по свойствам максимальных подгрупп силовских подгрупп;
- найдены критерии разрешимости и метанильпотентности групп в терминах слабо нормальных подгрупп.
Работа имеет теоретический характер. Результаты курсовой работы могут быть использованы при изучении слабо нормальных, квазинормальных и слабо квазинормальных подгрупп.
Литература
1.Боровиков, М.Т. Группы с перестановочными подгруппами взаимно простых порядков / М.Т. Боровиков // Вопросы алгебры. Выпуск 5. - Минск: Университетское, 1990. - С. 80-82.
2.Боровиков, М.Т. О 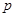 -разрешимости конечной группы / М.Т. Боровиков // Арифметическое и подгрупповое строение конечных групп / Под редакцией М.И. Салука. - Минск: Наука и техника, 1986. - С. 3-7. -разрешимости конечной группы / М.Т. Боровиков // Арифметическое и подгрупповое строение конечных групп / Под редакцией М.И. Салука. - Минск: Наука и техника, 1986. - С. 3-7.
3.Го Веньбинь. 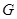 -накрывающие системы подгрупп для классов -накрывающие системы подгрупп для классов 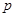 -сверхразрешимых и -сверхразрешимых и 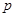 -нильпотентных конечных групп / Го Веньбинь, К.П. Шам, А.Н. Скиба // Сиб. мат. журнал. - 2004. - Т. 45, № 3. - С. 75-92. -нильпотентных конечных групп / Го Веньбинь, К.П. Шам, А.Н. Скиба // Сиб. мат. журнал. - 2004. - Т. 45, № 3. - С. 75-92.
4.Пальчик, Э.М. О группах, все 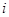 -максимальные подгруппы которых перестановочны с силовской подгруппой / Э.М. Пальчик // ИАН БССР. Сер. физ.-матем. наук. - 1968. - № 1. - С. 45-48. -максимальные подгруппы которых перестановочны с силовской подгруппой / Э.М. Пальчик // ИАН БССР. Сер. физ.-матем. наук. - 1968. - № 1. - С. 45-48.
5.Пальчик, Э.М. О конечных группах с перестановочными подгруппами / Э.М. Пальчик // Докл. АН БССР. - 1967. - Т. 11, № 5. - С. 391-392.
6.Пальчик, Э.М. О группах, все 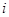 -максимальные подгруппы которых перестановочны с силовской подгруппой. II / Э.М. Пальчик, Н.П. Конторович // ИАН БССР. Сер. физ.-матем. наук. - 1969. - № 3. - С. 51-57. -максимальные подгруппы которых перестановочны с силовской подгруппой. II / Э.М. Пальчик, Н.П. Конторович // ИАН БССР. Сер. физ.-матем. наук. - 1969. - № 3. - С. 51-57.
7.Подгорная, В.В. Полунормальные подгруппы и сверхразрешимость конечных групп / В.В. Подгорная // Весцi НАН Беларусi. Сер. фiз.-матэм. навук. - 2000. - № 4. - С. 22-25.
8.Подгорная, В.В. Факторизации конечных групп дисперсивными и сверхразрешимыми подгруппами / В.В. Подгорная // Веснiк Вiцебскага дзяржаунага Унiверсiтэта. - 1999. - № 4(14). - С. 80-82.
9.Поляков, Л.Я. Конечные группы с перестановочными подгруппами / Л.Я. Поляков // Конечные группы. - Минск: Наука и техника, 1966. - С.75-88.
10.Самусенко (Подгорная), В.В. О конечных группах с заданными минимальными добавлениями к подгруппам / В.В. Самусенко // Вопросы алгебры. Выпуск 13. - 1998. - С. 177-182.
|