Дипломна робота
Методи дослідження мереж масового обслуговування
РЕФЕРАТ
Дипломна бакалаврська робота:
73 сторінки, 7 джерел, 7 таблиць, 5 рисунків.
Перелік ключових слів:
мережа масового обслуговування, рівняння балансу, теорема ВСМР, теорема Нортона, декомпозиція мережі.
Об’єкт дослідження:
мережі масового обслуговування.
Мета роботи:
огляд методів розрахунку та дослідження мереж МО.
ЗМІСТ
ВСТУП
РОЗДІЛ 1. ОСНОВНІ ПОНЯТТЯ І ОЗНАЧЕННЯ
1.1 Механізм обслуговування
1.2 Дисципліна обслуговування
1.3 Маршрутна матриця і потоки в мережах
1.4 Інші означення
РОЗДІЛ 2. СКЛАДАННЯ РІВНЯННЬ ЛОКАЛЬНОГО БАЛАНСУ ДЛЯ МЕРЕЖМАСОВОГО ОБСЛУГОВУВАННЯ
2.1 Однорідні експоненціальні мережі масового обслуговування
2.1.1 Рівняння глобального балансу для замкнених мереж
2.1.2 Вигляд розв’язку в мультиплікативній формі
2.1.3 Мережі, що залежать від навантаження
2.1.4 Показники якості функціонування однорідних мереж
2.2 Мережі МО з кількома класами повідомлень
2.2.1 Опис змішаної мережі
2.2.2 Теорема ВСМР
2.2.3 Відкриті мережі масового обслуговування з кількома класами повідомлень
2.2.4 Розширення теореми ВСМР
РОЗДІЛ 3. МЕТОД АНАЛІЗУ СЕРЕДНІХ ЗНАЧЕНЬ
3.1 Загальне описання методу
3.2 Однорідна замкнена мережа масового обслуговування, що залежить від навантаження
3.3 Обчислення основних співвідношень
РОЗДІЛ 4. ОБЧИСЛЕННЯ ХАРАКТЕРИСТИК МЕРЕЖ МО
4.1 Метод Бузена
4.2 Обчислення характеристик мережі масового обслуговування
РОЗДІЛ 5. МЕТОД ДЕКОМПОЗИЦІЙНОЇ АПРОКСИМАЦІЇ
5.1 Апроксимація функцій розподілу475.2 Теорема Нортона для аналізу замкнених і розімкнених локально-збалансованих мереж масового обслуговування
5.3 Наближений декомпозиційний алгоритм
5.4 Декомпозиція розімкнених мереж масового обслуговування на рівні перших моментів
РОЗДІЛ 6. МЕТОД ПОЛІНОМІАЛЬНОЇ АПРОКСИМАЦІЇ
6.1 Опис методу
6.2 Оцінка обчислювальної складності
РОЗДІЛ 7. ПРИКЛАД РОЗРАХУНКУ МЕРЕЖІ МАСОВОГО ОБСЛУГОВУВАННЯ
ВИСНОВКИ
ПЕРЕЛІК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
ДОДАТОК
ВСТУП
Одним з розділів теорії масового обслуговування є мережі масового обслуговування. Поява цього розділу пов'язана з вирішенням практичних задач проектування обчислювальних систем та мереж. Перші підходи до аналізу мереж масового обслуговування (МО) були розроблені у 1960-70 pp. математиками Й.Джексоном, В.Гордоном та Ж.Ньюелом. Однак ці роботи не знайшли широкого практичного застосування до появи в 1971 р. роботи Ф.Мура, у якій було показано, що мережі МО є адекватними моделями функціонування обчислювальних систем. Подальший розвиток області застосування теорії мереж МО пов'язаний з удосконалюванням апаратного та програмного забезпечення обчислювальних систем.
Реклама

Складність та різноманіття підходів щодо дослідження функціонування мереж МО створюють значні труднощі для спеціалістів суміжних областей, які бажають використовувати цю теорію для вирішення практичних задач. В той же час достатня завершеність математичних результатів і практичні потреби розробників обчислювальних мереж зумовили необхідність систематизованого викладу методів аналізу мереж МО. Теоретичні дослідження мереж МО і їх практичне застосування знайшли відображення в численних статтях і оглядах, які орієнтовані в основному на математиків, а також в окремих розділах монографій.
У роботі основні методи дослідження мереж МО розділені на дві групи – аналітичні та наближені. Розглянутий у розділі 1 метод дослідження локально-збалансованих мереж МО дозволяє отримати розв'язок в зручній мультиплікативній формі. Але пряме обчислення стаціонарних ймовірностей станів та інших характеристик мережі є досить складною процедурою. У зв'язку з цим у розділі 4 розглянуті ефективні рекурентні алгоритми розрахунку мереж МО. Метод аналізу середніх значень дозволяє обчислити такі важливі показники функціонування мережі MO, як середні довжини черг та час дожидання, продуктивність мережі та ін., не удаючись до розрахунку нормалізуючої константи.
Область застосування аналітичних моделей мереж МО у значній мірі обмежується через припущення щодо експоненціального характеру обслуговування. У цьому випадку, враховуючи, що методи точного аналізу немарківських мереж МО мало перспективні при дослідженні реальних систем, використовують наближені методи, які розглянуті у 5-6 розділах. Основний підхід полягає в апроксимації довільної функції розподілу послідовністю функцій розподілу, які допускають раціональне перетворення Лапласа, і відшуканні точного розв'язку для одержаної мережі МО в мультиплікативній формі.
У роботі також наведений приклад розрахунку мережі масового обслуговування одним із методів та відповідна програма для обчислення характеристик.
Реклама

РОЗДІЛ Ι. ОСНОВНІ ПОНЯТТЯ ТА ОЗНАЧЕННЯ
Предметом вивчення мереж МО є методи кількісного аналізу черг при взаємодії множини центрів обслуговування і потоків повідомлень.
Мережа МО є сукупністю скінченного числа М обслуговуючих центрів, в якій циркулюють повідомлення, які переходять відповідно до маршрутної матриці з одного центру в іншій. Під центром обслуговування розуміють систему масового обслуговування, що складається з А однакових приладів 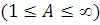 і буфера об'ємом і буфера об'ємом 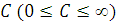 . При . При 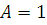 центр називають однолінійним, при центр називають однолінійним, при 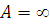 — нескінченнолінійним. Надалі, якщо спеціально не обумовлено, вважатимемо, що об'єм буфера в центрі обслуговування — нескінченнолінійним. Надалі, якщо спеціально не обумовлено, вважатимемо, що об'єм буфера в центрі обслуговування 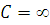 . .
Якщо у момент надходження повідомлення всі обслуговуючі прилади центру зайняті, то повідомлення займає чергу в буфері, де чекає початку обслуговування. Черги є наслідком стохастичного характеру надходження і обслуговування повідомлень в центрі.
1.1 МЕХАНІЗМ ОБСЛУГОВУВАННЯ
Механізм обслуговування характеризується кількістю роботи по обробці повідомлення, яка вимірюється в різних одиницях залежно від природи центру обслуговування. Швидкодія обслуговуючого приладу в центрі визначається кількістю роботи, яка виконується ним в одиницю часу. Відношення кількості роботи при обслуговуванні одного повідомлення до швидкодії, яка називається тривалістю обслуговування повідомлення, а також величина µ, зворотна середній тривалості обслуговування, — інтенсивність обслуговування, одиницею вимірювання якої служить повідомлення в секунду, є важливими поняттями теорії мереж МО. Загальна інтенсивність обслуговування і
-го центру може залежати від числа повідомлень 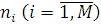 , що знаходяться в центрі (як на обслуговуванні, так і в черзі). Наприклад, інтенсивність обслуговування центру, що складається з , що знаходяться в центрі (як на обслуговуванні, так і в черзі). Наприклад, інтенсивність обслуговування центру, що складається з 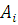 однакових обслуговуючих приладів, визначається виразом однакових обслуговуючих приладів, визначається виразом
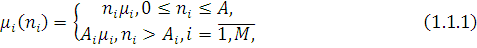
де 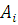 - кількість однакових обслуговуючих приладів у і-му центрі. - кількість однакових обслуговуючих приладів у і-му центрі.
Нехай 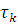 — тривалість обслуговування k-го повідомлення. Якщо випадкові величини — тривалість обслуговування k-го повідомлення. Якщо випадкові величини 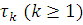 незалежні в сукупності і володіють однаковою функцією розподілу F(t), то таке обслуговування називається рекурентним. Основні аналітичні результати в теорії мереж МО одержані для випадку, коли перетворення Лапласа функції розподілу часу обслуговування незалежні в сукупності і володіють однаковою функцією розподілу F(t), то таке обслуговування називається рекурентним. Основні аналітичні результати в теорії мереж МО одержані для випадку, коли перетворення Лапласа функції розподілу часу обслуговування
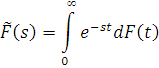
є раціональною функцією вигляду
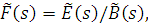
де 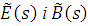 — відповідно поліноми степеня d і d1 — відповідно поліноми степеня d і d1
Клас функцій розподілу, що володіють раціональним перетворенням Лапласа, є достатньо широкий і включає експоненціальний розподіл, розподіл Ерланга, гіперекспоненціальний розподіл та ін. Характеристики деяких цих розподілів наведені в табл. 1.1.
Таблиця 1.1 Характеристики деяких розподілів
Тип
розподілу
|
Функція розподілу |
Математичне сподівання |
Дисперсія |
Перетворення Лапласа |
| Експоненціальний |
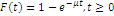
|
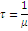 |
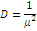 |
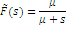 |
Ерланга
k- го порядку
|
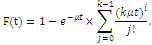
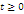
|
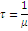 |
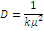 |
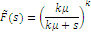 |
Гіперекспоненціальний k- го
порядку
|
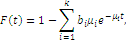
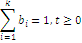
|
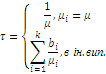 |

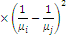
|
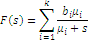 |
Вигляд перетворення Лапласа функції розподілу Ерланга k-го порядку показує, що воно є k- кратною згорткою експоненціального розподілу з середнім 1/kµ. Тому розподіл Ерланга k-го порядку можна інтерпретувати як розподіл тривалості обслуговування повідомлення на k послідовно сполучених однолінійних центрах обслуговування (етапах), причому тривалість обслуговування в кожному однолінійному центрі має експоненціальний розподіл з параметром kµ.
1.2 ДИСЦИПЛІНА ОБСЛУГОВУВАННЯ
Дисципліна обслуговування відображає правило, відповідно до якого здійснюється вибір повідомлення для обслуговування в центрі. Розрізняють безпріорітетні і пріоритетні дисципліни обслуговування. Прикладом безпріорітетних дисциплін є дисципліна обслуговування «першим прийшов — першим обслужений» (ПППО), відповідно до якої повідомлення, що надійшло в центр, стає в кінець черги повідомлень, які чекають обслуговування, якщо всі прилади центру зайняті, і негайно починає обслуговуватися, якщо вільний хоча б один прилад.
Хорошою ілюстрацією пріоритетних дисциплін є правило вибору повідомлення за принципом «останнім прийшов — першим обслужений» (ОППО). При обслуговуванні за принципом ОППО, повідомленню, яке щойно надійшло, привласнюється щонайвищий пріоритет і воно або починає негайно обслуговуватися, перериваючи обслуговування попередніх повідомлень (абсолютний пріоритет), або стає першим в черзі повідомлень, які чекають обслуговування (відносний пріоритет). Щодо повідомлення, обслуговування якого було перерване, можливі різні припущення: воно або покидає центр обслуговування (втрачається), або повертається в початок черги (обслуговування цього повідомлення або починається наново, або з перерваного місця).
Окрім дисципліни обслуговування ПППО і ОППО в теорії мереж МО велику роль відіграють ще дві дисципліни — розділення процесора (РП) і обслуговування без очікування (ОБО). У однолінійних центрах з дисципліною обслуговування РП кожне повідомлення незалежно від його положення в черзі обслуговується з інтенсивністю, обернено пропорційною кількості п повідомлень в центрі (іншими словами, кожне повідомлення обслуговується 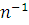 c). c).
1.3 МАРШРУТНА МАТРИЦЯ І ПОТОКИ В МЕРЕЖАХ
Перехід повідомлення з одного центру після закінчення обслуговування в ньому в іншій здійснюється відповідно до заданого маршруту, під яким розуміється послідовність відвідуваних повідомленням центрів мережі. Маршрут повідомлення по мережі МО задається матрицею маршрутів P, вид якої залежить від того, чи є мережа МО відкритою або замкненою. У відкриту мережу МО повідомлення надходять із зовнішнього джерела і можуть покидати мережу після завершення обслуговування. Якщо прийняти зовнішнє джерело за новий центр мережі і позначити індексом 0, то маршрут у відкритій мережі задається стохастичною матрицею 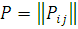 , де , де 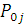 і і 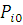 — відповідно імовірність надходження в j-й центр повідомлення з джерела і імовірність покидання повідомленням мережі після закінчення обслуговування в і-му центрі; — відповідно імовірність надходження в j-й центр повідомлення з джерела і імовірність покидання повідомленням мережі після закінчення обслуговування в і-му центрі; 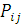 — імовірність того, що повідомлення, що йде з i-го центру, перейде в j-й центр — імовірність того, що повідомлення, що йде з i-го центру, перейде в j-й центр 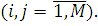
Очевидно, що виконується рівність
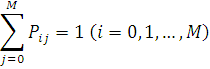
Потік повідомлень, який входить з джерела в мережу визначається сумісним розподілом випадкових величин 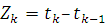 , де , де 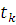 — моменти надходження повідомлень — моменти надходження повідомлень 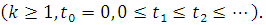 Якщо випадкові величини Zk
незалежні в сукупності, то такий потік називають потоком з обмеженою післядією і для його визначення достатньо задати набір функцій розподілу Якщо випадкові величини Zk
незалежні в сукупності, то такий потік називають потоком з обмеженою післядією і для його визначення достатньо задати набір функцій розподілу 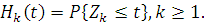 Важливу роль в теорії систем і мереж МО виконує рекурентний потік, для якого Важливу роль в теорії систем і мереж МО виконує рекурентний потік, для якого 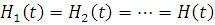 . Окремим випадком рекуррентного потоку є пуассонівський потік, для якого . Окремим випадком рекуррентного потоку є пуассонівський потік, для якого 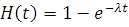 , де інтенсивність потоку λ може залежати від загального числа повідомлень N, що знаходяться в мережі. , де інтенсивність потоку λ може залежати від загального числа повідомлень N, що знаходяться в мережі.
Для визначення потоків, що циркулюють в стаціонарному режимі у відкритій мережі МО, введемо коефіцієнти передачі ei
такі, що ei
λ(N) є загальною інтенсивністю потоку повідомлень в i-й центр мережі. Інтенсивність ei
λ(N) складається з інтенсивності надходження повідомлень в і-й центр з джерела 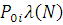 і інтенсивності надходження від інших центрів і інтенсивності надходження від інших центрів 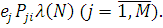 Таким чином, величини ei
задовольняють наступній системі лінійних рівнянь: Таким чином, величини ei
задовольняють наступній системі лінійних рівнянь:
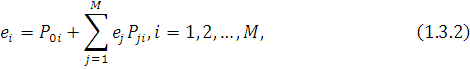
розв’язок якої через припущення про те, що стохастична матриця маршрутів Р є невиродженою, існує і єдиний.
У замкненій мережі МО повідомлення ззовні не надходять і не покидають мережу; кількість повідомлень, що циркулюють в ній, постійна і дорівнює N. Матриця Р, що визначає випадкові маршрути руху повідомлень, так же само, як і для відкритої мережі, передбачається стохастичною і нерозкладною, але не містить в цьому випадку нульових стовпця і рядка (джерело повідомлень відсутнє). Система лінійних рівнянь (1.3.2) набуде вигляду

Число незалежних рівнянь в системі (1.3.3) на одиницю менше кількості змінних, так що її рішення єдине з точністю до мультиплікативної константи. Іншими словами, якщо 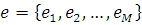 — розв’язок системи рівнянь (1.3.3), то при — розв’язок системи рівнянь (1.3.3), то при 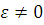 розв’язком є і розв’язком є і 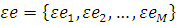 . Для відшукання однозначного розв’язку системи рівнянь (1.3.3) достатньо довільно задати значення ei
,наприклад покласти ei
=1. У цьому випадку величину ei
можна інтерпретувати як середнє число відвідувань повідомленням центру . Для відшукання однозначного розв’язку системи рівнянь (1.3.3) достатньо довільно задати значення ei
,наприклад покласти ei
=1. У цьому випадку величину ei
можна інтерпретувати як середнє число відвідувань повідомленням центру 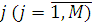 між двома послідовними відвідуваннями ним першого центру. між двома послідовними відвідуваннями ним першого центру.
Нехай 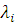 — потік, що проходить через — потік, що проходить через 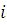 -й центр -й центр 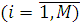 в стаціонарному режимі. Тоді вираз в стаціонарному режимі. Тоді вираз 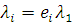 зв'язує потоки, що проходять через i-й і перший центри мережі. зв'язує потоки, що проходять через i-й і перший центри мережі.
1.4 ІНШІ ВИЗНАЧЕННЯ
В силу статистичної однорідності повідомлень, що циркулюють у відкритих і замкнених мережах МО, такі мережі називають однорідними. При цьому однорідну мережу МО називатимемо експоненціальною, якщо функції розподілу 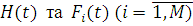 є експоненціальними, і немарківською, якщо хоча б одна з цих функцій є довільною. є експоненціальними, і немарківською, якщо хоча б одна з цих функцій є довільною.
Природним узагальненням однорідних мереж МО є мережі з кількома класами повідомлень, відмінними як маршрутами, так і тривалістю обслуговування в центрах. Така мережа може бути відкритою, замкненою або змішаною. Змішана мережа МО відкрита для одних класів повідомлень, які надходять в неї ззовні і після закінчення обслуговування покидають її, і замкнена для інших класів (кількість повідомлень кожного з таких класів усередині мережі постійна).
Основні підходи до дослідження мереж МО з кількома класами базуються або на прямому методі відшукання виразів для ймовірностей станів мережі з використанням техніки складання рівнянь локального балансу, або на методі складання рекурентних рівнянь для середніх значень.
РОЗДІЛ 2. СКЛАДАННЯ РІВНЯНЬ ЛОКАЛЬНОГО БАЛАНСУ ДЛЯ МЕРЕЖ МО
2.1 ОДНОРІДНІ ЕКСПОНЕНЦІАЛЬНІ МЕРЕЖІ
Опис математичного дослідження мереж МО доцільно почати з методів дослідження простих однорідних експоненціальних мереж, тобто мереж МО, в яких функції розподілу тривалості обслуговування в центрах є експоненціальними, а вхідні потоки повідомлень — пуассонівськими (якщо мережа є відкритою). Саме для мереж цього типу, був відзначений чудовий факт, що полягає у тому, що стаціонарна імовірність станів мережі має мультиплікативну форму. Цей факт є основою для подальших аналітичних досліджень більш загальних мереж МО, а також розробки ефективних алгоритмів розрахунку характеристик мереж МО.
2.1.1 РІВНЯННЯ ГЛОБАЛЬНОГО БАЛАНСУ ДЛЯ ЗАМКНЕНИХ МЕРЕЖ
Розглянемо однорідну замкнену мережу МО з багатолінійними центрами, дисципліною обслуговування ПППО, в якій циркулюють N повідомлень відповідно до матриці маршрутів 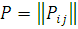 . Тривалість обслуговування повідомлення приладом i-го центру розподілена за експоненціальним законом з параметром . Тривалість обслуговування повідомлення приладом i-го центру розподілена за експоненціальним законом з параметром 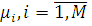 , так, що загальна інтенсивність обслуговування будь-якого центру визначається виразом (1.1.1). Розглянемо багатовимірний випадковий процес , так, що загальна інтенсивність обслуговування будь-якого центру визначається виразом (1.1.1). Розглянемо багатовимірний випадковий процес
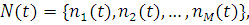
де 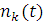 — число повідомлень, що знаходяться в k-му центрі (у черзі і на обслуговуванні) у момент t ( — число повідомлень, що знаходяться в k-му центрі (у черзі і на обслуговуванні) у момент t (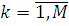 ), і позначимо через ), і позначимо через
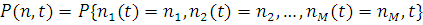
імовірність того, що у момент t мережа знаходиться в стані 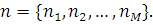
Позначимо через S(N,M) множину М-вимірних векторів з невід’ємними цілочисельними координатами
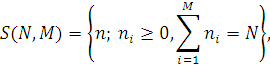
потужність якої (кількість станів) дорівнює 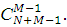
Випадковий процес N(t), який визначений на просторі станів S(N,M), є марківським, оскільки тривалості обслуговування в центрах мережі розподілені за експоненціальним законом. Аналізуючи можливі переходи цього процесу за проміжок часу 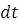 і переходячи до границі при і переходячи до границі при 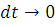 , одержуємо наступну систему прямих диференціальних рівнянь Колмогорова: , одержуємо наступну систему прямих диференціальних рівнянь Колмогорова:
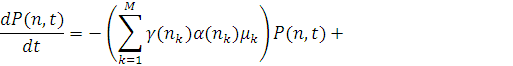
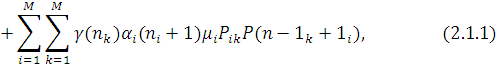
де 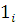 - — вектор, i-я координата якого дорівнює 1, а інші дорівнюють нулю; функція - — вектор, i-я координата якого дорівнює 1, а інші дорівнюють нулю; функція 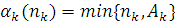 визначає число повідомлень, що знаходяться на обслуговуванні в k-му центрі ( визначає число повідомлень, що знаходяться на обслуговуванні в k-му центрі (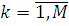 ), коли загальне число повідомлень в ньому дорівнює ), коли загальне число повідомлень в ньому дорівнює 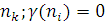 при ni
=0 і при ni
=0 і 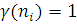 при при  . .
Розглянемо розв’язання системи (2.1.1) в стаціонарному режимі, який в замкненій мережі МО завжди існує. Прирівнюючи до нуля похідні в лівій частині системи рівнянь (2.1.1), для ймовірностей стаціонарного розподілу марківського процесу N(t)
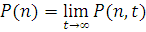
з урахуванням тотожності 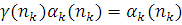 одержуємо наступну систему лінійних різницевих рівнянь: одержуємо наступну систему лінійних різницевих рівнянь:
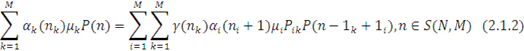
Ліва частина є швидкістю переходів із стану n, а права — швидкість переходів в цей стан. Рівняння (2.1.2) називають рівнянням глобального балансу.
2.1.2 ВИГЛЯД РОЗВ’ЯЗКУ В МУЛЬТИПЛІКАТИВНІЙ ФОРМІ
Переходячи до розв’язання системи рівнянь (2.1.2), введемо функцію
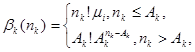
яка може бути представлена також рекурсивно:
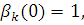
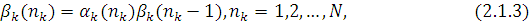
введемо заміну змінних в (2.1.2):
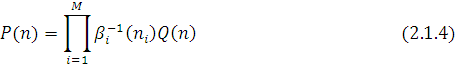
Після підстановки (2.1.4) в (2.1.2) одержимо нову систему рівнянь відносно Q(n):
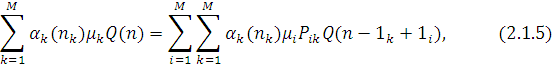
Якщо представити Q(n) у вигляді функції М невідомих параметрів xi
:

і підставити у вираз (2.1.5), то (2.1.5) набуває наступного простого вигляду:
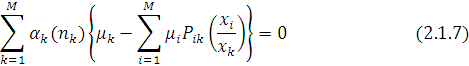
З метою подальшого спрощення останньої системи рівнянь припустимо, що всі N повідомлень знаходяться в j-му центрі 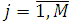 і, отже, в решті центрів повідомлення відсутні. Враховуючи, що функція і, отже, в решті центрів повідомлення відсутні. Враховуючи, що функція 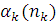 в цьому випадку за означенням дорівнює нулю для всіх в цьому випадку за означенням дорівнює нулю для всіх 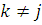 , одержуємо , одержуємо

або, ввівши позначення 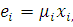
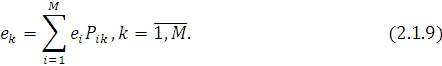
Отже, невідомі параметри xk
визначаються з системи лінійних рівнянь (2.1.9), рішення якої в силу припущення про вид маршрутної матриці Р єдине з точністю до мультиплікативної константи ε.
Таким чином, стаціонарний розподіл ймовірності станів даної замкненої однорідної експоненціальної мережі МО має вигляд
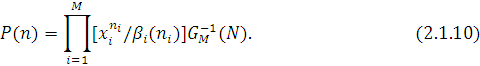
Нормалізуюча константа 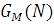 визначається з умови нормування визначається з умови нормування
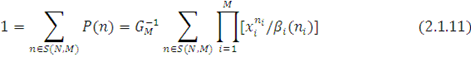
Тут підсумовування ведеться по всіх 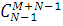 можливих станах вектора можливих станах вектора
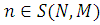 . .
З (2.1.11) витікає, що

Підставляючи (2.1.12) в (2.1.10) і враховуючи, що 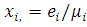 , одержуємо остаточно , одержуємо остаточно
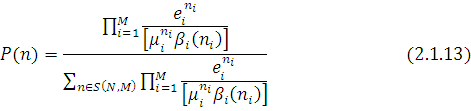
З останнього виразу видно, що стаціонарні імовірності Р(n) не залежать від константи ε з точністю, до якої визначаються значення вектора ε, і мають вид добутку, співмножники якого 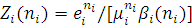 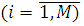 є стаціонарні імовірності станів i-го центру, що розглядається окремо від мережі. є стаціонарні імовірності станів i-го центру, що розглядається окремо від мережі.
Формули (2.1.12) і (2.1.13) дозволяють визначати різні імовірнісні характеристики мережі МО. Наприклад, ймовірність того, що кількість повідомлень в і-му однолінійному центрі 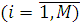 більше або рівне n, має вигляд більше або рівне n, має вигляд
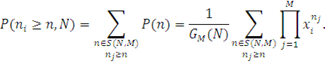
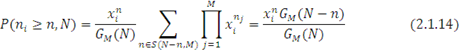
З останнього виразу, з урахуванням того, що
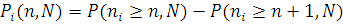 , визначається граничний розподіл числа повідомлень, що знаходяться в i-му вузлі , визначається граничний розподіл числа повідомлень, що знаходяться в i-му вузлі 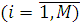 : :
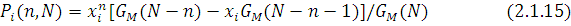
Вирази (2.1.10), (2.1.15) і (2.1.13) справедливі відповідно для мереж,що не залежать від навантаження, і мереж, в яких залежність інтенсивності обслуговування центру від числа повідомлень у ньому визначається функцією (1.1.1).
2.1.3 МЕРЕЖІ, ЩО ЗАЛЕЖАТЬ ВІД НАВАНТАЖЕННЯ
Перейдемо до розгляду більш загального класу відкритих та замкнених мереж МО, що залежать від навантаження, у яких інтенсивність вхідного потоку і інтенсивність обслуговування в центрах є відповідно довільними функціями числа повідомлень в мережі і в центрах обслуговування. Для дослідження характеристик таких мереж МО використовувається техніка складання рівнянь локального балансу
Стаціонарні імовірності станів замкненої однорідної експоненціальної мережі, що залежить від навантаження, задовольняють наступній системі лінійних рівнянь:
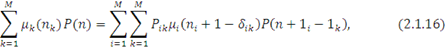
яка виводиться так само, як система рівнянь (2.1.2). Тут 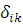 — символ Кронекера. — символ Кронекера.
Підставляючи в (2.1.16) рівняння (2.1.9), яке записане у вигляді
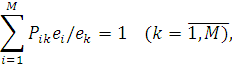
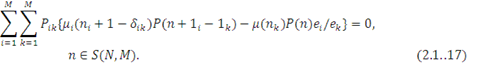
Очевидно, що рівняння глобального балансу (2.1.17) виконується, якщо вираз, що стоїть у фігурних дужках, рівний нулю:
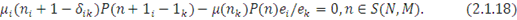
Таким чином, рівняння (2.1.18), яке називають рівнянням локального балансу, є достатньою (але не необхідною) умовою глобального балансу (2.1.19). З рекуррентного рівняння (2.1.18) безпосередньо випливає, що стаціонарна імовірність Р(n) має наступний вигляд:

де введене позначення  а нормалізуюча константа а нормалізуюча константа 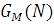 визначається з умови нормування визначається з умови нормування 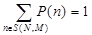 і дорівнює і дорівнює
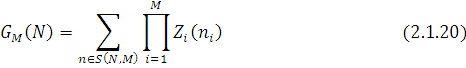
Таким чином, ми знову одержали розв’язок, що має мультиплікативну форму.
Для відкритої мережі МО з інтенсивністю вхідного потоку 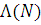 стаціонарні імовірності Р(n), що визначаються за допомогою міркувань, аналогічних виводу формул (2.1.2), (2.1.16), мають вигляд стаціонарні імовірності Р(n), що визначаються за допомогою міркувань, аналогічних виводу формул (2.1.2), (2.1.16), мають вигляд
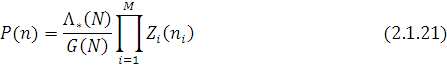
де позначено 
Стаціонарний розподіл Р(n) існує і єдиний, якщо збігається ряд
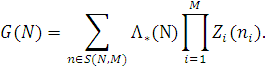
У частковому випадку, коли інтенсивність вхідного потоку не залежить від числа повідомлень в мережі і дорівнює Λ, маємо
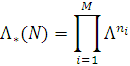
В цьому випадку (2.1.21) набуде вигляду

Тут Pi
(ni
) — стаціонарна імовірність того, що в і-му центрі, що розглядається ізольовано, знаходиться ni
, повідомлень: 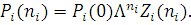
Вираз (2.1.22), відомий як теорема розкладання Джексона, показує, що дана мережа є сукупністю незалежних центрів обслуговування з пуассонівськими вхідними потоками з параметрами 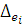 , і інтенсивностями обслуговування , і інтенсивностями обслуговування
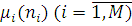 , залежить від довжини черги. , залежить від довжини черги.
Таким чином, для відкритих і замкнених експоненціальних мереж розв’язок має мультиплікативну форму, що допускає декомпозицію мережі на ізольовані центри. Одержаний результат є нетривіальним, оскільки потоки у відкритих і замкнених експоненціальних мережах МО з довільною маршрутною матрицею не є пуассонівськими; він має вирішальне значення для розробки ефективних обчислювальних алгоритмів.
2.1.4 ПОКАЗНИКИ ЯКОСТІ ФУНКЦІОНУВАННЯ ОДНОРІДНИХ МЕРЕЖ
Основною метою при використанні моделей мереж МО для аналізу обчислювальних систем і мереж є відшукання різних показників якості функціонування або характеристик мереж МО. Ми розглянули одну з найважливіших таких характеристик — розподіл імовірності станів Р(n). Перейдемо тепер до визначення інших характеристик імовірності однорідних експоненціальних МО, що залежать від навантаження.
По аналогії з формулою (2.1.15) граничний розподіл числа повідомлень в М-му (граничному) центрі визначається у вигляді
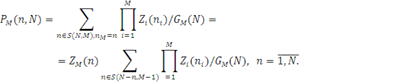
З урахуванням виразу (2.1.20) для нормалізуючої константи маємо
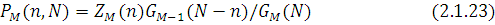
Граничний розподіл в будь-якому центрі 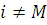 може бути одержаний шляхом перенумерації центрів так, щоб даний центр став граничним. Для одержаної таким чином мережі застосовується вираз (2.1.23). Легко бачити, що для центру М, який не залежить від навантаження може бути одержаний шляхом перенумерації центрів так, щоб даний центр став граничним. Для одержаної таким чином мережі застосовується вираз (2.1.23). Легко бачити, що для центру М, який не залежить від навантаження 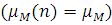 , вираз (2.1.23) перетвориться до вигляду (2.1.15). В цьому випадку при визначенні характеристик вузлів з номерами i=1,2,…,M-1 додаткова перенумерація не потрібна. , вираз (2.1.23) перетвориться до вигляду (2.1.15). В цьому випадку при визначенні характеристик вузлів з номерами i=1,2,…,M-1 додаткова перенумерація не потрібна.
Інтенсивність потоку повідомлень, що виходить, з і-го центру λi
(N) за означенням дорівнює середньому числу заявок, що обслуговуються в ньому за одиницю часу. Таким чином,
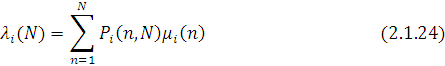
З визначення  слідує, що слідує, що

Підставляючи (2.1.25) і (2.1.23) в (2.1.24), одержуємо для 
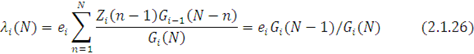
Для випадку, коли інтенсивність обслуговування в i-му центрі описується виразом (1.1.1), продуктивність λi
(N) може бути визначена через середню кількість зайнятих приладів в і-му центрі ui
(n):
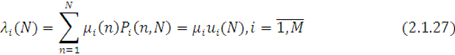
де ui
(n) задовольняє наступному співвідношенню:
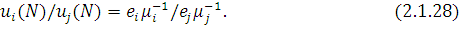 . .
Співвідношення (2.1.28) дозволяє визначити характеристики зайнятості і пропускної спроможності для всіх центрів, якщо розраховані або виміряні характеристики одного вузла.
З (2.1.27) і (2.1.28) встановлюється рівність нормованих пропускних спроможностей для кожного центру

Із співвідношення 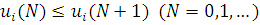 слідує, що при слідує, що при 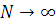 один з центрів, наприклад j-й, виявиться насиченим, так що один з центрів, наприклад j-й, виявиться насиченим, так що 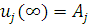 . Очевидно, що пропускна спроможність цього центру при . Очевидно, що пропускна спроможність цього центру при 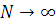 буде буде 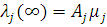 і значення і значення 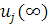 , ,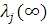 для решти центрів мережі можуть бути визначені з (2.29). Цей прийом часто використовується при дослідженні деяких асимптотичних властивостей замкнених мереж масового обслуговування. для решти центрів мережі можуть бути визначені з (2.29). Цей прийом часто використовується при дослідженні деяких асимптотичних властивостей замкнених мереж масового обслуговування.
Математичне сподівання числа повідомлень в М-му центрі з урахуванням виразу (2.1.23) має вигляд
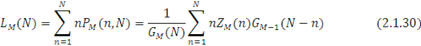
Для вузла, що не залежить від навантаження, вираз, що описує середню довжину черги в центрі, спрощується:
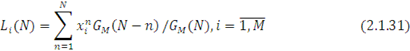
Відповідно до формули Літтла середній час перебування повідомлень в i-му центрі обслуговування Ti
(N) дорівнює відношенню середньої довжини черги до середньої інтенсивності вхідного потоку. У стаціонарному режимі інтенсивність вихідного потоку дорівнює інтенсивності вхідного потоку, тому
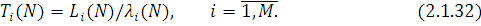
Особливий інтерес представляє час циклу Vi
(N) — середнє значення інтервалу часу між моментом виходу з i-го центру до моменту першого надходження вказаного повідомлення в цей центр. Якщо ei
=1, то величину ej
можна інтерпретувати як середнє число відвідувань повідомленням j-го центру між двома послідовними відвідуваннями i-го центру. Отже, сумарний середній час, проведений повідомленням за час циклу в j-му центрі, складає 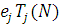 . Звідси . Звідси

Підставляючи в (2.1.33) вираз (2.1.32) і враховуючи співвідношення (2.1.29), яке в даному випадку має вигляд 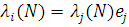 , маємо: , маємо:
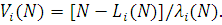
Таким чином, час циклу 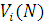 однозначно визначається середньою довжиною черги і продуктивністю і-го центру. однозначно визначається середньою довжиною черги і продуктивністю і-го центру.
2.2 МЕРЕЖІ МАСОВОГО ОБСЛУГОВУВАННЯ З КІЛЬКОМА КЛАСАМИ ПОВІДОМЛЕНЬ
Однорідні експоненціальні мережі МО володіють рядом обмежень, які в значній мірі звужують область їх практичного застосування. До їх числа відносяться: по-перше, припущення про експоненціальний розподіл тривалості обслуговування повідомлень у кожному центрі; по-друге, обмеження на дисципліну обслуговування в центрах, яке передбачає обслуговування за принципом ПППО; по-третє, припущення про статистичну однорідність повідомлень, що циркулюють в мережі. Розглянемо тепер мережі МО, в яких зняті всі згадані вище обмеження, — змішані мережі МО з кількома класами повідомлень і широким набором дисциплін обслуговування в центрах.
2.2.1 ОПИС ЗМІШАНОЇ МЕРЕЖІ
Змішана мережа МО складається з кінцевого числа М центрів обслуговування, між якими відповідно до маршрутної матриці Р циркулює R різних класів повідомлень. Під час переходу з одного центру в іншій повідомлення можуть змінювати клас так, що повідомлення r-того класу може стати повідомленням s-го класу 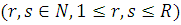 . .
Маршрут в змішаній мережі з кількома класами задається матрицею 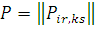 , де , де 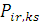 — імовірність того, що повідомлення r-то класу, що закінчило обслуговування в i-му центрі, перейде в k-й центр і стане повідомленням s-го класу. — імовірність того, що повідомлення r-то класу, що закінчило обслуговування в i-му центрі, перейде в k-й центр і стане повідомленням s-го класу.
На парах (ir) визначається марківський ланцюг з матрицею переходів Р, який можна розкласти на L ергодичних неперетинних підланцюгів, множина станів кожного з яких E1
, E2
, …, EL
.
Нехай nir
— число повідомлень класу r в i-му центрі в стані мережі n; Nj
=M(n, Ej
) і N=M(n) — відповідно число повідомлень в підланцюзі Ej
і в мережі МО в стані n. Тоді виконуються співвідношення
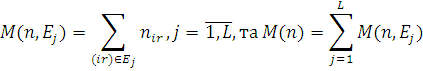
причому, якщо Nj
= M(n, Ej
) = const при 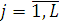 , дана мережа є замкненою. , дана мережа є замкненою.
Вхідний потік, який надходить в розімкнену мережу із зовнішнього джерела, може бути заданий різними способами. У першому випадку з джерела надходить один пуассонівський потік, інтенсивність якого Λ(M(n)) є функцією загального числа повідомлень в мережі при її стані n. Вхідне повідомлення надходить в i-й центр і стає повідомленням класу r з імовірністю P0, ir
, яка не залежить від стану мережі. У другому випадку є L пуассонівських вхідних потоків повідомлень, які надходять у відповідні підланцюги. Інтенсивність j-го потоку 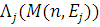 є функцією числа повідомлень в j-му підланцюзі є функцією числа повідомлень в j-му підланцюзі 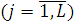 . Повідомлення j-го потоку, що виходить з джерела, з імовірністю Pj, ir
надходить в i-й центр і стає повідомленням r-того класу, якщо . Повідомлення j-го потоку, що виходить з джерела, з імовірністю Pj, ir
надходить в i-й центр і стає повідомленням r-того класу, якщо 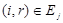 , та , та
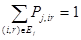 . У відкритій мережі МО вимога класу r, що закінчила обслуговування в і-му центрі, покидає мережу з імовірністю . У відкритій мережі МО вимога класу r, що закінчила обслуговування в і-му центрі, покидає мережу з імовірністю
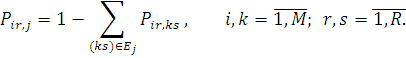
Для довільного підланцюга справедлива наступна система рівнянь згідно (1.3.2):
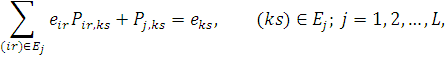
де 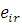 — відносна інтенсивність потоку повідомлень классу r, який проходить через центр і. Якщо — відносна інтенсивність потоку повідомлень классу r, який проходить через центр і. Якщо 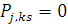 для всіх для всіх 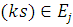 , то мережа замкнена по відношенню до підланцюга Еj
. В цьому випадку , то мережа замкнена по відношенню до підланцюга Еj
. В цьому випадку 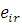 визначаються з точністю до мультиплікативної константи. Якщо визначаються з точністю до мультиплікативної константи. Якщо 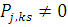 хоча б для однієї пари хоча б для однієї пари 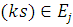 , то , то 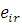 визначається однозначно. визначається однозначно.
Для завершення опису змішаної мережі МО залишається задати дисципліну і механізм обслуговування в центрах мережі. Вважатимемо, що мережа складається з центрів наступних чотирьох типів.
Центр типу 1. Обслуговування повідомлень в центрі здійснюється відповідно до дисципліни ПППО
. Тривалість обслуговування повідомлень всіх класів має один і той же експоненціальний розподіл з інтенсивністю 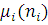 , яка залежить від числа повідомлень в центрі ni.
. Стан ni
центру визначається вектором , яка залежить від числа повідомлень в центрі ni.
. Стан ni
центру визначається вектором 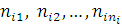 , де , де 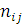 – номер класу повідомлення, що стоїть j
-м в черзі – номер класу повідомлення, що стоїть j
-м в черзі 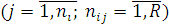
Центр типу 2. Обслуговування повідомлень в однолінійному центрі здійснюється відповідно до дисципліни РП
. Тривалість обслуговування повідомлення r-го класу, r=1, 2, ..., R, розподілена за законом Коксу з параметрами
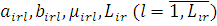 і середнім і середнім
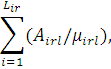
де 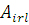 —імовірність того, що повідомлення класу r досягає l-ї стадії обслуговування в і-му вузлі. Стан центру —імовірність того, що повідомлення класу r досягає l-ї стадії обслуговування в і-му вузлі. Стан центру 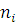 визначається вектором визначається вектором 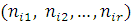 , де , де 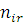 – вектор – вектор 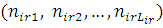 , l-та координата якого , l-та координата якого 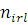 означає число повідомлень r-го класу в і-му центрі, які знаходяться на l
-му етапі обслуговування. Число повідомлень r-го класу в i
-му центрі складає означає число повідомлень r-го класу в і-му центрі, які знаходяться на l
-му етапі обслуговування. Число повідомлень r-го класу в i
-му центрі складає 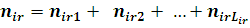 , а загальне число повідомлень в центрі , а загальне число повідомлень в центрі 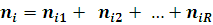 . Таким чином, швидкість завершення обслуговування повідомлення r-го класу, що знаходиться на l-му етапі у стані ni
центру, дорівнює . Таким чином, швидкість завершення обслуговування повідомлення r-го класу, що знаходиться на l-му етапі у стані ni
центру, дорівнює 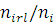 . Після завершення обслуговування повідомлення покидає центр з імовірністю birl
и переходить до наступної стадії з імовірністю airl
. . Після завершення обслуговування повідомлення покидає центр з імовірністю birl
и переходить до наступної стадії з імовірністю airl
.
Центр типу 3. Багатолінійний центр з числом обслуговуючих приладів, рівним або більшим максимальної кількості повідомлень в цьому центрі, і дисципліною обслуговування ОБО
(обслуговуванням без очікування). Стан центру і розподіл тривалості обслуговування, що має раціональне перетворення Лапласа, описуються так само, як і для центру другого типу.
Центр типу 4. Однолінійний центр з дисципліною обслуговування ОППО
(«останнім прийшов — першим обслужений»). Так само, як для вузлів другого і третього типів, розподіл тривалості обслуговування має раціональне перетворення Лапласа і може відрізнятися для повідомлень різних класів. Стан центру 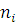 визначається вектором визначається вектором 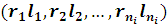 . де . де 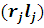 — пара, що характеризує повідомлення, що стоїть j-м в черзі, при дисципліні обслуговування ОППО
, rj
— номер класу повідомлення і lj
— номер перерваного етапу обслуговування. Обслуговування перерваного повідомлення починається з того етапу, на якому воно було перерване. — пара, що характеризує повідомлення, що стоїть j-м в черзі, при дисципліні обслуговування ОППО
, rj
— номер класу повідомлення і lj
— номер перерваного етапу обслуговування. Обслуговування перерваного повідомлення починається з того етапу, на якому воно було перерване.
2.2.2 ТЕОРЕМА ВСМР
Назва теореми – складено з перших літер прізвищ авторів: Baskett F., Chandy K., Muntz R., Palacios F.) Через зроблені припущення і означення процес, що описує функціонування змішаної мережі МО, є марківським. Стан мережі є вектором 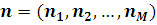 , де , де 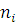 характеризує стан i-го центру і має структуру, що залежить від типів центрів мережі, описаних вище. характеризує стан i-го центру і має структуру, що залежить від типів центрів мережі, описаних вище.
Рівняння глобального балансу для знаходження стаціонарного розподілу P(n) ймовірностей станів мережі записуються по аналогії з (2.1.16) в загальному вигляді таким чином:
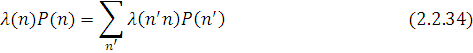
для будь- якого стану n, n’, де λ(n) — інтенсивність виходу мережі із стану n; λ(n’, n) — інтенсивність переходу мережі із стану n’ в стан n. Відшукання стаціонарного розподілу P(n) безпосередньо з системи рівнянь (2.2.34) представляє складну задачу, тому звичайно використовується підхід, пов'язаний з отриманням рівнянь локального балансу, техніка складання яких для однорідних замкнених мереж була розглянута в 1.1. В даному випадку суть складання рівнянь локального балансу полягає в прирівнюванні інтенсивності входу мережі в стан, при якому повідомлення починає обслуговуватися з певного етапу, до інтенсивності виходу мережі з цього стану, при якому повідомлення закінчує цей етап обслуговування. З кожним повідомленням зв'язується етап обслуговування. Якщо повідомлення обслуговується, то етап визначений, якщо воно стоїть в черзі, то для дисципліни обслуговування ПППО
це буде перший етап, для ОППО
— перерваний етап. При такому підході кожне рівняння системи (2.2.34) можна представити у вигляді ряду рівнянь локального балансу, виконання яких, як вже наголошувалося, є достатньою (але не необхідною) умовою виконання рівнянь глобального балансу.
ВСМР- теорема
. Для змішаної мережі МО, кожен центр якої належить до одного з вказаних чотирьох типів, стаціонарний розподіл ймовірностей станів існує і має мультиплікативний вигляд:
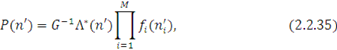
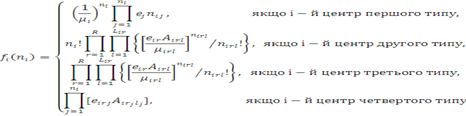
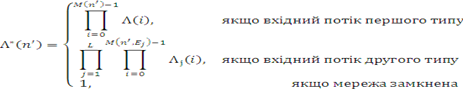
Стаціонарний розподіл існує, якщо збігається ряд
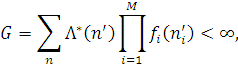
де G — нормалізуюча константа.
У практичних додатках докладний опис станів вузлів, що включає, наприклад, етап обслуговування і порядок розташування повідомлень у вузлі, не є істотним. Основний інтерес представляють агреговані стани вузлів 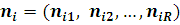 і відповідні стани мережі і відповідні стани мережі 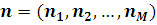 . Ймовірності стаціонарного агрегованого стану мережі P(n) можна одержати підсумовуванням P(n’) по всіх станах n’. В силу мультиплікативності P(n’) це еквівалентно підсумовуванню множників . Ймовірності стаціонарного агрегованого стану мережі P(n) можна одержати підсумовуванням P(n’) по всіх станах n’. В силу мультиплікативності P(n’) це еквівалентно підсумовуванню множників 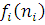 по всіх станах вузлів по всіх станах вузлів 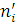 при фіксованих при фіксованих 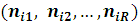 . Якщо позначити одержані множники через Zi
(ni
), то вираз для P(n) набуде вигляду . Якщо позначити одержані множники через Zi
(ni
), то вираз для P(n) набуде вигляду
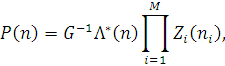
де нормалізуюча константа G і функція 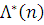 визначаються так само, як і в (2.2.35), а Zi
(ni
) залежить від типу i-го вузла визначаються так само, як і в (2.2.35), а Zi
(ni
) залежить від типу i-го вузла 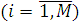 і має наступний вигляд: і має наступний вигляд:
якщо і
-й вузол першого типу,
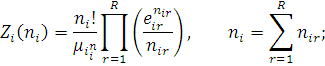
якщо і-
й вузол другого або четвертого типу,
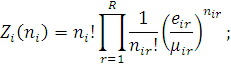
якщо i
-й вузол третього типу,
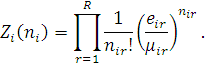
Таким чином, стаціонарний розподіл стану мережі P(n) має мультиплікативний вигляд і, що особливо важливе, не залежить від функції розподілу тривалості обслуговування в центрах (а тільки від відповідних середніх значень).
2.2.3 ВІДКРИТІ МЕРЕЖІ МО З КІЛЬКОМА КЛАСАМИ ПОВІДОМЛЕНЬ
Для відкритих мереж, коли інтенсивність вхідного потоку повідомлень з джерела не залежить від стану мережі, можливі подальші спрощення. Розглянемо спочатку закон розподілу числа повідомлень в мережі без розділення повідомлень на різні класи. В цьому випадку стан і
-го центру характеризується числом повідомлень в ньому ni
, а стан мережі —вектором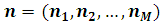 і вираз для P(n)
набуде наступного простого вигляду: і вираз для P(n)
набуде наступного простого вигляду:
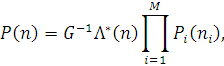
Де
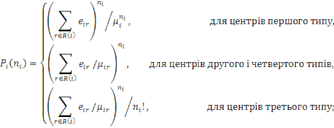
Для відкритої мережі система рівнянь для відшукання відносних інтенсивностей потоків має єдиний розв’язок 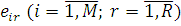 і, отже, інтенсивність потоку повідомлень r- того класу, що надходять в i-й вузол, і, отже, інтенсивність потоку повідомлень r- того класу, що надходять в i-й вузол, 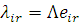 . Для випадку, коли інтенсивність обслуговування в центрах відкритої мережі не залежить від числа повідомлень в центрі з урахуванням позначення . Для випадку, коли інтенсивність обслуговування в центрах відкритої мережі не залежить від числа повідомлень в центрі з урахуванням позначення
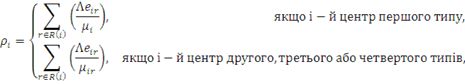
вираз для стаціонарного розподілу станів мережі набуває наступного вигляду:
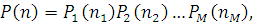
Де
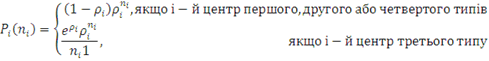
2.2.4 РОЗШИРЕННЯ ТЕОРЕМИ ВСМР
Розглянуті в 1.2 відкриті, замкнені і змішані мережі, що задовольняють умовам теореми ВСМР, мають широке практичне застосування при дослідженні обчислювальних систем і мереж. Проте природно виникає наступне питання: чи обмежений клас мереж, для яких виконується властивість мультиплікативності, лише мережами, що включають чотири типи центрів обслуговування? Частково відповідь на це питання дається в роботі Мунтца, де показано, що для розглянутих чотирьох типів центрів обслуговування, характерна властивість 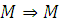 — пуассонівський характер надходження повідомлень спричиняє за собою пуассонівський потік повідомлень на виході системи. Показано, що мережа центрів обслуговування, що володіють властивістю — пуассонівський характер надходження повідомлень спричиняє за собою пуассонівський потік повідомлень на виході системи. Показано, що мережа центрів обслуговування, що володіють властивістю 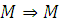 , має мультиплікативну форму стаціонарних ймовірностей станів. , має мультиплікативну форму стаціонарних ймовірностей станів.
У ряді інших робіт одержана значна кількість теоретичних результатів, які розширюють теорему ВСМР. Зокрема, в роботі Ноетзела введена узагальнена дисципліна обслуговування LBPS
(Last Batch Processor Sharing), яка визначає великий клас дисциплін обслуговування, при яких стаціонарні ймовірності станів мережі МО мають мультиплікативну форму для довільного розподілу тривалості обслуговування в центрах мережі.
Зупинимося детальніше на практично важливому узагальненню теореми ВСМР, розглянутому в роботі Лема,у якій сформульовані достатні умови мультиплікативності мереж МО з більш загальної, ніж в умовах теореми ВСМР, залежністю інтенсивностей потоків, що надходять, від стану мережі МО.
Розглянемо відкриту ВСМР- мережу, в яку надходить L пуассонівських потоків повідомлень. Додатково до позначень п.2.2.2 введемо вектор агрегованого стану мережі
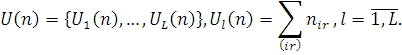
На множині L - вимірних, цілочисельних, невід’ємних векторів задані два набори функцій: 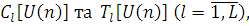 які можуть приймати значення на множині {0, 1}. Повідомлення l
-го підланцюга, що надходить у мережу, приймається на обслуговування, якщо функція втрат які можуть приймати значення на множині {0, 1}. Повідомлення l
-го підланцюга, що надходить у мережу, приймається на обслуговування, якщо функція втрат 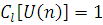 , і втрачається, якщо , і втрачається, якщо 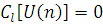 . Функція . Функція 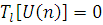 , якщо у момент відходу з мережі повідомлення l
- го підланцюга нове повідомлення вказаного під ланцюга миттєво вводиться в мережу, і , якщо у момент відходу з мережі повідомлення l
- го підланцюга нове повідомлення вказаного під ланцюга миттєво вводиться в мережу, і 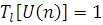 в іншому випадку. в іншому випадку.
Введемо наступні позначення:
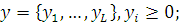
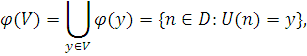
де D і V — відповідно допустимі множини векторів n та U(N) . Тоді справедлива наступна теорема.
Теорема
. Нехай функція втрат 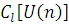 і функції і функції 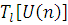 задовольняють умові задовольняють умові
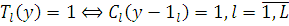 для всіх пар y і у—1l
з V. Тоді стаціонарний розподіл ймовірностей станів мережі МО має мультиплікативну форму: для всіх пар y і у—1l
з V. Тоді стаціонарний розподіл ймовірностей станів мережі МО має мультиплікативну форму:
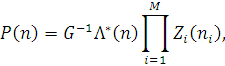
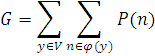
нормалізуюча константа.
РОЗДІЛ 3. МЕТОД АНАЛІЗУ СЕРЕДНІХ ЗНАЧЕНЬ
3.1 ЗАГАЛЬНЕ ОПИСАННЯ МЕТОДУ
Розглянемо спочатку застосування методу аналізу середніх значень для розрахунку замкненої однорідної експоненціальної мережі МО, що не залежить від навантаження, яку позначимо через D(N). Якщо обслуговування у вузлах мережі D(N) здійснюється відповідно до дисципліни ПППО, то середній час очікування Ti
(N)в i-му центрі складається з середньої тривалості обслуговування повідомлення τi
, яке щойно надійшло, і середньої тривалості обслуговування всіх повідомлень, що знаходилися в i-му центрі τi
νi
(N), де νi
(N) — середня кількість повідомлень в i-му центрі у момент надходження нового повідомлення. Таким чином,
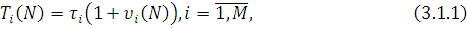
і для визначення νi
(N) необхідно досліджувати стаціонарний режим марківського ланцюга, що описує функціонування мережі в моменти надходження повідомлень в i-й центр. Стаціонарні імовірності станів мережі D(N)у момент надходження повідомлень в i-й центр співпадають із стаціонарними імовірностями станів мережі D(N-1) для довільного моменту часу. Звідси безпосередньо витікає, що 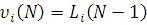 , де , де 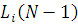 — середня кількість повідомлень в i-му центрі мережі D(N-1), та (3.1.1) набуває вигляду: — середня кількість повідомлень в i-му центрі мережі D(N-1), та (3.1.1) набуває вигляду:
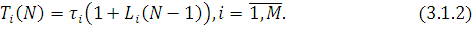
Щоб одержати рекурентний алгоритм для розрахунку середніх характеристик мережі, необхідно знайти співвідношення, яке зв'язує величини Li
(N) и Ti
(N). Таке співвідношення витікає з формули Літтла, застосованої до i-го центру:
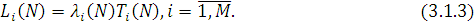
де λi
(N)- інтенсивність потоку повідомлень, що надходять в i-й центр.
Якщо позначити через i*
номер довільного виділеного центру мережі, то:
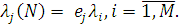
де- ej
однозначно визначається рівняннями
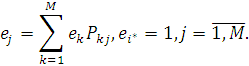
а продуктивність виділеного центру 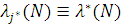 з урахуванням формули Літтла має вигляд: з урахуванням формули Літтла має вигляд:

Враховуючи початкові умови 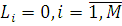 ,за допомогою системи рівнянь ,за допомогою системи рівнянь
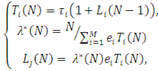
можна рекуррентно по N розраховувати середні характеристики однорідної мережі МО, інтенсивності обслуговування центрів якої не залежать від навантаження
3.2 ОДНОРІДНА ЗАМКНЕНА МЕРЕЖА МО, ЩО ЗАЛЕЖИТЬ ВІД НАВАНТАЖЕННЯ
Перш ніж переходити до виводу рекурсивних співвідношень для середніх характеристик мережі МО, вузли якої залежать від навантаження, визначимо співвідношення для граничних розподілів 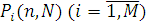 . Вираз для граничного розподілу довжини черги в i-му центрі (i=1,2,…,M) може бути представлено у вигляді: . Вираз для граничного розподілу довжини черги в i-му центрі (i=1,2,…,M) може бути представлено у вигляді:
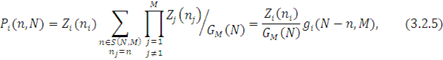
де gi
(n,M)- нормалізуюча константа мережі, в якій відсутній і-й центр і циркулює n повідомлень.
Підставляючи в останній вираз  і враховуючи що і враховуючи що
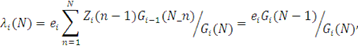
одержимо:
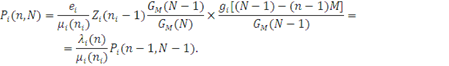
Звідси витікає
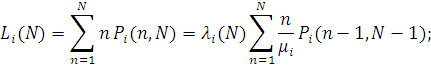
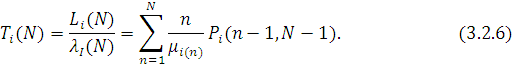
Якщо i-й центр включає 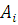 однотипних обслуговуючих приладів, однотипних обслуговуючих приладів,
то  , і вираз (3.2.6) набуде вигляду: , і вираз (3.2.6) набуде вигляду:
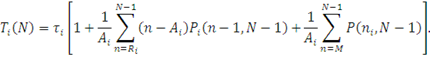
Але перша сума в останньому виразі означає середнє число повідомлень в черзі i-го центру для мережі D(N-1) (виключаючи повідомлення, що знаходяться на обслуговуванні):
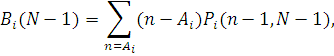
а друга — імовірність того, що всі обслуговуючі прилади зайняті:
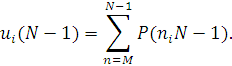
Таким чином, в даному випадку
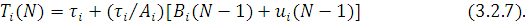
Співвідношення (3.2.5), (3.2.6)разом з виразами (3.2.3), (3.2.4) та початковими умовами 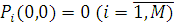 дозволяють рекурентно по ni
визначати основні характеристики мережі МО, яка залежить від навантаження. дозволяють рекурентно по ni
визначати основні характеристики мережі МО, яка залежить від навантаження.
3.3 ОБЧИСЛЕННЯ
ОСНОВНИХ СПІВВІДНОШЕНЬ
Розглянутий алгоритм аналізу середніх значень легко поширюється для випадку мережі МО з кількома класами повідомлень.
Позначимо через 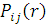 імовірність того, що повідомлення класу імовірність того, що повідомлення класу 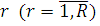 після закінчення обслуговування в i–му центрі надходить у центр j (j,i = 1, 2, …, M). Агрегований стан мережі позначимо через після закінчення обслуговування в i–му центрі надходить у центр j (j,i = 1, 2, …, M). Агрегований стан мережі позначимо через 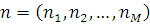 , де , де 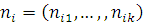 та та 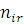 – кількість повідомлень r–го класу в i–му центрі. Величина – кількість повідомлень r–го класу в i–му центрі. Величина 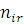 повинна задовольняти наступні умови: повинна задовольняти наступні умови:
1) 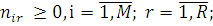
2) 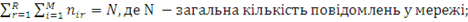
3) 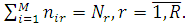
Множину можливих станів можна визначити наступним чином
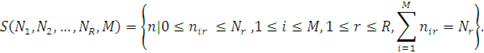
Без обмеження спільності вважатимемо, що повідомлення не можуть змінювати клас при переході з одного центру в інший (мережа, у якій повідомлення змінюють належність до класу, може бути перетворена в еквівалентну мережу, у якої така зміна відсутня). Позначимо через 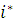 номер довільного виділеного центру мережі. Тоді інтенсивність потоку повідомлень r-го класу, що проходять через i-й центр номер довільного виділеного центру мережі. Тоді інтенсивність потоку повідомлень r-го класу, що проходять через i-й центр 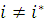
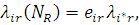
де 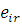 — середнє число відвідувань повідомленням класу r центру j між двома відвідуваннями ним виділеного центру. Значення — середнє число відвідувань повідомленням класу r центру j між двома відвідуваннями ним виділеного центру. Значення 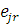 однозначно визначаються з системи рівнянь однозначно визначаються з системи рівнянь
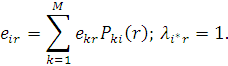
Для мережі МО з кількома класами повідомлень і центрами обслуговування, що залежать від навантаження для обчислення 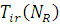 , потрібен попередній розрахунок розподілу довжини черги , потрібен попередній розрахунок розподілу довжини черги 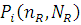 , яка може бути представлена у вигляді , яка може бути представлена у вигляді
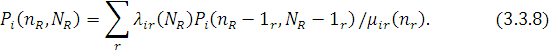
Покажемо, що середній час очікування повідомлень r-го класу в i-му центрі, що залежить від навантаження, може бути виражений через характеристики мережі 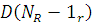 таким чином: таким чином:
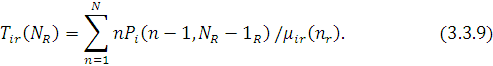
Дійсно, з визначення 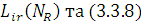 маємо маємо
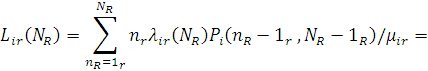
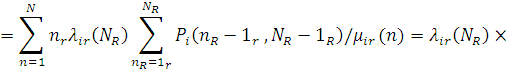
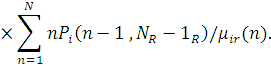
РОЗДІЛ 4. ОБЧИСЛЕННЯ ХАРАКТЕРИСТИК МЕРЕЖ МАСОВОГО ОБСЛУГОВУВАННЯ
Розглянуті в попередніх параграфах методи дослідження локально-збалансованих мереж МО дозволяють отримати розв’язок в зручній мультиплікативній формі. Проте вказаний розв’язок залежить від нормалізуючої константи, що має відносно простий вигляд для відкритих мереж МО, але є сумою добутків 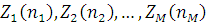 для замкнених мереж. Кількість доданків в цій сумі відповідає потужності простору станів мережі і навіть для однорідних замкнених мереж складає для замкнених мереж. Кількість доданків в цій сумі відповідає потужності простору станів мережі і навіть для однорідних замкнених мереж складає 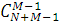 . Внаслідок комбінаторного зростання простору станів мережі МО при збільшенні числа центрів, класів та повідомлень потужність простору станів мережі швидко зростає, так що прямий розрахунок нормалізуючої константи (наприклад, по формулі (2.1.20)) є досить складним для мереж великої розмірності. . Внаслідок комбінаторного зростання простору станів мережі МО при збільшенні числа центрів, класів та повідомлень потужність простору станів мережі швидко зростає, так що прямий розрахунок нормалізуючої константи (наприклад, по формулі (2.1.20)) є досить складним для мереж великої розмірності.
Тому розроблено спеціальні методи обчислення стаціонарних ймовірностей станів і інших характеристик замкнених мереж МО, сукупність яких є окремим розділом теорії мереж МО.
Основою більшості таких алгоритмів є рекурентний метод Бузена (алгоритм згортки).
4.1 МЕТОД БУЗЕНА
Відповідно до цього методу алгоритм розрахунку нормалізуючої константи
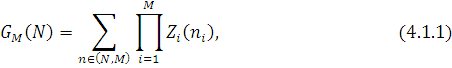
де множник 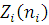 згідно (2.1.26), (2.1.34) має вигляд згідно (2.1.26), (2.1.34) має вигляд
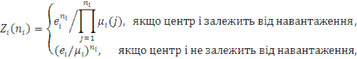
а простір станів мережі
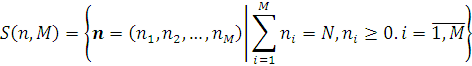
зводиться до простої ітеративної процедури, суть якої полягає в наступному.
Розглянемо функцію
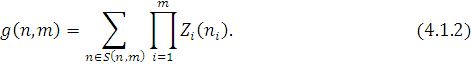
Очевидно, що при 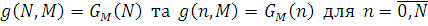 при m>1маємо при m>1маємо
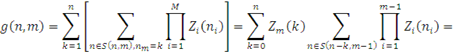
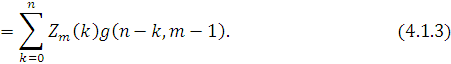
Таким чином, для мережі, що складається з центрів, інтенсивність обслуговування яких залежить від навантаження

Якщо центр т не залежить від навантаження, той вираз (4.1.3) можна спростити. В цьому випадку
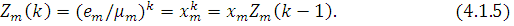
Підставивши (4.1.5) у вираз (4.1.3), після спрощень одержуємо
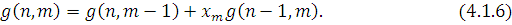
Формули (4.1.6) і (4.1.3) дозволяють здійснювати рекурентне обчислення g(n, m) при початкових умовах 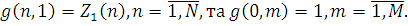 У табл. 4.1 і 4.2 показаний схематичний опис алгоритму Бузена. Стовпці таблиці заповнюються послідовно зверху вниз. Якщо центр т не залежить від навантаження, то елементи стовпця т обчислюються по формулі (4.1.6), інакше – використовується вираз (4.1.4) і для відшукання Zj
(k) застосовується рекурентний вираз У табл. 4.1 і 4.2 показаний схематичний опис алгоритму Бузена. Стовпці таблиці заповнюються послідовно зверху вниз. Якщо центр т не залежить від навантаження, то елементи стовпця т обчислюються по формулі (4.1.6), інакше – використовується вираз (4.1.4) і для відшукання Zj
(k) застосовується рекурентний вираз
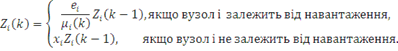
Шукане значення нормалізуючої константи 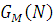 знаходиться у нижньому правому куті таблиці. знаходиться у нижньому правому куті таблиці.
ТАБЛИЦЯ 4.1 Метод Бузена. Центри не залежать від навантаження.
m
n
|
1 |
2 |
… |
m-1 |
m |
… |
M |
| 0 |
1 |
1 |
… |
1 |
1 |
… |
1 |
| 1 |
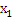 |
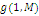
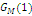
|
| … |
… |
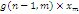

|
… |
| n-1 |
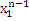 |
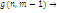 |
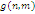 |
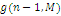
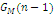
|
| n |
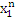 |
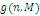
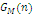
|
| … |
… |
… |
| N |
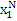 |
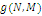
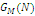
|
ТАБЛИЦЯ 4.2 Метод Бузена. Центри залежать від навантаження.
Подальше спрощення обчислювальної процедури можливе в окремому випадку мереж, що залежать від навантаження, коли m-й центр мережі містить Am
однакових обслуговуючих приладів. При цьому інтенсивність обслуговування m-го центру:
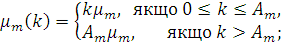
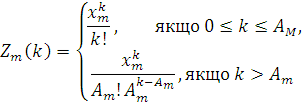
Останній вираз можна записати у рекуррентному вигляді
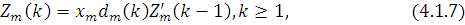
де 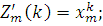
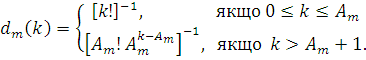
Підставляючи (4.1.7) в (4.1.3), одержуємо
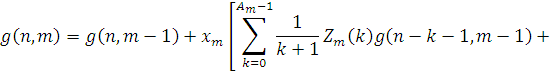
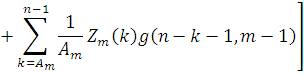
Після перетворень маємо остаточно

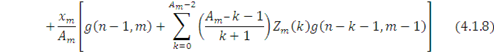
Для мережі, що не залежить від навантаження 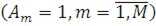 , вираз (4.1.8) співпадає з (4.1.6). Якщо , вираз (4.1.8) співпадає з (4.1.6). Якщо  , то , то
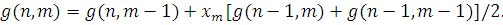
вираз (4.1.8) дозволяє значно скоротити обчислення по порівнянню з прямим використовуванням формули (4.1.3) для випадку, коли центр т складається з кількох однакових обслуговуючих центрів.
Відмітимо, що нормалізуючі константи, які обчислені в результаті роботи описаного вище алгоритму не є однозначними, оскільки залежать від конкретного вибору величин 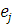 , які визначаються з системи рівнянь , які визначаються з системи рівнянь
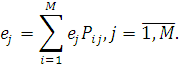
Розв’язок цієї системи рівнянь, єдиний з точністю до мультиплікативної константи, тому конкретне значення нормалізуючи констант 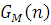 можна одержати шляхом довільного завдання можна одержати шляхом довільного завдання 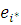 , наприклад , наприклад 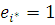 . .
4.2 ОБСЧИСЛЕННЯ ХАРАКТЕРИСТИК МЕРЕЖІ МО
Стаціонарні ймовірності граничного розподілу кількості повідомлень в і-му центрі мережі, що не залежить від навантаження, розраховуються по формулі:
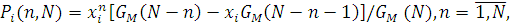
де нормалізуючі константи  визначаються з останнього стовпця табл. 4.1. Для мережі, що залежить від навантаження, формула (4.1.1) описує граничний розподіл визначаються з останнього стовпця табл. 4.1. Для мережі, що залежить від навантаження, формула (4.1.1) описує граничний розподіл 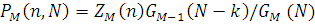 лише для граничного центру М. Для відшукання граничного розподілу кількості повідомлень в будь-якому центрі іпри обчисленні величин g(n,m) у табл. 4.1 необхідно перенумерувати центри так, щоб i-й центр став граничним, і повторно застосувати алгоритм Бузена. лише для граничного центру М. Для відшукання граничного розподілу кількості повідомлень в будь-якому центрі іпри обчисленні величин g(n,m) у табл. 4.1 необхідно перенумерувати центри так, щоб i-й центр став граничним, і повторно застосувати алгоритм Бузена.
Розглянемо алгоритм обчислення граничного розподілу 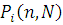 , який дозволяє не перенумеровувати повторно центри. Введемо допоміжну функцію , який дозволяє не перенумеровувати повторно центри. Введемо допоміжну функцію
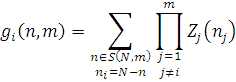
Цю функцію можна розглядати як нормалізуючу константу мережі, у якій відсутній і
-й центр,и циркулює рівно n
повідомлень. Легко також бачити, що
 . З урахуванням нової допоміжної функції граничний розподіл приймає вигляд . З урахуванням нової допоміжної функції граничний розподіл приймає вигляд
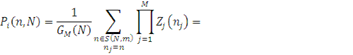
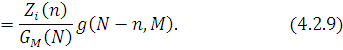
Залишається відшукати алгоритм для обчислення допоміжної функції 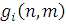 . З умови нормування маємо . З умови нормування маємо
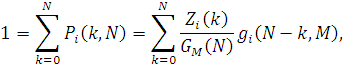
звідки витікає, що
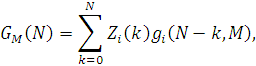
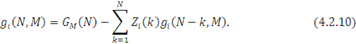
У разі, коли i-й центр містить Ai
однакових обслуговуючих приладів, маємо
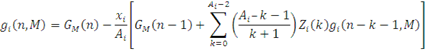
В частинному випадку при Ai
=2
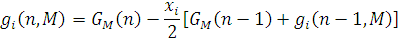
Значення допоміжної функції 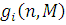 у виразі (4.2.10) розраховуються ітераційно з початковою умовою у виразі (4.2.10) розраховуються ітераційно з початковою умовою 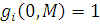
Інші характеристики мережі, що є функціями нормалізуючої константи 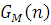 , обчислюються по формулах, розглянутих в розділі 1. , обчислюються по формулах, розглянутих в розділі 1.
РОЗДІЛ 5. МЕТОД ДЕКОМПОЗИЦІЙНОЇ АПРОКСИМАЦІЇ
Далі ми приділимо увагу методам наближеного аналізу мереж МО. Причина використання наближених методів полягає в необхідності дослідження мереж МО з блокуваннями, пріоритетами і, що особливо важливе, з довільними функціями розподілу тривалості обслуговування в центрах мережі і рекурентним вхідним потоком. Наближені методи аналізу мереж МО, за допомогою яких вдається досягти компромісу між суперечливими вимогами адекватного моделювання реальних систем і простоти відшукання рішення в мультиплікативній формі, звичайно засновані або на апроксимації довільних законів узагальненим розподілом Коксу, або на розширенні властивості мультиплікативності за межі області його застосування, на постулюванні незалежності там, де випадкові величини слабо залежні, на дифузійній або декомпозиційній апроксимації або на імітаційному моделюванні. Слід зазначити, що така класифікація умовна, оскільки багато наближених методів базуються на сумісному використанні перерахованих підходів.
Імітаційне моделювання є універсальним засобом наближеного дослідження мереж МО, але вимагає значних витрат часу при розробці і використанні програм моделювання. Основні проблеми полягають в оцінці точності результатів і тривалості моделювання (правило зупинки).
Інші методи розглянемо детальніше.
В рамках декомпозиційної апроксимації широке практичне застосування знайшли наступні підходи.
Перший з них, пов'язаний із застосуванням математично еквівалентних перетворень мережі МО, базується на теоремі Нортона. Наближене дослідження мережі МО з довільними розподілами тривалості обслуговування в цьому випадку здійснюється шляхом переходу до еквівалентної мережі з експоненціальними обслуговуючими центрами. При цьому критеріями еквівалентності є наступні умови: сума середніх значень довжин черг в замкненій мережі дорівнює N; пропускна здатність обслуговуючих центрів пропорційна відносній інтенсивності потоків.
Другий підхід базується або на виділенні в початковій мережі слабо зв'язаних підмереж з подальшою оцінкою інтегральних характеристик мережі з похибкою, яка є функцією ступеня зв'язності підмереж, або на декомпозиції мережі на центри обслуговування, які аналізуються окремо, і на складанні рівнянь балансу середніх і дисперсії потоків для розрахунку характеристик мережі в цілому.
Декомпозиційна апроксимація є одним з найбільш перспективних методів, які дозволяють з одного боку збільшити ефективність аналізу мереж МО в розрахунковому відношенні, а з іншого – отримати досить точні оцінки характеристик моделей, які не можуть бути розраховані точними моделями.
5.1 АПРОКСИМАЦІЯ ФУНКЦІЙ РОЗПОДІЛУ
Якщо функції розподілу тривалості обслуговування в центрах мережі допускають раціональне перетворення Лапласа і обслуговування повідомлень в центрах мережі здійснюється відповідно до дисципліни РП
, ОБО
або ОППО
, то відповідно до теореми ВСМР стаціонарні імовірності станів мережі задовольняють мультиплікативній формі і мають вигляд 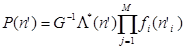 . Таким чином, один із способів наближеного дослідження немарківських мереж МО полягає в апроксимації довільних функцій розподілу тривалості обслуговування повідомлень в центрах мережі узагальненим розподілом Кокса. Строге обґрунтування можливості такої апроксимації дається наступною теоремою. . Таким чином, один із способів наближеного дослідження немарківських мереж МО полягає в апроксимації довільних функцій розподілу тривалості обслуговування повідомлень в центрах мережі узагальненим розподілом Кокса. Строге обґрунтування можливості такої апроксимації дається наступною теоремою.
Теорема
. Нехай Q(x) — довільна функція розподілу, яка задовольняє умові Q(0)=0, і 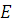 — клас нескінченних сумішей ерланговськіх розподілів. Тоді для будь-яких — клас нескінченних сумішей ерланговськіх розподілів. Тоді для будь-яких 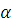 і і 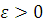 знайдеться такий розподіл знайдеться такий розподіл 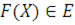 , що , що
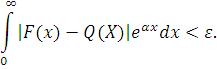
Вказана теорема залишається справедливою і при апроксимації кінцевими сумішами розподілів Ерланга.
На практиці звичайно розглядають дві основні характеристики функції розподілу: математичне сподівання τ=M[t] і дисперсію D=M[t2
]-M2
[t], де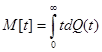 та та 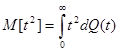 .Таке завдання функції розподілу обґрунтовується тим, що характеристики багатьох систем МО визначаються тільки першими двома моментами функції розподілу тривалості обслуговування. .Таке завдання функції розподілу обґрунтовується тим, що характеристики багатьох систем МО визначаються тільки першими двома моментами функції розподілу тривалості обслуговування.
Покажемо тепер, що апроксимація функцій розподілу із заданими значеннями τ і ω може бути ефективно проведена при ω<1 узагальненим розподілом Ерланга, а при ω>1 гіперекспоненціальним розподілом другого порядку.
Розглянемо узагальнений розподіл Коксу для випадку, коли µ1
= µ2
=… µk
=µ, a0
=1, ar
=1 при 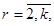 bk
=1. Таким чином, після першого етапу повідомлення може закінчити обслуговування з імовірністю b1
або продовжувати обслуговування на етапах, що залишилися, з імовірністю a1
=1-b1
. Вираз для перетворення Лапласа узагальненого розподілу Кокса в цьому випадку набуває вигляду bk
=1. Таким чином, після першого етапу повідомлення може закінчити обслуговування з імовірністю b1
або продовжувати обслуговування на етапах, що залишилися, з імовірністю a1
=1-b1
. Вираз для перетворення Лапласа узагальненого розподілу Кокса в цьому випадку набуває вигляду
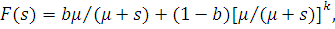
де введене позначення b=b1
. Диференціюючи F(s), одержуємо:
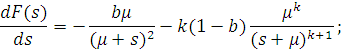
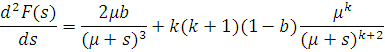
Використовуючи відоме співвідношення для визначення початкових моментів розподілу

Знаходимо
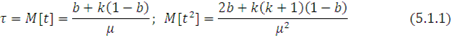
Підставляючи (5.1.1) у вираз для коефіцієнтів варіації

маємо:
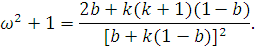
З останнього рівняння знаходимо шукане значення імовірності:
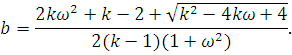
Таким чином, при 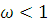 апроксимація функцій розподілу може здійснюватися узагальненим розподілом Ерланга з параметрами b і k, визначеними вище. Інтенсивність обслуговування на етапі r знаходиться з виразу для M[t]: апроксимація функцій розподілу може здійснюватися узагальненим розподілом Ерланга з параметрами b і k, визначеними вище. Інтенсивність обслуговування на етапі r знаходиться з виразу для M[t]:
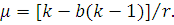
При 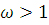 апроксимацію зручно проводити за допомогою гіперекспоненціального розподілу. Розглянемо гіперекспоненціальний розподіл другого порядку з числом етапів k=2 і щільністю розподілу апроксимацію зручно проводити за допомогою гіперекспоненціального розподілу. Розглянемо гіперекспоненціальний розподіл другого порядку з числом етапів k=2 і щільністю розподілу
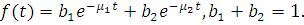 Приймаючи Приймаючи 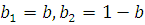 і здійснюючи перетворення, аналогічні розглянутому вище випадку, одержуємо: і здійснюючи перетворення, аналогічні розглянутому вище випадку, одержуємо:
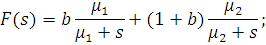
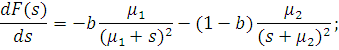
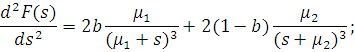
Звідси знаходимо:
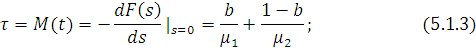
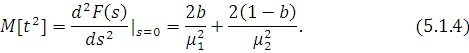
Щоб виконувалася умова (5.1.2), покладемо
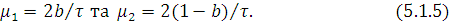
Підставляючи (5.1.3) — (5.1.5) у вираз для коефіцієнта варіації (5.1.2) і розв’язуючи відповідне квадратне рівняння, одержуємо
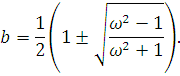
Оскільки сума коренів b1
+b2
=1, то можна використовувати будь-який з них. Таким чином, узагальнені ерланговський і гіперекспоненціальний розподіли цілком визначаються першими двома моментами і перекривають весь діапазон значень коефіцієнтів варіації від 0 до 1 і від 1 до ∞.
Розглянутий спосіб апроксимації функцій розподілу тривалості обслуговування в центрах мережі приводить до значного збільшення простору станів мережі МО і, отже, може бути використаний лише для мереж невеликої розмірності.
5.2 ТЕОРЕМА НОРТОНА ДЛЯ АНАЛІЗУ ЗАМКНЕНИХ І РОЗІМКНЕНИХ ЛОКАЛЬНО-ЗБАЛАНСОВАНИХ МЕРЕЖ МО
Розглянемо однорідну мережу МО з М центрами обслуговування, яка задовольняє умовам локального балансу і ймовірностями переходу, що задаються матрицею маршрутів 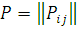
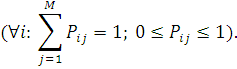
Нехай ei
— відносна інтенсивність потоку повідомлень в i-му центрі, яка задовольняє векторне рівняння еР=е. У замкненій мережі розв’язок векторного рівняння єдиний з точністю до мультиплікативної константи.
Декомпозиція такої мережі на основі теореми Нортона дозволяє звести початкову мережу МО до еквівалентної з двома центрами обслуговування. При цьому перший центр двохвузлової мережі збігається з i-м центром початкової мережі 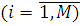 , а другий (композиційний), є еквівалентом частини мережі, що залишилася, володіє експоненціально розподіленим часом обслуговування з параметром , а другий (композиційний), є еквівалентом частини мережі, що залишилася, володіє експоненціально розподіленим часом обслуговування з параметром 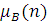 , який залежить від числа повідомлень в ньому. , який залежить від числа повідомлень в ньому.
Теорема.
Граничний розподіл числа повідомлень в i-му центрі початкової мережі збігається з відповідним розподілом еквівалентної мережі, якщо параметр 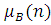 композиційного центру дорівнює інтенсивності композиційного центру дорівнює інтенсивності 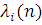 надходження повідомлень в i-й центр початкової мережі, в якій надходження повідомлень в i-й центр початкової мережі, в якій 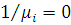 . .
Розглянемо детальніше застосування цієї теореми на прикладі замкненої мережі МО (рис. 5.1 ). Для обчислення статистичних характеристик i-го центру мережі на рис.5.1 підмережа В замінюється композиційним центром (рис. 5.2). Інтенсивність обслуговування повідомлень композиційним центром визначається підмережею В, яка співпадає з мережею на мал. 5.1 у всьому, за винятком того, що замість i-го центру вводиться пряме з'єднання - i-й центр замикається (рис.5.2). Інтенсивність 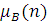 встановлюється рівній продуктивності встановлюється рівній продуктивності 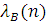 замкненої підмережі В. Таким чином, для повного визначення еквівалентної мережі необхідно обчислити (аналітично або за допомогою імітаційної моделі) або виміряти продуктивності замкненої підмережі В. Таким чином, для повного визначення еквівалентної мережі необхідно обчислити (аналітично або за допомогою імітаційної моделі) або виміряти продуктивності 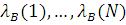 підмережі В, в якій циркулює 1,2,…,N повідомлень. підмережі В, в якій циркулює 1,2,…,N повідомлень.
Рисунок 5.1 Декомпозиція мережі МО

Рисунок 5.2 Мережа з композиційним центром

Для однорідної замкненої локально-збалансованої мережі МО з довільною структурою алгоритм обчислення інтенсивності 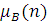 включає наступні кроки. включає наступні кроки.
Крок 1. Ініціалізація: 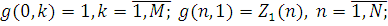 де функція де функція
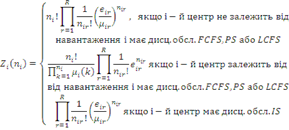
а функція 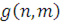
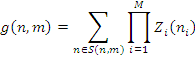
Крок 2. Цикл по L=1,…,i-1,i+1,…,M та по 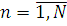 для обчислення правого граничного стовпця нормалізуючої константи підмережі В з елементами g(n,m), для обчислення правого граничного стовпця нормалізуючої константи підмережі В з елементами g(n,m), 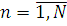 , де , де
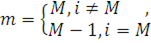
Крок 3. Обчислення інтенсивності обслуговування композиційного центру за формулою 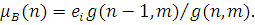
Теорема Нортона залишається справедливою і для неоднорідних локально-збалансованих мереж МО. Для замкненої мережі МО з R класами повідомлень в цьому випадку з метою побудови еквівалентної мережі повинні бути обчислені для усіх 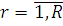 продуктивності продуктивності 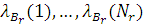 підмережі В. У розімкненій мережі всі центри, за винятком даного i-го центру, замінюються одним композиційним пуассонівським джерелом, яке генерує повідомлення всіх класів. Кожен клас генерується незалежно, і інтенсивність потоку r-го класу повідомлень підмережі В. У розімкненій мережі всі центри, за винятком даного i-го центру, замінюються одним композиційним пуассонівським джерелом, яке генерує повідомлення всіх класів. Кожен клас генерується незалежно, і інтенсивність потоку r-го класу повідомлень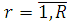 , який надходить з композиційного джерела, встановлюється рівній продуктивності , який надходить з композиційного джерела, встановлюється рівній продуктивності 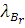 підмережі В. підмережі В.
5.3 НАБЛИЖЕНИЙ ДЕКОМПОЗИЦІЙНИЙ АЛГОРИТМ
Описаний вище декомпозиційний підхід є основою наближеного алгоритму розрахунку середніх характеристик замкнених мереж МО з довільною функцією розподілу тривалості обслуговування в центрах. Вказаний ітераційний алгоритм базується на теоремі Нортона і передбачає апроксимацію мережі з довільною функцією розподілу тривалості обслуговування в центрах еквівалентною експоненціальною мережею. Інтенсивності обслуговування в центрах еквівалентної мережі C1
, С2
,…,СM
вибираються так, щоб виконувалися наступні умови:
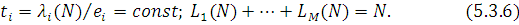
Перша умова відображає закон рівності нормалізованих пропускних спроможностей (пропускна здатність центру i пропорціональна відносній інтенсивності потоку ei
). Друга полягає у тому, що в замкненій мережі сума середніх значень довжин черг повинна дорівнювати N. Відмітимо, що обидві умови не залежать від виду функцій розподілу і дисциплін обслуговування в центрах мережі.
Формально вказані умови можна представити у вигляді системи М нелінійних рівнянь з М невідомими:
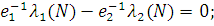

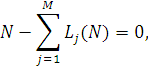
де 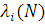 і Li
(N)— функції змінних C1
, С2
,…,СM і Li
(N)— функції змінних C1
, С2
,…,СM
Перейдемо від задачі розв’язання системи нелінійних рівнянь (5.3.7) до еквівалентної задачі мінімізації функції
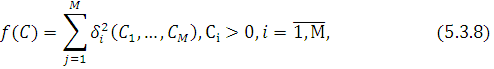
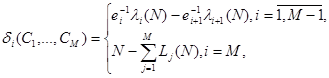
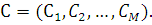
Ввівши бар’єрну функцію 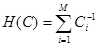 задачу (5.3.8) можна замінити задачею безумовної мінімізації функції задачу (5.3.8) можна замінити задачею безумовної мінімізації функції

де γ — ваговий коефіцієнт.
Алгоритм розв’язування початкової задачі розрахунку характеристик замкненої мережі з довільно розподіленою тривалістю обслуговування у вузлах може базуватися або на рішенні оптимізаційної задачі (5.3.9), або на безпосередній перевірці умов (5.3.6). Проте в обох випадках алгоритм реалізує ітеративну процедуру перетворення початкової мережі в мережу з двома центрами. Вказана мережа включає i-й центр початкової мережі 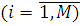 з довільною функцією розподілу тривалості обслуговування і додатковий (композиційний) центр з експоненціальним розподілом тривалості обслуговування. з довільною функцією розподілу тривалості обслуговування і додатковий (композиційний) центр з експоненціальним розподілом тривалості обслуговування.
Один з найбільш ефективних наближених підходів дослідження характеристик таких двохвузлових мереж заснований на апроксимації довільної функції розподілу узагальненим розподілом Коксу. При цьому, залежно від значення коефіцієнта варіації wi
=1, wi
<1 або wi
>1 функція розподілу часу обслуговування в центрі апроксимується відповідно експоненціальним, узагальненим ерланговськім або гіперекспоненціальним розподілом.
Ітераційний обчислювальний алгоритм включає наступні основні кроки.
Крок 1. Ініціалізація: інтенсивності обслуговування Ci
встановлюються рівними інтенсивностям µi
, заданим для початкової мережі, тобто 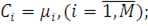 встановлюється в нуль лічильник числа ітерацій d. встановлюється в нуль лічильник числа ітерацій d.
Крок 2. Для кожного i-го центру 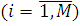 визначаються параметри композиційного центру µB
(n), визначаються параметри композиційного центру µB
(n),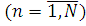 В залежності від значення коефіцієнта варіації В залежності від значення коефіцієнта варіації 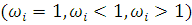 функція розподілу часу обслуговування в i-му центрі апроксимується відповідно експоненціальним, узагальненим ерланговоким або гіперекспоненціальним розподілом. функція розподілу часу обслуговування в i-му центрі апроксимується відповідно експоненціальним, узагальненим ерланговоким або гіперекспоненціальним розподілом.
Крок 3. Розраховується замкнена мережа з двома центрами. Обчислюються продуктивність λi
(N) і середня довжина черги Li
(N).
Крок 4. Якщо 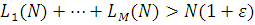 , де , де 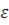 — задана точність розв’язку, то для тих i, для яких — задана точність розв’язку, то для тих i, для яких 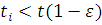 , встановлюється , встановлюється 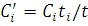
(тут 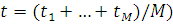 . Якщо таких центрів немає, то для усіх i встановлюється . Якщо таких центрів немає, то для усіх i встановлюється 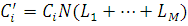 та здійснюється перехід до кроку 7. та здійснюється перехід до кроку 7.
Крок 5. Якщо 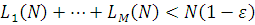 , то для тих i, для яких , то для тих i, для яких
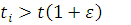 встановлюється встановлюється 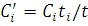 . Якщо таких центрів немає, то для усіх і встановлюється . Якщо таких центрів немає, то для усіх і встановлюється 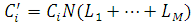 і здійснюється перехід до кроку 7. і здійснюється перехід до кроку 7.
Крок 6. Якщо 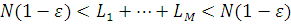 , то для всіх i встановимо , то для всіх i встановимо
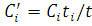 . Алгоритм завершує роботу, якщо виконуються всі нерівності . Алгоритм завершує роботу, якщо виконуються всі нерівності
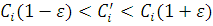 . Інакше здійснюється перехід до кроку 7. . Інакше здійснюється перехід до кроку 7.
Крок 7. Встановлюється 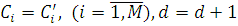 і здійснюється перехід до кроку 2. і здійснюється перехід до кроку 2.
5.4 ДЕКОМПОЗИЦІЯ РОЗІМКНЕНИХ МЕРЕЖ МО НА РІВНІ ПЕРШИХ
МОМЕНТІВ
В основі даного методу декомпозиції розімкнених однорідних мереж МО лежать наступні два припущення: потоки, що циркулюють в мережі, взаємно незалежні; функції розподілу інтервалів часу між послідовними надходженнями повідомлень в центри і часу обслуговування визначаються першими двома моментами. В рамках зроблених припущень формулюється і розв'язується основна задача декомпозиційної апроксимації — складання і рішення систем рівнянь щодо перших двох моментів (математичного сподівання і дисперсії ) розподілу інтервалів часу між повідомленнями в потоках, що циркулюють по мережі.
Значення 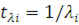 визначаються безпосередньо з рівнянь балансу потоків в центрах: визначаються безпосередньо з рівнянь балансу потоків в центрах:
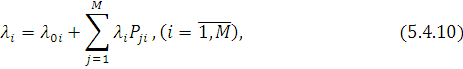
де 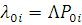 — інтенсивність потоку повідомлень в i-й центр з джерела; — інтенсивність потоку повідомлень в i-й центр з джерела; 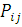 — елементи матриці маршрутів. — елементи матриці маршрутів.
Визначимо дисперсії інтервалів часу між повідомленнями у вихідних потоках. Для цього розглянемо два послідовні моменти 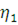 та та 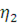 закінчення обслуговування повідомлень в і-му центрі. Величина закінчення обслуговування повідомлень в і-му центрі. Величина 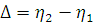 істотно залежить від стану центру в моменти закінчення обслуговування. Якщо в момент істотно залежить від стану центру в моменти закінчення обслуговування. Якщо в момент 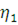 в центрі є хоча б одне повідомлення, яке чекає обслуговування, то величина Δ дорівнює часу обслуговування наступного повідомлення. Якщо в момент в центрі є хоча б одне повідомлення, яке чекає обслуговування, то величина Δ дорівнює часу обслуговування наступного повідомлення. Якщо в момент 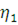 в центрі відсутні повідомлення, то Δ складається з часу обслуговування і часу до надходження наступного повідомлення (залишкового часу) Позначимо: в центрі відсутні повідомлення, то Δ складається з часу обслуговування і часу до надходження наступного повідомлення (залишкового часу) Позначимо: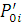 — ймовірність того, що у момент закінчення обслуговування в i-му центрі відсутні повідомлення; — ймовірність того, що у момент закінчення обслуговування в i-му центрі відсутні повідомлення; 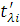 і і 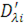 - середнє значення і дисперсія залишкового часу. Тоді для - середнє значення і дисперсія залишкового часу. Тоді для 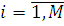 , одержимо: , одержимо:


де 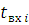 і і 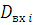 — відповідно середнє значення і дисперсія інтервалів часу між повідомленнями вхідного потоку i-го центру; — відповідно середнє значення і дисперсія інтервалів часу між повідомленнями вхідного потоку i-го центру;  і і 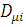 , — середнє значення і дисперсія часу обслуговування повідомлень в центрі i. Відмітимо, що в стаціонарному режимі , — середнє значення і дисперсія часу обслуговування повідомлень в центрі i. Відмітимо, що в стаціонарному режимі

де 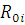 — ймовірність відсутності повідомлень в i-му центрі. З урахуванням цих співвідношень з (5.4.12) витікає, що — ймовірність відсутності повідомлень в i-му центрі. З урахуванням цих співвідношень з (5.4.12) витікає, що 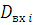 залежить від двох невідомих параметрів залежить від двох невідомих параметрів 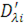 і і 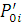 або або 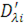 і і 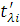 . .
Введемо в (5.4.12) рівняння перетворення дисперсії
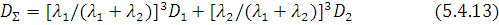
для суми двох незалежних потоків та
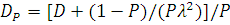
для просіяного потоку (P — ймовірність покидання повідомленням потоку).
Формули (5.4.12) i (5.4.13) дозволяють одержати систему рівнянь балансу дисперсій потоків, аналогічну рівнянням (5.4.10):
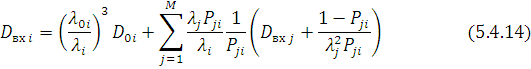
де 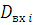 — дисперсія інтервалів часу між сусідніми повідомленнями потоку, що надходять в i-й центр. — дисперсія інтервалів часу між сусідніми повідомленнями потоку, що надходять в i-й центр.
РОЗДІЛ 6. МЕТОД ПОЛІНОМІАЛЬНОЇ АПРОКСИМАЦІЇ
6.1 ОПИС МЕТОДУ
На стадії передпроектного обстеження значення початкових даних для проектування обчислювальних систем і мереж відомі лише приблизно. Тому витрати на підвищення точності результатів моделювання на цій стадії проектування виявляються невиправданими. В цьому випадку необхідно використовувати найпростіші методи аналізу. До числа таких методів відноситься метод поліноміальної апроксимації, який дозволяє здійснювати декомпозицію мережі МО на рівні першого моменту розподілу інтервалів часу між повідомленнями в потоках, що циркулюють по мережі.
Розглянемо замкнену однорідну мережу МО, яка складається з М центрів, в яких циркулюють N повідомлень відповідно до матриці маршрутів 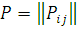 . Припускаться, що функція розподілу часу обслуговування в i-му центрі є довільною із заданими першими двома моментами . Припускаться, що функція розподілу часу обслуговування в i-му центрі є довільною із заданими першими двома моментами
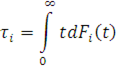
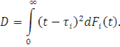
Нехай 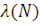 - інтенсивність потоку повідомлень через виділений центр (наприклад, перший). Тоді в стаціонарному режимі роботи мережі МО - інтенсивність потоку повідомлень через виділений центр (наприклад, перший). Тоді в стаціонарному режимі роботи мережі МО
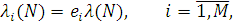
де відносна інтенсивність потоку однозначно визначається із системи рівнянь:
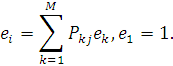
Використовуючи формулу Літтла, загальну кількість повідомлень в мережі МО можна представити в наступному вигляді:
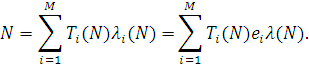
Тут 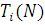 — час перебування повідомлення в i-му центрі. — час перебування повідомлення в i-му центрі.
Проведемо заміну змінної 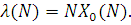 Тоді середній час циклу (час між надходженнями повідомлень у виділений центр) Тоді середній час циклу (час між надходженнями повідомлень у виділений центр)
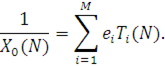
Даний метод заснований на декомпозиції початкової мережі на окремі незалежні центри і використанні аналога формули Поллячека — Хінчина для оцінки часу перетворення повідомлень в центрі:
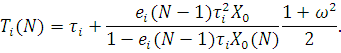
Таким чином, задача наближеного аналізу замкненої мережі МО може бути сформульована як задача розв’язання рівняння

відносно змінної X0
(N), де 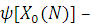 поліном степеня M: поліном степеня M:
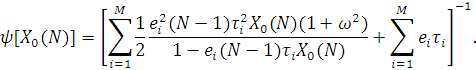
Розв’язок отриманого поліноміального рівняння при умові 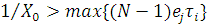 існує і єдиний. З вибраного виду полінома Р(Х) слідує, що при існує і єдиний. З вибраного виду полінома Р(Х) слідує, що при 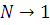 і і 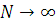 розв’язок рівняння (6.1.1) асимптотично збігається з точним значенням. розв’язок рівняння (6.1.1) асимптотично збігається з точним значенням.
6.2. ОЦІНКА ОБЧИСЛЮВАЛЬНОЇ СКЛАДНОСТІ МЕТОДУ
Оцінку обчислювальної складності методу поліноміальної апроксимації проведемо для однорідних експоненціальних мереж. Для експоненціального розподілу тривалості обслуговування в центрах мережі рівняння (6.1.1) приймає вигляд:
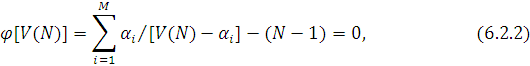
де уведені позначення 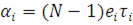 та та 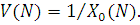
При розв’язанні рівняння (6.2.2) використовується обмеження 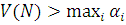 та один з ітераційних методів, наприклад метод поділу навпіл, який дає оцінку зверху кількості арифметичних операцій та один з ітераційних методів, наприклад метод поділу навпіл, який дає оцінку зверху кількості арифметичних операцій
Нехай ε — необхідна точність розв’язку. Позначимо 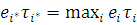 . Вважаючи без обмеження спільності . Вважаючи без обмеження спільності 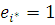 , одержуємо кількість ітерацій, необхідних для відшукання розв’язку з точністю ε: , одержуємо кількість ітерацій, необхідних для відшукання розв’язку з точністю ε: 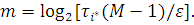 Помітимо, що Помітимо, що
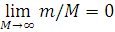
тобто, при великій кількості центрів число ітерацій 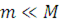
РОЗДІЛ 7. Приклад розрахунку мережі МО
Розглянемо модель замкненої ієрархічної мережі МО, схема якої зображена на рисунку 7.1. У цій мережі циркулює N=30 заявок, у відповідності з маршрутною матрицею. Заявка, яка виходить з головного центру 1 потрапляє у один з аналітичних центрів 2-11, у яких проходить первинну обробку, а потім у центрах
12-18 вторинну та сортировку щодо призначення їх у виконуючі системи 19-20. Після закінчення обслуговування у центрах19-20 виконана заявка потрапляє у головний центр 1, у якому вона замінюється новою, та надходить у центри 2-11.
Якщо у момент надходження повідомлення у один із центрів він зайнятий, то повідомлення займає місце у буфері, у якому очікує звільнення приладу (дисципліна обслуговування ПППО). Буфер з необмеженим числом місць дожидання.
Рисунок 7.1 Приклад мережі МО

Далі приведена маршрутна матриця (табл.7.1) та інтенсивності обслуговування у центрах 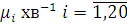 (табл.7.2). (табл.7.2).
Таблиця 7.1 Маршрутна матриця
i
j
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 1 |
0 |
0,1 |
0,05 |
0,15 |
0,1 |
0,05 |
0,1 |
0,05 |
0,15 |
0,2 |
0,05 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,25 |
0,15 |
0,1 |
0,05 |
0,11 |
0,3 |
0 |
0 |
| 3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,15 |
0,1 |
0,25 |
0,3 |
0,1 |
0,05 |
0 |
0 |
| 4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,05 |
0,1 |
0,25 |
0,1 |
0,15 |
0,3 |
0 |
0 |
| 5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,1 |
0,3 |
0,1 |
0,25 |
0,15 |
0,05 |
0 |
0 |
| 6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,3 |
0,25 |
0,05 |
0,1 |
0,15 |
0,1 |
0 |
0 |
| 7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,15 |
0,3 |
0,25 |
0,05 |
0,1 |
0,1 |
0 |
0 |
| 8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,1 |
0,25 |
0,3 |
0,15 |
0,1 |
0,05 |
0 |
0 |
| 9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,3 |
0,05 |
0,1 |
0,15 |
0,25 |
0,1 |
0 |
0 |
| 10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,1 |
0,15 |
0,05 |
0,3 |
0,1 |
0,25 |
0 |
0 |
| 11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,05 |
0,05 |
0,1 |
0,1 |
0,25 |
0,3 |
0,15 |
0 |
0 |
| 12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,5 |
0,5 |
| 13 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,67 |
0,33 |
| 14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,5 |
0,5 |
| 15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,75 |
0,25 |
| 16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,25 |
0,75 |
| 17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,83 |
0,17 |
| 18 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,25 |
0,75 |
| 19 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 20 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Таблиця 7.2 Інтенсивності обслуговування.
| i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
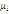 |
1 |
0,12 |
0,125 |
0,5 |
0,21 |
0,56 |
0,25 |
0,65 |
0,27 |
0,27 |
0,15 |
0,21 |
0,19 |
0,15 |
0,12 |
0,17 |
0,25 |
0,3 |
0,54 |
0,63 |
Значення 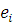 знаходимо з системи рівнянь: знаходимо з системи рівнянь:
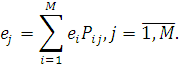
Як зазначено у розділі 1, одно із значень 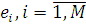 може вибиратися довільно. Покладемо для зручності може вибиратися довільно. Покладемо для зручності 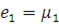 , де , де 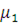 – інтенсивність обслуговування головного центру 1. Маємо такі значення коефіцієнтів передачі – інтенсивність обслуговування головного центру 1. Маємо такі значення коефіцієнтів передачі 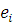 : :
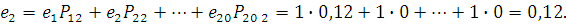
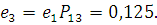
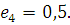
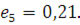

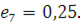
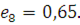
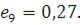
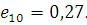
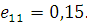
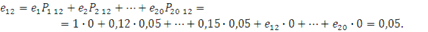

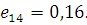
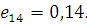
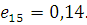
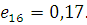
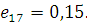
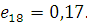
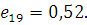
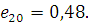
Відносні коефіцієнти використання і-го центру дорівнюють 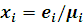 : :
Таблиця 7.3 Відносні коефіцієнти використання і-го центру.
| i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
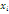 |
1 |
0,83 |
0,4 |
0,3 |
0,476 |
0,089 |
0,4 |
0,769 |
0,55 |
0,74 |
0,33 |
0,23 |
0,8 |
1,08 |
1,18 |
1,01 |
0,59 |
0,575 |
0,963 |
0,761 |
За допомогою методу Бузена знаходимо значення 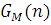 . Заповнюємо таблицю, використовуючи формулу . Заповнюємо таблицю, використовуючи формулу 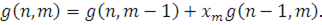
У правому стовпці таблиці отримані значення нормалізуючої константи 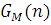 . Тепер знайдемо основні характеристики функціонування мережі. . Тепер знайдемо основні характеристики функціонування мережі.
За формулою (2.1.31)
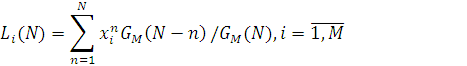
визначимо середню довжину черги у і-му центрі.
Інтенсивність вихідного потоку повідомлень з і-го центру 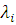 за означенням дорівнює середньому числу повідомлень, які були обслуговані у ньому за одиницю часу. Обчислимо інтенсивність у кожному центрі за формулою (2.1.26) за означенням дорівнює середньому числу повідомлень, які були обслуговані у ньому за одиницю часу. Обчислимо інтенсивність у кожному центрі за формулою (2.1.26)
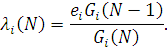
Середній час перебування повідомлення в і-му центрі обслуговування 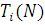 дорівнює відношенню середньої довжини черги до середньої інтенсивності вихідного потоку, тобто (2.1.32) дорівнює відношенню середньої довжини черги до середньої інтенсивності вихідного потоку, тобто (2.1.32)
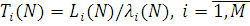 . .
Обчислимо у кожному центрі:
Таблиця 7.3 Результати розрахунку показників функціонування мережі
| № центру i |
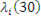 |
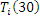 |
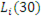 |
| 1 |
1,0000 |
2,980328 |
2,980328 |
| 2 |
0,0999 |
17,09798 |
1,708593 |
| 3 |
0,0500 |
8,824672 |
0,440875 |
| 4 |
0,1499 |
1,990151 |
0,298257 |
| 5 |
0,0999 |
5,726601 |
0,572036 |
| 6 |
0,0499 |
1,472157 |
0,073526 |
| 7 |
0,0999 |
4,41441 |
0,440875 |
| 8 |
0,0499 |
1,255889 |
0,062713 |
| 9 |
0,1497 |
4,915428 |
0,736029 |
| 10 |
0,1992 |
6,459583 |
1,286915 |
| 11 |
0,0498 |
6,881465 |
0,342598 |
| 12 |
0,0498 |
4,483347 |
0,223145 |
| 13 |
0,1507 |
10,31031 |
1,553436 |
| 14 |
0,1458 |
28,09523 |
4,095602 |
| 15 |
0,1161 |
55,61827 |
6,455276 |
| 16 |
0,1377 |
22,84074 |
3,144646 |
| 17 |
0,1172 |
6,980735 |
0,818049 |
| 18 |
0,1364 |
5,728309 |
0,781422 |
| 19 |
0,4032 |
6,481892 |
2,613804 |
| 20 |
0,368404 |
3,72383 |
1,371875 |
ВИСНОВКИ
Важливим розділом теорії масового обслуговування є мережі масового обслуговування. За допомогою мереж СМО моделюють багато типів транспортних, технологічних та обчислювальних систем, процеси надання медичної допомоги, обслуговування пасажирів та ін. У роботі Ф.Мура було показано, що мережі МО є адекватними моделями функціонування обчислювальних систем. Подальший розвиток області застосування теорії мереж МО пов'язаний з удосконалюванням апаратного та програмного забезпечення обчислювальних систем.
Постановкою задачі дипломної роботи є дослідження математичних підходів та методів, які використовуються для аналізу і розрахунку показників функціонування мереж МО.
Мережа МО є сукупністю кінцевого числа обслуговуючих центрів, в якій циркулюють повідомлення, які переходять відповідно до маршрутної матриці з одного центру в іншій.Якщо у момент надходження повідомлення всі обслуговуючі прилади центру зайняті, то повідомлення займає чергу в буфері, у якому чекає початку обслуговування. У загальному випадку мережу МО можна зобразити у вигляді графа, вершинами якого є одноканальні або багатоканальні СМО. Розрізняють розімкнені та замкнені мережі. Для замкненої стохастичної мережі не існує зовнішніх джерел вимог, тобто в ній завжди знаходиться однакова кількість вимог. У розімкненій мережі існують джерела і стоки вимог. Розглянемо детальніше основні підходи до їх розрахунку.
Для найпростіших однорідних експоненціальних мереж стаціонарні ймовірності станів мережі мають мультиплікативну форму
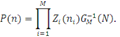
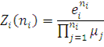
Цей факт є основою для подальших аналітичних досліджень та розробки ефективних алгоритмів розрахунку більш загальних мереж. Нормалізуюча константа 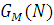 визначається з умов нормування визначається з умов нормування
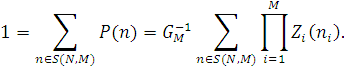
Для розімкнених мереж МО вона має відносно простий вигляд, а для замкнених є сумою добутків 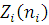 . .
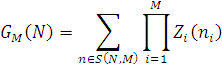
Прямий розрахунок нормалізуючої константи є досить трудомісткою процедурою. Основою багатьох алгоритмів розрахунку стаціонарних ймовірностей мережі є рекурентний метод Бузена. Відповідно до нього алгоритм розрахунку нормалізуючої константи зводиться до простої ітеративної процедури. При початкових умовах 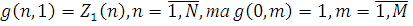 формула формула
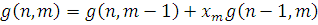
дозволяє рекурентно обчислити 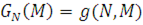 . А інші характеристики мережі, такі як середня довжина черги у і-му центрі, середній час перебування повідомлення в і-му центрі та ін. є функціями від нормалізуючої константи. . А інші характеристики мережі, такі як середня довжина черги у і-му центрі, середній час перебування повідомлення в і-му центрі та ін. є функціями від нормалізуючої константи.
При дослідженні мереж МО точними методами накладається обмеження, що час обслуговування у центрах мережі має експоненціальний розподіл. Причина використання наближених методів полягає в необхідності дослідження мереж МО з довільними функціями розподілу тривалості обслуговування в центрах мережі і рекурентним вхідним потоком.
Найбільш простим наближеним методом аналізу мереж МО є метод поліноміальної апроксимації. Для замкнутої однорідної мережі МО, яка складається з M центрів, та у якій циркулює N повідомлень відповідно до маршрутної матриці, функція розподілу часу обслуговування в і-му центрі є довільною з першими двома моментами:
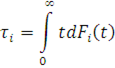
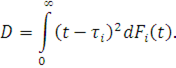
Нехай 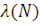 - інтенсивність потоку повідомлень через виділений центр. Позначимо - інтенсивність потоку повідомлень через виділений центр. Позначимо 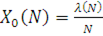 . Тоді задача наближеного аналізу замкненої мережі МО формулюється як задача розв’язання рівняння . Тоді задача наближеного аналізу замкненої мережі МО формулюється як задача розв’язання рівняння
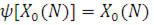
відносно змінної X0
(N), де 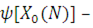 поліном степеня M: поліном степеня M:
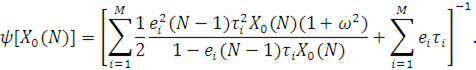
де позначено 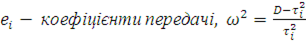
Відомим наближеним методом є метод декомпозиційної апроксимації. Мережа МО з довільними функціями розподілу часу обслуговування замінюється еквівалентною мережею з експоненціальними обслуговуючими центрами. Декомпозиція замкнутої мережі з М центрами обслуговування за теоремою Нортона зводиться до еквівалентної мережі з двома центрами. При цьому перший центр двохвузлової мережі співпадає з і-м центром початкової мережі, а 2-й (композиційний), який є еквівалентом іншої частини мережі, має експоненціальний час розподілу обслуговування з параметром 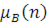 , що залежить від числа повідомлень в ньому, і дорівнює інтенсивності надходження повідомлень в і-й центр початкової мережі. , що залежить від числа повідомлень в ньому, і дорівнює інтенсивності надходження повідомлень в і-й центр початкової мережі.
Розглянемо модель замкненої ієрархічної мережі МО, схема якої зображена на рисунку 7.1. У цій мережі циркулює N=30 заявок, у відповідності з маршрутною матрицею. Якщо у момент надходження повідомлення у один із центрів він зайнятий, то повідомлення займає місце у буфері, у якому очікує звільнення приладу. Буфер з необмеженим числом місць дожидання. Обслуговуючі центри – з експоненцільно розподіленим часом обслуговування заявок. Середній час обслуговування у центрах заданий. Застосувавши розглянутий метод Бузена, знаходимо нормалізуючу константу, та обчислюємо такі показники функціонування мережі, як середня довжина черги у центрах, інтенсивність вихідного потоку та середній час перебування повідомлення у кожному центрі.
ПЕРЕЛІК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Томашевський В.М. Моделювання систем. – К.: Видавнича група ВН, 2005. – 352 с.
2. Жожикашвили В.А., Вишневский В.М. Сети массового обслуживания. Теория и применение к сетям ЭВМ. – М.: Радио и связь, 1988. -192 с.
3. Кузин Л.Т. Основы кибернетики: В2-х тт. Т. 2. Основы кибернетических моделей. Учеб. Пособие для вузов. – М.: Энергия,1979. – 584 с.
4. Беляков В.Г., Митрофанов Ю.И. к исследованию замкнутых сетей массового обслуживания большой размерности//Автоматика и телемеханика. – 1981. - №7. – С.61-69.
5. Вишневский В.М., Герасимов А.И. Исследование потоков в замкнутых экспоненциальных сетях массового обслуживания//Проблемы управления и теории информации. – 1983. Т. 12, №6.
6. Яшков С.Ф. Анализ очередей в ЭВМ. – М.:Радио и связь, 1989, 216с.
7. Шварц М. Сети ЭВМ. Анализ и проектирование. – М.: Радио и свіязь, 1981. – 336 с.
ДОДАТОК
Програма розрахунку показників функціонування мережі
#include<iostream.h>
#include<conio.h>
#include<iomanip.h>
#include<math.h>
#include<stdlib.h>
int main(){
int i,j,p;
double g[31][20],x[20],e[20],mu[20],L[20],lam[20],T[20];
e[0]=1;
e[1]=0.1;
e[2]=0.05;
e[3]=0.15;
e[4]=0.1;
e[5]=0.05;
e[6]=0.1;
e[7]=0.05;
e[8]=0.15;
e[9]=0.2;
e[10]=0.05;
e[11]=0.05;
e[12]=0.15;
e[13]=0.16;
e[14]=0.14;
e[15]=0.17;
e[16]=0.15;
e[17]=0.17;
e[18]=0.52;
e[19]=0.48;
mu[0]=1;
mu[1]=0.12;
mu[2]=0.125;
mu[3]=0.5;
mu[4]=0.21;
mu[5]=0.56;
mu[6]=0.25;
mu[7]=0.65;
mu[8]=0.27;
mu[9]=0.27;
mu[10]=0.15;
mu[11]=0.21;
mu[12]=0.19;
mu[13]=0.15;
mu[14]=0.12;
mu[15]=0.17;
mu[16]=0.25;
mu[17]=0.3;
mu[18]=0.54;
mu[19]=0.63;
for(i=0;i<20;i++) x[i]=e[i]/mu[i];
for(i=0;i<31;i++) g[i][0]=pow(x[0],i);
for(j=0;j<20;j++) g[0][j]=1;
for(j=1;j<20;j++){
for(i=1;i<31;i++) g[i][j]=x[j]*g[i-1][j]+g[i][j-1];}
cout<<"Normalizujucha constanta GM(N):"<<g[30][19]<<endl;
for(i=0;i<20;i++){
cout<<"x["<<i<<"]="<<x[i]<<" "<<endl;}
cout<<"serednja dovzhina chergi v i-mu centri"<<endl;
for(i=0;i<20;i++){
for(p=0;p<31;p++){L[i]+=pow(x[i],p)*g[30-p][19]/g[30][19];}}
for(i=0;i<20;i++) cout<<"L["<<i<<"]="<<L[i]<<" "<<endl;
cout<<"Serednja intensivnist vyhidnogo potoku povidomlen z i-go centru"<<endl;
for(i=0;i<20;i++){ lam[i]=e[i]*g[29][i]/g[30][i];}
for(i=0;i<20;i++){
cout<<"lam["<<i<<"]="<<lam[i]<<" "<<endl;}
cout<<"Serednij chas perebuvannja povidomlennjya v i-mu centri"<<endl;
for(i=0;i<20;i++){ T[i]=L[i]/lam[i];}
for(i=0;i<20;i++){
cout<<"T["<<i<<"]="<<T[i]<<" "<<endl;}
getch();
}
|