Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Челябинский государственный университет»

Кафедра математических методов в экономике

КУРСОВАЯ РАБОТА

ЭКОНОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ

РЫНКА ВТОРИЧНЫХ ТРЁХКОМНАТНЫХ КВАРТИР МЕТАЛЛУРГИЧЕСКОГО РАЙОНА

г. ЧЕЛЯБИНСКА

Факультет экономический Исполнитель Е.В.Ашмарина

Специальность «Математические Группа ЭММ 301

методы в экономике» Научный руководитель

Дата защиты _____________ А.М. Набиев, к.э.н., доцент

Оценка __________________

Челябинск

2005

Содержание

Введение

В данной работе методы эконометрического анализа применяются с целью моделирования состояния рынка вторичного жилья. Рассматривается вторичный рынок трёхкомнатных квартир Металлургического района

г. Челябинска.

Актуальность исследования вытекает из необходимости формализации существующих критериев оценки стоимости продаваемых квартир, т.к. часто на практике нет четко обоснованных критериев и моделей для её определения. Преобладает способ оценивания цены предложения квартиры, имеющий основой субъективные критерии, которые могут не совпадать у разных оценщиков.

Этим объясняется необходимость нахождения модели, описывающей состояние вторичного рынка квартир, обоснованной объективными методами.

Объектом исследования выбрана совокупность трёхкомнатных квартир Металлургического района на вторичном рынке г. Челябинска.

В качестве предмета исследования выступает оценка продажной цены квартиры.

Целью работы является исследование зависимости цены предложения трехкомнатных квартир на вторичном рынке Металлургического р-на г.Челябинска в 2005 году от характеристик этих квартир.

Основным методом исследования является регрессионный анализ.

Для нахождения оценок параметров эконометрической модели, проведения тестов, определяющих значимость найденных оценок и модели в целом, использовался пакет EViews-3.

1. Описание предметной области

1.1 Общее представление о Металлургическом районе.

Формирование рынка вторичного жилья Металлургического района г. Челябинска имеет ряд особенностей. Чтобы иметь представление о нем, адекватное настоящему времени, необходимо рассмотреть условия его становления в нескольких аспектах.

1. Исторический аспект.

В 1943 году на пустующей местности за северной границей г. Челябинска, за рекой Миасс, был построен Челябинский Металлургический Завод.

В связи с этим на прилегающей к заводу территории был основан жилой поселок – соцгород. В 1946 году ему был официально присвоен статус самостоятельного территориально-административного образования, именуемого ныне Металлургическим районом [2, с.6].

В 50-70 годы двадцатого века велась активная застройка района, большинство жилых объектов построено именно в это время. Поэтому на рынке преобладает старое жилье, новостроек существенно меньше. За последние годы и в настоящее время строится, преимущественно, элитное жильё, оно перекупается, продается вторично, что существенно меняет обстановку на рынке вторичного жилья.

2. Территориальный аспект.

Напрямую связан с историей возникновения района.

Металлургический район располагается в северной части города Челябинска. Его естественной границей с юга является река Миасс. С севера район граничит с Каштакским бором.

Район значительно отдален и обособлен промышленной зоной от остальной части города. По сути, он представляет собой отдельное территориальное образование.

3. Экологический аспект.

На территории района размещено большое количество крупных промышленных предприятий (в их числе металлургический гигант «Мечел»).

В связи с этим сложившаяся экологическая ситуация весьма неблагоприятна, т.к. большинство атмосферных выбросов заводов оседает в границах района.

4. Социальный аспект.

Металлургический район в силу специфики своего возникновения является «рабочим районом», т.е. большинство его населения составляют работники заводов. Чаще всего жилые дома строились самими заводами непосредственно для своих рабочих и служащих. Поэтому здесь изначально ставка делалась на недорогое жилье, не на комфорт и благоустроенность, а на обеспечение жильем максимального количества семей.

Отсюда низкое качество и маленький метраж квартир.

Рассмотренные аспекты позволяют получить исчерпывающее представление о причинах формирования рынка вторичного жилья Металлургического района именно в таком виде, в котором он существует на сегодняшний день.

Главной его особенностью является очень низкая продажная цена квартир по сравнению с более благополучными районами г. Челябинска.

1.2 Описание факторов, рассматриваемых в исследовании.

Для проведения статистического анализа и эконометрического моделирования рынка вторичных трёхкомнатных квартир на основе объявлений о продаже квартир была построена выборка, содержащая 121 наблюдение. Перечень данных приведен в Приложении 1.

Изучив объявления и предметную область, можно сказать, что целесообразно проводить оценку продажной цены квартиры по следующим факторам:

1. жилая площадь (в м2);

2. остальная площадь (общая площадь – жилая площадь) (в м2);

3. количество этажей в доме;

4. номер этажа квартиры;

5. количество балконов;

6. материал стен дома;

7. наличие ремонта в квартире;

8. наличие квартирной железной двери.

9. наличие подъездного домофона;

10. серия квартиры;

11. удобство положения дома;

12. застекленность балкона;

13. привлекается ли посредник для продажи квартиры;

Некоторые факторы, выбранные для построения модели цены предложения вторичных трёхкомнатных квартир, имеют ряд особенностей, описанных ниже.

1.2.1. Серия.

Из анализа выборки следует, что целесообразно рассматривать следующие квартирные серии:

- «хрущевка»;

- «брежневка»

- 121;

- полнометражная;

- ленинградский проект;

- элитная.

Серийность квартиры является её качественным фактором, поэтому каждая из указанных серий в модели обозначается фиктивной переменной (имеет значение 0, если квартира не принадлежит указанной серии, и значение 1, если принадлежит).

Квартиры, включенные в выборку и имеющие другую серию, не указанную в перечисленных (например, «индивидуальный проект»), имеют значение ноль у всех перечисленных фиктивных переменных, обозначающих принадлежность к серии.

Фактор «серия» включает в себя такие характеристики квартиры как высота потолков, планировка, санузел и другие особенности проекта.

1.2.2 Удобство положения.

В Металлургическом районе нет чётко выраженного единственного центра, близостью к которому можно было бы определять удобство положения дома.

Поэтому под удобством положения будем подразумевать соответствие места расположения квартиры следующим критериям:

- близость к остановке транспорта (лучше к нескольким видам транспорта);

- близость к крупным продовольственным магазинам, супермаркетам;

- близость к различным учреждениям сферы обслуживания (иные магазины, парикмахерские, отделения связи, кафе, аптеки);

- близость к учреждениям культуры (библиотеки, дворцы культуры), спорта (спортивные залы, бассейн, дворцы спорта, спортивные базы, стадионы) и досуга (парк культуры и отдыха).

Факторы, отрицательно влияющие на удобство положения квартиры:

приближенность к заводам и городской свалке.

1.2.3 Второстепенные факторы с точки зрения экономического смысла.

Следующие факторы включаются в статистическую выборку данного исследования, т.к. встречаются в абсолютном большинстве объявлений о продаже квартир.

Но с точки зрения экономического смысла они могут оказаться незначимыми в создаваемой модели продажной цены квартиры. Эту гипотезу следует проверить на дальнейших этапах исследования.

Тем не менее, эти факторы включаются в исследование, т.к. они необходимы для адекватности модели предметной области и, к тому же, априорных оснований для обоснования их незначимости недостаточно.

Рассмотрим такие факторы более подробно.

1. Железная дверь

- есть в большинстве квартир приведенной выборки, поэтому может не являться значимым фактором.

2. Застекленность балкона

- стоимость застекления балкона несравнимо меньше стоимости квартиры и, предположительно, существенно не влияет на её цену.

3. Домофон

- может оказаться незначимым по этой же причине.

4. Наличие телефона.

Т.к. Металлургический район практически полностью телефонизирован, то телефоны установлены в абсолютном большинстве квартир. Они могут отсутствовать в домах на окраинах, что учитывает уже имеющийся фактор «удобство положения», или в новостройках.

В результате описания предметной области и анализа объявлений о продаже квартир выявлено 19 факторов, от которых, предположительно, зависит продажная цена квартиры. Они включаются в модель, т.к. наиболее полно раскрывают характеристики квартиры.

Также в разделе выдвинут ряд предположений о возможной незначимости некоторых факторов и обоснованы причины этого явления. Эти гипотезы предстоит проверить на дальнейших этапах работы.

2. Постановка задачи

В данной курсовой работе рассматривается задача построения аналитической формулы средней стоимости квартиры в зависимости от факторов, влияющих на эту стоимость.

Зависимая переменная: Y - оценка продажной цены квартиры (в тыс.руб).

Независимые переменные: факторы, от которых, предположительно, зависит цена предложения квартиры.

Они разделяются на 2 типа:

1. количественные – имеют единицы измерения;

2. качественные (фиктивные) – имеют значение 0, если квартира не обладает указанным в факторе качеством, и 1, если обладает.

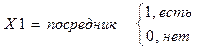
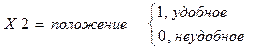
Х 3 = этажей в доме (штук)

Х 4 = номер этажа

Х 5 = жилая площадь (в м2)

Х 6 = остальная площадь (в м2)

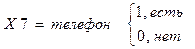
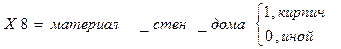
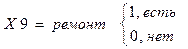
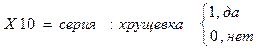
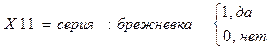
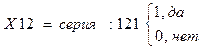
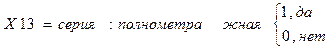
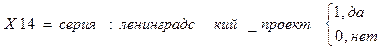
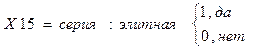
Х 16 = количество балконов

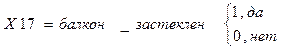
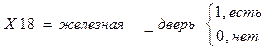
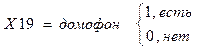
Для описания эконометрической модели зависимости продажной цены квартиры от указанных факторов выбрана модель регрессионного уравнения, в частности, модель множественной регрессии.

В качестве параметров модели предполагается использовать весовые коэффициенты при отобранных факторах (в модели весовые коэффициенты обозначены С1,…, С19).

В работе предполагается рассмотреть три типа регрессионных моделей:

1. линейную: Y=C1+C2*X1+C3*X2+…+C20*X19

2. полулогарифмическую:

LOG(Y)=C1+C2*X1+C3*X2+…+C20*X20

3. логарифмическую:

LOG(Y) =C1+C2*X1+C3*X2+C6*LOG(X5)+С(7)*LOG(X6)+…+C20*X19

Т.о. определены набор регрессоров, включаемых в модель, и функциональные формы моделей, далее рассматриваемых в работе.

3. Моделирование.

На этапе моделирования ставится задача построения различных регрессионных моделей продажной цены квартир – линейной, полулогарифмической и логарифмической.

3.1 Линейная модель.

В соответствии с методическими указаниями к выполнению данной курсовой работы за начальную модель примем модель множественной линейной регрессии, включающей все рассматриваемые факторы:

Таблица 3.1 Результаты оценки параметров модели 1.1.

В скобках под оценками коэффициентов модели приведены их стандартные ошибки.

Выделены те параметры модели, для которых гипотеза о значимости коэффициентов подтвердилась на 5% уровне значимости, т.е. значение Prob.< 0,05 и значения стандартной ошибки меньше оцениваемых коэффициентов в 2 раза и более.

Значимыми оказались факторы:

1. Х2 - удобство положения увеличивает цену на 98.35 тыс. руб.;

2. Х6 - остальная площадь (общая площадь – жилая площадь) увеличивает цену (цена одного квадратного метра: 12.07 тыс. руб.). Т.е. при увеличении остальной площади на 1 кв. метр стоимость квартиры возрастает на 12.07 тыс. руб.

3. Х13 - полнометражная серия квартиры увеличивает цену на 162.16 тыс. руб.;

4. Х15 - элитная серия квартиры увеличивает цену на 1587.57 тыс. руб.;

5. Х16 - наличие каждого балкона увеличивает цену на 139.24 тыс. руб.

Коэффициент детерминации получился равным R-squared=0.82, т.е. весьма близким к единице. Исходя из этого, можно сделать предположение о близости построенного уравнения к выборке.

Значение Prob(F-statistic)=0, следовательно, уравнение в целом абсолютно значимо.

Для выявления эффекта мультиколлинеарности оцениваем матрицу парных коэффициентов корреляции (она приведена в Приложении 2).

Значение коэффициента парной корреляции между факторами X5 и X6 равно 0.41, что может повлечь эффект мультиколлинеарности.

Исходя из экономического смысла, можно объединить эти факторы, просуммировав их (т.к. Х5 - жилая площадь, Х6 – остальная площадь).

Коэффициент парной корреляции между X3 (количество этажей в доме) и X4 (№ этажа) равен 0.48, а между Х3 и X8 (материал стен дома) его значение равно 0.7, что также может обусловить появление мультиколлинеарности.

В связи с этим, введем вместо Х3 и Х4 регрессор (Х3/Х4), которую можно интерпретировать как «соотношение этажности дома и этажа квартиры».

На основании больших значений коэффициентов парной корреляции со многими регрессорами (см. приложение 2), больших стандартных ошибок и больших значений Prob. (> 0.05) исключаем незначимые регрессоры.

Можно предположить, что приведенные ниже факторы незначимы по следующим причинам:

1. Х1 – наличие посредника.

Незначим в связи с невозможностью достоверного определения участия посредника в продаже квартиры.

2. Х7 – наличие телефона;

Х17 – застекленный балкон;

Х18 – железная дверь;

Х19 – домофон.

Незначимость данных факторов подтверждает предположения, выдвинутые в п. 1.2.3 данной работы.

3. Х8 – материал стен дома.

Фактор незначим, так как коррелирует с этажностью дома (пяти-, четырёх- и трёхэтажные дома чаще всего строят из кирпича, а высотные дома – панельные).

4. Х10 – серия: хрущевка;

Х11 – брежневка.

Можно предположить, что факторы незначимы из-за возможной корреляции с величиной площади квартиры. К тому же указанные серии чаще всего имеют старые дома и существенных особенностей, способных сильно влиять на продажную цену квартиры, эти проекты не имеют.

5. Х14 – серия: ленинградский проект.

Фактор незначим, т.к. в выборки присутствует всего несколько квартир, обладающих этим признаком. К тому же, серия не обладает ярко выраженными особенностями, способными существенно повлиять на цену квартиры.

Незначимые факторы из модели удаляются постепенно, т.к. исключив все их одновременно, мы рискуем потерять на самом деле значимые регрессоры, освобожденные от влияния незначимых.

Исходя из внесенных изменений в учитываемые факторы, строится модель 1.2.

Таблица 3.2 Результаты оценки параметров модели 1.2.

Значимыми оказались все факторы, включенные в регрессию.

Значение коэффициента детерминации получилось равным R-squared=0.80, т.е. близким к единице. Т.о. можно выдвинуть предположение о близости построенного уравнения к выборке.

Скорректированный коэффициент детерминации имеет значение

Adjusted R-squared=0.78, что также указывает на возможность предыдущего утверждения.

Коэффициента детерминации полученной модели меньше, чем у исходного уравнения, где R-squared=0.82. Но разница между скорректированным и простым коэффициентами детерминации меньше, что свидетельствует о лучшем качестве полученной модели.

Значение Prob(F-statistic)=0, следовательно, уравнение в целом абсолютно значимо.

3.2 Полулогарифмическая модель..

Начальная полулогарифмическая модель включает в себя все рассматриваемые регрессоры.

Таблица 3.3 Результаты оценки параметров модели 2.1.

Значимые регрессоры выделены жирным шрифтом.

Все значимые факторы имеют положительные коэффициенты, что говорит об их прямом влиянии на цену кватиры.

Значимыми являются следующие факторы (в скобках указано, на сколько % изменится цена при наличии данного фактора - для качественных факторов и при увеличении данного фактора на единицу – для количественных факторов):

Х2 – удобство положения дома (0.09 %);

Х5 – величина жилой площади (0.004 %);

Х6 – величина остальной площади (0.01 %);

Х9 – наличие ремонта (0.06);

Х13 – полнометражная серия квартиры (0.12 %);

Х15 – элитная серия квартиры (0.64 %);

Х16 – количество балконов (0.08 %).

Факторы, незначимые в данной модели 2.1, одинаковы с незначимыми факторами модели 1.1. Поэтому объяснение возможных причин их незначимости также аналогичны. Они подробно изложены в разделе 3.1.

Незначимые регрессоры удаляются постепенно, т.к. в связи с возможным наличием мультиколлинеарности некоторые из них могут оказаться значимыми при освобождении от влияния действительно незначимых факторов. Т.о. строится модель 2.2.

Таблица 3.4 Результаты оценки параметров модели 2.2.

.

Коэффициент детерминации получился равным R-squared=0.78, т.е. весьма близким к единице, что говорит о возможной близости построенного уравнения к выборке.

Скорректированный коэффициент детерминации имеет значение

Adjusted R-squared=0.76, что также может говорить о корректности предыдущего утверждения.

Значение Prob(F-statistic)=0, следовательно, уравнение в целом абсолютно значимо.

Коэффициенты при всех учтенных в данной модели факторах значимы.

3.3 Логарифмическая модель.

Начальная логарифмическая модель содержит все 20 имеющихся регрессоров.

Таблица 3.5 Результаты оценки параметров модели 3.1

Значимые регрессоры выделены жирным шрифтом.

Незначимыми оказались те же, факторы, что и в модели 1.1. В разделе 3.1 приводится обоснование возможных причин их незначимости.

Постепенно удаляя из модели незначимые факторы, переходим к скорректированной полулогарифмической модели 3.2.

Таблица 3.6 Результаты оценки параметров модели 3.2.

.

Коэффициент детерминации получился равным R-squared=0.78, т.е. весьма близким к единице, что, возможно, говорить о близости построенного уравнения к выборке. Скорректированный коэффициент детерминации имеет значение Adjusted R-squared=0.76, что также может говорить о корректности предыдущего утверждения.

Значение Prob(F-statistic)=0, следовательно, уравнение в целом абсолютно значимо. Коэффициенты при всех учтенных в данной модели факторах значимы.

Т.о. на этапе моделирования построено 3 различные значимые модели (линейная, полулогарифмическая, логарифмическая), оценивающие зависимость цены предложения трёхкомнатной квартиры на рынке вторичного жилья Металлургического района от различных факторов.

4. Идентификация и интерпретация полученных моделей.

На этапе идентификации модели проводится её тестирование и коррекция на гетероскедастичность, после чего каждая из трёх полученных моделей интерпретируется.

4.1 Суть гетероскедастичности.

Для нахождения оценок линейных регрессионных зависимостей применяется метод наименьших квадратов (МНК).

Однако, МНК требует выполнения условий Гаусса-Маркова, которые гарантируют состоятельность, несмещенность и эффективность найденных оценок [1, с.23]. Нарушение этих условий может давать оценки с плохими статистическими свойствами. Одной из ключевых предпосылок МНК является условие постоянства дисперсии случайных отклонений. Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Её невыполнимость называется гетероскедастичностью (непостоянством дисперсии отклонений) [3, с.230].

Т.о. при гетероскедастичности оценки коэффициентов получаются неэффективными. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющимися [3, с.232].

4.2 Проверка и коррекция на гетероскедастичность.

Проверка на гетероскедастичность построенных моделей осуществляется в пакете EViews-3 с помощью теста Уайта. В нашем случае его результаты говорят о том, что гипотеза о гомоскедастичности не подтвердилась для любой из трёх моделей.

Проведем коррекцию на гетероскедастичность для каждой из них.

Сделать поправку на гетероскедастичность и «улучшить» оценку матрицы ковариаций позволяет метод расчета стандартных ошибок по форме Уайта, автоматически реализуемый в EViews-3. Результаты коррекции линейной, полулогарифмической и логарифмической моделей на гетероскедастичность приведены ниже.

4.2.1. Коррекция на гетероскедастичность модели 1.2.

Таблица 4.1 Скорректированная на гетероскедастичность модель 1.2.

Малая значимость регрессора Х5+Х6 (Prob.=0.28), обозначающего общую площадь квартиры, вероятнее всего обусловлена связью между метражом квартиры и её серией.

Такие квартирные серии, как 121 (Х12), полнометражная (Х13), элитная (Х15), обладая рядом особенностей, изначально несут в себе информацию о стоимости квартиры.

Целесообразно ввести новый регрессор Х20:

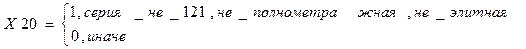
Включение регрессора Х20 в модель позволит освободить переменные, описывающие принадлежность квартиры к указанным сериям, от влияния фактора метражности. Возможно, это улучшит качество оценок параметров модели и увеличит их значимость. Коррекция на гетероскедастичность новой модели 1.3 дает следующие результаты.

Таблица 4.2 Результат коррекции на гетероскедастичность модели 1.3.

Полученная модель имеет вид:

Yt=322.76+102.24*X2t+23.57*X3t/X4t+4.38*(X5t+X6t)*Х20+417.43*X12t+

(118.53) (31.49) (10.12) (2.12) (132.78)

+528.82*X13t+2211.76*X15t+152.11*X16t, t=1…121

(129.84) (417.33) (36.70)

Значение коэффициента детерминации получилось равным R-squared=0.79, из чего может следовать близость построенного уравнения к выборке. Скорректированный коэффициент детерминации имеет значение

Adjusted R-squared=0.78, т.е. он отличается от R-squared незначительно, что также говорит в пользу предыдущего утверждения.

Значение Prob(F-statistic)=0, следовательно, уравнение в целом абсолютно значимо.

Рассмотрим экономический смысл значимых регрессоров и их влияние на цену предложения квартиры.

1. Х2 - удобство положения увеличивает цену на 102.24 тыс. руб.

2. Х3/Х4 – увеличение соотношения этажности дома и этажа квартиры на единицу увеличивает цену на 23.57 тыс. руб.

3. (Х5+Х6)*Х20 – при увеличении общей площади квартиры (не относящейся к 121, полнометражной и элитной сериям) на 1 кв. метр, её цена предложения возрастает на 4.38 тыс. руб.

Введенный регрессор Х20 исключает влияние фактора метражности в таких квартирных сериях, как 121, полнометражная и элитная. Поэтому непосредственный фактор метража (Х5+Х6) учитывается только при определении цены на квартиры серий, отличных от перечисленных.

4. Х12 – принадлежность квартиры к 121 серии увеличивает её цену на 417.43 тыс.руб.

5. Х13 – полнометражная серия квартиры увеличивает её цену на 528.82 тыс. руб.

6. Х15 – элитная серия квартиры имеет самую большую значимость среди коэффициентов полученной модели. Принадлежность квартиры к элитному типу жилья увеличивает её продажную стоимость на 2211.76 тыс. руб.

7. Х16 – каждый балкон увеличивает цену продажи квартиры на 152.11 тыс. руб.

4.2.2. Коррекция на гетероскедастичность полулогарифмической

модели 2.2.

Таблица 4.3 Результаты коррекции на гетероскедастичность модели 2.2.

Построенная модель имеет вид:

LOG(Yt ) = 6.3 5 + 0.09*X2t + 0.006*(X5t + X6t) - 0.09*X8t + 0.06*X9t –

(0.12) (0.02) (0.002) (0.03) (0.02)

- 0.10*X10t + 0.11*X13t + 0.62*X15t + 0.06*X16t, t=1...121.

(0.03) (0.04) (0.20) (0.03)

В скобках под коэффициентами указаны их стандартные ошибки.

Коэффициент детерминации получился равным R-squared=0.77, что, возможно, говорит о близости построенного уравнения к выборке.

Скорректированный коэффициент детерминации имеет значение

Adjusted R-squared=0.75. Можно сказать, что он незначительно отличается от R-squared, что, вполне вероятно, свидетельствует о верности предыдущего утверждения.

Значение Prob(F-statistic)=0, следовательно, уравнение в целом абсолютно значимо. Коэффициенты при всех учтенных в данной модели факторах значимы.

Следующие факторы увеличивают продажную цену квартиры (коэффициенты > 0):

Х2 – удобство положения (0.09 %);

Х5 + Х6 – общая площадь (0.006 %);

Х9 – наличие ремонта (0.06 %);

Х13 – полнометражная серия (0.11 %);

Х15 – элитная серия (0.62 %);

Х16 – количество балконов (0.06 %).

В скобках указано, на сколько процентов увеличится продажная цена квартиры при увеличении приведенного фактора на 1 единицу (для количественных факторов) и при наличии данного фактора (для качественных факторов, описываемых фиктивными переменными).

Экономическая интерпретация положительного влияния этих факторов на стоимость квартиры подробно изложена разделе п. 5.2.1.

Факторы, уменьшающие продажную цену квартиры (коэффициенты < 0):

А) Х8 – материал стен дома (кирпич). Если дом построен из кирпича, то цена квартиры уменьшается на 0.09 %. Отрицательное влияние на цену вызвано тем, что в Металлургическом районе кирпичные, в основном, старые дома, в которых квартиры дешевле, чем в новостройках.

Б) Х10 – серия: хрущевка уменьшает стоимость квартиры на 0.1 %.

Это можно объяснить тем, что «хрущевки» являются устаревшими и наименее благоустроенными из всех квартирных серий.

4.2.3. Коррекция на гетероскедастичность логарифмической

модели 3.2.

Таблица 4.4 Результаты коррекции на гетероскедастичность модели 3.2.

Построенная модель имеет вид:

LOG(Yt) =4.34+0.09*X2t+0.04*LOG(X3t/X4t)+0.53*LOG(X5t+X6t)+0.06*Х9+

(0.45) (0.03) (0.02) (0.11) (0.02)

+0.14*X13t +0.73*X15t+0.08*X16t, t=1…121

(0.03) (0.17) (0.03)

Коэффициент детерминации получился равным R-squared=0.78, т.е. весьма приближенным к единице, что говорит о возможной близости построенного уравнения к выборке. Скорректированный коэффициент детерминации имеет значение Adjusted R-squared=0.76, т.е он незначительно отличается от R-squared, что, возможно, тоже свидетельствует о корректности предыдущего утверждения.

Значение Prob(F-statistic)=0, следовательно, уравнение в целом абсолютно значимо.

Все факторы, учтенные в модели, являются значимыми (Prob.<0.05).

Коэффициенты при всех регрессорах положительны, т.е. наличие указанных факторов увеличивает продажную цену квартиры.

Перечень линейных регрессоров (скобках указано, на сколько % увеличится цена при наличии данного фактора):

Х2 – удобство положения (0.09 %);

Х13 – полнометражная серия (0.14 %)

Х15 – элитная серия (0.73 %);

Х16 – количество балконов (при увеличении на 1 цена увеличивается на 0.08 %).

Перечень логарифмических регрессоров (в скобках указано, на сколько % изменится цена при изменении данного фактора на 1 %):

Х3/Х4 – соотношение этажности дома и номера этажа квартиры (0.04 %);

Х5+Х6 – общая площадь (0.53 %).

Вывод: сравнивая вид каждой модели до и после коррекции на гетероскедастичность, можно сказать, что оценки коэффициентов не изменились. Зато стандартные ошибки возросли в несколько раз. Это свидетельствует о расширении доверительных интервалов для оценок коэффициентов регрессии.

5. Верификация

На этапе верификации необходимо провести проверку качества построенных моделей и выбрать наиболее точную из них.

5.1 Тест на функциональную форму модели.

Тестом на ошибку спецификации регрессии является RESET -тест . Идея этого теста заключается в том, что если исходная модель для Yt верна, то добавление нелинейных функций не должно помогать объяснять Yt [1, с.36].

Reset-тест автоматически реализован в EViews-3. При его проведении было установлено, что функциональная форма всех трёх моделей верна.

5.2 Выбор конкурирующих моделей.

Выбор лучшей модели осуществляется по нескольким критериям.

Рассмотрим каждый из них.

5.2.1 Значимость коэффициентов регрессии ( t -тест).

Исходя из данных имеющейся статистической выборки, определяются оценки коэффициентов уравнения регрессии. Для каждого коэффициента рассчитывается значение t-статистики (статистики Стьюдента). Это эмпирическое значение затем сравнивается с табличным значением t-критерия Стьюдента с таким же количеством степеней свободы. Если табличное значение статистике меньше эмпирического, то коэффициент значим.

В пакете EViews-3 процедура расчета t-статистики осуществляется автоматически, одновременно с оцениванием коэффициентов регрессии. На основе t-статистики также определяется значение Prob. – это вероятность того, что коэффициент незначим. Если значение Prob.< 0.05, то гипотеза о незначимости отвергается.

На этапе устранения мультиколлинеарности из всех трёх моделей были исключены незначимые регрессоры. Исключением являются только те регрессоры, отсутствие которых в модели противоречило её экономическому смыслу.

5.2.2. Значимость модели в целом ( F -тест).

Значимость построенных уравнений регрессии определяется с помощью критерия Фишера и соответствующей статистики. Если на соответствующем уровне значимости

F эмпирическое > F табличное, то гипотеза о незначимости уравнения отвергается.

В EViews-3 автоматически рассчитывается Prob(F-statistic).

Если Prob(F-statistic) < 0.05, то гипотеза о незначимости уравнения отвергается.

Для каждой из построенных моделей значение Prob(F-statistic)=0, т.е. все уравнения являются значимыми.

5.2.3 Соответствие модели выборочным данным ( R ² , R ² _adj ).

Коэффициент детерминации R² показывает, насколько модель близка к исходной выборке. Чем ближе R² к единице, тем точнее модель. Но при включении в модель новых регрессоров R² всегда увеличивается, хотя к улучшению качества модели это фактически не приводит. Чтобы проверить, действительно ли новые вводимые регрессоры делают модель лучше, необходимо вычислять скорректированный коэффициент детерминации R² _{adj .} Чем ближе R² _adj к R² , тем точнее модель описывает выборку.

Таблица 5.1 Сравнение коэффициентов детерминации.

Во всех построенных моделях скорректированный и простой коэффициенты детерминации очень близки и друг к другу, и к единице.

Это может свидетельствовать о соответствии полученных моделей данным исходной выборки.

Значения R² _adj и R² максимальны у линейной модели.

5.2.4 Критерий минимума стандартной ошибки регрессии.

Таблица 6.2 Стандартные ошибки регрессии.

Основываясь на перечисленных критериях, можно сделать вывод, что наилучшими характеристиками обладает линейная модель. Она и будет являться конечным результатом данной курсовой работы.

5.3 Проверка качества модели по контрольной выборке.

Дополнительно к уже имеющимся исходным данным была сделана статистическая выборка. Она содержит 32 данное, которые расположены в Приложении 3.

Эти данные подставляются в выбранную логарифмическую модель. Прогнозные цены на квартиры, полученные в этой модели, сравниваются с уже имеющимися статистическими данными, и делается вывод о качестве прогноза логарифмической модели.

Для определения ошибки прогноза используется формула:

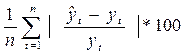
Т.о. ошибка прогноза продажной цены квартиры в построенной логарифмической модели составляет 6.42 %.

6. Интерпретация окончательной модели

В ходе написания курсовой работы было проведено эконометрическое моделирование рынка вторичных трёхкомнатных квартир Металлургического района г. Челябинска.

С помощью эконометрического анализа были выделены наиболее значимые факторы, влияющие на цену предложения квартиры на рынке

Результатом моделирования стало построение трёх регрессионных уравнений – линейного (модель 1.3), полулогарифмического (модель 2.2) и логарифмического (модель 3.2). При помощи ряда тестов модели были скорректированы, и среди них выбрана одна, наиболее точная, - модель 1.3, которая имеет следующий вид:

Yt=322.76+102.24*X2t+23.57*X3t/X4t+4.38*(X5t+X6t)*Х20+417.43*X12t+

(118.53) (31.49) (10.12) (2.12) (132.78)

+528.82*X13t+2211.76*X15t+152.11*X16t, t=1…121

(129.84) (417.33) (36.70)

.

Рассмотрим экономический смысл значимых регрессоров и их влияние на цену предложения квартиры.

1. Х2 - удобство положения увеличивает цену на 102.24 тыс. руб.

Является одним из наиболее значимых факторов, что в точности соответствует объективным критериям рынка жилья.

Действительно, квартира, имеющая более удобное и выгодное расположение, всегда имеет большую стоимость, чем аналогичная квартира, не обладающая эти качеством.

2. (Х5+Х6)*Х20 – при увеличении общей площади квартиры (не относящейся к 121, полнометражной и элитной сериям) на 1 кв. метр, её цена предложения возрастает на 4.38 тыс. руб.

С точки зрения экономического смысла метраж квартиры является главным фактором формирования её стоимости. Но цена 1 квадратного метра жилой площади, найденная в модели (4.38 тыс. руб.), весьма занижена по сравнению с реальной. Тем не менее, это не противоречит логике.

Низкая цена 1 кв. метра объясняется тем, что метраж здесь – простая количественная оценка, не учитывающая важных особенностей квартиры, например, удобства её расположения.

К тому же, модель содержит константу С=322.76, которая не зависит от различных характеристик квартиры и всегда включается в её стоимость. Величину константы можно интерпретировать как основу продажной цены любой трёхкомнатной квартиры. Сам факт того, что квартира трёхкомнатная, дает представление об её возможных размерах. Метраж конкретизирует эти представления. Поэтому С можно рассматривать как характеристику размера квартиры. А т.к. значение константы достаточно велико (322.76), это объясняет малую стоимость 1 кв. метра жилой площади в полученном уравнении.

Введенный регрессор Х20 исключает влияние фактора метражности в таких квартирных сериях, как 121, полнометражная и элитная. Принадлежность квартиры к этим сериям уже определяет ряд её важнейших свойств, в том числе фиксирует метраж (чаще всего у квартир одной серии значение жилой площади одинаково), определяет основную часть стоимости квартиры.

Поэтому непосредственный фактор метража (Х5+Х6) учитывается только при определении цены на квартиры серий, отличных от перечисленных.

Т.о. в формировании цены на одни квартиры фактор метражности может иметь определяющее значение (при этом коэффициент максимален). В других же случаях метражность не является единственным ведущим фактором и основная доля цены определяется иными факторами.

3. Х12 – принадлежность квартиры к 121 серии увеличивает её цену на 417.43 тыс. руб.

Это объясняется тем, что квартиры указанной серии располагаются в домах-новостройках, обладающих удачной планировкой, раздельным санузлом, лифтом, мусоропроводом, большими лоджиями, встроенным отоплением и прочими удобствами. К тому же, этот фактор определяет часть стоимости квартиры, обусловленную её метражом.

4. Х13 – полнометражная серия квартиры увеличивает её цену на 528.82 тыс. руб.

Квартиры этой серии имеют такие положительные характеристики как высокие потолки, удобство планировки и большая площадь. К тому же фактор полнометражности квартиры берет на себя нагрузку по части стоимости, обусловленной метражом.

5. Х15 – элитная серия квартиры имеет самую большую значимость среди коэффициентов полученной модели. Принадлежность квартиры к элитному типу жилья увеличивает её продажную стоимость на 2211.76 тыс. руб.

Это связано с тем, что элитные дома наиболее благоустроенны, комфортабельны и являются самыми новыми. Большинство элитных квартир относится к рынку первичного жилья, но и на вторичном рынке они постепенно появляются. Их число невелико по сравнению с давно построенными домами, но они имеют ряд особенностей, существенно влияющими на облик рынка вторичного жилья Металлургического района, и, следовательно, на его построенную модель.

Стоимость 1 кв. метра элитного жилья существенно выше стоимости 1 кв. метра квартиры другой серии. К тому же, квартиры этой серии обладают очень большой площадью, стоимость которой и отражает полученный коэффициент.

6. Х16 – каждый балкон увеличивает цену продажи квартиры на 152.11 тыс. руб.

Несомненно, этот показатель положительно влияет на стоимость квартиры. Но с точки зрения объективного состояния рынка жилья, его значение сильно завышено, т.к. стоимость 1 кв. метра балкона не может быть больше стоимости 1 кв. метра жилой площади.

Тем не менее, коэффициент значим и включается в модель.

7. Х3/Х4 – увеличение соотношения этажности дома и этажа квартиры на единицу увеличивает цену на 23.57 тыс. руб.

Построенная модель показывает, что цена квартиры линейно зависит от регрессора Х3/Х4. Это означает, что с уменьшением этажа квартиры её цена увеличивается, т.е. самые дорогие квартиры располагаются на начальных этажах. Т.о. наибольшую цену продажи имеют квартиры первого этажа, наименьшую – последнего.

Этот вывод противоречит распространенному мнению, что наименьшую стоимость имеют квартиры первого и последнего этажей дома, а наибольшую – квартиры, занимающие средние этажи. Согласно этому соображению, график зависимости цены квартиры от соотношения этажности дома и этажа квартиры (Х3/Х4) должен иметь следующий схематичный вид:

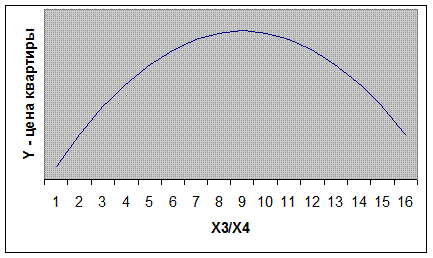
Рис. 7.1 Вид графика квадратичной зависимости цены от соотношения этажности дома и этажа квартиры.

Здесь величина Х3/Х4 изменяется от 1 до 16, т.к. 16 - это максимальная величина этажности, встречающаяся в анализируемой статистической выборке.

Т.о. зависимость цены квартиры от фактора Х3/Х4 должна быть квадратичной, а коэффициент при этом регрессоре – отрицательным.

Чтобы проверить эту гипотезу, строится новая модель 1.4. Она получается с помощью замены в модели 1.3 регрессора Х3/Х4 на регрессор (Х3/Х4)^2.

Таблица 7.1 Результаты оценки параметров модели 1.4.

Для сравнения качества моделей 1.3 и 1.4 ниже приведена аналогичная таблица для исходной модели 1.3.

Таблица 7.2 Результаты оценки параметров модели 1.3.

Сопоставляя оценки этих двух моделей, можно сделать следующие выводы:

1. Коэффициент при регрессоре Х3/Х4 в модели 1.3 значим

(Prob.= 0.0217), а коэффициент при регрессоре (Х3/Х4)^2 незначим

(Prob.= 0.0750).

2. Значения простого и скорректированного коэффициентов детерминации в модели 1.3 больше, чем в модели 1.4.

Т.о. приведение регрессора Х3/Х4 к квадратичной форме ухудшает качество модели, поэтому оно нецелесообразно.

Исходя из изложенного выше, можно сделать вывод, что цена предложения квартиры линейно зависит от соотношения этажности дома и этажа квартиры. График, схематично описывающий эту зависимость, представлен на рисунке 7.2.

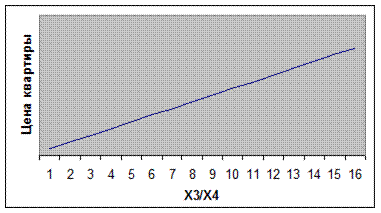
Рис. 7.2. Вид графика линейной зависимости цены от соотношения этажности дома и этажа квартиры.

Цена максимальна при наибольшей высоте дома и наименьшем этаже квартиры. Этот фактор актуален для высотных домов, где наиболее ценятся начальные этажи.

Максимальную цену продажи имеют квартиры первого этажа. Причиной может являться тот факт, что часто такие квартиры продаются под магазины, что и увеличивает их цену.

Недостатками построенной модели являются большие значения стандартных ошибок и неабсолютная точность прогноза (6.42 %). Это объясняется неточностью публикуемых в объявлениях данных и завышением реальной оценочной цены квартиры с расчетом на возможный торг. В оценке цены квартиры очень силен субъективный фактор. Часто квартиры, расположенные в одном доме и имеющие примерно одинаковые характеристики, оцениваются хозяевами с разницей в несколько десятков, а иногда и сотню тысяч рублей.

Тем не менее, модель является значимой и соответствующей ряду тестов, определяющих её качество.

Заключение

В ходе проведенной работы было построено три регрессионные модели, описывающие зависимость продажной цены квартиры от ряда факторов, - линейная, полулогарифмическая и логарифмическая. Вследствие проведенного тестирования и анализа из трёх построенных моделей была выбрана наиболее точно описывающая выборку и значимая – линейная модель.

Особенностью конечной модели оказалось то, что на цену предложения квартиры положительно влияют следующие факторы:

1. Удобство положения дома.

2. Соотношения этажности дома и этажа квартиры.

3. Общая площадь квартиры.

4. Принадлежность квартиры к 121 серии.

5. Принадлежность квартиры к полнометражной серии.

6. Принадлежность квартиры к элитной серии.

7. Количество балконов.

Построенная модель обладает несколькими интересными особенностями.

Во-первых, величина общей площади влияет на цену квартир, не принадлежащих 121, полнометражной и элитной сериям. А для квартир перечисленных серий сама серийность является фактором, в числе прочих характеристик определяющим метражность, а значит и стоимость жилой площади. Тем самым, цена квартиры зависит от её серии.

Во-вторых, между продажной ценой квартиры и соотношением этажности дома и номера этажа квартиры существует прямая линейная зависимость. Т.о. наиболее высокую цену имеют квартиры первых этажей.

Построенная в ходе выполнения данной курсовой работы линейная регрессионная модель зависимости продажной цены квартиры от перечисленных факторов описывает текущее состояние вторичного рынка трёхкомнатных квартир Металлургического района г. Челябинска.

Она является результатом выполнения данной курсовой работы.

Список использованной литературы:

1. «Из рук в руки» 14 февраля 2005 г.

2. «Из рук в руки» 31 марта 2005 г.

3. «Из рук в руки» 11 апреля 2005 г

4. «Из рук в руки» 2 мая 2005 г.

5. «Тумба» 19 февраля 2005 г.

6. «Тумба» 9 апреля 2005 г.

7. «Тумба» 30 апреля 2005 г.

8. www.74dom.ru 10 марта 2005 г.

9. www.chelreal.ru 11 марта 2005 г.

10. В.Н. Павленко, А.М. Набиев, Е.А. Постников, М.А. Хрыкина. Практикум по эконометрике. - Челябинск, 2004 г.

11. И.И. Елисеева, С.В. Курышева, Т.В. Костеева. Эконометрика. – Москва, «Финансы и статистика», 2001г.

12. Наш дом – Металлургический район. – Челябинск, «Гаро», 1995.

13. С.А. Бородич. Эконометрика. – Минск, «Новое знание», 2001г.