На основе данных выданных преподавателем необходимо:
1. Определить параметры следующих уравнений регрессии:
а) линейного;
б) гиперболического;
в) степенного;
г) показательного (экспоненциального);
д) логарифмического;
е) параболического.
2. Оценить качество каждой модели взаимосвязи с помощью средней ошибки аппроксимации и показателя детерминации.
3. На основании результатов, полученных в пункте 2, выбрать уравнение регрессии, наилучшим образом описывающее взаимосвязь между фактором х
и результативным признаком у
.
4. По выбранной модели взаимосвязи сделать точечный прогноз для значения фактора равного 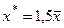 . .
| Вар №29
|
| X |
Y |
После сортировки: |
X |
Y |
| 10,83 |
5,21 |
1,03 |
0,62 |
| 12,84 |
5,55 |
1,20 |
1,30 |
| 7,11 |
4,69 |
1,31 |
1,30 |
| 1,31 |
1,30 |
1,34 |
0,97 |
| 10,45 |
5,19 |
3,55 |
3,20 |
| 3,55 |
3,20 |
4,13 |
2,24 |
| 5,35 |
4,50 |
4,23 |
2,98 |
| 4,23 |
2,98 |
4,32 |
3,26 |
| 5,34 |
3,47 |
4,67 |
2,89 |
| 4,32 |
3,26 |
5,27 |
3,66 |
| 6,09 |
3,68 |
5,34 |
3,47 |
| 11,66 |
5,69 |
5,35 |
4,50 |
| 7,06 |
3,43 |
5,44 |
2,87 |
| 6,21 |
3,93 |
5,66 |
3,50 |
| 6,97 |
3,57 |
6,09 |
3,68 |
| 5,44 |
2,87 |
6,21 |
3,93 |
| 5,66 |
3,50 |
6,24 |
4,42 |
| 13,94 |
6,53 |
6,97 |
3,57 |
| 1,03 |
0,62 |
7,06 |
3,43 |
| 4,13 |
2,24 |
7,11 |
4,69 |
| 13,30 |
5,83 |
7,26 |
4,69 |
| 1,20 |
1,30 |
8,56 |
4,87 |
| 8,56 |
4,87 |
10,45 |
5,19 |
| 1,34 |
0,97 |
10,83 |
5,21 |
| 7,26 |
4,69 |
11,66 |
5,69 |
| 6,24 |
4,42 |
11,70 |
5,29 |
| 4,67 |
2,89 |
12,05 |
5,49 |
| 12,05 |
5,49 |
12,84 |
5,55 |
| 5,27 |
3,66 |
13,30 |
5,83 |
| 11,70 |
5,29 |
13,94 |
6,53 |
1. Определение параметров уравнений регрессии
1.1. Линейное уравнение регрессии
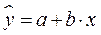
Система нормальных уравнений в общем виде:
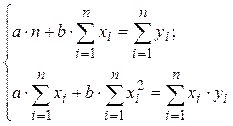
Система нормальных уравнений с вычисленными коэффициентами
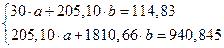
Решение системы:
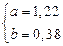
Построенное уравнение регрессии:
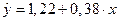
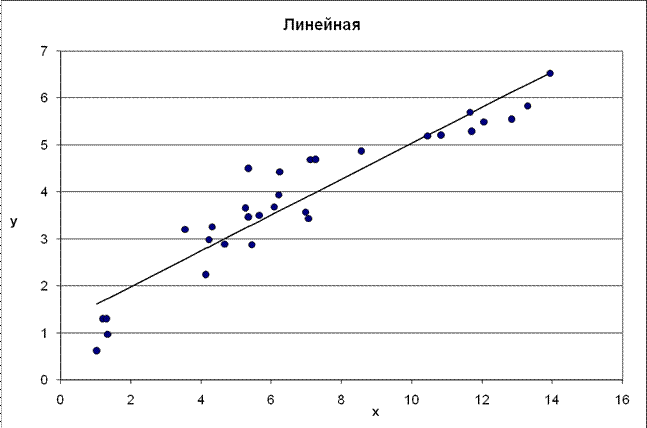
Рис. 1. График линейного уравнения регрессии
1.2. Гиперболическое уравнение регрессии
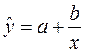
Система нормальных уравнений в общем виде:
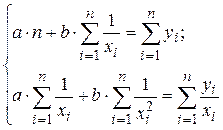
Система нормальных уравнений с вычисленными коэффициентами
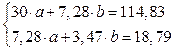
Решение системы:
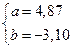
Построенное уравнение регрессии:
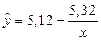
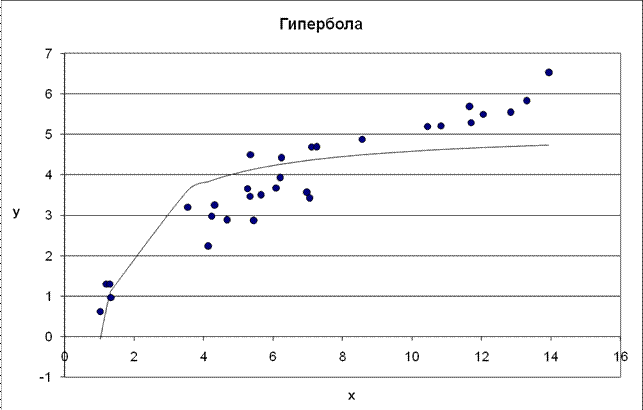
Рис. 2. График гиперболического уравнения регрессии
1.3. Степенное уравнение регрессии
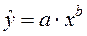
Система нормальных уравнений в общем виде:
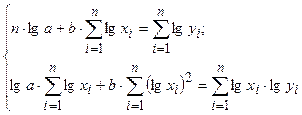
Система нормальных уравнений с вычисленными коэффициентами
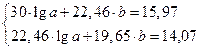
Решение системы:
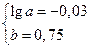
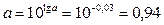
Построенное уравнение регрессии:
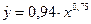
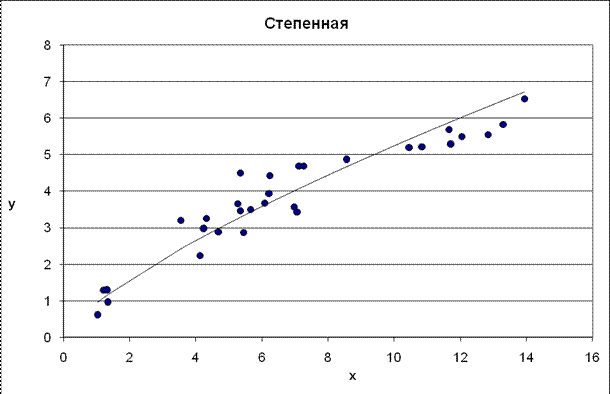
Рис. 3. График степенного уравнения регрессии
1.4. Показательное уравнение регрессии
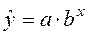
Система нормальных уравнений в общем виде:
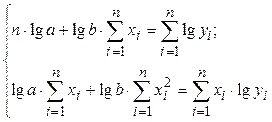
Система нормальных уравнений с вычисленными коэффициентами
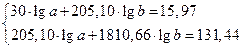
Решение системы:
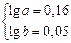
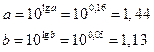 ; ;
Построенное уравнение регрессии:
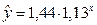
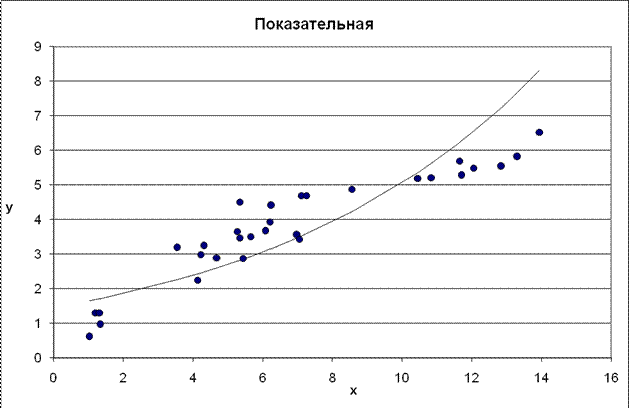
Рис. 4. График показательного уравнения регрессии
1.5. Логарифмическое уравнение регрессии
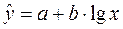
Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами
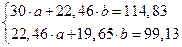
Решение системы:
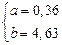
Построенное уравнение регрессии:
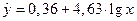
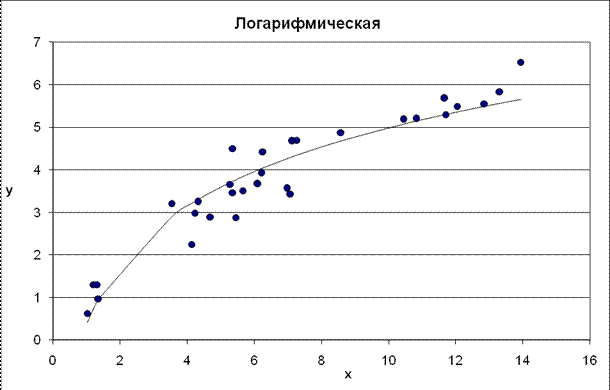
Рис. 5. График логарифмического уравнения регрессии
1.6. Параболическое уравнение регрессии
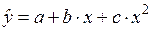
Система нормальных уравнений в общем виде:
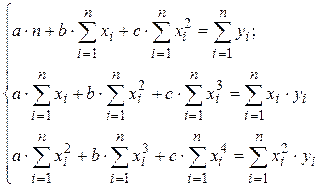
Система нормальных уравнений с вычисленными коэффициентами
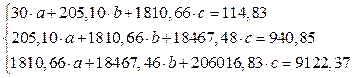
Решение системы:
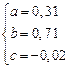
Построенное уравнение регрессии: 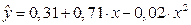
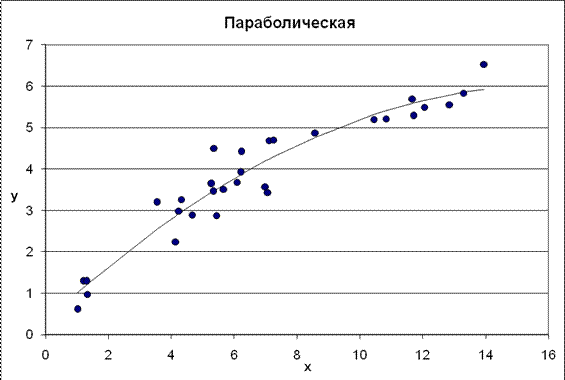
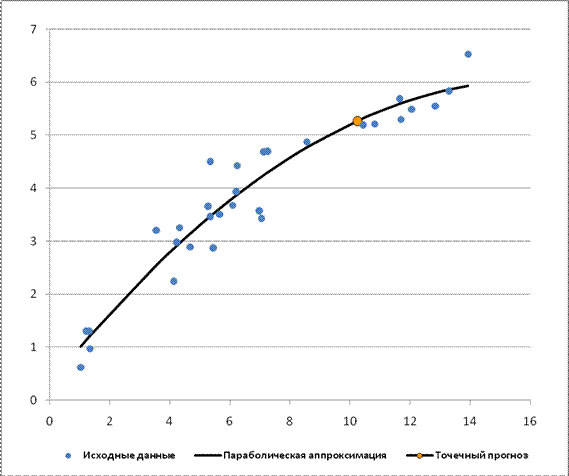
Рис. 6. График параболического уравнения регрессии
2. Оценка качества построенных уравнений регрессии
Средняя ошибка аппроксимации:
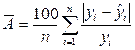
Показатель детерминации:
Реклама

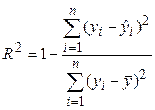
| Название
|
Уравнение
|
A
, %
|
R2
|
| Линейная |
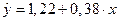
|
18,56 |
0,88 |
| Гипербола |
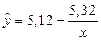
|
23,05 |
0,72 |
| Степенная |
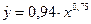
|
12,75 |
0,90 |
| Показательная |
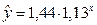
|
25,51 |
0,62 |
| Логарифмическая |
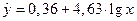
|
12,49 |
0,91 |
| Параболическая |
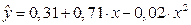
|
11,39 |
0,92 |
3. Выбор уравнения регрессии
На основании результатов, полученных в пункте 2, можно сделать вывод, что наиболее подходящей для описания взаимосвязи между результативной переменной у
и фактором х
является параболическая функция, поскольку эта функции имеет наиболее близкое к единице значение показателя детерминации и наименьшую ошибку аппроксимации.
4. Построение точечного прогноза
Среднее значение фактора
 . .
Значение фактора, для которого строится точечный прогноз (на основании задания)
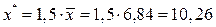 . .
Точечный прогноз состоит в подстановке значения фактора х
* в выбранное для описания взаимосвязи уравнение:
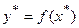 . .
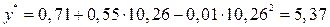
Министерство образования и науки российской федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Российский государственный торгово-экономический университет
Тульский филиал
(ТФ ГОУ ВПО РГТЭУ)
КОНТРОЛЬНАЯ РАБОТА
По дисциплине «Эконометрика»
Вариант № 29
Выполнила: Проверил:
Студентка 3 курса Якушин
На базе СПО Дмитрий Иванович
специальности «Финансы и кредит» к.т.н., доц.,
Захарова Ю.В.
Тула 2010 год
|