| Содержание
Введение
§1. Определение линейного оператора. Примеры
§2. Непрерывные линейные операторы в нормированном пространстве. Ограниченность и норма линейного оператора
§3. Обратный оператор. Спектр оператора и резольвента
§4. Оператор умножения на непрерывную функцию
§5. Оператор интегрирования
§6. Оператор дифференцирования
§7. Оператор сдвига
Заключение
Введение
Наиболее доступными для изучения среде операторов, действующих в линейных нормированных пространствах, являются линейные операторы. Они представляют собой достаточно важный класс операторов, так как среди них можно найти операторы алгебры и анализа.
Целью дипломной работы является показать некоторые из линейных операторов, исследовать их на непрерывность и ограниченность, найти норму ограниченного оператора, а также спектр оператора и его резольвенту.
В первом и втором параграфах приведены основные сведения теории операторов: определение линейного оператора, непрерывности и ограниченности линейного оператора, его нормы. Рассмотрены некоторые примеры.
В третьем параграфе даны определения обратного оператора, спектра оператора и его резольвенты. Рассмотрены примеры.
В четвертом параграфе исследуется оператор умножения на непрерывную функцию: Ах(t) = g(t)x(t).
В пятом параграфе приведен пример оператора интегрирования Аf(t)=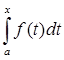 . .
В седьмом параграфе исследуется оператор сдвига Af(x) = f(x+a).
Показана линейность, непрерывность, ограниченность, найдена норма, точки спектра и резольвента всех трех операторов.
В шестом параграфе исследуется оператор дифференцирования Дf(x)=f/
(x), в пространстве дифференцируемых функции D[
a
,
b
]
. Показана его линейность. Доказано, что Д не является непрерывным оператором, а также как из неограниченности оператора следует его разрывность.
§1. Определение линейного оператора. Примеры
Определение 1.
Пусть Ex
и Ey
[1]
– линейные пространства над полем комплексных (или действительных) чисел. Отображение А: Ex
® Ey
называется линейным оператором
, если для любых элементов х1
и х2
пространства Ex
и любого комплексного (действительного) числа 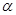 выполняются следующие равенства [2]
: выполняются следующие равенства [2]
:
1. А(х1
+х2
) = Ах1
+ Ах2
;
Реклама

2. А(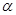 х) = х) = 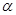 А(х); А(х);
Примеры линейных операторов:
1) Пусть Е = Е1
– линейное топологическое пространство. Оператор А задан формулой:
Ax = x для всех x 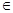 Е. Е.
Такой оператор, переводящий каждый элемент пространства в себя является линейным и называется единичным оператором.
2) Рассмотрим D[
a
,
b
]
– пространство дифференцируемых функций, оператор дифференцирования Д в пространстве D[
a
,
b
]
задан формулой:
Дf(x) = f/
(x).
Где f(x) 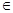 D[a, b]
, f/
(x) D[a, b]
, f/
(x) 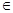 C[a, b]
. C[a, b]
.
Оператор Д определен не на всем пространстве C[
a
,
b
]
, а лишь на множестве функций имеющих непрерывную производную. Его линейность, очевидно, следует из свойств производной.
3) Рассмотрим пространство С[-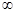 , + , +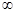 ]
– пространство непрерывных и ограниченных функций, оператор А сдвигает функцию на const a: ]
– пространство непрерывных и ограниченных функций, оператор А сдвигает функцию на const a:
Аf(x) = f(x+a).
Проверим линейность оператора А:
1) А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g).
Исходя из определения суммы функции, аксиома аддитивности выполняется.
2) A(kf(x)) = kf(x+a) = kA(f(x)).
Верна аксиома однородности.
Можно сделать вывод, что А – линейный оператор.
4) Пусть 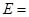 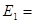 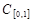 (пространство непрерывных функций на отрезке [0,1], и дано отображение (пространство непрерывных функций на отрезке [0,1], и дано отображение 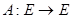 1
, заданное формулой: 1
, заданное формулой:
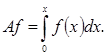
Так как интеграл с переменным верхним пределом от непрерывной функции является функцией дифференцируемой, а, следовательно, непрерывной, то 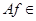 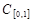 . В силу линейности определенного интеграла данное отображение является линейным оператором. . В силу линейности определенного интеграла данное отображение является линейным оператором.
§2. Непрерывные линейные операторы в нормированном
пространстве. Ограниченность и норма линейного оператора
Пусть 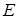 , , 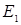 – нормированные пространства. – нормированные пространства.
Определение 2 .
Оператор А: Е 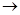 Е1
называется непрерывным
в точке Е1
называется непрерывным
в точке 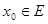 , если какова бы не была последовательность xn , если какова бы не была последовательность xn
 x0
, А(xn
) сходится к А(x0
). То есть, при p (xn
, x0
) x0
, А(xn
) сходится к А(x0
). То есть, при p (xn
, x0
)  0, p (А(xn
), А(x0
)) 0, p (А(xn
), А(x0
))  0. 0.
Известно и другое (равносильное) определение непрерывности линейного оператора.
Определение 3.
Отображение А называется непрерывным
в точке x0
, если какова бы не была окрестность[3]
U точки y0
= А (x0
) можно указать окрестность V точки x0
такую, что А(V)  U. U.
Иначе 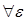 >0 >0  >0, что как только p (x, x0
) < >0, что как только p (x, x0
) < 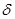 , p (f(x), f(x0
)) < , p (f(x), f(x0
)) < 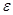 . .
Теорема 1.
Если линейный оператор непрерывен в точке х0
= 0, то он непрерывен и в любой другой точке этого пространства.
Доказательство.
Линейный оператор А непрерывен в точке х0
=0 тогда и только тогда, когда 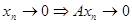 . Пусть оператор А непрерывен в точке х0
=0. Возьмем последовательность точек пространства хn
®х1
, тогда хn
–х1
®0, отсюда А(хn
–х1
)®А(0)=0, т. е. А(хn
–х1
)®0. . Пусть оператор А непрерывен в точке х0
=0. Возьмем последовательность точек пространства хn
®х1
, тогда хn
–х1
®0, отсюда А(хn
–х1
)®А(0)=0, т. е. А(хn
–х1
)®0.
Реклама

Так как А – это линейный оператор, то А(хn
–х1
)®Ахn
–Ах0
, а тогда
Ахn
-Ах0
® 0, или Ахn
®Ах0
.
Таким образом, из того, что линейный оператор А непрерывен в точке х0
=0, следует непрерывность в любой другой точке пространства.
т. д-на.
Пример.
Пусть задано отображение F(y) = y(1) пространства С[0, 1]
в R. Проверим, является ли это отображение непрерывным.
Решение.
Пусть y(x) – произвольный элемент пространства С[0, 1]
и yn
(x) – произвольная сходящаяся к нему последовательность. Это означает:
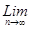 p (yn
, y) = p (yn
, y) = 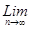 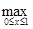 |yn
(x)- y(x))| = 0. |yn
(x)- y(x))| = 0.
Рассмотрим последовательность образов: F(yn
) = yn
(1).
Расстояние в R определено следующим образом:
p (F(yn
), F(y)) = |F(yn
) - F(y))| = | yn
(1) - y(1)| 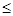 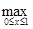 |yn
(x)- y(x))|=p(yn
,y), |yn
(x)- y(x))|=p(yn
,y),
то есть p (F(yn
), F(y)) 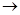 0. 0.
Таким образом, F непрерывно в любой точке пространства С[
a
,
b
]
, то есть непрерывно на всем пространстве.
С понятием непрерывности линейного оператора тесно связано понятие ограниченности.
Определение 4.
Линейный оператор А: Е 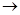 Е1
называется ограниченным
, если можно указать число K>0 такое, что Е1
называется ограниченным
, если можно указать число K>0 такое, что
||Аx|| 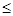 K||x||. (1) K||x||. (1)
Теорема 2.
Среди всех констант K, удовлетворяющих (1), имеется наименьшее.
Доказательство:
Пусть множество S – множество всех констант K, удовлетворяющих (1), будучи ограниченным снизу (числом 0), имеет нижнюю грань k. Достаточно показать, что k 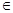 S. S.
По свойству нижней грани в S можно указать последовательность (kn
), сходящуюся к k. Так как kn
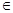 S, то выполняется неравенство: |А(x)| S, то выполняется неравенство: |А(x)| 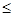 kn
||x||, (x kn
||x||, (x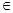 E). Переходя в этом неравенстве к пределу E). Переходя в этом неравенстве к пределу
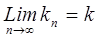
получаем |А(x)| 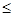 k||x||, где (x k||x||, где (x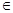 E), (k E), (k 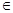 S). S).
т. д-на.
Определение 5.
Наименьшая из этих констант K, для которых выполняется неравенство (1), называется нормой
оператора А и обозначается ||A||[4]
.
||А|| 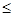 K, для K, для  K, подходящего для (1), то есть |А(x)| K, подходящего для (1), то есть |А(x)| 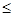 ||А||||x||, где ||А||||x||, где
||А|| = 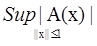  x x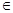 E. E.
Между ограниченностью и непрерывностью линейного оператора существует тесная связь, а именно справедлива следующая теорема.
Теорема 3.
Для того, чтобы линейный оператор А действующий из Ex
в Ey
был ограничен, необходимо и достаточно, чтобы оператор А был непрерывен.
Необходимость
:
Дано: А – ограничен;
Доказать: А – непрерывен;
Доказательство:
Используя теорему 1 достаточно доказать непрерывность А в нуле.
Дано, что ||Аx|| 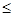 K||x||. K||x||.
Докажем, что А непрерывен в нуле, для этого должно выполняться 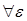 >0, >0, 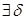 >0 что ||x||< >0 что ||x||< 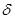 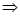 ||Ax|| < ||Ax|| < 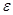 . .
Выберем 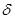 так, чтобы K*||x|| < так, чтобы K*||x|| < 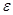 , ||x|| < , ||x|| < 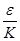 , (К>0), значит , (К>0), значит 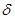 = = 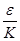 , тогда если ||x||< , тогда если ||x||< 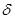 , то ||Аx|| , то ||Аx|| 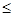 K||x|| < K K||x|| < K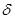 = = 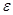
Непрерывность в нуле доказана, следовательно доказана непрерывность в 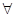 точке. точке.
Достаточность
:
Дано: А – непрерывен;
Доказать А – ограничен;
Доказательство:
Допустим, что А не ограничен. Это значит, что числу 1 найдется хотя бы один соответственный вектор x1
такой, что ||A x1
|| > 1|| x1
||.
Числу 2 найдется вектор x2
, что ||A x2
|| > 2|| x2
|| и т.д.
Числу n найдется вектор xn
, что ||A xn
|| > n|| xn
||.
Теперь рассмотрим последовательность векторов yn
= 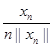 , где , где
||yn
|| = 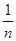 . .
Следовательно последовательность yn
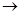 0 при n 0 при n  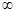 . .
Так как оператор А непрерывен в нуле, то Аyn
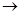 0, однако 0, однако
||Аyn
|| = ||A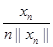 || = || = 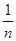 ||Axn
|| ||Axn
||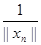 > n|| xn
|| > n|| xn
||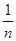 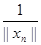 = 1, получаем противоречие с Аyn = 1, получаем противоречие с Аyn
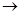 0, то есть А – ограничен 0, то есть А – ограничен
Для линейных операторов ограниченность и непрерывность оператора эквивалентны.
Примеры.
1) Покажем, что норма функционала[5]
F(y) = 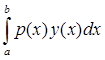 в C[
a
,
b
]
, где p(x) – непрерывная на [a,b] функция, равна в C[
a
,
b
]
, где p(x) – непрерывная на [a,b] функция, равна 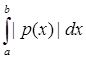 . .
По определению 5: ||F|| = 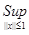 |F(x)| = |F(x)| = 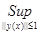 | |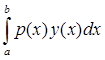 |. |.
|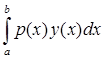 | | 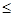 | |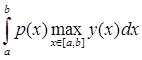 | = | | = | y(x)|| y(x)||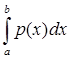 | | 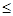 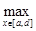 |y(x)|| |y(x)||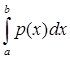 |; |;
||F|| = 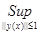 ( ( |y(x)|| |y(x)||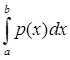 |) = |) = 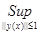 ||y(x)||| ||y(x)|||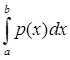 | = | | = |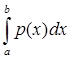 | | 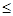 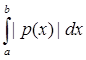 . .
Таким образом, норма F(y) = 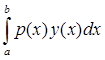 будет ||F|| = будет ||F|| = 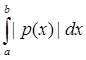 ; ;
2) Найдем норму функционала, определенного на C[0, 2], где p(x)=(x-1)
F(y) = 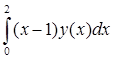 . .
По выше доказанному ||F|| = 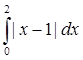 = 1. = 1.
§3.
Обратный оператор. Спектр оператора и резольвента
Пусть 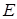 , , 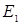 – нормированные пространства, – нормированные пространства, 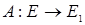 – линейный оператор, DA
- область определения оператора,
а RA
– область значений. – линейный оператор, DA
- область определения оператора,
а RA
– область значений.
Определение 6.
Оператор А называется обратимым
, если для любого элемента у, принадлежащего RA
, уравнение Ах=у имеет единственное решение.
Если оператор А обратим, то каждому элементу у, принадлежащему RA
, можно поставить в соответствие единственный элемент х, принадлежащий DA
и являющийся решением уравнения Ах=у. Оператор, осуществляющий это соответствие, называется обратным оператором
к оператору А и обозначается А-1
.
Теорема 4.
Для того чтобы линейный оператор 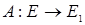 имел ограниченный обратный оператор необходимо и достаточно, чтобы выполнялось неравенство: имел ограниченный обратный оператор необходимо и достаточно, чтобы выполнялось неравенство:
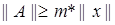 , (m>0). , (m>0).
Доказательство:
Достаточность.
Пусть выполняется данное неравенство. Тогда равенство Ax=0 возможно лишь тогда, когда x – нулевой вектор. Получим 0 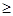 m*||x||, отсюда ||x|| m*||x||, отсюда ||x|| 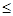 0, но так как норма не может быть <0, то x=0. А обращается в ноль лишь на нулевом векторе. Итак, А-1
существует. 0, но так как норма не может быть <0, то x=0. А обращается в ноль лишь на нулевом векторе. Итак, А-1
существует.
Докажем его ограниченность.
y=Ax.
x=A-1
y, норма ||A-1
y||=||x||, но ||x|| 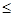 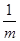 ||Ax||= ||Ax||=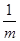 ||y||. ||y||.
Отсюда ||A-1
y|| 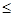 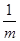 ||y||, то есть обратный оператор существует и он ограничен. ||y||, то есть обратный оператор существует и он ограничен.
Если за m возьмем наибольшую из возможных, то получим, что ||A-1
||=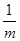 . .
Необходимость.
Пусть от А имеется ограниченный обратный А-1
на нормированном пространстве.
Итак, ||A-1
y|| 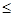 М||y||. М||y||.
Подставляем значение y и значение A-1
y,получим ||x|| 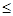 M||Ax|| (М всегда можно считать положительным числом). M||Ax|| (М всегда можно считать положительным числом).
Отсюда ||Ax|| 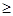 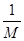 ||x||. ||x||.
Положим 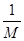 =m, получим ||Ax|| =m, получим ||Ax|| 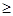 m||x||. m||x||.
т. д-на.
В теории операторов важную роль играет понятие спектра оператора. Рассмотрим это понятие сначала для конечномерного пространства.
Определение 7.
Пусть А – линейный оператор в n-мерном пространстве Еn
. Число λ называется собственным значением
оператора А, если уравнение Ах=λх имеет ненулевые решения. Совокупность всех собственных значений называется спектром
оператора А, а все остальные значения λ – регулярными.
Иначе говоря, λ есть регулярная точка, если оператор 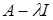 , где I – единичный оператор, обратим, При этом оператор (А – λI)-1
, как и всякий оператор в конечномерном пространстве, ограничен. Итак, в конечномерном пространстве существуют две возможности: , где I – единичный оператор, обратим, При этом оператор (А – λI)-1
, как и всякий оператор в конечномерном пространстве, ограничен. Итак, в конечномерном пространстве существуют две возможности:
1) уравнение Ах=λх имеет ненулевое решение, то есть λ является собственным значением для оператора А; оператор (А – λI)-1
при этом не существует;
2) существует ограниченный оператор (А – λI)-1
, то есть λ есть регулярная точка.
В бесконечном пространстве имеется еще и третья возможность, а именно:
3) оператор (А – λI)-1
существует, то есть уравнение Ах=λх имеет лишь нулевое решение, но этот оператор не ограничен.
Введем следующую терминологию. Число λ мы назовем регулярным
для оператора А, действующего в линейном нормированном пространстве Е, если оператор (А – λI)-1
, называемый резольвентой
оператора А, определен на всем пространстве Е и непрерывен.
Совокупность всех остальных значений λ называется спектром
оператора А. Спектру принадлежат все собственные значения оператора А, так как, если (А – λI)х=0 при некотором х≠0, то оператор (А – λI)-1
не существует. Их совокупность называется точечным спектром
. Остальная часть спектра, то есть совокупность тех λ, для которых (А – λI)-1
существует, но не непрерывен, называется непрерывным спектром.
Итак, каждое значение λ является для оператора А или регулярным, или собственным значением, или точкой непрерывного спектра. Возможность наличия у оператора непрерывного спектра – существенное отличие теории операторов в бесконечномерном пространстве от конечномерного случая.
Определение 8.
Оператор 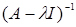 , где , где 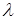 – регулярная точка оператора А, называется резольвентой[6]
оператора А и обозначается – регулярная точка оператора А, называется резольвентой[6]
оператора А и обозначается 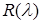 (или (или 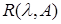 ). ).
Теорема 5.
Пусть 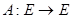 – линейный непрерывный оператор, – линейный непрерывный оператор, 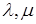 его регулярные числа. Тогда его регулярные числа. Тогда 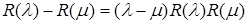 . .
Доказательство.
Умножим обе части равенства на 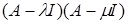 : : 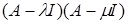 ( (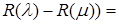 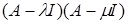 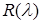 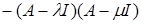 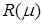 = =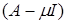 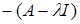 = =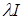 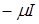 . С другой стороны получим . С другой стороны получим 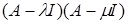 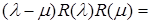 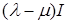 . Так как числа . Так как числа 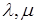 – регулярные для оператора А, то оператор – регулярные для оператора А, то оператор 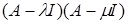 имеет обратный. Значит, из равенства имеет обратный. Значит, из равенства 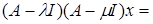 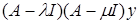 следует, что следует, что 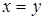 . Значит, утверждение теоремы верно. . Значит, утверждение теоремы верно.
т. д-на.
Примеры.
1) Рассмотрим в пространстве C[0,1]
оператор умножения на независимую переменную t: Ax = tx(t).
Уравнение Аx= x принимает в этом случае вид: x принимает в этом случае вид:
tx(t) -  x(t) = y(t), x(t) = y(t),
решение x(t) этого уравнения есть функция, тождественно ему удовлетворяющая.
Если  лежит вне отрезка [0, 1], то уравнение Аx= лежит вне отрезка [0, 1], то уравнение Аx=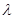 x имеет при любом y(t) единственное непрерывное решение: x имеет при любом y(t) единственное непрерывное решение:
x(t) = 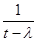 y(t), y(t),
откуда следует, что все такие значения параметра  являются регулярными, и резольвента есть оператор умножения на являются регулярными, и резольвента есть оператор умножения на 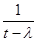 : :
R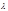 (y) =
(y) = 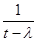 y(t). y(t).
Все значения параметра, принадлежащие отрезку[0, 1], являются точками спектра. В самом деле, пусть  0 0
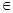 [0, 1]. Возьмем в качестве y(t) какую-нибудь функцию, не обращающуюся в нуль в точке [0, 1]. Возьмем в качестве y(t) какую-нибудь функцию, не обращающуюся в нуль в точке  0
, y( 0
, y( 0
) = a 0
) = a 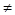 0. Для такой функции равенство (t - 0. Для такой функции равенство (t -  0
)x(t) = y(t), не может тождественно удовлетворяться ни при какой непрерывной на отрезке [0, 1] функции x(t), ибо в точке t = 0
)x(t) = y(t), не может тождественно удовлетворяться ни при какой непрерывной на отрезке [0, 1] функции x(t), ибо в точке t = 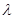 0
левая часть его равна нулю, в то время как правая отлична от нуля. Следовательно, при 0
левая часть его равна нулю, в то время как правая отлична от нуля. Следовательно, при 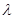 = = 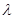 0
уравнение Аx= 0
уравнение Аx= x не имеет решения для произвольной правой части, что и доказывает принадлежность x не имеет решения для произвольной правой части, что и доказывает принадлежность  0
спектру оператора A. Вместе с тем ни одна точка спектра не является собственным значением, так как решение однородного уравнения (t - 0
спектру оператора A. Вместе с тем ни одна точка спектра не является собственным значением, так как решение однородного уравнения (t - 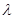 )x(t) = 0, )x(t) = 0,  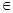 [0, 1], при любом t, отличном от [0, 1], при любом t, отличном от  , а следовательно, в силу непрерывности и при t = , а следовательно, в силу непрерывности и при t =  , обращается в нуль, т.е. тождественно равно нулю. , обращается в нуль, т.е. тождественно равно нулю.
2) Пусть оператор А действующий из Е 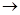 Е, задается матрицей А= Е, задается матрицей А=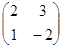 . .
Аx = 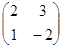 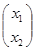 = = 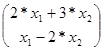 . .
Введем обозначения:
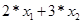 = y1 = y1
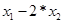 = y2 = y2
x1
, x2
, y1
, y2
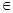 E; E;
A -  *I = *I = 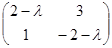 , найдем определитель A - , найдем определитель A -  *I: *I:
D(A -  *I) = *I) = 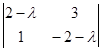 = (2- = (2- )*(-2- )*(-2- ) – 3 = ) – 3 =  2
– 7; 2
– 7;
Если определитель отличен от нуля, то есть если  не есть корень уравнения не есть корень уравнения 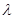 2
– 7 = 0, следовательно, все такие значения параметра 2
– 7 = 0, следовательно, все такие значения параметра  регулярные. регулярные.
Корни уравнения  2
– 7 = 0 образуют спектр: 2
– 7 = 0 образуют спектр:
 1
= 1
= 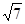 ; ;  2
= - 2
= -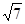 ; ;
 1
, 1
,  2
– собственные значения. 2
– собственные значения.
Найдем собственные векторы для собственных значений 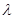 : :
при  = = 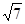 получаем: получаем:
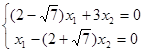
откуда x1
= (2+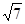 )x2
; 1-й собственный вектор: ((2+ )x2
; 1-й собственный вектор: ((2+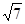 )x, x); )x, x);
при  = - = -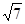 получаем: получаем:
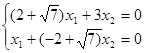
откуда x1
= (2 - 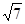 )x2
; 2-й собственный вектор: ((2 - )x2
; 2-й собственный вектор: ((2 - 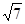 )x, x); )x, x);
§4.
Оператор умножения на непрерывную функцию
Рассмотрим пространство  непрерывных на отрезке непрерывных на отрезке 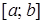 функций, и оператор А, заданный формулой: функций, и оператор А, заданный формулой:
Ах(t) = g(t) x(t).
g(t) - функция, непрерывная на [a, b]; a,b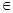 R. R.
Проверим является ли оператора А линейным, то есть, по определению 1, должны выполняться аксиомы аддитивности и однородности.
1) Аксиома аддитивности: A(f+g) = A(f) + A(g).
A(f+g) = (g(t)+f(t))x(t) = g(t)x(t)+f(t)x(t) = A(f) + A(g).
2) Аксиома однородности: A(k*f) = k*A(f).
A(k*f) = A(k*x(t)) = k*g(t)x(t) = kA(x(t)) = k*A(f).
По средствам арифметических операции над функциями, аксиомы аддитивность и однородность выполняются. Оператор А является линейным по определению.
3) Проверим, является ли А непрерывным, для этого воспользуемся определением непрерывности:
p (fn
(x), f0
(x))  0 0  p (A fn
(x), Af0
(x)) p (A fn
(x), Af0
(x)) 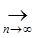 0. 0.
Оператор А, действует в пространстве C[
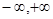 ]
, в котором расстояние между функциями определяется следующим образом:
]
, в котором расстояние между функциями определяется следующим образом:
p (fn
(x), f0
(x)) =  | fn
(x) - f0
(x)|. | fn
(x) - f0
(x)|.
Решение:
p (A xn
(t), Ax0
(t)) = 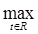 |Axn
(t) - Ax0
(t)| = |Axn
(t) - Ax0
(t)| = 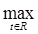 |xn
(t)g(t) - x0
(t)g(t)| |xn
(t)g(t) - x0
(t)g(t)| 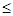 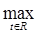 |g(t)| |g(t)| 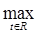 |xn
(t) - x0
(t)| = |xn
(t) - x0
(t)| = 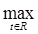 |g(t)|p (xn
(t), x0
(t)) |g(t)|p (xn
(t), x0
(t)) 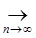 0. 0.
Итак, p (A xn
(t), Ax0
(t)) 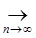 0. Следовательно по определению 2 оператор А является непрерывным, а по теореме 3 он ограничен. 0. Следовательно по определению 2 оператор А является непрерывным, а по теореме 3 он ограничен.
4) Оператор А ограниченный, следовательно у него можно найти норму.
По определению 5: ||A||=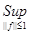 |A(f)|. |A(f)|.
Решение.
||A||=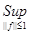 |A(f)|= |A(f)|=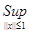 |g(t)x(t)|. |g(t)x(t)|.
|g(t)x(t)| 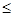 |g(t) |g(t) 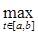 x(t)| = |g(t)| | x(t)| = |g(t)| |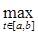 x(t)| x(t)| 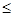 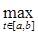 |x(t)| |g(t)|. |x(t)| |g(t)|.
||A||=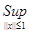 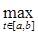 |x(t)| |g(t)| = |x(t)| |g(t)| = 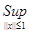 ||x(t)|| |g(t)| ||x(t)|| |g(t)| 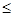 |g(t)|. |g(t)|.
Норма оператора А: ||A|| = |g(t)|.
5) Обратимость оператора А, его спектр и резольвента.
Возьмем произвольное число 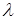 и составим оператор и составим оператор 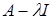 : :
(А-
l
I
) x
(t) = (g(t) –l ) х(t).
Чтобы найти обратный оператор, нужно решить уравнение 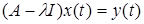 относительно функции относительно функции 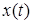 . Это возможно, если . Это возможно, если 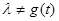 для любого для любого 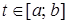 : :
 . .
Если число 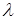 не является значение функции g(t), то знаменатель не обращается в 0, и функция не является значение функции g(t), то знаменатель не обращается в 0, и функция 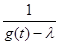 непрерывна на данном отрезке, а, значит, ограничена: существует такое число С, что на всем отрезке непрерывна на данном отрезке, а, значит, ограничена: существует такое число С, что на всем отрезке 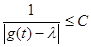 . Отсюда следует, что оператор . Отсюда следует, что оператор 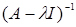 является ограниченным. является ограниченным.
Если же 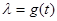 , то оператор , то оператор 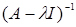 не существует. Следовательно, спектр оператора состоит из всех l = g(t). не существует. Следовательно, спектр оператора состоит из всех l = g(t).
Резольвента оператора имеет вид 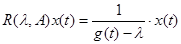 . .
Отметим, что точки спектра 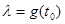 , , 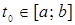 , не являются собственными числами. Не существует такой непрерывной функции , не являются собственными числами. Не существует такой непрерывной функции 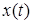 , для которой , для которой 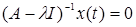 , или , или 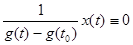 . Поэтому весь спектр данного оператора является непрерывным. . Поэтому весь спектр данного оператора является непрерывным.
Вывод:
Оператор A, заданный формулой: Ах(t) = g(t)x(t), где g(t) - функция, непрерывная на [a, b], a,b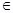 R: R:
1. линейный;
2. непрерывный;
3. ограниченный, с нормой ||A|| = |g(t)|;
4. обратим при 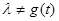 , для любого , для любого 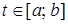 ; ;
5. спектр оператора состоит из всех l = g(t); спектр данного оператора является непрерывным;
6. резольвента имеет вид 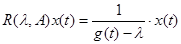 . .
§5.
Оператор интегрирования
Рассмотрим оператор интегрирования, действующий в пространстве непрерывных функций - C[
a
,
b
]
, определенных на отрезке [a,b], заданный следующим образом:
Аf(t) = 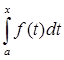 . .
f(t) – функция, непрерывная на [a, b],t 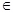 [a,x]; x [a,x]; x 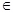 [a,b]; a,b [a,b]; a,b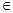 R; R;
Поскольку 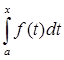 - интеграл с переменным верхним пределом, есть функция от верхнего предела – F(x), a - интеграл с переменным верхним пределом, есть функция от верхнего предела – F(x), a 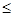 x x 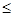 b; Следовательно можно утверждать, что А – оператор. b; Следовательно можно утверждать, что А – оператор.
Проверим оператор A на линейность. По определению 1:
1) Аксиома аддитивности: A(f+g) = A(f) + A(g).
A(f+g) = 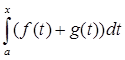 = = 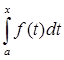 + + 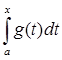 = A(f) + A(g). = A(f) + A(g).
2) Аксиома однородности: A(kf) = kA(f).
A(kf) = 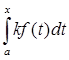 = k* = k*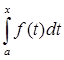 = kA(f). = kA(f).
Исходя из свойств интеграла:
1. интеграл от суммы, есть сумма интегралов;
2. вынесение const за знак интеграла.
Можно сделать вывод: оператор А является линейным.
3) Проверим, является ли А непрерывным, для этого воспользуемся определением непрерывности:
p (fn
(t), f0
(t)) 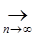 0 0 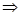 p (A fn
(t), Af0
(t)) p (A fn
(t), Af0
(t)) 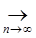 0. 0.
Оператор А, действует в пространстве C[
a
,
b
]
, в котором расстояние между функциями определяется следующим образом:
p (fn
(t), f0
(t)) = 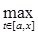 | fn
(t) - f0
(t)|. | fn
(t) - f0
(t)|.
Решение:
p (A fn
(t), Af0
(t)) = 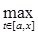 | |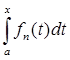 - - 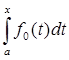 |. |.
|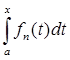 - - 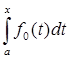 | = | | = |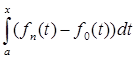 | | 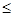  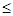 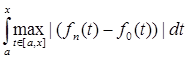 = p (fn
(t), f0
(t)) = p (fn
(t), f0
(t)) 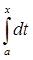 = p (fn
(t), f0
(t)) (x-a) = p (fn
(t), f0
(t)) (x-a) 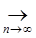 0 0
a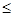 x x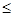 b. b.
Таким образом p (A fn
(t), Af0
(t)) 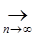 0. следовательно по определению 2 оператор А непрерывен. 0. следовательно по определению 2 оператор А непрерывен.
4) Непрерывный оператор является ограниченным (теорема 3):
|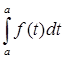 | | 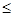 | |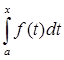 | | 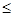 | |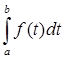 | |
|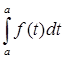 | = 0; | | = 0; |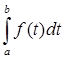 | = |b-a|. | = |b-a|.
0 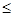 | |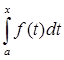 | | 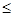 |b-a|. |b-a|.
5) Оператор А ограниченный, следовательно у него можно найти норму. Найдем норму оператора А (используя определение ||A||=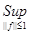 |A(f)|): |A(f)|):
||A|| = 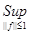 |A(f)| = |A(f)| = 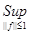 | |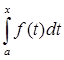 | | 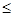 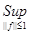 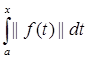 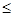 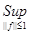 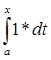 = (x-a); = (x-a);
a  x x  b; b;
Норма оператора А: ||A|| = (b-a);
6) Обратимость интегрального оператора и его спектр.
Возьмем пространство S = {f 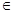 C[0,
b
]
/ f(0) = 0} с нормой ||f|| = C[0,
b
]
/ f(0) = 0} с нормой ||f|| = 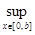 |f(x)|. |f(x)|.
В пространстве S рассмотрим оператор А:
Аf = 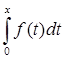
x 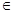 [0,b], t [0,b], t 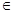 [0,x]; [0,x];
Найдем оператор обратный к (A - 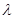 *I), *I), 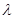 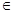 R; R;
(A - 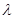 *I)*f = g *I)*f = g
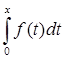 - - 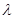 *f(x) = g(x) (1) *f(x) = g(x) (1)
Пусть функции f и g дифференцируемы;
Продифференцируем уравнение (1), получим:
f - 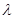 *f/
= g/
(2) *f/
= g/
(2)
Это уравнение (2) – дифференциальное неоднородное линейное уравнение. Решим это уравнение, используя метод Бернулли.
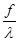 - f/
= - f/
= 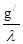
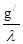 - - 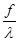 + f/
= 0 (3) + f/
= 0 (3)
Представим решение уравнения в виде: f(x) = U(x)*V(x), тогда уравнение (3) примет вид:
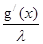 - - 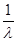 *U*V + U/
*V + U*V/
= 0 *U*V + U/
*V + U*V/
= 0
U/
*V + U*V/
- 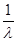 *U*V = - *U*V = - 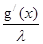
U/
*V + U*(V/
- 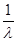 *V) = - *V) = - 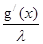 (4) (4)
Решаем однородное линейное уравнение:
V/
- 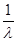 *V = 0 *V = 0
V/
= 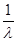 *V *V
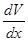 = = 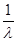 *V *V
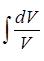 = = 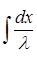
LnV = 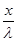 + c + c
V = 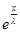 * *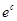 , пусть , пусть 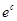 = с1 = с1
V = с1
*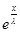
Подставим частное решение однородного уравнения в уравнение (4) при условии, что V/
- 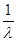 *V = 0. *V = 0.
Получим уравнение:
U/
* с1
*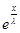 = - = - 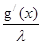
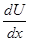 = - = -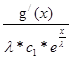
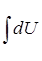 = - = - 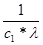 * *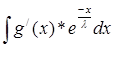
U = -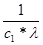 * *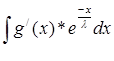
Подставим U и V в f(x) = U(x)*V(x) и получим:
f(x) = с1
*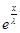 *(- *(-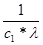 )* )*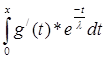
найдем интеграл Y = 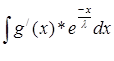 , интегрируем по частям: , интегрируем по частям:
dz = g/
(x)dx;
z = 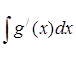 = g(x); = g(x);
j = 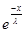 ; ;
dj = - 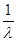 * *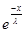 dx; dx;
Y = g(x)* 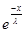 + + 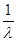 * *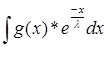
Подставим полученное значение в выражение f(x), которое примет вид:
f(x) = -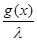 - - 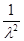 * *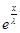 * *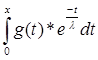 ; ;
Получим оператор В:
Bg = -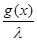 - - 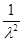 * *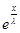 * *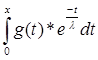 ; ;
x  [0,b], t [0,b], t  [0,x], g(x) [0,x], g(x) 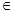 S, S, 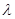 - произвольное число. - произвольное число.
Оператор В не существует, если 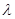 = 0; = 0;
Рассмотрим ограниченность оператора В для всех 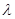 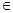 R, R, 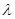 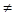 0; 0;
||Bg|| = ||f(x)|| = 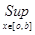 |f(x)| = |f(x)| = 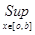 |- |-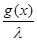 - - 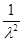 * *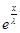 * *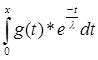 | | 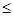 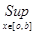 (| (|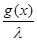 | + | | + |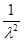 * *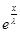 * *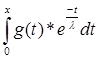 |) |)  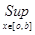 | |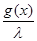 | + | + 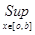 | |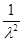 * *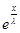 * *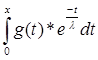 | | 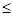 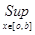 | |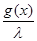 | + | + 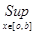 | |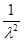 * * |* |*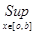 |g(x)* |g(x)* 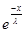 |*|x| |*|x| 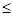 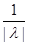 * *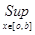 |g(x)| + |g(x)| + 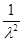 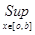 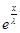 * *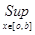 |g(x)|* |g(x)|* 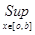 (| (|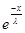 |*|x|) |*|x|) 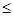 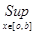 |g(x)|*( |g(x)|*( 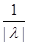 + + 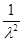 * *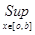 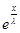 * *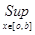 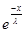 *b); *b);
При 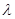 > 0 > 0
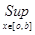 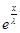 = = 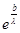 ; ;
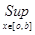 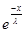 = 1; = 1;
При 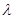 < 0 < 0
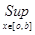 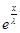 =1; =1;
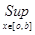 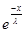 = = 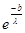 ; ;
Эти оба случая можно записать в общем виде: 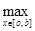 {1, {1,  }, тогда }, тогда
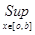 |g(x)|*( |g(x)|*( 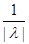 + + 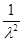 * *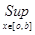 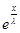 * *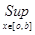 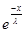 *b) *b) 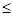 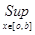 |g(x)|*( |g(x)|*( 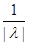 + + 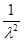 * *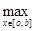 {1, {1, 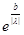 }*b) = ||g(x)||*( }*b) = ||g(x)||*( 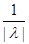 + + 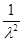 * *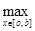 {1, {1, 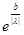 }*b); }*b);
Итак:
||Bg|| 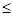 ||g(x)||*( ||g(x)||*( 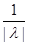 + + 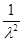 * *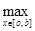 {1, {1, 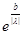 }*b); }*b);
То есть В – ограничен.
Осталось проверить, что В – оператор, обратный к (A - 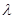 *I). *I).
Если это так, то произведение этих операторов равно единичному оператору или же (A - 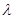 *I)*(Bg) = g(x). *I)*(Bg) = g(x).
Итак, нужно доказать, что
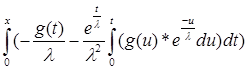 + g(x) + + g(x) + 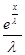 * *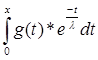 = g(x) = g(x)
или
-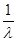 * *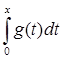 - - 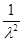  + + 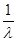 * *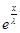 * *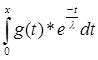 = 0; (*) = 0; (*)
Возьмем производную от левой части (*) и получим:
-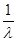 *g(x) - *g(x) - 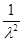 * *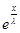 * *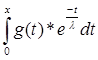 + + 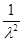 * *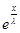 * *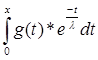 + + 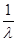 * * * *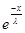 * g(x) = - * g(x) = -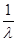 *g(x) + *g(x) + 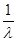 *g(x) - *g(x) - 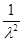 * *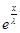 * *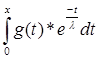 + + 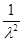 * *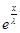 * *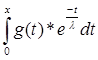 = 0; = 0;
Следовательно, выражение (*) = const. Но, так как при x=0 выражение (*) (точнее его левая часть) равно 0, то и const=0. Значит В – обратный оператор к (A - 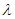 *I) в S. *I) в S.
Итак, мы получили ограниченный оператор В, обратный к (A - 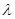 *I), который существует при *I), который существует при 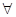 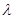 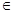 R, за исключением R, за исключением 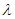 =0, то есть все возможные =0, то есть все возможные 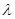 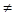 0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение 0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение 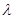 при которых В не существует, то есть при которых В не существует, то есть 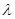 =0. =0.
Вывод:
Оператор интегрирования, действующий в пространстве непрерывных функций – C[
a
,
b
]
, определенных на отрезке [a,b], заданный следующим образом: Аf(t) = 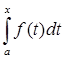 , где f(t) – функция, непрерывная на [a, b], t , где f(t) – функция, непрерывная на [a, b], t 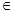 [a,x]; x [a,x]; x 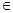 [a,b]; a,b [a,b]; a,b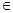 R: R:
1. линейный;
2. непрерывный;
3. ограниченный: 0 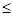 | |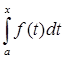 | | 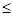 |b-a|; |b-a|;
4. норма A: ||A|| = (b-a);
5. резольвента оператора А: R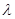 (A) = -
(A) = -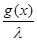 - - 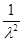 * *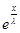 * *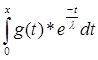 , где , где
x 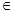 [0,b], t [0,b], t 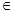 [0,x], g(x) [0,x], g(x) 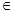 S, S = {f S, S = {f 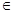 C[0,
b
]
/ f(0) = 0} с нормой ||f||= C[0,
b
]
/ f(0) = 0} с нормой ||f||=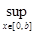 |f(x)|, g(x) = |f(x)|, g(x) = 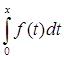 - -  *f(x), *f(x),  - произвольное число. - произвольное число.
6. Спектр оператора А: 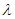 =0. =0.
§6.
Оператор дифференцирования.
Рассмотрим оператор дифференцирования Д действующий в пространстве дифференцируемых функций – D[
a
,
b
]
, заданный следующим образом:
Дf(x) = f/
(x);
Функция f(x) 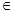 D[a, b]
, f/
(x) D[a, b]
, f/
(x) 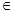 C[a, b]
; C[a, b]
;
Проверим оператор Д на линейность, по определению 1:
1) Аксиома аддитивности: Д(f+g) = Д(f) + Д(g).
Д(f+g) = (f+g)/
= f/
+ g/
= Д(f) + Д(g).
2) Аксиома однородности: Д(kf) = kД(f).
Д(kf) = (kf) /
= k(f)/
= kД(f).
Исходя из свойств производной:
1. производная от алгебраической суммы нескольких функций равна алгебраической сумме их производных;
2. постоянный множитель можно вынести за знак производной.
Можно утверждать, что Д – линейный оператор.
3) Для линейных операторов ограниченность и непрерывность оператора эквивалентны, это следует из теоремы 3.
3.1) Для начала покажем, что Д не является непрерывным оператором.
Задан оператор Дf(x) = f/
(x) подпространства E 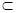 C[0, 2 C[0, 2 ]
, состоящего из непрерывно дифференцируемых функций, в пространство C[0, 2 ]
, состоящего из непрерывно дифференцируемых функций, в пространство C[0, 2 ]
. ]
.
Рассмотрим f0
(x) = 0  C[0, 2 C[0, 2 ]
и последовательность функций fn
(x)= ]
и последовательность функций fn
(x)=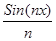 . .
В пространстве E  C[0, 2 C[0, 2 ]
: p (f0
, fn
) = ]
: p (f0
, fn
) = 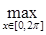 | |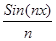 | = | = 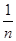  0, следовательно fn 0, следовательно fn
 f0
. f0
.
Рассмотрим последовательность образов: Д(fn
) = cos(nx).
Имеем:
p (Дfn
, Дf0
) = 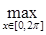 |cos(nx)| |cos(nx)| 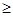 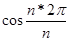 = 1. = 1.
Это означает, что Дfn
не может сходиться к Дf0
, то есть отображение Д терпит разрыв в f0
.
Поскольку оператор не является непрерывным, то, следовательно, он и не является ограниченным.
3.2) Теперь покажем, как из неограниченности оператора следует его разрывность.
Пусть оператор Д действует из C[0, 1]
в C[0, 1]
, оператор Дf(x) = f/
(x);
Этот оператор определен не на всем пространстве непрерывных функций, а лишь на подпространстве непрерывных функций, имеющих непрерывную производную.
В пространстве C[0, 1]
норма ||f|| = 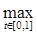 |f(t)|. |f(t)|.
Возьмем из C[0, 1]
последовательность fn
(t) = tn
. Она ограничена в C[0, 1]
: ||fn
(t)|| = 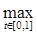 |tn
| = 1. |tn
| = 1.
Рассмотрим Д fn
(t): Д fn
(t) = f/
n
(t) = n tn-1
;
||f/
n
(t)|| = 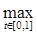 |n tn-1
| = n. |n tn-1
| = n.
В результате получили, что оператор Д переводит ограниченное множество в неограниченное, значит, по определению этот оператор не является ограниченным, а по теореме 3 не является непрерывным.
Вывод:
Оператор дифференцирования Д действующий в пространстве дифференцируемых функций – D[
a
,
b
]
, заданный следующим образом: Дf(x)=f/
(x), где функция f(x) 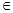 D[
a
,
b
]
, f/
(x) D[
a
,
b
]
, f/
(x) 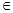 C[
a
,
b
]
: C[
a
,
b
]
:
1. линейный;
2. не ограниченный;
3. не непрерывный.
§7.
Оператор сдвига
Рассмотрим оператор А, действующий в пространстве непрерывных и ограниченных функций – C[
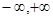 ]
, заданный следующим образом:
]
, заданный следующим образом:
Af(x) = f(x+a).
Функции f(x), f(x+a)  C[ C[
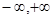 ]
, a
]
, a 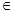 R, f(x+a) – непрерывная и ограниченная функция. R, f(x+a) – непрерывная и ограниченная функция.
Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы :
1) Аксиома аддитивности: А(f+g) = А(f) + А(g).
А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g).
По определению суммы функции, аксиома верна.
2) Аксиома однородности: А(kf) = kА(f).
A(k*f(x)) = k*f(x+a) = k*A(f(x)).
Аксиомы 1 и 2 верны, следовательно можно сделать вывод, что А – линейный оператор.
3) Проверим является ли оператор A непрерывным, для этого воспользуемся определением непрерывности:
p (fn
(x), f0
(x)) 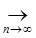 0 0 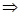 p (A fn
(x), Af0
(x)) p (A fn
(x), Af0
(x)) 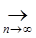 0. 0.
Оператор А действует в пространстве C[
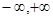 ]
, в котором расстояние между функциями определяется следующим образом:
]
, в котором расстояние между функциями определяется следующим образом:
p (fn
(x), f0
(x)) = 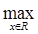 | fn
(x) - f0
(x)|. | fn
(x) - f0
(x)|.
Решение:
p (A fn
(x), Af0
(x)) = 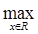 |Afn
(x) - Af0
(x)| = |Afn
(x) - Af0
(x)| = 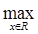 |fn
(x+a) - f0
(x+a)| = |fn
(x+a) - f0
(x+a)| = 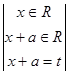 = = 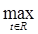 |fn
(t) - f0
(t)| = p (fn
(t), f0
(t)) |fn
(t) - f0
(t)| = p (fn
(t), f0
(t)) 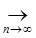 0. 0.
Таким образом p (A fn
(x), Af0
(x)) 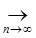 0. Следовательно оператор А непрерывен. 0. Следовательно оператор А непрерывен.
4) Непрерывный оператор является ограниченным, а у ограниченного оператора есть норма, найдем норму оператора А (по определению 5):
||A|| = 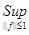 |Af| = |Af| = 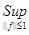 |f(x+a)| |f(x+a)| 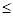 1. 1.
Поскольку ||f|| = 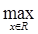 |f(x)| |f(x)| 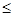 1. 1.
Норма А: ||A|| = 1.
5) Обратимость оператора А: Af(x) = f(x+a)
Такой оператор A сдвигает функцию на const a; обратный к A оператор будет сдвигать функцию на const (-a):
A-1
f(x) = f(x-a).
6) Спектр оператора А.
Рассмотрим пространство непрерывных функций – С[0, +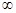 )
, имеющих конечный предел на )
, имеющих конечный предел на 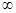 : :
Af(x) = f(x+a), a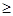 0. 0.
Вопрос о спектре оператора А касается разрешимости в пространствах С[0,
b
)
и С[а,+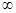 )
. )
.
Введем функцию V(x) = 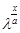 при | при |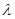 |<1, |<1, 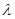 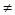 0, найдем ее предел: 0, найдем ее предел:
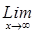 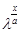 = 0 = 0
Следовательно рассмотренная функция входит в пространство С[0,+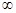 )
. )
.
Теперь рассмотрим V(x+a) = 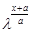 = = 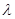 * *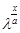 = = 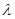 *V(x). *V(x).
Для 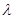 =0 подберем непрерывную функцию = 0 при x =0 подберем непрерывную функцию = 0 при x 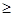 а и не равную 0 при x а и не равную 0 при x 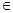 [0, a]. Для этой функции A(V(x)) = 0 то есть она является собственным вектором для числа 0; функция V(x) = с, так же удовлетворяет разностному отношению [0, a]. Для этой функции A(V(x)) = 0 то есть она является собственным вектором для числа 0; функция V(x) = с, так же удовлетворяет разностному отношению 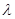 V(x) - V(x+a) = 0. Значит V(x) - V(x+a) = 0. Значит 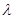 =1 =1 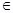 точечному спектру и в том и в другом пространстве. И все точки внутри единичного круга точечному спектру и в том и в другом пространстве. И все точки внутри единичного круга 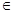 точечному спектру. точечному спектру.
Покажем, что остальные точки окружности 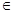 точечному спектру оператора А в пространстве С[0, + точечному спектру оператора А в пространстве С[0, +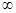 )
. )
.
Рассмотрим U(x) = 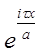 и число и число 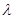 = = 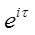 (| (|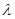 | = 1); | = 1);
U(x+a) = 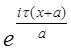 = = 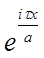 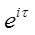 = = 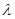 U(x); U(x);
U(x) = 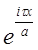 = Cos( = Cos(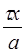 ) + iSin( ) + iSin(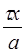 ), принадлежит пространству С[0,
b
)
так как мнимая и действительная части – функции ограниченные, но не принадлежат пространству С[
a
, + ), принадлежит пространству С[0,
b
)
так как мнимая и действительная части – функции ограниченные, но не принадлежат пространству С[
a
, +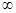 )
так как не имеют конечного предела на )
так как не имеют конечного предела на 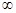 . .
Если точки лежат вне единичного круга, то они регулярные для оператора А в 2-х пространствах.
Покажем, что в пространстве С[0, +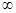 )
точки )
точки 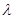 = = 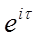 , , 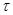 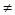 2 2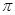 n не будут собственными числами. n не будут собственными числами.
Докажем это от противного: пусть найдется 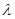 = = 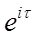 , , 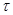 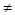 2 2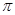 n – собственное число, тогда найдется функция f(x) n – собственное число, тогда найдется функция f(x) 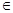 С[0, + С[0, +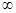 )
, что )
, что
f(x+a) = 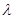 f(x). f(x).
Применим оператор А n раз: f(x+n*a) = 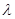 n
f(x), тогда n
f(x), тогда
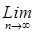 f(x+na) = f(x+na) = 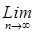 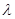 n
f(x), у левой части предел конечен; n
f(x), у левой части предел конечен;
правая часть предела не имеет, так как не имеет предела последовательность 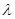 n
= n
= 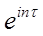 = Cos( = Cos(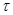 n) + iSin( n) + iSin(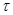 n). n).
Следовательно 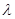 = = 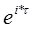 , , 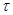 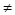 2 2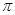 n собственным числом не является. n собственным числом не является.
Эти точки будут принадлежать спектру оператора А в пространстве С[0,+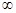 )
, так как спектр замкнутое множество и граница единичного круга должна принадлежать спектру оператора А в пространстве С[0, + )
, так как спектр замкнутое множество и граница единичного круга должна принадлежать спектру оператора А в пространстве С[0, +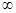 )
. )
.
Сделаем вывод:
При |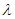 |>1 все точки регулярные
; |>1 все точки регулярные
;
При |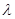 |<1 и |<1 и 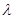 =1 – точки спектра; =1 – точки спектра;
При 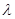 = = 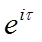 , , 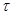 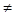 2 2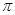 n – точки непрерывного спектра. n – точки непрерывного спектра.
Вывод:
Оператор А, действующий в пространстве непрерывных и ограниченных функций – C[
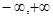 ]
, заданный следующим образом: Af(x) = f(x+a), где функции f(x), f(x+a)
]
, заданный следующим образом: Af(x) = f(x+a), где функции f(x), f(x+a) 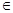 C[ C[
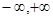 ]
, a
]
, a 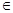 R, f(x+a) – непрерывная и ограниченная функция: R, f(x+a) – непрерывная и ограниченная функция:
1. линейный;
2. непрерывный и ограниченный;
3. норма А: ||A|| = 1;
4. A-1
f(x) = f(x-a);
5. Спектр оператора А:
· при |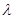 |<1 и |<1 и 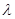 =1 – точки спектра; =1 – точки спектра;
· при 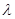 = = 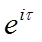 , , 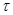 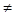 2 2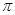 n – точки непрерывного спектра; n – точки непрерывного спектра;
· При |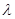 |>1 все точки регулярные. |>1 все точки регулярные.
Заключение
В ходе проделанной работы были рассмотрены основные определения теории линейных операторов: непрерывность, ограниченность, норма, спектр оператора и резольвента. Проведено исследование четыре оператора: оператор умножения на непрерывную функцию, оператор интегрирования, оператор дифференцирования, оператор сдвига. Можно сказать, что поставленные цели были достигнуты.
Список литературы
1. Колмогоров, А.Н. Элементы теории функций и функционального анализа [Текст]/ А.Н. Колмогоров, С.В. Фомин. – М.: Наука; Главная редакция физико–математической литературы, 1972.
2. Соболев, В.И. Лекции по дополнительным главам математического анализа [Текст] / В.И. Соболев. - М.: Наука, 1968.
3. Петров, В.А., Виленкин, Н.Я, Граев, М.И. Элементы функционального анализа в задачах [Текст]/ В.А. Петров, Н.Я. Виленкин, М.И. Граев под ред. О.А. Павлович. - М.: Просвещение, 1978.
4. Данфорд, Н. Линейные операторы. Общая теория [Текст]/ Н. Данфорд, Дж.Т. Шварц; под ред. А.Г. Костюченко; пер. с англ. Л.И. Головина, Б.С. Литягина. – М.: Издательство иностранной литературы, 1926.
[1]
Ex
и Ey
- линейные многообразия, то есть если x, y 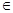 Ex
, то Ex
, то 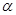 x + x + 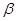 y y 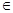 Ey
, при Ey
, при 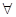 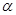 , , 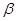 . .
Ex
– область определения А;
Ey
- область значения А;
[2]
Равенства 1 и 2 определяются как аксиомы аддитивности и однородности;
[3]
Шаром
в метрическом пространстве называется совокупность элементов
x
пространства, удовлетворяющих условию
p
(
xn
,
x
0
) < а.
Шар
D
(
x
0
,
a
).
Если
p
(
xn
,
x
0
) 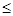 а, то
D
(
x
0
,
a
) – замкнутый шар. а, то
D
(
x
0
,
a
) – замкнутый шар.
Если
p
(
xn
,
x
0
) = а, то
S
(
x
0
,
a
) – сфера.
Всякий шар метрического пространства, содержащий точку
y
, называется окрестностью
точки
y
.
[4]
Свойства нормы оператора.
1) Если оператор 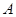 ограничен, ограничен, 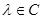 , то и оператор , то и оператор 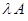 ограничен, причем ограничен, причем 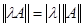 . .
2) Если операторы 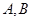 ограничены, то и оператор ограничены, то и оператор 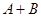 ограничен, причем ограничен, причем 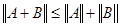 и и 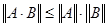 . .
[5]
Линейный функционал, есть частный случай линейного оператора. Именно, линейный функционал есть линейный оператор, переводящий пространство E в числовую прямую.
[6]
Резольвента – это функция комплексного переменного со значениями во множестве операторов, определенная на множестве регулярных чисел данного оператора.
|