ЧИСЕЛЬНЕ РОЗВ’ЯЗАННЯ ЗАДАЧ оптимального керування
1 Дискретизація задачі із закріпленим лівим і вільним правим кінцем. Необхідні умови оптимальності
Розглянемо неперервну задачу оптимального керування
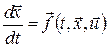 ,(1) ,(1)
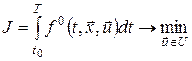 ,(2) ,(2)
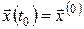 , , 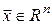 , , 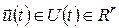 . (3) . (3)
Виконаємо дискретну апроксимацію даної задачі. Для цього розіб’ємо відрізок 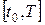 точками точками  , , 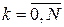 і будемо обчислювати значення цільового функціонала і закону руху тільки в точках розбиття: і будемо обчислювати значення цільового функціонала і закону руху тільки в точках розбиття: 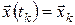 , , 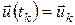 , , 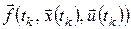 . Закон руху в цьому випадку можна записати у вигляді: . Закон руху в цьому випадку можна записати у вигляді:
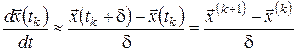 . .
Тепер дискретна задача оптимального керування, що апроксимує неперервну задачу (1) – (3), матиме вигляд:
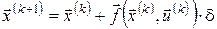 , , 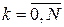 , (4) , (4)
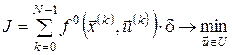 , (5) , (5)
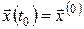 (6) (6)
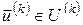 , , 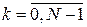 . (7) . (7)
Для пошуку оптимального розв’язку отриманої дискретної задачі може бути застосований метод множників Лагранжа. Функція Лагранжа має вигляд:
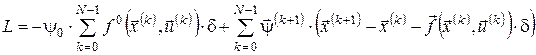 , ,
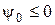 ,(8) ,(8)
де 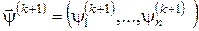 . .
Обмеження на керування введемо далі, під час реалізації чисельного методу. Відзначимо, що перед першим доданком стоїть знак «–», оскільки 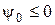 і якщо не додавати «–», то характер екстремуму початкової функції зміниться. і якщо не додавати «–», то характер екстремуму початкової функції зміниться.
Якщо 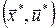 – локально-оптимальний процес для задачі (4) – (7), то існують такі нерівні одночасно нулю множники Лагранжа – локально-оптимальний процес для задачі (4) – (7), то існують такі нерівні одночасно нулю множники Лагранжа 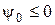 , , 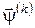 , , 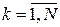 , , 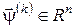 , що матимуть місце наступні умови: , що матимуть місце наступні умови:
1. 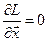 або або
 , ,
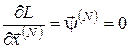 , ,
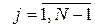 . (10) . (10)
2. 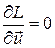 або або
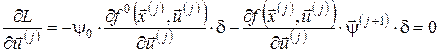 , ,
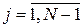 . (11) . (11)
Із (9) одержимо ітераційні співвідношення для спряжених змінних 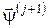 , а з (10) – співвідношення для , а з (10) – співвідношення для 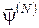 : :
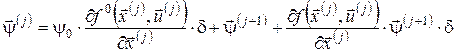
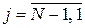 , (12) , (12)
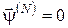 . (13) . (13)
Перепишемо співвідношення (12) у вигляді:
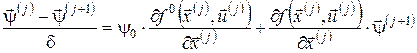 . .
Очевидно, що останнє співвідношення є аналогом спряженої системи для неперервних задач керування. Дійсно,
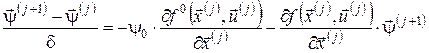 . .
Якщо 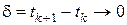 , то з останнього співвідношення одержимо , то з останнього співвідношення одержимо
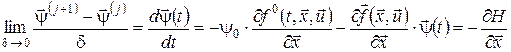 . .
Зі співвідношення (13) випливає, що 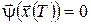 . .
Сформулюємо критерій оптимальності для задачі (4) – (7). Вважатимемо, що функції 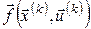 , , 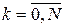 неперервно-диференційовані за змінними неперервно-диференційовані за змінними 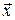 і опуклі за і опуклі за 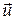 . Тоді для локально-оптимального процесу . Тоді для локально-оптимального процесу 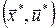 існують такі множники Лагранжа існують такі множники Лагранжа 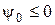 , , 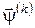 , , 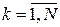 , , 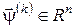 , не всі рівні нулю одночасно, що матимуть місце необхідні умови екстремуму: , не всі рівні нулю одночасно, що матимуть місце необхідні умови екстремуму:
1) умови стаціонарності в точці 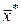 : :
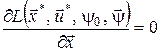 ; ;
2) 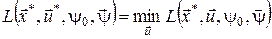 . (14) . (14)
Розпишемо (14), використовуючи вираз для функції Лагранжа:
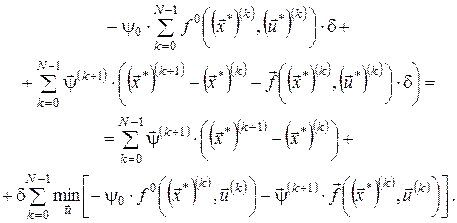
Перетворимо вираз під знаком мінімуму, переходячи до довільного 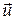 : :
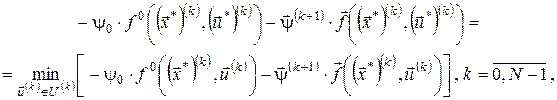
Або
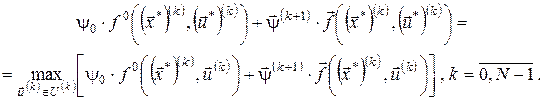
Якщо 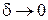 , то з останнього співвідношення одержимо , то з останнього співвідношення одержимо
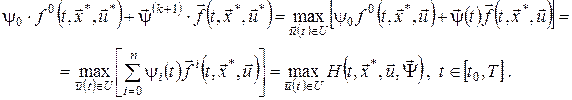
2 Ітераційний метод розв’язання дискретної задачі оптимального керування з двійним перерахуванням
Розглянемо ітераційний метод пошуку оптимального керування задачі (4) – (7). Суть методу полягає в тому, що на кожній ітерації обчислюються два вектори: 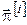 і і 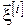 . Перший із них містить . Перший із них містить 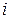 -е наближення для керувань у моменти часу -е наближення для керувань у моменти часу 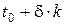 для системи (14), при для системи (14), при 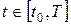 , а другий – , а другий – 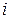 -е наближення для фазових станів системи в ці ж моменти часу. Отже, на кожній ітерації ми одержуємо процес -е наближення для фазових станів системи в ці ж моменти часу. Отже, на кожній ітерації ми одержуємо процес 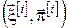 , що є , що є 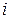 -м наближенням до шуканого оптимального процесу. -м наближенням до шуканого оптимального процесу.
Реклама

Контроль у методі подвійного перерахування полягає в повторному перерахуванні результатів задачі і порівнянні отриманих даних для різних значень кроку розбиття. У випадку розбіжності виконується корекція і обчислення повторюються.
Розглянемо алгоритм методу.
1. Задаємо крок розбиття 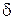 та точність обчислень та точність обчислень 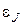 . .
2. Задаємо початкове наближення – припустимий набір керувань на кожному кроці – початкову стратегію керування:
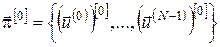 , , 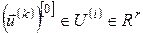 , , 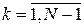 , ,
де 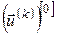 – наближення керування в момент – наближення керування в момент 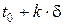 на ітерації на ітерації 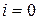 . .
3. За визначеною в п. 2 стратегією керування 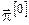 будуємо фазову траєкторію процесу будуємо фазову траєкторію процесу
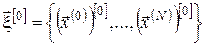 , , 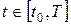 , , 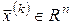
на початкової ітерації 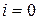 , використовуючи початкові умови і різницеві співвідношення, що апроксимують рівняння руху: , використовуючи початкові умови і різницеві співвідношення, що апроксимують рівняння руху:
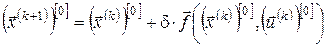
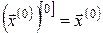 , , 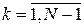 . .
4. Визначаємо початкове наближення 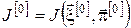 відповідно до (5). відповідно до (5).
5. Знаходимо спряжені змінні за формулами (12) – (13).
Визначаємо наступні наближення до оптимального керування  , ,
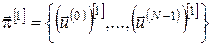
в момент 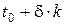 як розв’язки задачі (15) або (16): як розв’язки задачі (15) або (16):
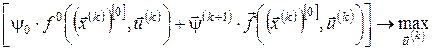 , , 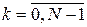 . .
7. Обчислюємо відповідну стратегії 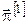 траєкторію траєкторію
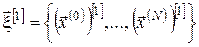
за формулами (4), (6):
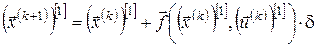 , , 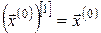 , , 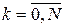 . .
8. Знаходимо наступне наближення цільового функціонала
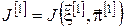 за формулою (5). за формулою (5).
9. Якщо 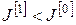 , то переходимо до п. 10, інакше вважаємо, що , то переходимо до п. 10, інакше вважаємо, що
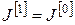 , , 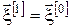 , , 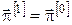 і переходимо до п. 13. і переходимо до п. 13.
10. Перевіряємо, чи виконується задана точність обчислень. Якщо
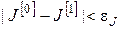 і і 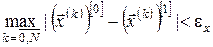 , ,
то переходимо до п. 13, інакше – до п. 11.
11. Позначаємо
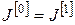 , , 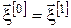 , , 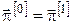 . .
12. Виконуємо наступний крок ітераційного методу – п. 5.
13. Позначаємо
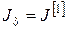 , , 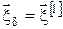 , , 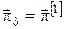 – розв’язок, отриманий із кроком розбиття – розв’язок, отриманий із кроком розбиття 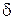 . .
1 Якщо крок 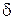 не ділився, то переходимо до п. 15, інакше – до п. 1 не ділився, то переходимо до п. 15, інакше – до п. 1
15. Ділимо крок
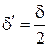 . Тоді . Тоді 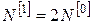 і переходимо до п. 2 при і переходимо до п. 2 при 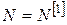 . .
1 Перевіряємо задану точність. Якщо
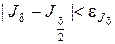 і і 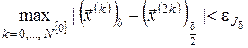 , ,
то переходимо до п. 18, інакше переходимо до п. 17.
17. Позначаємо
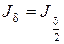 , , 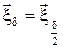 , , 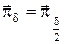 , , 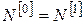 , і переходимо до п. 15 – наступного кроку подвійного перерахування. , і переходимо до п. 15 – наступного кроку подвійного перерахування.
18.  , , 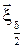 , , 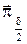 – розв’язок задачі. – розв’язок задачі.
Кінець алгоритму.
3. Оптимальне стохастичне керування: формулювання із зовнішнім інтегралом
Розглянемо відображення 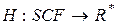 , що задане формулою , що задане формулою
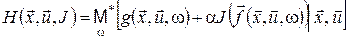 , (17) , (17)
за таких припущень:
параметр 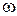 приймає значення з вимірного простору приймає значення з вимірного простору 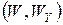 . Для будь-якої фіксованої пари . Для будь-якої фіксованої пари 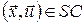 задана ймовірнісна міра задана ймовірнісна міра 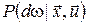 на просторі на просторі 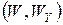 , а символ , а символ 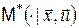 у формулі (12) означає зовнішній інтеграл відносно цієї міри. Отже, у формулі (12) означає зовнішній інтеграл відносно цієї міри. Отже,
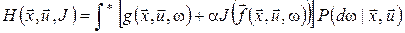 ; ;
функції 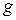 і і 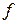 відображують множину відображують множину 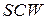 відповідно в множини відповідно в множини 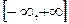 і і 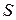 , тобто , тобто 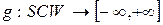 , , 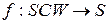 ; ;
скаляр 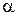 додатний. додатний.
Формули (1), (6) є окремими випадками відображення 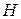 з (12). Очевидно, що відображення (1) для детермінованої задачі випливає з (12), якщо множина з (12). Очевидно, що відображення (1) для детермінованої задачі випливає з (12), якщо множина 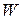 складається з єдиного елемента, а відображення (6) (для стохастичної задачі зі зліченним простором збурень) відповідає випадку, коли множина складається з єдиного елемента, а відображення (6) (для стохастичної задачі зі зліченним простором збурень) відповідає випадку, коли множина 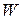 зліченна, а зліченна, а 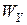 є є 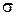 -алгеброю, складеною із всіх підмножин -алгеброю, складеною із всіх підмножин 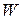 . .
Реклама

Очевидно, що відображення 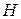 з (12) задовольняє припущенню монотонності. Якщо на множини з (12) задовольняє припущенню монотонності. Якщо на множини 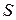 , , 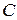 і функції і функції 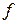 , , 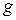 і і 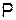 накласти вимоги вимірності, то витрати за накласти вимоги вимірності, то витрати за 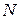 кроків кроків 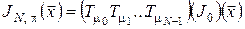 можна визначити в термінах звичайного інтегрування для будь-якої стратегії можна визначити в термінах звичайного інтегрування для будь-якої стратегії 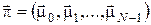 , для якої функції , для якої функції 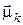 , , 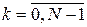 вимірні. вимірні.
Для початкового стану 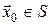 і стратегії і стратегії 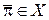 ймовірнісні міри ймовірнісні міри
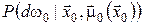 , ..., , ..., 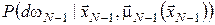
у сукупності із системою рівнянь
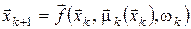 , , 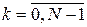 (18) (18)
визначають єдину міру 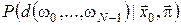 на на 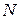 -кратному прямому добутку -кратному прямому добутку 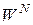 копій простору копій простору 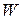 . У випадку, якщо . У випадку, якщо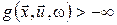 , , 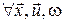 , і виконується одна з умов , і виконується одна з умов
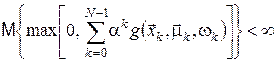 або або
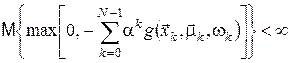 , ,
то функція витрат за 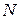 кроків, що відповідає вимірній стратегії кроків, що відповідає вимірній стратегії 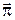 , приводиться до звичайного вигляду , приводиться до звичайного вигляду
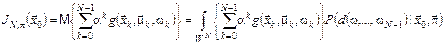 , ,
де стани 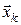 , , 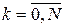 виражено як функції змінних виражено як функції змінних 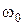 , ..., , ..., 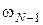 за допомогою рівнянь (13) та початкового стану за допомогою рівнянь (13) та початкового стану 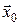 . .
Рекурентне співвідношення методу динамічного програмування для розв’язання багатоетапних задач оптимального стохастичного керування зі скінченним горизонтом можна записати так:
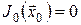 , , 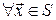 , ,
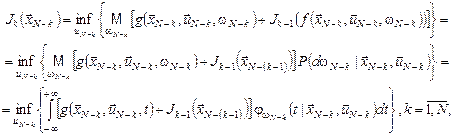
де 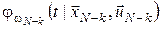 – щільність розподілу величини – щільність розподілу величини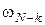 . .
4 Оптимальне стохастичне керування:мультиплікативний функціонал витрат
Розглянемо відображення 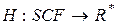 , що задане формулою , що задане формулою
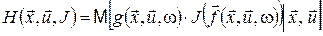 , (19) , (19)
за припущення, що параметр 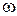 приймає значення зі зліченної множини приймає значення зі зліченної множини 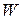 відповідно до заданого розподілу ймовірностей, що залежать від стану відповідно до заданого розподілу ймовірностей, що залежать від стану 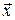 і керування і керування 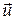 . Вважатимемо також, що . Вважатимемо також, що 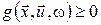 , , 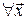 , , 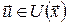 , , 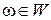 . Тоді відображення . Тоді відображення 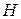 з формули (14) задовольняє припущенню монотонності. з формули (14) задовольняє припущенню монотонності.
Якщо 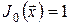 , , 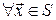 , то задача оптимального керування з мультиплікативним функціоналом витрат і скінченним горизонтом , то задача оптимального керування з мультиплікативним функціоналом витрат і скінченним горизонтом 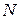 матиме такий вигляд: матиме такий вигляд:
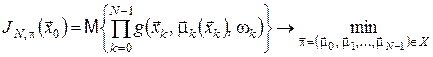 , (20) , (20)
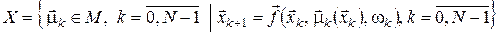 . (21) . (21)
а відповідна задача з нескінченним горизонтом:
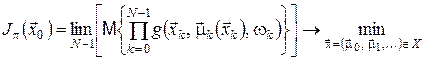 , (22) , (22)
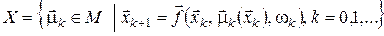 . (23) . (23)
Границя в (23) існує, якщо 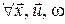 : : 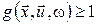 або або 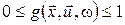 . .
Самостійний інтерес становить задача з експоненціальною функцією витрат
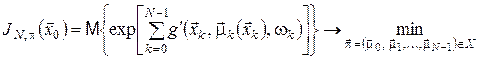 , ,
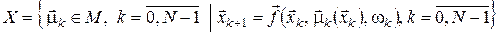 , ,
де 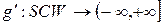 . .
Для розв’язання багатоетапних задач оптимального стохастичного керування з мультиплікативним функціоналом витрат використовується таке рекурентне співвідношення алгоритму динамічного програмування:
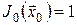 , , 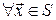 , ,
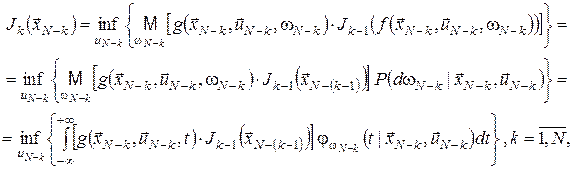
де 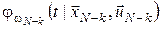 – щільність розподілу величини – щільність розподілу величини 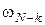 . .
5. Мінімаксне керування
Розглянемо задачу керування системою, у якій некерованими впливами є стратегії супротивника (або явища природи) 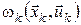 , , 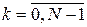 , що обираються залежно від поточного стану , що обираються залежно від поточного стану 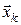 і керування і керування 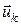 . Вважатимемо, що припустимі стратегії супротивника приймають значення із множини . Вважатимемо, що припустимі стратегії супротивника приймають значення із множини 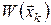 , , 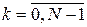 . Будемо обчислювати стратегію керування . Будемо обчислювати стратегію керування  , орієнтуючись на найгіршу поведінку супротивника. Розглянемо відображення , орієнтуючись на найгіршу поведінку супротивника. Розглянемо відображення 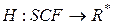 , задане формулою , задане формулою
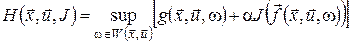 , ,
за таких припущень:
параметр 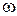 приймає значення з деякої множини приймає значення з деякої множини 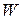 , а , а 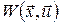 – непуста підмножина – непуста підмножина 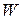 при будь-яких при будь-яких 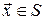 , , 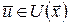 ; ;
функції 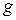 і і 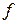 відображують множину відображують множину 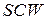 в множини в множини 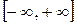 та та 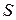 відповідно, тобто відповідно, тобто 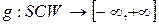 , , 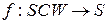 ; ;
скаляр 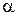 додатний. додатний.
За таких умов припущення про монотонність для відображення 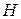 має місце. Якщо при цьому має місце. Якщо при цьому 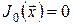 , , 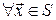 і і 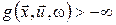 для всіх для всіх 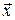 , , 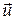 , , 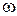 , то відповідну , то відповідну 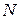 -крокову задачу мінімаксного керування можна сформулювати так: -крокову задачу мінімаксного керування можна сформулювати так:
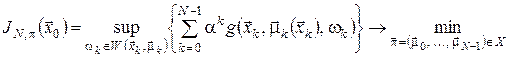 , (17) , (17)
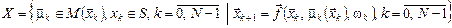 . (18) . (18)
Задача з нескінченним горизонтом формулюється аналогічно:
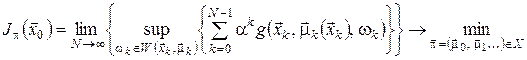 , (24) , (24)
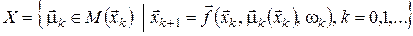 . (25) . (25)
Границя у співвідношенні (25) існує при виконанні будь-якої з умов:
· 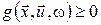 , , 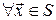 , , 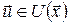 , , 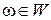 ; ;
· 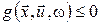 , , 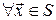 , , 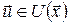 , , 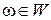 ; ;
· 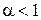 , , 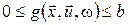 , , 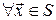 , , 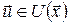 , , 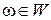 і деякого і деякого 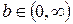 . .
Для розв’язання багатокрокових мінімаксних задач оптимального стохастичного керування рекурентне співвідношення алгоритму динамічного програмування використовується у такому вигляді:
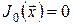 , , 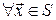 , ,
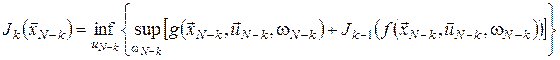 , ,
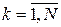 . .
|