Отзыв руководителя
на аттестационную работу «Оптимизация ректификации фракции в простых и сложных колоннах» бакалавра Смеляковой Анастасии Александровны
Аттестационная работа Смеляковой А.А. была направлена на поиск оптимальных схем разделения промышленной фракции легких углеводородов.
В результате работы Смеляковой Анастасией Александровной было освоено компьютерное моделирование химико-технологических процессов, изучены подходы к синтезу и оптимизации технологических схем разделения, методы моделирования парожидкостного равновесия. С использованием программного комплекса PRO II был проведен достаточно большой объем экспериментальных исследований.
В ходе выполнения квалификационной работы бакалавра Смелякова А.А. проявила себя как самостоятельный и инициативный исследователь. Следует отметить, что Смелякова А.А. принимала участие в 56 Научно-Техической Студенческой конференции МИТХТ, где заняла первое место.
Несомненно, работа заслуживает отличной оценки, а соискатель -присуждения степени бакалавра техники и технологии.Руководитель д-т.н., проф. Тимошенко А.В.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ТОНКОЙ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ ИМЕНИ М.В. Ломоносова
Кафедра Химии и Технологии Основного Органического Синтеза
Аттестационная работа по теме:
«Оптимизация ректификации фракции этан-пропен-пропан в простых и
сложных колоннах»
Руководители работы: д.т.н., проф.
аспирант
соискатель
А. В. Тимошенко
Л. В. Иванова
А. А. СмеляковаМосква 2004
Оглавление
ВВЕДЕНИЕ
ЛИТЕРАТУРНЫЙ ОБЗОР
Общие подходы к синтезу технологических схем разделения
Поливариантность организации технологического процесса разделения
4
Критерии оптимизации
5
Методы синтеза технологических схем разделения 7
Методы синтеза, основанные на эвристических правилах 8
Метод динамического программирования 9
Метод ветвей и границ10
Интегрально-гипотетический метод10
Эволюционный метод11
Информационно- энтропийный метод11
Разделение смеси пропен – пропан13
ПОСТАНОВКА ЗАДАЧИ
РАСЧЕТНАЯ ЧАСТЬ
Методы и алгоритмы исследования 23
Модели парожидкостного взаимодействия
Модель NRTL28
Модель Соав-Редлих-Квонг (SRK)28
Модель Пенг-Робинсон29
Выбор адекватной модели
30
Синтез схем ректификации для разделения смеси этан-пропен-пропан
32
Реклама

Разделение смеси по схемам из простых и сложных колонн
ВЫВОДЫ
СПИСОК ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЕ.
Введение
Процессы ректификации являются одними из самых энергоемких процессов химической технологии, и их эффективность часто определяет экономику производства в целом. В ряде случаев на разделение методом ректификации смесей органических продуктов затрачивается до 70% всей энергии, необходимой для их производства. Такие особенности производственных процессов как непрерывность и многотоннажность приводят к тому, что даже относительно невысокие снижение энергозатрат, повышение качества товарных фракций обеспечивают значительный экономический эффект для технологии в целом.
Поэтому синтез оптимальных технологических схем ректификационного разделения является одной из важных проблем в химической технологии. Сложность выбора оптимального технологического решения связана, с одной стороны, с высокой вариантностью схем разделения, а с другой, зависимостью структуры оптимальной схемы от исходного состава питания.
В данной работе для разделения смеси этан-пропен-пропан предлагается использовать схемы не только из простых двухсекционных колонн, но и комплексы с частично связанными тепловыми и материальными потоками. В ряде случаев применение сложных колонн позволяет снизить энергозатраты на разделение из-за приближения к термодинамической обратимости за счет структурных особенностей схем разделения.
Литературный обзор
Общие подходы к синтезу технологических схем разделения
Любую технологическую схему разделения можно представить как набор операторов разделения (ректификационных, экстракционных, абсорбционных и других колонн), определенным образом связанных друг с другом.
Задача синтеза оптимальной технологической схемы разделения в самом общем виде заключается в следующем: при известных составе и состоянии сырья, получаемого в результате химических реакций (т. е. в реакционной подсистеме), и заданных компонентах или фракциях, которые должны быть выделены, и их качестве необходимо выбрать: методы, которые могут быть применены на каждом этапе разделения, оптимальный набор разделительных операторов, оптимальную схему потоковых взаимосвязей между операторами и оптимальные параметры работы каждого оператора (оптимальные не по отдельным операторам, а для всей схемы разделения).
При разработке и проектировании можно поставить несколько задач: достигнуть минимальных энергетических затрат; достигнуть минимальных капитальных затрат; получить продукты необходимой степени чистоты; достигнуть максимального выхода целевых продуктов; выбрать наиболее устойчивые режимы работы аппаратов; достигнуть минимального сброса химических продуктов в окружающую среду. Решение всех этих задач одновременно, как правило, невыполнимо, так как наблюдаются конкурентные ситуации.
Реклама

Поливариантность организации технологического процесса разделения
Задача создания оптимальных схем разделения продуктов основного органического и нефтехимического синтеза является наиболее сложной. Сложность этой задачи определяется, прежде всего, поливариантностью выбора структуры технологической схемы. Если рассматривать только ректификационное разделение на чистые компоненты гомогенных зеотропных смесей, то число вариантов технологических схем может быть выражено следующим соотношением, предложенным С. В. Львовым [1]:
Z=[2(n-1)]!/[n!(n-1)!]
(1)
где n-число разделяемых компонентов.
Так, для разделения смеси, состоящей из 7 компонентов, возможно 132 различных варианта схемы ректификации, а для смеси из 10 компонентов - 4862. Сложность заключается
в том, что ни один из вариантов не может быть отброшен без тщательного исследования, так как любой из них может оказаться оптимальным в данной области переменных (состав исходной смеси, набор относительных летучестей компонентов, давления). Если же учесть число возможных типовых процессов разделения (S), то число вариантов технологических схем разделения значительно увеличится и может быть определено по следующей формуле:
Z=[2(n-1)]!/[n!(n-1)!] Sn-1
(2)
Критерии оптимизации
Поливариантность организации технологического процесса ректификации приводит к необходимости выбора такой целевой функции, с помощью которой можно было бы из допустимого множества вариантов однозначно оценивать конкретный вариант технологической схемы. К целевой функции предъявляются следующие требования: она должна быть численной и однозначной, а также универсальной, учитывающей адекватно как все затраты (стоимость) производства, так и все доходы (прибыль) при функционировании производства. Если целевая функция выбрана правильно, то ее максимальное или минимальное значение будет критерием оптимизации предложенного варианта технологии. В общем случае критерий оптимизации является функцией входных, выходных параметров и управляющих воздействий:
Ф=Ф(X1
,X2
,….Xn
,Y1
,Y2
,…Yn
,U1
,U2
,…Un
).
В качестве критериев оптимизации могут быть использованы различные экономические (себестоимость продукции, приведенные затраты, средняя прибыль и т.п.) и технологические (качество продуктов, разделительный потенциал и т. п.) критерии. Тот или иной критерий выбирается в зависимости от конкретной постановки задачи. Как правило, в качестве критерия оптимизации выбираются минимальные суммарные приведенные затраты на разделение для всей схемы в целом. Точный расчет приведенных затрат весьма трудоемок и требует расчета всего оборудования, входящего в технологическую схему разделения. Поэтому для предварительных оценок часто используют другие критерии, пропорциональные такого рода экономическим зависимостям, например, энергозатраты на разделение, так как они составляют большую часть от общих затрат (от 50 до 80 %). Для процесса ректификации энергозатраты определяются количеством тепла, подведенного в куб колонны и могут быть вычислены по формуле, предложенной в [2]:
Q = λΣDi
(Rmin
+l) -для i-ой колонны3)
Q = λΣDj
(Rmin
+l)-для j-ой схемы4)
λΣ-мольная теплота испарения жидкости, кипящей в кубе;
Di
-поток отбираемого дистиллята;
Rmin
-минимальное флегмовое число для 1-ой колонны.
Общий алгоритм выбора оптимальных технологических схем разделения основан на определении всего множества возможных схем разделения и последующей дискриминации их на основе выбранного критерия оптимизации.
Методы синтеза технологических схем разделения
Для проведения синтеза оптимальных технологических схем необходимо знать:
Физико - химические и химические свойства как чистых компонентов, так и всех смесей, составляющих данную многокомпонентную смесь. Наиболее важно знать температуры кипения компонентов и смесей, параметры фазового равновесия. Важна также химическая активность компонентов и их термическая стойкость в процессе разделения. Эти свойства позволяют выявить все термодинамические, химические и технологические ограничения, которые необходимо учитывать при синтезе технологических схем разделения.
Возможности различных методов разделения, области их использования, преимущества и недостатки.
Конструктивные особенности и возможности применения различных разделительных аппаратов, располагать классификацией таких аппаратов с описанием их основных характеристик.
Структуру технологических комплексов различного функционального действия, состоящих из ряда аппаратов и применяемых для разделения смесей, обладающих определенными специфическими свойствами. Эти комплексы позволяют преодолеть различные технологические ограничения, связанные с азеотропией, и получить продукты нужного состава. Комплексы могут состоять как из однотипных, так и разнотипных разделительных аппаратов.
Методы синтеза технологических схем разделения. Для применения методов, основанных на применении вычислительной техники, необходимо располагать математическими моделями как отдельных элементов и комплексов, так и системы в целом.
Методы оптимизации технологических схем разделения. Важно помнить, что оптимизацию технологической схемы необходимо начинать с оптимизации структуры диаграммы фазового равновесия разделяемой смеси, которая определяет термодинамические ограничения, связанные с азеотропией, и, следовательно, последовательность выделения компонентов или фракций. Далее могут быть использованы методы, базирующиеся на применении ЭВМ с использованием как глобальных критериев оптимизации (например, минимальные суммарные затраты), так и частных.
Методы синтеза, основанные на эвристических правилах
Эти методы заключаются в том, что в результате предварительного анализа действующих схем разделения формируется набор специальных правил, определяющих стратегию синтеза технологических схем [3,4]. Эти правила в целом отражают физико -химические закономерности протекающих процессов и могут быть формализованы для использования в процессе компьютерного моделирования.
Эвристические правила, преложенные различными авторами [5-10], сводятся к следующим:
Для зеотропных смесей при ректификационном методе разделения предпочтение отдается «прямой» последовательности разделения, то есть последовательности, в которой компоненты выделяется один за другим, начиная с компонента, обладающего наибольшей летучестью (имеющего наименьшую температуру кипения) в отдельных колоннах;
Компонент, содержание которого существенно превышает содержание всех остальных компонентов исходной смеси, должен отбираться первым в общей последовательности выделения компонентов или фракций компонентов;
Процесс разделения наиболее трудноразделимой пары компонентов или наиболее трудноразделимых фракций должен проводиться последним в общей последовательности разделения;
Наиболее «агрессивный» по воздействию на аппаратуру компонент должен выводиться из системы разделения в первую очередь;
Выбирается вариант схемы, в котором отношение количеств верхнего и нижнего продуктов в каждой колонне близко к единице;
Выбирается вариант схемы, в котором разделение осуществляется в порядке уменьшения различий в значениях относительных летучестей разделяемых ключевых компонентов;
Разделяющий агент необходимо выделять непосредственно после аппарата, в который он вводился.
Рассмотренные правила не охватывают все методы и случаи разделения. Они часто противоречат друг другу и отражают некоторые приближенные оценки, применимые, главным образом, к ректификации зеотропных смесей, состоящих из химически и термически стойких веществ.
Синтез технологических схем только на основе указанных эвристических правил не может быть осуществлен достаточно надежно. Некоторые из этих правил все же могут быть использованы в случае выделения отдельных фракций при разделении полиазеотропных смесей или на определенном этапе, когда разделяются уже зеотропные смеси. Такой этап возможен после выделения азеотропообразующих компонентов азеотропной подсистемы, после «удаления» азеотропов и выделения «агрессивных» компонентов, а также химически активных и термически нестойких веществ.
По мере накопления опыта разделения различных смесей список эвристических правил будет, безусловно, дополняться, а сами правила трансформироваться и в ряде случаев расширяться. Вместе с тем наиболее полно и точно можно осуществить синтез технологических схем разделения (TCP) на основе глубокого изучения физико - химических свойств разделяемых смесей и анализа термодинамических закономерностей.
Эвристики часто могут выступать в качестве ограничений на количество вариантов схем и позволяют свести задачу синтеза технологических схем к анализу значительно меньшего числа вариантов. При этом остаются трудности формализации отбора и генерирования эвристик.
Метод динамического программирования
В последнее время метод динамического программирования используется достаточно широко при синтезе технологических схем разделения. Идея метода впервые была предложена в работе [11] ив дальнейшем нашла свое развитие в работах [12 — 20]. Метод заключается в том, что оптимальные схемы синтезируют шаг за шагом, начиная с конца схемы. В данном случае технологическая схема рассматривается как многостадийный процесс разделения без обратных массовых и энергетических потоков. На начальном этапе рассматриваются колонны, в которых делятся бинарные смеси, а далее трех-, четырехкомпонентные и т.д., с учетом оптимального варианта на предыдущем этапе.
В каждом случае отыскивается оптимальная по отношению к принятому критерию технологическая схема разделения. Следовательно, принцип динамического программирования заключается в том, что любая часть оптимального пути является оптимальной. Это позволяет отыскать оптимальный путь поэтапно, используя на каждом этапе части этого пути, найденные на предыдущих этапах.
В конечном счете, можно вычислить значения критерия оптимальности для всех схем и выбрать оптимальный вариант. Достоинством данного метода синтеза оптимального варианта технологической схемы разделения многокомпонентных смесей является строгий математический подход и снижение размерности задачи, то есть сокращение расчетов всех возможных колонн при разделении многокомпонентной смеси. Однако учет рециркулируемых потоков существенно усложняет метод динамического программирования.
В связи с этим данный метод широко используется для синтеза технологических схем разделения идеальных и зеотропных смесей и весьма ограниченно для азеотропных.
Метод ветвей и границ
Является другим методом синтеза оптимальных технологических схем разделения, заключающийся генерировании дерева разделения исходной смеси и выделении на этом дереве методом «поиска глобину» оптимальной схемы разделения [21]. При этом используются соответствующие верхние и нижние оценки критерия оптимальности синтезируемой схемы разделения. Согласно методу ветвей и границ, расчет каждого варианта схемы производится от начала схемы к ее концу. Некоторое сокращение числа рассматриваемых вариантов различных элементов достигается путем отбрасывания «ветвей дерева» разделения, если значения критерия оптимальности для части схемы превосходит значение верхней оценки критерия оптимальности. За значение верхней оценки критерия оптимальности принимается его значение для наилучшей из рассчитанных к данному моменту схем разделения. Недостатком этого метода является то, что одни и те же разделительные элементы, входящие в разные схемы рассчитываются многократно, то есть в каждой схеме. Вместе с тем методом ветвей и границ дает достаточно надежные результаты (так же как и предыдущий метод) в случае разделения зеотропных смесей. Что касается азеотропных смесей, то использование его в предлагаемом виде невозможно.
Интегрально-гипотетический метод
Идея интегрального метода, который был впервые сформулирован в работе [22], предполагает синтез от некоторой всеобъемлющей глобальной схемы к конкретной оптимальной схеме разделения. Глобальная схема должна включать все возможные варианты. Таким образом, интегрально-гипотетический метод включает в себя два основных этапа:
синтез гипотетической обобщенной технологической схемы разделения;
анализ и оптимизация гипотетической обобщенной технологической схемы.
В целом решение задачи синтеза оптимальной схемы разделения с использованием этого метода сводится к решению задачи определения значений коэффициентов структурного разделения потоков и параметров элементов, входящих в исходную гипотетическую схему, которые обеспечивают оптимальное функционирование системы. Таким образом, задача синтеза в данном случае сводится к непрерывной оптимизации. Синтез оптимальных схем с использованием этого метода связан с большим объемом
вычислений. В этом случае постоянно приходится сталкиваться с локальным оптимумом, и трудно найти глобальный оптимум, соответствующий оптимальному варианту схемы.
Эволюционный метод
Основы данного метода для разделения одного потока питания на два продуктовых потока изложены в работах [23 - 26]. Метод заключается в том, что для исходной (принятой за основу) схемы разделения генерируются «соседние» схемы разделения с помощью определенных правил. Затем из них выбирается схема, по которой достигается разделение с меньшими затратами. И вновь генерируются «соседние» с выбранной схемой. Процесс прекращают, если найдена схема, характеризующаяся минимальными затратами [27]. Таким образом, общая стратегия эволюционного метода включает следующие этапы:
синтез какого-либо простейшего исходного варианта схемы;
определение в соответствии с некоторым коэффициентом эффективности наименее эффективного элемента в исходном варианте;
исключение этого элемента из схемы;
модификация данного элемента;
стыковка модифицированного элемента с оставшейся частью схемы и коррекция схемы;
определение коэффициента эффективности для вновь полученного варианта схемы. Указанные этапы итерационно повторяются до тех пор, пока не будет синтезирована оптимальная схема.
Недостатком этого метода является, как было указано ранее, значительная вероятность получения локальных оптимумов.
Информационно- энтропийный метод
Информационно-энтропийный подход, разработанный Майковым с сотрудниками [28, 29], можно рассматривать как разновидность эвристического метода, хотя он имеет определенное теоретическое обоснование. Согласно этому методу оптимальная схема разделения сопоставляется с наиболее эффективным процессом получения информации [30]. Следовательно, оптимальной системе соответствует максимум суммы информационных критериев разделительной способности всех разделительных аппаратов. Применение информационно - энтропийного подхода приводит к тем же результатам, что и при использовании эвристического правила дихотомии. Сравнение получаемых этим методом оптимальных вариантов технологических схем с вариантами, являющимися оптимальными
по приведенным затратам, показали значительное его расхождение.
Кроме рассмотренных применяется также рекурсивный метод и метод «случайных матриц». В ряде случаев можно использовать сочетание нескольких методов.
Разделение смеси пропен-пропан
Высокими энергетическими затратами характеризуется процесс разделения близкокипящей смеси нропен - пропан. В связи с этим для такой смеси все большее применение в промышленности находят новые технологические схемы со связанными материальными и тепловыми потоками и с тепловым насосом. Некоторые примеры таких схем рассматриваются ниже.
В работе [31] сообщается о применении теплового насоса на верхнем продукте для разделения смеси пропен - пропан. При компримировании паров верхнего продукта (пропена) до необходимого давления получается избыток тепла, который снимается в специальных концевых холодильниках водой или воздухом (рис.1).
Сравнение технологических показателей и затрат энергии при ректификации смеси пропен - пропан по разным схемам представлено в табл. 1.
Таблица 1. Показатели эффективности применения обычной и усовершенствованной схем ректификации смеси пропен-пропан
| Схема с тепловым
|
| Показатели процесса
|
насосом на верхнем
|
Общая схема
|
| продукте(рис 1,б)
|
| Давление, МПа
|
| в верху колонны до компрессора |
0.795 |
1,86 |
| после компрессора |
2,07 |
— |
| Температура,
° С
|
| верха колонны |
15 |
63 |
| на входе в кипятильник |
57 |
— |
| низа колонны |
24 |
55 |
| Тепло кипятильника, МВт |
7,6 |
7,6 |
| Расход пара, т/ч |
— |
11,8 |
| Расход электроэнергии на компрессор, МВт |
2,05 |
— |
| Расход охлаждающей воды, м3
/ч |
207 |
575 |
| Стоимость относительная общая |
65,4 |
100 |
| в том числе пара |
— |
85 |
| электроэнергии |
60,2 |
— |
| охлаждающей воды |
5,2 |
15 |
| Экономия энергии, % |
34,5 |
— |
Для пропеновых колонн, обеспечивающих получение пропена чистотой 99,5%(об.) и выше, рекомендуется усовершенствованна технологическая схема (рис. 1,6), при которой затраты на компримирование и охлаждение паров верхнего продукта меньше, так как только часть потока паров компримируется до 1,38 МПа и с температурой 35°С подается в кипятильник. Остальной поток паров дожимается до 1,86 МПа и охлаждается водой или воздухом.
Существенным преимуществом схем с тепловым насосом при разделении смеси пропен — пропан является значительное увеличение их относительных летучестей при пониженном давлении процесса, что приводит в итоге к снижению не только энергетических, но и капитальных затрат, требуемых для получения заданных высоких показателей разделения этой смеси.
В таблице 2 приведены усредненные сравнительные данные по параметрам и основным затратам для обычных и усовершенствованных схем с тепловым насосом при разделении пропен - пропан.
Таблица. 2. Показатели процесса разделения по схеме с тепловым насосом
| Показатели процесса и характеристика оборудования
|
Общая схема |
Схемы с тепловым насосом
|
| с обычным
|
с новым
|
| оборудованием
|
оборудованием
|
| Давление, МПа |
| в верху колонны |
1.9 |
0,86 |
0,86 |
| после компрессора |
— |
1,78 |
1,38 |
| температура, °С |
| в верху колонны |
46 |
14 |
14 |
| в низу колонны |
57 |
24 |
24 |
| Число реальных тарелок |
277 |
200 |
200 |
| Расстояние между тарелками, мм |
456 |
456 |
330 |
| Число колонн |
2 |
2 |
1 |
| Диаметр колонны, м |
5040 |
4420 |
4120 |
| Высота колонны, м |
77,4 |
61 |
79,5 |
| Флегмовое число |
14 |
10,6 |
10,6 |
| Тепло кипятильника, МВт |
29,6 |
29,3 |
29,3 |
| Разность температур в кипятильнике,°С |
55,5 |
19,5 |
5,5 |
| Поверхность кипятильника, м2
|
824 |
2420 |
2370 |
| Тепло конденсатора, МВт |
29,6 |
4,37 |
2,46 |
| Поверхность конденсатора, м2
|
5950 |
1070 |
583 |
| Расход охлаждающей воды, м /ч |
2320 |
483 |
253 |
| Мощность компрессора, МВт |
— |
4,32 |
2,42 |
| Расход пара, т/ч |
45,6* |
15,9** |
8,9** |
| Стоимость оборудования |
| (относительная) и энергетические |
| затраты, % |
| в том числе |
| колонны |
| насос орошения |
64,7 |
24,3 |
18,3 |
| теплообменник |
0,3 |
— |
— |
| компрессор и паровая турбина |
14,1
|
9,0 |
10,4 |
| пар |
— |
28,2 |
15,8 |
| охлаждающая вода |
17,8 |
9,7 |
5,4 |
| 3,1 |
0,6 |
0,3 |
* Пар низкого давления
** Пар высокого авления
Как видно из приведенных данных, экономия только на одной колонне перекрывает дополнительные затраты на компрессор. Колонна во всех случаях делается из двух самостоятельных частей. Энергетические затраты при применении теплового насоса уменьшаются примерно на 50%. Минимальные затраты соответствуют разности температур в кипятильнике 5°С при старых конструкциях, на практике обычно для разделения смеси пропен - пропан принимают 6°С.
В работе [32] приводят сравнительные данные по разделению смеси пропен — пропан в каскаде из двух последовательно работающих колонн по обычной схеме и в каскаде из четырех последовательно - параллельно работающих колонн по схеме со связанными тепловыми потоками (рис.2).
Рис. 2. Схема разделения смеси пропен — пропан в каскаде из двух последовательно работающих колонн (а) и в системе последовательно-параллельно работающих колонн со связанными тепловыми потоками (б): I — исходная смесь; П — пропен; III — пропан.
В таблице 3 приведены расходные показатели процесса и основные конструктивные размеры колонн.
| Таблица. 3. Показатели процесса разделения |
фракции пропен - пропан |
| Показатели процесса и характеристика
|
Обычная
|
Двухколонная система
|
| оборудования
|
схема
|
Колонна 1
|
Колонна 2
|
| Расход сырья, кмоль/ч |
600 |
291 |
309 |
| Содержание пропена в сырье, мольн. доли |
0,6 |
0,6 |
0,6 |
| Расход дистиллята, кмоль/ч |
351* |
170,3 |
180,7 |
| Содержание пропена в дистилляте, мольн. доли |
0,99 |
0,99 |
0,99 |
| Расход остатка, кмоль/ч |
249 |
120,7 |
128,7 |
| Содержание пропена в остатке, мольн. доли |
0,05 |
0,05 |
0,05 |
| Давление, МПа |
1,93 |
2,83 |
1,93 |
| Относительная летучесть смеси |
1,14-1,08 |
1,10-1,065 |
1,14-1,08 |
| Число тарелок |
200 |
200 |
180 |
| Номер тарелки питания (счет тарелок снизу) |
62 |
65 |
51 |
| Расстояние между тарелками, мм |
610 |
610 |
610 |
| Эффективность тарелок, % |
100 |
100 |
100 |
| Число колонн |
2 |
2 |
2 |
| Диаметр колонны, м |
3,2 |
2,85 |
2,29 |
| Флегмовое число |
15,9 |
23,5 |
16,6 |
| Поверхность кипятильника, м |
178 |
122 |
1030 |
| Температура в кипятильнике, °С |
55 |
77 |
55 |
| Поверхность конденсаторов, м |
1410 |
— |
752 |
| Температура орошения, °С |
47 |
67 |
47 |
| Расход пара, т/ч |
15,2 |
8,2 |
— |
| Давление пара, МПа |
5,0 |
5,0 |
— |
| Расход воды, м3
/ч |
1,39 |
— |
0,75 |
| Разность температур воды и паров продукта в |
| конденсаторе, °С |
6 |
— |
6 |
* 54,4 тыс.т. пропена в год
** R/Rmin
=1,15
Применение схемы последовательно - параллельно работающих колонн существенно сокращает расход охлаждающей воды и водяного пара. Кроме того, значительно снижается и стоимость оборудования — колонн и конденсаторов. Сравнение двухколонной системы из последовательно - параллельно работающих колонн и схемы с тепловым насосом для условий разделения этой же смеси показало значительное преимущество первой: экономическая эффективность от применения этой схемы увеличивается в 1,8 раза.
При разделении пропен - пропановой фракции примеси среднелетучих компонентов (ацетилена, пропандиена и метилацетилена) предлагается выделять в системе колонн со связанными тепловыми и материальными потоками (рис.3) [33]. В соответствии с приведенными схемами боковой отгон со средних тарелок (тарелок питания) с повышенным содержанием примесей подается на разделение в полную ректификационную колонну, где выделяется пропан (рис.3,а) или пропен (рис.3,6), в значительной степени свободный от примесей. Поток нижнего или верхнего продуктов второй колонны подается затем в первую колонну, и в среднее сечение концентрационной или отгонной частей колонны. В зависимости от целевого продукта(пропана и пропена ) примеси отбираются с верха или с низа второй колонны.
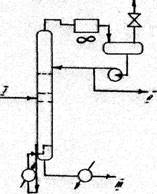
В работе [34] проанализированы три технологические схемы четкого разделения смеси пропен - пропан (рис.4). Каждая схема рассчитана на разделение 20 т/ч исходной фракции с получением 11,128 т/ч (90 тыс. т. в год) 95%-го пропена. Схема а соответствует обычной ректификации в простой колонне с кипятильником на паре низкого давления (0,1 МПа) с воздушным и водяным охлаждением пропана. Схема б соответствует ректификации в двух параллельно работающих колоннах со связанными тепловыми потоками - низкого и высокого давления с рекуперацией тепла пара из верха колонны высокого давления за счет его конденсации в кипятильнике колонны высокого давления. Схема в соответствует ректификации в колонне с тепловым насосом на верхнем продукте. Основные параметры технологического режима ректификационных колонн для рассматриваемых схем приведены в табл.4
 I I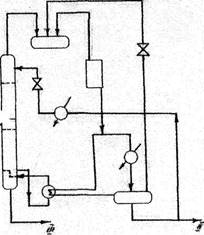 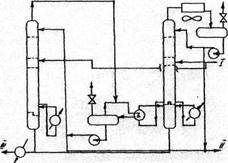
Рис. 4. Технологические схемы ректификации смеси пропей — пропан:
а -обычная; б -с тепловым насосом на верхнем продукте; в -с параллельно работающими колоннами; I — исходная смесь пропен-пропан; II пропей; III-пропан.
Таблица 4. Основные параметры технологического режима колонн при разделении смеси пропен - пропан (рис.4)
| Показатели
|
Схема а
|
Схема б
|
Схема
в
|
| Колонна низкого давления
|
Колонна
высокого давления
|
Температура,°С
верха колонны
конденсации верхнего продукта выхода из компрессора
орошения
низа колонны
Давление, МПа
верха колонны
в емкости орошения
Кратность орошения
|
40
38
-
38
55
1,67 1,6
9,7
|
40
38
-
38
55
1,67 1,6
9,7
|
63
62
-
62
79
2,87 2,8 15,4
|
20
45
48
38
35
1,0 1,85 8,4
|
Материальный баланс процесса разделения типичной пропен - пропановой фракции (в т/ч) приведен ниже:
| Компоненты
|
Сырье
|
Дистиллят
|
Остаток
|
| Этан |
0,135 |
0Д35 |
— |
| Пропен |
11,746 |
10,572 |
1,174 |
| Пропан |
5,929 |
0,421 |
5,508 |
| Изобутан |
1,803 |
— |
1,803 |
| н-Бутан |
0,016 |
— |
0,016 |
| Бутен |
0,371 |
— |
0,371 |
| Z |
20,000 |
11,128 |
8,872 |
Сравнение стоимости затрат при разделении смеси пропен - пропан при помощи различных схем (по отношению к общей стоимости разделения в простой колонне) таково:
| Капитальные
|
Эксплутационные
|
Общие
|
| затраты
|
затраты
|
затраты
|
| Схема а |
41 |
59 |
100 |
| Схема б |
54,6 |
43,2 |
97,8 |
| Схема в |
| привод компрессора |
| от паровой турбины |
36,9 |
32,1 |
69 |
| привод компрессора |
| от электродвигателя |
33 |
33,7 |
66,7 |
Как видно из приведенных данных, применение схемы с тепловым насосом может обеспечить значительную экономию энергетических и капитальных затрат на разделение, однако степень уменьшения их существенным образом зависит от технико - экономических показателей процесса разделения - от стоимости электроэнергии и водяного пара. Необходимо отметить также, что надежное расчетное сравнение схем ректификации смеси пропен - пропан с получением практически чистого пропена возможно только на основе достаточно точных термодинамических данных по фазовому равновесию.
Постановка задачи
Целью данной работы являлась структурная и параметрическая оптимизация технологической схемы разделения фракции этан-пропен-пропан для снижения энергозатрат на разделение.
Для достижения поставленной цели необходимо:
• выбрать математическую модель парожидкостного равновесия, адекватно описывающую экспериментальные данные;
• синтезировать схемы разделения;
• произвести расчет ректификации и выбрать решение, обеспечивающее минимальные энергозатраты.
Расчетная часть
Методы и алгоритмы исследования
В настоящей работе для математического моделирования схем ректификации использован лицензионный программный комплекс PRO/II with PROVISION компании SIMSCI corp., обеспечивающий моделирование и расчет технологических схем ректификации.
PRO/II - компьютерный комплекс для инженерных расчетов процессов органического синтеза и нефтехимии, технологии полимеров и др. Он объединяет базы данных химических компонентов и расширенных методов расчета термодинамических свойств с гибкими методами расчета аппаратов. Программа обладает вычислительными средствами для выполнения расчетов всех материальных и энергетических балансов необходимых для моделирования большинства статических процессов. Экспертные системы, расширенная обработка входных данных и проверка ошибок обеспечивают его высокую эффективность и надежность.
Расчет ректификации
Все алгоритмы ректификации в программе PRO/П представляют собой строгие модели равновесных ступеней контакта. В каждой модели решаются тепловой и материальный балансы и уравнения равновесия жидкость - пар.
Программа PRO/II предлагает четыре различных алгоритма моделирования ректификационных колонн:
алгоритм Inside/Out (I/O),
алгоритм Sure,
алгоритм Chemdist и
алгоритм ELDIST.
Алгоритм I/O может быть использован для решения большинства задач нефтепереработки и обладает высоким быстродействием. В настоящей работе расчет колонн ректификации проводился по этому алгоритму.
Алгоритм подразделяется на внешний и внутренний циклы. Во внутреннем цикле решаются тепловой и материальный балансы и обеспечиваются заданные требования. Во внутреннем цикле используются упрощенные термодинамические модели для энтальпий и коэффициентов равновесия жидкость - пар. Это, вместе с упрощенными моделями и
выбором первичных переменных, позволяет решить внутренний цикл быстро и надежно. Во внешнем цикле параметры упрощенной термодинамической модели обновляются на основе новых значений состава и результатов строгих термодинамических расчетов. Решение достигнуто, когда строго рассчитанные значения энтальпий и коэффициентов равновесия соответствуют значениям, рассчитанным в упрощенных термодинамических моделях, и удовлетворяют заданным требованиям.
На рис. 5 показана схематическая диаграмма простой ступени контакта.
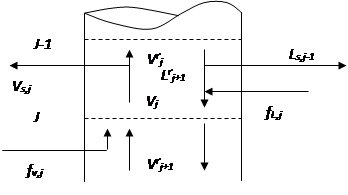
Рис. 5. Схема простой ступени контакта алгоритма I/O.
Тепловой баланс для ступени контакта j выглядит следующим образом:
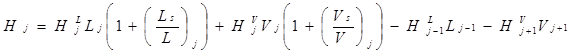
где: V
—
расход пара, покидающего ступень контакта; L
-
расход жидкости, покидающей ступень контакта;
Ls —
жидкостной боковой погон;
Vs
- паровой боковой погон;
Материальный баланс по компоненту для данной ступени контакта через расходы жидкости и паров при следующей зависимости для равновесных составов обеих фаз:
где К
представляет собой соотношение равновесной фугитивности пар - жидкость, может быть записан как:
(7)
где:
l
- расход жидкого компонента;
v
- расход парового компонента;
f
- расход компонента сырья.
Поскольку К
принято постоянным, то система уравнений материального баланса является линейной и формирует тридиагональную матрицу системы.
Во внешнем цикле алгоритма Inside/Out обновляются параметры упрощенной термодинамической модели и проверяется сходимость. Во внутреннем цикле уравнения ректификации решаются для текущих упрощенных термодинамических моделей. Проверка сходимости во внешнем цикле, следовательно, сравнивает значения энтальпий и коэффициентов фазового равновесия жидкость - пар, строго рассчитанные из нового состава, получившегося в результате расчетов внутреннего цикла. Полученное решение является окончательным.
Объект исследования
Для решения поставленной задачи нами было выбрана трехкомпонентная зеотропная смесь: этан - пропен - пропан.
Индивидуальные свойства компонентов представлены в таблице 1.
Таблица 5.
Физико - химические свойства компонентов
| Компоненты |
Молекулярная масса, г/моль |
Плотность,
кг/м3
|
Температура кипения, °С |
Критическая температура,
°С
|
Критическое давление, кг/см3
|
| Этан |
30,0700 |
356,05 |
-88,63 |
32,30 |
49,802 |
| Пропен |
42,0810 |
521,49 |
-47,70 |
91,80 |
47,115 |
| Пропан |
44,0970 |
507,20 |
-42,07 |
96,67 |
43,334 |
Самый легко летучий компонент в исследуемой смеси, этан, содержится в природных и попутных газах и представляет собой бесцветный, горючий газ. Его используют для получения сажи, так же как сырье для производства СО и Н2
и в дальнейшем для получения моторных топлив.
Пропан также представляет собой бесцветный газ, который растворим в органических растворителя и не растворим в воде. Его применяют как топливо для двигателей внутреннего сгорания, для получения сажи, в смеси с бутаном в баллонах используют как топливо в быту.
Пропен при обычных условиях является газом. Главным способами получения в промышленности пропена служат процессы расщепления нефтяных фракций или углеводородных газов (каталитический и термический крекинги, пиролиз). Кроме того, пропен получают дегидрированием пропана. Ввиду своей реакционной способности пропен занял одно из ведущих мест как исходное вещество для органического синтеза.
Изначально, компоненты исследуемой смеси входят в состав широкой фракции легких углеводородов, получаемые в процессе нефтедобычи. Она содержит довольно широкий спектр углеводородов состава C1
- C7
которые в дальнейшем разделяются на узкие фракции:
• метан - водородную
• метан - этановую
• этан - этиленовую
• пропан - пропиленвую
• изопентановую
• гексановую и другие.
Для исследования применимости сложных колонн нами была выбрана простейшая из многокомпонентных смесей, не образующая азеотропов. Фракция этан-пропен-пропан оказалась в этом отношении весьма подходящей.
Модели парожидкостного взаимодействия
Модель NRTL
Уравнение NRTL (non-random two-liquid - неслучайное двужидкостное) было разработано Реноном и Праузницем с целью использовать концепцию локального состава, для избежания неспособности уравнения Вильсона к предсказанию разделения фаз жидкость — жидкость. Полученное в результате уравнение оказалось довольно хорошим для описания широкого диапазона систем, в высокой степени неидеальных смесей и для частично несмешивающихся систем. Выражение для коэффициента активности имеет вид:
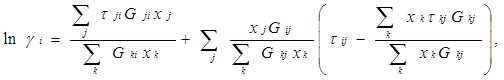 (8) (8)
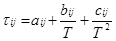 где: (когда единицей измерения является °К): где: (когда единицей измерения является °К):
Результирующее уравнение определяет коэффициент активности жидкости для каждой бинарной пары с точки зрения трех параметров. Выражения для параметров могут быть расширены с целью включения в них зависимости от температуры. В зависимости от выражений, использованных для параметров, уравнение может иметь три, пять, шесть или восемь параметров.
Модель Соав-Редлих-Квонг (
SRK
)
В 1972 г. для улучшения предсказания парового давления чистых компонентов и парожидкостного равновесия многокомпонентных смесей Соав предложил следующую температурную зависимость:
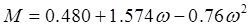 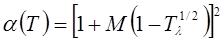 (9)(10) (9)(10)
где T
γ
- приведенная температура, Т/Тс
ω —
ацентрический фактор
Константы в уравнении (10) были получены из преобразования данных по паровому давлению для ограниченного числа обычных углеводородов. Эти пределы использования
уравнения состояния SRK ограничены неполярными компонентами.
Уравнение состояния Соав-Редлих-Квонга - это модификация уравнения состояния Редлиха-Квонга (которое основано на уравнении Ван-дер-Ваальса). Соав заменил член
a
/
T
0,5
более общей температурной зависимостью а(Т).
Выражение получило следующий вид:
P = RT/(V-b)-a(T)/V(V + b)
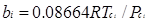  Где Где 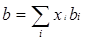
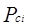 , - критические температура и давление для i-ro компонента , - критические температура и давление для i-ro компонента
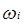 . —
ацентрический фактор для компонента i . —
ацентрический фактор для компонента i
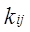 - константа бинарного взаимодействия для компонентов i и j - константа бинарного взаимодействия для компонентов i и j
Введение члена альфа позволило улучшить предсказание парового давления для чистых компонентов. Комбинированная формула для вычисления а(Т) с введенным членом ]$г
означает улучшение предсказания свойств смеси.
Использование формулировки Соава для предсказания свойств смеси включает в себя два этапа. Во-первых, для каждого из компонентов подбирается ацентрический фактор компонента (ом) таким образом, чтобы точно предсказать давление паров компонента. Во-вторых, из экспериментальных данных для бинарных систем с компонентами i и j, для которых достигается фазовое равновесие, определяется параметр kij.
Модель Пенга-Робинсона
Уравнение состояния Пенга-Робинсона было опубликовано в 1976 году и является модификацией уравнения Редлиха-Квонга. Во многих отношениях оно похоже на уравненеие SRK, но все же он разработано для улучшения предсказания плотности жидкости. Как и в случае уравнения Соава-Редлиха-Квонга, в уравнении Пенга-Робинсона присутствует температурная зависимость а(Т) и выражение имеет следующий вид:
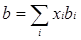 где: где:
- 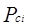  критические температура и давление для компонента i критические температура и давление для компонента i
ω i -
ацентрический фактор для компонента i
K
ij
. -
константа бинарного взаимодействия для компонентов i и j
Введением члена а было достигнуто улучшение предсказания давления пара чистых компонентов, а добавлением члена K
ij
в комбинированную формулу для вычисления а(Т)
означало улучшение предсказания свойств смесей.
Использование уравнения Пенга-Робиысона включает в себя два шага, аналогичные предыдущей модели.
Выбор адекватной модели
Систематическое исследование процессов ректификации требует выбора адекватной модели парожидкостного равновесия. В настоящей работе расчетньш эксперимент поставлен на примере разделения многокомпонентной модельной смеси этан - пропан - пропен.
Выбор модели описания парожидкостного взаимодействия для смесей этан-пропан, пропан-пропен, пропен-этан производился на основании сопоставления экспериментальных и расчетных данных. Расчет парожидкостного равновесия проведен с использованием программного комплекса PRO/IL На основании имеющегося опыта практического использования и общих рекомендаций по применению выбрано несколько моделей ПЖР, реализованных в программном комплексе: I - NRTL, II - модель SRK, III - модель Пенг -Робинсон.
Нами были получены экспериментальные данные по парожидкостному равновесию для следующих бинарных составляющих: этан - пропан, пропен - пропан, этан - пропен.
В качестве критерия сравнения для статистической обработки результатов было выбрано среднее относительное отклонение описания паровой фазы, δ.
(11)
где N- количество экспериментальных точек фазового равновесия.
Таким образом, нами было произведено сравнение трех бинарных составляющих по заданному критерию. Результаты представлены в Приложении и Табл. 6.
Таблица. 6.
Результаты моделирования парожидкостного равновесия
| Смесь
|
δ,%
|
| NRTL
|
SRK
|
PR
|
| Этан — пропен |
1,272 |
1,392 |
0,966 |
| Пропел - пропан |
0,835 |
1,250 |
1Д52 |
| Этан-пропан |
0,862 |
1,042 |
1,289 |
Из таблицы видно, что модель NRTL наилучшим образом описывает экспериментальные данные, поэтому для дальнейшего описания ПЖР мы воспользуемся моделью локальных составов.
Будем использовать уравнение с тремя параметрами: bij
, bij,
aij
.
Найденные значения параметров бинарного взаимодействия приведены в табл.7.
Таблица 7.
Параметры бинарного взаимодействия для модели NRTL
| Бинарная пара
|
bij
|
bij
|
aij
|
| Этан —пропан Пропен — пропан Этан - пропен |
-103,454
-54,7269 217,216
|
443,987 142,146
-216,315
|
1
0,9 0,972611
|
Синтез схем ректификации для разделения смеси этан-пропен-пропан
Для разделения трехкомпонентной зеотропной смеси нами было предложено четыре технологические схемы (рис. 6-7). Две из них являются последовательностью из простых двухсекционных колонн, две другие - являются комплексами из сложных колонн с боковыми секциями. В ряде случаев применение сложных колонн оправдано за счет приближения к термодинамической обратимости за счет структурных особенностей. Кроме того, такие схемы требуют меньшее число кипятильников и дефлегматоров, что может привести к значительному снижению энергозатрат на разделение. Но следует помнить, что такие технологические схемы целесообразно применять при невысокой четкости разделения и содержании среднекипящего компонента более 20%.
Рассмотрим предложенные схемы более подробно.
Схема 1 представляет собой последовательность простых двухсекционных колонн, работающих в режиме первого заданного разделения (рис. 6а, в). Согласно этой схеме в качестве дистиллата колонны 1 выделяют практически чистый этан, а кубовый продукт колонны 1 поступает на дальнейшее разделение. В колонне 2 происходит отделение пропена и пропана.
работает в режиме второго заданного разделения, что позволяет выделить в качестве кубового
продукта тяжелокипящий пропан. Дистиллат колонны 1 направляют на дальнейшее разделение на этан и пропен в колонну 2.
Используя широко развитые методы синтеза схем, основанные на теории графов [5, 6, 7, 8], нами синтезированы технологические схемы разделения трехкомпонентной смеси этан - пропен - пропан, содержащие сложные колонны (рис.6 б, г, 7 б, г). Схемами-прообразами являются описанные схемы 1 и 2. Для трансформации схем 1 и 2 представим их в виде графов (рис. 6 в, г, 7 в, г). Структуры 3 и 4 получают путем стягивания по ориентированному ребру, эксплицирующему потоки между колоннами. Полученные схемы-образы являются структурами с частично (рис. 6 б, г, 7 б, г) связанными тепловыми и материальными потоками.
Синтезированная схема 3 (рис. 6 б) представляет собой сложную колонну с боковой укрепляющей секцией. Схема содержит два дефлегматора и один кипятильник. Схема 4 (рис. 7 б), напротив, отличается наличием двух кипятильников и одного дефлегматора, представляя тем самым сложную колонну со стриппинг-секцией.
Таким образом, нами предложено четыре схемы разделения, представленные на рис. 8.
Схема 1 Схема 2
Схема 1 Схема 2
Схема 3 Схема 4
Рис. 8. Технологические схемы разделения смеси этан-пропен-пропан
Разделение смеси по схемам из простых и сложных колонн
Итак, нами было предложено четыре схемы ректификации.
Сравнение энергопотребления схем проводили по критерию минимальных энергозатрат, которые вычисляли как сумму тепловых нагрузок на кипятильники колонн. Все аппараты технологической схемы работают при давлении 40 кг/см2
.
Все расчеты проводили на 20 тон/час исходной смеси различных составов с помощью программного комплекса PRO П. Известно, что концентрационный симплекс исходных составов питания делится на области оптимальности, в каждой из которой оптимальна своя технологическая схема. Размер и положение этих областей определяется составом питания разделяемой смеси при прочих равных параметрах. Поэтому нами были выбраны 4 различных состава, указанных в таблице 8.
Таблица. 8. Исследуемые составы питания
| Состав 1
|
Состав 2
|
Состав 3
|
Состав 4
|
| Этан
|
0,33 |
0,50
|
0,50 |
0,01
|
| Пропен |
0,33 |
0,10
|
0,40
|
0,55 |
| Пропан
|
0,34
|
0,40
|
0,10
|
0,44
|
Этан
ПропенПропан
Рис. 9. Исходные составы питания концентрационного симплекса Состав 1 является эквимолярньм и находится в центре концентрационного симплекса, составы 2 и 3 и 4 смещены к его граням (рис. 9). Отметим также, что состав 4 является промышленным.
Мы также рассмотрели два различных набора значений по чистоте получаемых
продуктов. В первом случае концентрацию среднекипящего компонента задавали равной 95% мольн., во втором - 90%мольн., чистота остальных компонентов равна 99% для обоих вариантов.
В ходе расчетов для каждой технологической схемы нами были определены оптимальные положения тарелок питания, обеспечивающих минимальное энергопотребление в кубы колонн.
Для определения оптимальной тарелки питания в каждой колонне потребовалось проведение серии расчетов. В проектном варианте расчета в каждой колонне варьировали тарелку питания по высоте аппарата и сравнивали значения флегмового числа и тепловых нагрузок. В качестве примера на рис. 10 приведем зависимости энергозатрат на разделение и флегмового число от положения тарелки питания для первой схемы состава 1.
Тарелка питания
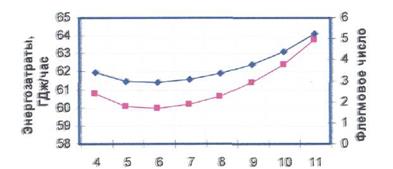
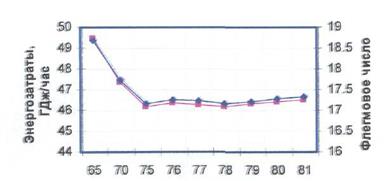
Рис. 10. Зависимость энергозатрат на разделение и флегмового числа от положения тарелки питания для схемы 1 состава 1. а - для колонны выделения этана, б - для колонны разделения пропена – пропана.
Отметим, что для других технологических схем зависимости энергозатрат и флегмового числа носят идентичный характер. Поэтому рассмотрим окончательные результаты расчетов, представленные в табл. 9
Таблица. 9. Результаты параметрической оптимизации технологических схем при чистоте пропена 95%
| оптим. тар.
|
Qкип.,
ГДж/час
|
Q конд. ГДж/час
|
Qсум
кип.,
ГДж/час
|
Qcyм
конд.,
ГДж/час
|
| кол 1/ко л 2
|
кол 1 |
/ко л 2
|
кол 1 |
/ко л 2
|
| Состав 1
|
| схема 1 |
6/75 |
7,004 |
39,155 |
-6,8653 |
-39,098 |
46,167 |
-45,963 |
| схема 2 |
81/17 |
51,94 |
10,28 |
-51,82 |
-10,16 |
62,21 |
-61,98 |
| схема 3 |
31/40 |
328,41 |
-300,49 |
-28,143 |
328,41 |
-328,64 |
| схема 4 |
78/15 |
47,146 |
33,414 |
-79,981 |
80,56 |
-79,981 |
| Состав 2
|
| схема 1 |
7/15 |
5,965
|
14,337 |
-5,413 |
-14,276
|
20,302 |
-19,689 |
| схема 2 |
86/7 |
21,764 |
3,3177 |
-21,241 |
-3,2246 |
25,0817 |
-24,4656 |
| схема 3 |
24/29 |
393,36 |
-419,03 |
-11,345 |
393,36 |
-430,37 |
| схема 4 |
85/17 |
25,966 |
0,27609 |
-25,65 |
26,243 |
-25,65 |
| Состав 3
|
| схема 1 |
5/66 |
6,6171 |
40,975 |
-6,4001 |
-40,934 |
47,592 |
-47,334 |
| схема 2 |
84/5 |
77,54 |
5,02 |
-77,47 |
-4,84 |
82,56 |
-82,31 |
| схема 3 |
25/38 |
415,2 |
-405,2 |
-8,3288 |
415,2 |
-413,53 |
| схема 4 |
70/20 |
57,097 |
1,0929 |
-57,947 |
58,19 |
-57,947 |
| Состав
4 |
| схема 1 |
10/77 |
5,2894 |
57,845 |
-5,2917 |
-57,721 |
63 ,135 |
-63,0127
|
| схема 2 |
80/10 |
380,01 |
0,41624 |
-379,91 |
-0,41622 |
380,43 |
-380,33 |
| схема 3 |
20/56 |
254,9 |
-44,025 |
-210,78 |
254,9 |
-254,81 |
| схема 4 |
80/20 |
60,955 |
4,00 |
-64,815 |
64,955 |
-64,815 |
Из приведенных данных видно, что для всех исследуемых составов оптимальной является первая технологическая схема, которая обеспечивает минимальное энергопотребление в кубы колонн. Это можно объяснить ее структурой. Продуктом первой колонны является компонент (этан), относительная летучестькоторого в два раза превышает остальные компоненты. Выделение этою компонента из смеси облегчает дальнейшее разделение пары пропен-пропан во второй колонне.Рассмотрим результаты более подробно.
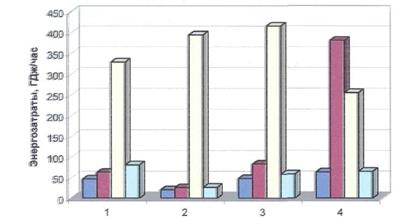
 Номер состава питания Номер состава питания
Рис. 11. Зависимость энергозатрат на разделение от соста
Из рис. 11 видно явное преимущество схемы 1 над остальными. Применение же схемы 3 нецелесообразно во всех случаях. Схема с боковой укрепляющей секцией, предназначенной для удаления тяжелых примесей из целевого компонента, требует больших энергозатрат на разделение. Энергозатраты в куб основной колонны этой схемы превышает остальные на порядок. Как показывает расчет для всех исследуемых составов, намного более выгодно проводить разделение пары пропен-пропан по схеме из последовательности простых двухсекционных колонн (схема 1). Что касается остальных технологических схем, то на первый взгляд их различие не так велико. Однако проанализируем полученные
Таблица. 10. Результаты сравнения технологических схем при чистоте пропена 95%
Qi
|
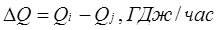 |
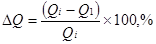 |
| Номер исходного состава питания
|
| 1
|
2 |
3 |
4 |
1 |
2
|
3 |
4 |
| Схема 2 |
16.04 |
4.77 |
34.97 |
317.29 |
25.788 |
19.05 |
42.35 |
83.40 |
| Схема 3 |
282.24 |
373.05 |
367.60 |
191.76 |
85.94 |
94.83 |
88.53 |
75.23 |
| Схема 4 |
34.39 |
5.94 |
10.59 |
1.82 |
42.69 |
22.63 |
18.21 |
2.80 |
результаты более подробно. В табл. 10 представлены результаты сравнения технологических схем по отношению к оптимальной (схеме 1).
Для состава 1 первая технологическая схема является, несомненно, лучшим вариантом разделения. Ближайший конкурент (схема 2) превышает ее по энергозатратам на 25%.
Если взглянуть на абсолютную разницу в энергопотреблении схем, то для состава 2 видно, что разница между схемами 1, 2 и 4 не велика. Однако в процентном соотношении она достигает порядка 20%. Схемы 2 и 4 в некоторой степени могут быть конкурентоспособны между собой, их различие составляет 4%. Следует заметить, что состав 2, содержание пропена в котором минимально (10%), обеспечивает минимальные энергозатраты для схем 1,2, и 4 по отношению к другим исследуемым составам.
Результаты для состава 3 несколько похожи с составом 1. Здесь также оптимальной является первая технологическая схема, а ближайшая после нее схема 4 отличается на ~ 20%.
В случае состава 4 можно говорить о равенстве энергозатрат на разделение для схем 1 и 4. Их различие составляет 1,82 ГДж/час или 2,8%. Исследуемый состав исходного питания находится близко к грани областей оптимальности данных схем.
С некоторой долей приближения можно говорить о том, что область, в которой оптимальна схема 4, находится в нижней левой части концентрационного симплекса. Она начинается при содержании среднекипящего компонента более 55% и прилегает к ребру пропен-пропан. Ранее авторами было показано, что подобные схемы с частично связанными тепловыми и материальными потоками могут быть оптимальны при содержании среднекипящего компонента более 30%. Наше исследование также подтверждает данное утверждение.
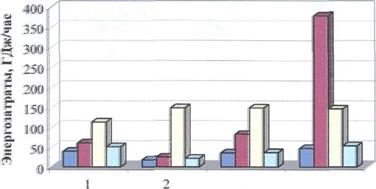
Нами был проведен аналогичный расчет при чистоте среднекипящего компонента 90%. Для каждой технологической схемы бьшо найдено оптимальное положение тарелок питания, при котором энергопотребеление в кубы колонн минимальны. Результаты представлены на рис. 12.
3
 Номер состава питания Номер состава питания
□ Схема 1
□ Схема 3
□ Схема 2
□ Схема 4
Рис. 12. Зависимость энергозатрат на разделение от состава исходного питания при чистоте пропена 90%
Не будем приводить тщательный анализ энергозатрат для каждого состава в отдельности. Отметим лишь то, что полученные результаты полностью пропорциональны предыдущему случаю. Это наглядно видно на рис. 12.
Таблица. 11. Результаты сравнения технологических схем по отношению к схеме 1 при чистоте пропена 90%
Qi
|
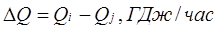 |
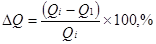 |
| Номер исходного состава питания
|
| 1
|
2 |
3 |
4 |
1 |
2 |
3 |
4 |
| Схема 2 |
21.05 |
6.66 |
47.13 |
330.87 |
35.06 |
27.45 |
57.48 |
87.61 |
| Схема 3 |
73.71 |
130.30 |
113.20 |
98.59 |
65.40 |
88.10 |
76.45 |
67.82 |
| Схема 4 |
11.85 |
4.00 |
1.36 |
6.51 |
23.31 |
18.52 |
3.75 |
12.21 |
По результатам табл. 11 можно судить о количественном изменении области оптимальности. Вероятно, ее граница сместилась ближе к составу 3, чем объясняется относительно небольшая разница энергозатрат схем 1 и 4 в этой точке исходного питания.
Ниже в табл. 4 приведены результаты сравнения технологических схем при различных требованиях к качеству пропена.
Таблица. 12. Результаты сравнения при различной чистоте пропена
| Качество пропена 95% |
Качество пропена 90% |
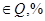
|
Оптии.тар.
кол1/кол2
|
Qсум.кип.,
ГДж/час
|
Оптии.тар.
кол1/кол2
|
Qсум.кип.,
ГДж/час
|
| Состав1 |
| схема1 |
6/75 |
46,16 |
5/70 |
38,99 |
15.54 |
| схема2 |
81/17 |
62,21 |
81/16 |
60,04 |
3.48 |
| схемаЗ |
31/40 |
328,41 |
29/46 |
112,70 |
65.68 |
| схема 4 |
78/15 |
80,56 |
79/13 |
50,84 |
36.89 |
| Состав 2 |
| схема1 |
7/85 |
20,30 |
14/86 |
17,60 |
13.30 |
| схема2 |
86/7 |
25,08 |
85/9 |
24,26 |
3.27 |
| схемаЗ |
24/29 |
393,36 |
17/35 |
147,90 |
62.40 |
| схема 4 |
85/17 |
26,24 |
76/25 |
21,60 |
17.69 |
| Состав 3 |
| схема1 |
5/66 |
47,59 |
5/68 |
34,87 |
26.73 |
| схема2 |
84/5 |
82,56 |
84/5 |
82,00 |
0.67 |
| схемаЗ |
25/58 |
415,2 |
27/35 |
148,07 |
64.33 |
| схема 4 |
70/20 |
58,19 |
78/20 |
36,23 |
37.73 |
| Состав 4 |
| схема1 |
10/77 |
63,135 |
10/85 |
46,79 |
25.88 |
| схема2 |
80/10 |
380,43 |
80/10 |
377,66 |
0.72 |
| схемаЗ |
20/56 |
254,9 |
13/59 |
145,38 |
42.96 |
| схема 4 |
80/20 |
64,955 |
85/29 |
53,30 |
17.94 |
Как уже отмечалось при снижении требований к качеству среднекипящей фракции с 95 до 90 %, произошло количественное изменение результатов. Качественно общая картина не изменилась. В какой-степени энергозатраты на разделение снизились (см. 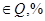 в табл. 12), однако схема 1 из простых двухсекционных колонн осталась по-прежнему оптимальной. в табл. 12), однако схема 1 из простых двухсекционных колонн осталась по-прежнему оптимальной.
Итак, нами было рассмотрено разделение смеси этан-пропен-пропан в четырех вариантах организации процесса. Мы исследовали влияние на энергозатраты различных требований к чистоте продуктовых фракций для четырех составов исходного питания. В результате было выявлено, что схема 1, состоящая из простых двухсекционных колонн и работающая в режиме первого заданного разделения является оптимальной с точки зрения энергопотребления для всех исследуемых случаев. Лишь в случае состава 4 (0,01-0,55-0,44) при чистоте пропена 95% наблюдается конкурентная ситуация оптимальной схемы 1 со схемой 4, содержащей сложную колонну с боковой исчерпывающей секцией. Различие в их энергопотреблении не превышает 3%. Условное равенство этих же технологических схем наблюдается и в случае 90%-го качества пропена, но уже для состава 3 (0,50-0,40-0,10). Таким образом, можно говорить о предпочтении использования схемы с боковой исчерпывающей секцией при содержании среднекипящего компонента (пропена) более 55%. На остальных областях концентрационного симплекса оптимальна схема из простых двухсекционных колонн, работающая по первому заданному разделению.
Выводы
1. При фиксированном суммарном числе ступеней разделения для всех исследуемых составов питания оптимальной является схема, состоящая из простых двухсекционных колонн, работающая по первому заданному разделению.
2. Нами было предположено существование области оптимальности схемы, содержащей сложную колонну с боковой исчерпывающей секцией при содержании среднекипящего компонента (пропена) более 55%.
3. При снижении качества пропена с 95% до 90% оптимальной остается схема, состоящая из простых двухсекционных колонн, работающая в режиме первого заданного разделения.
Список литературы
1.Львов СВ. Некоторые вопросы ректификации бинарных и многокомпонентных смесей.
М.: Изд. АН СССР, 1960,163с.
2. Тимофеев B.C., Серафимов Л.А. Принципы технологии основного органического и нефтехимического синтеза. М: Изд. Химия, 1992,431с.
3. Петлюк Ф.Б., Серафимов Л.А. Многокомпонентная ректификация : теория и расчет. М.:Химия, 1983, 303с.
4.Петлюк Ф.Б., Исаев Б.А. Расчетное исследование различных схем установок газофракционирования. Нефтепереработка и нефтехимия, 1978, №1, с.22.
5.Береговых В.В., Корабельников В.В., Серафимов Л.А. Выбор оптимальной технологической схемы ректификации тройных зеотропных смесей. Хим. - фарм. журн.,1984, №3,с.350-355.
6.Береговых В.В., Корабельников В.В., Серафимов Л.А. Стратегия синтеза и анализа технологических схем ректификации. Хим. - фарм. журн., 1985, №3, с.202 - 207.
7.Underwood A. Fractional distillation of multicomponent mixtures // Chem. Eng. Progr.,1948, v.44, №8, p. 598 -613.
8.Исаев Б.А. « Разработка методов синтеза и исследование оптимальных технологических схем ректификации многокомпонентных смесей», дисс. На соискание степени к.т.н., МИТХТ, М.,1988.
9. Tedder D.W., Rudd D.F., Parametric Studies in Industrial Distillation, Part I. Design Comparisons, AIChE J., v.24, p. 303 (1978).
10.Friedler F., Tarjan K., Huang Y.W., Fan L.T. Graph - theoretic Approach to Process Synthesis : Axioms and Theoremes // Chm. Eng. Sci. 1992.,v.47, №8, p. 1973.
И. Беллман Р. Динамическое программирование. - M.: Изд-во иностр. лит., 1960. - 400с.
12.Кафаров В.В., Мешалкин В.П., Перов В.Л. Математические основы автоматизированного проектирования химических производств. - М.: Химия, 1979. -320с.
13. Rathore R.N.S., VanWormer K.A., Powers G.I. Synthesis Distillation Systems with Energy Integration. // AIChE J.- 1974, v.20, №5, p.940-950.
14. Rathore R.N.S., VanWormer K.A., Powers G.I. Synthesis Strategies for Multicomponent
Separation Systems with Energy Integration. // AIChE J. - 1974, v.20, №3, p.491-502.
15.Косунов А.О. Синтез систем ректификации многокомпонентных смесей: Автореф. дисс.канд. техн. наук. // М.: МХТИ. - 1976,17с.
16.Кафаров В.В., Петлюк Ф.Б., Гройсман С.А., Телков Ю.К., Белов М.В. Синтезоптимальных схем ректификации многокомпонентных смесей методом динамическогопрограммирования. // ТОХТ. - 1975, т.9, №2, с.262-269.
17.Кафаров В.В., Бояринов А.И., Новиков А.И., Косунов А.О. Стратегия синтеза сложныхсхем ректификации многокомпонентных смесей. Автоматизация химическихпроизводств. // НИИТЭХИМ. - 1975, вып.6, с.36-41.
18.42.Кафаров В.В., БояриновА.И., Ветохин В.Н., Новиков А.И., ЩипинЮ.К.,
Гартман Т.Н. Системный анализпроцессов разделения.// Доклады I Всесоюзной
конференции по математическомумоделированию сложных химико-технологических систем. - Ереван, 1975, с.99-105.
19.Косунов А.О., Кафаров В.В., Бояринов А.И., Новиков А.И. Синтез сложных схем разделения многокомпонентных смесей. // Труды МХТИ. -1975, вып.88, с.33-41.
20.Гройсман С.А. Анализ и синтез технологических схем разделения смесей углеводородов в промышленности основного органического синтеза: Автореф. дис. ...канд. техн. наук. // М: МИТХТ. - 1977,24с.
21.Westberg A.W., Stephanopoulos G., Studies in Process synthesis - I. Branch and Bound Strategy with list Techniques for the Synthesis of Separation Schemes, Chem. Eng. Sci., 30, 963,1975.
22.Umeda Т., Hirai A., Inchikawa A. - Chem. Eng. Sci., 1972, v.27, p. 795 - 804.
23.King C.J, Gantz D.W., Barner F.J. Systematic Evolutionary Process Synthesis. // Ind. and Eng.Process Des. and Develop. -1972, v.l 1, №2, p.271-283.
24.Stephanopoulus G., Westerberg A.W. Studies of Process Synthesis. // Chem. Engng. Sci. -1976, v.31,№3, p. 195-204.
25.Seader Y.D., Westerberg A.W. Combined Heuristic and Evolutionary Strategy for Synthesis of Simple Separation Sequences. // AIChE J. - 1977, v.23, №6, p.951-954.
26.Machalec V., Motard R, Bauman E. Evolutionary search for optimal process flowsheet. // Сотр. and Chem. Eng. ~ 1978, v.l, №2, p.149-160.
27.King C.J., Gantz D.W., Barner F.J., Ind. and Eng. Process Des and Develop, 1972, v.l 1, №2, p. 271-283.
28.Майков В.П., Вилков Г.Г., Гальцов А.В. Термоэкономическое оптимальное проектирование многоколонных ректификационных установок. // Хим. и технол. топлив и масел. - 1971, №6, с.19-26.
29.Майков В.П. Системно-структурное исследование оптимальных тепло и массообменных аппаратов и установок: Автореф. дисс.... доктора техн. наук. // М.: МИХМ. -1972, 32с.
30. Майков В.П. Докт. дисс, М., МИХМ, 1972.
31.Wolf C.W., Weiber D.W., Ragi E. G. - Oil and Gas J., 1975, v.73, № 35, p. 85-88.
32.Tyrens B.D., Luyben W.L.- Hydrocarbon Processing, 1975, v.54, № 7, p.93-96.
33.Александров А.И. Перегенка и ректификация в нефтепереработке, М., Химия, 1981
34.Schulze - Trautmann H., Erdo'l und Kohle, Erdgas - Petrochem. ver. Brennstoff- chem., 1976,
B. 29, № 9, S. 403-407.
Приложение
Математический вид и параметры моделей парожидкостного равновесия
Модель NRTL
Выражение для коэффициента активности:

 где: (когда единицей измерения является ˚K); где: (когда единицей измерения является ˚K);

Таблица 1, Параметры бинарного взаимодействия для модели NRTL
Бинарная пара
|
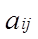 |
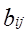 |
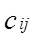 |
| Этан — пропан Пропен — пропан Этан — пропен |
-103,454
-54,7269 217,216
|
443,987 142,146
-216,315
|
1
0,9 0,972611
|
Модель SRK
P = RT/(V-b)-a(T)/V(V + b)
Где 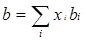 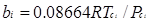 , ,
  , - критические температура и давление для i-ro компонента , - критические температура и давление для i-ro компонента
ω i
-
ацентрический фактор для компонента i
K
ij
. -
константа бинарного взаимодействия для компонентов i и j
Таблица 2, Параметры бинарного взаимодействия для модели SRK
| Бинарная пара
|
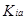 |
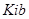 |
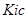 |
| Этан - пропан Пропен — пропан Этан — пропен |
-2,42222 0,187708
-0,22966
|
535,875
-66,8417 45,4099
|
2016,59
-11,6603 16140,6
|
Модель Пенга – Робинсона

 где: где:
-   критические температура и давление для компонента i критические температура и давление для компонента i
ω i -
ацентрический фактор для компонента i
K
ij
. -
константа бинарного взаимодействия для компонентов i и j
Таблица 3. Параметры бинарного взаимодействия для модели PR
| Бинарная пара
|
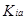
|
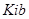
|
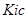
|
| Этан - пропан Пропен - пропан Этан - пропен |
-0,690433
-0,76273 0,000644
|
86,5762
-279,786 8Д3883
|
15530,5 199825 2364,41 |
МОДЕЛИРОВАНИЕ ПАРОЖИДКОСТНОГО РАВНОВЕСИЯ
Таблица 4. Бинарная пара: этан-пропан. Модель NRTL.
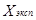 |
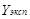 |
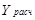 |
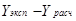 |
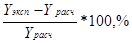 |
| 0,0006 |
0,045 |
0,0445 |
0.0004 |
0.963 |
| 0.044 |
0,273 |
0,2698 |
0.0032 |
1.182 |
| 0,0447 |
0,2799 |
0,2764 |
0.0035 |
1.256 |
| 0,0906 |
0,4404 |
0,4292 |
0.0112
|
2.606 |
| 0.0936 |
0,4501 |
0,4376 |
0.0125 |
2.856 |
| 0,095 |
0.4623 |
0,4479 |
0.0143 |
3.200 |
| 0,2305 |
0,6865 |
0,6813 |
0.0051 |
0.755 |
| 0,2357 |
0,6882 |
0,6839 |
0.0043 |
0.625 |
| 0Д844 |
0,737 |
0,7332 |
0.0037 |
0.509 |
| 0.2943 |
0,7694 |
0,7619 |
0.0074 |
0.973 |
| 0,2969 |
0,7704 |
0,7636 |
0.0068 |
0.886 |
| 0,3305 |
0,7871 |
0,7816 |
0.0055 |
0.698 |
| 0,4294 |
0,8394 |
0,8379 |
0.0014 |
0.172 |
| 0,4213 |
0,8439 |
0,8416 |
0.0022 |
0.264 |
| 0,5339 |
0.8908 |
0.8905 |
0.0002 |
0.025 |
| 0,5314 |
0,892 |
0,8918 |
0.0001 |
0.012 |
| 0,5752 |
0,9096 |
0,9094 |
0.0001 |
0.016 |
| 0.5762 |
0,9055 |
0.9067 |
0.0013 |
0.142
|
| 0.7766 |
0.959 |
0,9595 |
0.0005 |
0.054 |
| 0,7822 |
0,9613 |
0,9616 |
0.0004 |
0.039 |
Средняя относительная ошибка: 0,862
Таблица 5. Бинарная пара: этан-пропан. Модель SRK.
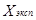
|
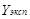
|
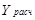
|
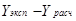
|
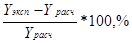 |
| 0,0006 |
0,045 |
0.0408 |
0.0041 |
10.121 |
| 0,044 |
0,273 |
0,2705 |
0.0024 |
0.891 |
| 0,0447 |
0,2799 |
0,2774 |
0.0025 |
0.897 |
| 0,0906 |
0,4404 |
0,4353 |
0.0050 |
1.151 |
| 0,0936 |
0,4501 |
0,4441 |
0.0059 |
1.339 |
| 0,095 |
0,4623 |
0,4551 |
0.0072 |
1.581 |
| 0,2305 |
0.6865 |
0,6845 |
0.0019 |
0.283 |
| 0,2357 |
0,6882 |
0,6869 |
0.0013 |
0.186 |
| 0,2844 |
0,737 |
0,7347 |
0.0022 |
0.303 |
| 0,2943 |
0.7694 |
0.7620 |
0.0073 |
0.963 |
| 0,2969 |
0,7704 |
0,7637 |
0.0067 |
0.875 |
| 0,3305 |
0,7871 |
0,7811 |
0.0060 |
0.765 |
| 0,4294 |
0,8394 |
0,8366 |
0.0027 |
0.325 |
| 0,4213 |
0,8439 |
0,8400 |
0.0038 |
0.453 |
| 0,5339 |
0.8908 |
0,8891 |
0.0017 |
0Л89 |
| 0,5314 |
0,892 |
0,8901 |
0.0018 |
0.206 |
| 0,5752 |
0,9096 |
0,9078 |
0.0018 |
0.195 |
| 0,5762 |
0,9055 |
0,9045 |
0.0009 |
0.105 |
| 0,7766 |
0,959 |
0,9590 |
0.0000 |
0.000 |
| 0,7822 |
0.9613 |
0,9612 |
0.0001 |
0.010 |
Средняя относительная ошибка: 1,042
Таблица 6, Бинарная пара: этан — пропан. Модель PR,
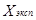
|
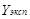
|
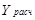
|
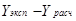
|
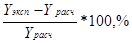 |
| 0,0006 |
0,045 |
0,0397 |
0.0052 |
13.159 |
| 0,044 |
0,273 |
0,2700 |
0.0029 |
1.075 |
| 0,0447 |
0,2799 |
0,2767 |
0.0031 |
1.135 |
| 0,0906 |
0,4404 |
0,4343 |
0.0060 |
1.386 |
| 0,0936 |
0,4501 |
0,4439 |
0.0062 |
1.395 |
| 0,095 |
0,4623 |
0,4552 |
0.0071 |
1.558 |
| 0,2305 |
0,6865 |
0,6823 |
0.0042 |
0.614 |
| 0,2357 |
0,6882 |
0,6863 |
0.0019 |
0.274 |
| 0,2844 |
0,737 |
0,7336 |
0.0034 |
0.462 |
| 0,2943 |
0,7694 |
0,7608 |
0.0085 |
1.120 |
| 0,2969 |
0,7704 |
0,7625 |
0.0079 |
1.035 |
| 0,3305 |
0,7871 |
0,7803 |
0.0067 |
0.861 |
| 0,4294 |
0,8394 |
0,8361 |
0.0033 |
0.390 |
| 0,4213 |
0,8439 |
0,8395 |
0.0043 |
0.518 |
| 0,5339 |
0,8908 |
0,8888 |
0.0019 |
0.215 |
| 0,5314 |
0,892 |
0,8899 |
0.0021 |
0.233 |
| 0,5752 |
0,9096 |
0,9076 |
0.0020 |
0.216 |
| 0,5762 |
0,9055 |
0,9043 |
0.0011 |
0.125 |
| 0,7766 |
0,959 |
0,9589 |
0.0001 |
0.006 |
| 0,7822 |
0,9613 |
0,9612 |
0.0001 |
0.010 |
Средняя относительная ошибка: 1,289
Таблица 7. Бинарная пара: пропен - пропан. Модель NRTL.
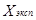
|
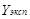
|
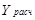
|
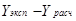
|
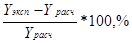 |
| 0.1778 |
0.1868 |
0.1865 |
0.0003 |
0.146 |
| 0.1765 |
0.1878 |
0.1874 |
0.0004 |
0.218 |
| 0.3738 |
0.3875 |
0.3910 |
0.0035 |
0.886 |
| 0.3764 |
0.5621 |
0.5442 |
0.0179 |
3.291 |
| 0.5514 |
0.5635 |
0.5660 |
0.0025 |
0.440 |
| 0.5527 |
0.5518 |
0.5560 |
0.0042 |
0.753 |
| 0.5615 |
0.5658 |
0.5691 |
0.0033 |
0.586 |
| 0.5761 |
0.7958 |
0.7866 |
0.0092 |
1.165 |
| 0.7912 |
0.796 |
0.7957 |
0.0003 |
0.032 |
Средняя относительная ошибка: 0,835.
Таблица 8. Бинарная пара: пропен - пропан. Модель SRK.
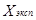
|
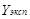
|
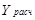
|
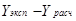
|
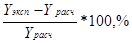 |
| 0.1778 |
0.1868 |
0.1928 |
0.0060 |
3.120 |
| 0.1765 |
0.1878 |
0.1817 |
0.0060 |
3.321 |
| 0.3738 |
0.3875 |
0.3838 |
0.0037 |
0.964 |
| 0.3764 |
0.5621 |
0.5664 |
0.0043 |
0.759 |
| 0.5514 |
0.5635 |
0.5603 |
0.0032 |
0.571 |
| 0.5527 |
0.5518 |
0.5543 |
0.0026 |
0.468 |
| 0.5615 |
0.5658 |
0.5613 |
0.0044 |
0.790 |
| 0.5761 |
0.7958 |
0.7906 |
0.0051 |
0.649 |
| 0.7912 |
0.796 |
0.7911 |
0.0048 |
0.607 |
Средняя относительная ошибка: 1,250.
Таблица 9. Бинарная пара: пропен - пропан. Модель PR.
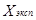
|
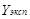
|
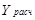
|
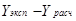
|
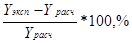 |
| 0.1778 |
0.1868 |
0.1928 |
0.0060 |
3.121 |
| 0.1765 |
0.1878 |
0.1918 |
0.0040 |
2.067 |
| 0.3738 |
0.3875 |
0.3874 |
0.0001 |
0.031 |
| 0.3764 |
0.5621 |
0.5764 |
0.0143 |
2.481 |
| 0.5514 |
0.5635 |
0.5603 |
0.0032 |
0.571 |
| 0.5527 |
0.5518 |
0.5604 |
0.0086 |
1.542 |
| 0.5615 |
0.5658 |
0.5614 |
0.0044 |
0.790 |
| 0.5761 |
0.7958 |
0J963 |
0.0005 |
0.062 |
| 0.7912 |
0.796 |
0.7912 |
0.0048 |
0.607 |
Средняя относительная ошибка: 1,252.
Таблица 10. Бинарная пара: этан - пропен. Модель NRTL.
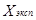
|
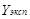
|
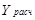
|
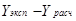
|
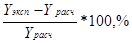 |
| 0.062 |
0.111 |
0.111 |
0.000 |
0.076 |
| 0.130 |
0.205 |
0.207 |
0.002 |
0.982 |
| 0.199 |
0.277 |
0.284 |
0.007 |
2.316 |
| 0.269 |
0.330 |
0.343 |
0.013 |
3.808 |
| 0.338 |
0.357 |
0.357 |
0.000 |
0.117 |
| 0.350 |
0.350 |
0.351 |
0.001 |
0.333 |
Средняя относительная ошибка: 1,272.
Таблица 11. Бинарная пара: этан - пропен. Модель SRK.
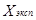
|
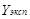
|
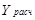
|
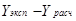
|
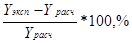 |
| 0.062 |
0.111 |
0.111 |
0.000 |
0.316 |
| 0.130 |
0.205 |
0.203 |
0.002 |
1.208 |
| 0.199 |
0.277 |
0.273 |
0.004 |
1.456 |
| 0.269 |
0.330 |
0.327 |
0.003 |
0.936 |
| 0.338 |
0.357 |
0.361 |
0.004 |
1.206 |
| 0.350 |
0.350 |
0.362 |
0.012 |
3.228 |
Средняя относительная ошибка: 1,392.
Таблица 12. Бинарная пара: этан - пропен. Модель PR.
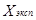
|
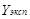
|
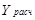
|
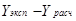
|
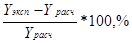 |
| 0.062 |
0.111 |
0.111 |
0.000 |
0.239 |
| 0.130 |
0.205 |
0.203 |
0.002 |
0.850 |
| 0.199 |
0.277 |
0.272 |
0.005 |
1.729 |
| 0.269 |
0.330 |
0.326 |
0.004 |
1.307 |
| 0.338 |
0.357 |
0.357 |
0.000 |
0.036 |
| 0,350 |
0.350 |
0.356 |
0.006 |
1.638 |
Средняя относительная ошибка: 0,966.
|