5 ВЛИЯНИЕ ТЕМПЕРАТУРЫ
НА СКОРОСТЬ ХИМИЧЕСКИХ РЕАКЦИЙ
5.1 Уравнение Аррениуса
Скорость химической реакции зависит не только от концентрации, но и от температуры. Как показывает опыт, скорость большинства реакций увеличивается при повышении температуры в 2 ÷ 4 раза на каждые 10 градусов.
Приближенной характеристикой зависимости скорости реакции от температуры является коэффициент реакции γ – отношение константы скорости при температуре Т+10
к константе скорости при температуре Т
:
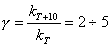 . (5.1)
. (5.1)
Это соотношение, называемое правилом Вант–Гоффа, может быть применено лишь для приблизительных, ориентировочных расчетов. Это правило не выполняется при высоких температурах, когда температурный коэффициент скорости (γ) перестает быть постоянным, приближаясь к единице. Однако для узкого интервала температур правило Вант–Гоффа часто бывает полезным.
Расчеты показывают, что увеличение скорости реакции при повышении температуры не может быть объяснимо лишь возрастанием числа столкновений. Это происходит потому, что не каждое столкновение частиц приводит к химической реакции. Лишь тогда, когда сталкивающиеся молекулы обладают определенной энергией, столкновение может быть эффективным и привести к химической реакции. Эти предположения были впервые высказаны А. Аррениусом. Согласно ученому, к реакции приводит столкновение лишь тех молекул, энергия которых больше определенной величины Еа
.
Таким образом, химическое взаимодействие осуществляется только между соударяющимися молекулами, которые достигли определенного энергетического уровня, характерного для данной реакции, ее энергетического барьера. Такие молекулы часто называют активными.
На основе взглядов Аррениуса была разработана теория активных соударений на базе молекулярно-кинетических представлений. Предложено считать активными столкновения, в которых суммарная энергия сталкивающихся возбужденных молекул А*
и В*
равна или больше Еа
. При столкновении молекулы сближаются до расстояния, которое называется эффективным диаметром столкновений dэфф
и при котором электроны и атомы одной молекулы попадают в поле действия электрических сил, возбуждаемых частицами другой молекулы. Только при таких условиях может произойти разрыв связей в исходных веществах и образование новых молекул. В первом приближении
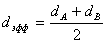 . (5.2)
. (5.2)
Все молекулы, запас энергии которых не ниже энергетического барьера реакции, находятся в особом состоянии, которое принято называть переходным, или состоянием активированного комплекса. Можно предположить, что система в состоянии активированного комплекса характеризуется тем, что в ней уже нет исходных веществ, но нет еще и продуктов реакций; исходные вещества переходят в продукты реакции.
Реклама

Покажем схематически переход от исходных веществ А и В к продуктам реакции С и Д через состояние активированного комплекса А….В (рис. 5.1)
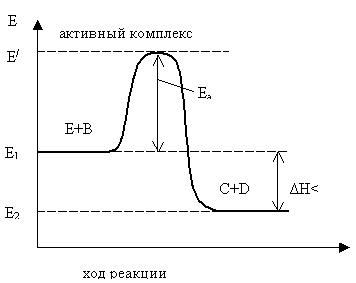
Рисунок 5.1 – Изменение энергии в ходе экзотермической реакции
Примем средний уровень энергии молекул исходных веществ в системе равным Е1
, а среднюю энергию переходного состояния – Е|
, то разность Е|
- Е1
будет выражать энергию активации данной реакции – Еа
. Энергия системы в переходном состоянии максимальна, а это значит, что активный комплекс крайне неустойчив. По ходу реакции он превращается в продукты взаимодействия С и D. В рассматриваемом примере средний уровень энергии молекул продуктов реакции Е2
ниже среднего уровня энергии молекул исходных веществ Е1
. Это означает, что процесс протекает с выделением энергии (реакция экзотермическая).
Средний уровень энергии молекул продуктов реакции Е2
может быть выше среднего уровня энергии молекул исходных веществ Е1
(рис. 5.2).
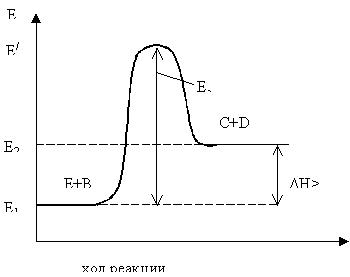
Рисунок 5.2 – Изменение энергии в ходе эндотермической реакции
Процесс протекает с поглощением энергии (реакция эндотермическая). Разность Е2
– Е1
равна тепловому эффекту процесса ΔН
.
Зависимость константы скорости реакции от температуры Аррениусом была представлена в виде:
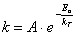 , (5.3)
, (5.3)
где А
– предэкспотенциальный множитель, не зависящий от температур;
Т
– температура, К;
R
– газовая постоянная;
Eа
– энергия активации (кал/моль, Дж/моль).
В химической кинетике часто пользуются уравнением Аррениуса в логарифмической форме:
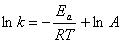 (5.4)
(5.4)
или
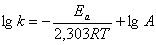 . (5.5)
. (5.5)
Из уравнений (5.4) (5.5) следует, что зависимость 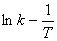 линейна (рис. 5.3)
линейна (рис. 5.3)
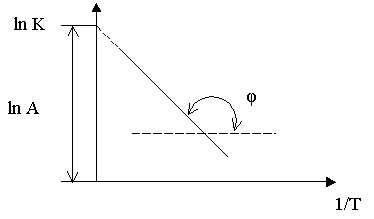
от температуры
Линейная зависимость (
lnk-
1/T)
позволяет определить энергию активации Еа
по тангенсу наклона прямой 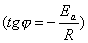 и предэкспотенциальный множитель А по отрезку, отсекаемому прямой на оси ординат, когда 1/Т
=0.
и предэкспотенциальный множитель А по отрезку, отсекаемому прямой на оси ординат, когда 1/Т
=0.
Дифференцируя уравнение 5.4 по температуре, получим:
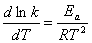 . (5.6)
. (5.6)
Величина 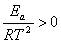 , логарифм константы скорости, а следовательно, и сама константа с температурой возрастает.
, логарифм константы скорости, а следовательно, и сама константа с температурой возрастает.
Энергию активации можно также найти из уравнения (5.6), проинтегрировав его от Т1
до Т2
:
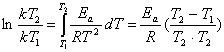
или
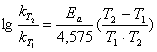 . (5.7)
. (5.7)
Из уравнения 5.7 можно определить величину энергии активации, если известны значения констант скорости при двух температурах: Т1
и Т2
.
Реклама

5.2 Связь энергии активации с тепловым эффектом
Пусть протекает реакция:
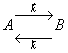
Тогда для прямой реакции
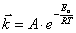 и
и 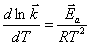 ;
;
для обратной реакции
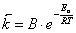 и
и 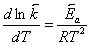 ,
,
вычитая из первого уравнения второе, получим:
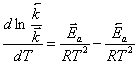 ,
,
но 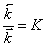 ,
,
где К
– константа равновесия,
тогда
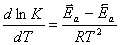 .
.
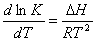 ,
,
где ΔН
– тепловой эффект реакции.
Сравнив два последние уравнения, получим:
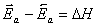 . (5.8)
. (5.8)
Из уравнения 5.8 следует, что разность между энергиями активации прямой и обратной реакции равна тепловому эффекту.
Контрольные вопросы:
1. Правило Вант–Гоффа. Что такое температурный коэффициент реакции?
2. Изменение энергии активации в ходе экзотермической реакции.
3. Изменение энергии активации в ходе эндотермической реакции.
4. Дать определение энергии активации. Что такое активированный комплекс?
5. Уравнение Аррениуса. Как зависит константа химической реакции от температуры?
6. Вывести уравнения связи энергии активации с тепловым эффектом.
|