| Введение
Электронные средства связи это техника передачи информации из одного места в другое в виде электрических сигналов, посылаемых по проводам, кабелю, оптоволоконным линиям или вообще без направляющих линий. Направленная передача по проводам обычно осуществляется из одной конкретной точки в другую, как, например, в телефонии или телеграфии. Ненаправленная передача, напротив, обычно используется для передачи информации из одной точки на множество других точек, рассеянных в пространстве, т.е. в широковещательных целях. Примером ненаправленной передачи может служить радиовещание. Каждый этап развития электроники сопровождался значительным повышением надежности электронных компонентов. При этом удавалось также существенно уменьшить размеры, потребляемую мощность и стоимость многих видов электронной аппаратуры. Широкое применение такой техники, как компьютеры, волоконно-оптические линии, спутники связи, телефоны прямого набора, видеотелефоны, транзисторные радиоприемники и кабельное телевидение, привело к полному пересмотру традиционной классификации методов связи. Сейчас уже практически не отождествляют передачу по проводам с прямой адресной связью, а беспроводную передачу – с радиовещанием. Вероятно, наиболее сильное влияние на развитие техники связи оказало значительное увеличение пропускной способности средств связи как по эфиру, так и по проводам. Эта возросшая пропускная способность используется для постоянно увеличивающегося глобального трафика телевидения, телефонии и цифровой информации.
Спутники связи. Первые спутники связи, размещавшиеся на околоземных орбитах в начале 1960-х годов, несли аппаратуру пассивного типа и служили лишь ретрансляторами сигнала. Современные спутники связи обычно выводятся на геостационарную орбиту высотой 35 900 км над поверхностью Земли. На каждом спутнике имеется 10 или большее число микроволновых приемников и передатчиков. Современный спутник позволяет передавать через океаны на целые континенты несколько телевизионных программ и обеспечивать работу более десятков тысяч телефонных каналов.
Кабели. Во время Первой мировой войны специалисты по технике связи разработали метод использования пары проводов для одновременной передачи нескольких телефонных разговоров. Этот метод, названный частотным уплотнением каналов, основан на возможности передачи по паре проводов широкого спектра звуковых частот. При этом сигналы каждого из нескольких передатчиков разносятся по частоте (с помощью модуляции) и полученный более высокочастотный объединенный сигнал передается на приемный терминал, где разделяется на составляющие сигналы посредством демодуляции. Телефонный кабель с защитной оболочкой может содержать от десятков до сотен скрученных проводных пар, каждая из которых позволяет обеспечить работу до 24 телефонных каналов. Однако кабелям, состоящим из проводных пар, присущи определенные ограничения. С превышением некоторой частоты сигналы, передаваемые по одной паре, начинают создавать помехи сигналам соседней пары. Чтобы решить эту проблему, была разработана передающая среда нового типа – коаксиальный кабель. Такой кабель, содержащий 22 коаксиальные пары, может обеспечить одновременную работу 132 000 телефонных каналов. Каждая пара в таком кабеле представляет собой центральный провод, заключенный в трубку второго проводника. Центральный проводник и трубка электрически изолированы друг от друга.
Импульсно-кодовая модуляция. Этот способ передачи сигналов средствами цифровой техники особенно удобен при использовании больших интегральных схем (БИС и СБИС), а также волоконно-оптических линий. Такая цифровая (ИКМ) передача речи и ТВ-сигналов в конце концов заменит другие средства связи. При использовании импульсно-кодовой модуляции сигналы речи или изображения можно разделять на множество малых временных интервалов; на каждом интервале ряд импульсов постоянной амплитуды представляет сигнал. Эти импульсы посылаются на принимающую станцию вместо оригинальных сигналов. Одно из преимуществ ИКМ связано с тем, что дискретные электронные импульсы постоянной амплитуды нетрудно отличить от случайных помех произвольной амплитуды (электростатического происхождения), которые в той или иной степени присутствуют в любой среде передачи. Такие импульсы можно передавать, по существу, без помех от стороннего шума, так как их легко отделить. ИКМ используется для самых разных сигналов. Телеграфные и факсимильные сообщения, а также другие данные, которые ранее пересылались по телефонным линиям другими методами, можно гораздо более эффективно передавать в импульсной форме. Трафик таких неречевых сигналов непрерывно возрастает; существуют также системы, позволяющие передавать смешанные сигналы речи, данных и видеоинформации.
Видеотелефон. Новые средства электроники позволяют дополнять изображениями передаваемую по телефону звуковую информацию. Видеопередачи между конференц-залами, находящимися в нескольких городах, используются для того, чтобы избежать необходимости переездов участников конференций. Видеопередачи начали широко применяться для обучения – лекции передаются из одной аудитории в другую (удаленную) и записываются на видеоленту для использования в тех же целях.
Системы кабельного телевидения. Хотя лазерное излучение и миллиметровые волны могут быть использованы для вещания, ограничения, обусловленные поглощением в атмосфере, и разные помехи другого рода удается преодолеть лишь ценой больших затрат. Поэтому при поиске путей расширения вещания, позволяющих избежать ограничений, связанных с использованием электромагнитных излучений, все больше используются кабельные системы. Для кабельного телевидения требуется прокладка кабелей от передающих до принимающих станций, расположенных, например, в домах. Радиослушатель или телезритель кабельного вещания не испытывает неудобств от замираний, двоения изображений и других помех. Кроме того, благодаря тому, что число каналов, передаваемых по кабелю, практически неограниченно (тогда как обычная станция ТВ-вещания передает в данный момент лишь одну программу), телезрителю предоставляется гораздо более широкий выбор программ. Модемы. В последнее время модемы становятся неотъемлемой частью компьютера. Установив модем на компьютер, перед вами открывается новый мир. Модем позволяет, не выходя из дома, получать доступ к базам данных, которые могут быть удалены от вас на многие тысячи километров. Кроме того, воспользовавшись глобальными сетями (RelCom, FidoNet, Internet) можно принимать и посылать электронные письма не только внутри города, но и в любой конец земного шара. Глобальные сети дают возможность не только обмениваться почтой, но и участвовать во всевозможных конференциях, получать новости по любой интересующей вас тематике. Интернет. Глобальная компьютерная сеть, охватывающая весь мир. Сегодня интернет имеет около 19 миллионов абонентов в более чем 150 странах мира. Ежемесячно размер сети увеличивается на 7-10%. Интернет образует как бы ядро, обеспечивающее связь различных информационных сетей, принадлежащих различным учреждениям во всем мире, одна с другой. Если ранее сеть использовалась исключительно в качестве среды передачи файлов и сообщений электронной почты, то сегодня решаются более сложные задачи распределенного доступа к ресурсам. Около двух лет назад были созданы оболочки, поддерживающие функции сетевого поиска и доступа к распределенным информационным ресурсам, электронным архивам. Кроме того интернет предоставляет уникальные возможности дешевой, надежной и конфиденциальной глобальной связи по всему миру. Это оказывается очень удобным для фирм имеющих свои филиалы по всему миру, транснациональных корпораций и структур управления. Обычно, использование инфраструктуры интернета для международной связи обходится значительно дешевле прямой компьютерной связи через спутниковый канал или через телефон.
Реклама

Реклама

1.
Теоретические и практические основы грамматик
1.1
Теория конечных автоматов
Конечный автомат (КА) – абстрактное вычислительное устройство с фиксированным и конечным объемом памяти, которое на входе читает цепочки (последовательности символов некоторого алфавита), а на выходе сообщает об их принадлежности к некоторому множеству, для распознания которого он построен.
Принцип работы конечных автоматов различных уровней широко применяется в вычислительных устройствах как на аппаратном, так и на программном уровнях: это компиляторы, трансляторы программ, различные кодировщики, антивирусные программы и т.п. В принципе работу любой программы можно представить как работу цепочки конечных автоматов различной сложности. В процессе построения конечного автомата должны быть определены следующие параметры:
а) входной алфавит V конечного автомата (конечное множество входных символов, которые будет распознавать КА);
б) конечное множество состояний S;
в) начальное состояние КА – s0
(состояние, с которого начинает работу КА при обработке новой цепочки);
г) множество допускающих состояний – Sдоп
(подмножество состояний, с элементами которого сравнивается достигнутое КА состояние после прихода символа "конец цепочки");
д) таблица переходов (управляющая таблица), которая паре "текущее состояние – входной символ" ставит в соответствие новое состояние КА из множества состояний S).
– В множество входных символов обязательно включают особый символ "конец цепочки", который сообщает КА о том, что нужно достигнутое состояние si
сравнить с элементами множества Sдоп
и, если si
Î Sдоп,
пропустить цепочку; в противном случае цепочка отвергается.
В коде программы этот символ будет иметь вид « * ». Часто при распознании цепочек возникает ситуация, когда невозможно текущей паре "состояние – входной символ" поставить в соответствие новое состояние. По сути это означает, что цепочка не принадлежит распознаваемому множеству, хотя она и не просмотрена до символа "конец цепочки". Такие ситуации в таблице переходов помечаются символом "error"; попав в такое состояние, КА отвергает проверяемую цепочку и переходит в начальное состояние.
КА всегда начинает работать из начального состояния s0
. Символы распознаваемой цепочки поступают посимвольно, начиная с первого, и изменяют состояния КА в соответствии с таблицей переходов. После поступления символа "конец цепочки" достигнутое автоматом состояние фиксируется и сравнивается с множеством допускающих состояний. На основании этого сравнения цепочка допускается или отвергается.
По сути КА работает как фильтр, который пропускает "правильные" цепочки. Другая трактовка КА – компактный алгоритм распознания регулярных, в том числе и бесконечных множеств, который строит программист перед началом кодирования.
Построение КА для распознания заданного множества цепочек – процесс творческий и неоднозначный. Теоретически для распознания одного и того же множества цепочек можно построить бесконечное множество КА. Описанный выше принцип распознания применим далеко не ко всякому регулярному множеству. Он эффективен в следующих случаях:
– распознаваемые цепочки содержат определенные сочетания символов в начале, конце или (и) середине цепочки;
– распознаваемые цепочки содержат ограниченное число повторений определенных символов или их сочетаний (не больше n; точно n; не меньше n, причем n = 1,2,3);
– распознаваемые цепочки содержат запрет на определенные сочетания символов в начале, конце или (и) во всей цепочке;
– распознаваемые цепочки содержат комбинации названных выше ограничений.
1.1.2 Эквивалентные состояния КА
Состояния s и t двух различных конечных автоматов эквивалентны тогда и только тогда, когда первый КА, начав работу из состояния s, будет допускать те же цепочки, что и второй КА, начав работу из состояния t. Если эти состояния начальные, то эти автоматы э
квивалентны.
Два состояния конечного автомата эквивалентны тогда и только тогда, когда, начав работу из этих состояний, конечный автомат будет допускать одни и те же цепочки.
Другими словами, если для двух состояний КА нет различающей цепочки, то такие состояния эквивалентны (различающая – такая цепочка символов, которая приводит КА из сравниваемых состояний к различным конечным результатам).
Эквивалентные состояния, принадлежащие одному КА, не нарушая эквивалентности, можно заменить одним (в таблице переходов оставить одну из строк эквивалентных состояний, удалив остальные, при этом заменить имена удаленных состояний на оставленное).
1.1.3
Недостижимые состояния КА
Недостижимыми называются такие состояния КА, которые не могут быть достигнуты из начального состояния воздействием любых входных символов.
Не нарушая эквивалентности, такие состояния можно исключить из таблицы переходов КА. Процедура поиска недостижимых состояний следующая:
Шаг 1: записать одноэлементное множество, в которое входит начальное состояние.
Шаг 2: дополнить это множество состояниями, в которые переходит КА из состояний, уже присутствующих в множестве при воздействии любых входных символов.
Шаг 3: если на шаге 2 множество не пополняется новыми элементами, то получен исчерпывающий список достижимых состояний; остальные состояния КА недостижимы
Конечный автомат, в котором исключены недостижимые и эквивалентные состояния называется минимальным КА.
1.2 Грамматики
1.2.1 Общие сведения
В расширенном представлении под термином "язык" понимают всякое средство общения, состоящее из:
– знаковой системы, т.е. множества допустимых последовательностей знаков;
– множества смыслов этой системы;
– соответствия между последовательностями знаков и смыслами, делающими осмысленными допустимые последовательности знаков.
Знаками могут быть буквы алфавита, математические обозначения, звуки, ритуальные действия и т.д. Hаука об осмысленных знаковых системах называется семиотикой. Hаиболее исследованными являются знаковые системы, у которых знаками являются символы алфавита. Правила, определяющие множество текстов (допустимых последовательностей знаков), образуют синтаксис языка; описание множества смыслов и соответствия между текстами и смыслами – семантику языка. К таким знаковым системам относятся естественные языки, языки различных областей науки, языки программирования.
Семантика языка существенно зависит от назначения языка, в то время, как для синтаксиса можно сформулировать понятия и методы, не зависящие от назначения и целей языка. Для исследования синтаксиса сложился специальный математический аппарат – теория формальных грамматик, в котором язык понимается уже не как средство общения, а как множество формальных объектов – последовательностей символов алфавита. Эти последовательности называют цепочками и язык понимают как множество цепочек.
Пусть задан алфавит V, в котором можно построить множество V*
(читается – итерация алфавита V) цепочек. Формальный язык L в алфавите V – это подмножество цепочек из V* (
L Ì
V*)
. Описание формальных языков осуществляется с помощью формальных порождающих грамматик (формальных грамматик).
Формальная порождающая грамматика G (в дальнейшем – грамматика G) – это формальная система, определяемая четверкой объектов:
G[Z] = (VN, VT, Z, P),
где VN - алфавит нетерминалов (вспомогательных символов);
VT – алфавит терминалов (основных символов);
Z – начальный символ (аксиома) грамматики;
P – конечное множество правил.
Hетерминалы принято обозначать большими буквами латинского алфавита, терминалы – малыми буквами. В алфавит нетерминалов обязательно входит начальный символ грамматики.
Каждое правило из множества P имеет вид x - y, – где x, y цепочки, состоящие из терминальных и нетерминальных символов. В дальнейшем будем рассматривать грамматики, содержащие только правила, левые части которых состоят из одного нетерминального символа (контекстно–свободные грамматики). При этом должно быть хотя бы одно правило, левая часть которого – начальный символ грамматики.
Грамматика описывает бесконечный язык, если хотя бы одно из правил рекурсивно, т. е. в правой части содержится его левая часть в явном или неявном виде.
Сентенциальная форма – любая цепочка терминальных и нетерминальных символов, которая получается на любом шаге процесса вывода. Множество сентенциальных форм можно получить из дерева вывода, обходя его по узлам и соблюдая следующие правила:
– начинать обход с самого левого узла;
– обход надо совершать так, чтобы при переходе к следующему узлу образованное поддерево не включало, как элемент, предыдущее поддерево.
Фраза – часть сентенциальной формы, выводимая из одного нетерминала за несколько шагов. Для простой фразы шаг вывода равен 1.
Одну и ту же цепочку можно получить, применяя правила в различных последовательностях (деревья выводов различны). Если для однозначности в процессе вывода на каждом шаге применять правило к самому левому(правому) нетерминалу в сентенциальной форме, то получим левосторонний(правосторонний) вывод.
Таким образом:
– Каждой цепочке выводимой в заданной грамматике соответствует одно или несколько деревьев вывода.
– Каждому дереву соответствует один или больше выводов.
– Каждому дереву соответствует единственный правый и единственный левый выводы.
– Если каждой цепочке, выводимой в данной грамматике, соответствует единственное дерево вывода, то такая грамматика называется однозначной (в правой части каждого правила такой грамматики содержится не более одного нетерминала).
Языком L(G), порождаемым грамматикой G, называется множество всех цепочек в алфавите терминальных символов VT, выводимых из начального символа грамматики.
1.2.2 Классификация грамматик
Общепринятой классификацией грамматик и порождаемых ими языков является иерархия Хомского, содержащая четыре типа грамматик (рисунок 1):
| 0-й тип
|
Правила имеют вид: x - y, где x и y – любые цепочки терминалов и нетерминалов
|
| С фразовой структурой.
|
1-й тип
|
Правила имеют вид x - y, где | x | <= | y | (правая цепочка не короче левой).
|
| контекстно–зависимые
(КЗ)
|
2-й тип
|
вид правил A - y, где A – нетерминал, y – любая цепочка
|
| контекстно–свободные (КС)
|
3-й тип – автоматные грамматики (вид правил A - aB или A - b или A-e где a,b–терминалы; A,B–нетерминалы;e-пустая цеп).
|
Рисунок 1 – Классификация грамматик
Каждый тип грамматик включает грамматики более высоких типов, как частные случаи.
Для построения распознавателей грамматик, других целей очень часто необходимо преобразовать правила исходной грамматики к соответствующему виду. При этих преобразованиях язык, порождаемый исходной и полученными после преобразования грамматиками не должен меняться.
1.2.3 Эквивалентные преобразования грамматик
Для построения распознавателей грамматик, других целей часто необходимо преобразовывать правила исходной грамматики к соответствующему виду. При этом язык, порождаемый исходной и полученными после преобразования грамматиками, не должен меняться.
Две грамматики эквивалентны, если они порождают один и тот же язык(одни и те же цепочки терминальных символов).Рассмотрим ряд процедур, которые всегда приводят к эквивалентным преобразованиям.
В множестве Р правил грамматики G непродуктивным называют нетерминал, из которого нельзя получить цепочку терминалов. Для поиска в множестве правил непродуктивных нетерминалов используется следующее свойство.
Свойство А: Если все символы правой части правила продуктивны, то продуктивен и символ, стоящий в его левой части.
Алгоритм поиска непродуктивных нетерминалов в множестве правил P грамматики G:
– составить список нетерминалов для которых найдется хотя бы одно правило, правая часть которого состоит только из терминалов;
– если найдется такое правило, что все нетерминалы, стоящие в его правой части уже занесены в список, то добавить в список нетерминал стоящий в его левой части;
– если на предыдущем шаге список не пополняется, то получен исчерпывающий список всех продуктивных нетерминалов.
Hетерминалы грамматики не попавшие в список, построенный по приведенному выше алгоритму, являются непродуктивными и, не нарушая эквивалентности, из множества правил Р можно удалить все правила, содержащие такие нетерминалы.
В множестве правил грамматики недостижимым называют нетерминал, который не участвует в процессе вывода. цепочек. Для поиска недостижимых нетерминалов используется следующее свойство.
Свойство Б: Если нетерминал в левой части правила является достижимым, то достижимы все нетерминалы, стоящие в правой части этого правила.
Алгоритм поиска недостижимых нетерминалов в множестве правил P грамматики G:
– образовать одноэлементный список из начального нетерминала грамматики;
– если в множестве Р найдено правило, левая часть которого уже в списке, то включить в список все нетерминалы из его правой части;
– если на предыдущем шаге список не пополняется, то получен исчерпывающий список всех достижимых нетерминалов.
Hетерминалы грамматики не попавшие в список, построенный по приведенному выше алгоритму, являются недостижимыми и, не нарушая эквивалентности, из множества правил Р можно удалить все правила, содержащие такие нетерминалы.
Не нарушая эквивалентности, можно также исключить правила такого вида: A - A или A - B, B - C, C - A (циклический блок правил).
1.2.5
Построение
грамматик
для заданного КА
Любое регулярное множество, которое распознается КА, можно описать с помощью автоматной грамматики. Алгоритм построения грамматики следующий:
– Начальное состояние КА - начальный символ грамматики.
– Алфавит КА (без символа конец цепочки–"┤") - терминальные символы грамматики.
– Множество состояний КА - нетерминальные символы грамматики.
– Если в таблице переходов КА есть переход из состояния А
в состояние В при воздействии входного символа х
– ввести правило следующего вида: А - xB.
– Если D– допускающее состояние КА, то ввести правило следующего вида: D-*,
где *– пустая цепочка(для отвергающих состояний правил нет).
– Закончить составление правил, когда будут обработаны все непустые клетки управляющей таблицы ("0" – пустая клетка).
2. Разработка программного продукта
2.1 Современные требования к программным продуктам
– Удобный, легкий в обращении интерфейс.
– В программе необходимо предусмотреть неквалифицированные действия пользователя.
– К программе должна прилагаться специально разработанная справочная система.
– Программа должна работать в разных операционных системах.
– Надёжность работы программы.
2.2 Область прикладного применения ПП
Представленный мною ПП является наглядным пособием для всех желающих изучить такую тему дискретной математики, как «Построение грамматики для заданного пользователем конечного автомата».
2.3 Обоснование выбора средств реализации
Программа написана в среде программирования Delphi 7.0 под Windows.
Основные характеристики среды разработки Delphi.
Delphi - это комбинация нескольких важнейших технологий:
–Высокопроизводительный компилятор в машинный код
– Объектно-ориентированная модель компонент
– Визуальное (а, следовательно, и скоростное) построение приложений из программных прототипов
– Масштабируемые средства для построения баз данных
Компилятор в машинный код. Компилятор, встроенный в Delphi, обеспечивает высокую производительность, необходимую для построения приложений в архитектуре “клиент-сервер”. Этот компилятор в настоящее время является самым быстрым в мире, его скорость компиляции составляет свыше 120 тысяч строк в минуту на компьютере 486DX33. Он предлагает легкость разработки и быстрое время проверки готового программного блока, характерного для языков четвертого поколения (4GL) и в то же время обеспечивает качество кода, характерного для компилятора 3GL. Кроме того, Delphi обеспечивает быструю разработку без необходимости писать вставки на Си или ручного написания кода (хотя это возможно).
В процессе построения приложения разработчик выбирает из палитры компонент готовые компоненты как художник, делающий крупные мазки кистью. Еще до компиляции он видит результаты своей работы - после подключения к источнику данных их можно видеть отображенными на форме, можно перемещаться по данным, представлять их в том или ином виде. В этом смысле проектирование в Delphi мало чем отличается от проектирования в интерпретирующей среде, однако после выполнения компиляции мы получаем код, который исполняется в 10-20 раз быстрее, чем то же самое, сделанное при помощи интерпретатора. Кроме того, компилятор компилятору рознь, в Delphi компиляция производится непосредственно в родной машинный код, в то время как существуют компиляторы, превращающие программу в так называемый p-код, который затем интерпретируется виртуальной p-машиной. Это не может не сказаться на фактическом быстродействии готового приложения.
Объектно-ориентированная модель программных компонент. Основной упор этой модели в Delphi делается на максимальном реиспользовании кода. Это позволяет разработчикам строить приложения весьма быстро из заранее подготовленных объектов, а также дает им возможность создавать свои собственные объекты для среды Delphi. Никаких ограничений по типам объектов, которые могут создавать разработчики, не существует. Действительно, все в Delphi написано на нем же, поэтому разработчики имеют доступ к тем же объектам и инструментам, которые использовались для создания среды разработки. В результате нет никакой разницы между объектами, поставляемыми Borland или третьими фирмами, и объектами, которые вы можете создать. В стандартную поставку Delphi входят основные объекты, которые образуют удачно подобранную иерархию из 270 базовых классов.
2.4 Структура разрабатываемого программного продукта.

Рисунок 2 – Структура разрабатываемого программного продукта
Рассматриваемая структура изображена на рисунке 2.
2.5 Блок-схема
Функциональная схема разработанного программного продукта приведена на рисунке 3.
     нет нет
да
Рисунок 3 – Функциональная схема программного продукта
2.6 Работа с ПП, справочной системой
Справочная система представлена в виде Web-страницы, что вызывается gри нажатии F7. Ссылка на адрес её расположения указана в листинге программы: WinExec('C:\Program Files\Internet Explorer\Iexplore.exe F:\Моя курсовая работа\Моя Web-страница\Справка.mht',1);
Запустите Primer4. Всплывает окно (рисунок 4):

Рисунок 4 – Главная форма
Вводим состояния и алфавит (рисунок 5):
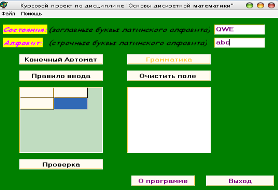
Рисунок 5 – Главная форма с заполненными строками
Нажимаем на кнопку «Конечный Автомат». Заполняем управляющую таблицу. Проверим конечный автомат (рисунок 6):
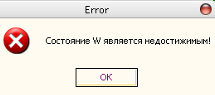
Таблица 1 – Компоненты программы
| Имя компонента в модуле
|
Назначение компонента
|
События компонента
|
Назначение обработчиков событий
|
Примечания
|
| MainMenu
|
Самая главная форма, где расположены все компоненты
|
| BitBtn1
|
Кнопка для создания конечного автомата
|
OnClick
|
Создание управляющей таблицы.
|
| BitBtn2
|
Кнопка выхода
|
OnClick
|
Закрытие программы.
|
| BitBtn3
|
Кнопка для создания граматики.
|
OnClick
|
Создания првил грмматики.
|
| BitBtn4
|
Кнопка для вызова правил ввода.
|
OnClick
|
Открывается форма с правилами ввода.
|
| BitBtn5
|
Кнопка проверки конечного автомата.
|
OnClick
|
Проверка конечного автомата на недостижимые символы.
|
| BitBtn6
|
Кнопка очистки поля
|
OnClick
|
Очищает поле, где расположены правила найденной грамматики.
|
| BitBtn7
|
Кнопка вызова справки о программном продукте.
|
OnClick
|
| Edit
|
Cтрока для ввода символов состояния и алфавита.
|
Ввод символов состоянии и алфавита конечного автомата.
|
| StringGrid
|
Компонент для управляющей таблицы
|
| ListBox
|
Поле для правил грамматики
|
В таком случае, невозможно построить грамматику. Строим конечный автомат, в котором все состояния достижимы. И только тогда строим грамматику. В таблице 1 предоставлена информация о компонентах программы.
3. Руководство пользователя, инструкция инсталяции
3.1 Требования к аппаратным средствам
При разработке программного комплекса было создано Win32 – приложение.
Требования к аппаратным средствам:
– Windows 95, Windows NT 4.0 и выше
– 2 Mb дискового пространства для минимальной конфигурации (только выполняемые файлы)
– 3 Mb дискового пространства для нормальной конфигурации (выполняемые файлы и тексты модулей, а также справка)
– Процессор 80486 (лучше 80586)
– 16 Mb RAM
3.2 Особенности запуска и работы с программой
Для нормального функционирования программного продукта следует выполнить следующее:
– Ознакомиться с файлом readme.txt;
– Создать папки на компьютере с таким адресом:
– 'C:\Program Files\Internet Explorer\Iexplore.exe F:\Моя курсовая работа\Моя Web-страница\Справка.mht
– Извлечь в данную папку все файлы из архива, копировать туда исполняющий файл программы (Primer4.exe), проследить чтобы также там был файл Справка. mht.
– Для начала работы с ПП запустите Primer4.exe.
3.3 Тестовые варианты программы (печатный и прописной вариант)
Для проверки работы программы можно использовать предложенные ниже тестовые варианты. В программе специально предусмотрены 2 тестовых варианта, которые будут рассмотрены ниже. При сравнении результатов анализа вручную и работы программы мы видим, что результат одинаков, что свидетельствует о правильности работы программы.
Пример 1.
Запустим файл Primer4.
exe.
Вводим состояния и алфавит (рисунок 7) и заполянем управляющую таблицу (рисунок 8):
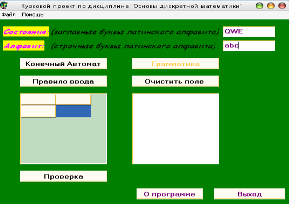
Рисунок 7 – Ввод состояний и алфавита
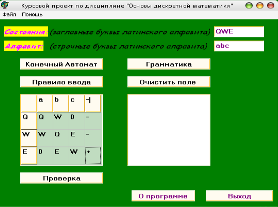
Рисунок 8 – Заполнение управляющей таблицы.
Строим грамматику (рисунок 9):
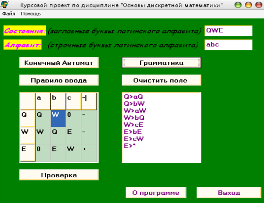
Рисунок 9 – Полученная граматика
Пример 2.
Запустим файл Primer4.
exe.
Вводим состояния и алфавит (рисунок 10), заполняем управляющую таблицу (рисунок 11):
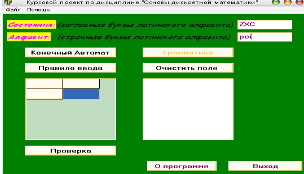
Рисунок 10 - Ввод состояний и алфавита
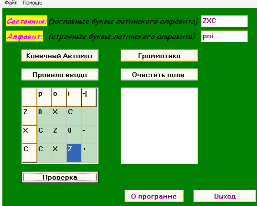
Рисунок 11 - Заполнение управляющей таблицы
Строим грамматику (рисунок 12):
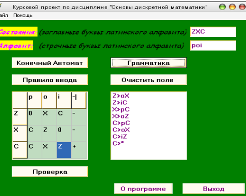
Рис.12 – Полученная граматика
Выводы
В рамках данной курсовой работы мною была разработана программа построения грамматики для заданного конечного автомата. А также я ознакомилась с теорией конечных автоматов и грамматик, научилась писать программы - конструкторы для построения автоматных грамматик закрепила умение работы в среде Delphi 7.0. Была создана справочная система в виде Web-страницы, в которой находится подробная справка по работе с программы продуктом. Написано вступление, где рассматривается общий обзор средств электронной связи.
Список литературы
1 Яблонский С.В. «Введение в дискретную математику: Учеб. пособие для вузов» / С.В Яблонский, - М.: Наука, 1986 – 384с.
2 «Разработка приложений в среде Delphi», -М.: Издательский дом “Вильямс”,2000.-464 с.
3 Грис Д.П. « Конструирование компиляторов для цифровых вычислительных машин» / Д.П. Грис, – М.: Мир, 1975. – 544 с.
4 Кузнецов О.П. «Дискретная математика для инженера» / О.П. Кузнецов, Г.М. Адельсон-Вельский, – М: Энергоатомиздат, 1988.– 480 с.
5 Лебедев А.Н.«Моделирование в научно-технических исследованиях» / А.Н.Лебедев, - М.:Москва 1989.-519с.
6 Суворова Н.И. «Информационное моделирование. Величины, объекты, алгоритмы » / Н.И. Суворова, - М.:2002.
7 Богдан М.П. «Краткий курс лекций по дисциплине “ Основы дискреной математики”» / М.П. Богдан, – Краматорск: ДГМА,2002.
8 Новиков Ф.А. «2Дискретная математика для программистов» / Новиков Ф.А., – СПб: Питер, 2000. – 304с.
Приложение
А
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons, Grids, Menus, HtmlHlp;
type
TForm1 = class(TForm)
StringGrid1: TStringGrid;
BitBtn1: TBitBtn;
Edit1: TEdit;
Label1: TLabel;
Edit2: TEdit;
Label2: TLabel;
Label4: TLabel;
Label5: TLabel;
BitBtn2: TBitBtn;
MainMenu1: TMainMenu;
N1: TMenuItem;
N2: TMenuItem;
N3: TMenuItem;
N4: TMenuItem;
N5: TMenuItem;
N6: TMenuItem;
ListBox1: TListBox;
BitBtn3: TBitBtn;
N7: TMenuItem;
N8: TMenuItem;
BitBtn4: TBitBtn;
BitBtn5: TBitBtn;
N9: TMenuItem;
BitBtn6: TBitBtn;
BitBtn7: TBitBtn;
procedure BitBtn1Click(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
procedure N2Click(Sender: TObject);
procedure N4Click(Sender: TObject);
procedure N5Click(Sender: TObject);
procedure N6Click(Sender: TObject);
procedure BitBtn3Click(Sender: TObject);
procedure N7Click(Sender: TObject);
procedure N8Click(Sender: TObject);
procedure BitBtn4Click(Sender: TObject);
procedure BitBtn5Click(Sender: TObject);
procedure N9Click(Sender: TObject);
procedure BitBtn6Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure BitBtn7Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses unit2,unit4,unit3;
var Sostin:set of char;
procedure TForm1.BitBtn1Click(Sender: TObject);
var s1,s2,s:string;
i,j:integer;
begin
s1:=Edit2.Text;
s2:=Edit1.Text;
StringGrid1.ColCount:=Length(s1)+2;
StringGrid1.RowCount:=length(s2)+1;
StringGrid1.Cells[Length(s1)+1,0]:='-|';
for i:=1 to Length(s2) do
StringGrid1.Cells[0,i]:=s2[i];
for i:=1 to Length(s1) do
StringGrid1.Cells[i,0]:=s1[i];
for i:=1 to length(s2)-1 do
for j:=i+1 to length(s2) do
if (s2[i]=s2[j]) then begin
MessageBox(form1.Handle,'Введи правильно состояния не должны повторяться!!!','Error',mb_ok or mb_iconerror);
edit1.SetFocus;
exit;
end;
for i:=1 to length(s2) do
if not ((s2[i]>='A') and (s2[i]<='Z')) then begin
MessageBox(form1.Handle,'Введите правильно состояния!!!', 'Error',mb_ok or mb_iconerror);
edit1.SetFocus;
exit;
end;
for i:=1 to length(s1)-1 do
for j:=i+1 to length(s1) do
if (s1[i]=s1[j]) then begin
MessageBox(form1.Handle,'Введи правильно буквы алфавита не должны повторяться!!!','Error',mb_ok or mb_iconerror);
edit2.SetFocus;
exit;
end;
for i:=1 to length(s1) do
if not ((s1[i]>='a') and (s1[i]<='z')) then begin
MessageBox(form1.Handle,'Введите правильно буквы алфавита!!!','Error',mb_ok or mb_iconerror);
edit2.SetFocus;
exit;
end;
for i:=0 to stringgrid1.ColCount-1 do
StringGrid1.ColWidths[i]:=(Stringgrid1.ClientWidth div stringgrid1. ColCount)-1;
for i:=0 to stringgrid1.RowCount-1 do
StringGrid1.RowHeights[i]:=(Stringgrid1.ClientHeight div stringgrid1. RowCount)-1;
Sostin:=['0'];
s:=Edit1.Text;
for i:=1 to Length(s) do
Sostin:=Sostin+[s[i]];
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
close;
end;
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
close;
end;
procedure TForm1.N2Click(Sender: TObject);
begin
close;
end;
procedure TForm1.N4Click(Sender: TObject);
begin
form3.ShowModal;
end;
procedure TForm1.N5Click(Sender: TObject);
begin
form2.ShowModal;
end;
procedure TForm1.N6Click(Sender: TObject);
var s1,s2:string;
i,j:integer;
begin
s1:=Edit2.Text;
s2:=Edit1.Text;
StringGrid1.ColCount:=Length(s1)+2;
StringGrid1.RowCount:=length(s2)+1;
StringGrid1.Cells[Length(s1)+1,0]:='-|';
for i:=1 to Length(s2) do
StringGrid1.Cells[0,i]:=s2[i];
for i:=1 to Length(s1) do
StringGrid1.Cells[i,0]:=s1[i];
for i:=1 to length(s2)-1 do
for j:=i+1 to length(s2) do
if (s2[i]=s2[j]) then begin
MessageBox(form1.Handle,'Введи правильно состояния не должны повторяться!!!','Error',mb_ok or mb_iconerror);
edit1.SetFocus;
exit;
end;
for i:=1 to length(s2) do
if not ((s2[i]>='A') and (s2[i]<='Z')) then begin
MessageBox(form1.Handle,'Введите правильно состояния!!!',' Error',mb_ok or mb_iconerror);
edit1.SetFocus;
exit;
end;
for i:=1 to length(s1)-1 do
for j:=i+1 to length(s1) do
if (s1[i]=s1[j]) then begin
MessageBox(form1.Handle,'Введи правильно буквы алфавита не должны повторяться!!!','Error',mb_ok or mb_iconerror);
edit2.SetFocus;
exit;
end;
for i:=1 to length(s1) do
if not ((s1[i]>='a') and (s1[i]<='z')) then begin
MessageBox(form1.Handle,'Введите правильно буквы алфавита!!!','Error',mb_ok or mb_iconerror);
edit2.SetFocus;
exit;
end;
for i:=0 to stringgrid1.ColCount-1 do
StringGrid1.ColWidths[i]:=(Stringgrid1.ClientWidth div stringgrid1. ColCount)-1;
for i:=0 to stringgrid1.RowCount-1 do
StringGrid1.RowHeights[i]:=(Stringgrid1.ClientHeight div stringgrid1. RowCount)-1;
end;
procedure TForm1.BitBtn3Click(Sender: TObject);
var i,j:integer;
stroka:string;
begin
ListBox1.Items.Clear;
for i:=1 to Stringgrid1.RowCount-1 do begin
stroka:='';
for j:=1 to Stringgrid1.ColCount-1 do begin
if (stringgrid1.Cells[j,i]>='A') and (stringgrid1.Cells[j,i]<='Z') then begin
stroka:=stroka+stringgrid1.Cells[0,i];
stroka:=stroka+'>'+stringgrid1.Cells[j,0];
stroka:=stroka+stringgrid1.Cells[j,i];
ListBox1.Items.Add(stroka);
end
else if (stringgrid1.Cells[j,i]='+') then begin
stroka:=stroka+stringgrid1.Cells[0,i];
stroka:=stroka+'>'+'*';
ListBox1.Items.Add(stroka);
end;
stroka:='';
end;
end;
end;
procedure TForm1.N7Click(Sender: TObject);
var i,j:integer;
stroka:string;
begin
ListBox1.Items.Clear;
for i:=1 to Stringgrid1.RowCount-1 do begin
stroka:='';
for j:=1 to Stringgrid1.ColCount-1 do begin
if (stringgrid1.Cells[j,i]>='A') and (stringgrid1.Cells[j,i]<='Z') then begin
stroka:=stroka+stringgrid1.Cells[0,i];
stroka:=stroka+'>'+stringgrid1.Cells[j,0];
stroka:=stroka+stringgrid1.Cells[j,i];
ListBox1.Items.Add(stroka);
end
else if (stringgrid1.Cells[j,i]='+') then begin
stroka:=stroka+stringgrid1.Cells[0,i];
stroka:=stroka+'>'+'*';
ListBox1.Items.Add(stroka);
end;
stroka:='';
end;
end;
end;
procedure TForm1.N8Click(Sender: TObject);
begin
form4.ShowModal;
end;
procedure TForm1.BitBtn4Click(Sender: TObject);
begin
form4.ShowModal;
end;
procedure TForm1.BitBtn5Click(Sender: TObject);
const Dop=['+','-'];
var dost:set of char;
i,j:integer;
sost:string;
nedost:boolean;
begin
for i:=1 to StringGrid1.RowCount-1 do
for j:=1 to StringGrid1.ColCount-1 do begin
if (j=StringGrid1.ColCount-1) then
if not (StringGrid1.Cells[j,i][1] in Dop) then begin
ShowMessage('Введен неверный символ!Н');
StringGrid1.Row:=i;
StringGrid1.Col:=j;
exit;
end
else
continue;
if not (StringGrid1.Cells[j,i][1] in Sostin) then begin
ShowMessage('Введен неверный символ!');
StringGrid1.Row:=i;
StringGrid1.Col:=j;
exit;
end;
end;
nedost:=false;
dost:=[];
sost:=StringGrid1.Cells[0,1];
dost:=dost+[sost[1]];
for i:=1 to StringGrid1.RowCount-1 do
for j:=1 to StringGrid1.ColCount-2 do begin
sost:=StringGrid1.Cells[j,i];
if (not (sost[1] in dost)) and (StringGrid1.Cells[0,i][1] in dost) then
dost:=dost+[sost[1]];
end;
for i:=1 to StringGrid1.RowCount-1 do
if not (StringGrid1.Cells[0,i][1] in dost) then begin
MessageBox(form1.Handle,pchar('Состояние '+StringGrid1.Cells[0,i][1]+' является недостижимым!!!'),'Error',mb_iconerror or mb_ok);
nedost:=true;
end;
if not nedost then
BitBtn3.Enabled:=true;
end;
procedure TForm1.N9Click(Sender: TObject);
begin
WinExec('C:\Program Files\Internet Explorer\Iexplore.exe F:\Моя курсовая работа\Моя Web-страница\Справка.mht',1);
end;
procedure TForm1.BitBtn6Click(Sender: TObject);
begin
ListBox1.Clear;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
Sostin:=[];
end;
procedure TForm1.BitBtn7Click(Sender: TObject);
begin
form2.ShowModal;
end;
end
|