| Учреждение образования Белорусский Государственный университет информатики и радиоэлектроники
Курсовой проект
«Проектирование устройств фильтрации»
Минск 2007 г.
2. Методика расчёта устройств фильтрации на операционных усилителях
3. Вывод передаточной функции фильтра
Фильтр Чебышева 8-ого порядка с неравномерностью в полосе пропускания 78%.
Передаточная характеристика фильтра нижних частот:
Построение графиков в нормированной системе координат:
ФНЧ
Построим амплитудно-частотную характеристику:
Фаза-частотная характеристика:
Характеристика рабочего затухания:
Характеристика группового время запаздывания:
Импульсная характеристика фильтра:
Переходная характеристика:
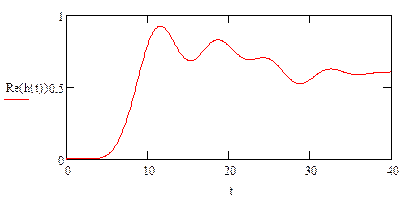
2Операция денормирования:
Передаточная характеристика.
Фаза-частотная характеристика.
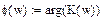
Характеристика рабочего затухания.
Хар-ка группового время запаздывания
Импульсная характеристика:
Переходная характеристика.
4.Разработка принципиальной схемы фильтра, расчёт элементов.
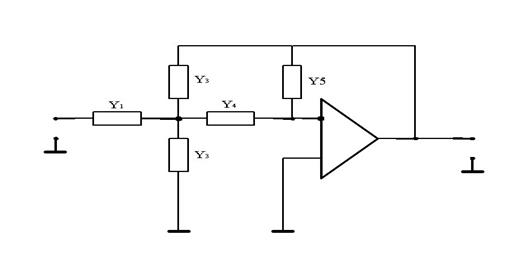 Постоим принципиальную схему фильтра нижних частот ( вид аппроксимации: Чебышева ) второго порядка на операционном усилителе. Фильтр нижних частот пропускает низкочастотные составляющие сигнала и задерживает высокочастотные, исходя из этого присутствие разделительных конденсаторов в ветвях схемы необходимо. Но в какой именно ветви должны стоять конденсаторы не известно, поэтому во все ветви поставим проводимости. Постоим принципиальную схему фильтра нижних частот ( вид аппроксимации: Чебышева ) второго порядка на операционном усилителе. Фильтр нижних частот пропускает низкочастотные составляющие сигнала и задерживает высокочастотные, исходя из этого присутствие разделительных конденсаторов в ветвях схемы необходимо. Но в какой именно ветви должны стоять конденсаторы не известно, поэтому во все ветви поставим проводимости.
Равенство токов обеспечивается тем, что операционный усилитель не потребляет тока. Ток I4 протекает через проводимость Y4 и втекает в ветвь с проводимостью Y5 без потерь.Выразим токи в ветвях через проводимости.
Разделим все члены уравнения на Uвых, для того чтобы возможно было определить коэффициент передачи.
Получим передаточную характеристику
Общая же формула передаточной характеристики фильтра нижних частот имеет вид:
Сравним два выражения.Из выражения видно, что числитель не зависит от частоты. Анализируя выражения передаточной характеристики фильтра сделал вывод о том, что проводимости Y4, Y3 и Y1 должны заменить резисторы, а проводимости Y2 и Y5 – емкости.
С учётом этого построим принципиальную схему фильтра.
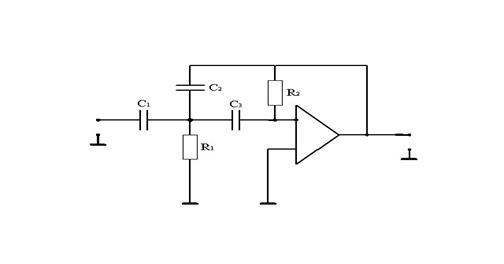 
 Если сравнить это выражение с передаточной характеристикой ФНЧ, то можно составить систему уравнений: Если сравнить это выражение с передаточной характеристикой ФНЧ, то можно составить систему уравнений:
В данной системе три уравнения и пять неизвестных. Встаёт вопрос: какие из этих величин обозначить константами. Сейчас производство довольно хорошо научилось делать разделительные конденсаторы и количество номинальных значений ёмкостей в них значительно больше чем сопротивлений у резисторов
Реклама

( значение погрешности в величинах также меньше ), поэтому решив эту систему задав ёмкости С1 и С2 постоянными величинами получим :
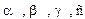 Так рассчитаем элементы четырёх фильтров второго прядка. Элементы второго фильтра второго порядка рассчитываются аналогично первому. Но здесь значения альфа и бэтта необходимо брать применительно ко второму элементу фильтрации нашего фильтра. Значения берутся в денормированном виде Так рассчитаем элементы четырёх фильтров второго прядка. Элементы второго фильтра второго порядка рассчитываются аналогично первому. Но здесь значения альфа и бэтта необходимо брать применительно ко второму элементу фильтрации нашего фильтра. Значения берутся в денормированном виде
4.2 Проверим правильность формул и найдём численные значения сопротивлений и ёмкостей применительно к каждому каскаду.
1. Первый фильтр второго порядка:
2. Второй фильтр второго порядка
3. Третий фильтр второго порядка
:
4. Четвёртый фильтр второго порядка
:
Запишем выражение передаточной функции для каждого каскада фильтрации, но уже с учётом выражений для сопротивлений и ёмкостей. Так как фильтр чётного порядка, то для вычисления используется одна формула:
Составляя общий коэффициент передачи для фильтра 8-ого порядка необходимо перемножить коэффициенты передачи каждого промежуточного каскада фильтрации:
Теперь если построить график амплитудно-частотной характеристики, то можно сделать вывод, что элементы фильтра с многопетлевой обратной связью рассчитаны верно. Графики совпадают.
|