| Федеральное государственное образовательное учреждение среднего профессионального образования
«Омский промышленно-экономический колледж»
КУРСОВАЯ РАБОТА
по дисциплине «Математические методы»
Тема: «Теория игр»
Выполнил:
Каримов Руслан Ринатович
3 курс, БП 2 - 117
Руководитель:
Белгородцева Наталья Александровна
Оценка:________________
Дата защиты:___________
2010
Содержание
Введение
Обзор литературы
1. Основные понятия теории игр
2. Игры с противодействием и нулевой суммой
3. Графический метод решения игровых задач с нулевой суммой
3.1 Решение задач графическим методом
4. Сведение задач теории игр к задачам линейного программирования
4.1 Решение задач
5. Игры с природой (без противодействия)
5.1 Решение задач
Заключение
Список используемой литературы
Введение
Проблема выполнения различных вычислений была актуальна во все времена. По мере развития общественно-экономических отношений усложнялись поставленные задачи, которые для своего решения требовали разработки новых методов вычислений. На смену простейшим арифметическим и геометрическим вычислениям пришли алгебраические и тригонометрические вычисления. Организация современного производства требует не только наличия современных станков и оборудования, но и разработки новых технологических процессов и современных методов управления производством. Для решения каждой из поставленных задач разрабатываются математические модели, анализируя которые удается найти наилучшее решение поставленной задачи. Создание математической модели – сложная кропотливая работа, которая в современных условиях под силу коллективам разработчиков. Для создания математической модели одного и того же объекта различные коллективы могут использовать различный математический аппарат. После создания математической модели специалистами-аналитиками за дело принимаются специалисты-программисты, которые реализуют созданную модель в виде программных кодов. Далее с математической моделью работают специалисты-практики. Целенаправленно воздействуя на модель, они изучают ее поведение и подбирают оптимальный режим работы для реального объекта. Одной из таких моделей является игровая модель и поиск стратегий поведений в условиях полной или частичной неопределенности. В очень редких (исключительных) случаях для игровых моделей можно определить количественную оценку или указать оптимальное решение. В игровых моделях не ставится задача найти какое-то числовое решение, а требуется лишь или очертить область возможных решений, или предоставить некоторые дополнительные сведения о возможном развитии событий и рекомендовать правила поведения.
Реклама

Обзор литературы
Для написания курсовой работы по дисциплине «Математические методы» на тему «Теория игр» я воспользовался следующей литературой:
-« Математические методы в программировании » : / Агальцов В.П., Волдайская И.В. Учебник : – М . : ИД «ФОРУМ» : ИНФРА-М, 2006. – 224с. : ил. – (Профессиональное образование). – (Учимся программировать).
-Лекции по дисциплине «Математические методы».
-«Математические методы: Учебник» / Партика Т.Л., Попов И.И. – М: ФОРУМ: ИНФРА, 2005.
-«Математическое программирование» / Костевич Л., издательство «Новое знание», 2003.
В одной из книг например «Математические методы в программировании»: / Агальцов В.П., Волдайская И.В. Учебник : – М . : ИД «ФОРУМ» : ИНФРА-М, 2006 написано понятней, если сравнивать с другими книгами, которыми я пользовался. Но в этой книге есть темы, которые отсутствуют или объяснены без теории, а на конкретном примере и тогда сложнее понять, о чем идет речь данной теме. Тогда я обращаюсь к другим источникам литературы в них, конечно, есть теория, но она сложнее и более углубленная. В одном из источников мне понравилась тема «Игры с природой (без противодействия)» и я решил изучить ее самостоятельно.
1.
Основные понятия теории игр
Цель теории игр – выработка рекомендаций для различного поведения игроков в конфликтной ситуации, т.е. выбор оптимальной стратегии для каждого из них. Различают два больших класса игровых моделей: модели без противодействия (или их еще называют «играми с природой») и модели с противодействием (действия конкурентов на рынке).
Игры с противодействием часто называют конфликтными ситуациями, которые широко распространены в обществе. Например, конкурентная борьба в экономике, в спортивных соревнованиях, состязание сторон в ходе судебного заседания и т.д. Игровая модель, в отличии от конфликтной ситуации, строится по определенным законам, а игроки придерживаются определенных правил.
Развитие игры во времени представляется как ряд последовательных «ходов». Ходы могут быть сознательные и случайные. Случайный ход – результат, получаемый не решением игрока, а каким либо механизмом случайного выбора (покупательский спрос, задержка с поставкой материалов и т.п.). Сознательный ход – выбор игроком одного из возможных вариантов действия (стратегий) и принятие решения о его осуществлении.
Реклама

Конфликтная же ситуация, строго говоря, развивается спонтанно.
Участниками игры (конфликтной ситуации) могут быть минимум два человека (парная игра) или несколько человек (множественная игра). Игра развивается по оговоренным правилами. Игроки по очереди делают свои ходы. Естественно, перед каждым ходом игрок может или сохранить предыдущую стратегию или применить новую стратегию. Если игрок при выборе очередного хода придерживаются каких-либо правил, то такая игра носит название стратегической. Однако игрок во время игры может менять вариант своего поведения (но не правил), т.е. сменить стратегию.
Возможные варианты (исходы) игры сводятся в прямоугольную таблицу (табл. 1.1) – платежную матрицу, в которой строки соответствуют различным стратегиям игрока А, столбцы – стратегиям игрока В, ai j называется выигрыш первого игрока.
Таблица 1.1
| Стратегии
|
В1
|
В2
|
…
|
В n
|
| А1
|
a11
|
a12
|
…
|
a1n
|
| А2
|
a21
|
a22
|
…
|
a2n
|
| …
|
…
|
…
|
…
|
…
|
| А m
|
am1
|
am2
|
…
|
amn
|
Если игра содержит ограниченное количество стратегий, то такая игра называется конечной. В противном случае – бесконечной.
Стратегия, приносящая игроку максимальный выигрыш, называется оптимальной. Для нахождения оптимальной стратегии необходимо проанализировать все возможные стратегии и рассчитывать на то, что разумный противник на каждую из них будет отвечать такой, при которой выигрыш игрока А минимален. Обычно минимальные числа в каждой строке обозначаются α i и выписываются в виде добавочного столбца матрицы (табл. 1.2). В каждой строке будет свое α i = min aij . Предпочтительной для игрока А является стратегия, при которой α i обращается в максимум, т.е.
α = max (min aij),
где α – гарантированный выигрыш (максимин).
Если придерживаться максиминной стратегии, то при любом поведении стороны В (конкурента) гарантирован выигрыш, во всяком случае не меньше α . Поэтому α называют также ценой игры – тот гарантированный минимум, который можно обеспечить при наиболее осторожной (перестраховочной) стратегии.
Очевидно, что аналогично распределения можно провести и для конкурента В, который должен рассмотреть все свои стратегии, выделяя для каждой из них максимальные значения выигрыша:
β = min (max aij),
которое дает минимаксный выигрыш, или минимакс.
Такая β – стратегия – минимаксная, придерживаясь которой стороне В гарантировано, что в любом случае она проигрывает не больше β, поэтому β называют верхней ценой игры.
Если α = β = С, то число С называют чистой ценой игры или седловой точкой.
Для игры с седловой точкой нахождение решения состоит в выборе пары максиминной и минимаксной стратегий, которые являются оптимальными, так как любое отклонение от этих стратегий приводит к уменьшению выигрыша первого игрока и увеличению проигрыша второго игрока по сравнению с ценой игры С.
Таблица 2
| В1
|
В2
|
…
|
В n
|
α i
|
| А1
|
a11
|
a12
|
…
|
a1n
|
α 1
|
| А2
|
a21
|
a22
|
…
|
a2n
|
α 2
|
| …
|
…
|
…
|
…
|
…
|
…
|
| А m
|
am1
|
am2
|
…
|
amn
|
α i
|
| βi
|
β1
|
β2
|
…
|
βn
|
Наиболее полно разработан математический аппарат игр с нулевой суммой, когда выигрыш одного игрока равен проигрышу другого игрока, т.е. общая сумма выигрыша всех игроков равна нулю.
При построении игровых моделей предполагается, что каждый из игроков будет выбирать только лучшую (для себя) стратегию.
Результатом исследования игровой модели является определение наиболее осторожной стратегии поведение игрока, либо обеспечение гарантированного выигрыша (как правило, минимального), либо сведение к минимуму проигрыша. Риски при получении большого выигрыша не учитываются и не оцениваются.
Таким образом, результаты исследования игровых моделей указывают на оптимальную стратегию поведения (гарантированный выигрыш), а какой стратегией воспользуется игрок в реальной жизни – дело самого игрока.
2.
Игры с противодействием и нулевой суммой
Предположим, что имеются две конкурирующие фирмы, выпускающие однотипные товары. Для обеспечения наибольшей прибыли обе фирмы разработали стратегии реализации товара. В общем случае это можно записать в виде матрице (табл. 1.1).
 Пусть фирма А разработала четыре стратегии, а фирма В – пять стратегий. Пусть фирма А разработала четыре стратегии, а фирма В – пять стратегий.
 То есть фирма А - А1; А2; А3; А4 Аi , где i = 1,4. То есть фирма А - А1; А2; А3; А4 Аi , где i = 1,4.
  Фирма В соответственно - В1; В2; В3; В4; В5 Вj , где j = 1,5. Фирма В соответственно - В1; В2; В3; В4; В5 Вj , где j = 1,5.
Каждая фирма от реализации своей стратегии предполагает получить какой-то доход (табл. 2.1).
Таблица 2.1
| Стратегии
|
В1
|
В2
|
В3
|
В4
|
В5
|
| А1
|
5
|
8
|
7
|
5
|
4
|
| А2
|
1
|
10
|
5
|
5
|
6
|
| А3
|
2
|
4
|
3
|
6
|
2
|
| А4
|
3
|
5
|
4
|
4
|
3
|
Если фирма А выберет первую стратегию, то минимальный доход составит 4. Минимальный доход от второй стратегии – 1; от третьей – 2; от четвертой – 3. У фирмы В имеется в наличии пять стратегий. Использование первой стратегии обернется убытком в 1 единицу; второй (убыток) – 4; третьей – 3, четвертой – 4 и пятой – 2.
На первый взгляд фирма А должна избрать вторую стратегию (А2), чтобы получить выигрыш 10, но в ответ вторая фирма изберет первую стратегию (В1) и выигрыш фирмы А составит только 1.
Поэтому цель первой фирмы можно сформулировать так: получить максимальный доход из возможных минимальных. Введем в табл. 2.1 дополнительную строку и дополнительный столбец, в которых укажем возможные минимальные прибыли и максимальные (табл. 2.2).
Таблица 2.2
| Стратегии
|
В1
|
В2
|
В3
|
В4
|
В5
|
Минимальная прибыль фирмы А
|
| А1
|
5
|
8
|
7
|
5
|
4
|
4
|
| А2
|
1
|
10
|
5
|
5
|
6
|
1
|
| А3
|
2
|
4
|
3
|
6
|
2
|
2
|
| А4
|
3
|
5
|
4
|
4
|
3
|
3
|
| Максимальный убыток фирмы В
|
5
|
10
|
7
|
6
|
6
|
Исходя из данных (табл. 2.2) фирме А надо придерживаться стратегии А1 , а фирме В – стратегии В1 . Таким образом, гарантированный минимальный доход фирмы А составит 4, а минимально возможный убыток, который понесет фирма В, составит 5 (минимально возможный проигрыш).
Минимальный гарантированный выигрыш называется нижней ценой игры. При плохой игре фирмы В выигрыш может быть и большим.
Минимально возможный проигрыш называется верхней ценой игры.
Для нашего примера нижняя цена игры составляет 4 (минимальный гарантированный выигрыш фирмы А), а верхняя цена игры – 5 (минимально возможный проигрыш фирмы В). Приведенные выше рассуждения хороши, если конкурирующая фирма заранее не знает, как себя поведет противник. Если конкурирующая фирма ознакомлена с планами конкурента, то она может выбрать другую стратегию (отличную от осторожной стратегии) и получить больший выигрыш (доход).
Таким образом, приведенные осторожные стратегии являются неустойчивыми по отношению к дополнительной информации.
На практике иногда случается, что нижняя цена игры равна верхней цене игры. В этом случае говорят об устойчивых стратегиях игроков (конкурирующих фирм) или о задачах с седловой точкой. Задача с седловой точкой представлена в (табл. 2.3).
Таблица 2.3
| Стратегии
|
В1
|
В2
|
В3
|
В4
|
В5
|
Минимальная прибыль фирмы А
|
| А1
|
4
|
8
|
7
|
5
|
4
|
4
|
| А2
|
1
|
10
|
5
|
5
|
6
|
1
|
| А3
|
2
|
4
|
3
|
6
|
2
|
2
|
| А4
|
3
|
5
|
4
|
4
|
3
|
3
|
| Максимальный убыток фирмы В
|
4
|
10
|
7
|
6
|
6
|
Стратегии обоих противников в задачах с седловой точкой называются оптимальными и не зависят от дополнительно полученной информации. В специальной литературе доказано, что если при исследовании игровой модели известна вся предыстория (все ранее сделанные ходы), то существуют оптимальные (чистые) стратегии поведения игроков (конкурентов).
Если игровая задача не имеет седловой точки, то на практике конкурирующие фирмы (игроки) используют смешанные стратегии, т.е. попеременно используют две или более стратегий. В этом случае использование фирмой А нескольких стратегий можно записать как сумму вероятностей использования каждой стратегии Sa= p1+ p2+ …+ pm .
Соответственно, использование нескольких стратегий фирмой В можно записать Sb= q1+ q2+ …+ qn . Поэтому в общем случае исследование игровой модели сводится к определению вероятностей использования конкретных стратегий каждой фирмой (игроком).
3. Графический метод решения игровых задач с нулевой суммой
Суть графического метода состоит в том, что из матрицы удаляют дублирующие и поглощаемые строки и столбцы. Дублирующими называют полностью одинаковые строки или столбцы. Доминирующей строкой называется такая строка, которая содержит элементы, большие или равные соответствующим элементам другой строки, называемой поглощаемой. Доминирующим столбцом называется такой, который содержит элементы, меньше или равные соответствующим элементам другого столбца, который называется поглощаемым.
Воспользуемся табл. 2.1.
Строка (стратегия) А1 является доминирующей по отношению к строке (стратегии) А4 , так как содержит элементы, большие соответствующих элементов строки А4 . Соответственно строка А4 является поглощаемой и из дальнейшего рассмотрения удаляется (табл. 3.1).
Таблица 3.1
Первый шаг упрощения таблицы
| Стратегии
|
В1
|
В2
|
В3
|
В4
|
В5
|
| А1
|
5
|
8
|
7
|
5
|
4
|
| А2
|
1
|
10
|
5
|
5
|
6
|
| А3
|
2
|
4
|
3
|
6
|
2
|
Первый столбец является доминирующим по отношению ко второму, третьему и четвертому столбцам (поглощаемым). Поступаем аналогично (табл. 3.2).
Таблица 3.2
Второй шаг упрощения таблицы
| Стратегии
|
В1
|
В5
|
| А1
|
5
|
4
|
| А2
|
1
|
6
|
| А3
|
2
|
2
|
Еще раз рассматриваем строки. Первая строка поглощает третью строку. Поглощаемые строки (столбцы) содержат самые плохие стратегии. Окончательно получим (табл. 3.3).
Таблица 3.3
Третий шаг упрощения таблицы
| Стратегии
|
В1
|
В5
|
| А1
|
5
|
4
|
| А2
|
1
|
6
|
Вероятность использования первой фирмой первой стратегии обозначим через p1. Тогда вероятность использования второй стратегии первым игроком будет p2 = 1- p1 . Ожидаемый выигрыш фирмы А от применения
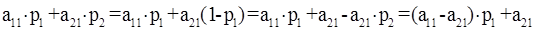 (3.1) (3.1)
вторым игроком первой стратегии составит:
Аналогичным способом получим ожидаемый выигрыш фирмы А от применения вторым игроком:
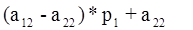 (3.2) (3.2)
В выражения (3.1) и (3.2) подставим конкретные значения.
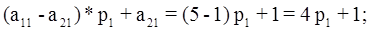
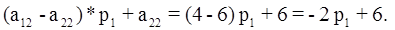
На оси х отложим две точки 0 и 1. Через эти точки проведем прямые линии, параллельные оси у. Затем в первое выражение подставим 0 вместо p1, а потом – единицу. И по двум точкам построим прямую линию.
Аналогично построим вторую прямую линию. Пересечение двух прямых линий и даст решение задачи (рис. 3.1).
Рис. 3.1 . Графический способ определения стратегий фирмы А
4p1 + 1= - 2p1 + 6
4p1 + 2p1 = - 1 + 6
6p1 = 5
p1 = 0,83
Итак, вероятность использования первой стратегии фирмой А
составляет 0,83 (p
1
= 0,83), а второй стратегии p2
= 1 – 0,83 – соответственно 0,17 (p
2
= 0,17).
Аналогично определим оптимальную стратегию поведения фирмы В:
Пусть у1 – вероятность выбора второй игрой 5 стратегией, у2 - 6 стратегией. (p4 + p5 = 1, p5 = 1- p4)
(a11 – a12) · у1 + a12 = (5 – 4) у1 + 4 = у1 + 4;
(a21 – a22) · у1 + a22 = (1 – 6) у1 + 6 = -5 у1 + 6.
Рис. 3.2 . Графический способ определения стратегий фирмы В
у1
+ 4 = -5 у1
+ 6
6 у1
=
2
у1
=
0,33
Вероятность использования первой стратегии фирмой В
составляет 0,33 (у
1
= 0,33), а второй стратегии у
2
=
1- 0,33 – соответственно 0,67 (у
2
= 0,67).
3.1 Решение задач графическим методом
Пример 1: Рассмотрим игру заданной платежной матрицей:
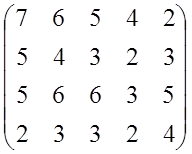 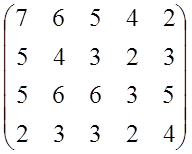
Решение:
Проверим есть ли седловая точка :
α = max (2,2,3,2) = 3
β = min (7,6,6,4,5) = 4 α ≠ β
Седловой точки нет, игра в чистых стратегиях не решается. Найдем смешанную стратегию игроков. Посмотрим, можно ли удалить не выгодную стратегию для игроков. Для первого игрока невыгодной считается та стратегия, которая, обеспечивает выигрыш меньший, чем какая либо другая. Для второго игрока считается та стратегия не выгодной, которая обеспечить проигрыш больший, чем другая стратегия.
| Невыгодные стратегии для первого игрока:
|
4, 2
|
| Невыгодные стратегии для второго игрока:
|
1, 2, 3
|
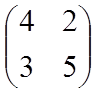
Пусть p
1
– вероятность с которой первый
игрок должен применять 1 стратегию, p
3
– вероятность применения 3 стратегией, p
3
=
1- p
1
.
Ожидаемый выигрыш 1 игрока, если второй выбрал 4 стратегию:
p1 · 4 + (1 - p1) · 3 = p1 + 3;
Ожидаемый выигрыш 1 игрока, если второй выбрал 5 стратегию:
p1 · 2 + (1 - p1) · 5 = -3 p1 + 5;
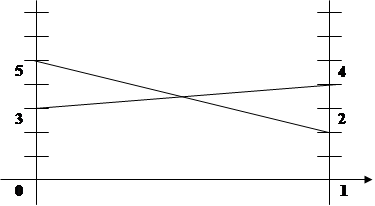
p
1
+ 3 = -3 p
1
+ 5
4 p
1
= 2
p
1
= 1/2 , p
3
=1/2 .
Первому игроку для получения гарантированного выигрыша 3,5 (1/2+3) рекомендуется чередовать стратегии 1 и 3.
Рассмотрим второго игрока.
Пусть p4 – вероятность выбора вторым игроком 4 стратегией, p5 - 5 стратегией. (p4 + p5 = 1, p5 = 1- p4)
Ожидаемые проигрыш второго игрока, если первый выберет 1 стратегию.
p4 · 4 + (1- p4) · 2 = 2 p4 + 2
Ожидаемые проигрыш второго игрока, если первый выберет 3 стратегию.
p4 · 3 + (1- p4) · 5 = -2 p4 + 5
2 p
4
+ 2 = -2 p
4
+5
4 p
4
=3
p
4
=3/4
p
5
=1/4
ν = 3/4 · 2 + 2 = 3,5
Ответ : Из 4 игр 3 надо сыграть 4 стратегией, 1 игру – 5 стратегией, и тогда проигрыш будет не больше 3,5, для первого игрока 1 надо сыграть 2 стратегией и 1 – второй стратегией.
Пример 2: Решить игру, заданную матрицей
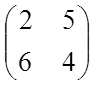
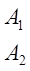
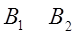
Решение:
Проверим если ли седловая точка:
α = max (2,4) = 4
β = min (6,5) = 5 α ≠ β
седловой точки нет, игра в чистой стратегии не решается. Найдем смешанную стратегию игроков. Т.к. игровая матрица задана первоначально в размерности 2×2, значит убирать столбцы или строки не нужно.
Ожидаемый выигрыш 1 игрока если второй выбрал 1 стратегию:
А1 · 2 + (1 - А1) · 6 = -4А1 + 6;
Ожидаемый выигрыш 1 игрока если второй выбрал 2 стратегию:
А1 · 5 + (1 - p1) · 4 = А1 + 4;
- 4 А1
+ 6 = А1
+ 4
- 4 А1
+ А1
= 4 – 6
- 5 А1
= - 2
А1
= 2/5 , А2
= 3/5.
Первому игроку для получения гарантированного выигрыша 4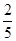 , ,
(2/5+4) рекомендуется играть 1 стратегией.
Рассмотрим второго игрока.
Пусть В1 – вероятность выбора второй игрой 4 стратегией,
(В1 + В2 = 1, В2 = 1- В1)
Ожидаемый проигрыш второго игрока, если первый выберет 1 стратегию.
В1 · 2 + (1- В1) · 5 = - 3 В1 + 5
Ожидаемый проигрыш второго игрока, если первый выберет 2 стратегию.
В1 · 6 + (1- В1) · 4 = 2 В1 + 4
- 3 В1
+ 5 = 2 В1
+ 4
- 3 В1
– 2 В1
= 4 – 5
- 5 В1
= - 1
В1
= 1/5 , В2
= 4/5.
ν = 1/5 · 2 + 4 = 4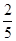
Ответ : Из 2 игр 2 надо сыграть 1 стратегией, 1 игру – 2 стратегией, и тогда проигрыш будет не больше 4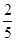 . .
Пример 3: Решить игру, заданную матрицей
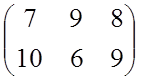
Проверим если ли седловая точка:
α = max (7,6) = 7
β = min (10,9,9) = 9 α ≠ β
седловой точки нет, игра в чистой стратегии не решается. Найдем смешанную стратегию игроков. Посмотрим, можно ли удалить не выгодную стратегию для игроков. Для первого игрока невыгодной считается та стратегия, которая, обеспечивает выигрыш меньший, чем какая либо другая. Для второго игрока считается та стратегия не выгодной, которая обеспечить проигрыш больший, чем другая стратегия.
| Невыгодная стратегия для второго игрока:
|
3
|
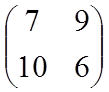
Ожидаемый выигрыш 1 игрока, если второй выбрал 1 стратегию:
p
1
· 7 + (1 -
p
1
) · 10 = -3
p
1
+ 10;
Ожидаемый выигрыш 1 игрока, если второй выбрал 2 стратегию:
p1 · 9 + (1 - p1) · 6 = 3 p1 + 6;
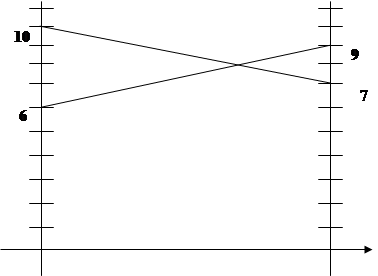
-
3p
1
+ 10 = 3 p
1
+ 6
-
3p
1
-
3p
1
= -10 + 6
-
6p
1
= -4
p
1
= 2/3 , p
2
=1/3 .
Первому игроку для получения гарантированного выигрыша 7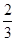 , (2/3+7) рекомендуется играть 1 стратегией. , (2/3+7) рекомендуется играть 1 стратегией.
Рассмотрим второго игрока.
Ожидаемые проигрыш второго игрока если первый выберет 1 стратегию.
p4 · 7 + (1- p4) · 9 = -2 p4 + 9
Ожидаемые проигрыш второго игрока если первый выберет 2 стратегию.
p4 · 10 + (1- p4) · 6 = 4 p4 + 6
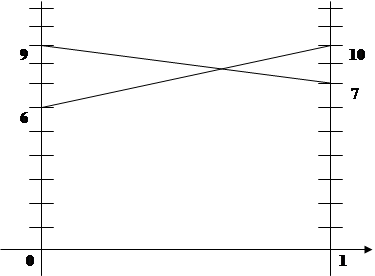
-
2p
4
+ 9 = 4 p
4
+ 6
-
2p
4
-
4p
4
= 6 – 9
-
6p
4
= -3
р4
= 1/2 , p
5
=1/2 .
Ответ : Из 2 игр (для первого) 2 надо сыграть 3 стратегией и 1 – 3 стратегией, (для второго) 1 надо сыграть 2 стратегией и 1 – 2 стратегией.
Пример 4: Решить игру, заданную матрицей
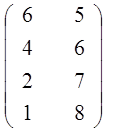
Проверим если ли седловая точка:
α = max (5,4,2,1) = 5
β = min (6,8) = 6 α ≠ β
седловой точки нет, игра в чистой стратегии не решается. Найдем смешанную стратегию игроков.
Посмотрим можно ли удалить не выгодную стратегию для игроков Для первого игрока невыгодной считается та стратегия, которая, обеспечивает выигрыш меньший, чем какая либо другая. Для второго игрока считается та стратегия не выгодной, которая обеспечить проигрыш больший, чем другая стратегия.
| Невыгодная стратегия для первого игрока:
|
2,3
|

Ожидаемый выигрыш 1 игрока, если второй выбрал 1 стратегию:
p
1
· 6 + (1 - p
1
) · 1 = 5 p
1
+ 1;
Ожидаемый выигрыш 1 игрока, если второй выбрал 2 стратегию:
p
1
· 5 + (1 - p
1
) · 8 = -3 p
1
+ 8;
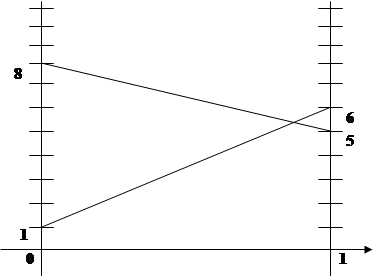
5 p1
+ 1 = -3 p1
+ 8
5 p1
+
3p1
= 8 – 1
8 p1
= 7
p1
= 7/8 , p2
=1/8 .
Рассмотрим второго игрока.
Ожидаемые проигрыш второго игрока, если первый выберет 1 стратегию.p4 · 6 + (1- p4) · 5 = p4 + 5
Ожидаемые проигрыш второго игрока, если первый выберет 2 стратегию.
p4 · 1 + (1- p4) · 8 = -7 p4 + 8
p4
+ 5 = -7 p4
+ 8
p4
+ 7 p4
= 8 – 5
8 p4
= 3
р
4
= 3/8 , p5
=5/8 .
u
= 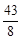 . .
Ответ : Из 4 игр (для первого) 7 надо сыграть 8 стратегией и 1 – 8, (для второго) 3 надо сыграть 8 стратегией и 5 – 8.
4. Сведение задач теории игр к задачам линейного
программирования
Предположим, что цена игры положительна (u > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.
Свойство 1. Тройка (хо, yо, u) является решением игры G = (Х,Y,А) тогда и только тогда, когда (хо, yо, кu +а) является решением игры G(Х,Y,кА+а), где а – любое вещественное число, к > 0.
Свойство 2. Для того, чтобы хо = (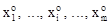 ) была оптимальной смешанной стратегией матричной игры с матрицей А и ценой игры u, необходимо и достаточно выполнение следующих неравенств ) была оптимальной смешанной стратегией матричной игры с матрицей А и ценой игры u, необходимо и достаточно выполнение следующих неравенств
 (j = (j = 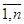 ) ) 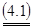
Аналогично для игрока 2 : чтобы yо = (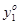 , ..., , ...,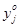 , ..., , ...,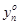 ) была оптимальной смешанной стратегией игрока 2 необходимо и достаточно выполнение следующих неравенств: ) была оптимальной смешанной стратегией игрока 2 необходимо и достаточно выполнение следующих неравенств:
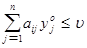 (i = (i = 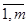 ) ) 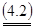
Из последнего свойства вытекает: чтобы установить, является ли предполагаемые (х, y) и u решением матричной игры, достаточно проверить, удовлетворяют ли они неравенствам (*) и (**). С другой стороны, найдя неотрицательные решения неравенств (*) и (**) совместно со следующими уравнениями
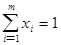 , , 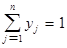 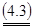
получим решение матричной игры.
Итак, пусть дана матричная игра с матрицей А порядка m х n. Согласно свойству 7 оптимальные смешанные стратегии х = (х1, ..., хm), y = (y1, ..., yn) соответственно игроков 1 и 2 и цена игры u должны удовлетворять соотношениям.
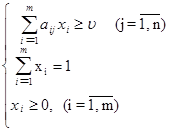 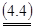
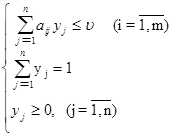 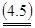
Разделим все уравнения и неравенства в (4.4) и (4.5) на u (это можно сделать, т.к. по предположению u > 0) и введём обозначения:
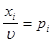 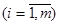 , , 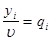 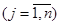 , ,
Тогда (1) и (2) перепишется в виде:
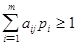 , , 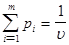 , , 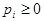 , , 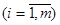 , ,
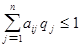 , , 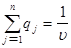 , , 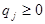 , , 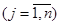 . .
Поскольку первый игрок стремится найти такие значения хi и, следовательно, pi , чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений pi 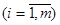 , при которых , при которых
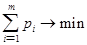 , , 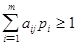 . . 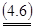
Поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры u была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj, 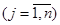 , при которых , при которых
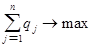 , , 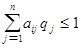 . . 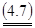
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).
Решив эти задачи, получим значения pi 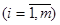 , qj , qj 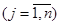 и u.Тогда смешанные стратегии, т.е. xi и yj получаются по формулам: и u.Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:
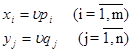 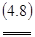
4.1 Решение задач
Пример 5: Найти решение игры, определяемой матрицей.
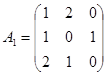
Решение.
Составим теперь пару взаимно-двойственных задач :
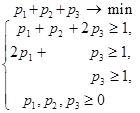 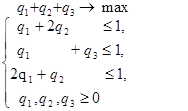
Решим вторую из них
| Б.п.
|
q1
|
q2
|
q3
|
q4
|
q5
|
q6
|
Решение
|
å
|
Отношение
|
| 
|
-1
|
-1
|
-1
|
0
|
0
|
0
|
0
|
-3
|
|  q4 q4
|
1
|
2
|
0
|
1
|
0
|
0
|
1
|
5
|
—
|
| q5
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
4
|
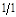
|
| q6
|
2
|
1
|
0
|
0
|
0
|
1
|
1
|
5
|
—
|
| Б.п.
|
q1
|
q2
|
q3
|
q4
|
q5
|
q6
|
Решение
|
å
|
Отношение
|
| 
|
0
|
-1
|
0
|
0
|
1
|
0
|
1
|
1
|
|   q4 q4
|
1
|
2
|
0
|
1
|
0
|
0
|
1
|
5
|
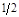
|
| q3
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
4
|
—
|
| q6
|
2
|
1
|
0
|
0
|
0
|
1
|
1
|
5
|
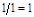
|
| Б.п.
|
q1
|
q2
|
q3
|
q4
|
q5
|
q6
|
Решение
|
å
|
Отношение
|
| 
|
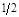
|
0
|
0
|
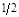
|
1
|
0
|
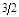
|
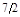
|
| q2
|
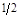
|
1
|
0
|
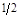
|
0
|
0
|
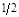
|
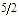
|
| q3
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
4
|
| q6
|

|
0
|
0
|
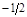
|
0
|
1
|
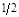
|
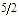
|
Из оптимальной симплекс-таблицы следует, что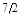
(q1, q2, q3) = (0;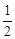 ; 1), ; 1),
а из соотношений двойственности следует, что
( p1, p2, p3) = (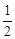 ; 1; 0). ; 1; 0).
Следовательно, цена игры с платёжной матрицей А1 равна
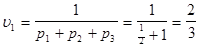 . . 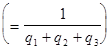 , ,
а игры с платёжной матрицей А:
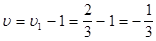 . .
При этом оптимальные стратегии игроков имеют вид:
Х = (х1, х2, х3) = (uр1; uр2; uр3) = 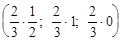 = = 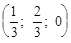
Y = (y1, y2, y3) = (uq1; uq2; uq3) = 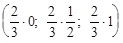 = = 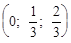 . .
5. Игры с природой (без противодействия)
В играх с противодействием фирме А (одному игроку) противостоит другая фирма – В (игрок). Фирма В выбирает целенаправленную стратегию поведения с тем, чтобы уменьшить выигрыш фирмы А (следовательно, и свой проигрыш).
В играх с природой вторым игроком является природа, которая действует («выбирает» стратегии) случайным образом. То есть она может или улучшать положение первого игрока, или ухудшать. Поэтому существует несколько критериев оценки результатов исследования игровой модели.
1. Критерий Вальде (пессимистический).
В соответствии с этим критерием следует применять самую осторожную стратегию, которая сведет к минимуму вероятность (риск) проигрыша и доставит минимальную прибыль. Эта стратегия обеспечивается критерием:
max (min a ij ).(5.1)
где минимум выбирается по каждой строке.
То есть этот критерий совпадает с нижней ценой игры.
2. Критерий максимума (оптимистический).
Этот критерий полагает, что природа будет максимально благосклонна к игроку. Можно выбирать самые авантюристические стратегии и они будут реализоваться
max (max a ij ).(5.2)
где максимум выбирается по каждой строке.
3. Критерий Гурвица.
Критерий Гурвица занимает промежуточное значение между критерием Вальде и критерием максимума. Сам игрок определяет вероятность своего «везения»
max (α min a ij + (1- α) max a ij ) .(5.3)
Ответственное лицо, принимающее решение, определяет значение коэффициента α. Если потери могут быть весьма значительными, то значение коэффициента α приближается к единице, иначе к 0.
4. Критерий Сэвиджа.
Этот критерий анализирует возможные риски от применения каждой из стратегий и выбирает такую стратегию, которая обеспечивает приемлемые потери. Риски по каждой стратегии определяются по формуле:
r ij = max a ij - a ij.(5.4)
То есть из максимально возможного выигрыша при данном состоянии природы вычитается выигрыш, полученный от использования выбранной стратегии. Каждый элемент матрицы рисков обозначает потери, которые понесет фирма (точнее, недополученную прибыль), если для каждого текущего состояния природы будет выбрана неоптимальная стратегия. Оптимальная стратегия может быть определена по формуле:
min (max (max a ij - a ij).(5.5)
где максимум выбирается в каждом конкретном столбце.
Для примера возьмем таблицу стратегий (табл. 5.1) и составим для нее таблицу рисков (табл. 5.2).
Если фирма (игрок) выберет стратегию А1, а природа реализует стратегию В1 , то фирма получит максимально возможную прибыль 5 (недополученная прибыль составит 0). Фирма угадала состояние природы. Но если природа реализует стратегию В4, то фирма вместо максимально возможной прибыли 12 получит прибыль 5, а недополученная прибыль составит 7.
Таблица 5.1
Таблица стратегий
| Стратегии
|
В1
|
В2
|
В3
|
В4
|
В5
|
| А1
|
5
|
8
|
7
|
5
|
4
|
| А2
|
1
|
10
|
5
|
5
|
6
|
| А3
|
2
|
4
|
3
|
6
|
2
|
| А4
|
3
|
5
|
4
|
12
|
3
|
| max a ij
|
5
|
10
|
7
|
12
|
6
|
Таблица 5.2
Таблица рисков
| Стратегии
|
В1
|
В2
|
В3
|
В4
|
В5
|
| А1
|
0
|
2
|
0
|
7
|
2
|
| А2
|
4
|
0
|
2
|
7
|
0
|
| А3
|
3
|
6
|
4
|
6
|
4
|
| А4
|
2
|
5
|
3
|
0
|
3
|
5.1 Решение задач
Пример 1: Швейная фабрика на летний сезон может реализовать два вида костюмов: 1200 костюмов по цене 520 руб. и 200 костюмов по цене 1000 руб., если погода будет жаркой. Если погода будет холодной, то фабрика может реализовать 650 костюмов первого вида и 700 костюмов второго вида.
Определить план выпуска костюмов каждого вида и прибыль, полученную от их реализации.
Решение
:
Швейная фабрика располагает двумя стратегиями: А1 - погода будет жаркой и А2 – погода будет холодной.
Если фабрика воспользуется первой стратегией и погода действительно будет жаркой, то прибыль фабрики составит:
1200 · 520 + 200 · 1000 = 624 000 + 200 000 = 824 000 руб.
Если фабрика воспользуется первой стратегией, но погода будет холодной, то прибыль фабрики составит:
650 · 520 + 200 · 1000 – (1200 – 650) · 520 = 338 000 + 200 000 – 286 000 = 252 000 руб.
Если фабрика воспользуется второй стратегией и погода действительно будет холодной, то прибыль фабрики составит:
650 · 520 + 700 · 1000 = 338 000 + 700 000 = 1 038 000 руб.
Если фабрика воспользуется второй стратегией, но погода будет жаркой, то прибыль фабрики составит:
650 · 520 + 200 · 1000 – (700 – 200) · 1000 = 338 000 + 200 000 – 500 000 = 38 000 руб.
Составим матрицу прибыли (таб. 5.3).
Таблица 5.3
Матрица прибыли
| Стратегии
|
В1
|
В2
|
| А1
|
824 000
|
252 000
|
| А2
|
38 000
|
1 038 000
|
α = max (252 000; 38 000) = 252 000 руб.
β = min (824 000; 1 038 000) = 824 000 руб.
Таким образом, цена игры находится в диапазоне от 252 000 руб. до 824 000 руб.
Минимальный гарантированный доход швейной фабрики составит 252 000 руб., но возможен и доход в 824 000 руб.
Определим план выпуска изделий швейной фабрикой. Вероятность выбора стратегии А1 обозначим через х1, а вероятность выбора стратегий А2 – через х2. Учитывая, что х2 = 1 - х1,можем записать:
(a11 – a12)· х1 + a12 = (824 000 – 38 000)· х1 + 38 000 = 786 000 х1 + 38 000;
(a21 – a22)· х1 + a22 = (252 000 – 1 038 000) · х1 + 1 038 000 = -786 000 х1 + 1 038 000;
786 000 х1 + 786 000 х1 = 1 038 000 – 38 000
1 572 000 х1 = 1 000 000
х1 = 0,64; х2 = 1 – 0,64х2 = 0,36;
0,64 (1200; 200) + 0,36 (650; 700) = (1002; 380).
Цена игры составит: 786 000 х1 + 38 000 = 541 040 руб.
Таким образом, план выпуска изделий таков: 1002 костюма первого вида и 380 костюмов второго вида, и при любых погодных условиях швейная фабрика получит прибыль не менее 541 000 руб.
Определим критерии.
1. Критерий Вальде:
max (min a ij) = max (38 000; 252 000) = 252 000 руб.
Швейной фабрике целесообразно использовать стратегию А1 .
2. Критерий максимума:
max (max a ij ) = max (824 000; 1 038 000) = 1 038 000 руб.
Швейной фабрике целесообразно использовать стратегию А2 .
3. Критерий Гурвица:
пусть α = 0,4 , тогда для стратегии А1
α min a ij + (1 - α) max a ij = 0,4 · 252 000 + (1 – 0,4) · 824 000 = 595 200 руб.
для стратегии А2
α min a ij + (1 - α) max a ij = 0,4 · 38 000 + (1 – 0,4) · 1 038 000 = 638 000 руб.
Швейной фабрике целесообразно использовать стратегию А2 .
4. Критерий Сэвиджа:
Максимальный элемент в первом столбце – 824 000, во втором столбце – 1 038 000.
Матрица рисков будет иметь вид:

Швейной фабрике целесообразно использовать стратегию А1 или А2 .
Заключение
При написании курсовой работы по дисциплине «Математические методы» на тему «Теория игр» у меня возникли проблемы с теоретической частью курсовой работы. Мне приходилось брать одну литературу и искать нужную информацию, а потом, если в ней не полностью раскрыта тема, то брал следующую, а в ней более труднее приходилось разбираться, так как один автор пишет, как он понимает, а другой - свои взгляды на тему. Но я смог преодолеть эту непреодолимую пропасть.
Список литературы
1. « Математические методы в программировании » : / Агальцов В.П., Волдайская И.В. Учебник : – М . : ИД «ФОРУМ» : ИНФРА-М, 2006. – 224с. : ил. –(Профессиональное образование). – (Учимся программировать).
2. Лекции по дисциплине « Математические методы ».
3. «Математические методы: Учебник» / Партика Т.Л., Попов И.И. – М: ФОРУМ: ИНФРА, 2005.
4.«Математическое программирование» / Костевич Л., издательство «Новое знание», 2003.
|