| Федеральное агентство по образованию
ГОУ ВПО Воронежский государственный технический университет
Факультет автоматики и электромеханики
Кафедра автоматики и информатики в технических системах
КУРСОВОЙ ПРОЕКТ
По дисциплине: “Электрический привод”
Тема: “Проектирование электропривода пассажирского лифта”
Расчетно-пояснительная записка
Воронеж 2008 г.
Содержание
Введение
1. Техническое задание
1.1 Описание конструкции рабочей машины и технологического процесса ее работы.
1.2 Кинематическая схема механизма
1.3 Краткое описание работы пассажирского лифта
1.4 Расчет подъемных канатов.
1.5 Расчет канатоведущего шкива.
1.6 Выбор мощности двигателя лифта
1.7 Производительность пассажирских лифтов
2. Определение передаточного числа редуктора
3. Расчет нагрузочной диаграммы.
4. Выбор схемы включения электродвигателя
5. Расчет статических механических и электромеханических характеристик
6. Расчет кинематической схемы механической части ЭП
7. Расчет динамики механической части ЭП
8. Расчет переходных процессов
9. Проверка двигателя
10. Расчет энергетических показателей ЭП
11. Точность остановки кабины
Заключение.
Список литературы
Введение
Широкое внедрение электрического привода во все отрасли промышленности и все возрастающие требования к статическим и динамическим характеристикам электропривода предъявляют повышение требования к профессиональной подготовке студентов, специализирующихся в области электропривода. Несомненно, важное место в этой подготовке занимает курсовое проектирование, где студент закрепляет полученные теоретические знания и приобретает практические навыки разработки автоматизированных электроприводов.
Цель курсового проектирования: углубление теоретических знаний по курсу “Электрический привод”; закрепление практических навыков расчета электроприводов и выбора технических средств их реализации. В курсовом проекте предусматривается на основе анализа режимов работы промышленной установки спроектировать автоматизированный электропривод для обеспечения ее работы с учетом особенностей конструкции установки и требований технологического режима.
Спроектировать привод движения пассажирского лифта согласно технологическому процессу, описанному в разделе «Описание конструкции, назначения рабочей машины и технологического процесса работы».
Реклама

Исходные данные на проектирование
Вариант №3
| Скорость кабины
|
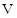 , м/с , м/с
|
0.71
|
| Грузоподъемность
|
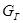 , кг , кг
|
320
|
| Вес кабины
|
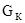 , Н , Н
|
6500
|
| Погрешность остановки
|
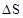 , мм , мм
|
20
|
| Предельное ускорение
|
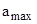 , м/с2 , м/с2
|
1.5
|
| Диаметр шкива
|
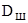 , мм , мм
|
800
|
| Посадочный этаж
|
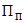
|
5
|
Приведение исходных данных на проектирование к международной системе единиц.
Вес кабны 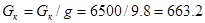 кг. кг.
Диаметр шкива 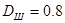 м м
Погрешность остановки 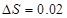 м м
Лифт – это подъемник прерывистого действия с вертикальным движением кабины по жестким направляющим, установленными в огражденной со всех сторон шахте.
Пассажирские лифты подразделяют на три группы в зависимости от скорости движения кабины:
тихоходные – до 0.5 м/с
быстроходные – до 1 м/с
скоростные – свыше 1 м/с.

  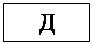
Рис.1. Кинематическая схема лифта.
В кинематической схеме (рис.1) обозначены:
1
– двигатель
2
– тормозная муфта
3
– редуктор
4
– соединительная муфта
5
– канатоведущий шкив
6
– канаты
7
– кабина
8
– противовес
В современных лифтах преимущественно применяют кинематические схемы с верхним расположением ЭП (рис.1). При таком размещении уменьшается число перегибов канатов, что увеличивает их долговечность, повышается КПД, уменьшается нагрузка на опорные конструкции, снижается стоимость. Проектируемый мною лифт относится именно к этой схеме.
Кинематическая схема с верхним расположением ЭП работает следующим образом: движение от двигателя (1) передается на канатоведущий шкив (5) через тормозную муфту (2), редуктор (3) и соединительную муфту (4), который с помощью канатов(6) приводит в движение кабину(7) и противовес(8).
Рассмотрим назначение некоторых элементов кинематической схемы.
Редуктор необходим для уменьшения частоты вращения ротора двигателя и увеличения крутящего момента двигателя.
Противовес необходим для полного уравновешивания кабины, частичного уравновешивания груза и уменьшения статического момента сопротивления, создаваемого кабиной и грузом.
Привод лифта должен обеспечить остановку кабины с отклонением уровней пола и кабины , которая зависит от величины начальной скорости при различных предельных ускорениях. Для этого подход к этажу производится на более низкой скорости с последующим включением тормозной муфты, с помощью которой осуществляется полная остановка кабины.
К основным параметрам работы лифта относятся: скорость движения кабины 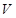 , м/c; ускорение a
,м/с2
; рывок скорости a
,м/с3
. , м/c; ускорение a
,м/с2
; рывок скорости a
,м/с3
.
Для быстроходных лифтов величина предельного ускорения и замедления составляет 1.5 м/c2
, для скоростных лифтов – 2.5 м/с2
. При этом рывок скорости не должен превышать 3…10 м/с3
.
Реклама

Кабины лифтов имеют предохранительные устройства, обеспечивающие остановку кабины при обрыве или ослаблении несущих канатов и при превышении скорости движения на 20-40% от номинальной. В этом случае ловители заклинивают кабину между направляющими.
Одним из основных требований, предъявляемых к электроприводу пассажирских лифтов, является плавность движения, которая определяется величиной ускорения в начале движения и торможения при остановке.
Производительность лифта определяется его средней скоростью, для увеличения которой необходимо сократить время разгона и торможения кабины. Однако большие ускорения оказывают нежелательные воздействия на людей, поэтому для пассажирских лифтов ускорение а≤2м/с2
. При таком ускорении величина рывка скорости не должна превышать 20 м/с3
.
Оптимальная диаграмма работы лифта представлена на рис.2.

рис.2. Тахограмма работы лифта.
По характеру изменения скорости она может быть разбита на пять участков:
А
– разгон кабины;
Б
– движение с номинальной скоростью;
В
– снижение скорости до посадочной;
Г
– подход на пониженной скорости к этажу;
Д
– торможение до полной остановки кабины.
Определяем максимальное расчетное статическое натяжение ветви каната 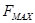 , Н. При этом учтем, что в зданиях с количеством этажей менее десяти вес подвесного кабеля и тяговых канатов не учитывается. , Н. При этом учтем, что в зданиях с количеством этажей менее десяти вес подвесного кабеля и тяговых канатов не учитывается.
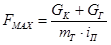 , ,
где: 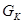 - вес кабины, Н; - вес кабины, Н;
 - грузоподъемность лифта, Н; - грузоподъемность лифта, Н;
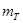 - число канатов; - число канатов;
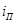 - кратность полиспата.; - кратность полиспата.;
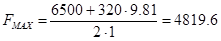 Н. Н.
Вычислим разрывное усилие каната 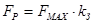 , ,
где 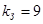 - коэффициент запаса прочности каната, определяемый по таблице 4.1. [1]. - коэффициент запаса прочности каната, определяемый по таблице 4.1. [1].
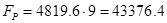 Н. Н.
Теперь по таблице 4.2 выберем диаметр каната, соблюдая условие 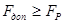 , где , где 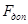 - допустимое разрывное усилие, кH. - допустимое разрывное усилие, кH.
Выбираем канат типа 10.5-ГЛ-В-Н диаметром 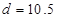 мм, мм, 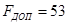 кH. кH.
По рассчитанному диаметру каната определим ширину канатоведущего шкива:
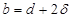 , где , где 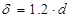
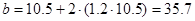 мм мм
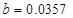 м м
Масса шкива:
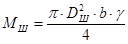 , ,
где 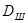 - диаметр шкива , м; - диаметр шкива , м;
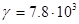 - удельный вес , - удельный вес , 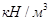 . .
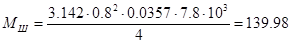 кг. кг.
Момент инерции шкива:
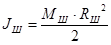 , ,
где 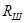 - радиус шкива , м; - радиус шкива , м;
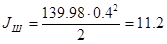 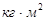 . .
Определим массу противовеса:
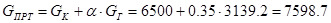 Н, Н,
где 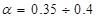 - коэффициент неуравновешенности, - коэффициент неуравновешенности,
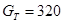 кг. – грузоподъемность, кг. – грузоподъемность,
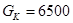 Н - вес кабины. Н - вес кабины.
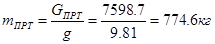
Определим время, затрачиваемое на круговой рейс (Т).
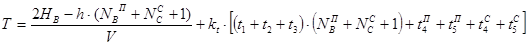 , где: , где:
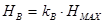 - вероятная высота подъема кабины, м; - вероятная высота подъема кабины, м;
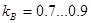 - коэффициент вероятности высоты подъема; - коэффициент вероятности высоты подъема;
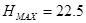 м – максимальная высота подъема; м – максимальная высота подъема;
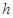 – путь, проходимый кабиной при разгоне до номинальной скорости и при торможении от номинальной скорости до полной остановки. – путь, проходимый кабиной при разгоне до номинальной скорости и при торможении от номинальной скорости до полной остановки.
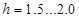 м; м;
V – скорость движения кабины;
V=0.71 м/с;
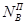 и и 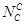 - число вероятных остановок при подъеме и спуске; - число вероятных остановок при подъеме и спуске;
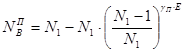 ; ; 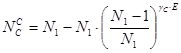 , где: , где:
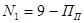 - число возможных остановок выше посадочного этажа - число возможных остановок выше посадочного этажа 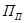 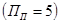 ; ;
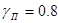 и и 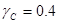 - коэффициенты заполнения при подъеме и спуске соответственно; - коэффициенты заполнения при подъеме и спуске соответственно;
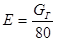 - вместимость лифта, определяемая его грузоподъемностью - вместимость лифта, определяемая его грузоподъемностью 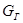 и средним весом одного человека; и средним весом одного человека;
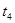 и и 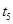 - время, затрачиваемое на вход и выход пассажиров при подъеме и спуске; - время, затрачиваемое на вход и выход пассажиров при подъеме и спуске;
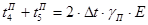
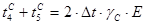 , ,
где 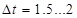 - время, затрачиваемое на вход и выход одного пассажира; - время, затрачиваемое на вход и выход одного пассажира;
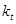 - коэффициент, учитывающий дополнительные задержки, - коэффициент, учитывающий дополнительные задержки, 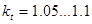
Рассчитаем необходимые значения:
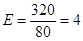 человека; человека;
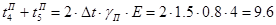 с; с;
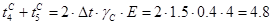 с; с;
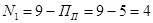
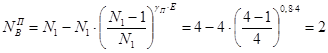 ; ;
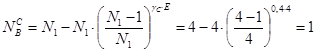 ; ;
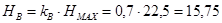 м. м.
Определим время Т:
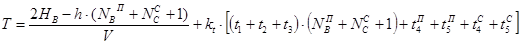
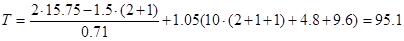 с. с.
Время работы двигателя:
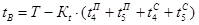
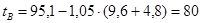 с. с.
Продолжительность включения двигателя:
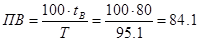 %. %.
Расчет мощности двигателя лифта сводится к предварительному выбору мощности по статическим нагрузкам, построению полной нагрузочной диаграммы с учетом переходных процессов и к дальнейшей проверке по методу эквивалентного тока или момента.
Мощность двигателя механизма подъема в установившемся режиме:
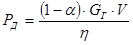 , ,
где: 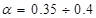 - коэффициент неуравновешенности, - коэффициент неуравновешенности,
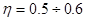 - общий КПД для реальных подъемно-транспортных установок. - общий КПД для реальных подъемно-транспортных установок.
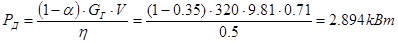
Произведем перерасчет мощности с учетом ближайшего стандартного значения:
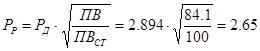 кВт. кВт.
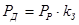 , где , где 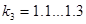 - коэффициент, учитывающий динамические нагрузки двигателя. - коэффициент, учитывающий динамические нагрузки двигателя.
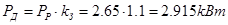
По полученным данным выберем двигатель асинхронный двухскоростной для привода лифтов АНП1805А6/24.
Асинхронные двигатели для привода лифтов удовлетворяют требованиям стандартов, за исключением требований к пусковым характеристикам (МЭК 34-12). Эти двигатели изготавливают в малошумном исполнении. Для них регламентирован уровень шума не только в стационарном режиме работы, но и в переходных режимах – при пуске двигателя и при переключении частоты вращения с высшей на низшую.
Паспортные данные выбранного двигателя запишем в таблицу:
| Номинальная мощность
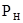 , кВт , кВт
|
3
|
---
|
| Номинальная частота вращения
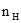 , об/мин , об/мин
|
940
|
205
|
| КПД 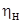 , % , %
|
78
|
---
|
| Cos f
|
0.65
|
---
|
| Номинальный ток А, при 380 В
|
8.9
|
14.5
|
| Номинальный момент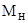 , Нм , Нм
|
30.5
|
| 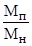
|
2.3 -2.8
|
³1.8
|
| 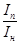
|
5
|
---
|
| 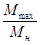
|
2.6-3.1
|
³1.8
|
| Отношение максимального тормозного момента к номинальному моменту
|
---
|
2.3-2.8
|
| Допустимое количество пусков в час
|
120
|
| Динамический момент ротора  , , 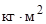
|
0.156
|
| Предельный коэффициент инерции системы
|
7.0
|
| Масса, кг
|
130
|
Производительность пассажирских лифтов определяется количеством человек, перевозимых лифтом за один час:
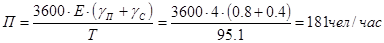
Предварительно выбранный двигатель имеет синхронную частоту вращения 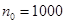 об/мин. Допустим, что нагруженный двигатель будет работать в номинальной точке механической характеристики об/мин. Допустим, что нагруженный двигатель будет работать в номинальной точке механической характеристики 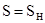 . .
Номинальная скорость равна:
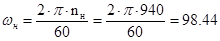 рад/с, рад/с,
где 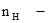 номинальная частота вращения двигателя. номинальная частота вращения двигателя.
Определим передаточное число редуктора:
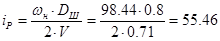 , ,
где 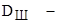 диаметр канатоведущего шкива, м. диаметр канатоведущего шкива, м.
Выберем стандартное значение передаточного числа редуктора 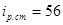 . .
Статический момент механизма на его валу
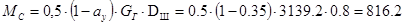 Нм, Нм,
Момент инерции механизма
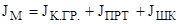
где 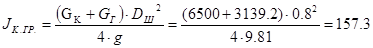 кг×м2
момент инерции кабины с грузом, приведенный к валу шкива, кг×м2
, кг×м2
момент инерции кабины с грузом, приведенный к валу шкива, кг×м2
,
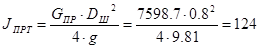 кг×м2
момент инерции противовеса, приведенный к валу шкива. кг×м2
момент инерции противовеса, приведенный к валу шкива.
Теперь мы можем рассчитать момент инерции механизма:
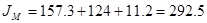 , кг×м2
. , кг×м2
.
Момент инерции механизма, приведённый к валу двигателя:
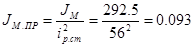 , кг×м2
. , кг×м2
.
Суммарный момент инерции:
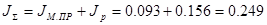 , кг×м2
. , кг×м2
.
Определим фактическую скорость движения кабины:
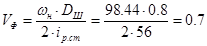 , м/с. , м/с.
Отклонение от заданной скорости:
 , ,
где V – заданная скорость.
Рассчитаем время стоянки при подъеме и спуске:
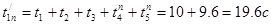
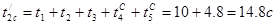
Время пуска и торможения при заданном ускорении:

Путь, проходимый с установившейся скоростью:
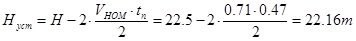
Время движения с установившейся скоростью:
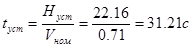
При торможении двигатель отключается от сети и накладывается механический тормоз, следовательно, время работы двигателя при подъеме и спуске:
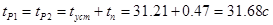
Время работы при подъеме и спуске:
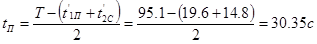
Рассчитаем статические моменты при подъеме и спуске кабины:
Статический момент механизма при прямом направлении энергии, приведённый к валу двигателя:
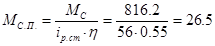 , Н×м. , Н×м.
Статический момент механизма при обратном направлении энергии, приведённый к валу двигателя:
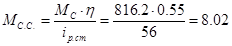 , Н×м. , Н×м.
Рассчитаем динамический момент при подъеме и спуске кабины:
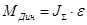
где 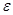 -угловое ускорение. -угловое ускорение.
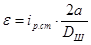
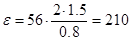 рад/с2 рад/с2
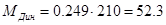 Нм Нм
Суммарный момент равен:
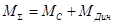
Статическая мощность механизма при прямом направлении энергии (подъем кабины) рассчитаем по формуле:
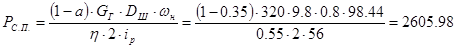 , Вт, , Вт,
Статическая мощность механизма при обратном направлении энергии (спуск кабины) рассчитаем по формуле:
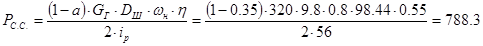 , Вт. , Вт.
Эквивалентная мощность:
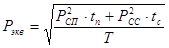 ; ;
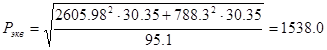 Вт.
Вт.
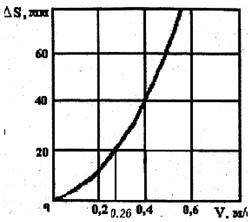
Рис. 4.3. Зависимость погрешности остановки лифта от величины начальной скорости при ускорении 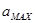
Теперь, пользуясь графиками (рис.4.3), по указанным 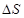 и и 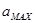 , определим посадочную скорость торможения: , определим посадочную скорость торможения: 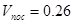 м/с. м/с.
Время движения кабины на каждом этаже кругового рейса можно рассчитать по формуле:
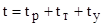 с, (1) с, (1)
где 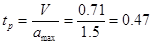 , с – время разгона, , с – время разгона,
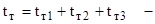 время торможения, время торможения,
где 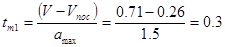 , с – время перехода с номинальной , с – время перехода с номинальной
скорости на посадочную скорость.
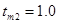 , с – время подхода к этажу на посадочной скорости, , с – время подхода к этажу на посадочной скорости,
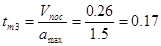 , с – время торможения от , с – время торможения от 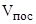 до полной остановки, до полной остановки,
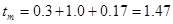 с; с;
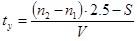 , – время движения на установившейся скорости, с, , – время движения на установившейся скорости, с,
где 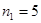 , , 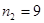 – порядковые номера этажей; – порядковые номера этажей;
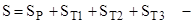 путь, проходимый кабиной при разгоне и торможении, м; путь, проходимый кабиной при разгоне и торможении, м;
где 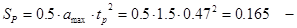 путь разгона, м; путь разгона, м;
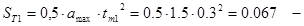 путь торможения от путь торможения от 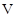 до до 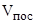 с
, м; с
, м;
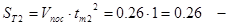 путь подхода к этажу на посадочной скорости, м; путь подхода к этажу на посадочной скорости, м;
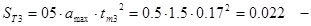 путь торможения от путь торможения от 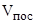 до остановки, м. до остановки, м.
Следовательно, путь, проходимый кабиной при разгоне и торможении будет равен
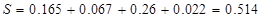 , м. , м.
Рассчитаем время движения для отдельных этапов цикла работы. При 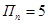 число вероятных остановок на спуске число вероятных остановок на спуске 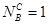 , на подъеме , на подъеме 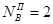 . Цикл работы лифта (условно) будет состоять из: подъема с пятого на седьмой . Цикл работы лифта (условно) будет состоять из: подъема с пятого на седьмой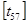 , подъема с седьмого на девятый , подъема с седьмого на девятый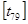 , и спуска с девятого на пятый , и спуска с девятого на пятый 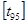 (завершение кругового рейса). (завершение кругового рейса).
Рисунок 3.2. Схема цикла работы лифта.
Такой цикл работы лифта выбран из условия максимально допустимой нагрузки на двигателе при посадочном этаже 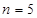 . .
Нагрузочная диаграмма рабочей машины приведена на рисунке 3.3.
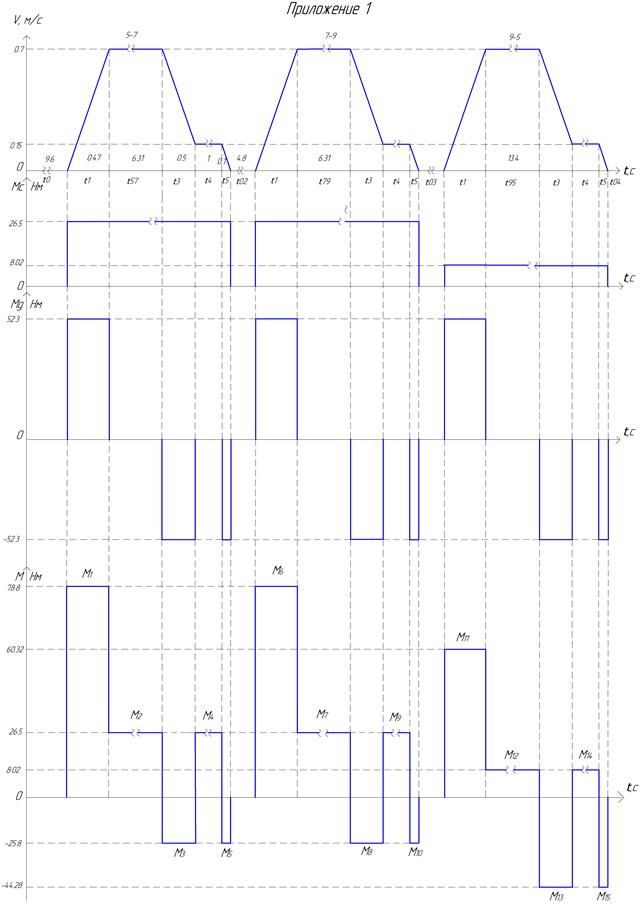
Рисунок 3.2. Нагрузочная диаграмма рабочей машины.
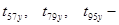 время установившегося движения, с. время установившегося движения, с.
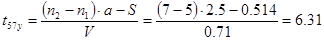 , с, , с,
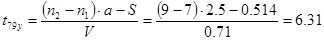 , с , с
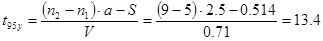 , с, , с,
4. Выбор схемы включения электродвигателя
В соответствии с требованиями технологического режима принципиальная электрическая схема включения электродвигателя, приведенная на рисунке 4.1, обеспечивает:
1 Пуск электродвигателя (контактор К1).
2 Изменение направления движения (вращения ротора) (контактор К3 – прямое включение, контактор К4 - обратное).
3 Рекуперативное торможение с высокой скорости вращения на низкую обеспечивается контактором К2 и отключением К1.
4 Торможение с помощью Электромагнитного тормоза (контактор К5).
5 Защиту двигателя от перегрева (тепловое реле в цепи статора низкоскоростной и высокоскоростной обмоток двигателя).
6 Защиту от токов короткого замыкания (автоматический выключатель QF1).
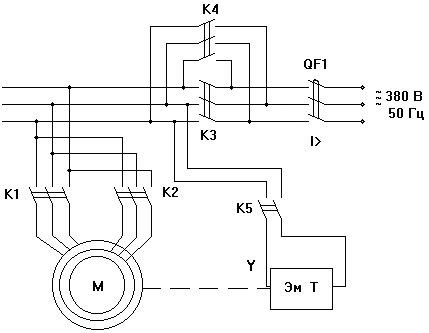
Рисунок 4.1 – Схема включения электродвигателя
Для высокой скорости:
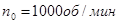 ; ; 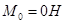 ; ; 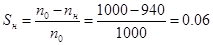
Из соотношения 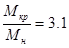 находим находим 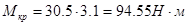
Найдём критическое скольжение:
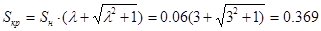 , где , где 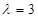
Найдём частоту вращения при критическом моменте по формуле:
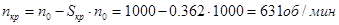
Дли низкой скорости
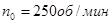 ; ; 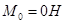 ; ; 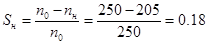
Из соотношения 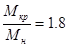 находим находим 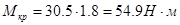
Найдём критическое скольжение:
 , где , где 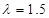
Найдём частоту вращения при критическом моменте по формуле:
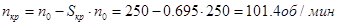
Найдём критический момент для низкой скорости в генераторном режиме по формуле:
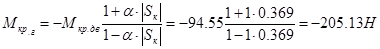 , где , где 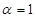
Для расчета механических характеристик (МХ) будем использовать уточненную формулу Клосса, т.к. выбранный двигатель меньше 100 кВт.
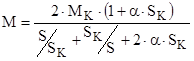 , Н×м. , Н×м.
Неизвестные параметры отдельно для высокоскоростной и низкоскоростной обмоток 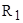 , , 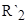 , , 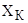 получим из формулы критического момента получим из формулы критического момента 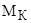 и и 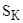 . Приближенно примем, что . Приближенно примем, что 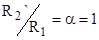 , т.е. , т.е.
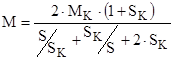 (5.1) (5.1)
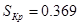 . Затем из формулы . Затем из формулы 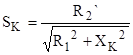 , учитывая, что , учитывая, что 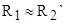 найдем найдем 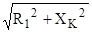 : :
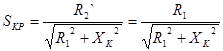 , ,
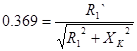 , отсюда , отсюда 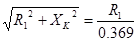 . .
Теперь подставим полученное выражение в формулу критического момента 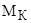 в двигательном режиме, а также известные паспортные данные: в двигательном режиме, а также известные паспортные данные:
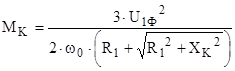 ; ;
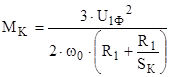 . .
Выразим 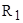 из полученного выражения: из полученного выражения:
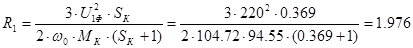 Ом. Ом.
Из уравнения критического скольжения выразим значение 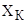
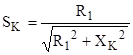 ; ;
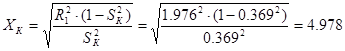 Ом. Ом.
Для низкоскоростной обмотки расчет проводится аналогичным образом. После расчета мы получили, что: 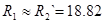 Ом, Ом, 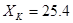 Ом. На низкоскоростной обмотке при рекуперативном торможении критический момент не вписывается в диапазон Ом. На низкоскоростной обмотке при рекуперативном торможении критический момент не вписывается в диапазон 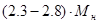 , потому что при расчёте было принято допущение , потому что при расчёте было принято допущение 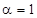 , то есть , то есть 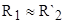 . Следовательно, для низкоскоростной обмотки данное допущение неприемлемо. Из справочных данных следует, что кратности пускового и критического момента для низкоскоростной обмотки одинаковы: . Следовательно, для низкоскоростной обмотки данное допущение неприемлемо. Из справочных данных следует, что кратности пускового и критического момента для низкоскоростной обмотки одинаковы: 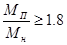 , , 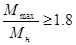 . Примем допущение, что . Примем допущение, что 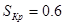 . .
Из справочной литературы определим критические моменты:
 Н×м; Н×м;
С учётом значений критических моментов и скольжения по формуле Клосса методом последовательных приближений определим коэффициент 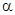
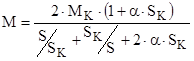 , Н×м; , Н×м;
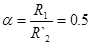 . .
Из уравнения для критического скольжения определим подкоренное выражение
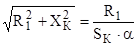 . .
Подставим подкоренное выражение в формулу критического момента, откуда определим сопротивление 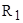
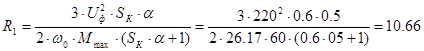 Ом. Ом.
Приведённое сопротивление ротора
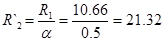 Ом. Ом.
Реактивное сопротивление
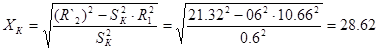 Ом. Ом.
По формуле Клосса строим ЕМХ для обеих обмоток (рисунок 5.1).
Механическая характеристика

Рисунок 5.1. ЕМХ на низкоскоростной (2р=24) и высокоскоростной (2р=6) обмотках.
Расчет статических электромеханических характеристик
Электромеханические характеристики (ЭМХ) также рассчитываем для высокоскоростной и низкоскоростной обмоток.
Для построения ЭМХ будем пользоваться формулой для тока ротора I2
`:
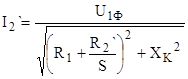 (5.2) (5.2)
Рассмотрим случаи, когда 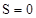 , , 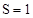 , , 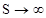 , , 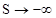 . .
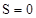 , т.е. , т.е.  . Следовательно . Следовательно 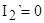 , т.к. , т.к. 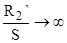 . .
1) 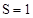 , т.е. , т.е. 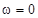 (условие пуска). В этом случае: (условие пуска). В этом случае:
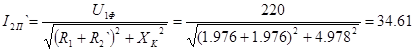 А. А.
2) 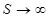 , т.е. , т.е. 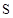 > >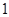 . Следовательно . Следовательно 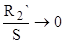 . В результате имеем: . В результате имеем:
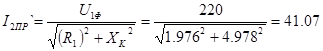 А. А.
3) 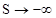 . В этом случае . В этом случае
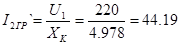 А. А.
Аналогичные расчеты делаем для низкоскоростной обмотки:
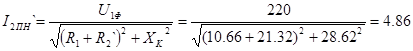 А, А,
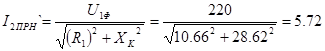 А, А,
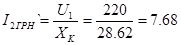 А. А.
По полученным формулам построим графики ЭМХ двухскоростного двигателя для высокоскоростной и низкоскоростной обмоток (рисунок 5.2).
Электромеханическая характеристика
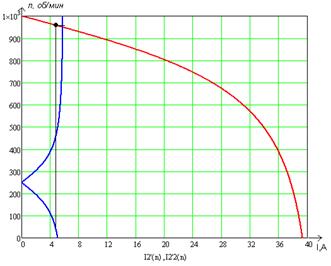
Рисунок 5.2 – графики ЭМХ двухскоростного двигателя
Отталкиваясь от кинематической схемы механизма можно перейти к расчётной схеме. Для этого приводят скорости, моменты инерции, массы и силы к валу двигателя. В основе приведения лежит закон сохранения энергии.
Согласно кинематической схеме механизма (рисунок 2.1) производим дальнейший переход к расчетной схеме.
Из кинематической схемы (рисунок 2.1) механизма видно, что она является разветвленной, но если допустить, что между шкивом и противовесом связи абсолютно жесткие, когда кабина находится в крайнем нижнем положении, то можно считать схему последовательной.
Приведем параметры механической части электропривода к валу двигателя.
Радиус приведения поступательно движущихся масс определим по формуле:
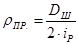 , м (6.1) , м (6.1)
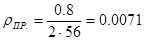 м м
Приведённый момент инерции канатоведущего шкива вычислим по формуле:
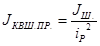 , кг∙м2
(6.2) , кг∙м2
(6.2)
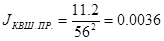 кг∙м2 кг∙м2
Приведённый момент инерции противовеса:
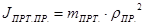 , кг∙м2
, (6.3) , кг∙м2
, (6.3)
где 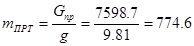 кг (6.4) кг (6.4)
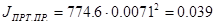 кг∙м2
. кг∙м2
.
Приведённый момент инерции кабины:
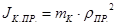 , кг∙м2
, (6.5) , кг∙м2
, (6.5)
где 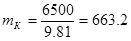 , кг – масса кабины лифта (6.6) , кг – масса кабины лифта (6.6)
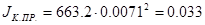 , кг∙м2 , кг∙м2
Приведённый момент инерции груза:
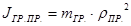 , кг∙ м2
(6.7) , кг∙ м2
(6.7)
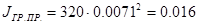 , кг∙м2 , кг∙м2
Жесткость одного каната ориентировочно можно определить по формуле:
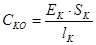 , Н/м (6.8) , Н/м (6.8)
где ЕК
=107
– модуль упругости каната, Н/см2
;
SK
– площадь сечения каната, см2
;
lK
– длина каната (высота подъема), м.
Площадь SK
, м 2
определится по формуле:
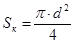 ,
см 2
(6.9)
,
см 2
(6.9)
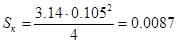 см 2 см 2
Тогда:
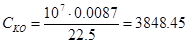 Н∙м Н∙м
При числе канатов, равном двум, суммарная жёсткость равна:
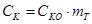 , Н∙м (6.10) , Н∙м (6.10)
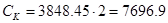 Н∙м Н∙м
Жёсткость каната, приведённая к валу двигателя:
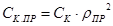 , Н∙м (6.11) , Н∙м (6.11)
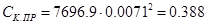 Н∙м Н∙м
Примем величину жёсткости муфты 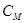 =75000 Н∙м. Тогда жёсткость муфты, соединяющий редуктор и шкив, приведённая к валу двигателя определяется по формуле: =75000 Н∙м. Тогда жёсткость муфты, соединяющий редуктор и шкив, приведённая к валу двигателя определяется по формуле:
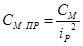 , Н∙м (6.12) , Н∙м (6.12)
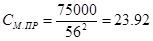 Н∙м Н∙м
Момент инерции редуктора и тормозной муфты J1
, кг∙м2
примем равным:
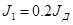 , кг∙м2
(6.13) , кг∙м2
(6.13)
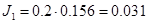 кг∙м2 кг∙м2
Расчетная схема исходной многомассовой механической части электропривода (МЧ ЭП) представлена на рисунке 6.1:
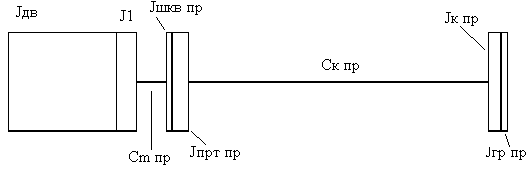 Рисунок 6.1 Рисунок 6.1
Перейдем к трёхмассовой расчётной схеме с помощью формул:
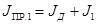 , кг∙м2
(6.14) , кг∙м2
(6.14)
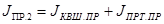 , кг∙м2
(6.15) , кг∙м2
(6.15)
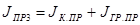 , кг∙м2
(6.16) , кг∙м2
(6.16)
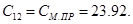 H∙м H∙м
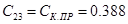 H∙м H∙м
Согласно формулам (3.14), (3.15), (3.16) имеем:
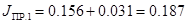 кг∙м2 кг∙м2
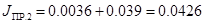 кг∙м2 кг∙м2
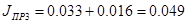 кг∙м2 кг∙м2
Получим трехмассовую расчетную схему следующего вида:
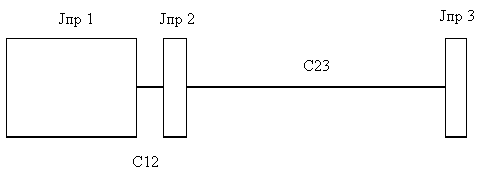
Рисунок 6.2 - Трехмассовая расчетная схема механической части электропривода
Приведём трехмассовую схему к двухмассовой:
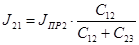 , кг∙м2
(6.17) , кг∙м2
(6.17)
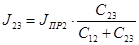 , кг∙м2
(6.18) , кг∙м2
(6.18)
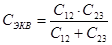 , H∙м (6.19) , H∙м (6.19)
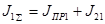 , кг∙м2
(6.20) , кг∙м2
(6.20)
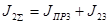 , кг∙м2
(6.21) , кг∙м2
(6.21)
Получим:
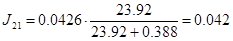 кг∙м2
; кг∙м2
;
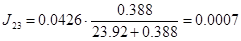 кг∙м2
; кг∙м2
;
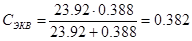 H∙м; H∙м;
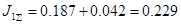 кг∙м2
; кг∙м2
;
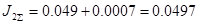 кг∙м2
. кг∙м2
.
Получим двухмассовую расчетную схему следующего вида:
Определим суммарный момент инерции:
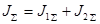 , кг∙м2
(6.22) , кг∙м2
(6.22)
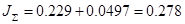 кг∙м2 кг∙м2
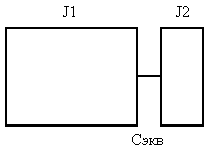
Рисунок 6.3 - Двухмассовая расчетная схема механической части электропривода
Соотношение масс: 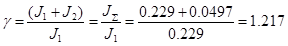
Уравнения движения для двухмассовой механической системы с учётом оператора p имеют вид:
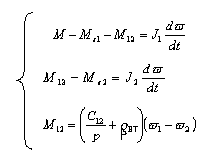
(7.1)
где  - коэффициент внутреннего вязкого трения. - коэффициент внутреннего вязкого трения.
Структурная схема двухмассовой механической части строится на основании системы уравнений (7.1) , описывающих динамику системы и представлена на рисунке 7.1:
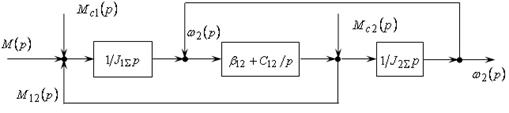
Рисунок 7.1 - Структурная схема двухмассовой механической части
В приведенной схеме учтены силы внутреннего вязкого трения коэффициентом 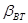 .Управляющим воздействием здесь является электромагнитный момент двигателя М, H∙м, а возмущающим – моменты сопротивления нагрузки .Управляющим воздействием здесь является электромагнитный момент двигателя М, H∙м, а возмущающим – моменты сопротивления нагрузки 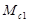 и и 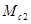 , H∙м. Регулируемыми переменными являются скорости , H∙м. Регулируемыми переменными являются скорости 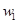 и и 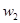 ,1/c, ,1/c, 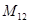 , H∙м - нагрузка упругой связи. , H∙м - нагрузка упругой связи.
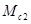 , Н∙м – момент сопротивления , приложенный ко второй массе, определим по формуле: , Н∙м – момент сопротивления , приложенный ко второй массе, определим по формуле:
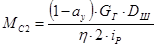 , H∙м (7.2) , H∙м (7.2)
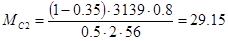 H∙м H∙м
Момент сопротивления, приложенный к первой массе, составляет (1-5)% от 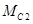 , H∙м: , H∙м:
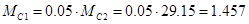 H∙м; H∙м;
Частоту свободных колебаний механической части рассчитаем по формуле:
 , с-1
(7.3) , с-1
(7.3)
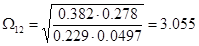 с-1 с-1
Из структурной схемы (рисунок 7.1) найдём передаточную функцию 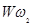 по управляющему воздействию, в качестве которого выступает момент двигателя М(p), H∙м . Получим: по управляющему воздействию, в качестве которого выступает момент двигателя М(p), H∙м . Получим:
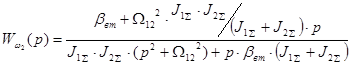 (7.4) (7.4)
Для нахождения коэффициента внутреннего вязкого трения 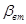 воспользуемся формулами: воспользуемся формулами:
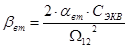 , (7.5) , (7.5)
где 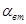 - коэффициент затухания. - коэффициент затухания.
Определим 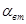 по формуле: по формуле:
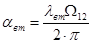 , с-1
, (7.6) , с-1
, (7.6)
где  =(0.1..0.3)=0.2 – логарифмический декремент затухания. =(0.1..0.3)=0.2 – логарифмический декремент затухания.
Тогда по формуле (7.6) имеем:
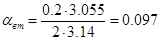 , с-1 , с-1
Отсюда по формуле (7.5) получим:
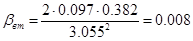
Коэффициент резонансного усиления:
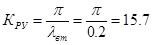
Уравнения движения для двухмассовой механической системы с учётом оператора p и ранее посчитанных величин имеют вид:
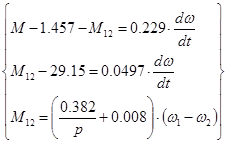
Осуществив переход в частотную область путем замены р на j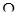 , где , где 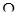 - частота вынужденных колебаний, 1/с , в передаточной функции - частота вынужденных колебаний, 1/с , в передаточной функции 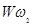 (р) и преобразовав к виду, удобному для выделения амплитудно- и фазочастотной характеристики, получим данные характеристики. Для построения использована программа MATLAB. (р) и преобразовав к виду, удобному для выделения амплитудно- и фазочастотной характеристики, получим данные характеристики. Для построения использована программа MATLAB.
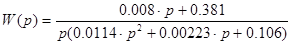
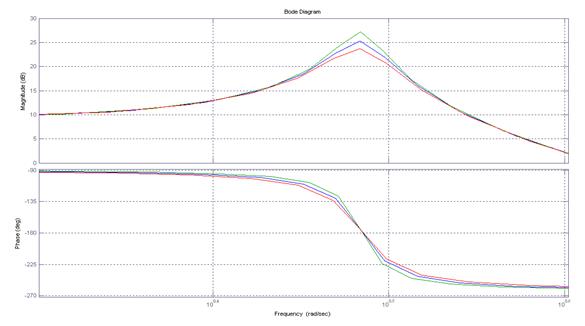
Рисунок 7.2 - Графики АЧХ и ФЧХ для w2
(t) по М(р)
Из рисунка видно влияние коэффициента 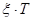 , при его изменении в пределах , при его изменении в пределах 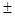 20% (0.00178; 0.00223; 0.00268) на величину резонансного пика: максималый пик соответствует минимальному значению коэффициента, минимальный пик соответствует максимальному значению коэффициента. 20% (0.00178; 0.00223; 0.00268) на величину резонансного пика: максималый пик соответствует минимальному значению коэффициента, минимальный пик соответствует максимальному значению коэффициента.
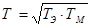 ; ; 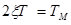 ; ;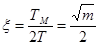
т.о. ЭП с линейной механической
характеристикой вследствие электромагнитной инерции представляет собой при жестких механических связях колебательное звено, показатели колебательности которого 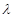 и и 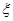 зависят только от соотношения постоянных времени m
= ТМ
/ ТЭ
, а быстродействие определяется электромагнитной постоянной времени ТЭ
или при данном m
-механической постоянной времени ТМ
. При работе на естественной характеристике значение ТЭ
лежит в пределах ТЭ
=0,01-0,1 с. зависят только от соотношения постоянных времени m
= ТМ
/ ТЭ
, а быстродействие определяется электромагнитной постоянной времени ТЭ
или при данном m
-механической постоянной времени ТМ
. При работе на естественной характеристике значение ТЭ
лежит в пределах ТЭ
=0,01-0,1 с.
Покажем влияние величины логарифмического декремента затухания λ при его изменении в пределах (0,1; 0,15; 0,3) на величину резонансного пика:
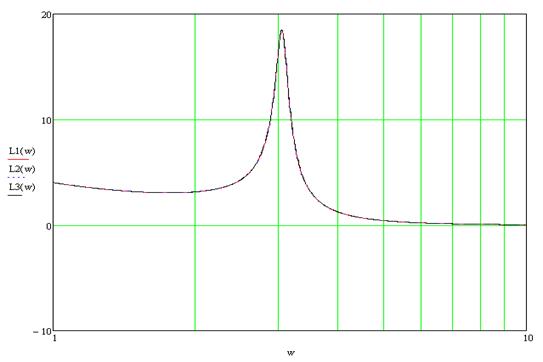
Рисунок 7.3 – График влияния величины логарифмического декремента затухания λ, на величину резонансного пика.
Из рисунка видно, что резонансный пик изменяется не значительно.
Покажем влияние на величину резонансного пика моментов инерции масс двухмассовой системы (для всех случаев логарифмический декремент затухания λ=0.2):
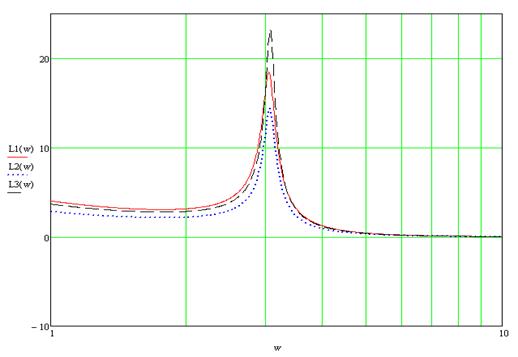 Рисунок 7.4 – График влияния моментов инерции на величину резонансного пика. Рисунок 7.4 – График влияния моментов инерции на величину резонансного пика.
Сплошной линией показана ЛАЧХ системы при значении ранее рассчитанных моментов инерции масс системы 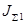 =0.229 и =0.229 и 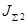 =0.0497. Этому случаю соответствует среднее значение резонансного пика. =0.0497. Этому случаю соответствует среднее значение резонансного пика.
Штриховой линией показана ЛАЧХ системы при увеличении момента инерции первой массы на 50% 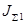 =0.344 , момент инерции второй массы оставлен без изменения =0.344 , момент инерции второй массы оставлен без изменения 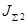 =0.0497. Это приводит к общему опусканию ЛАЧХ и уменьшению резонансного пика. =0.0497. Это приводит к общему опусканию ЛАЧХ и уменьшению резонансного пика.
Пунктирной линией показана ЛАЧХ системы при увеличении момента инерции второй массы на 50% 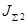 =0.0745 , момент инерции первой массы оставлен без изменения =0.0745 , момент инерции первой массы оставлен без изменения 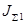 =0.229. Это приводит к общему подниманию ЛАЧХ и увеличению резонансного пика. =0.229. Это приводит к общему подниманию ЛАЧХ и увеличению резонансного пика.
Для общей оценки устойчивости системы и определения запасов устойчивости определим положение корней характеристического уравнения передаточной функции W(p) по управляющему воздействию:
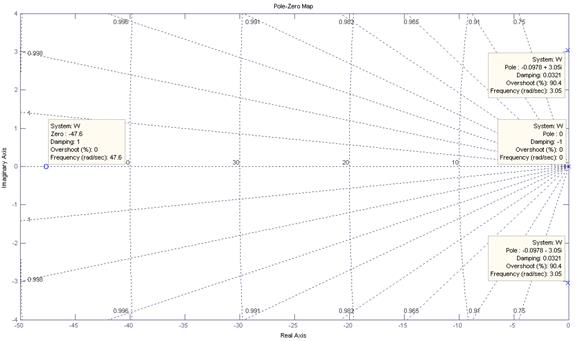
Рисунок 7.5 – Положение корней характеристического уравнения.
Один из полюсов лежит в начале координат на комплексной плоскости, значит система является колебательной.
Характер движения ЭП w1
(t), w2
(t) и изменение момента упругой деформации во времени М12
(t) при наличии диссипативных сил /1/:
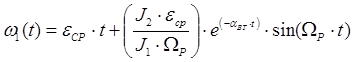 , с-1
(7.7) , с-1
(7.7)
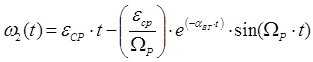 , с-1
(7.8) , с-1
(7.8)
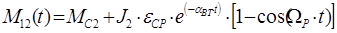 , H∙м (7.9) , H∙м (7.9)
где 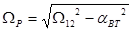 - резонансная частота, с-1
(7.10) - резонансная частота, с-1
(7.10)
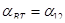 - коэффициент затухания, с-1
; - коэффициент затухания, с-1
;
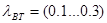 - логарифмический декремент затухания. - логарифмический декремент затухания.
Тогда по формуле (7.10) имеем:
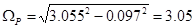 , с-1 , с-1
Среднее ускорение 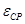 , с-2
, определится по формуле: , с-2
, определится по формуле:
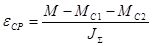 , с-2
, (7.11) , с-2
, (7.11)
где 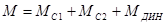 , H∙м (7.12) , H∙м (7.12)
Перепишем формулу (7.12) в виде:
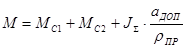 , H∙м (7.13) , H∙м (7.13)
Тогда имеем:
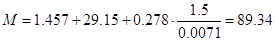 H∙м H∙м
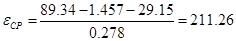 с-2 с-2
Тогда по формулам (7.7), (7.8), (7.9) запишем:
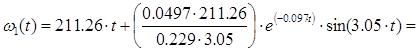
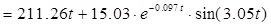 с-1 с-1
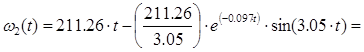
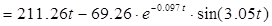 с-1 с-1
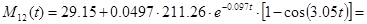
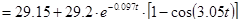 H∙м H∙м
Динамический коэффициент 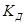 определится по формуле: определится по формуле:
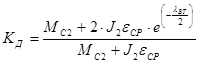 (7.14) (7.14)
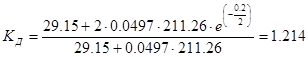

  Рисунок 7.6 – График переходных процессов угловых скоростей двухмассовой МЧЭП Рисунок 7.6 – График переходных процессов угловых скоростей двухмассовой МЧЭП
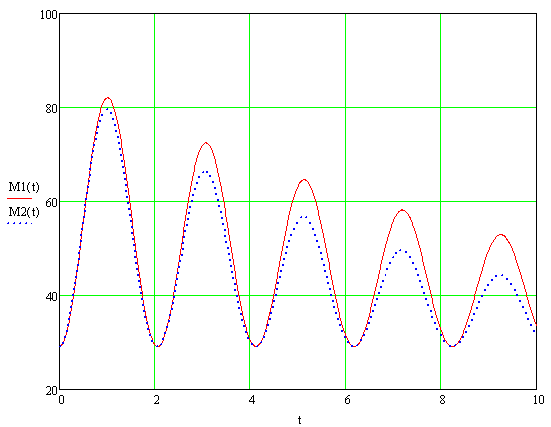
Рисунок 7.7 – График переходного процесса момента упругой деформации.
Сплошной линией показаны колебания момента при ранее выбранном значении логарифмического декремента затухания λ=0.2; пунктирной линией показаны колебания момента при увеличении логарифмического декремента затухания до λ=0.3.
По графику определим М12
max
=82.05 Нм
Фактическое отношение 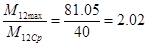
Динамический коэффициент который характеризует условия работы механического оборудования и является одним из основных показателей динамических качеств электропривода.
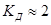 т.е упругие колебания вдвое увеличивают рабочие нагрузки передач, кинетическая энергия в основном переходит в энергию упругих деформаций, не вызывая дополнительные динамические нагрузки. т.е упругие колебания вдвое увеличивают рабочие нагрузки передач, кинетическая энергия в основном переходит в энергию упругих деформаций, не вызывая дополнительные динамические нагрузки.
Помимо прямых критериев оценки демпфирующих способностей электропривода существуют косвенные критерии, в частности критерий, основанный на оценке отвода энергии колебаний за один цикл в электрическую часть системы, где энергия поглощается имеющимися диссипативными элементами (активными сопротивлениями). Наличие недемпфированного резонанса на частоте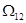 свидетельствует об отсутствии электромеханической связи, которая характеризуется коэффициентом электромеханической связи. свидетельствует об отсутствии электромеханической связи, которая характеризуется коэффициентом электромеханической связи.
Коэффициент электромеханической связи:
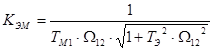
Постоянную времени ТМ1
определим из следующего соотношения:
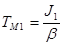 , ,
где 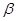 - жёсткость механической характеристики на рабочем участке. - жёсткость механической характеристики на рабочем участке.
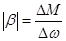
Для расчета механических характеристик (МХ) будем использовать формулу Клосса,
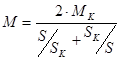 , H∙м, (7.15) , H∙м, (7.15)
где 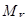 , H∙м – критический момент двигателя, , H∙м – критический момент двигателя,
Номинальная скорость равна:
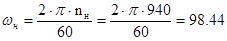 рад/с, рад/с,
номинальное скольжение
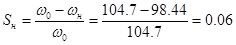 ; ;
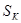 - критическое скольжение, - критическое скольжение,
критическое скольжение 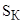 : :
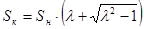 , где λ= Ммах
/Мн
=2.69; , где λ= Ммах
/Мн
=2.69;
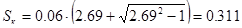 ; ;
С учётом рассчитанных значений:
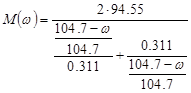
М(84)=294 Нм;
М(47)=106.5 Нм;
Жёсткость механической характеристики:
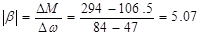
Определим постоянную времени ТМ1
:
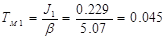 ; ;
Электромагнитную постоянную времени ТЭ
определим по формуле:
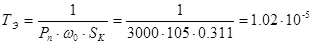
Частота электромеханического резонанса:
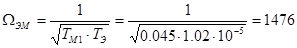 с-1 с-1
Коэффициент электромеханической связи:
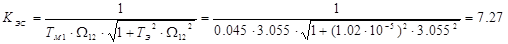
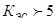 , можно утверждать, что демпфирующее действие ЭП пренебрежимо мало вследствие высокой жесткости механической характеристики двигателя. Такие условия свидетельствуют о возможности повышения демпфирующей способности ЭП за счет смягчения жесткости характеристики, увеличения инерционности системы регулирования скорости или других мер. , можно утверждать, что демпфирующее действие ЭП пренебрежимо мало вследствие высокой жесткости механической характеристики двигателя. Такие условия свидетельствуют о возможности повышения демпфирующей способности ЭП за счет смягчения жесткости характеристики, увеличения инерционности системы регулирования скорости или других мер.
Структурная схема двухмассовой системы, в которой входным воздействием является момент нагрузки МС2
:

Передаточная функция по возмущающему воздействию:
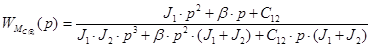 ; ;
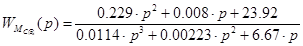
Частотные характеристики системы:
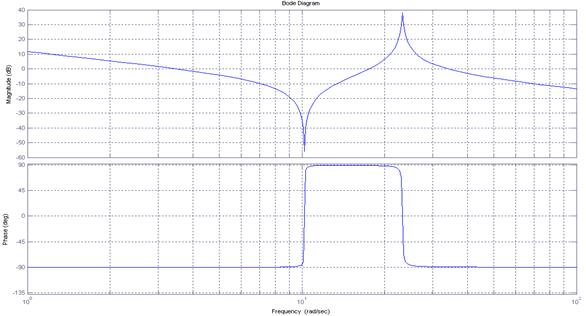
Рисунок 7.8 – Частотные характеристики.
Определим положение нулей и полюсов передаточной функции на комплексной плоскости:
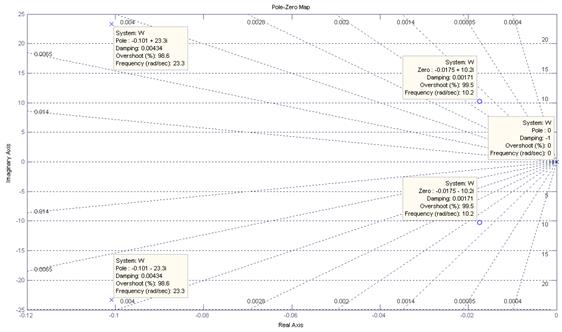
Рисунок 7.9 – Положение нулей и полюсов передаточной функции.
Нахождение одного из корней характеристического равнения, являющегося полюсом, в начале координат на комплексной плоскости говорит о колебательном характере системы.
Методика построения пусковой диаграммы зависит от мощности двигателя. Т.к. выбранный двигатель малой мощности, то мы будем пользоваться уточненной методикой. В нашем случае механические характеристики нелинейные, следовательно, применим графоаналитические методы (в частности метод последовательных интервалов).
Алгоритм построения переходного процесса:
– рисуем оси угловой частоты, момента, момента инерции и времени; при этом масштабы первых трёх осей выбираются произвольно, а масштаб оси времени рассчитывается по формуле:
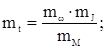
– в левом квадранте изображаем механическую характеристику;
– с учётом статического момента перерисовываем механическую характеристику;
– разбиваем область механической характеристики на произвольное количество участков; разбиение проводим параллельно оси моментов;
– заменяем участки ограниченные механической характеристикой равными по площадям прямоугольниками (преобразуем нелинейную характеристику в ступенчатую);
– из каждого эквивалентного прямоугольника опускаемся перпендикуляры на ось моментов;
– из начала координат циркулем сносим получившиеся точки на ось угловой скорости (для пуска на положительную область, а для генератора на отрицательную);
– из точки суммарного приведённого момента инерции проводим лучи, соединяющие полученные точки на оси угловой скорости;
– параллельным переносом для каждого значения угловой скорости сносим в правый квадрант построенные лучи.
– Построим электромеханическую характеристику двигателя во втором квадранте и найдем точки ее пересечения с границами участков, на которые разбиваем кривую динамического момента.
– из каждой точки пересечения опускаемся перпендикуляры на ось моментов;
– из начала координат циркулем сносим получившиеся точки на ось угловой скорости;
– из точки суммарного приведённого момента инерции проводим лучи, соединяющие полученные точки на оси угловой скорости;
Для каждого значения 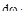 в первом квадранте откладывается величина тока двигателя в первом квадранте откладывается величина тока двигателя 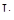 , которая принимается постоянной в течение времени , которая принимается постоянной в течение времени 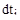 и приращения скорости и приращения скорости 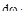 . В конце построений кривые заменим плавными линиями . В конце построений кривые заменим плавными линиями 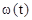 и и 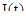 . .
Все рисунки представлены в приложении 2.
При пуске 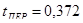 с, при торможении с, при торможении 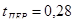 с с
Графики переходных процессов при спуске лифта отличаются величиной статического момента, что скажется на длительности динамических режимов, сохранив их характер.
Проверку двигателя по нагреву осуществляют сравнивая ток статора с номинальным током двигателя. Величину току статора определим по формуле:
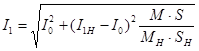 (9.1) (9.1)
где I1н
, Mн
, sн
– соответственно номинальные значения тока статора, момента и скольжения;
M, s – текущие значения момента и скольжения двигателя в установившемся режиме работы.
I0
– ток холостого хода, А.
Ток в одной из фаз обмотки статора определим по формуле:
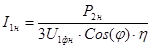 , А , А
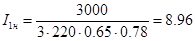 А А
Подставим значения в уравнение (9.1):
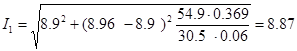
Номинальный ток при составляет I
н
=
8.9 А.
Выбранный двигатель имеет номинальный ток
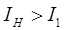
Выбранный нами двигатель подходит по нагреву.
Опираясь на нагрузочную диаграмму, рассчитаем эквивалентный момент:
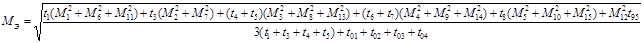 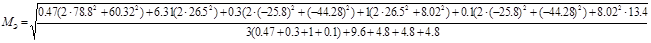 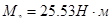
Выбранный двигатель имеет номинальный момент 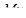 больший по сравнению с эквивалентным моментом больший по сравнению с эквивалентным моментом 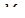 . Выбранный нами двигатель устраивает по перегрузке. . Выбранный нами двигатель устраивает по перегрузке.
Определим реальную продолжительность включения из нагрузочной диаграммы:
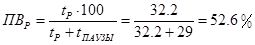 . .
Потери энергетической мощности имеют место в установившихся и переходных процессах /6/, /5/.
В установившемся режиме потери:
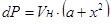 , Вт, , Вт,
где 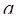 – коэффициент потерь, характеризующий отношение постоянных потерь к переменным при номинальной нагрузке (для лифтовых АД – коэффициент потерь, характеризующий отношение постоянных потерь к переменным при номинальной нагрузке (для лифтовых АД 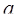 =(0.5…0.9)=0.8 =(0.5…0.9)=0.8
Определим значения сопротивлений R1, R2’ , xk
из формул :
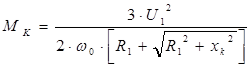 ; ;
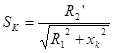
Приняв R1= R2’, получим:
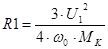
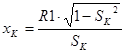

Определим номинальные токи ротора 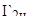 отдельно для высокоскоростной и низкоскоростной обмоток с соответствующими параметрами обмоток: отдельно для высокоскоростной и низкоскоростной обмоток с соответствующими параметрами обмоток:
1) для высокоскоростной обмотки:
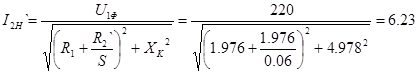 , А. , А.
2) для низкоскоростной обмотки:
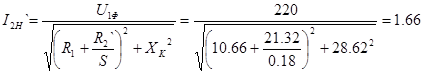 , А. , А.
Определим токи ротора 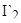 отдельно для высокоскоростной и низкоскоростной обмоток в установившемся режиме на подъеме: отдельно для высокоскоростной и низкоскоростной обмоток в установившемся режиме на подъеме:
1) для высокоскоростной обмотки:
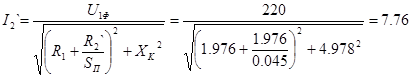 , А. , А.
2) для низкоскоростной обмотки:
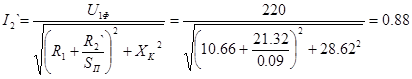 , А. , А.
Определим токи ротора 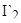 отдельно для высокоскоростной и низкоскоростной обмоток в установившемся режиме на спуске: отдельно для высокоскоростной и низкоскоростной обмоток в установившемся режиме на спуске:
1) для высокоскоростной обмотки:
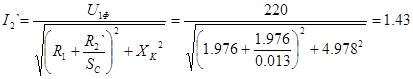 , А. , А.
2) для низкоскоростной обмотки:
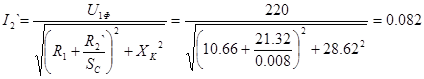 , А , А
где 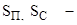 соответственно скольжение при подъеме и спуске лифта. соответственно скольжение при подъеме и спуске лифта.
Определим переменные потери в номинальном режиме работы для высокоскоростной обмотки.
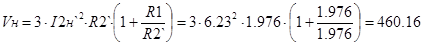 Вт Вт
Определим переменные потери в номинальном режиме работы для низкоскоростной обмотки.
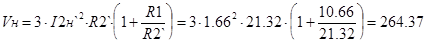 Вт Вт
Определим потери мощности для высокоскоростной обмотки:
1) при подъеме:
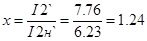
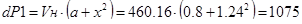 , Вт. , Вт.
2) при спуске:
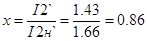
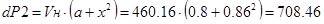 , Вт. , Вт.
Определим потери мощности для низкоскоростной обмотки:
1) при подъеме:
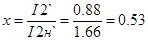
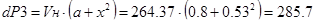 , Вт. , Вт.
2) при спуске:
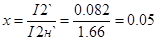
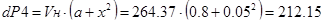 , Вт. , Вт.
Умножив потери мощности на соответствующие временные промежутки установившегося режима, получим потери энергии в установившемся режиме:
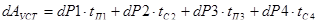 , Дж, , Дж,
где tП1
, tC
2
– соответственно время установившегося режима при подъеме и спуске на высокоскоростной обмотке; tП3
, tC
4
– соответственно время установившегося режима при подъеме и спуске на низкоскоростной обмотке, с.
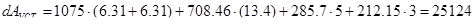 , Дж. , Дж.
Определим потери энергии в переходных режимах.
Потери при пуске на холостом ходу:
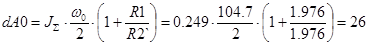 , Дж. , Дж.
Для пуска под нагрузкой:
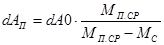 , Дж, , Дж,
где 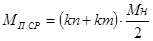 - средний пусковой момент двигателя, Н*м; кm - перегрузочная способность двигателя, кп – кратность пускового момента. - средний пусковой момент двигателя, Н*м; кm - перегрузочная способность двигателя, кп – кратность пускового момента.
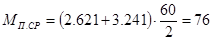 , Н.
м. , Н.
м.
Определим потери энергии для пуска под нагрузкой отдельно при пуске вверх dA1 и пуске вниз dA2 кабины:
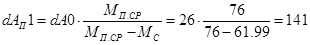 , Дж, , Дж,
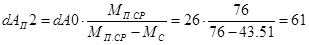 , Дж. , Дж.
При рекуперативном торможении происходит преобразование запасенной кинетической энергии вращающегося ротора в электроэнергию, за вычетом потерь отдается в сеть.
В первом приближении выделяющаяся энергия в режиме рекуперации без учета потерь на электромеханическое преобразование составят
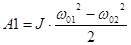 , Дж, , Дж,
где ω01
и ω02
– соответственно синхронные скорости высокоскоростной и низкоскоростной обмоток, 1/с.
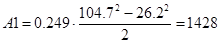 , Дж. , Дж.
Потери энергии при рекуперативном торможении:
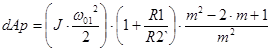 , Дж, , Дж,
где 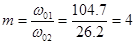 ,R1, R2` - сопротивления низкоскоростных обмоток, Ом. ,R1, R2` - сопротивления низкоскоростных обмоток, Ом.
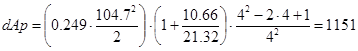 , Дж. , Дж.
Энергия отдаваемая в сеть
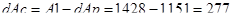 ,Дж ,Дж
Общие потери энергии за круговой рейс определяются как сумма потерь энергии в переходных и установившихся режимах работы электропривода. Для выбранного кругового рейса получим:
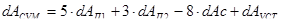 , Дж. , Дж.
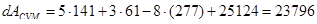 , Дж. , Дж.
КПД двигателя за круговой рейс
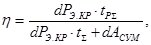
где РЭ.КР
– эквивалентная мощность на валу двигателя за круговой рейс, Вт; tР.СУМ
– суммарное время работы электродвигателя за круговой рейс, с.
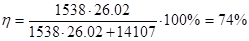
Среднецикловой коэффициент мощности в асинхронных приводах рассчитывают по формуле
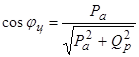
где Ра
– активная мощность двигателя, кВт;
Qa
– реактивная мощность, кВАР.
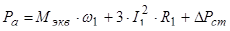
где Мэкв
– эквивалентный момент за цикл работы, Н∙м;
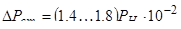 – потери в стали. – потери в стали.
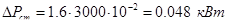
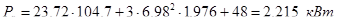
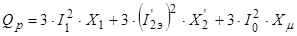
где I0
– ток холостого хода двигателя, А;
Xμ
– реактивное сопротивление контура намагничивания.
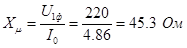
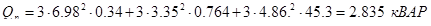
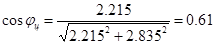
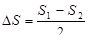 ; ;
где 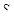 - путь, пройденный кабиной с пассажирами; - путь, пройденный кабиной с пассажирами;
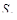 - путь, пройденный кабиной без пассажиров. - путь, пройденный кабиной без пассажиров.
Для расчета S будем использовать формулу:
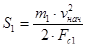 , где , где 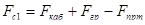 - статическая сила, с учетом пассажиров; - статическая сила, с учетом пассажиров;
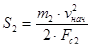 , где , где 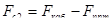 - статическая сила, без учета пассажиров; - статическая сила, без учета пассажиров;
где 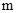 – масса механизма, приведенная к валу двигателя; – масса механизма, приведенная к валу двигателя;
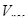 - посадочная скорость; - посадочная скорость;
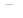 - статическое усилие, действует со стороны механизма; - статическое усилие, действует со стороны механизма;
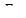 - тормозное усилие, действует со стороны тормоза. - тормозное усилие, действует со стороны тормоза.
Масса 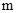 определяется по формуле: определяется по формуле:
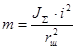 , где , где
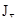 - суммарный момент инерции механизма; - суммарный момент инерции механизма;
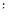 - передаточное число редуктора; - передаточное число редуктора;
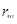 - радиус шкива. - радиус шкива.
Найдем 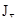 при пустом лифта: при пустом лифта:
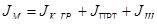 , где , где
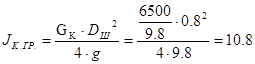 - момент инерции кабины без груза, приведенный к валу шкива, кг×м2
. - момент инерции кабины без груза, приведенный к валу шкива, кг×м2
.
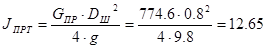 - момент инерции противовеса, приведенный к валу шкива, кг×м2
, - момент инерции противовеса, приведенный к валу шкива, кг×м2
,
Теперь мы можем рассчитать момент инерции механизма:
 , кг×м2
; , кг×м2
;
Момент инерции механизма, приведённый к валу двигателя:
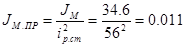 , кг×м2
; , кг×м2
;
Суммарный момент инерции при отсутствии груза:
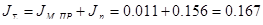 , кг×м2
; , кг×м2
;
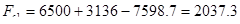 Н; Н;
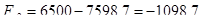 Н. Н.
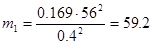 кг; кг;
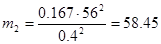 кг, кг,
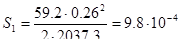 м, м,
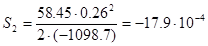 м, м,
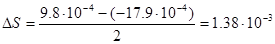 м. м.
Точность остановки составляет 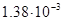 м. , что является почти идеальным случаем остановки кабины пассажирского лифта и гораздо меньше м. , что является почти идеальным случаем остановки кабины пассажирского лифта и гораздо меньше 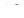 заданного по условию (0.02м). Данная система не требует применения фрикционного тормоза для обеспечения заданной точности остановки. заданного по условию (0.02м). Данная система не требует применения фрикционного тормоза для обеспечения заданной точности остановки.
В данной курсовой работе был спроектирован электропривод пассажирского лифта. Проектирование можно разбить на несколько этапов.
На первом этапе производится выбор рода тока и типа электропривода. Выбираем электропривод на переменном токе и применяем двухскоростной асинхронный двигатель с короткозамкнутым ротором.
Далее, согласно заданным параметрам, производится предварительный расчет мощности двигателя. По полученным данным выбирается двухскоростной асинхронный двигатель. В условиях проекта, мной выбран двигатель АНП 1805А6/24.
На следующем этапе строится нагрузочная диаграмма, из которой определяется момент прикладываемый к валу двигателя. В расчете я получил, что момент прикладываемый к валу равен приблизительно 23.72 Нм. Выбранный двигатель способен развить момент 30.5 Нм. Следовательно, двигатель подходит по перегрузке.
Проверка по нагреву осуществляется сравнением эквивалентного тока за цикл с номинальным током двигателя. Целесообразно выполнить проверку только для высокоскоростной обмотки, поскольку низкоскоростная обмотка имеет малое время работы и потому не оказывает существенного влияния на вычисляемый эквивалентный ток. Полученное значение тока равно 8.87А. Выбранный двигатель имеет номинальный ток 8.9А., больший по сравнению с эквивалентным. Значит, выбранный двигатель подходит по перегреву, а так же выбранный нами двигатель устраивает по перегрузке.
Однако выбранный двигатель обеспечивает фактическую скорость движения кабины равную 0.7 м/c. Но это не является существенным, так как отклонение от заданной условием задания скорости составляет 1.4%.
Произведена оценка энергетических показателей ЭП. В результате высоких динамических нагрузок двигатель выбран завышенной мощности, что вызвало снижение энергетических показателей ЭП. КПД составляет 74%, коэффициент мощности cosφ = 0.61.
Реальная загрузка лифта не является постоянной величиной, поэтому следующим этапом проектирования является проверка точности остановки кабины на уровне этажа. В данном проекте точность остановки составляет 12 мм, что удовлетворяет заданным параметрам курсового проекта.
Список литературы
1 Ключев В.И., Терехов В.М. Электропривод и автоматизация общепромышленных механизмов. Учебник для вузов, М.: Энергия, 1980.-360 с.
2 Автоматизированный электропривод /Под общ. ред. Н.Ф.Ильчинко, М.Г.Юнькова. – М.: Энергоатомиздат, 1990. – 544 с.
3 Ключев В.И. Теория электропривода. Учебник для вузов, М.: Энергоиздат, 1985. – 568 с.
|