|
При записи механизма реакции или при выдвижении набора механизмов (набора гипотез о механизмах) необходимо учитывать основные теоретические положения (постулаты, законы, принципы) и эвристические правила, которые позволяют оценить вероятность отнесения той или иной реакции к элементарным стадиям. Количественный ответ на этот вопрос дают пока еще очень трудоемкие профессионально выполненные квантово-химические расчеты. Поэтому использование простых правил и представлений о реакционной способности очень полезно.
В этом разделе мы рассмотрим очень кратко основные выводы и следствия различных теорий элементарной стадии, повторив и основные понятия химической кинетики.
Основные понятия химической кинетики
Концентрация вещества C определяется количеством молекул (или молей) в единице объема.
Число частиц должно быть большим, чтобы величину концентрации С можно было рассматривать как величину статистическую и одинаковую в любой части реакционного объема.
В системе устанавливается равновесное распределение частиц по внутренним степеням свободы (энергиям) и по скоростям поступательного движения – максвелл-больцмановское распределение (МБР). Между возбужденными и невозбужденными состояниями устанавливается статистическое (термическое) равновесие, характеризуемое одной температурой. Если химические реакции не нарушают термического МБР, то кинетику таких реакций называют “равновесной”. К равновесной кинетике относятся большинство реакций в газах, растворах и на поверхности при T < 1000о
С. Неравновесная кинетика исследует фотохимические, плазмохимические реакции, процессы горения и взрыва.
Взаимодействие нескольких частиц (реагентов) с образованием молекул (частиц), называемых продуктами реакции, проходящее через один потенциальный барьер, называют элементарным актом химического процесса. Многократное повторение таких актов с участием большого числа молекул (частиц), называют элементарной реакцией или элементарной стадией (ЭС).
Число участников (реагентов) ЭС называют молекулярностью ЭС. Молекулярность m есть сумма стехиометрических коэффициентов участников ЭС (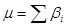 ). ).
Скорость реакции. Изменение количества молей i-того участника стадии (∆ni
) в результате химической реакции определяется скоростью ri
образования или расходования ni
, временем реакции t и объемом V:Dni
= j(ri
, t, V). Поэтому скорость реакции ri
есть производная второго порядка от ni
по V и t:
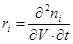 (1) (1)
Если ri
одинакова по всему объему и V = const (закрытая система), то Dni
µV, и дифференцирование по V заменяется делением на V:
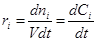 (2) (2)
Если в открытой системе реакция стационарна, то Dni
µt, и дифференцирование по t заменяется делением на t (реактор идеального вытеснения):
Реклама

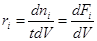 (3) (3)
где Fi
– мольный поток (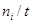 ). ).
Если выполнены оба условия (безградиентный проточный реактор, реактор полного смешения), то скорость 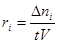 или или 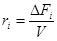 . .
Скорость j-той стадии при V = const есть производная степени глубины реакции c по времени в единице объема
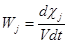 , где , где 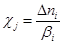 (4) (4)
отсюда
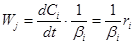 (5) (5)
Изложенные соображения справедливы и для участников итоговых уравнений стационарных, квазистационарных и нестационарных реакций.
Основные законы, постулаты и принципы
Рассмотрим основные законы, постулаты, принципы и эвристические правила, лежащие в основе теории элементарной стадии:
Законы сохранения массы и элементов в ходе химической реакции (в закрытой системе):
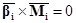 (6) (6)
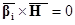 (7) (7)
где 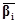 – вектор-строка стехиометрических коэффициентов участников реакции, – вектор-строка стехиометрических коэффициентов участников реакции, 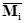 – вектор-столбец молекулярных масс участников реакции, H – атомная (молекулярная) матрица. – вектор-столбец молекулярных масс участников реакции, H – атомная (молекулярная) матрица.
Закон сохранения энергии
.
Закон действия масс (Гульдберг–Вааге, Вант-Гофф). Согласно этому закону скорость элементарной стадии в одном направлении пропорциональна произведению концентраций реагентов в степенях, соответствующих стехиометрическим коэффициентам в уравнении стадии
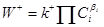 (8) (8)
Для реакции  (9) (9)
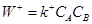 (10) (10)
где k+
– константа скорости (удельная скорость при 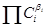 = 1). Сумма bi
соответствует молекулярности реакции, а показатель bi
называют порядком реакции. В случае ЭС суммарный порядок совпадает с молекулярностью. = 1). Сумма bi
соответствует молекулярности реакции, а показатель bi
называют порядком реакции. В случае ЭС суммарный порядок совпадает с молекулярностью.
- Постулат о необходимости соударений молекул (частиц) для реализации химического превращения. Даже в случае мономолекулярных реакций основой всех теорий считается схема Линдеманна-Христиансена, согласно которой молекула реагента А в реакции А ® В приобретает необходимую для превращения в В энергию в результате столкновения с любыми молекулами М (инертного газа, продукта и с другой молекулой реагента).
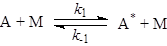
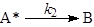
В случае квазистационарности по [А*
]
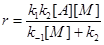 (11) (11)
При больших концентрациях М (больших давлениях)
k–1
[M] >> k2
и 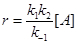 . .
При низких концентрациях М лимитирующей становится первая стадия в прямом направлении с уравнением 2го
порядка. Вероятность соударений двух молекул в бимолекулярной реакции или фактор соударений 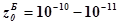 см3
/сек существенно ниже фактора (вероятности) тройных соударений см3
/сек существенно ниже фактора (вероятности) тройных соударений 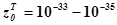 см6
/сек, поэтому вероятность таких реакций низка. Тримолекулярные реакции в подавляющем числе примеров являются блоками бимолекулярных ЭС. см6
/сек, поэтому вероятность таких реакций низка. Тримолекулярные реакции в подавляющем числе примеров являются блоками бимолекулярных ЭС.
Простые соображения, вытекающие из теории соударений в газовой фазе, позволяют сформулировать первое очень важное правило отбора – молекулярность (m) элементарной стадии не превышает 2 (m£ 2).
Реклама

В газовой фазе частицы сталкиваются по всему объему. В жидкой фазе – только в свободном объеме клетки из молекул растворителя. В первой сфере такой клетки молекулу реагента А окружает 8 – 12 молекул растворителя. Для того, чтобы столкнуться, молекулы A и B в этом случае должны в результате диффузии попасть из клеток Asol
и Bsol
в общую клетку (AB)sol
, т.е. образовать так называемую диффузионную пару. Поскольку свободный объем клетки Vf
составляет 0,2 – 2% от V растворителя, частота столкновений в таком объеме будет больше, чем в объеме V газовой фазы. Экспериментальное отношение констант скорости kж
/ kг
одинаковых бимолекулярных элементарных реакций в неполярных растворителях составляет 10 – 150. Очевидно, что вероятность соударения трех частиц в одной клетке не увеличится заметно по сравнению с газофазными реакциями, а вероятность образования диффузионной тройки в одной клетке ниже вероятности образования диффузионной пары.
В реакциях таких сложных молекул, как ферменты, молекулярность отдельных стадий также не превышает двух. Однако, в случае ферментов в активном центре фермента возможно многоцентровое связывание и синхронное участие в элементарном акте большого числа (3 – 4) активных групп. Таким образом, по отношению к комплексу фермент-субстрат (ES) реакция является, например, бимолекулярной (ES + H2
O), а в полости активного центра происходит многоцентровой процесс. Сильное падение энтропии активации в этом случае компенсируется повышением энтропии за счет изменения третичной структуры белка и его дегидратации в результате вызванной образованием комплекса ES перестройки белка.
- Принцип микроскопической обратимости (постулат) исходит из обратимости любого элементарного акта, т.е. из обратимости любого микроскопического процесса, протекающего на молекулярном уровне. В макроскопическом описании больших ансамблей молекул (частиц) появляются МБР, статистические термодинамические характеристики (DH, DS) и, соответственно, возможность необратимости. Сумма элементарных актов в прямом направлении, т.е. макроскопический процесс, компенсируется суммой элементарных актов в обратном направлении при достижении равновесия. Микроскопически обратимый процесс в макроскопической системе может быть необратимым. В макросистеме обратимых стадий, каждая стадия (реакция) самостоятельно доходит до равновесия, когда изменение химического потенциала Dm (или химического сродства А) станет равным нулю
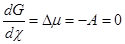 ( (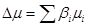 ) (12) ) (12)
Равенство Dm = DG = –А = 0 означает и равенство скоростей прямой и обратной реакции W+
= W–
.
- Принцип детального равновесия (ПДР) определяет статистическое соотношение между константами скорости прямого (k+
) и обратного (k–
) элементарного процесса в условиях МБР, как константу равновесия этого процесса (k+
/k–
= K). ПДР следует из ПМО и равенства скоростей W+
= W–
в точке химического равновесия (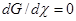 ). ПДР есть макроскопическое проявление ПМО. Взяв в качестве постулата принцип микроскопической обратимости при равновесии в форме W+
= W–
, получим ПДР и обратно, положив k+
/k–
= K в качестве постулата, приходим к равенству W+
= W–
при равновесии. Например, запишем для реакции (9) ). ПДР есть макроскопическое проявление ПМО. Взяв в качестве постулата принцип микроскопической обратимости при равновесии в форме W+
= W–
, получим ПДР и обратно, положив k+
/k–
= K в качестве постулата, приходим к равенству W+
= W–
при равновесии. Например, запишем для реакции (9)
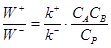 (13) (13)
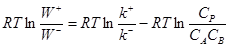 (14) (14)
Примем k+
/k–
= K, тогда 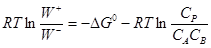 , т.е. , т.е.
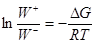 (15) (15)
Из (15) следует, что при 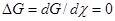 W+
= W–
. W+
= W–
.
Рассмотренный вывод справедлив для случая идеальных газов и идеальных растворов. Из ПМО следует ряд важных следствий, касающихся механизмов сложных реакций. Приведем одно из них – сложная реакция в прямом и обратном направлениях проходит через те же самые ЭС и интермедиаты.
- Закон (уравнение) Аррениуса описывает фундаментальное свойство константы скорости ЭС в условиях МБР – экспоненциальную зависимость от температуры
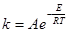 (16) (16)
Экспериментально, уравнение (16) было получено Худом в 1885 г. Зависимость такого вида была предсказана Вант-Гоффом в рамках равновесной термодинамики (1883 г.) и обоснована Аррениусом в рамках статистической физики (1889 г.). Классический механизм бинарных соударений молекул как упругих шаров приводит к выражению
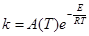 (17) (17)
С учетом необходимой ориентации молекул получим простейшую форму уравнения
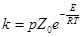 (18) (18)
где p – стерический фактор, Z0
– фактор соударений или общее число соударений. Энергия Е – энергия активации ЭС в уравнениях (17 – 18) есть разность между средней энергией реагирующих частиц и средней энергией всех частиц.
Экспоненциальный множитель в уравнениях выражает долю “активных” столкновений, т.е. тех столкновений, энергия которых равна или выше энергии барьера Е. Такое выражение – следствие того, что основной вклад в Еакт
в газовой фазе вносит поступательное движение молекул А и В.
Величины предэкспонентов в уравнениях (16) и (17) для мономолекулярных (АМ
), бимолекулярных (АБ
) и тримолекулярных (АТ
) реакций составляют 1013
сек–1
, 1010–11
л·моль-1
·сек–1
и 106
– 108
л·моль-2
·сек–2
, соответственно.
В рамках теории переходного состояния (или активированного комплекса) константа скорости ЭС (9)
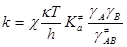 , (19) , (19)
где 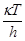 – частота перехода через барьер, сек–1
, c – трансмиссионный коэффициент, определяющий долю активированных комплексов, переваливающих через барьер, – частота перехода через барьер, сек–1
, c – трансмиссионный коэффициент, определяющий долю активированных комплексов, переваливающих через барьер, 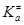 – термодинамическая константа равновесия образования активированного комплекса в условиях МБР всех частиц, gi
– коэффициенты активности реагентов и активированного комплекса – термодинамическая константа равновесия образования активированного комплекса в условиях МБР всех частиц, gi
– коэффициенты активности реагентов и активированного комплекса 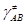 . .
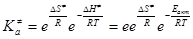 (20) (20)
Из общих принципов, важных для химической кинетики и полезных для определения статуса химической реакции как элементарной стадии, отметим еще два принципа.
Принцип независимости химических реакций.
Одновременное протекание множества ЭС в реагирующей системе подчиняется принципу (постулату) независимости химических реакций (В.Оствальд): все элементарные химические реакции протекают независимо. Связь между реакциями осуществляется на уровне материальных балансов, за счет изменения концентраций реагентов.
Согласно этому принципу, прямая и обратная элементарные реакции также протекают независимо, и это позволяет установиться химическому равновесию (см. ПМО).
- Принцип наименьшего движения Райса и Теллера. Согласно этому принципу, ЭС будет протекать быстро, с низкой Eакт
, если в ходе этой ЭС:
– происходит наименьшее движение ядер, т.е. движение с минимальным изменением координат ядер;
– происходит наименьшее движение электронов, т.е. такое, при котором изменение электронных оболочек не приводит к изменению валентного состояния.
Если в системе происходит незначительное изменение координат ядер, то это означает, что термы реагентов и продуктов близки. А чем ближе термы, тем ниже, в общем случае, величина барьера (Eакт
). Однако, это не всегда так. Путь наименьшего движения может и не совпадать с путем наименьшей энергии. Условие наименьшего движения электронов более универсально. В случае мономолекулярных реакций, например, это условие означает, что электронное строение реакционного центра реагирующей молекулы должно быть близко к электронному строению активированного комплекса для того, чтобы величина барьера (или 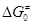 ) была небольшой. ) была небольшой.
Энергетические правила отбора ЭС рассматривают случаи, когда причиной больших значений 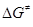 являются термохимические особенности ЭС. являются термохимические особенности ЭС.
- Эндотермические ЭС. В этом случае величина 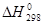 определяет нижний предел Еакт
, поскольку в подавляющем большинстве случаев максимумы на кривых потенциальной энергии и свободной энергии расположены при одном и том же значении координаты реакции. В случае, если определяет нижний предел Еакт
, поскольку в подавляющем большинстве случаев максимумы на кривых потенциальной энергии и свободной энергии расположены при одном и том же значении координаты реакции. В случае, если 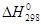 велика, например велика, например 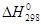 = 40000 кал/моль, а типичная величина предэкспонента бимолекулярной реакции SN
2-типа 1011
л×моль–1
×сек–1
(интервал значений А 1010
–1012
л×моль–1
×сек–1
), величина константы скорости k составит при 298 К = 40000 кал/моль, а типичная величина предэкспонента бимолекулярной реакции SN
2-типа 1011
л×моль–1
×сек–1
(интервал значений А 1010
–1012
л×моль–1
×сек–1
), величина константы скорости k составит при 298 К
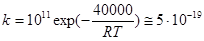 л×моль–1
×сек–1
. л×моль–1
×сек–1
.
Для того, чтобы скорость стадии (Wj
) была не ниже 0,01 моль×л–1
×ч–1
(практически приемлемая скорость), произведение концентраций реагентов в реакции типа (6) должно равняться
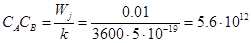 моль2
×л–2
, моль2
×л–2
,
что, естественно, нереально. При этом же значении скорости для CA
CB
= 10–4
моль2
×л–2
k = 2,8×10–2
л×моль–1
×сек–1
, откуда Еакт
@ 17000 кал/моль.
Таким образом, в зависимости от температуры реакции и ожидаемой скорости стационарного или квазистационарного процесса можно задать ограничения на величину 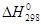 при выборе какой-либо реакции на роль ЭС. при выборе какой-либо реакции на роль ЭС.
Использование величины 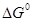 в качестве термодинамического критерия в случае ЭС не является столь же жестким, как для оценок реализуемости брутто-процесса (итоговой реакции). В последнем случае для выбора условий реакции (P, T) оценивают в качестве термодинамического критерия в случае ЭС не является столь же жестким, как для оценок реализуемости брутто-процесса (итоговой реакции). В последнем случае для выбора условий реакции (P, T) оценивают 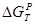 , Kравн
и равновесный выход продукта, который из любых соображений должен быть большим. В случае ЭС образования промежуточного соединения Х , Kравн
и равновесный выход продукта, который из любых соображений должен быть большим. В случае ЭС образования промежуточного соединения Х
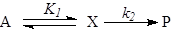 (21) (21)
допустимой концентрацией Х является такая, которая обеспечит положительное сродство (А > 0, Dm < 0) первой стадии и достаточную скорость образования Р на второй стадии, зависящую также и от k2
.
W1
> 0 при 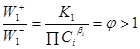
В стадии образования Х (21)
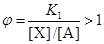 . .
В рассмотренном примере происходит кинетическое сопряжение двух ЭС через общий интермедиат Х, позволяющее проводить процесс синтеза продукта Р, с термодинамически невыгодной первой стадией. Сопряжение первой термодинамически невыгодной стадии (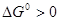 или даже или даже 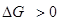 , т.е. А < 0) с быстрой второй смещает равновесие первой стадии вправо или даже меняет ее направление, увеличивает А и поэтому разность , т.е. А < 0) с быстрой второй смещает равновесие первой стадии вправо или даже меняет ее направление, увеличивает А и поэтому разность 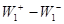 в пределе вырастает до величины в пределе вырастает до величины 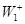 . .
Полезно еще раз уточнить некоторые понятия в связи с рассмотренными выше проблемами. Любая кинетически обратимая стадия (взаимно-обратная, двухсторонняя реакция), протекающая в закрытой системе при неизменных внешних условиях Р, Т, является термодинамически необратимым процессом (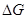 = Dmi
< 0), поскольку система самопроизвольно движется от исходного состояния к конечному равновесному. Кинетически необратимой стадией будет такая ЭС, для которой на протяжении всего процесса до степени конверсий реагента А a = 0,999 отношение = Dmi
< 0), поскольку система самопроизвольно движется от исходного состояния к конечному равновесному. Кинетически необратимой стадией будет такая ЭС, для которой на протяжении всего процесса до степени конверсий реагента А a = 0,999 отношение 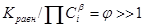 ( (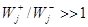 ). Например, если Kравн
@ 1015
, то на всем протяжении процесса от a = 0 до a = 0,999 величина j >> 1 и отношение ). Например, если Kравн
@ 1015
, то на всем протяжении процесса от a = 0 до a = 0,999 величина j >> 1 и отношение 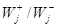 меняется в интервале 1012
¸ 107
, сохраняясь очень большим в течении всего процесса. Другими словами меняется в интервале 1012
¸ 107
, сохраняясь очень большим в течении всего процесса. Другими словами
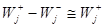
Процессы такого типа можно считать кинетически необратимыми.
- Эмпирические зависимости Еакт
и 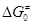 от термодинамических характеристик стадии. На основании экспериментальных наблюдений (Бренстед, Белл, Поляни) и теоретических соображений Беллом, Эвансом и Поляни был сформулирован принцип линейности свободных энергий (ПЛСЭ), называемый также правилом БЭП. В ряду однотипных элементарных реакций эти принципы отражают связь величин от термодинамических характеристик стадии. На основании экспериментальных наблюдений (Бренстед, Белл, Поляни) и теоретических соображений Беллом, Эвансом и Поляни был сформулирован принцип линейности свободных энергий (ПЛСЭ), называемый также правилом БЭП. В ряду однотипных элементарных реакций эти принципы отражают связь величин 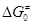 и и 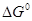 или Еакт
и или Еакт
и 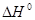 , т.е. связь кинетических и термодинамических характеристик, которая была аппроксимирована линейными уравнениями , т.е. связь кинетических и термодинамических характеристик, которая была аппроксимирована линейными уравнениями
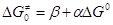 (22) (22)
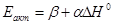 (23) (23)
Коэффициенты уравнения (23) найдены Н.Н. Семеновым для ряда ЭС радикалов с молекулами (уравнение Поляни-Семенова).
Eэкзо
= 11,5 – 0,25|DH0
| (24)
Eэндо
= 11,5 + 0,75|DH0
| (25)
где DH0
– энтальпия стадии по абсолютной величине.
Правило БЭП позволяет при отборе ЭС использовать в качестве ограничения сверху не значения DH0
, а величины Еакт
, что делает отбор ЭС более точным.
Принципиально важным является безусловно вопрос о виде функции E = f(DH0
). Еще Поляни (30е годы ХХ века) было ясно, что ПЛСЭ или уравнение Поляни являются лишь грубой линейной аппроксимацией в узком интервале термодинамических величин DG0
и DH0
более сложных функций, например, квадратичного уравнения (26)
 (26) (26)
Уравнение типа (26) было позднее получено для реакций переноса электрона (Р.Маркус, 1956 г.), предложено по аналогии для переноса протона (Р.Маркус, 1968) и уточнено и теоретически обосновано В.Г.Левичем, Р.Р.Догонадзе и А.М.Кузнецовым (1965 – 1975 гг). Получены параболические и более сложные степенные уравнения для расчета Еакт
стадий радикальных реакций по значениям DH0
.
|