Департамент образования и науки Краснодарского края
ГОУ СПО Краснодарский педагогический колледж №3 Краснодарского края
Выпускная квалификационная работа
Формы работы на уроках математики в процессе решения текстовых задач
Студентка 4 курса
Школьного отделения
Базарнова Екатерина Николаевна
Руководитель: Гавриш Г.Н.
2010 г.
Оглавление
Введение
Глава 1. Формы работы младших школьников на уроках математики
1.1 Урок математики. Содержание урока, его построение. Подготовка учителя к уроку
1.2 Использование различных форм работы младших школьников в процессе решения текстовой задачи
Глава 2. Решение текстовых задач в начальной школе
2.1 Понятие «текстовая задача» и ее структура
2.2 Процесс решения текстовых задач
2.3 Обучение решению задач. Уровни сформированности умений младших школьников решать задачи. Критерии уровней
2.4 Методические приемы, используемые в работе над текстовой задачей в начальной школе
2.5 Примеры использования различных форм работы младших школьников в процессе решения текстовой задачи
Глава 3. Формирование умений младших школьников решать текстовые задачи
3.1 Диагностика уровня сформированности умений младших школьников решать задачи
3.2 Повышение уровня сформированности умений младших школьников решать задачи
3.3 Динамика уровней сформированности умений младших школьников решать задачи
Заключение
Список литературы
Введение
Математическое образование играет исключительную роль во всей образовательной структуре. Математика является не только базой естественных наук и экономики, но и важнейшей составляющей интеллектуального развития школьников.
Многие ведущие российские ученые такие, как В.А. Гусев, Г.В. Дорофеев, Н.Б. Истомина, Ю.М. Колягин, Л.Г. Петерсон и другие, отмечают необходимость математического развития младшего школьника в учебной деятельности: «начальный курс математики способствует продвижению ученика в общем развитии, становлению нравственных позиций личности ребенка» [19, 121].
Начальный курс математики раскрывается на системе целесообразно подобранных задач. Значительное место занимают в этой системе текстовые задачи. Они необходимы для того, чтобы сформировать у учащихся важные для обыденной жизни знания, а на их базе – умения и навыки, связанные с решением постоянно возникающих проблемных ситуаций.
Реклама

Но чтобы решить проблему, нужно понять ее суть, сформулировать задачу словесно, создать математическую интерпретацию решаемой проблемы, выбрать методы и способы достижения поставленной цели. Через решение задач дети знакомятся с важными в познавательном и воспитательном отношении фактами. Поскольку процесс решения текстовой задачи зачастую может быть организован не единственным образом, то важным показателем математической обученности индивида является его умение выбрать наиболее рациональный способ решения поставленной задачи. Поэтому очень важно научить школьников в широком смысле слова работать с задачей.
Каждая конкретная учебно-математическая задача предназначена для достижения чаще всего не одной, а нескольких целей: педагогической, учебной, дидактической, а формулировки этих целей подсказывает содержание самой задачи. Справедливо считать, что любая задача, включенная в урок, должна быть обязательно решена на этом уроке, решение доведено до конца и записано соответствующим образом. В результате деятельность учащихся на уроке зачастую однообразна, так как наполнена большим объемом механической и непродуктивной работы. Чтобы этого избежать и чтобы дети не уставали на уроке, с энтузиазмом принимались за работу, необходимо использование разнообразных форм и методов проведения урока в целом и решения текстовых задач в частности. Вариативность методов обучения математике помогает учащимся глубже окунуться в тему, более осознанно усвоить учебный материал, научиться общаться с коллективом, развивать самостоятельность. К сожалению, большинство статей в периодической печати и специальной литературе дают нам лишь общие знания о формах работы на уроках математики.
Курс обучения младших школьников математике по программе М.И Моро предполагает формирование у детей ряда представлений и понятий, ознакомление учащихся с некоторыми теоретическими фактами, формирование умений и отработка соответствующих навыков применения теоретических знаний. Коме того, программа предполагает доступное детям обобщение учебного материала, понимание общих принципов и законов, лежащих в основе изучаемых математических фактов, осознание тех связей, которые существуют между рассматриваемыми явлениями. Рассматриваемые в начальном курсе математики основные понятия, отношения, взаимосвязи и закономерности раскрываются на системе соответствующих конкретных задач. Важно научить детей самостоятельно находить пути решения предлагаемых программой задач, применять простейшие общие подходы к их решению [16, 235].
Реклама

В.Н. Рудницкая в своей программе по математике для начальной школы важнейшей целью ставит создание благоприятных условий для полноценного интеллектуального развития ребенка на уровне, соответствующем его возрастным особенностям и возможностям, и обеспечение необходимой и достаточной математической подготовки ученика для дальнейшего обучения [17].
В программе И.И. Аргинской говорится, что «Исходя из общей цели, стоящей перед обучением в системе Л.В. Занкова, начальный курс математики должен решать следующие задачи:
– дать представление о математике как науке, обобщающей существующие и происходящие в реальной жизни явления и способствующей тем самым познанию окружающего мира, созданию его широкой картины;
– сформировать знания, умения и навыки, необходимые ученикам в жизни и для успешного продолжения обучения в основном звене школы» [19, 122].
Программа И.И. Аргинской по математике для начальной школы нацелена на то, что можно назвать истинным умением решать задачи. Оно выражается, прежде всего, в решении задач без соотнесения их со знакомыми, ранее отработанными типами, а на основе распутывания той ситуации, которая отражена в данной конкретной задаче, и перевода ее на язык математических отношений [19, 123].
В основе программы Н.Б. Истоминой лежит методическая концепция, выражающая необходимость целенаправленной и систематической работы по формированию у младших школьников приемов умственной деятельности: анализа и синтеза, сравнения, классификации, аналогии и обобщения, в процессе усвоения математического содержания. Именно перечисленные приемы умственной деятельности составляют основу деятельности, связанной с решением текстовых задач [16, 265].
Современная методическая наука располагает совокупностью средств для достижения конкретных поставленных дидактических задач. Еще на этапе планирования уроков учитель подумывает систему методов и приемов учебно-воспитательной работы, сочетание различных форм организации деятельности школьников, методику применения средств обучения.
Отечественная начальная школа нацелена преимущественно на классно-урочную форму работы. Исследованиями психологов и наблюдениями учителей и методистов констатируется разделение коллектива класса по уровням успешности в обучении. Причинами такой дифференциации являются как социальные факторы, так и психические, физиологические особенности конкретных учащихся, психологические проблемы межличностных отношений школьников и т.п. В каждом конкретном случае такие причины и их сочетания индивидуальны. Поэтому для обеспечения наибольшей успешности целого класса в освоении учебного материала учителю желательно построить такой учебно-воспитательный процесс, в котором каждый ученик, независимо от его потенциала, будет вести активную познавательную деятельность.
На наш взгляд, такую возможность дает грамотно спланированное и реализованное на уроках сочетание различных форм организации деятельности учащихся. Учителя и методисты в специальной литературе, на совещаниях, семинарах, форумах подчеркивают, что применение одного и того же метода (методического приема, средства обучения) отнюдь не гарантирует одинакового уровня усвоения знаний учащимися.
Те учащиеся, которые в сравнении со своими одноклассниками более мотивированы на обучение, имеют определенный интерес к учебе, обладают достаточно высокими показателями развития внимания, памяти, речи, умеют организовывать собственную учебную деятельность и т.п., воспринимают учебный материал осознанно, глубоко, без видимых затруднений. Такие учащиеся в основном без видимых затруднений устанавливают связи между новым материалом и ранее изученным, а также применяют полученные знания в жизни, устанавливая межпредметные связи.
Другие учащиеся, которые испытывают затруднения в учебе, как правило, не обладают высокими показателями в развитии психических процессов, слабо мотивированы на учебную деятельность, не проявляют интереса к учебе. Усвоение материала на уроке такими школьниками поверхностно, непрочно. В обыденной жизни полученные знания, как правило, не находят применения. Вследствие этого для школьника создается некий замкнутый круг: знания нужны только для дальнейшей учебы, а учеба состоит лишь в приобретении новых знаний.
Раскрыть для всего класса значимость учения, показать взаимосвязи изучаемых вопросов и возможности приложения теории к практике уже в младшем школьном возрасте позволяет сочетание форм организации деятельности учащихся на уроке. Чувствуя ответственность перед классом при фронтальной работе, обмениваясь опытом (передавая или перенимая его) с одноклассниками в групповой работе, выполняя посильную деятельность при индивидуальной работе, младшие школьники получают более комфортные условия для успешного усвоения знаний по программе.
В настоящее время отечественная методическая литература предлагает инновационные разработки уроков, мультимедийные презентации, тренировочные пособия по математике, предназначенные для обучения младших школьников. Однако, на наш взгляд, эти источники носят несистемный характер, как правило, сфера их применения неширока. В связи с эти необходимость обобщения передового педагогического опыта в обучении решению текстовых задач становится бесспорной.
Отсюда вытекает проблема исследования – необходимость поиска ответа на вопрос: какие формы организации деятельности учащихся на уроках математики могут быть использованы учителем для выработки умения у учащихся решать текстовые задачи?
В качестве объекта исследования рассматривается весь процесс обучения младших школьников решению задач.
Предметом исследования являются формы работ учащихся на уроках математики в процессе решения текстовых задач.
Целью исследования является: на основе теоретического изучения форм и методов работы на уроках математики в процессе решения текстовых задач разработать методические рекомендации для учителей младших классов по использованию различных форм работы на уроках математики при решении текстовых задач.
Гипотеза: если на уроках математики систематически применять разнообразные формы работы с учащимися при обучении решению задач, то уровень их умения решать текстовые задачи повысится.
Для достижения поставленной цели необходимо решить ряд задач:
1) Раскрыть содержания понятий «формы работы на уроке математики в начальной школе», «уровень сформированности умений младших школьников», «текстовая задача»;
2) Изучить методику использования различных форм организации деятельности учащихся на уроках математики при решении текстовых задач;
3) Изучить характеристики уровней сформированности умений младших школьников решать текстовые задачи и соответствующие им критерии;
4) Разработать систему заданий для диагностики уровней развития умений младших школьников решать текстовые задачи;
5) Разработать фрагменты уроков, связанных с решением текстовых задач, с использованием разнообразных форм работы над текстовой задачей.
Методы исследования:
Теоретические:
· анализ научной, методической, периодической литературы по теме работы;
· изучение, анализ и обобщение передового опыта – с целью создания теоретической базы исследования.
Эмпирические:
· анализ учебной документации младших школьников;
· беседа с учителем начальной школы;
· анкетирование родителей учащихся;
· тестирование учащихся – с целью определения уровней сформированности умений младших школьников решать текстовые задачи.
Теоретической базой исследования явились труды известных педагогов (Истоминой Н.Б., Белошистой А.В., Аргинской И.И. и др.), раскрывшие сущность понятий «урок», «формы работы на уроках математики в начальной школе», «уровень сформированности умений младших школьников», «текстовая задача», описавших общие положения методики работы над текстовыми задачами в начальной школе. Так, в книге Т.Е. Демидова и А.П. Тонких «Теория и практика решения текстовых задач» [8, 5], наиболее полно раскрывается понятие текстовой задачи и ее структуры, приводится классификация текстовых задач, описываются методы и способы решения задач.
Особенности учащихся младших классов, которые необходимо принимать во внимание учителю при подготовке уроков математики и при решении текстовых задач, описаны в трудах психологов (Гусева В.А., Талызина Н.Ф. и др.). Например, в книге Л.В. Шелеховой «Сюжетные задачи по математике в начальной школе» [25, 30] подробно описана реализация индивидуального подхода к учащимся при обучении решению задач, приведена классификация видов самостоятельной работы школьников в зависимости от дидактической цели конкретного урока. В этой же книге приводится дифференциация учебных заданий по уровню творчества, по трудности, по объему учебного материала, по степени самостоятельности учащихся.
Дополнительная методическая и учебная литература (Петерсон Л.Г., Моро М.И., Демидова Т.Е. и др.), статьи (Сластенин Р.А., Царева С.Е., Басангова Р.Б., Смолеусова Т.В. и др.) в журналах «Начальная школа», «Начальная школа Плюс До и После», «Первое сентября», стали основой для обобщения современного передового педагогического опыта практикующих учителей и формирования банка фрагментов уроков, связанных с решением текстовых задач в начальной школе. Так, например, А.В Белошистая в статье «Вопросы обучения решению задач» [3, 73] рассматривает формирование и развитие умения представлять себе словесно заданную ситуацию как основное содержание подготовительного этапа к работе над задачей.
При проведении исследования широко использовались ресурсы сети Internet (http://wikipedia.org, http://5ka.su и др.), на страницах которой современные учителя обмениваются опытом, публикуют новейшие разработки уроков и их фрагментов, демонстрируют мультимедийное сопровождение к урокам математики.
Практическая значимость исследования представлена в виде рекомендаций учителям начальной школы по организации и применению разнообразных форм работы на уроке при обучении младших школьников решению текстовых задач.
Глава 1. Организация учебного процесса по математике в начальной школе
В настоящей главе раскрывается сущность понятий «урок» и «форма организации обучения», перечисляются требования к организации и проведению урока математики в начальной школе. Кроме того, приводится сравнительная характеристика известных форм работы на уроке математики.
1.1 Урок математики. Содержание урока, его построение. Подготовка учителя к уроку
Основной формой организации учебно-воспитательной работы с учащимися в школе является урок, сущность которого раскрывается в дидактике. Рассмотрим некоторые определения этого понятия, сформулированные в педагогической литературе.
Урок – это динамичная и вариативная основная форма организации учебного процесса, при которой в рамках точно установленного времени учитель занимается с определенным составом учащихся – с классом – по твердому расписанию, используя разнообразные методы и средства обучения для решения поставленных задач образования, развития и воспитания [14].
Урок – форма организации учебной деятельности в школе, при которой учитель занимается в рамках точно установленного времени с постоянным составом учащихся – с классом, по твердому расписанию, используя разнообразные методы для достижения поставленных им дидактических задач, определяемых требованиями учебной программы [29].
Урок – форма организации обучения с целью овладения учащимися изучаемым материалом (знаниями, умениями, навыками, мировоззренческими и нравственно-эстетическими идеями). Такая форма применяется при классно-урочной системе обучения и проводится для класса, то есть относительно постоянного учебного коллектива [35].
Современный урок – это организованное педагогом духовное общение группы, содержанием которого является научное знание, а ключевым результатом – интеллект каждого субъекта урочного общения, его духовное обогащение [29].
Сопоставляя приведенные определения понятия «урок», выделим основные его характерные черты (основные характеристики):
· урок является отрезком учебно-воспитательного процесса, ограниченным во времени;
· урок подчинен достижению заблаговременно поставленной основной дидактической цели и реализации сопутствующих задач;
· содержание урока подбирается в соответствии с целями и задачами урока, а также с учетом общедидактических требований, предъявляемых к уроку математики в начальной школе;
· средства и методы обучения подбираются учителем с перспективой наиболее полного достижения целей урока;
· организация учебной деятельности учителя и учащихся планируется (и, возможно, корректируется в ходе урока) с учетом особенностей обучаемого коллектива.
Следует отметить, что общий взгляд на понятие урока вполне можно распространить и на урок математики в начальной школе:
· современный урок математики в начальной школе продолжается 40 минут;
· каждый урок математики в начальной школе подчинен одой из следующих дидактических задач: подготовка к восприятию и усвоению нового материала, предусмотренного программой, собственно ознакомление с новым материалом, повторение и систематизация ранее изученных вопросов;
· в содержание современного урока математики в начальной школе включаются в том или ином виде все разделы начального курса математики, а именно: нумерация целых неотрицательных (возможно, дробных, отрицательных) чисел, арифметические действия, величины, текстовые задачи, алгебраический и геометрический материал;
· в качестве средств обучения на современном этапе чаще других используются учебники, тетради на печатной основе, интерактивная доска, мультимедийная аппаратура, наглядные средства обучения. Методы обучения математике в начальных классах в зависимости от целей конкретного урока могут быть как догматическими, проблемными, деятельностными;
· в ходе урока при необходимости учитель оперативно вносит коррективы в его план.
Главную роль среди перечисленных характеристик урока играют его цели: образовательные, воспитательные и развивающие. Этим целям всецело подчиняется выбор остальных характеристик урока. К образовательным целям урока математики относится формирование математических знаний, умений и навыков, предусмотренных учебной программой. Однако формировать надо не только математические, но и общеучебные знания, умения и навыки, позволяющие более рационально организовать учебную деятельность младших школьников при изучении математики. В единстве с обучением осуществляются цели воспитания и развития личности учащегося.
Учебные программы по математике предусматривают решение определенных воспитательных и развивающих задач. Для усиления воспитывающего и развивающего воздействий обучения учитель обязан тщательно анализировать соответствующие возможности математики и выделять воспитательную и развивающую цели каждого урока.
Выбор оптимальных для данного контингента младших школьников методов обучения — одна из самых трудных методических проблем. Выбор методов не будет оптимальным, если избранный метод не удовлетворяет хотя бы одному из условий, от которых он зависит, а именно:
1) методы обучения соответствуют целям урока (обучающей, воспитывающей и развивающей);
2) метод обучения соответствует особенностям содержания изучаемого материала (его сложности, новизне, характеру);
3) метод обучения выбирается с учетом особенностей учащихся класса (уровень развития их мышления, уровень знаний и умений, сформированность навыков учебного труда, уровень воспитанности учащихся, уровень их самостоятельности и др.);
4) метод обучения определяется с учетом оснащенности кабинета дидактическими материалами, техническими средствами обучения;
5) при выборе метода обучения учитываются эргономические условия (время проведения урока по расписанию, наполняемость класса и т. д.);
6) выбранный метод обучения соответствует индивидуальным особенностям учителя (его чертам характера, уровню овладения тем или другим методом, его отношениям с классом и др.).
Еще одна важная методическая характеристика урока – деятельность учителя и учащихся – будет рассмотрена ниже, в пункте 1.2 настоящей выпускной квалификационной работы.
Рассматривая урок с точки зрения логики процесса обучения, мы придем к понятию «структура урока».
В дидактике исследуется понятие «общая дидактическая структура урока», сущность и компоненты которой усматриваются на рисунке №1 [32]:
Раскрывая структуру урока математики в начальной школе, важно выделить основные этапы урока (комбинированного типа) из множества возможных его этапов:
1. Постановка цели урока перед учащимися.
2. Ознакомление с новым материалом.
3. Закрепление нового материала: а) на уровне воспроизведения информации и способов деятельности, б) на уровне творческого применения и добывания знаний.
4. Проверка знаний, умений и навыков.
5. Систематизация и обобщение изученного материала (по теме, разделу и т.п.).
В основе успешности обучения младших школьников математике лежит ряд требований к организации и проведению урока [20]. Во-первых, для каждого урока обязательным является первый из названных выше этап ― постановка цели, выбор остальных этапов обусловлен целью урока.
Опираясь на мотивы учения, необходимо привлечь учащихся к предстоящей на уроке работе, вызвать потребность в познании, в самоконтроле и самооценке своей деятельности. В течение всего урока учитель изучает реакцию учащихся на все происходящее на уроке.
Для практики обучения очень важно, чтобы цель урока, поставленная учителем, была понята учеником. Осознанные учеником цель и учебно-познавательная задача помогают ему действовать активно и ускоряют процесс получения результата своих учебных действий.
Очевидно, что одна структура урока может обеспечить более интересную и активную деятельность учащихся, чем другая. И надо стремиться к тому, чтобы урок оптимально обеспечивал активную познавательную деятельность всех учащихся класса.
Общая цель урока (единство обучения, воспитания и развития) порождает новые по содержанию и структуре уроки математики.
Второе важное требование к уроку математики – это рациональное построение его содержания. Бесспорно, что на уроке математики главным является его математическое содержание, которое должно глубоко отражать логику данного учебного предмета и быть определяющим во всем, что делается на уроке. Именно на базе математического содержания урока у учащихся формируются три вида умений и навыков: математические, общеинтеллектуальные (приемы умственной деятельности), умения и навыки учебной деятельности.
Важно обучать учащихся не столько математическим фактам самим по себе, сколько приобщать школьников к методам математики, развивать у них мышление. В каждом уроке важно выделить стержневую идею его математического содержания и вокруг нее сгруппировать все остальное.
Третье требование к уроку – это оптимальный выбор средств, методов и приемов обучения и воспитания на уроке.
Большая роль в отборе средств, методов и приемов работы на уроке отводится учителю. Успех дела зависит здесь во многом от того, насколько глубоко проникает учитель в специфику учебного материала, насколько умело ставит учебно-познавательные задачи, учитывая при этом уровень общей и математической подготовки учащихся, их личностные качества и прогнозируя результаты использования того или иного средства, метода или приема.
Выбирая средства, методы и приемы обучения, необходимо помнить, что нельзя их универсализировать. Ни одно из средств, ни один из методов, взятых изолированно, не смогут обеспечить достижения поставленных целей обучения.
Специфика самого учебного предмета «математика» такова, что основным в обучении младших школьников являются наглядно-вербальные средства в различных сочетаниях. Урок математики характеризуется комплексным применением наглядных и технических средств обучения.
Таким образом, мы видим, что в настоящее время понятие урока вообще и, в частности, урока математики в начальной школе хорошо раскрыто в специальной литературе. На протяжении десятилетий практически неизменными остаются взгляды на его целевую направленность, содержание, сочетание методов и средств обучения.
1.2 Формы работы младших школьников на уроках математики
Формы организации обучения (организационные формы) – это внешнее выражение согласованной деятельности учителя и учащихся, осуществляемой в определенном порядке и режиме. Они имеют социальную обусловленность, возникают и совершенствуются в связи с развитием дидактических систем [29]. Учебный процесс предполагает органическое единство средств, методов и приемов работы с организационными формами обучения. Каждому методу, приему обучения соответствует своя организационная форма, определяющаяся отношениями между учителем и учащимися и учащихся между собой. Учитель управляет всей учебной деятельностью на уроке, используя при этом различные ее формы. В дидактике принята следующая классификация форм учебной деятельности, в основе которой лежит количественная характеристика коллектива учащихся, взаимодействующих с учителем в данный момент урока:
· общие или фронтальные (работа со всем классом);
· индивидуальные (с конкретным учащимся);
· групповые (звено, бригада, пара и т. д.).
Первая предполагает совместные действия всех учащихся класса под руководством учителя, вторая — самостоятельную работу каждого ученика в отдельности; групповая — учащиеся работают в группах из трех-шести человек или в парах. Задания для групп могут быть одинаковыми или разными. Названные формы организации учебной деятельности учителя и учеников выступают на уроке в различных сочетаниях и последовательностях. В современных условиях обучения достаточно четко ставится вопрос о применении и сочетании таких организационных форм работы на уроке, которые обеспечивали бы эффективное приобретение школьниками не только знаний, умений и навыков, но и ценного опыта нравственных и коллективистских отношений. Огромная роль в достижении дидактических целей урока принадлежит коллективным формам работы (по сравнению с другими формами), поскольку они:
– позволяют уплотнять время урока,
– создают ситуации взаимообучения учащихся,
– существенно влияют на развитие личности.
Фронтальной формой организации учебной деятельности учащихся называется такой вид совместной деятельности учителя и учащихся на уроке, когда все ученики одновременно выполняют одинаковую, общую для всех работу, всем классом обсуждают, сравнивают и обобщают ее результаты. Учитель ведет работу со всем классом одновременно, общается с учащимися непосредственно в ходе своего рассказа, объяснения, показа, вовлечения школьников в обсуждение рассматриваемых вопросов и т.д. Это способствует
· установлению особенно доверительных отношений и общения между учителем и учащимися, а также учащихся между собой;
· воспитывает в детях чувство коллективизма;
· позволяет учить школьников рассуждать и находить ошибки в рассуждениях своих товарищей по классу;
· формировать устойчивые познавательные интересы школьников;
· активизировать их деятельность [34].
Условно механизм взаимодействия учителя (У) со школьниками (Ш) и школьников между собой изображен на рисунке №2.

Рис.2 Взаимодействие учителя и учащихся при фронтальной форме организации учебной деятельности класса
Фронтальная форма учебной работы имеет ряд существенных недостатков. Она по своей природе нацелена на некоего абстрактного ученика, в силу чего в практике работы школы весьма часто проявляются тенденции к нивелированию учащихся, побуждению их к единому темпу работы, к чему ученики в силу разных причин (своей разноуровневой работоспособности, подготовленности, реального фонда знаний, умений и навыков) не готовы. Ученики с низкими учебными возможностями работают медленно, хуже усваивают материал, им требуется больше внимания со стороны учителя, больше времени на выполнение заданий, больше тренировочных упражнений, чем ученикам с высокими учебными возможностями. Более успешные в учебе школьники нуждаются не в увеличении количества заданий, а в усложнении их содержания, в заданиях поискового, творческого типа, работа над которыми способствует развитию таких школьников и усвоению знаний на более высоком уровне.
Поэтому для максимальной эффективности учебной деятельности учащихся нельзя считать фронтальную форму организации деятельности школьников идеальной, необходимо использовать наряду с фронтальной формой организации учебной работы на уроке и другие.
Фронтальная форма организации учебной деятельности школьников должна применяться на тех этапах урока, где она целесообразна и удобна. Такими этапами являются, например, изучение нового материала и его первичное закрепление. Применение же вновь приобретенных знаний в измененных условиях требует индивидуального подхода к учащимся. Лабораторные или практические работы лишь организуют фронтально. Содержание заданий, их формулировки и уровень сложности разрабатываются с перспективой максимального развития каждого ученика.
Индивидуальная форма организации работы учащихся на уроке предполагает, что каждый ученик получает для самостоятельного выполнения задание, специально для него подобранное в соответствии с его подготовкой и учебными возможностями. В качестве таких заданий может быть работа с учебником, другой учебной литературой, разнообразными источниками (справочники, словари, энциклопедии, хрестоматии и т.д.), написание изложений, сочинений, рефератов, докладов, проведение всевозможных наблюдений и т.д. На уроках математики индивидуально подобранные упражнения чаще всего представлены в виде тренировочных упражнений – задач, примеров, уравнений и т.п.
Широко используется индивидуальная работа в программированном–обучении. Программированное обучение [греч. programma — публичное объявление, распоряжение, указ] — обучение по заранее разработанной программе, в которой полностью предусмотрены действия как учащихся, так и педагога (или заменяющей его обучающей машины) [35].
Условно взаимодействие учителя и школьников при индивидуальной форме организации учебной деятельности класса изображено на рисунке №3.

Рис.3 Взаимодействие учителя и учащихся при индивидуальной форме организации учебной деятельности класса
В педагогической литературе выделяют два вида индивидуальных форм организации выполнения заданий: индивидуальную и индивидуализированную.
Первая характеризуется тем, что деятельность ученика по выполнению общих для всего класса заданий осуществляется без контакта с другими школьниками, но в едином для всех темпе; вторая предполагает учебно-познавательную деятельность учащихся над выполнением специфических заданий. Именно она позволяет регулировать темп продвижения в учении каждого школьника сообразно его подготовке и возможностям.
Одним из наиболее эффективных путей реализации индивидуальной формы учебной деятельности школьников на уроке являются дифференцированные индивидуальные задания. К ним относятся задания с печатной основой, которые освобождают учащихся от механической работы и позволяют при меньшей затрате времени значительно увеличить объем эффективной самостоятельной работы. Причем для слабоуспевающих учеников дифференциация должна проявляться не столько в дифференциации заданий, сколько в мере оказываемой помощи учителем. Он наблюдает за работой школьников, следит, чтобы они работали правильными приемами, дает советы, формулирует наводящие вопросы.
Однако этого недостаточно. Не менее важным является контроль учителя за ходом выполнения заданий, его своевременная помощь в разрешении возникающих у учащихся затруднений. Если учитель в процессе индивидуальной работы школьников замечает, что некоторые ученики не справляются с заданием, учитель может прервать индивидуальную работу и дать всему классу–дополнительное–разъяснение.
Индивидуальную работу допустимо проводить на всех этапах урока, при решении различных дидактических задач ― для усвоения новых знаний и их первичного закрепления, для формирования и закрепления умений и навыков, для обобщения и повторения изученного, для контроля, для овладения исследовательским методом и т.д.
Недостатком индивидуальной формы организации работы учащихся на уроке является то, что при выполнении заданий школьники практически не общаются друг с другом, приобретаемый опыт самостоятельной деятельности не становится достоянием коллектива, не обсуждается вместе с товарищами по классу и учителем. Эти недостатки можно компенсировать в практической работе учителя сочетанием индивидуальной формы организации учебной деятельности школьников с групповой либо фронтальной (звеньевой, бригадной, кооперативно-групповой, парной). Кроме того, подготовка и реализация индивидуальной формы работы на уроке требует от учителя существенной затраты времени уже на этапе замысла и разработки, а также высокого мастерства при управлении самим процессом и при анализе полученных результатов.
Для организациигрупповой (звеньевой) формы учебной работы учащихсяучителю необходимо тщательно продумать все вопросы, которые связаны с образованием групп, распределением обязанностей внутри групп и объемом работы каждой группы.
Величина групп может быть различной. Она колеблется в пределах от двух до шести человек. Состав групп меняется в зависимости от содержания и характера предстоящей работы. При этом не менее половины группы должны составлять ученики, способные успешно–заниматься–самостоятельной–работой.
«Руководители групп» из числа учащихся и состав самих групп могут варьироваться на разных учебных дисциплинах. Учащиеся подбираются по принципу объединения школьников разного уровня обученности, внеурочной информированности по данному предмету, совместимости учащихся, что позволяет им взаимно дополнять и компенсировать достоинства и недостатки друг друга. В группе не должно быть негативно настроенных друг к другу учащихся.
Групповая работа может быть однородной и неоднородной. Однородная групповая работа предполагает выполнение небольшими группами учащихся одинакового для всех задания, а дифференцированная – выполнение различных заданий разными группами. В ходе работы членам одной группы разрешается совместное обсуждение хода и результатов работы, обращение–за–советом–друг–к–другу.
При групповой форме работы учащихся на уроке в значительной степени возрастает и индивидуальная помощь каждому нуждающемуся в ней ученику, как со стороны учителя, так и со стороны учащихся-консультантов.
Групповая форма работы учащихся на уроке наиболее применима и целесообразна при проведении практических, лабораторных работ и работ-практикумов по естественнонаучным предметам, при отработке навыков разговорной речи на уроках иностранного языка (работа в парах), на уроках трудового обучения при решении конструктивно-технических задач, при изучении текстов, копий исторических документов и т.п.
На уроках математики в начальной школе групповая работа может быть применена на этапе отработки вычислительных навыков, при закреплении знаний некоторых теоретических фактов (связи между компонентами арифметических действий, решение уравнений, действия с величинами). В ходе такой работы максимально используются коллективные обсуждения результатов, взаимные консультации при выполнении сложных измерений или расчетов, при изучении правил, исторических документов и т.п. Вся групповая деятельность школьников при этом вполне успешно сочетается с интенсивной–самостоятельной–работой каждого учащегося.
Правильно организованная групповая работа представляет собой вид коллективной деятельности, она успешно может протекать при четком распределении работы между всеми членами группы, взаимной проверке результатов работы каждого, полной поддержке учителя, его оперативной помощи.
Групповая деятельность учащихся на уроке складывается из следующих элементов:
1. Предварительная подготовка учащихся к выполнению группового задания, постановка учебных задач, краткий инструктаж учителя.
2. Обсуждение и составление плана выполнения учебного задания в группе, определение способов его решения (ориентировочная деятельность), распределение–обязанностей.
3.–Работа–по–выполнению–учебного–задания.
4. Наблюдение учителя и корректировка работы группы и отдельных учащихся.
5. Взаимная проверка и контроль над выполнением задания в группе.
6. Сообщение учащихся по вызову учителя о полученных результатах, общая дискуссия в классе под руководством учителя, дополнение и исправление, дополнительная информация учителя и формулировка окончательных выводов.
7. Индивидуальная оценка работы групп и класса в целом [34].
Схематически взаимодействие учителя и групп школьников представлено на рисунке №4.
 
Рис.4 Взаимодействие учителя и учащихся при групповой форме организации учебной деятельности класса
Успех групповой работы учащихся зависит, прежде всего, от мастерства учителя, от его умения распределять свое внимание таким образом, чтобы каждая группа, и каждый ее участник в отдельности, ощущали заботу учителя, его заинтересованность в их успехе, в нормальных плодотворных межличностных отношениях. Всем своим поведением учитель обязан выражать заинтересованность в успехе как сильных, так и слабых учащихся, вселять им уверенность в успехах, проявлять уважительное отношение к–слабым–ученикам.
Достоинства групповой организации учебной работы учащихся на уроке очевидны. Результаты совместной работы учащихся весьма ощутимы как в приучении их к коллективным методам работы, так и в формировании положительных нравственных качеств личности. Но это не говорит о том, что групповая форма организации учебной работы может быть признана идеальной, универсальной. Ею нельзя ограничивать разнообразие форм работы учащихся в классе, ее нельзя противопоставлять другим формам.
Групповая форма несет в себе и ряд недостатков. Среди них наиболее существенными являются: трудности комплектования групп и организации работы в них; учащиеся в группах не всегда в состоянии самостоятельно разобраться в сложном учебном материале и избрать самый экономный путь его изучения. В результате, слабые ученики с трудом усваивают материал, а сильные нуждаются в более трудных, оригинальных заданиях, задачах.
Только в сочетании с другими формами обучения школьников на уроке — фронтальной и индивидуальной — групповая форма организации работы учащихся приносит ожидаемые положительные результаты.
Сочетание этих форм, выбор наиболее оптимальных вариантов этого сочетания определяется учителем в зависимости от решаемых учебно-воспитательных задач на уроке, от учебного предмета, специфики содержания, его объема и сложности, от специфики класса и отдельных учеников, уровня их учебных возможностей и, конечно, от стиля отношений учителя и учащихся, отношений учащихся между собой, от той доверительной атмосферы, которая установилась в классе, от постоянной готовности оказывать друг другу помощь.
Необходимо подчеркнуть, что характеристика известных форм организации деятельности учащихся вполне применима к урокам математики в начальной школе. На основе изучения методической литературы нами установлено, что передовой педагогический опыт современных учителей основан на поиске оптимального сочетания форм организации деятельности школьников на уроках.
Фронтальная, групповая и индивидуальная формы работы учащихся по-разному способствуют реализации образовательных, воспитательных и развивающих задач. Поэтому необходимо рациональное их сочетание, продуманный выбор той или иной формы с учетом особенностей учебного предмета, содержания изучаемого материала, методов обучения, возрастных особенностей учащихся.
Глава 2. Текстовые задачи в начальном курсе математики
В настоящей главе раскрывается сущность понятия «текстовая задача», описывается ее структура, приводится классификация задач по разным основаниям, дается характеристика этапам обучения решать текстовые задачи. Также рассмотрены примеры дифференцирования задач по уровню их сложности.
2.1 Понятие «текстовая задача» и ее структура
С термином «задача» люди постоянно сталкиваются в повседневной жизни, как на бытовом, так и на профессиональном уровне. Каждому из нас приходится решать те или иные проблемы, которые зачастую мы называем задачами. Это могут быть общегосударственные задачи (освоение космоса, воспитание подрастающего поколения, оборона страны и т.п.), задачи определенных коллективов и групп (сооружение объектов, выпуск литературы, установление связей и зависимостей и др.), а также задачи, которые стоят перед отдельными личностями.
К решению разноплановых жизненных задач школьников начинают готовить уже в младшем школьном возрасте в процессе обучения математике.
Решая задачи, учащиеся приобретают новые или закрепляют, углубляют и систематизируют уже имеющиеся математические знания. Обучающая функция текстовых задач может быть продемонстрирована задачами, в которых
· раскрывается конкретный смысл арифметических действий,
· вводятся рациональные приемы вычислений и соответствующие им правила,
· выполняются табличные или внетабличные вычисления,
· используются соотношения между различными единицами измерения величин и т.д.
Более того, существующие межпредметные связи начального курса математики с другими учебными дисциплинами позволяют отработать умение читать, повторить грамматические нормы (правописание словарных слов, применение изучаемых правил орфографии, правил сокращения слов и т.д.).
Задачи выполняют развивающую функцию по отношению к учащимся младших классов. В процессе решения текстовых задач отрабатываются умения
· выполнять операции анализа и синтеза, абстрагирования и конкретизации,
· проводить рассуждения по аналогии,
· обобщать способы решения типовых задач
· находить признаки абстрактных математических понятий в реальных объектах и, следовательно, устанавливать связь теоретических знаний в области математики с жизнью.
Большое значение имеет решение задач и в воспитании личности учащихся:
· прививается культура мышления, общения и выражения собственных мыслей,
· вырабатывается умение слушать мнение учителя и одноклассников, анализировать и оценивать услышанное,
· вырабатывается аккуратность в ведении записей,
· расширяется кругозор,
· воспитывается чувство коллективизма среди школьников и т.д.
Поэтому важно, чтобы учитель имел глубокие представления о текстовой задаче, о её структуре, умел решать такие задачи различными способами и передавал эти знания своим ученикам.
Проблема решения и чисто математических задач, и задач, возникающих перед человеком в процессе его производственной или бытовой деятельности, изучается издавна. Однако до настоящего времени нет общепринятой трактовки самого понятия «задача». В широком смысле слова под задачей понимается некоторая ситуация, требующая исследования и разрешения человеком (или решающей системой).
Отдельно стоят математические задачи, решение которых достигается специальными математическими средствами и методами. Среди них выделяют задачи научные (например, теорема Ферма, проблема Гольбаха и др.), решение которых способствует развитию математики и ее приложений, и задачи учебные, которые служат для формирования необходимых математических знаний, умений и навыков у разных групп обучаемых (школьников, слушателей курсов, студентов и др.) и направлены на изменение качеств личности обучаемого (не знал — знаю, не умел — умею и т.п.).
Положив в основание классификации число действий, которые необходимо выполнить для решения задачи, выделяют простые и составные задачи. Задачу, для решения которой нужно выполнить одно арифметическое действие, называют простой. Задачу, для решения которой нужно выполнить два или большее число действий, называют составной.
Учебные математические задачи различаются по характеру их объектов. В одних задачах все объекты математические (числа, геометрические фигуры, функции и т.п..), в других объектами являются реальные объекты (люди, животные, автотранспортные и механические средства, сплавы, жидкости и т.д.) или их свойства и характеристики (количество, возраст, скорость, производительность, длина, масса и т.п.). Задачи, все объекты которых математические (доказательства теорем, вычислительные упражнения, установление признаков изучаемого математического понятия и т.д.), часто называют математическими заданиями.
Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими и т.д.). Перечисленные названия берут начало от способа записи (задача представлена в виде текста), сюжета (описываются реальные объекты, явления, события), характера математических выкладок (устанавливаются количественные отношения между значениями некоторых величин, связанные чаще всего с вычислениями). В последнее время наиболее распространенным является термин «текстовая задача».
Классификация задач по различным основаниям приведена в таблице №1.
Таблица №1. Классификации задач по различным основаниям
| № |
Основание
классификации
|
Виды задач |
Видовая характеристика |
| 1. |
Цели
решения задач
|
научные |
способствовать развитию математики и ее приложений, науки в целом |
| учебные |
формирование математических знаний, умений и навыков у обучаемых |
| 2. |
Характер
объектов
|
математические задания |
все объекты математические |
| текстовые |
хотя бы один объект является реальным предметом или явлением |
| 3. |
Количество
данных
|
с избыточными данными |
содержат информацию, которая не нужна для выполнения требования задачи |
| с недостающими данными |
содержат недостаточно информации для выполнения требования задачи |
| 4. |
Уровень
сложности
|
типовые |
решение задачи состоит в стереотипном воспроизведении заученных действий |
| творческо-воспроизводящие |
решение задачи требует некоторой модификации заученных действий в изменившихся условиях |
творческие,
эвристические
|
решение задачи требует поиска
новых, еще неизвестных способов действий
|
| 5. |
Количество
выполняемых при решении действий
|
простые |
для решения задачи требуется
выполнить одно действие
|
| составные |
для решения задачи требуется выполнить более одного действия |
Текстовая задача
– описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения [29].
Придерживаясь современной терминологии, можно сказать, что текстовая задача представляет собой словесную модель ситуации, явления, события, процесса и т.п. Как в любой модели, в текстовой задаче описывается не все событие или явление, а лишь его количественные и функциональные характеристики [8].
Математическая задача – это связанный лаконический рассказ, в котором введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в условии [8].
Любая текстовая задача состоит из двух частей: условия и требования (вопроса). Числовые значения величин и существующие между ними зависимости, т.е. количественные и качественные характеристики объектов задачи и отношений между ними, называют условием
(или условиями
) задачи.
В условии сообщаются сведения об объектах и некоторых величинах, характеризующих данные объекты, об известных и неизвестных значениях этих величин, об отношениях между ними. В задаче обычно не одно, а несколько условий, которые называют элементарными.
Требования задачи – это указание того, что нужно найти. Они могут быть сформулированы как в вопросительной, так и в повествовательной форме, их также может быть несколько. Величину, значение которой требуется найти, называют искомой величиной, а числовые значения искомых величин – искомыми, или неизвестными.
Систему взаимосвязанных условий и требований называют высказывательной моделью задачи. Для того чтобы уяснить структуру задачи, надо выявить ее условия и требования, т.е. построить высказывательную модель задачи.
Рассматривая задачу в узком смысле этого понятия, в ней можно выделить следующие составные элементы:
1. Словесное изложение сюжета, в котором явно или в завуалированной форме указана функциональная зависимость между величинами, числовые значения которых входят в задачу;
2. Числовые значения величин или числовые данные, о которых говорится в тексте задачи;
3. Задание, обычно сформулированное в виде вопроса, в котором предлагается узнать неизвестные значения одной или нескольких величин.
Каждая задача – это единство условия и цели. Если нет одного из этих компонентов, то нет и задачи. Это очень важно иметь в виду, чтобы проводить анализ текста задачи с соблюдением такого единства. Это означает, что анализ условия задачи необходимо соотносить с вопросом задачи и, наоборот, вопрос задачи анализировать направленно с условием. Их нельзя разрывать, так как они составляют одно целое. Иногда задачи формулируются таким образом, что часть условия или всё условие включено в одно предложение с требованием задачи.
Рассмотрим задачу: «На тракторе «Кировец» колхозное поле площадью 600 га можно вспахать за 10 дней, а на тракторе «Казахстан» – за 15 дней. На вспашку поставлены оба трактора. За сколько дней будет вспахано это поле?»
В приведенной задаче имеется несколько величин, часть из которых известна (площадь поля, время работы каждого трактора в отдельности), часть неизвестна (производительности тракторов в отдельности и совместно, время совместной работы тракторов). Все неизвестные величины будут определены в процессе решения задачи, хотя соответствующие требования не сформулированы. Искомым является единственное требование о вычислении времени совместной работы тракторов, поскольку именно оно заключено в требовании задачи.
В реальной жизни довольно часто возникают самые разнообразные задачные ситуации. Сформулированные на их основе задачи могут содержать избыточную информацию, то есть такую, которая не нужна для выполнения требования задачи. Например: «Маша купила 6кг яблок, а ее подруга Света на 3кг больше. Сколько заплатила Маша за свою покупку, если 1кг яблок стоит 35 рублей?»
На основе возникающих в жизни задачных ситуаций могут быть сформулированы и задачи, в которых недостаточно информации для выполнения требований. Так в задаче: «Найти длину и ширину участка прямоугольной формы, если известно, что длина больше ширины на 3 метра» – недостаточно данных для ответа на её вопрос. Чтобы выполнить эту задачу, необходимо её дополнить недостающими данными.
Трудность задачи является психолого-дидактической категорией и представляет собой совокупность многих субъективных факторов, зависящих от особенностей личности школьников, например, таких как интеллектуальные возможности и интересы учащегося, степень новизны и т.д. По трудности можно выделить три типа задач:
1. Задачи, решение которых состоит в стереотипном воспроизведении заученных действий. Степень трудности данных задач связана с тем, насколько сложным является навык воспроизведения действий и насколько он прочно освоен. Последний фактор становится основным. Чем более прочны навыки у человека, тем легче они воспроизводятся и тем менее подвергаются дезорганизующему влиянию различных условий и, прежде всего, эмоций.
Турист проехал на автомашине 146 км, а на пароходе на 50 км меньше, чем на автомобиле. Оставшийся путь турист прошел пешком. Сколько километров турист прошел пешком, если весь путь составил 254 км?
2. Задачи, решение которых требует некоторой модификации заученных действий в изменившихся условиях. Степень трудности в данном случае связана с количеством и разнородностью элементов, которое необходимо координировать наряду с описанными выше особенностями.
Турист проехал на автомашине 146 км, на пароходе на 50 км меньше, чем на автомобиле. Пешком турист прошел 12 км. Сколько километров проплыл турист на пароходе, если весь его путь составил 254км?
a) Измените условия, чтобы остались только те данные, которые нужны для решения задачи;
b) Измените вопрос и условия, чтобы в задаче не было лишних данных.
3. Задачи, решение которых требует поиска новых, еще неизвестных способов действий. К данным задачам относятся такие, которые, требуют творческой активности, эвристического поиска новых, неизвестных схем действий или необычной комбинации известных. При этом сюжетная задача должна отвечать учебным целям, главным образом, через правильное соотношение в ней новизны, ранее усвоенного материала и приемов его применения.
Например: «Турист отправился в путешествие, во время которого он ехал на автомашинах, плыл на пароходе и, конечно, шел пешком. На протяжении всего путешествия он наблюдал за очарованием природы и восхищался старинной архитектурой.
На основе приведенного текста составьте задачу так, чтобы ее решением было числовое выражение
a) 264 – (146 + (146 – 50))
b) 146 + (146 – 40) + (146 – 40) : 2»
Учащимся предлагают задачи с возрастающей степенью трудности, которые решаются последовательно – от первого к последнему. По количеству и качеству решенных задач можно судить о навыке ребенка, связанного с той или иной темой. Если ребенок не смог справиться с каким-либо заданием, то он должен объяснить, что вызвало у него затруднение. Это позволит преподавателю скорректировать свою обучающую деятельность относительно каждого ребенка.
Задачи и их решение занимают в обучении школьников весьма существенное место и по времени, и по их влиянию на умственное развитие ребенка.
Важно, чтобы учитель имел глубокие представления о текстовой задаче, о её структуре, умел решать такие задачи различными способами и передавал эти знания своим ученикам.
2.2 Процесс решения текстовых задач
Одной из важнейших проблем обучения математике является формирование у учащихся умения решать текстовые задачи.
Ответ на требование задачи получается в результате ее решения. Решить задачу в широком смысле этого слова – это, значит, раскрыть связи между данными, указанными условием задачи, и искомыми величинами, определить последовательность применения общих положений математики (правил, законов, формул и т.п.), выполнить действия над данными задачи, используя эти общие положения, и получить ответ на требование задачи или доказать невозможность его выполнения.
Термин «решение задачи» широко применяется в математике. Этим термином обозначают связанные между собой, но все же не одинаковые понятия:
1) решением задачи называют результат, то есть ответ на требование задачи;
2) решением задачи называют процесс нахождения этого результата, то есть всю деятельность человека, решающего задачу, с момента начала чтения задачи до окончания решения;
3) решением задачи называют лишь те действия, которые производят над условиями и их следствиями на основе общих положений математики для получения ответа задачи [21, 62].
Решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придётся работать, те инструменты, с помощью которых выполняется эта работа.
Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Основная особенность текстовых задач состоит в том, что в них не указывается прямо, какое именно действие (или действия) должно быть выполнено для получения ответа на требование задачи.
Итак, различают общий и частный подходы к решению задач. Названия не случайны. Частный подход связан с решением задач частных видов. Общий подход основан на том, что есть общее при решении любых задач – этапы решения, которые вычленил Д.Пойа. Количество этапов и их содержание примерно одинаково у разных авторов, что говорит об объективном характере существования соответствующих этапов в деятельности решающего. Базовым считаются четыре этапа решения задачи (см. рисунок №5).
 |
Общий
(4 этапа решения любой задачи)
|
|
Частный
(основан на видах, типах задач)
|
|
Рис.№5. Классификация подходов к решению текстовых задач
Важнейшим этапом решения задачи является первый этап – восприятие задачи (анализ текста). Цель этапа – понять задачу, т.е. выделить все множества и отношения, величины и зависимости между ними, числовые данные, лексическое значение слов.
Результатом выполнения этого этапа является понимание задачи, так как с точки зрения психологии восприятие текста – это его понимание. Не поймешь задачу – не решишь ее. Для того чтобы добиться понимания задачи, полезно воспользоваться разными приемами, которые накопились в современной методике.
Приемы выполнения анализа задачи:
- драматизация, обыгрывание задачи;
- разбиение текста задачи на смысловые части;
- постановка специальных вопросов;
- переформулировка текста;
- перефразирование задачи (заменить термин содержанием; заменить описание термином, словом; заменить слово синонимом; убрать несущественные слова; конкретизировать, добавив не меняющие смысл подробности);
- построение модели (схема, рисунок, таблица, чертеж, предметная модель, выражение);
- определение вида задачи и выполнение соответствующей схемы – краткой записи.
Второй этап – поиск плана решения. Долгие годы методисты именно этот этап называли основным, но до него надо еще дойти, добраться. Цель этапа – соотнести вопрос с условием.
Данный этап требует рассуждений, но если их осуществлять устно, как часто бывает, то многие дети, особенно «визуалы», не освоят умения искать план решения задачи. Нужны приемы графической фиксации подобных рассуждений. Такие приемы, как граф-схема и таблица рассуждений, существуют в российской методике более 100 лет.
Приемы выполнения этапа:
- рассуждения (от условия к вопросу; от вопроса к условию; по модели; по словесному заданию отношений);
- составление уравнения;
- частный подход решения задач, название вида, типа задачи [21, 63].
Третий этап решения задачи – выполнение плана – наиболее существенный этап, особенно при арифметическом решении задачи. Цель этапа – выполнить операции в соответствующей математической области (арифметика, алгебра, геометрия, логика и др.) устно или письменно.
Приемы выполнения этапа:
- арифметические действия, оформленные выражением, по действиям (без пояснения, с пояснением, с вопросами);
- измерение, счет на модели;
- решение уравнений;
- логические операции;
Анализ школьной практики свидетельствует, что на уроках математики при решении текстовых задач преимущественное внимание уделяется второму и особенно третьему этапам. Первый этап считается пройденным, если ученики смогли сказать, что в задаче дано, и что нужно найти.
Четвертый этап – проверка выполненного решения. Цель этапа – убедиться в истинности выбранного плана и выполненных действий, после чего сформулировать ответ задачи.
Это самый нелегальный этап. Большинство учителей убеждено в том, что если дети во время решения задачи проверяли себя (по действиям с пояснением или с вопросами), то в другой проверке они не нуждаются.
Приемы выполнения этапа:
До решения:
- прикидка ответа или установление границ с точки зрения здравого смысла, без математики.
Во время решения:
- по смыслу полученных выражений;
- осмысление хода решения по вопросам
После решения задачи:
- решение другим способом;
- решение другим методом;
- подстановка результата в условие;
- сравнение с образцом;
- составление и решение обратной задачи.
Все четыре этапа решения задачи одинаково важны. Только выполнение всех этапов позволяет считать решение завершенным полностью.
Становится совершенно ясно, что овладение умениями выполнять перечисленные этапы решения задач протекает не только в начальной школе, но и на дальнейших ступенях–обучения.
2.3 Обучение решению задач. Уровни сформированности умений младших школьников решать задачи. Критерии уровней
Обучение решению задач – это специально организованное взаимодействие учителя и учащихся, цель которого – формирование у учащихся умения решать задачи.
Чтобы выявить характер и условия такого взаимодействия, нужно разобраться в том, что значит умение решать задачи.
Любое умение – это качество человека, а именно: его готовность и возможность успешно осуществлять определенные действия. В методической литературе принято выделять два основных типа умения решать задачи:
– общее умение решать задачи;
– умение решать задачи определенного вида (частное умение решать задачи).
Чтобы успешно формировать эти умения, нужно знать, в чем и как они проявляются, каковы их структура и операциональный состав, какие компоненты являются вариативными, изменяемыми, а какие – инвариатными, неизменяемыми.
Общее умение решать задачи проявляется при решении человеком (испытуемым) незнакомой задачи, т.е. задачи такого вида, способ решения которой неизвестен решающему.
При формировании общего умения решать задачи предметом изучения и основным содержанием обучения процессу решения задач являются методы и способы решения задач, приемы, помогающие осуществлению каждого этапа и всего процесса решения в целом.
Условно общее умение решать текстовые задачи представлено на рисунке №6.
Умение решать задачи определенных видов состоит из:
– знаний о видах задач, способов решения задач каждого вида;
– умения «узнать» задачу данного вида, выбрать соответствующий ей способ решения и реализовать его на «узнанной» задаче. Обучение умению решать задачи определенного вида включает в себя усвоение детьми сведений о видах задач, способов решения задач каждого вида (данного вида) и выработку умения выделять задачи соответствующих видов, выбирать способы решения, адекватные виду задачи, применять эти способы к решению конкретных задач.

Рис. №6 Структура общего умения решать текстовые задачи
При формировании у школьников умения решать задачи определенных видов предметом изучения и основным содержанием обучения являются виды задач, способы и образцы решения задач конкретных видов. Это является одной из наиболее сложных методических проблем, с которыми сталкивается учитель при обучении детей. И это естественно, так как решение задач вообще и математических в частности, по своей сути – процесс творческий, требующий продуктивной деятельности.
Условно структура умения решать задачи определенных видов изображено на рисунке №7.
Если рассматривать формирование умения решать задачи с точки зрения требований, предъявляемых школой, то достаточно научиться решать набор так называемых стандартных задач, используя многократное повторение задач каждого типа вплоть до выработки и запоминания образца решения.
В этом случае действительно можно говорить даже не о формировании умения, а об автоматизированном навыке решения задач, как это делает Л.Г. Петерсон в своем пособии для учителей первых классов.

Рисунок №7. Структура умения решать задачи определенных видов
Методы обучения решению задач «вырастают» из знаний о задаче и процессе их решения. Нельзя подменять эти понятия, но и нельзя осмысленно обучать решению задач, не упорядочив знания о решении задач.
Термин «умение» имеет два значения:
1) Как первоначальный уровень овладения каким-либо простым действием. В этом случае навык рассматривается как высший уровень овладения этим действием, автоматизированное его выполнение: умение переходит в навык.
2) Как способность осознанно выполнять сложное действие с помощью ряда навыков. В этом случае навык – это автоматизированное выполнение элементарных действий, из которых состоит сложное действие, выполняемое с помощью умения.
Диагностичными показателями владения умениями обычно являются конкретные действия и их комплексы, выполняемые относительно конкретно поставленных задач в контексте обучения. Вместе с тем, в структуре любого действия можно выделить общие элементы, реализация которых необходима при воспроизведении каждого конкретного умения. Владение этими элементами может служить объективными показателями сформированности умения:
· построение алгоритма (последовательности) операций выполнения конкретных действий в структуре умения;
· моделирование (планирование) практического выполнения действий, составляющих данное умение;
· выполнение комплекса действий, составляющих данное умение;
· самоанализ результатов выполнения действий, составляющих умение в сопоставлении с целью деятельности.
При определении уровня сформированности умений и навыков младших школьников по математике обычно учитывают сформированность их устных и письменных вычислительных навыков, сформированность умения решать задачи, ориентироваться в геометрических понятиях.
Применительно к решению текстовых задач в отечественной начальной школе используется следующая шкала уровней.
- Высокому уровню сформированности умения решать задачи соответствуют работы и ответы, в которых ученик может самостоятельно и безошибочно решить задачу (составить план, решить, объяснить ход решения и точно сформулировать ответ на вопрос задачи).
- Среднему уровню сформированности умения решать задачи соответствуют работы и ответы, в которых ученик допускает отдельные неточности в формулировках, допускает ошибки в вычислениях и решениях задач, но исправляет их сам или с помощью учителя. При этом в работах не должно быть более одной грубой и трех-четырех негрубых ошибок.
- Низкому уровню сформированности умения решать задачи соответствуют работы и ответы, в которых ученик не справляется с решением задач и вычислениями в них даже с помощью учителя. Допускает 2 и более грубых ошибки.
2.4 Методические приемы, используемые в обучении решению текстовых задач в начальной школе
Чтобы научить ребенка работе над текстовой задачей, учитель может использовать различные приемы обучения, соответствующие совершенствованию логического мышления и творческих способностей детей.
Выше (см. пункты 2.2, 2.3) были описаны традиционно используемые приемы работы над текстовой задачей. Рассмотрим еще несколько конкретных примеров работы над задачей [12, 41].
Прием, основанный на предложенных объектах, сюжете, вспомогательной модели (приложение №1). Данный прием рассчитан на учащихся второго-третьего классов.
На доске заранее вывешиваются карточки с объектами «овощи», «свекла», «морковь», «картофель», а также вспомогательная модель задачи.
Учитель дает учащимся следующие команды:
– Выберите слова, характеризующие сюжет задачи. (Школьники вырастили овощи.)
– Где выращивают школьники овощи? (На пришкольном участке).
– Какое слово из предложенных объектов, записанных в столбце, общее? (Овощи.)
– Соотнесите предложенные объекты со схемой, указав количественные характеристики. (Целое – овощи. Количество овощей неизвестно. Части: свекла – 20 кг, морковь – 12 кг, картофель – 8 кг).
– Сформулируйте текст задачи. (Школьники вырастили на пришкольном участке 20 кг свеклы, 12 кг моркови и 8 кг картофеля. Сколько килограммов овощей вырастили школьники?)
– О какой величине говорится в задаче? (О массе.)
– Как иначе можно сформулировать требование? (Какова масса собранного урожая?)
Далее учитель предлагает ученикам самостоятельно решить эту задачу в рабочих тетрадях.
20 + 12 + 8 = 40 (кг)
Ответ: 40 кг урожая собрали школьники.
Затем совместно с учителем дети проверяют правильность решения предложенной задачи. В качестве способа проверки могут выступать сравнение своего решения с выполненным на закрытой части доски, чтение решения вслух Прием составления задачи по предложенной программе действий. Данный прием развивает коммуникативные способности ребенка, способность неординарно мыслить, и рассчитан на учащихся не младше второго класса. На доске вывешиваются схемы (см. рисунок №8). Учитель предлагает учащимся составить по данной схеме задачу, а затем решить ее.
Дети составляют задачу: «Миша решил 3 уравнения и 7 примеров. На сколько больше примеров, чем уравнений, решил Миша? На сколько меньше уравнений, чем примеров, решил Миша?»
Решение:
7 – 3 = 4 (шт.)
Ответ: на 4 примера больше, чем уравнений, решил Миша.
Учитель спрашивает одного из учеников, как решить эту задачу и что в итоге получится. Остальные дети делают проверку.

Рис. №8 Схема для составления текстовой задачи
Алогичная работа проводится со следующей схемой (см. рисунок №9).

Рис. №9 Схема для составления текстовой задачи
«Миша нарисовал 2 рисунка, а Маша 4. Сколько всего рисунков нарисовали дети? На сколько рисунков больше нарисовала Маша, чем Миша?»
Решение:
1) 2 + 4 = 6 (шт.) – нарисовали вместе.
2) 4 – 2 = 2 (шт.) – Маша нарисовала больше Миши.
Ответ: 6 рисунков, на 2 рисунка.
Прием составления задачи на основе нескольких задач, содержащих один сюжет и часть общих объектов с их количественными характеристиками.
Цель данного приема состоит в том, чтобы учить школьников выделять основные структурные компоненты задачи (условие и требование). Подобрав специальным образом численные данные, учитель может использовать этот прием в любом классе начальной школы.
Задача 1. В школьную библиотеку привезли новые учебники. В первый день библиотекари расставили 210 учебников по русскому языку, во второй – 135 учебников по математике. Сколько учебников расставили библиотекари по полкам за два дня?
Задача 2. В школьную библиотеку привезли учебники. В первый день библиотекари расставили по полкам 210 учебников по русскому языку, во второй – 63 учебника по чтению. Сколько учебников расставили библиотекари по полкам за два дня?
Задача 3. В школьную библиотеку привезли учебники. В первый день библиотекари расставили по полкам 97 учебников по английскому языку, во второй – 63 учебника по чтению. Сколько расставили библиотекари по полкам за два дня?
Учитель дает следующие команды детям:
– Прочитайте задачи.
– Что общего в данных задачах? (Сюжет, требование).
– Что можно сказать об объектах и количественных характеристиках задач? (Часть объектов и их количественные характеристики в первой и второй задачах, а также во второй и третьей задачах одинаковые).
– Сформулируйте текст одной задачи, используя все объекты и их количественные характеристики. (В школьную библиотеку привезли новые учебники. Из них в первый день расставили по полкам 210 учебников по русскому языку и 97 по английскому языку, во второй – 135 учебников по математике и 63 учебника по чтению. Сколько учебников расставили библиотекари по полкам за два дня?)
Прием обучения составлению задач по предложенному решению с подробным пояснением.
Цель данного приема состоит в том, чтобы учить детей соотносить текстовую задачу с предложенным решением.
На доске дано решение этой задачи.
1) 3 + 15 = 18 – концертов дал детский хор в городе и в санатории.
2) 30 – 18 = 12 – концертов дал детский хор в сельских клубах
Учитель задает детям вопросы:
– Известно ли нам, где давал концерты детский хор? (В городе, санатории, сельских клубах.)
– Известно ли нам, сколько концертов дал хор в городе? (3 или 15)
– Известно ли нам, сколько концертов дал хор в санатории? (15 или 3)
– Сколько всего концертов дал хор? (30)
– Составьте задачу по первому равенству. (Детский хор дал 3 концерта в городе и 15 концертов в санатории. Сколько всего концертов дал детский хор в городе и в санатории?)
– Составьте задачу по второму равенству. (За лето детский хор дал 30 концертов. Из них 18 – в городе и санатории, а остальные в сельских клубах. Сколько концертов дал детский хор в сельских клубах?)
– Опираясь на решение задачи, сформулируйте требование задачи. (Узнать, сколько концертов дал детский хор в сельских клубах).
– Сформулируйте текст задачи, опираясь на два действия. (Детский хор дал 30 концертов. Из них 3 в городе, 15 – в санатории, а остальные – в сельских клубах. Сколько концертов дал детский хор в сельских клубах?)
Прием составления текста задачи по сюжетным рисункам с изменением действия (приложение №2).
Цель данного приема состоит в том, чтобы учить детей находить математические модели в реальной ситуации, учить переводить сюжетную ситуацию на математический язык. Подбирая соответствующие сюжеты, учитель может применить прием в любом классе начальной школы.
– По рисункам определите сюжет задачи. Как он меняется от первого рисунка ко второму? (Курица снесла яйца, из них вылупились цыплята).
– Назовите объекты задачи. (Курица, яйца, цыплята).
– С какими из них мы будем проводить вычислительные операции? (С яйцами.)
– Что вы можете сказать о количественной характеристике объектов на первом рисунке? (На первом рисунке изображены 4 яйца).
– На втором рисунке из яиц вылупились цыплята. Сколько их? (3)
– Сформулируйте требование задачи. (Сколько яиц осталось целыми?)
– Сформулируйте текст задачи. (Курица высидела 4 яйца. Через некоторое время из 3 яиц вылупились цыплята. Сколько яиц осталось целыми?)
Рассмотренные приемы работы над текстовой задачей достаточно разнообразны, однако, они рассчитаны в основном на учащихся с уровнем знаний выше среднего. У учеников, которые обладают низким или средним уровнем, эти приемы работы над текстовой задачей позволяют, с помощью учителя или других учащихся, повысить уровень их обученности.
2.5 Примеры использования различных форм работы младших школьников в процессе решения текстовых задач
В поисках путей более эффективного использования структуры уроков разных типов особую значимость приобретает форма организации учебной деятельности учащихся на уроке.
Ранее (см. пункт 1.2) были описаны признаки различных форм организации деятельности школьников на уроках математики. В пункте 2.2 была дана характеристика этапам решения задачи и приемам их выполнения. Эти приемы стандартно применяются учителями начальной школы при фронтальной форме работы над задачей. Ниже мы рассмотрим примеры реализации групповой и индивидуальной форм работы учащихся при решении текстовых задач.
Как известно, признаками групповой работы учащихся на уроке являются следующие:
— класс на данном уроке делится на группы для решения конкретных учебных задач;
— каждая группа получает определенное задание (либо одинаковое, либо дифференцированное) и выполняет его сообща под непосредственным руководством лидера группы или учителя;
— задания в группе выполняются таким способом, который позволяет учитывать и оценивать индивидуальный вклад каждого члена группы;
— состав группы непостоянный, он подбирается с учетом того, чтобы с максимальной эффективностью для коллектива могли реализоваться учебные возможности каждого члена группы.
Задания, решаемые некоторым количеством учащихся, можно разделить на две группы: репродуктивные и продуктивные.
К репродуктивным заданиям относится, например, решение арифметических сюжетных задач знакомых видов. От учащихся требуется при этом воспроизведение знаний и их применение в привычной ситуации – работа по образцу, выполнение тренировочных упражнений.
К продуктивным заданиям относятся упражнения, отличающиеся от стандартных. Ученикам приходится применять знания в измененной или в новой незнакомой ситуации, осуществлять более сложные мыслительные действия (например, поисковые, преобразующие), создавать новый продукт (составлять задачи, сочинять сказки на основе сюжетных задач). В процессе работы над продуктивными заданиями школьники приобретают опыт творческой деятельности.
Дифференцированная работа чаще всего организуется следующим образом: учащимся с низким и ниже среднего уровнем обученности предлагаются репродуктивные задания, а ученикам со средним, выше среднего и высоким уровнем обученности – творческие задания.
Рассмотрим групповую работу па примере конкретной задачи (1 класс).
«В вазе лежало 5 желтых и 2 зеленых яблока. 3 яблока съели. Сколько яблок осталось?»
Задание для 1-й группы учащихся с низким уровнем обученности. Решите задачу. Подумайте, можно ли ее решить другим способом.
Задание для 2-й группы учащихся со средним уровнем обученности. Решите задачу двумя способами. Придумайте задачу с другим сюжетом так, чтобы решение при этом не изменилось.
Задание для 3-й группы учащихся с уровнем обученности выше среднего. Решите задачу двумя способами. Составьте задачу, обратную данной, и решите ее.
Задание для 4-й группы учащихся с высоким уровнем обученности. Решите задачу двумя способами. Измените задачу так, чтобы ее можно было решить тремя способами. Решите полученную задачу тремя способами.
Следует отметить, что организация такой формы работы требует от учителя высокого уровня профессионального мастерства. Адекватное образование групп, распределение обязанностей внутри них, распределение учебного времени, разъяснение требований к оформлению записей, своевременная проверка качества выполнения задания должны быть продуманы с особой тщательностью, поскольку некоторые команды («Подумайте …», «Придумайте …», «Составьте …» и т.п.) чаще всего на уроках математики в младших классах выполняются фронтально, не сопровождаясь записями.
Можно предложить продуктивные задания всем ученикам. Но при этом детям с низким уровнем обученности даются задания с элементами творчества, в которых нужно применить знания в измененной ситуации, а остальным – творческие задания на применение знаний в новой ситуации.
Приведем пример дифференциации заданий для учащихся второго-третьего классов.
«Для новогодних подарков привезли 48 кг конфет. В пакетах было 12 кг конфет, в коробках – в три раза меньше, чем в пакетах, а остальные конфеты были в ящиках. Сколько килограммов конфет было в ящиках?»
Задание для 1-й группы учащихся с низким уровнем обученности. Решите задачу. Составьте задачу, обратную данной, и решите ее.
Задание для 2-й группы учащихся с ниже среднего уровнем обученности. Решите задачу. Придумайте задачу с другим сюжетом, но чтобы решение при этом не изменилось.
Задание для 3-й группы учащихся со средним уровнем обученности. Решите задачу. Измените вопрос к задаче так, чтобы она решалась в четыре действия.
Задание для 4-й группы учащихся с уровнем обученности выше среднего. Решите задачу. Составьте задачу, обратную данной, и решите ее. Измените вопрос и условия задачи так, чтобы данные об общем количестве конфет стали лишними. Запишите новую задачу и решите ее.
Задание для 5-й группы учащихся с высоким уровнем обученности. Решите задачу. Придумайте три различные задачи, с такими же данными, что и в приведенной задаче, используя жизненные ситуации.
При письменном решении задания, детям выдается образец выполнения работы
Кроме групповой, в обучении решению задач младших школьников может применяться и индивидуальная форма работы учащихся.
Под индивидуальной работой учащихся подразумевается работа, которая выполняется ими по заданию и под контролем учителя в специально запланированное для этого время на уроке. Назначение такой формы работы – развитие познавательных способностей школьников, их инициативы в принятии решения, творческого и логического мышления.
При организации индивидуальной работы необходимо учитывать ее строгую регламентацию в целостной системе учебных работ, степень ее трудности и сложности. Это обусловливает значимость научно обоснованной классификации самостоятельных работ. Все виды самостоятельной работы, применяемые в учебном процессе, можно классифицировать по следующим признакам: по дидактической цели, по характеру учебной деятельности учащихся, по содержанию, по степени самостоятельности и элементу творчества учащихся.
При организации учебного процесса самостоятельная работа подразумевает, с одной стороны, учебное задание, которое должен выполнить ученик, с другой – форму проявления соответствующей деятельности (мышления, запоминания, воображения) при выполнении учеником данного задания. При этом ребенок, в конечном счете, должен получить либо новые, ранее не известные ему знания, либо углубить и расширить сферы действия уже полученных знаний. Все это подразумевает индивидуальный подход к ребенку через внутриклассную дифференциацию.
Наиболее важное значение в этом направлении работы имеют принцип доступности и систематичности изучаемого материала, связь теории с практикой, принцип постепенности в нарастании трудности, принцип творческой активности, которые можно реализовать через различные виды помощи ученику.
Рассмотрим это на примере задачи (третий-четвертый класс).
«Мастер за 1 час работы делает 2 изделия. Сколько изделий он сделал за два дня, если в первый день он работал 3 часа, а во второй – 4?»
Наиболее распространенными видами помощи являются:
1. Образец выполнения задания: показ способа решения, образца рассуждения (например, в виде подробной записи решения задачи) и оформления.
Запись решения в виде числового выражения. Запись решения в данной форме осуществляется поэтапно:
1) 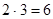 (шт.) – изготовлено в первый день; (шт.) – изготовлено в первый день;
2) 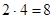 (шт.) – сделано во второй день; (шт.) – сделано во второй день;
3) 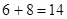 (шт.) – сделано всего. (шт.) – сделано всего.
Или:
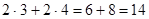 (шт.) – изготовлено мастером за два дня. (шт.) – изготовлено мастером за два дня.
2. Справочные материалы: памятки, инструкции, теоретическая справка в виде правила, формулы, таблицы единиц величин.
Для того, чтобы проверить правильность решения, составьте и решите обратную задачу к данной по следующим этапам:
1) Подставь в текст задачи найденное значение искомого, то есть вместо вопроса задачи поставьте в текст задачи ответ на него;
2) Выбери новое искомое;
3) Сформулируй новую задачу;
4) Реши составленную задачу;
5) Сравни полученное число с той данной величиной прямой задачи, которая была выбрана в качестве искомой величины;
6) На основе этого сравнения составь соответствующее умозаключение о правильности решения прямой задачи.
Роль индивидуальной работы школьников возрастает в связи с изменением целей обучения, его направленностью на формирование навыков творческой деятельности, а также в связи с компьютеризацией обучения.
Доля самостоятельных (индивидуальных) работ в учебном процессе увеличивается от класса к классу, В начальных классах на нее отводится не менее 20%.
Итак, изучив методическую литературу, мы пришли к следующим выводам:
− на современном этапе обучение младших школьников решению текстовых задач остается одним из важнейших направлений учебной деятельности, поскольку именно текстовые задачи являются связующим звеном между теоретическим обучением и применением знаний на практике;
− для всестороннего раскрытия понятия текстовой задачи и рассмотрения различных жизненных ситуаций в начальной школе предлагаются текстовые задачи, которые можно классифицировать по ряду оснований;
− решение любой текстовой задачи происходит по плану, включающему в себя ряд последовательных этапов;
− обучение решению задач проходит в двух направлениях: выработка общего умения решать текстовые задачи и выработка умений решать задачи определенного вида. Применительно к начальным классам чаще других реализуется первое из двух направлений. в соответствии с учебной программой, деятельность учителя и учащихся нацелена на выработку у младших школьников умений решать текстовые задачи;
− умение как психолого-педагогическая категория означает готовность и возможность человека (в данном контексте, младшего школьника) успешно выполнять какую-либо деятельность (в данном случае, решать текстовые задачи). В зависимости от уровня сформированности умения решать задачи учащихся можно разделить на три группы, соответственно с высоким, средним и низким уровнями. Критерии этих уровней описаны в методической литературе;
− для достижения поставленной дидактической цели в обучении младших школьников решению текстовых задач учителю необходимо варьировать и сочетать различные формы (индивидуальную, групповую, фронтальную) организации деятельности учащихся на уроках математики. Вспомогательные материалы, призванные оказать помощь учителю, содержатся в специально издаваемых методических пособиях, публикуются на страницах журналов и в сети Internet.
Глава 3.
Формирование умений младших школьников решать текстовые задачи
3.1 Диагностика уровня сформированности умений младших школьников решать задачи
Практическое исследование по теме работы было проведено в период преддипломной практики с 26 января по 5 марта 2010 года. Базой практики явилась МОУ СОШ №57 города Краснодара.
В качестве экспериментального был выбран 3 «А» класс. Учитель –Каргаполова Татьяна Ивановна (стаж работы 18 лет). Обучение математике ведется по программе «Школа – 2100», учебник Т.Е.Демидовой, С.А.Козловой, А.П.Тонких. В классе всего 24 учащихся, из них 12 мальчиков, 12 девочек.
Для обеспечения объективности эксперимента был выбран контрольный класс – 3 «Б». Учитель – Ильинская Елена Вячеславовна (стаж работы 14 лет). Обучение математике ведется по программе «Школа – 2100», учебник Т.Е.Демидовой, С.А. Козловой, А.П. Тонких. В классе всего 21 учащихся, из них 7 мальчиков, 14 девочек.
Педагогический эксперимент реализовывался в 3 этапа.
На первом этапе проведено определение уровня сформированности у учащихся экспериментального и контрольного классов умения решать текстовые задачи.
Цель: определить уровни сформированности умения младших школьников решать текстовые задачи.
Для достижения поставленной цели были выбраны различные методы исследования.
Одним из таких методов стала беседа с учителем с целью получения первичных представлений об уровне сформированности у учащихся класса умений решать текстовые задачи.
В ходе беседы учителю были заданы следующие вопросы:
1. Какое значение Вы придаете решению текстовых задач в начальной школе?
2. Какие виды типовых задач уже изучены в соответствии с программой?
3. Твердо ли знают учащиеся теоретические положения, на основе которых выбирают арифметические действия при решении задач?
4. Какие правила и законы вызывают наибольшее затруднение у учащихся?
5. С какими формами наглядного представления текстовых задач дети знакомы?
6. Какие формы наглядного представления задачи чаще всего Вы использовали на уроке?
7. Умеют ли школьники самостоятельно выбирать удобный способ наглядного представления задачи?
8. Умение решать какие типовые задачи наиболее твердо сформировано у школьников?
9. Успешно ли дети справляются с записью решения задачи в виде выражения?
10. Решение каких видов задач вызывают затруднения у школьников?
11. Какие виды типовых задач будут изучаться в ближайшее время?
12. Используете ли Вы какие-то инновационные методики для обучения школьников?
13. К помощи каких учащихся Вы рекомендуете прибегать при решении задачи на уроке?
14. Считаете ли Вы необходимым разбирать в классе задачу, которая задается для домашнего выполнения?
В ходе беседы выяснилось, что учитель считает решение задач важным связующим звеном между теоретическим и практическим обучением школьников. На момент начала преддипломной практики в программу включены практически все виды задач, предусмотренные начальным курсом математики. Теоретическими положениями, лежащими в основе выбора действий для решения задач, дети в основном владеют. В настоящий момент учащиеся чаще всего допускают ошибки при выборе формул для решения задач «на движение», поэтому учитель зачастую использует разнообразные приемы моделирования процессов (предметные картинки, составление схем, таблиц, диаграмм). Оформление решения задачи в виде выражения в некоторых частных случаях вызывает затруднения у учащихся, однако говорить о том, что это является закономерным, нельзя. Применительно к типовым задачам некоторых видов учащиеся обучены выбирать удобный способ решения, и они успешно справляются с этим видом деятельности. На уроках учитель часто применяет мультимедийные презентации. При разборе задачи в классе учитель рекомендует опираться на следующих учащихся: Багирову Эльвиру, Василенко Анастасию, Лысенко Кирилла, Гузова Антона и Трищук Анастасию. Если задача, предложенная в учебнике, не является стандартной, то учитель рекомендует работать над ней в классе, непосредственно на уроке. Для домашнего выполнения преимущественно предлагаются известные учащимся виды задач.
На данном этапе исследования было проведено анкетирование родителей с целью получения представлений об уровне сформированности умений решать текстовые задачи.
Вопросы анкеты приведены ниже.
1. Считаете ли Вы важным научить ребенка решать задачи? (Да, нет).
2. Осознает ли Ваш ребенок связь между реальной жизнью и решением задач на уроке? (Да; нет).
3. Успешно ли справляется Ваш ребенок с решением задач в домашнем задании? (Всегда – да; почти всегда – да; чаще справляется, чем нуждается в помощи; чаще нуждается в помощи, чем справляется самостоятельно; почти никогда не справляется самостоятельно; никогда не может решить задачу самостоятельно).
4. Уверенно ли Ваш ребенок выбирает арифметическое действие при решении задач? (Да; нет; однозначно ответить невозможно).
5. Оказываете ли Вы помощь ребенку при решении задач дома? (Да; нет; иногда).
6. Если на предыдущий вопрос Вы ответили «да», то опишите, в чем выражается эта помощь?
7. Как Вы считаете, чему необходимо уделить особое внимание при решении задач на уроке?
В результате проведения исследования нами определено, что практически все родители считают важным научить ребенка решать задачи. При решении задач дома дети практически всегда справляются с решением задачи самостоятельно, родители лишь иногда оказывают им помощь, задавая наводящие вопросы.
Кроме беседы и анкетирования был проведен тест для учащихся, цель которого состояла в определении частных умений младших школьников, связанных с решением текстовых задач.
Задания, включенные в тест, предполагают проверку следующих знаний, умений, навыков младших школьников (см. таблицу №2):
Таблица №2. Знания, умения и навыки младших школьников, связанные с решением текстовых задач
| № |
Характеристики ЗУН |
Номер задания |
| 1. |
Умение выделять структурные элементы в текстовой задаче |
1, 2 |
| 2. |
Умение выбирать арифметическое действие в процессе решения текстовой задачи |
2, 9 |
| 3. |
Умение соотносить реальную ситуацию с ее
математической моделью
|
4, 5, 6, 7, 8 |
| 4. |
Знания этапов решения текстовых задач и приемов их выполнения |
3, 9 |
| 5. |
Умения решать задачи разными способами |
10 |
Текст тестовых заданий приведен в приложении №3.
Качество выполненной учащимися работы оценивалось в условных баллах, что позволило разделить школьников на три группы в зависимости от уровня сформированности умений решать текстовые задачи (см. таблицу №3 и приложение).
К группе учащихся с высоким уровнем сформированности умений решать задачи отнесем учащихся с результатом 45 – 59 баллов (75 – 100% выполненных заданий); к среднему уровню отнесем учащихся с результатом 30 – 44 баллов (50 – 74% выполненных заданий), а к низкому уровню сформированности умений отнесем учащихся с результатом 0 – 43 баллов (0 – 49% выполненных заданий).
Таким образом, тест позволил сделать вывод о том, что в экспериментальном классе высоким уровнем сформированности умений решать задачи обладают 14 человек (58,3%), средним – 8 человек (33,3%), а низким – 2 человека (8,4 %).
Таблица №3. Оценочная таблица (в условных баллах)
| № |
Номер задания |
Максимальное количество баллов |
| 1. |
1 |
6 |
| 2. |
2 |
14 |
| 3. |
3 |
6 |
| 4. |
4 |
4 |
| 5. |
5 |
2 |
| 6. |
6 |
4 |
| 7. |
7 |
3 |
| 8. |
8 |
3 |
| 9. |
9 |
2 |
| 10. |
10 |
15 |
| ИТОГО: |
59 |
Аналогичные исследования были проведены в контрольном 3 «Б» классе.
Результаты исследований позволяют распределить учащихся этого класса по уровням сформированности умений решать задачи следующим образом:
- высокий уровень – 11 человек (52,4%)
- средний уровень – 8 человек (38%)
- низкий уровень – 2 человека (9,6%).
Соотношение между долями учащихся высокого, среднего и низкого уровней сформированности умений решать задачи отображено в ниже в таблице №4 и на диаграмме №1.
Таблица №4. Распределение учащихся экспериментального и контрольного классов в зависимости от уровня сформированности умений решать задачи
| Уровень сформированности умения решать задачи |
Экспериментальный класс |
Контрольный класс |
| Чел. |
% |
Чел. |
% |
| Высокий |
14 |
58,3 |
11 |
52,4 |
| Средний |
8 |
33,3 |
8 |
38,0 |
| Низкий |
2 |
8,4 |
2 |
9,6 |

Диаграмма №1. Соотношение уровней сформированности умений решать задачи на диагностическом этапе
По итогам исследования, проведенного на первом этапе педагогического эксперимента, можно заметить, что:
− как в экспериментальном, так и в контрольном классах, присутствуют три категории учащихся с соответственно высоким, средним и низким уровнями сформированности умений решать текстовые задачи;
− доля учащихся, обладающих высоким уровнем сформированности умений решать задачи, в обоих классах превосходит по численности остальные категории;
− группа учащихся с низким уровнем сформированности умений решать текстовые задачи в обоих классах самые малочисленные, однако такие учащиеся присутствуют.
Итак, на первом этапе эксперимента мы изучили уровни сформированности умений решать текстовые задачи у учащихся экспериментального и контрольного классов. На втором этапе мы будем вести целенаправленную работу по повышению уровней развития названных умений младших школьников. В качестве средства достижения поставленной цели мы выбрали сочетание различных форм организации учебной деятельности младших школьников на уроках при решении задач.
3.2
Повышение уровня сформированности умений младших школьников решать задачи
На формирующем этапе исследования дети работали с задачами, которые приведены в учебнике Т.Е.Демидовой, С.А.Козловой, А.П.Тонких «Математика» 3 класс, 2 часть, уроки №№ 60 – 72.
Рассмотрим, как реализовывался данный этап на примерах конкретных задач.
Урок 60, задача №8 в)
Цель: закреплять умение прямого и косвенного сравнения чисел.
Оборудование: учебник, мультимедийная аппаратура, слайды.
Тотошка и его друг Гектор решили сосчитать всех птиц в хозяйстве Джона и Анны. Оказалось, что на птичьем дворе живут 40 уток. Это на 70 птиц меньше, чем кур и на 12 больше, чем индеек. Сколько уток, кур и индеек живут на птичьем дворе Джона и Анны?
Учащиеся читают задачу про себя, затем вслух.
Учитель предлагает рассмотреть чертеж к задаче и дополнить его в соответствии с условием задачи (см. рисунок №10):
 Рис. №10. Предлагаемая модель к задаче
― Какие птицы изображены самым коротким отрезком? (мнения учащихся разделяются).
― Верно ли, что уток меньше, чем кур? На экране появляется вспомогательная запись 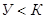 . (верно) . (верно)
― Верно ли, что уток меньше, чем кур и меньше, чем индеек? На экране появляется вспомогательная запись 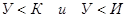 . (нет, уток больше, чем идеек) . (нет, уток больше, чем идеек)
― Значит, 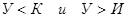 (слайд). Поэтому можно догадаться, что самым коротким должен быть отрезок, обозначающий количество индеек, а самым большим отрезком обозначаются куры. Дополним чертеж. Названия отрезков и численные данные учащиеся расставляют на отрезках (см. рисунок №10): (слайд). Поэтому можно догадаться, что самым коротким должен быть отрезок, обозначающий количество индеек, а самым большим отрезком обозначаются куры. Дополним чертеж. Названия отрезков и численные данные учащиеся расставляют на отрезках (см. рисунок №10):

Рис. №11 Схема к задаче
― Как обозначить вопрос задачи? (мнения учащихся разделяются: часть детей считает, что фигурная скобка нужна, другие дети считают, что фигурная скобка не нужна). Учитель обращает внимание, что вопрос можно понять по-разному. Однако поскольку узнавать количество каждого вида птиц не имеет смысла (количество уток известно по условию, то нечетко сформулированный вопрос следует понимать так: «Сколько ВСЕГО уток, кур и индеек живут на птичьем дворе Джона и Анны?» После этого учащиеся обозначают вопрос задачи фигурной скобкой (см. рисунок №12):
 
Рис. №12. Схема к задаче
― Каким действием узнать, сколько было кур? (сложением, потому что уток на 70 меньше, чем кур, а, значит, кур на 70 больше, чем уток).
― Каким действием узнать, сколько было индеек? (вычитанием, потому то их на 12 меньше, чем уток).
― Каким действием узнаем, сколько всего птиц было на ферме? (сложением).
Задача (урок 61, № 6, а)
Цель: учить устанавливать связи между данными и искомыми, отрабатывать умение решать задачи разными способами.
Оборудование: учебник, мультимедийная аппаратура, слайды.
Лика разложила 96 своих книг поровну на 8 полок книжного шкафа. Сколько книг было у Вити, если на каждую из восьми полок этого же шкафа он поставил на 2 книги меньше, чем Лика?
Дети читают приведенную задачу сначала про себя, затем один ученик зачитывает ее вслух.
Учитель задает детям вопросы:
¾ О чем говорится в задаче? (о книгах)
¾ Что делали с этими книгами? (раскладывали на полки)
¾ Что из задачи мы уже знаем? (Лика разложила 96 книг поровну на 8 полок, а Витя – на каждую полку поставил на 2 книги меньше)
¾ Что требуется узнать? (сколько книг было у Вити)
¾ Что мы можем узнать в первую очередь? (сколько книг на каждую полку поставила Лика).
¾ Для чего нам нужно это знать? (чтобы узнать, сколько книг положил Витя на каждую полку).
¾ Какое арифметическое действие надо выполнить, чтобы это узнать? (вычесть).
¾ Почему надо вычитать? (в задаче сказано «на 2 меньше»).
¾ Ответили ли мы вторым действием на вопрос задачи? (нет, так как требуется узнать, сколько всего у Вити книг).
¾ Каким действием мы будем узнавать, сколько всего книг у Вити? (умножением).
Далее учитель еще раз вместе с детьми проговаривает план решения и предлагает учащимся записать решение к себе в тетрадь. Самопроверка – сравнение с образцом решения (слайд).
После выполнения самопроверки по образцу учитель включает следующий слайд, на котором написаны выражения:
 . .
Учитель говорит, что два выражения на слайде тоже являются решением этой задачи. Но оформлено это решение не полностью. Учащимся требуется объяснить, на какие вопросы отвечают записанные выражения (Первым действием узнаем, на сколько книг меньше поставит Витя на полки шкафа, вторым действием узнаем, сколько книг у Вити).
Учитель просит учащихся сравнить два способа решения (ответ получен один и тот же, но второй способ на одно действие короче, чем первый).
Урок 61, задача №6 в)
Витя решил узнать, сколько времени он потратил за неделю на выполнение домашних заданий. Сколько минут он занимался в понедельник, если во вторник он затратил на выполнение домашнего задания 120 минут, в среду – 60 минут, в четверг – 80 минут, в пятницу – 40 минут, а всего в течение пяти дней он затратил на выполнение домашних заданий 500 минут?
Цель: повторить связи между компонентами и результатами арифметических действий, учить решать задачу разными способами
Оборудование: учебник, чертежи на доске.
Учащиеся читают задачу сначала про себя, а затем вслух. Выполняется разбор условия задачи:
− О чем говорится в задаче? (о времени, затраченном на выполнение домашних заданий)
− Как удобно изобразить все затраченное время? (отрезком). Один учащийся выполняет чертеж на доске, остальные работают в тетрадях.
− Сколько дней выполнял Витя домашние задания? (всего 5 дней, с понедельника по пятницу)
− Где надо показать рабочие дни? (это части отрезка)
− Отметьте эти части.
− Что означают числа 120, 60, 80 и 40? (время, затраченное на выполнение домашних заданий соответственно во вторник, среду, четверг и пятницу). Отметьте эти числа на чертеже.
− Что обозначает число 500? (все время, затраченное на выполнение домашних заданий за неделю). Покажите это на чертеже.
В итоге на доске и в тетрадях появляется чертеж (см. рисунок №13):

Рис. №13. Чертеж к задаче
− По чертежу перескажите задачу (учащиеся пересказывают условие, но в формулировке вопроса испытывают затруднение, поскольку общее затраченное время известно по условию – 500 минут).
− Надо ли выполнять какие-либо действия, чтобы ответить на поставленный вопрос? (нет)
− Можно ли что-нибудь изменить в задаче, чтобы она приобрела смысл? (да, следует поменять вопрос)
− Измените вопрос (сколько времени потратил Витя на выполнение домашних заданий в понедельник?)
− Отметьте вопрос на чертеже.
− Умеете ли вы решить такие задачи? (да)
− Какие действия надо выбрать для решения? (Первый способ – сначала сложение – «сколько времени затрачено на выполнение домашних заданий со вторника по пятницу», затем – вычитание. Второй способ – последовательно вычитать из общего времени, затраченного на выполнение домашних заданий, время, затраченное в отдельные дни).
− Можно ли решить эту задачу уравнением? (да. Неизвестным х обозначим время, затраченное на выполнение домашних заданий в понедельник. Сложим продолжительности занятий в каждый из пяти дней, приравняем к общей затрате времени за неделю. Затем решим уравнение)
− Решите задачу по вариантам. Первый ряд – через сложение, второй – используя только вычитание. Решение оформите в виде числовых выражений. Третий ряд решит эту задачу уравнением.
Проверка проводится с помощью интерактивной доски.
− Рассмотрите «цепочку», предложенную в учебнике (см. рисунок №14):

Рис №14 Арифметическая «цепочка»
− Что обозначают круги? (сумму времени, затраченного на выполнение домашних заданий в разные дни)
− Догадайтесь, зачем круги расположили в линию? (узнать первое в цепочке число можно, «вернувшись назад», то есть, выполнив обратные действия)
− Какое действие является обратным по отношению к сложению? (вычитание)
− Давайте хором посчитаем и узнаем, какие числа надо вписать в круги. (500 минус 40 – это 460; 460 минус 80 – будет 380; 380 минус 60 – это 320; 320 минус 120 – будет 200)
− Что показывает число 200? (продолжительность занятий Вити в понедельник).
− Итак, сколькими способами мы решили задачу? (четырьмя)
− Какой способ показался вам наиболее удобным? (последний, так как не требует долгого оформления).
− Сейчас потренируемся в составлении задач, которые можно решить при помощи «цепочки». На зеленых карточках – самые простые «цепочки», на синих – чуть сложнее, красные – самые сложные. Выберите себе такую карточку, какую захотите.
После этого желающим учащимся выдаются индивидуальные карточки (2-3 цветов) с «цепочками» (см. рисунок №15). Придумайте задачу по этой цепочке:
Низкий уровень сложности:


Средний уровень сложности:


Высокий уровень сложности:


Рис. №15. Индивидуальные карточки
Проверка – по желанию, фронтальная.
Урок 62, задача №6 б)
За две недели дрессировок Костя потратил 28 кусков сахара. Это треть тех запасов сахара, которые у него были. Сколько кусков сахара у Кости осталось? На сколько недель дрессировки хватит этих запасов, если каждую неделю щенок будет получать в 2 раза меньше сахара, чем в первую неделю?
Цель: повторить связи между пропорциональными величинами.
Оборудование: учебник, интерактивная доска.
Учащиеся читают задачу сначала про себя, затем – вслух.
− Рассмотрите таблицу на доске:
Получает сахара
каждый день
|
Количество
недель
|
Всего получил
сахара за все дни
|
| Потрачено |
| Осталось |
− Подходит ли таблица для краткой записи этой задачи? (дети считают, что подходит)
Учитель просит указать, как заполнить таблицу данными. На доске появляется запись:
Получает сахара
за каждый день
|
Количество недель |
Всего получил
сахара за все дни
|
| Потрачено |
? |
2 |
28 |
| Осталось |
?, в 2 раза м. |
? |
 |
− Без ответа на какой вопрос эту задачу решить невозможно? (сколько кусков сахара получал щенок за каждый день)
− Можно ли это узнать и каким действием? (учащиеся считают, что можно, действием деления)
− Почему вы считаете, что можно выбрать деление? (распределить затраченный сахар поровну)
− А есть ли такое условие в задаче? (учащиеся перечитывают задачу и убеждаются, что такого условия нет)
− Как исправить условие задачи, чтобы ее можно было решить? (дети исправляют условие задачи «За две недели дрессировок Костя потратил 28 кусков сахара, поровну за каждый день»)
− Составьте план решения задачи (первым действием узнаем, сколько кусков сахара получал щенок еженедельно в первую неделю; вторым действием узнаем, сколько кусков сахара получал щенок еженедельно во вторую неделю; третьим действием узнаем, сколько кусков сахара еще осталось у Кости; четвертым действием узнаем, на сколько недель хватит оставшегося сахара)
− Запишите решение по действиям с пояснениями. Один учащийся решает у доски, остальные – в тетрадях:
1) 28 : 2 = 14 (к.) – еженедельно в первую неделю
2) 14 : 2 = 7 (к.) – еженедельно во вторую неделю
3) 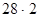 =56 (к.) – осталось сахара =56 (к.) – осталось сахара
4) 56 : 7 = 8 (нед.)
Ответ: на 8 недель хватит сахара.
− Рассмотрите чертеж. Что обозначают отрезки и их части?

Учащиеся отвечают: верхний отрезок обозначает количество израсходованного сахара. Нижний отрезок – это сахар, который еще остался. Его вдвое больше. Верхний отрезок разделен пополам, каждая половина – сахар, израсходованный за каждую неделю.
− Если бы щенок и дальше получал еженедельно столько сахара, сколько получал и раньше, то время осталось бы прежним или изменилось? (оно изменилось бы – увеличилось, так как сахара больше)
− Можно ли узнать, на сколько недель тогда хватило бы сахара? (да, умножением)
− А если еженедельный расход сахара уменьшить, то время изменится или нет? (оно еще увеличится, так как сахар будет расходоваться медленнее)
− Как узнать, на сколько хватит сахара? (время, полученное в первом действии, умножить еще на 2)
− Запишите решение. Один учащийся у доски, остальные в тетрадях:
1) 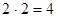 (нед.) – хватило бы сахара (нед.) – хватило бы сахара
2) 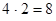 (нед.). (нед.).
Ответ: на 8 недель хватит сахара.
Урок 66, задача №4 а).
На рисунке 20 лещей, карасей в 3 раза больше, а окуней столько, сколько лещей и карасей вместе. Сколько на рисунке рыб?
Цель этой работы состоит в том, чтобы учить детей решать задачу алгебраическим способом.
Дети читают задачу. Учитель просит назвать условие задачи и ее вопрос.
Затем совместно с учащимися на доске появляется краткая запись этой задачи (см. рисунок №16)

     Л. – 20 Л. – 20
 К. – в 3 раза б. ? рыб К. – в 3 раза б. ? рыб
 О. – столько же О. – столько же
Рис. № 16 Краткая запись к задаче.
¾ Запишите вопросы, на которые можно ответить, пользуясь данным условием и запишите их решение.
Запись в тетрадях учащихся должна выглядеть следующим образом:
1. Сколько карасей на рисунке?
20 × 3 = 60
2. Сколько окуней?
20 + 60 = 80
3. Сколько всего рыб на рисунке?
20 + 60 + 80 = 160
Для индивидуальной работы учащимся предлагаются карточки с заданиями, разделенными по уровню сложности.
Карточка №1. (для слабоуспевающих учеников)
Задача: Оля собирала цветы: ромашки, васильки и колокольчики. Ромашек было 10, васильков было __ 4 _______, чем ромашек, а колокольчиков – _________, сколько ромашек и васильков вместе. Сколько цветов всего?
Задание: Дополни условие задачи так, чтобы ее решение задавалось выражением 10 + 10 × 4 + (10 + 10 × 4) и реши задачу.
Карточка №2. (для учащихся со средним уровнем обученности)
Задача: Оля собирала цветы: ромашки, васильки и колокольчики. Ромашек было ____, васильков было __ ____ больше, чем ромашек, а колокольчиков – _________, сколько ромашек и васильков вместе. Сколько ________ всего?
Задание. Дополни условие задачи так, чтобы ее решение задавалось выражением 10 + 10 × 4 + (10 + 10 × 4) и реши задачу.
Карточка №3. (для учащихся с высоким уровнем обученности)
Задача: Оля собирала цветы: ромашки, васильки и колокольчики. Ромашек было ____, васильков было __ ____ ________, чем ромашек, а колокольчиков – _________, сколько ________ и ________ вместе. Сколько _______ ______?
Задание. Дополни условие задачи так, чтобы ее решение задавалось выражением 10 + 10 × 4 + (10 + 10 × 4) и реши задачу.
Для проверки правильности выполнения задания целесообразно использовать интерактивную доску или мультимедийную презентацию.
Урок 68, задача №4 б.
Цель: повторить правило нахождения доли от числа, учить строить разнообразные вспомогательные модели к задаче.
Оборудование: учебник, мультимедийная аппаратура, слайды, карточки с выражениями.
Для украшения зала мальчики сделали 76 гирлянд из цветных фонариков. На украшение сцены пошло 16 гирлянд, третьей частью оставшихся гирлянд украсили стены, а остальными – вход в школу. Сколько гирлянд украшали вход в школу?
Дети сначала читают задачу, а затем отвечают на вопросы учителя:
¾ Какое изделие мальчики делали? (гирлянды)
¾ Сколько всего гирлянд они сделали? (76)
¾ Что украшали гирляндами дети? (сцену, стены и вход в школу)
¾ Сколько потребовалось гирлянд на сцену? (16)
¾ А на стены? (третья часть от оставшихся гирлянд)
¾ Что означает «третья часть числа»? (все оставшиеся гирлянды разделили на 3 равных части и взяли из них одну)
На доске вывешено несколько вспомогательных моделей задачи. Учитель говорит: «Найдите модель, подходящую к этой задаче» (см. рисунок №17). Учащиеся объясняют, почему нельзя выбрать модели №1 и №2, в качестве подходящей они выбирают модель №3.
  
Сц. – 16 г.
Ст. – 1/3 76 г.Вх. - ? г.
Рис. №17 Различные вспомогательные модели к задаче
Почему первая запись не подходит к этой задаче? (так как она неточная, не указано, 1/3 часть от какого количества гирлянд было использовано для украшения стен)
¾ А вторая? (так как она разъясняет только часть задачи)
¾ Что в задаче требуется узнать? (сколько гирлянд украшали вход в школу)
После разбора условия задачи учитель вывешивает на доску карточки с выражениями. На оборотной стороне карточек указан порядок действий для решения задачи (см. рисунок №18)
Рис. №18Карточки с выражениями
Затем учитель объясняет задание:
¾ Соберите решение задачи из предложенных выражений.
Учащиеся поочередно выходят к доске и, переворачивая карточки с выражениями, убеждаются в правильном выборе порядка действий. При этом учащиеся объясняют, на какой вопрос отвечают каждым выражением и почему выбирают именно такое арифметическое действие (см рисунок №19).
Рис. №19 Схема порядка действий в задаче
Затем учащиеся самостоятельно записывают решение задачи с пояснениями.
Запись должна выглядеть следующим образом:
1) 76 – 16 = 60 (г.) – осталось
2) 60 : 3 = 20 (г.) – украсили стены
3) 60 – 20 = 40 (г.) – пошло на вход в школу
Ответ: 40 гирлянд.
Пока учащиеся оформляют решение задачи в тетрадях, учитель заменяет некоторые карточки.
После того, как школьники оформили решение задачи, учитель опять обращает их внимание на карточки с выражениями и просит найти второй способ решения этой задачи. Учащиеся, как и в прошлый раз, поочередно выходят к доске и проставляют порядок действий, объясняя, на какой вопрос при этом можно ответить (см. рисунок №20).
Рис. №20 Схема порядка действий в задаче
Решение задачи вторым способом выполняется устно.
Урок 69, задача №7.
Цель: повторить основные понятия теории множеств, учить решать задачи разными способами, учить определять истинность или ложность высказываний.
Оборудование: учебник, мультимедийная аппаратура, слайды, карточки с предложениями, карандаши.
Для книг из классной библиотеки Костя сделал рисунок:
 Составь несколько высказываний к этому рисунку.
· Сколько всего книг о животных и книг с рассказами в этой библиотеке, если книг с рассказами 45, книг о животных 38, а книг с рассказами о животных 17?
Целью данной работы является закрепление знаний о множестве.
Учитель предлагает учащимся рассмотреть рисунок и назвать множества, которые на нем изображены (книги, рассказы, книги и рассказы о животных).
¾ Назовите элементы множества:
- рассказы (Л.Н. Толстой «Филиппок», В.Драгунский «Девочка на шаре» и другие),
- книги о животных (книга о кошках, В.Бианки «Синичкин календарь», Н.Сладков «Лесные тайнички»),
- рассказы о животных (Ю.Коринец «Ханг и Чанг», М.Ершова «Котята»)
Учитель показывает на слайде этот же рисунок, но частично раскрашенный (см. рисунок №21):
 Рис.№21 Множество книг.
Дети видят, что есть такое множество книг, которое не относится к рассказам, книгам о животных и рассказам о животных. Учитель просит привести примеры такого множества (книга А.В.Волкова «Волшебник Изумрудного города», К.Чуковский «Бармалей», Д.Р.Киплинг «Маугли» и другие)
После изучения рисунка учитель дает задание учащимся составить несколько высказываний к этому рисунку с использованием слов: некоторые, существует, не все, все.
Дети называют свои предложения:
- все книги о животных – это книги;
- не все рассказы – это книги;
- некоторые рассказы – книги;
- существуют книги – рассказы о животных.
Для индивидуальной работы можно предложить нескольким учащимся карточки со следующим заданием: оценить, верно ли что…
- некоторые книги о животных – это книги (верно);
- все рассказы – книги (неверно);
- все книги о животных являются рассказами (неверно);
- существуют книги не о животных, которые не являются рассказами (верно).
Далее дети читают ниже приведенную задачу.
¾ Что мы узнали из текста задачи? (книг с рассказами 45, книг о животных 38, а книг с рассказами о животных 17)
Учитель просит учащихся взять простые карандаши в руки и наклонной штриховкой отметить все рассказы. На фоне этой штриховки отметить число 45. Затем, изменив наклон штриховки, отметить все книги о животных, отметить на этом фоне число 38.
¾ Что заметили? (на рисунке не два, а три вида штриховки, есть штриховка «клеточкой»)
¾ Обведите яркой линией эту область. Какие книги в ней содержатся? (рассказы о животных).
¾ Сколько их, запишите. (внутри области учащиеся записывают число 17)
¾ Что нас просят узнать? (сколько всего книг о животных и книг с рассказами в этой библиотеке)
¾ Что мы будем узнавать в первую очередь? (сколько всего книг содержится во множествах, отмеченных наклонной штриховкой)
¾ Какое действие мы будем при этом выполнять? (сложение, так как мы будем узнавать, сколько книг всего)
¾ Что мы можем найти после этого? (сколько книг о животных и книг с рассказами в этой библиотеке)
¾ Как мы это определим? (из всех книг вычтем книги с рассказами о животных)
После разбора задачи ученики самостоятельно записывают решение в тетради. Оно должно выглядеть следующим образом:
1) 45 + 38 = 83 (кн.) – всего в библиотеке
2) 83 – 17 = 66 (кн.) – о животных и книг с рассказами
Ответ: 66 книг.
При выполнении этого задания можно провести индивидуальную работу для слабоуспевающих учащихся. Им раздаются карточки, в которых предложены другие способы решения этой задачи.
Например:
Карточка №1.

Задание: Найди на рисунке множество, в котором книг содержится 45 – 17. Закрась это множество синим цветом. Обведи красным карандашом множество, в котором книг содержится (45 – 17) + 38.
Карточка №2.

Задание: Найди на рисунке множество, в котором книг содержится 38 – 17. Закрась это множество синим карандашом. Обведи красным карандашом множество, в котором книг содержится (38 – 17) +45.
Карточка №3.

Задание: раскрась картинку всеми имеющимися способами. Реши задачу по действиям с пояснениями.
В качестве домашнего индивидуального задания можно предложить учащимся составить похожую задачу о предметах домашнего обихода, оформить рисунок.
Урок 70, задача №8 б)
Цель: повторить связи между пропорциональными величинами, учить решать задачи разными способами.
Оборудование: учебник,
Коля и Мишка варили кашу. Этой кашей они заполнили 2 кастрюли одинакового объема и 6 банок такого же объема. Сколько литров каши сварили мальчики, если в банки они разлили на 12 литров каши больше, чем в кастрюли?
Учитель предлагает разобрать эту задачу в форме игры. Учащиеся поочередно рассказывают о том, что известно из условия задачи. Побеждает тот, кто назовет данные последним. Также учитель обращает внимание детей, если они этого не сказали, на то, что кастрюли и банки имеют одинаковые вместимости.
¾ Могли бы мы решить задачу, если бы вместимость посуды была бы разной? Почему? (дети высказывают свою точку зрения с объяснением)
Далее учитель предлагает ученикам объединиться в пары и путем обсуждения найти решение этой задачи.
После этого идет проверка решения задачи.
Один из учеников выходит к доске и, комментируя, чертит схему к задаче (см. рисунок №22):

Рис.№22Схема к задаче
Другой ученик записывает решение задачи, комментируя его.
В итоге, в тетрадях учащихся должна появиться следующая запись:
1) 6 – 2 = 4 (шт.) – банок больше, чем кастрюль
2) 12 : 4 = 3 (л) – в одной банке или кастрюле
3) 2 + 6 = 8 (шт.) – банок и кастрюль одинаковой вместимости всего
4) 3 × 8 = 24 (л) – каши сварили мальчики
Ответ: 24 литра.
Для решения задачи другим способом можно организовать работу в малых группах. Для этого необходимо, чтобы учитель заранее приготовил карточки со следующими выражениями: 6 – 2; 12 : 4; 6 : 2; 3 × 2; 6 × 3; 6 + 18 и геометрические фигуры шести цветов. Дети поочередно вынимают из коробки по одной геометрической фигуре. Потом они садятся в группы по цветам, выбирают звеньевого и получают карточку с заданием. На этой карточке написано одно из шести выражений, суть задания состоит в том, чтобы дети объяснили, на какой вопрос задачи можно с его помощью ответить.
Когда все группы выполнили это задание, к доске выходят звеньевые и становятся в порядке, соответствующем решению задачи. После этого класс записывает решение. Оно выглядит следующим образом:
1) 6 – 2 = 4 (шт.) – банок больше, чем кастрюль
2) 12 : 4 = 3 (л) – в одной банке или кастрюле
3) 6 : 2 = 3 (раза) – банок больше, чем кастрюль
4) 3 × 2 = 6 (л) – каши в кастрюлях
5) 6 × 3 = 18 (л) – каши в банках
6) 6 + 18 = 24 (л) – каши сварили всего
Ответ: 24 литра.
Итак, на втором этапе эксперимента мы провели разные формы работ на уроке при решении текстовой задачи. На контрольном этапе мы будем повторно проводить тестирование учащихся с целью определения динамики уровня сформированности умений младших школьников решать текстовые задачи.
3.3 Динамика уровней сформированности умений младших школьников решать задачи
На контрольном этапе было проведено повторное тестирование учащихся экспериментального и контрольного классов с целью определения изменений в уровнях сформированности умений младших школьников решать задачи.
По результатам повторного исследования было выявлено, что в экспериментальном классе высоким уровнем сформированности умений решать задачи обладают 21 человек (87,5%), средним – 3 человека (12,5%). В контрольном классе результаты исследований следующие: высокий уровень – 12 человек (57,1%); средний уровень – 9 человек (42,9%)
Группы учащихся с низким уровнем умения решать задачи в обоих классах отсутствуют.
Соотношение между количеством учащихся высоких и средних уровней сформированности умений решать задачи можно увидеть в ниже приведенной таблице №5 и на диаграмме №2:
Таблица №5. Распределение учащихся экспериментального и контрольного классов в зависимости от уровня сформированности умений решать задачи на контрольном этапе
| Уровень сформированности умения решать задачи |
Экспериментальный класс |
Контрольный класс |
| Чел. |
% |
Чел. |
% |
| Высокий |
21 |
87,5 |
12 |
57,1 |
| Средний |
3 |
12,5 |
9 |
42,9 |
| Низкий |
0 |
0 |
0 |
0 |

Диаграмма №2. Соотношение уровней сформированности умений решать задачи на контрольном этапе
По итогам исследования, проведенного на контрольном этапе педагогического эксперимента, можно сказать, что в экспериментальном и контрольном классах на момент окончания эксперимента группы учащихся с низким уровнем сформированности умений решать задачи отсутствуют.
В контрольном классе доля учащихся с высоким уровнем сформированности существенно превосходит долю учащихся со средним уровнем сформированности этих же умений. В контрольном классе разница в количественном составе групп выражена менее резко.
Сравнивая распределение учащихся каждого класса по группам на диагностирующем и контрольном этапе, мы увидим результаты, отображенные в таблицах №6 и №7, а также на диаграммах №3 и №4:
Таблица №6. Динамика уровней сформированности умений решать задачи в экспериментальном 3-А классе
| Уровень сформированности умения решать задачи |
Диагностирующий этап |
Контрольный этап |
Динамика |
| Чел. |
% |
Чел. |
% |
Чел. |
% |
| Высокий |
14 |
58,3 |
21 |
87,5 |
+7 |
+29,2 |
| Средний |
8 |
33,3 |
3 |
12,5 |
-5 |
-20,8 |
| Низкий |
2 |
8,4 |
0 |
0 |
-2 |
-8,4 |
Таблица №7. Динамика уровней сформированности умений решать задачи в контрольном 3-Б классе
Уровень сформированности умения решать задачи
|
Диагностирующий этап |
Контрольный этап |
Динамика |
| Чел. |
% |
Чел. |
% |
Чел. |
% |
| Высокий |
11 |
52,4 |
12 |
57,1 |
+1 |
+4,7 |
| Средний |
8 |
38,0 |
9 |
42,9 |
+1 |
+4,9 |
| Низкий |
2 |
9,6 |
0 |
0 |
-2 |
-9,6 |

Диаграмма №3. Динамика уровней сформированности умений решать задачи в экспериментальном 3-А классе
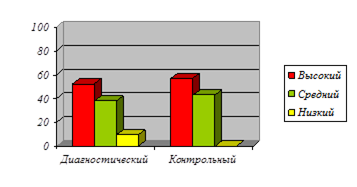
Диаграмма №3. Динамика уровней сформированности умений решать задачи в контрольном 3-Б классе
Таким образом, в ходе педагогического эксперимента нами установлено, что в результате систематического сочетания разнообразных форм организации деятельности учащихся на уроках математики при решении задач уровень соответствующих умений у учащихся экспериментального класса существенно возрос. В ходе формирующего этапа эксперимента учащиеся со средним уровнем умений решать текстовые задачи повысили этот уровень и отнесены в группу учащихся с высоким уровнем умения решать задачи. Те учащиеся, которые на диагностирующем этапе вошли в группу с низким уровнем умения решать задачи, в результате нашей работы повысили уровень своих умений и перешли в группу со средним уровнем умений решать задачи.
Аналогичные изменения произошли в контрольном классе. Однако в количественном отношении динамика выражена не столь резко, как в контрольном классе.
Мы считаем, что достигнутые в экспериментальном классе изменения в уровнях сформированности умений учащихся решать текстовые задачи произошли вследствие варьирования на уроках коллективной, групповой и индивидуальной форм работы младших школьников при решении задач.
Ильинская Е.В., учитель контрольного класса, не ставила своей целью повышение уровня умений школьников решать задачи. Более актуальной для учащихся класса она считает развитие свойств памяти школьников. Для достижения поставленной цели учителем организованы внеклассные занятия. Повышение уровня сформированности умений решать задачи у учащихся 3 «Б» класса Ильинская Е.В. объясняет систематическим включением задач в уроки в соответствии с материалами учебника и требованиями образовательной программы.
Таким образом, выдвинутая гипотеза «если на уроках математики систематически применять разнообразные формы работы с учащимися при обучении решению задач, то уровень их умения решать текстовые задачи повысится», подтверждена.
Заключение
Современная концепция начального образования школьников ориентирована на получение новых знаний в сочетании со всесторонним развитием личностной сферы ребенка. Все модели обучения имеют общую цель – развитие личности учащегося, формирование у него желания и умения учиться: «Миссия новой системы образования четко соотносится и с важнейшими социальными эффектами системы образования – это обеспечение социальной и духовной консолидации нации, конкурентоспособности и безопасности личности, общества и государства» [37].
В настоящее время на территории Росси обучение математике в начальных классах ведется по традиционной («Школа России», «Начальная школа ХХI века», «Школа 2100», «Гармония», «Перспективная начальная школа», «Классическая начальная школа», «Планета знаний», «Перспектива») и развивающим (Л.В. Занкова и Д.Б. Эльконина – В.В. Давыдова) системам [38].
Специалистам, работающим в области педагогики, совершенно понятно, что любой – важный, занимательный, интересный научный факт усваивается младшим школьником более глубоко и осознанно, если своевременно демонстрировать обучаемому значимость вновь приобретенных знаний для повседневной жизни. В этом смысле обучение математике в начальной школе связывает теоретическую и практическую составляющие дисциплины посредством системы текстовых задач.
В процессе изучения психолого-педагогической литературы мы установили, что текстовые задачи, включенные в начальный курс математики, призваны решать триединую задачу обучения математике: способствовать усвоению математических знаний, формированию и воспитанию личностных качеств младших школьников, развитию их психических процессов. С помощью текстовых задач учитель раскрывает сущность теоретических положений, отрабатывает умения выполнять вычислительные приемы, устанавливает межпредметные связи и демонстрирует приложение математических знаний и умений к решению жизненных задач.
Текстовые задачи, включенные в начальный курс математики, классифицируются по различным основаниям. Это позволяет с методической точки зрения так построить учебно-воспитательный процесс, что практически любой младший школьник имеет возможность усвоить связи, правила и законы, лежащие в основе выбора действий для решения задачи.
В зависимости от возраста учащихся на каждом уроке математики решаются типовые текстовые задачи (нахождение целого и части; умножение и деление суммы на число; задачи с пропорциональными величинами и т.д.), в результате чего можно говорить об отработке достаточно прочных умений и навыков школьников в решении этих видов задач.
Однако, по свидетельству учителей начальной школы, не у всех младших школьников процесс обучения решению задач проходит без затруднений. Возникновение проблем в усвоении учебного материала может быть вызвано целым рядом факторов личностного или социального характера. В результате коллектив класса разделяется на группы в зависимости от уровня сформированности умений, в частности, решать текстовые задачи.
С целью формирования и дальнейшей отработки умений и навыков, предусмотренных программой, учитель использует широкий арсенал методических средств управления учебно-воспитательным процессом. Школьников знакомят
· с различными способами наглядного представления текстовой задачи,
· с различными способами решения основных видов типовых задач,
· с различными приемами выполнения каждого из этапов решения задачи и пр.
Для работы над задачей на уроках используют различные методы обучения. Но, как показывают исследования психологов и педагогов, а также наблюдения учителей, один и тот же метод обучения не гарантирует одинакового уровня усвоения материала учащимися целого класса. В более полной мере учесть индивидуальные особенности младших школьников может помочь сочетание на уроках различных форм организации деятельности учащихся: коллективной, групповой и индивидуальной.
Каждая из этих форм имеет определенные преимущества по сравнению с остальными, но и не является универсальной. Применение одних форм позволяют раскрыться индивидуальному потенциалу учащегося, применение других открывают возможности для взаимного обучения между школьниками.
В период преддипломной практики мы исследовали динамику уровней развития умений младших школьников решать текстовые задачи через сочетание различных форм работы при решении задач.
На констатирующем этапе эксперимента было установлено, что в экспериментальном и контрольном классах присутствуют учащиеся с соответственно высоким, средним и низким уровнями сформированности умения решать задачи. Работа на формирующем этапе была нацелена на варьирование форм организации деятельности учащихся при решении задач на уроке. С этой целью нами были разработаны планы уроков, мультимедийные презентации, плакаты и индивидуальные дидактические материалы (карточки с дифференцированными заданиями). На контрольном этапе нами была изучена динамика уровней сформированности умений младших школьников решать текстовые задачи. В результате эксперимента установлено, что за период практики по вопросам, предусмотренным программой, уровень учащихся обоих классов решать текстовые задачи повысился.
Мы считаем, что полученный результат в экспериментальном классе обусловлен сочетанием форм работы учащихся при решении задач и использованием различных методических приемов реализации этих форм. По мнению Ильинской Елены Вячеславовны, учителя контрольного класса, повышение уровня умений ее учащихся решать задачи обусловлено проведением серии внеклассных занятий.
Таким образом, мы можем сделать вывод о том, что сочетание коллективной, групповой и индивидуальной форм работы младших школьников на уроке при решении задач действительно позволяет повысить уровень соответствующих умений учащихся. Тем самым гипотеза, сформулированная во введении к работе, подтверждена.
Полученный в ходе исследования результат позволяет нам сформулировать ряд рекомендаций для учителей начальной школы, которые заинтересованы в повышении уровня сформированности умений младших школьников решать текстовые задачи.
1. Прежде чем начать целенаправленную работу по повышению уровня сформированности умений младших школьников решать задачи, всесторонне оцените потенциальные возможности Ваших учащихся, изучите характер трудностей, которые они испытывают при решении задач, расспросите родителей школьников о том, в какой помощи, по их мнению, нуждается ребенок.
2. Изучите текстовые задачи, которые включены в учебник математики, по которому происходит обучение в классе. Классифицируйте эти задачи (например, на стандартные – по известным видам, и нестандартные).
3. В любой этап урока включайте устные упражнения, с помощью которых повторяются основания для выбора действий при решении задач. Целесообразно некоторые из задач предлагать не в словесной форме, а в виде условного ее изображения (краткой записи, таблицы, чертежа, рисунка и т.п.). Желательно, чтобы суть выполняемых упражнений постоянно видоизменялась (решить задачу, составить условие по модели или по решению, дополнить условие, убрать лишние данные, найти ошибки в рассуждениях, найти иной способ решения и т.п.). Кроме численных данных, на определенной ступени обучения допустимы буквенные. Это позволит учащимся более глубоко осознать изучаемые правила, связи между величинами и другие теоретические положения.
4. При планировании уроков не забывайте о ведущей роли учителя на занятии. Имейте в виду, что составленный план урока не всегда удается реализовать в полной мере. Еще на этапе подготовки урока предусмотрите альтернативную деятельность учащихся. Если запланированный ход урока не удалось реализовать, внимательно проанализируйте причины, которые помешали организовать работу в соответствии с Вашим планом. Учтите свои недостатки при планировании работы в дальнейшем.
5. При разработке плана урока разделите упражнения, которые будут выполнять школьники, на группы в соответствии с целесообразной формой организации деятельности учащихся. Убедитесь в том, что в выборе форм работы над задачей в Вашем плане нет однообразия. Формы деятельности школьников должны периодически сменять друг друга.
6. Помните, что при одной и той же форме организации деятельности учащихся при решении задачи возможны разнообразные методические подходы. Старайтесь строить учебную деятельность младших школьников таким образом, чтобы максимально использовать современные методы обучения, включайте в свои уроки проблемные ситуации, подталкивайте учащихся к активной мыслительной деятельности. Вступайте с учащимися в дискуссии, предлагайте школьникам выступать в роли учителя по отношению к одноклассникам.
7. Не бойтесь вести работу над задачей на достаточно высоком уровне сложности. Исследованиями психологов установлено, что хорошо успевающий по предмету учащийся при заниженных требованиях рано или поздно снижает уровень учебной мотивации. В то же время слабоуспевающий школьник, ориентируясь на своих более успешных в учебе одноклассников, в условиях высоких требований стремится в меру своих сил овладеть программными вопросами.
8. Используйте в своей работе современные методические материалы: электронные учебные пособия, мультимедийные сопровождения к урокам, разработки уроков в сети Internet и т.п.
9. При организации коллективной (фронтальной) работы старайтесь следить за тем, чтобы в активную деятельность были включены все учащиеся класса. Как правило, более коммуникабельные младшие школьники активны при решении задачи. Они отвечают на вопросы учителя, анализируют ответы одноклассников, формулируют вопросы к задаче, составляют план решения. Особого внимания требуют учащиеся, которые редко проявляют инициативу в коллективе. Включить таких школьников в работу можно специально адресованными вопросами, предложением продолжить начатую мысль, просьбой оценить услышанное и т.д. Помните, что одобрение успехов таких учащихся чрезвычайно важно для них. При необходимости дать негативную оценку работе этих учащихся постарайтесь подобрать такие слова, чтобы не унизить человеческое достоинство школьника, не спровоцировать его на замкнутость в коллективе.
10. При организации индивидуальной работы школьников при решении задач тщательно продумывайте уровень сложности предлагаемых заданий, способ оформления выполненного задания. В некоторых случаях учителю следует самому распределить задания по уровню сложности между учащимися. В других ситуациях право выбора уровня сложности предоставляйте самим школьникам. Поощряйте учащихся, которые сегодня показывают желание выполнить задание более высокого уровня сложности, чем выполнялось им вчера.
11. При организации групповой работы школьников по решению задач тщательно продумывайте количественный и списочный состав групп. Объединяйте в одну группу учащихся с разными успехами в обучении, с различными психологическими особенностями и т.п. Определите, какой деятельностью должна заниматься группа и что должно стать результатом ее работы. Обязанности внутри группы может распределять учитель, но если у учащихся есть желание самостоятельно распределить нагрузку внутри группы, не мешайте им в этом. Проконтролируйте лишь, чтобы на каждого школьника была возложена определенная обязанность.
12. Независимо от того, какой формой организации деятельности младших школьников вы воспользовались на данном уроке, обязательно подведите итоги работы класса в конце урока. Опишите, что, по Вашему мнению, удалось реализовать, а чего достичь не получилось. Выслушайте мнение детей о том, что показалось им наиболее продуктивным, а что вызвало определенные трудности. Результаты анализа по возможности учтите при планировании следующих уроков.
Наше общество стремительно развивается в информационном пространстве. Оно включается в постоянно расширяющуюся систему политических, социальных и экономических отношений со множеством зарубежных стран. Государственный заказ на гармонично развитых, образованных, творческих, грамотных и мобильных специалистов не утратит своей актуальности. Такие граждане в будущем вполне могут вырасти из современных младших школьников, поскольку отечественная педагогическая наука располагает всеми необходимыми для этого возможностями.
Список литературы
1. Аргинская И.И., Вороницына Е.В. Особенности обучения младших школьников математике // Первое сентября №24. 2005. с.12-21
2. Басангова Р.Б. Познавательная деятельность ученика в ходе решения задач // Начальная школа №3. 2002
3. Белошистая А.В. Вопросы обучения решению задач // Начальная школа Плюс До и После №10. 2002. с.73-79
4. Белошистая А.В. Методика обучения математике в начальной школе. Курс лекций. – М.: «Владос». 2007
5. Белошистая А.В. Обучение математике в начальной школе. Методическое пособие. – М.: «Academia», 2006
6. Гусев В.А. Психолого-педагогические основы обучения математике. – М. 2003.
7. Дебашинина Е.Ю. Самостоятельная работа на уроках математики в условиях развивающего обучения // Начальная школа №7. 2003. с.101-103
8. Демидов Т.Е., Тонких А.П. Теория и практика решения текстовых задач. - М.: «Academia». 2002
9. Ивлева Э.И. Организация взаимопомощи учащихся на уроках математики // Начальная школа №2. 2002
10. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: «Academia». 1998
11. Коджаспирова Г.М., Коджаспиров А.Ю. Педагогический словарь. – М.: «Academia». 2001
12. Матвеева Н.А. Методические приемы обучения составлению текстовых задач // Начальная школа №6. 2003. с.41-44
13. Матвеева Н.А. Различные арифметические способы решения задач // Начальная школа №3. 2001. с.29
14. Мижериков В.А. Психолого-педагогический словарь. – Ростов-на-Дону: «Феникс». 1998
15. Моро М.И., Бантова М.А. Математика 4 класс 2 часть. – М.: «Просвещение», 2004
16. Программы общеобразовательных учреждений начальных классов (1-4). Часть 1. – М.: «Просвещение». 2000
17. Программы четырехлетней начальной школы / руководитель проекта Н. Ф. Виноградова – М.: «Вента-Граф». 2004
18. Роганова Н.Ф. Разноуровневые задания по математике // Начальная школа №9. 2003. с.79-81
19. Сборник программ для четырехлетней начальной школы / система Л.В.Занкова – М.: «Учебная литература». 2004
20. Сластенин Р.А., Исаев И.Ф., Мищенко А.И. Педагогика. – М., 2002
21. Смолеусова Т.В. Этапы, методы и способы решения задачи// Начальная школа №12. 2003. с.62-67
22. Талызина Н.Ф. Индивидуальные формы работы // Педагогическая психология. М., 1998. с.170-173
23. Хакунова Ф.Л. Особенности организации самостоятельной работы обучаемых // Начальная школа №1. 2003
24. Царева С.Е. Обучение решению задач // Начальная школа №1. 1998
25. Шелехова Л.В. Сюжетные задачи по математике в начальной школе. – М.: «Чистые пруды». 2007
26. Шикова Р.Н. Особенности работы над задачами // Начальная школа №4. 1999. с.77
27. Яковлева Е.В. Организация дифференцированного подхода в процессе усвоения знаний младшими школьниками // Начальная школа №5. 2004. с.69-74
28. Ямалтдинова Д.Г. Организация самостоятельной творческой деятельности младших школьников на уроках // Начальная школа Плюс До и После №10. 2007. с.70-71
|