| 7.3. Теплоемкость твердых тел
§ 1. Понятие о квантовой теории теплоемкости. Фононы
Квантовая статистика устранила трудности в объяснении зависимости теплоемкости газов (в частности, двухатомных) от температуры. Согласно квантовой механике, энергия вращательного движения молекул и энергия колебаний атомов в молекуле могут принимать лишь дискретные значения. Если энергия теплового движения значительно меньше разности энергий соседних уровней энергии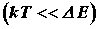
, то при столкновении молекул вращательные и колебательные степени свободы практически не возбуждаются. Поэтому при низких температурах поведение двухатомного газа подобно одноатомному.
Так как разность между соседними вращательными уровнями энергии значительно меньше, чем между колебательными, т. е.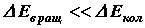 
, то с ростом температуры возбуждаются вначале вращательные степени свободы, в результате чего теплоемкость возрастает; при дальнейшем росте температуры возбуждаются и колебательные степени свободы и происходит дальнейший рост теплоемкости.
Функции распределения Ферми - Дирака для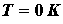 
и 
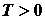заметно различаются (рис. 7.1) лишь в узкой области энергий (порядка 
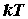). Следовательно, в процессе нагревания металла участвует лишь незначительная часть всех электронов проводимости. Этим и объясняется отсутствие заметной разницы между теплоемкостями металлов и диэлектриков, что не могло быть объяснено классической теорией.
Как уже указывалось, классическая теория не смогла объяснить также зависимость теплоемкости твердых тел от температуры, а квантовая статистика решила эту задачу. Так, А. Эйнштейн, приближенно считая, что колебания атомов кристаллической решетки независимы (модель кристалла как совокупности независимых колеблющихся с одинаковой частотой гармонических осцилляторов), создал качественную квантовую теорию теплоемкости кристаллической решетки. Она впоследствии была развита П. Дебаем, который учел, что колебания атомов в кристаллической решетке не являются независимыми (рассмотрел непрерывный спектр частот гармонических осцилляторов).
Рассматривая непрерывный спектр частот осцилляторов, П. Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам. Поэтому тепловое возбуждение твердого тела можно описать в виде упругих волн, распространяющихся в кристалле. Согласно корпускулярно-волновому дуализму свойств вещества, упругим волнам в кристалле сопоставляют фононы,
обладающие энергией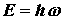 
. Фонон есть квант энергии звуковой волны
(так как упругие волны — волны звуковые). Фононы являются квазичастицами -
элементарными возбуждениями, ведущими себя подобно микрочастицам. Аналогично тому как квантование электромагнитного излучения привело к представлению о фотонах, квантование упругих волн привело к представлению о фононах.
Квазичастицы, в частности фононы, сильно отличаются от обычных частиц (например, электронов, протонов, фотонов), так как они связаны с коллективным движением многих частиц системы. Квазичастицы не могут возникать в вакууме, они существуют только в кристалле. Импульс фонона обладает своеобразным свойством: при столкновении фононов в кристалле их импульс может дискретными порциями передаваться кристаллической решетке - он при этом не сохраняется. Поэтому в случае фононов
говорят о квазиимпульсе.
Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе - Эйнштейна, так как фононы являются бозонами (их спин равен нулю). Фононы могут испускаться и поглощаться, но их число не сохраняется постоянным; поэтому в формуле (7.4) для фононов необходимо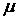 
, положить равным нулю.
Применение статистики Бозе-Эйнштейна к фононному газу-газу из невзаимодействующих бозе-частиц - привело П. Дебая к количественному выводу, согласно которому при высоких температурах, когда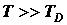 
(классическая область), теплоемкость твердых тел описывается законом Дюлонга и Пти , а при низких температурах, когда 
(квантовая область), - пропорциональна кубу термодинамической температуры: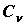 
~
.
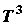В данном случае 
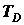- характеристическая
температура
Дебая
, определяемая соотношением 
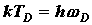, где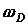 
- предельная частота упругих колебаний кристаллической решетки. Таким образом, теория Дебая объяснила расхождение опытных и теоретических (вычисленных на основе классической теории) значений теплоемкости твердых тел.
Модель квазичастиц - фононов - оказалась эффективной для объяснения открытого П. Л. Капицей явления сверхтекучести жидкого гелия. Теория сверхтекучести, созданная (1941) Л. Д. Ландау и развитая (1947) российским ученым Н. Н. Боголюбовым (р. 1909), применена впоследствии к явлению сверхпроводимости.
|
