Реферат
на тему:
Математична обробка результатів вимірювань
Прямими
називаються вимірювання, в результаті яких встановлюють безпосередньо шукане значення величини.
Результати спостережень Xl
,
Х2
,.... Хп
,
одержані за прямими вимірюваннями фізичної величини Q
,
називаються рівно
розсіяними,
якщо вони є незалежними, однаково розподіленими випадковими величинами. Рівнорозсіяні результати одержують при вимірюваннях, які проводяться одним або групою експериментаторів за допомогою однакових технічних засобів вимірювання та у незмінному зовнішньому середовищі.
Результати опрацьовуються по-різному, залежно від того, мало (п <
40) чи багато (п ≥
40) проведено спостережень.
При малій кількості результатів обробка їх проводиться у такій послідовності.
1. Визначається точкова оцінка істинного значення вимірюваної величини — середнє арифметичне значення результатів спостережень:
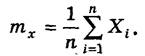 (1) (1)
2. Обчислюються випадкові відхилення результатів спостережень та їх квадрати:
 (2) (2)
3. Визначається середнє квадратичне відхилення результатів спостережень:
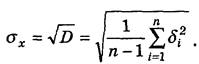 (3) (3)
4. Перевіряється нормальність розподілу результатів спостережень.
5. Визначається наявність грубих похибок, які відповідають відношенню δ
≥
3σ
. Результати з грубими помилками опускають і проводять обчислення для меншого числа спостережень з попередньою послідовністю.
6. Встановивши значення довірчої ймовірності залежно від точності вимірювань, визначається значення ймовірності випадкової похибки:
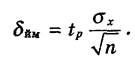 (4) (4)
7. Результат істинного значення записується у такому вигляді:
Q
=
mx
± д
й
м
;
при Р
= 0,9—0,9973,
або
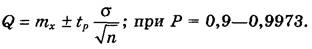 (5) (5)
Приклад.
Визначити істинне значення виміряної температури в апараті за низкою результатів спостережень (табл. 1) при заданій ймовірності р
= 0,95.
Таблиця
1
| Ms
|
t
°С
|
δ
°С
|
δ
2
t
|
| 1 |
123,5 |
+0,09 +0,05 |
0,0081 0,0025 |
| 2 |
123,8 |
+0,39 +0,35 |
0,1521 0,1225 |
| 3 |
123,6 |
+0,19 +0,15 |
0,0361 0,0225 |
| 4 |
123,7 |
+0,29 +0,25 |
0,0841 0,0625 |
| 5 |
123,9 |
+0,49 +0,45 |
0,2401 0,2025 |
| 6 |
123,0 |
-0,41 -0,45 |
0,1681 0,2025 |
| 7 |
123,4 |
-0,01 -0,05 |
0,0001 0,0025 |
| 8 |
123,2 |
-0,21 -0,25 |
0,0441 0,0625 |
| 9 |
123,1 |
-0,31 -0,35 |
0,0961 0,1225 |
| 10 |
123,3 |
-0,11 -0,15 |
0,0121 0,0225 |
| 11 |
101,2 |
-22,21 — |
493,284 — |
| 12 |
145,2 |
+21,79 — |
474,804 — |
| ∑ |
п
= 12 |
п =
10 |
п =
12 |
п
= 10 |
п
= 12 |
п =
10 |
| 1480,9 |
1234,5 |
-0,12 |
0,0 |
968,92 |
0,825 |
| mt
|
123,41 123,45 |
σ
t
=
8,9858 σ
t
= 0,3 |
1. Визначаємо точкову оцінку істинного значення вимірюваної величини, тобто середнє арифметичне даних спостережень (графа 2 табл. 1):
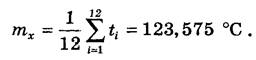
Одержане числове значення середнього арифметичного округляємо так, щоб випадкові відхилення не були більшими за дві-три значущі цифри при точних вимірюваннях. Отже, округляємо до значення t
= 123,41 °С.
2. Визначаємо відхилення результатів спостережень (графа 3 табл. 1). їх сума дорівнює 0,12, хоча повинна дорівнювати нулю. Проте два останніх спостереження мають значні відхилення, тому перевіряємо їх щодо наявності грубих відхилень за відношенням δ
≥
3σ
.
Реклама

3. Визначаємо середнє квадратичне відхилення результатів спостережень:
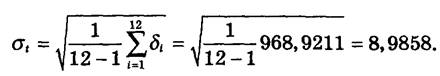
Згідно з правилом δ
≥
3σ
два останніх спостереження, відхилення яких наближаються до Зσ
, відносяться до результатів з грубими похибками і їх можна опустити з ряду спостережень, залишивши в ньому перші 10 спостережень. Повторюємо обробку результатів для 10 спостережень.
1. Визначаємо середнє арифметичне значення результатів спостережень:

2. Визначаємо відхилення результатів 10 спостережень:
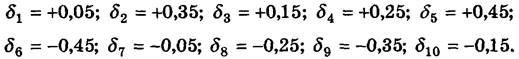
Їх сума дорівнює 0. Значних відхилень результатів спостережень не виявлено.
3. Визначаємо середнє геометричне відхилення результатів спостережень:
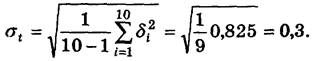
4. Виходячи з довірчої ймовірності 0,95 при 10 спостереженнях, знаходимо значення коефіцієнта Стьюдента tp
= 2,228.
5. Визначаємо довірчі межі відхилення вимірюваної величини:
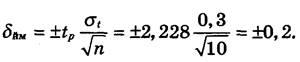
6. Визначаємо результат істинного значення вимірюваної температури та довірчі межі:

Список використаної літератури
В.Д.Цюцюра, С.В.Цюцюра. Метрологія
та основи
вимірювань
. Навч. посібн., К., "Знання -Прес", 2003
|