Реферат
на тему:
Моменти випадкових похибок
Функція розподілу результатів вимірювань чи похибок є універсальним способом опису розміщення випадкових похибок навколо істинного значення. Проте для визначення функцій розподілу необхідно виконати досить копітке наукове дослідження і складні обчислення. Тому цю роботу доцільно виконувати при розробці та дослідженні нових технічних засобів вимірювальної техніки.
Значно частіше випадкові похибки характеризуються за допомогою обмеженого числа спеціальних величин, які називаються моментами.
Початковим моментом к-го порядку результатів спостережень
називається інтеграл виду
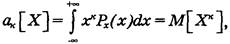 (1) (1)
що є математичним сподіванням степені X
к
.
З виразу (12) видно, що початковий момент збігається з математичним сподіванням результатів спостережень.
Центральним моментом к-го порядку результатів спостережень
називається інтеграл виду
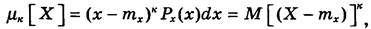 (2) (2)
який є математичним сподіванням величини (
X
- тх),
тобто у випадкової похибки к-
ї степені.
Обчислимо перший центральний момент:
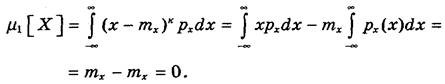 (3) (3)
Таким чином, перший центральний момент результатів спостережень дорівнює нулю.
Поряд з математичним сподіванням результатів спостережень велике значення має другий центральний момент — дисперсія
розподілу результатів спостережень та похибок вимірювань, яка позначається D[X]iD[δ
]:
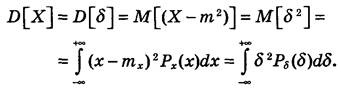 (4) (4)
Дисперсія розподілу випадкових похибок
дорівнює дисперсії розподілу результатів спостережень і характеризує їх розсіювання відносно математичного сподівання. Дисперсія розподілу зростає зі збільшенням елементів ймовірності P
δ
(
δ
)
dx
,
виникненням великих значень випадкових похибок, тобто зі збільшенням розсіювання результатів спостережень.
Якщо математичне сподівання результатів спостережень у механічній інтерпретації можна розглядати як абсцису центру тяжіння фігури, обмеженої кривою розподілу та віссю абсцис, то дисперсію — як момент інерції цієї фігури відносно вертикальної осі, яка проходить через центр тяжіння.
Дисперсія розподілу має розмірність квадрата вимірюваної величини, тому вона незручна для користування. Значно частіше в розрахунках використовується позитивне значення квадратного кореня з дисперсії, яке називається середнім квадратичним відхиленням результатів спостережень:
Реклама

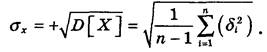 (5) (5)
Для характеристики розсіювання результатів спостережень найчастіше використовується математичне сподівання та дисперсія, оскільки вони визначають найважливіші ознаки розподілу: положення центру розподілу і степінь розсіювання результатів вимірювань відносно істинного значення вимірюваної величини.
У практиці вимірювань застосовуються різні закони розподілу випадкових похибок: трикутний, трапецієподібний, прямокутний, симетричний, нормальний. Проте найбільше значення має нормальний закон розподілу (закон Гаусса). Головна особливість нормального закону розподілу полягає в тому, що він є граничним
законом, до якого наближаються інші закони розподілу при типових для вимірювання умовах, при п→∞
. Теорією ймовірностей доводиться, що густина ймовірностей суми незалежних малих складових при необмеженому збільшенні їх числа наближається до нормального закону розподілу незалежно від того, які закони розподілу мали ці складові. Якщо врахувати, що випадкова похибка є результатом дії великої кількості випадкових чинників, роль кожного з
яких при точних вимірюваннях невелика, то стає зрозумілим значення нормального закону в теорії вимірювань.
Найчастіше при вивченні випадкових похибок використовується нормальний закон розподілу, диференціальна функція якого описується рівнянням:
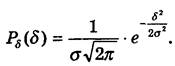 (6) (6)
На рис. 1 подано графік нормального розподілу випадкових похибок Р(
δ
).
Крива розподілу має дзвоноподібну форму і симетрична відносно осі ОР(
δ
).
Максимальна величина ймовірностей дорівнює 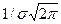 і досягається у точці О.
В міру віддалення від точки О
(вліво чи вправо) ймовірність Р(
δ
)
зменшується і асимптотично наближається до нуля, а ймовірність великих випадкових похибок зростає. і досягається у точці О.
В міру віддалення від точки О
(вліво чи вправо) ймовірність Р(
δ
)
зменшується і асимптотично наближається до нуля, а ймовірність великих випадкових похибок зростає.
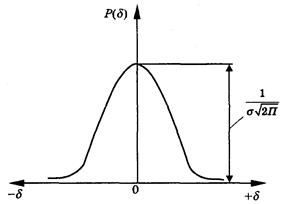
Рис.
1. Крива нормального розподілу випадкових похибок
Для диференційної функції розподілу результатів спостережень це рівняння набуває більш загального вигляду:
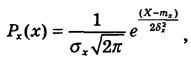 (7) (7)
де тх
— математичне сподівання;
σх
— середнє квадратичне відхилення результатів спостережень.
Для зручності обробки результатів експериментальних вимірювань слід використовувати диференціальну функцію нормованого нормального розподілу [1]:
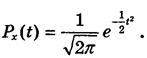 (8) (8)
Значення диференціальної функції нормованого нормального розподілу та інтегральна функція цього розподілу, яка визначається такою залежністю:
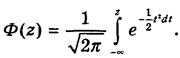 (9) (9)
Значне поширення нормального розподілу похибок у практиці вимірювань пояснюється центральною граничною теоремою теорії ймовірностей, яка є однією з визначних математичних теорем, розроблених видатними математиками: А. де Муавром, П. де Лапласом, К.Ф. Гауссом, П.Л. Чебишевим, A.M. Ляпуновим та ін.
Реклама

Центральна гранична теорема
стверджує, що розподіл випадкових похибок буде близьким до нормального кожного разу, коли результати спостережень формуватимуться під впливом великої кількості незалежних чинників, кожен з яких справляє лише незначний вплив порівняно із сумарним впливом інших.
Диференційні функції при нормальному законі розподілу результатів спостережень мають дзвоноподібну симетричну форму і забезпечують добре унаочнення про розсіювання результатів вимірювань та випадкових похибок.
При зменшенні середнього квадратичного відхилення σ
1
<σ
2
<σ
3
межі розподілу результатів звужуються (рис. 2), а вершина дзвону диференціальної функції піднімається вгору. Ймовірність виникнення малих похибок збільшується, а великих — зменшується, тобто зменшується розсіювання результатів вимірювання відносно дійсної величини і зростає точність вимірювання. Чим точніше виконано вимірювання, тим вище підійматиметься крива розподілу випадкових похибок і зменшуватиметься значення середнього квадратичного відхилення.
Для повного уявлення про точність вимірювань та надійність оцінки випадкових відхилень результатів вимірювань, особливо при обмеженій кількості значень вимірюваної величини, необхідно задатися довірчими межами, довірчим інтервалом та довірчою ймовірністю.
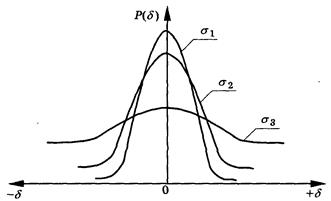
Рис.
2. Криві нормального розподілу випадкових похибок при різних значеннях середнього квадратичного відхилення σ
1
<σ
2
<σ
.
Довірчі межі випадкових похибок
— це верхня та нижня
межі інтервалу, в які похибки потрапляють із заданою ймовірністю Р
3
. Величина Р
3
називається довірчою ймовірністю.
Для визначення довірчих меж похибок необхідно знати густину розподілу похибок та ймовірність потрапляння похибок у довірчі межі. Якщо не ввести обмеження, то задача матиме множину розв'язків.
При відомому середньому геометричному значенні σ
довірчі межі ставляться за нижньою межею -σ
і верхньою межею +σ
. Довірчий інтервал має вигляд
Ір
=(тх
- σ;тх
+σ),
(10)
де тх
— середнє арифметичне значення результатів вимірювань.
Залежно від мети та точності вимірювань довірчі межі задаються -
tp
σ
або mx
-
tp
σ
і +
tp
σ
або mx
+
tp
σ
.
Довірчий інтервал значення вимірюваної величини має вигляд
Ір
= (тх
-
tp
σ
;
mx
+
tp
σ
).
(11)
Значення коефіцієнта tp
визначається шляхом зворотного інтерполювання інтегральної функції Ф(t) для вибраних довірчих ймовірностей при п→∞
наведені у табл. 1.
Таблиця
1
| P
|
0,683 |
0,90 |
0,95 |
0,98 |
0,99 |
0,995 |
0,9973 |
| t
р
|
1,00 |
1,645 |
1,96 |
2,33 |
2,58 |
2,80 |
3,00 |
Так, при нормальному розподілі похибок з ймовірністю 0,68, випадкові похибки δ
знаходяться у довірчих межах ±1σ
; з ймовірністю 0,95 — у межах подвійної середньої квадратичної похибки ±2σ
; з ймовірністю 0,9973 — у межах ±3σ
(рис. 3).
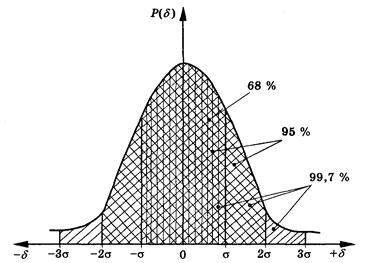
Рис.
3. Довірчі межі та довірчі ймовірності
при нормальному законі розподілу
Для звичайних технічних вимірювань, коли не вимагається високий ступінь надійності та точності, довірча ймовірність береться у межах 0,9—0,95.
Виходячи з нормального закону розподілу, можна розраховувати ймовірність виникнення випадкових похибок з різними значеннями.
Припустимо, що δ
= кσ
,
і визначимо ймовірності Р
їх виявлення для таких значень к:
0,5; 1; 2; 3; 4; 5; 5...
За даними табл. 2, загальна сума результатів спостережень з випадковими похибками до δ
≤
3σ
дорівнює 99,73 %. Звідси виникає правило
3σ
,
за яким при нормальному розподілі результати спостережень, випадкові похибки яких більші або рівні σ ≤
3σ
, можна виключити з ряду результатів, оскільки ймовірність їх появи дуже мала.
Таблиця
2
| к
|
0,5 |
1 |
2 |
3 |
4 |
5 |
| Р
|
0,635 |
0,317 |
0,045 |
0,0027 |
0,0001 |
0,000001 |
| % |
63,5 |
31,7 |
4,5 |
≈0,03 |
0,0001 |
0,00001 |
Список використаної літератури
В.Д.Цюцюра, С.В.Цюцюра. Метрологія
та основи
вимірювань
. Навч. посібн., К., "Знання -Прес", 2003
|