Національний Університет Біоресурсів і Природокористування
Кафедра економічної кібернетики
Курсова робота:
«Програмне генерування РВП(0; 1)»
Виконав
Студент 4-го курсу 3-ї групи
Лєвошко Д. М.
Київ - 2009
Зміст
Вступ
1. Способи генерування рівномірної випадкової послідовності
1.1 Табличний спосіб
1.2 Фізичне генерування
1.3 Програмний спосіб
2. Моделювання випадкових величин
3. Програмне генерація РВП(0; 1)
3.1 Генератори випадкових чисел
3.2 Визначення якості генераторів
3.3 Використання декількох генераторів
Висновок
Список використаної літератури
Вступ
Алгоритмічне (імітаційне) моделювання — це числовий метод дослідження систем і процесів за допомогою моделюючого алгоритму.
Кожного разу, коли на хід модельованого процесу впливає випадковий чинник, його вплив імітується за допомогою спеціально організованого розіграшу (жеребкування). При побудові стохастичних імітаційних моделей ці числа дають змогу генерувати випадкові події або випадкові величини з довільним розподілом.
Послідовності випадкових чисел використовуються в програмуванні в найрізноманітніших випадках, починаючи з моделювання (це найбільш часте вживання) і кінчаючи іграми і іншим розважальним програмним забезпеченням. Турбо Паськаль містить вбудовану функцію, звану Random, яка генерує випадкові числа. Random - це чудовий генератор випадкових чисел, але для деяких вживань вам може потрібно два або більш різних генераторів для забезпечення різних наборів випадкових чисел для різних завдань. Тому в даній курсовій роботі Random буде порівняний з двома іншими генераторами Ran1 і Ran2, та створено генератор, що поєднує роботу трьох генераторів.
Отже метою даної курсової роботи є дослідити методи програмного генерування рівномірно розподіленої випадкової послідовності на проміжку (0; 1). Та проаналізувати роботу деяких вже існуючих програмних генераторів РВП порівнявши їх з створеними генераторами Ran1 і Ran2.
Завдання курсової роботи:
- ознайомитися із способами генерування РВП(0; 1);
- вивчити програмні способі генерування випадкової послідовності;
- розглянути моделювання випадкових величин за допомогою чисел РВП(0; 1);
- ознайомитися з принципом роботі деяких генераторів РВП, проаналізувати якість їх роботи, та створити генератор, що поєднує роботу кількох генераторів тим самим генеруючи більш якісну послідовність.
Реклама

1. Способи генерування рівномірної випадкової послідовності
1.1 Табличний спосіб
Основна проблема в методі Монте-Карло полягає в тому, щоб дістати рівномірну випадкову послідовність чисел РВП, розподілених на відрізку [0, 1]. При побудові стохастичних імітаційних моделей ці числа дають змогу генерувати випадкові події або випадкові величини з довільним розподілом. У разі, коли для програмної реалізації використовуються мови моделювання (GPSS,
симула тощо), що забезпечені вмонтованими генераторами випадкових послідовностей чисел, програмістові немає потреби розробляти програми утворення таких чисел. Крім того, бібліотеки більшості ЕОМ включають спеціальні стандартні підпрограми, котрі можна використати з відповідною метою.
Проте в організаціях, які ще не мають достатнього досвіду створення імітаційних моделей, програмісти часто стикаються з тим, що потрібні їм стандартні підпрограми або взагалі не включені до бібліотеки стандартних підпрограм, або містять численні помилки. Тому виникає необхідність створювати програми породження РВП [0, 1].
Існують три способи дістати рівномірну випадкову послідовність чисел, розподілених на відрізку [0, 1]: табличний, програмний і фізичне генерування.
Фізичний пристрій чи програма на ЕОМ породження РВП [0, 1] називається генератором (датчиком)
випадкових чисел.
Табличний спосіб одержання РВП [0,1]
полягає ось у чому. Існують розроблені з допомогою фізичних або програмних датчиків спеціальні таблиці випадкових цифр. У процесі машинної імітації використовуються здебільшого випадкові числа у загальноприйнятій десятковій системі числення. Тому для створення випадкового числа у вигляді десяткового дробу із заданою кількістю значущих цифр після коми достатньо із будь-якого місця таблиці вибрати підряд потрібну кількість випадкових цифр. У табл. Д.1 наведено 2200 випадкових цифр, або 440 п’ятиёрозрядних випадкових чисел. Почавши, наприклад, з першого випадкового числа, сформуємо серію трирозрядниих РВП [0, 1]: 0,104; 0,802; 0,236; 0,824; 0,130 і т.д.
Зауважимо, що табличний метод у користуванні має як переваги, так і недоліки.
Переваги табличного методу:
1) числа можна діставати з надвисокою швидкістю, якщо таблицю записано в оперативну пам’ять;
2) можна повторювати спроби, що дуже важливо в разі проведення особливо відповідальних експериментів;
Реклама

3) забезпечується одноразова перевірка якості випадкових чисел.
Недоліки табличного методу:
1) таблиця займає багато місця в оперативній пам’яті;
2) запас чисел обмежений;
3) необхідна зовнішня пам’ять.
Тепер розроблено чимало таблиць випадкових цифр. У таблицях, що належать до ГОСТ 11.003-73 «Прикладна статистика. Рівномірно розподілені випадкові числа», наведено 8192 випадкові десяткові цифри. У світі відомі нині такі таблиці зі значно більшою кількістю цифр. Наприклад, фірма РЕНД (США) з допомогою спеціальної електронної апаратури побудувала таблицю, що містить близько мільйона цифр. Ця таблиця записана на магнітну стрічку, що дає змогу вводити цифри в пам’ять швидкодіючої ЕОМ.
Проте табличний метод породження РВП [0, 1] з огляду на повільний увід табличних даних у пам’ять ЕОМ і необхідність використовувати значний обсяг пам’яті, щоб зберігати їх, для машинної імітації вважається неефективним і застосовується здебільшого для ручних розрахунків. У дослідженнях на ЕОМ він застосовується нечасто, насамперед для налагодження програм або дублювання особливо важливих дослідів.
1.2 Фізичне генерування
До появи ЕОМ як генератори випадкових чисел використовувалися різні механічні пристрої — колесо рулетки, спеціальні гральні кості та пристрої, які перемішували фішки з номерами, що витягувалися вручну по одній. Деякі з таких засобів дають цілком задовільні результати в разі невеликої кількості фішок або чисел.
Останнім часом фізичне генерування РВП [0, 1] базується на використанні формули згідно з якою при генеруванні наступного m
-розрядного випадкового двійкового числа необхідно дістати m
реалізацій випадкової величини Z
, що набуває значення 0 або 1 з однаковою ймовірністю 0,5.
Реалізації 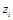 випадкової величини Z
можна дістати, скориставшись такими фізичними явищами: випадкової величини Z
можна дістати, скориставшись такими фізичними явищами:
радіоактивне випромінювання;
власні шуми електронних ламп.
Радіоактивне випромінювання
. Сутність методу, що грунтується на радіоактивному випромінюванні, полягає ось у чому.
1. Вибирається джерело радіоактивного випромінювання з інтенсивністю l.
2. Залежно від значення l вибирається відрізок часу Dt.
3. За допомогою лічильника визначається кількість частинок, що їх випромінює джерело за час Dt.
4. Застосовується схема:
1) якщо кількість частинок парна, то 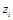 = 0; = 0;
2) якщо кількість частинок непарна, то 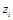 = 1. = 1.
Примітка.
Лічильник частинок працює у двійковій системі числення, тому значення 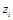 — число молодшого розряду. — число молодшого розряду.
Щоб дістати m
-розрядне випадкове двійкове число, достатньо m
разів звернутися до лічильника радіоактивних частинок.
Власні шуми електронних ламп.
Власними шумами електронних ламп називають явище існування вихідної напруги U
при нульовій вхідній. Посилюючи власні шуми, можна дістати реалізацію стаціонарного випадкового процесу U
(t
)
(рис.1.1).
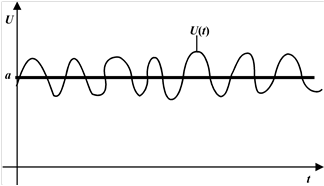
Рис. 1.1.
Графік функції U
(t
) (“власні шуми електронних ламп”)
Попередньо вибирають деякий рівень відсікання a,
для якого в довільний момент часу t
маєвиконуватись умова
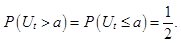
Випадкова величина 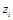 імітується за схемою імітується за схемою
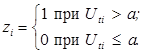 (1) (1)
Щоб дістати m
-розрядне випадкове двійкове число РВП [0, 1], досить провести m
вимірюваньшуму лампи в моменти часу 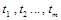 і скористатися перетворенням (1). і скористатися перетворенням (1).
Послідовність квазірівномірних випадкових чисел за допомогою фізичного генерування утворюється спеціальними електронними приставками до ЕОМ — фізичними генераторами випадкових чисел.
Для знаходження наступного випадкового числа РВП [0, 1] при проведенні машинних розрахунків досить один раз звернутися до цього пристрою.
Переваги методу фізичного генерування:
1) швидкість здобування чисел надвисока (проміжок часу звертання до електронного пристрою ЕОМ дуже малий);
2) місця в оперативній пам’яті не займає;
3) запас чисел не обмежений.
Недоліки методу фізичного генерування:
1) не можна повторити спроби (немає змоги фізичний датчик зафіксувати на певному випадковому числі);
2) потрібне періодичне коригування датчиків, оскільки фізичні властивості їх із часом змінюються;
3) необхідно мати спеціальний пристрій до ЕОМ.
Фізичне генерування випадкових чисел використовується здебільшого там, де дуже часто розв’язуються задачі методом Монте-Карло. Проте останніми роками навіть за цих умов надається перевага програмним генераторам випадкових чисел.
1.3 Програмний спосіб
При програмному способі наступне випадкове число 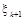 дістають за допомогою рекурентного співвідношення
дістають за допомогою рекурентного співвідношення
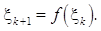
Генеровані так випадкові числа називаються псевдовипадковими
(псевдо
... від грец. y
e
u
d
o
V
— обман, вигадка, помилка; відповідає поняттям «несправжній», «неправильний»), оскільки між двома сусідніми числами існує залежність. Функцію 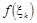 вибирають складною, що включає логічні перетворення, аби згадана залежність практично не впливала на результат. вибирають складною, що включає логічні перетворення, аби згадана залежність практично не впливала на результат.
Один із перших алгоритмів утворення випадкових чисел за допомогою рекурентного співвідношення — метод серединних квадратів,
запропонований 1946 року фон Нейманом і Метрополісом. Сутність його розкриємо спочатку на прикладі, а далі розглянемо загальний випадок.
Приклад.
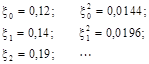
Загальний випадок.
Нехай 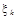 — m
-розрядне двійкове число (0 < — m
-розрядне двійкове число (0 < 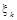 < 1), причому < 1), причому 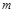 — парне. Загальний вигляд — парне. Загальний вигляд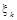 : :
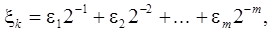
де коефіцієнти 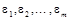 набувають значення 0 або 1. набувають значення 0 або 1.
Квадрат цього числа
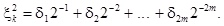
Виокремимо середні розряди цього числа і покладемо
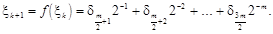
Як показали статистичні випробування, утворювані таким способом випадкові числа мають розподіл, близький до РВП [0, 1]. Очевидний недолік методу серединних квадратів полягає ось у чому. У разі відсутності заміни нульового значення випадкового числа, котре може з’явитися в результаті наступної спроби, якимось іншим, усі наступні числа послідовності будуть нулями.
Можливе циклічне повторення й інших цифр. Нехай, наприклад, потрібно дістати серію випадкових чотирицифрових десяткових чисел 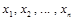 методом серединних квадратів. Розглянемо випадок, коли за початкове число даної серії взято 4500: методом серединних квадратів. Розглянемо випадок, коли за початкове число даної серії взято 4500:
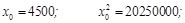
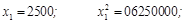
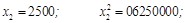
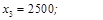 і т.д. і т.д.
Недоліки методу серединних квадратів обмежують його практичне застосування, хоча раніше до цього методу вдавалися завдяки його простоті.
Загальної теорії побудови псевдовипадкових чисел досі не створено. Вигляд фунції 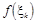 установлюють емпірично. Ця функція містить різні арифметичні та логічні операції. Якість утворюваних чисел перевіряється з допомогою спеціальних тестів. установлюють емпірично. Ця функція містить різні арифметичні та логічні операції. Якість утворюваних чисел перевіряється з допомогою спеціальних тестів.
Тепер майже всі стандартні бібліотечні програми обчислення послідовності рівномірно розподілених випадкових чисел грунтуються на конгруентних методах.
В основу кожного з них покладено поняття конгруентності.
Два цілі числа A
і B
конгруентні (порівнянні) за модулем m
(де m —
ціле число) тоді і тільки тоді, коли існує таке ціле число k,
що A – B = km
, тобто коли різниця A – B
ділиться на m
без остачі (числа A
та B
дають однакові остачі при діленні на абсолютну величину числа m
). Це визначення записується як 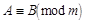 і читається «А
конгруентне В
за модулем m
». Наприклад, 13 º 3 (за модулем 10), 124 º 4 (за модулем 10), 5 º 1 (за модулем 4), 4339 º 39 (за модулем 100 ) і т.д. і читається «А
конгруентне В
за модулем m
». Наприклад, 13 º 3 (за модулем 10), 124 º 4 (за модулем 10), 5 º 1 (за модулем 4), 4339 º 39 (за модулем 100 ) і т.д.
Найвідомішими є такі конгруентні методи: мультиплікативний, мішаний і адитивний
Мультиплікативний конгруентний метод
(метод лишків)
Випадкове число 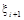 Î РВП [0, 1] дістаємо перетворенням цілих чисел Î РВП [0, 1] дістаємо перетворенням цілих чисел 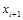 , що визначаються з допомогою рекурентного виразу , що визначаються з допомогою рекурентного виразу
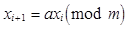 (2)
(2)
де a
і m
— невід’ємні цілі числа.
Згідно з (2) для знаходження наступного випадкового числа 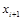 достатньо виконати такі дії: достатньо виконати такі дії:
1) взяти останнє випадкове число 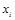 ; ;
2) помножити його на коефіцієнт a
;
3) добуток поділити на модуль m
;
4) остачу від ділення вважати шуканим випадковим числом 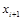 ; це буде одне з цілих чисел 0, 1, 2, 3, . . . , m –
1. ; це буде одне з цілих чисел 0, 1, 2, 3, . . . , m –
1.
Для генерування послідовності випадкових чисел 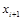 потрібно мати початкове число потрібно мати початкове число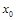 , множник a
і модуль m
. При виборі a
і m
потрібно виявити певну обережність. Коли a
= 1, то , множник a
і модуль m
. При виборі a
і m
потрібно виявити певну обережність. Коли a
= 1, то 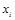 = = 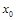 при будь-якому і .
Коли при будь-якому і .
Коли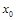 = 0, то = 0, то 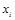 = 0 при довільному і .
Очевидно, що будь-який генератор псевдовипадкових чисел може дати лише скінченну множину цілих випадкових чисел; після чого послідовність повторюватиметься. = 0 при довільному і .
Очевидно, що будь-який генератор псевдовипадкових чисел може дати лише скінченну множину цілих випадкових чисел; після чого послідовність повторюватиметься.
Період (довжина)
послідовності залежить від розрядності ЕОМ та вибраного модуля, а статистичні властивості — від вибору початкового числа та множника. Отже, вибирати 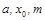 потрібно так, щоб забезпечити максимальний період і мінімальну кореляцію (автокореляцію). потрібно так, щоб забезпечити максимальний період і мінімальну кореляцію (автокореляцію).
Мультиплікативний конгруентний метод пояснимо, розглянувши процес генерування десяткових дробів 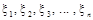 з десятьма знаками після коми. Перепишемо формулу (2), узявши з десятьма знаками після коми. Перепишемо формулу (2), узявши 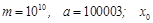 — довільне непарне число, що не ділиться на 5: — довільне непарне число, що не ділиться на 5:
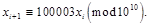
Нехай x
0
= 123456789, тоді
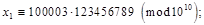
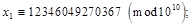
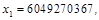
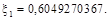
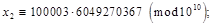
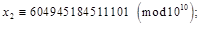
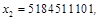
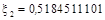 і т.д.
і т.д.
У системах ЕОМ типу IBM широко застосовується метод Хатчинсона. Двійкові числа в цих машинах подаються 32 розрядами: 31 розряд містить значущі цифри, крайній зліва розряд показує знак числа. За модуль беруть 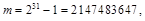 множник множник 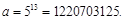 Максимальна довжина послідовності випадкових чисел дорівнює m
– 1; Максимальна довжина послідовності випадкових чисел дорівнює m
– 1; 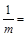 0,46566113 0,46566113 . Запишемо програму цього датчика випадкових чисел мовою фортран. . Запишемо програму цього датчика випадкових чисел мовою фортран.
SUBROUTINE RAND (N
1, N, R
)
1. N =
1220703125
´
N1
2. IF(N)3,
4,
4
3. N =
N +
2147483647 +
1
4. NI =
N
5. R =
N
6. R =
R
´
0.4656613E –
9
7. RETURN
8. END
У програмі 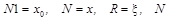 — ціле число між 1 і — ціле число між 1 і 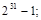 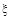 — випадкове число з плаваючою крапкою (оператори 5 і 6 дають результати з плаваючою крапкою). Від’ємне число N
може виникнути після команди 1 у результаті відкидання старших розрядів, тому оператор 3 змінює його значення. — випадкове число з плаваючою крапкою (оператори 5 і 6 дають результати з плаваючою крапкою). Від’ємне число N
може виникнути після команди 1 у результаті відкидання старших розрядів, тому оператор 3 змінює його значення.
Щоб дістати кілька послідовностей випадкових чисел РВП [0, 1], необхідно ввести різні значення початкових чисел: 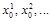 , а щоб повторити початковий відрізок будь-якої послідовності, достатньо всередині основної програми присвоїти відповідній змінній N
1її початкове значення і повторити весь цикл звертань до генератора. , а щоб повторити початковий відрізок будь-якої послідовності, достатньо всередині основної програми присвоїти відповідній змінній N
1її початкове значення і повторити весь цикл звертань до генератора.
Описаний генератор грунтовно перевірявся і показав досить добру якість випадкових чисел.
Мішані конгруентні методи
Побудова мішаних когруентних методів грунтується на залежності
xi
+1
º (axi
+ c
) (mod m
),
де с
— деяка константа.
Адитивний конгруентний метод
В основу цього методу покладено рекурентне співвідношення
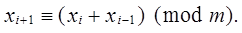
Існують і складніші адитивні методи.
Переваги програмного методу:
1) місця в оперативній пам’яті займає мало (близько десяти машинних команд);
2) можна повторити спроби;
3) забезпечується одноразова перевірка якості випадкових чисел;
4) не потрібні зовнішні пристрої.
Недоліки програмного методу:
1) відносно невелика швидкість утворення випадкових чисел;
2) запас чисел обмежений.
Порівнюючи переваги та недоліки трьох методів генерування РВП [0, 1], доходимо висновку, що програмний спосіб породження псевдовипадкових чисел найприйнятніший для застосування в імітаційному моделюванні.
2.
Моделювання випадкових величин
Алгоритмічне (імітаційне) моделювання — це числовий метод дослідження систем і процесів за допомогою моделюючого алгоритму.
Кожного разу, коли на хід модельованого процесу впливає випадковий чинник, його вплив імітується за допомогою спеціально організованого розіграшу (жеребкування). Таким способом будується випадкова реалізація модельованого явища, яка є одним із результатів дослідження. За результатами окремого досліду, звичайно, не можна робити висновок щодо закономірностей досліджуваного процесу. Але за великої кількості реалізацій середні характеристики (математичне сподівання, мода, медіана), що їх виробляє (генерує) модель, набувають стійких властивостей, котрі посилюються зі зростанням кількості реалізацій (прогонів). Звісно, залишається певний ризик, який характеризується тим, що модель є гомогенною, існує неповнота даних тощо.
Кидання жеребка можна здійснити вручну (вибором із таблиці випадкових чисел), але зручніше це робити за допомогою спеціальних програм, що входять до складу програмного забезпечення комп’ютера. Такі програми називають датчиками чи генераторами випадкових чисел.
У складі трансляторів майже всіх алгоритмічних мов є стандартні процедури (чи функції), котрі генерують випадкові (точніше, псевдовипадкові) числа, що є реалізаціями послідовності випадкових чисел із рівномірним законом розподілу.
Наприклад, у складі транслятора мови Visual Basic — стандартна функція RND, що видає випадкові дійсні числа одинарної точності в інтервалі (0; 1). Звернення до цієї функції може мати вигляд x = RND, де x — можливе значення (реалізація) випадкової величини, яка рівномірно розподілена на інтервалі (0; 1).
Моделювання випадкових подій:
1. Моделювання простої події
Нехай має місце подія А, імовірність настання котрої дорівнює Р(А). Потрібно обрати правило, у багаторазовому використанні якого частота появи події прямувала б до її ймовірності. Оберемо за допомогою датчика випадкових чисел, що мають рівномірний закон розподілу на інтервалі (0;1), деяке число x і визначимо ймовірність того, що x < Р(А). Для випадкового числа x, котре є реалізацією випадкової величини з рівномірним законом розподілу на інтервалі (0; 1), справедливою буде така залежність:
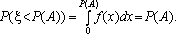
Отже, імовірність потрапляння випадкової величини в інтервал (0; Р(А)) дорівнює величині Р(А). Тому, якщо під час розіграшу число потрапило в цей інтервал, то слід вважати, що відбулася подія А. Протилежна подія (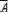 ) відбудеться з імовірністю (1 – Р(А)) у тому разі, коли x ? Р(А). ) відбудеться з імовірністю (1 – Р(А)) у тому разі, коли x ? Р(А).
Процедура моделювання простої події в імітаційній моделі описується алгоритмом, схема якого подана на рис. 2.1 (ДВЧ(x) — датчик випадкових чисел x, що відповідають рівномірному закону розподілу на інтервалі (0; 1).)

Рис. 2.1.
. Моделювання простої події
Оператор 1 звертається до датчика випадкових чисел, який генерує випадкове число x.
Оператор 2 здійснює перевірку умови x < Р(А). Якщо вона виконується, вважається, що відбулася подія А. У протилежному випадку вважається, що відбулася протилежна подія (А).
2. Моделювання повної групи несумісних подій
Нехай наявна повна група випадкових несумісних подій (ПГНП) А1, А2, …, Аk з імовірностями p1, p2, …, pk. При цьому виконується умова:
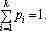
Поділимо інтервал (0; 1) на k відрізків, довжини яких відповідно дорівнюють p1, p2, …, pk.

Рис. 2.2.
. Моделювання повної групи несумісних подій
Якщо випадкова величина x, яка генерується датчиком випадкових чисел, що відповідають рівномірному закону розподілу на інтервалі (0; 1), припадає, наприклад, на відрізок pk–1, то це повинно означати, що відбулася подія Аk–1.
Справді, якщо позначити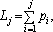 то виявиться справедливим вираз то виявиться справедливим вираз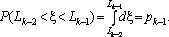
Процедура моделювання повної групи несумісних подій описується алгоритмом, схема якого наведена на рис. 2.2.

Рис. 2.3.
Схема алгоритму моделювання повної групи несумісних подій
Оператор 1 звертається до генератора випадкових чисел, що відповідають рівномірному закону розподілу на інтервалі (0; 1). Оператор 2 перевіряє умову потрапляння випадкової величини x в інтервал (0; L1). Якщо ця умова виконується, то вважається, що відбулася подія А1. Якщо ця умова не виконується, то алгоритм передбачає перевірку умов потрапляння випадкової величини в інші інтервали.
3. Моделювання дискретної випадкової величини
Розподіл дискретної випадкової величини може бути поданий у вигляді таблиці
| Хі |
Х1 |
Х2 |
… |
Хn |
| Pi |
P1 |
P2 |
… |
Pn |
Тут pj — імовірність того, що випадкова величина х набуває значення хj, j = 1, …, n.
Накладається також умова:
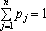
Поділимо інтервал (0; 1) на n відрізків, довжини котрих дорівнюють заданим імовірностям. Якщо випадкове число x, що формується генератором випадкових чисел, котрі відповідають рівномірному закону розподілу на інтервалі (0; 1), потрапляє до інтервалу pk, то випадкова величина х набуває значення хk. Отже, під час моделювання дискретної випадкової величини фактично використовується та сама процедура, що й за моделювання повної групи несумісних подій.
3. Програмне генерація РВП(0; 1)
3.1 Генератори випадкових чисел
Технічно термін "генератор випадкових чисел" - це абсурд; числа само по собі не є випадковими. Наприклад, 100 - це випадкове число? А 25? Що насправді означає цей термін, так це те, що створюється послідовність чисел, що з'являються випадковим чином. Це породжує складніше питання: що таке послідовність випадкових чисел? Єдино правильна відповідь: послідовність випадкових чисел – це послідовність, в якій всі елементи є незв'язаними. Це визначення наводить до такого парадоксу, що будь-яка послідовність може бути як випадковою, так і невипадковою залежно від того, як ця послідовність отримана. Наприклад, наступний рядок чисел 1 2 3 4 5 6 7 8 9 0 був отриманий друкуванням верхнього рядка клавіатури по порядку, таким чином послідовність звичайно не може розглядатися як що згенерувала випадковим чином. Але як бути, якщо ви отримаєте ту ж саму послідовність, виймаючи пронумерований тенісні кулі з боченка. В даному випадку це вже випадковим чином послідовність, що згенерувала. Даний приклад показує, що випадковість послідовності залежить від того, як вона була отримана, а не від неї самої. Пам'ятаєте, що послідовність чисел, що згенерувала комп'ютером, є детермінованою: кожне число, окрім першого, залежить від попередніх чисел. Технічно це означає, що комп'ютером може згенерувати лише квазівипадкова послідовність чисел. Проте, це вистачає для більшості завдань і в даній курсовій роботі такі послідовності для простоти називатимуться випадковими. У загальному випадку вважається добре, коли числа в послідовності випадкових чисел розподілені рівномірно (не плутайте це з нормальним розподілом або колоколообразной кривою). При рівномірному розподілі всі події рівноімовірні так, що діаграма рівномірного розподілу прагне до прямої горизонтальної лінії, а не до кривої.
До широкого поширення комп'ютерів всякий раз, коли необхідні були випадкові числа, вони виходили або киданням гральних кісток, або вийманням пронумерованих куль з ящика. У 1955 році фірма RAND опублікувала таблицю з 1 мільйона випадкових чисел, отриманих за допомогою обчислювальної машини. На ранній стадії розвитку обчислювальної техніки було розроблено багато методів генерації випадкових чисел, але більшість з них не знайшла вживання. Один дуже цікавий метод був розроблений Джоном фон Нейманом; його часто називають середньоквадратичним. У даному методі попереднє випадкове число зводиться в квадрат, а потім з результату виділяються середні цифри. Наприклад, якщо ви створюєте числа з трьох цифр, а попереднє число було 121, то зведення в квадрат дає результат 14641. Виділення трьох середніх цифр дає наступне випадкове число 464. Недоліком даного методу є те, що він має дуже короткий період повторення, званий циклом. З даної причини даний метод сьогодні не використовується.
Зараз найчастіше застосовується метод генерації випадкових чисел, що грунтується на використанні рівняння

при виконанні наступних умов

Відзначимо, що R - це попереднє число, а R - наступне. Даний метод інколи називають лінійним порівняльним методом. Формула така проста, що ви можете подумати, що генерувати випадкові числа просто. Проте, це пастка: наскільки добре працює дана формула, дуже сильно залежить від значення а, з і m. Вибір значень інколи більшою мірою мистецтво, ніж наука. Існують складні правила, які можуть допомогти вам вибрати значення; проте, ми розглянемо лише декілька простих правил і прикладів. Модуль (m) має бути досить великим, оскільки він визначає область випадкових чисел.
Операція узяття по модулю породжує залишок від ділення числа на модуль. Отже, 10 по модулю 4 рівне 2. Таким чином, якщо модуль дорівнює 12, то формулою породжуються числа від 0 до 11, а якщо модуль дорівнює 21425, то породжуються числа від 0 до 21424. Вибір множника а і прирости з є дуже складним завданням. У загальному випадку множник може бути задоволений великим, а приріст - маленьким. Безліч спроб і перевірок необхідна, аби створити хороший генератор. Як перший приклад тут приведений один з найчастіше використовуваних генераторів випадкових чисел. Рівняння, показане в Rаn1 використовується як основа для генератора випадкових чисел у ряді популярних мов.

Дана функція має три головні особливості. По-перше, випадкові числа насправді є цілими, хоча функція повертає дійсні числа. Даний метод працює з цілими числами, але генератори випадкових чисел, як це прийнято, повинні повертати числа в межах від 0 до 1, що означає, що це мають бути числа з плаваючою комою. По-друге, початкове значення задається через глобальну змінну а1. До першого виклику Ran1 змінна а1 має бути встановлена в 1. По-третє, в Ran1 випадкові числа діляться на модуль перш, ніж вони будуть повернені функцією, для того, щоб числа лежали в області від 0 до 1. Якщо ви поцікавитеся значенням глобальної змінної а1 до повернення рядка, то воно повинне лежати в області від 0 до 32748. Отже, коли а1 ділиться на 32749, отримане число буде більше або рівне 0 і менше 1. Багато генераторів випадкових чисел не застосовні, оскільки вони породжують не рівномірний розподіл або мають короткий цикл повторення. Навіть коли ці недоліки не дуже впадають в очі, вони можуть породити змішаний результат, якщо такий генератор використовується знову і знову. Рішення полягає в тому, аби створити різні генератори і застосовувати їх індивідуально або спільно для здобуття якісніших послідовностей випадкових чисел. Вживання декількох генераторів може згладити розподіл послідовності за рахунок зменшення малих змішень окремих генераторів. Далі приведена функція генерування випадкових чисел, звана Ran2, яка породжує хороший розподіл:

Обоє цих генератора випадкових чисел породжують хороші послідовності випадкових чисел. Проте залишаються питання: чи досить "випадковою" є послідовність? Чи хороші дані генератори?
3.2 Визначення якості генераторів
Ви можете застосувати різні тексти для визначення випадковості послідовності чисел. Жоден з тестів не скаже, що послідовність є випадковою, проте, він скаже, якщо вона не є такій. Тести можуть виявити не випадкові послідовності, але, якщо тест не знайшов недоліків, це не означає, що дана послідовність дійсно випадкова. Тести, проте, підвищують упевненість в генераторі випадкових чисел, який породив послідовність. Тепер ми коротко розглянемо декілька простих способів тестування послідовностей. Спершу розглянемо спосіб визначення того, наскільки близький розподіл чисел в послідовності відповідає очікуваному. Наприклад, ви намагаєтеся генерувати послідовність випадкових чисел від 0 до 9. Вірогідність появи кожної цифри дорівнює 1/10. Хай згенерувала наступна последовательность

Якщо ви підрахуєте число появ кожної цифри, то отримаєте результат

Далі вам слід відповісти самому собі на питання, чи досить схожий даний розподіл на очікуване вами. Пам'ятаєте: якщо генератор випадкових чисел хороший, він генерує послідовності випадково. У істинно випадковому варіанті всі послідовності можливі. Дійсно, як якась послідовність може бути не випадковою, якщо будь-яка послідовність можлива? Просто деякі послідовності менш схожі на те, якою має бути випадкова послідовність, чим інші. Ви можете визначити вірогідність того, що дана послідовність є випадковою, використовуючи критерій хі-квадрат. У критерії хі-квадрат очікувана кількість віднімається із спостережуваної кількості зустрічей числа в послідовності, що згенерувала. Цей результат називається V. Ви можете використовувати Vдля знаходження відсотка в таблиці значень хі-квадрат. Цей відсоток визначає вірогідність того, що була породжена випадкова послідовність. Мала таблиця хі-квадрат приведена на рисунку (3.1); ви можете знайти повні таблиці в більшості книг за статистикою

Рис. 3.1.
Мала таблиця хі-квадрат
Вибрані значення хі-квадрат. Для визначення вірогідності того, що послідовність не випадкова, знайдіть рядок в таблиці, показаній на рис. (3.1), з числом елементів послідовності; в даному випадку це 20. Потім шукайте число по рядку, яке більше V. В даному випадку це колонка 1. Це означає, що існує вірогідність 99% того, що приклад з 20 елементів матиме V більше 8,260. З іншого боку це означає, що існує вірогідність лише в 1% того, що послідовність, що перевіряється, згенерувала випадковим чином. Аби пройти через критерій хі-квадрат, вірогідність V должна знизитися до рівня від 25% до 75%. Проте ви можете протиставити цьому виводу питання: Оскільки всі послідовності можливі, як може дана послідовність мати лише однопроцентний шанс бути законною? Відповідь така: це всього лише вірогідність. Фактично, якщо ви застосовуєте критерій хі-квадрат, вам слід отримати декілька різних послідовностей і усереднений результат, аби уникнути відкидання хорошого генератора випадкових чисел. Будь-яка одинична послідовність може бути знехтувана, але ряд різних послідовностей після усереднювання повинен давати добрий результат. З іншого боку, послідовність може пройти через критерій хі-квадрат і не бути випадковою. Наприклад, послідовність 1 3 5 7 9 1 3 5 7 9 пройдет критерій хі-квадрат, але вона виглядає не дуже випадковою. В даному випадку згенерував пробіг по діапазону значень. Пробіг - це просто зростаюча або убуваючи послідовність чисел з довільним інтервалом. В даному випадку кожна група з п'яти цифр є зростаючою послідовністю і як така не може вважатися випадковою послідовністю.
Іншою характеристикою, належній оцінці, є довжина періоду: тобто, як багато чисел може згенерувати до початку повторення послідовності. Всі машинні генератори випадкових чисел завжди генерували послідовність, що повторюється. Чим довше період, тим краще генератор. Навіть якщо частота чисел усередині періоду розподілена рівномірно, числа не утворюють випадкову серію, оскільки дійсно випадкова серія не може досить повторюватися. У загальному випадку період в декілька тисяч чисел задовольняє більшості вживань.
Різні інші тести можуть бути застосовані для визначення якості генератора випадкових чисел. Напевно, можна написати більше програм для перевірки генераторів випадкових чисел, чим створити самих генераторів. Розглянемо ще один тест, який дозволить вам перевірити генератор випадкових чисел "візуально", використовуючи діаграму для демонстрації характеристик послідовності, що згенерувала. У ідеалі діаграма повинна грунтуватися на частоті кожного числа. Проте оскільки генератор може породжувати тисячі різних чисел, це не здійснимо. Замість цього створюватимуться діаграми, згруповані до десяти цифрам. Наприклад, оскільки породжувані числа лежать в області від 0 до 1, число 0.9365783 буде включено в групу 9, а число 0.34523445 буде включено в групу 3. Це означає, що діаграма виведення випадкових чисел має 10 ліній, кожна з яких представляє число попадань в групу. Програма також виводить середнє значення послідовності, яке може бути використане для виявлення змішення. Як і всі інші програми даної курсової роботи, наступна програма виконується лише на персональному комп'ютері IBM РС, який має адаптер кольорового графічного дисплея. Розроблені раніше функції Ran1 і Ran2, а також вбудована функція Турбо Паськаля Random, продемонстровані поруч для порівняння.


У даній програмі кожна функція генерує 1000 чисел і на основі цього створюються таблиці частот. Процедура Display малює всі три матриці частот на екрані після генерації кожного випадкового числа так, що ви можете спостерігати зростання частот. На рис.(3.2) показано виведення кожного генератора випадкових чисел після генерації 1000 чисел. Середні значення дорівнюють 0,489932 в Ran1, 0,4858311 y Ran2 і 0,494014 в Random. Це прийнятно.

Рис. 3.2.
Порівняння генераторів випадкових чисел
Для ефективного використання програми ви повинні спостерігати як за формою діаграми, так і за динамікою зростання, аби виявити короткі цикли, що повторюються. Наприклад, Ran2 генерує значно менше чисел в області від 0,9 до 0,999999, чим Random і Ran1. Звичайно даний текст не є всеосяжним, але він допоможе вам зрозуміти спосіб, яким генератор породжує числа, і прискорить процес аналізу генераторів.
3.3
Використання декількох генераторів
Один простий метод, який покращує властивості випадкових послідовностей, що породжуються трьома генераторами, полягає в комбінуванні їх під управлінням однієї головної функції. Дана функція вибирає між двома з них, грунтуючись на результаті третьої. За допомогою цього методу ви можете отримати дуже довгий період і зменшити вплив циклів і зсувів. Функція, звана CombRandom, показана тут, здійснює комбінування виводів генераторів Ran1, Ran2, Random:


Результат Ran2 використовується для того, щоб вирішити, Ran1 або Random видасть значення головної функції CombRandom. При такому методі період головної функції рівний або більше суми періодів Random і Ran1. Таким чином, даний метод робить можливим породження послідовності з дуже довгим періодом. Можна легко змінювати суміш Random і Ran1 зміною константи в операторові if, аби отримати бажаний вами розподіл між цими двома генераторами. Крім того, ви можете додати додаткові генератори і здійснювати вибір між ними для здобуття ще довшого періоду. Далі слідує програма для відображення діаграми CompRandom і її середнього значення. На рис.(3.3) показана фінальна діаграма після генерації 1000 чисел. Середнє значення CombRandom равно 0,493361.
Вивід, отриманий комбінуванням трьох генераторів випадкових чисел.

Рис. (3.3)
Фінальне відображення функції CombRandom
Висновок
Послідовність випадкових чисел – це послідовність, в якій всі елементи є незв'язаними.
Існують три способи дістати рівномірну випадкову послідовність чисел, розподілених на відрізку [0, 1]: табличний, програмний і фізичне генерування.
Кожен з них має як свої переваги так и недоліки.
Фізичний пристрій чи програма на ЕОМ породження РВП [0, 1] називається генератором (датчиком)
випадкових чисел.
Випадковість елементів послідовності призводить до такого парадоксу, що будь-яка послідовність може бути як випадковою, так і невипадковою залежно від того, як ця послідовність отримана. Згенеровані за допомогоу програмних методів випадкові числа називаються псевдовипадковими
(псевдо
... від грец. y
e
u
d
o
V
— обман, вигадка, помилка; відповідає поняттям «несправжній», «неправильний»), оскільки між двома сусідніми числами існує залежність. Функцію 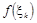 вибирають складною, що включає логічні перетворення, аби згадана залежність практично не впливала на результат. вибирають складною, що включає логічні перетворення, аби згадана залежність практично не впливала на результат.
Для перевірки якості РВП застосувати різні тексти для визначення випадковості послідовності чисел, хоча жоден з тестів не скаже, що послідовність є випадковою, проте, він скаже, якщо вона не є такій. Тести можуть виявити не випадкові послідовності, але, якщо тест не знайшов недоліків, це не означає, що дана послідовність дійсно може вважатися випадковою.
Для покращення властивості випадкових послідовностей, що породжуються генераторами, їх роботу комбінують під управлінням однієї головної функції. Дана функція вибирає між двома з них, грунтуючись на результаті третьої. За допомогою цього методу ви можете отримати дуже довгий період і зменшити вплив циклів і зсувів. В даній курсовій роботі розроблена функція, звана CombRandom, що здійснює комбінування виводів генераторів Ran1, Ran2, та функції Random Турбо Паськаль.
Список використаної літератури
1. Ситник В. Ф., Орленко Н. С. Імітаційне моделювання: Навч. посібник.—К.: КНЕУ, 1998.— 232 с.
2. Сытник В.Ф. Основы машинной имитации производственных и организационно-экономических систем. — К.: УМК ВО, 1988. — 188 с.
3. Советов Б.Я., Яковлев С.А. Моделирование систем. — М.: Высш. шк., 1985. — 271 с.
4. Клейн Дж. Статистические методы в имитационном моделировании. — М.: Статистика, 1978. — Т.1 — 222 с., Т.2 — 335 с.
5. Тарануха Н. А., Гринкруг Л. С. и др. Обучение программированию: язык Pascal. – М.: Солон-пресс, 2009. – 384с.
|