Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального учреждения
«Комсомольский-на-Амуре государственный технический университет»
Факультет Авиа - и кораблестроение
Кафедра Технология самолетостроения
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Динамика полёта»
Расчёт лётно-технических характеристик самолёта Ан-124
Студент группы 3ТС4ка-1 Ю.В.Евдокимова
Руководитель курсовой работы Г.А.Колыхалов
2006
Содержание
Введение
1. Аэродинамический расчет самолета
1.1 Расчет потребных тяг
1.2 Расчет располагаемых тяг
1.3 Определение летно-технических характеристик самолета
1.3.1 Минимальная теоретическая скорость установившегося горизонтального полета Vmin
теор
1.3.2 Наивыгоднейшая скорость горизонтального установившегося полета Vнв
(Мнв
)
1.3.3 Крейсерская скорость горизонтального установившегося полета Vкр
(Мкр
)
1.3.4 Максимальная скорость горизонтального установившегося полета Vmax
(Мmax
)
1.3.5 Вертикальная скорость самолета. Наивыгоднейшая скорость набора высоты. Время подъема
2. Расчет характеристик устойчивости и управляемости самолета
2.1 Определение средней аэродинамической хорды крыла (САХ)
2.2 Определение положения аэродинамического фокуса самолета
2.3 Расчет балансировочной кривой
Список использованных источников
Введение
Динамика полета - это наука о законах движения летательных аппаратов под действием аэродинамических, гравитационных и реактивных сил.
Она представляет собой сочетание в основном трех классических дисциплин: механики твердого тела, механики жидкости и газа и математики.
Среди широкого круга задач динамики полета большое практическое значение имеют задачи, связанные с изучением установившегося прямолинейного движения самолета. Решение их позволяет определить летные характеристики самолета, характеризуемые диапазонами возможных скоростей и высот, скороподъемностью, дальностью, продолжительностью полета и т. д.
При определении летно-технических характеристик самолета пользуются уравнением сил в проекции на оси траекторией системы координат, рассматривая при этом самолет как материальную точку переменной массы. А при расчетах устойчивости и управляемости самолета его рассматривают как твердое тело.
Реклама

Исходными данными для выполнения курсовой работы являются результаты курсовой работы по Аэродинамике «Расчёт аэродинамических характеристик самолёта Ан-124», его геометрические параметры, аэродинамические характеристики и крейсерские поляры.
Курсовая работа содержит расчеты, графики и рисунки, пояснения и обоснования расчета летно-технических характеристик, характеристик продольной устойчивости и управляемости самолета.
1. Аэродинамический расчет самолета
В задачу аэродинамического расчета входит определение, в зависимости от действующих на самолет внешних сил, кинематических параметров установившегося движения центра масс самолета, т.е. его летно-технических характеристик (ЛТХ). К ЛТХ относится максимальная скорость горизонтального установившегося полета на разных высотах, предельно возможная высота горизонтального полета, время подъема самолета на различные высоты (если движение при подъеме принимать как установившееся), дальность полета самолета и т.д.
Рассмотрим уравнения движения прямолинейного установившегося полета при наборе высоты без крена искольжения (вертикальная плоскость)
Pcos(α + φ) = X + mgsinθ ;
Y + Psin (α + φ) = mgsin θ, (1.1)
где α- угол между продольной осью Ох самолета и проекцией скорости V на плоскость симметрии самолета;
φ - угол между силой тяги двигателя Р и средней хордой крыла;
θ - угол наклона траектории образован направлением скорости V и местной горизонтальной плоскостью.
Так как в условиях решаемой задачи угол наклона траектории невелик (θ < 20˚), а угол (α + φ) относительно мал, то можно принять, что
P · cos (α + φ) = Р, P · sin (α + φ) = 0, cos θ = 1.
В этом случае уравнения движения примут вид
Р = X + m · g · sin · θ; Y = m ·g. (1.2)
Скорость или число M полета из второго уравнения
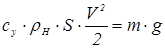 или или 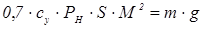 ; (1.3) ; (1.3)
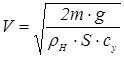 ; ; 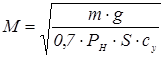 , ,
где ρН
- атмосферное давление на высоте Н; Н = 11000 м.
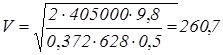 м/с ; м/с ; 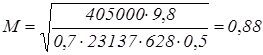 , ,
Как видно, скорость полета, потребная при заданном значении су
, в первом приближении (пренебрегаем составляющей силы тяги P · sin (α + φ)) не зависит от тяги двигателя, а значит, зависит только от значения су
. Необходимое условие установившегося полета - равновесие моментов сил, действующих на самолет,- выполняется летчиком путем соответствующего отклонения руля высоты.
Из первого уравнения системы (1.2), имеем sinθ = (P-X)/m·g , где аэродинамическое сопротивление X принимая равным потребной тяге Рn
, получим
Реклама

sinθ = (Р-Рn
) /m·g = Δρ/m·g(1.4)
Из (1.4) следует, что для того, чтобы выполнить полет по траектории, летчик должен посредством рычага управления двигателем обеспечить необходимую (располагаемую) силу тяги Р.
Таким образом, в первом приближении скорость полета зависит от значения су
, а наклон траектории к горизонту - от величины силы тяги двигателя Р.
Сила тяги двигателя в общем случае зависит от скорости и высоты полета и от положения дросселя. Обычно эта зависимость (для наглядности) задается графически в виде сетки кривых Р(М,Н) или P(V,H) для различных положений дросселя или аналитически.
В основе всех методов аэродинамического расчета лежит сопоставление значения какого-либо параметра, потребного для осуществления выбранного режима полета, со значением этого же параметра, которое обеспечивает двигатель, т.е. располагаемой величиной параметра. Очевидно, равенство потребной и располагаемой величин выбранного параметра является условием установившегося движения. В качестве параметра можно выбрать, например, силу тяги или мощность, развиваемую двигателем, расход топлива и др.
Метод аэродинамического расчета, основанный на сравнении величин потребной и располагаемой тяг (метод тяг), построенный Н.Е.Жуковским, - основной метод аэродинамического расчета.
В методе тяг условием установившегося полета является равенство потребной и располагаемой сил тяги.
Таблица 1 – Исходные данные на самолёт Ан-124
| Наименование параметров |
Обозначение, размерность |
Числовое значение |
Страна
Экипаж
Число мест пассажиров
|
nж
nпас
|
СССР
6
-
|
Размах крыла
Площадь крыла
Стреловидность крыла
Относительная толщина крыла: корн. / концев.
Диаметр фюзеляжа
|
l, м
S, м2
χ0,25
, град
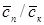
Dф
, м
|
73,3
628
30
0,14 / 0,10
8,7
|
Число и тип двигателей
Взлётная тяга одного двигателя
Взлётная мощность одного двигателя
|
nдв
Ро
, даН
Nо
, кВт
|
4, ТРДД
23450
-
|
Взлетная масса самолёта
Масса пустого снаряженного самолёта
Платная нагрузка
Запас топлива
|
mо
, кг
mп.сн.
, кг
mпл
, кг
mт
, кг
|
405000
25000
150000
230000
|
Дальность полёта
Крейсерская скорость
Крейсерская высота полёта
Скорость при заходе на посадку
Длина взлётной дорожки
Длина посадочной дорожки
|
L, км
Vкрейс
, км/ч
H, км
Vзах
, км/ч
Iвзл
, м
Iпос
, м
|
4500
800
11
200
2400
2400
|
Таблица 2 – Величины стандартной атмосферы
| Геометрическая высота Н, м |
Атмосферное давление Рн
, Н/м |
Температура Тн
, К |
Плотность ρн
, кг/м3
|
Скорость звука ан
, м/с |
| 0 |
103323,0 |
288,15 |
1,2492 |
340,28 |
| 2000 |
81065,0 |
275,14 |
1,0265 |
332,52 |
| 4000 |
62782,0 |
262,13 |
0,8356 |
324,56 |
| 6000 |
48144,0 |
249,13 |
0,6732 |
316,41 |
| 8000 |
36351,0 |
236,14 |
0,5363 |
308,05 |
| 11000 |
23137,0 |
216,66 |
0,3720 |
295,07 |
Для горизонтального установившегося полета без крена и скольжения при условий, что угол α + φ мал, имеем следующую систему уравнений
Р = Х, Y = m·g. (1.5)
Из первого уравнения, являющегося условием постоянства скорости, следует, что в горизонтальном установившемся полете тяга равна лобовому сопротивлению и называется потребной тягой Рn
= X . Второе уравнение системы (1.5) - условие постоянства высоты полета.
Итак, потребная тяга определяется силой лобового сопротивления для установившегося горизонтального полета на высоте Н и можетбыть вычислена по формулам
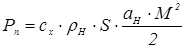 или или
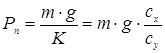 ; (1.6) ; (1.6)
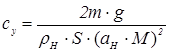 , (1.7) , (1.7)
где сх
- коэффициент аэродинамического сопротивления, берется с графика крейсерских поляр, полученных в РГЗпо аэродинамике для соответствующего числа М и режима полета, определяемого значением су
. Последнее определяется по формуле (1.7) и зависит от полетной массы самолета , скорости М и высоты полета Н через плотность воздуха ρН
и скорость звука аН
.
Все расчеты сводим в таблицу.
Таблица 3 – Расчет потребных тяг
| М
|
0,3
|
0,4
|
0,6
|
0,7
|
0,75
|
0,8
|
0,85
|
0,9
|
0,95
|
| Н = 0 |
су
|
0,97 |
0,546 |
0,24 |
0,17 |
0,15 |
0,14 |
0,12 |
0,1 |
0,097 |
| сх
|
0,036 |
0,012 |
0,017 |
0,019 |
0,023 |
0,04 |
0,063 |
0,09 |
0,139 |
| Рпотр
(Н) |
147303 |
87231 |
281138 |
443594 |
608580 |
1134000 |
2083725 |
3572100 |
5687536 |
| Н = 2000м |
су
|
1,237 |
0,696 |
0,31 |
0,23 |
0,2 |
0,17 |
0,15 |
0,14 |
0,12 |
| сх
|
0,07 |
0,02 |
0,019 |
0,021 |
0,025 |
0,042 |
0,066 |
0,095 |
0,144 |
| Рпотр
(Н) |
224527 |
114052 |
243261 |
362387 |
496125 |
980576 |
1746360 |
2693250 |
4762800 |
| Н = 4000м |
су
|
1,595 |
0,897 |
0,4 |
0,3 |
0,26 |
0,22 |
0,2 |
0,18 |
0,16 |
| сх
|
0,13 |
0,03 |
0,022 |
0,023 |
0,028 |
0,046 |
0,071 |
0,102 |
0,155 |
| Рпотр
(Н) |
323492 |
132595 |
218295 |
304290 |
427431 |
829882 |
1408995 |
2249100 |
3844969 |
| Н = 6000м |
су
|
2,08 |
1,17 |
0,52 |
0,4 |
0,33 |
0,3 |
0,26 |
0,23 |
0,21 |
| сх
|
0,21 |
0,075 |
0,028 |
0,03 |
0,033 |
0,053 |
0,079 |
0,109 |
0,169 |
| Рпотр
(Н) |
400716 |
254423 |
213715 |
297675 |
396900 |
701190 |
1205965 |
1880961 |
3194100 |
| Н = 8000м |
су
|
2,75 |
1,55 |
0,7 |
0,5 |
0,44 |
0,4 |
0,34 |
0,31 |
0,27 |
| сх
|
0,32 |
0,14 |
0,042 |
0,036 |
0,042 |
0,064 |
0,09 |
0,125 |
0,192 |
| Рпотр
(Н) |
461847 |
358491 |
238140 |
285768 |
378859 |
635040 |
1050618 |
1600403 |
2822400 |
| Н = 11000м |
су
|
4,34 |
2,43 |
1,08 |
0,8 |
0,7 |
0,61 |
0,54 |
0,48 |
0,43 |
| сх
|
0,691 |
0,35 |
0,11 |
0,053 |
0,076 |
0,098 |
0,128 |
0,174 |
0 |
| Рпотр
(Н) |
557854 |
571667 |
404250 |
262946 |
430920 |
637643 |
940800 |
1438763 |
0 |
Графики зависимости потребных тяг от числа М приведены в приложении А.
Тяга газотурбинного двигателя изменяется по высоте полета и скорости в зависимости от режима его работы и степени форсирования. Необходимо так же учесть уменьшение тяги за счет потерь скоростного напора в воздухозаборнике двигателя. Эти потери зависят от типа воздухозаборника (лобовой, боковой, длинный, короткий и др.), а на сверхзвуковых скоростях от чисел М и количества скачков уплотнения на входе. С учетом этих замечаний располагаемую тягу двигателей, установленных на самолете и работающих на расчетных высоте и скорости, можно представить так:
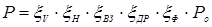 (1.8) (1.8)
Исходные данные для расчета:
· паспортная тяга всех двигателей Р0
= 93800;
· степень двухконтурности двигателей m = 8,0;
· температура в форсажной камере Тф
= 2000 К;
· коэффициент, учитывающий уменьшение тяги двигателей вследствие потерь скоростного напора во входных устройствах ξВ3
= 0,97;
· коэффициент, учитывающий изменение тяги двигателей в зависимости от режима его работы (от степени дросселирования) ξДР
= 0,72.
Расчетные формулы:
Коэффициент, учитывающий изменение тяги по скорости полета М и степени двухконтурности двигателей m:
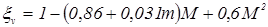 ; (1.9) ; (1.9)
Коэффициент, учитывающий изменение тяги двигателей по высоте полета:
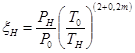 ; (1.10) ; (1.10)
где Р0
, РН
– атмосферное давление у земли и расчетной высоте;
Т0
, ТН
– температура воздуха у земли и на расчетной высоте.
Коэффициент, учитывающий увеличение тяги двигателя вследствие его форсирования:
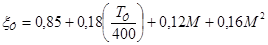 ; (1.11) ; (1.11)
располагаема тяга двигателей:
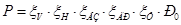 (1.12) (1.12)
Все расчеты сведем в таблицу.
Таблица 4 – Расчет располагаемых тяг
| М
|
0,3
|
0,4
|
0,6
|
0,7
|
0,75
|
0,8
|
0,85
|
0,9
|
0,95
|
| Н,м |
ξН
|
ξV
|
0,722 |
0,653 |
0,551 |
0,518 |
0,507 |
0,498 |
0,492 |
0,489 |
0,489 |
| ξФ
|
1,711 |
1,734 |
1,790 |
1,822 |
1,840 |
1,859 |
1,878 |
1,898 |
1,918 |
| 0 |
1 |
Р,Н |
80751 |
74042 |
64538 |
61810 |
60975 |
60502 |
60402 |
60686 |
61338 |
| 2000м |
0,927 |
Р,Н |
74824 |
68608 |
59801 |
57273 |
56499 |
56061 |
55969 |
56232 |
56836 |
| 4000м |
0,855 |
Р,Н |
69070 |
63360 |
55211 |
52878 |
52166 |
51727 |
51673 |
51914 |
52473 |
| 6000м |
0,787 |
Р,Н |
63523 |
58272 |
50777 |
58630 |
47977 |
47601 |
47524 |
47745 |
48260 |
| 8000м |
0,703 |
Р,Н |
56757 |
52066 |
45369 |
43451 |
42867 |
42532 |
42463 |
42660 |
43120 |
| 11000м |
0,625 |
Р,Н |
50468 |
46297 |
40342 |
38636 |
38117 |
37817 |
37757 |
37933 |
38342 |
Графики располагаемых тяг приведены в приложении А.
Используя построенные зависимости потребных и располагаемых тяг для горизонтального установившегося полета определяем ЛТХ самолета для каждой высоты полета.
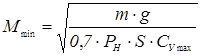 , , 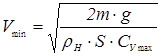 , (1.13) , (1.13)
где СУ
max
= – коэффициент подъемной силы, соответствующий критическому углу атаки.
Таким образом, эта скорость, при которой подъёмная сила ещё может уравновесить силу веса самолета на заданной высоте Нi
. Практически на Vmin
теор
летать нельзя, так как любая ошибка в пилотировании или вертикальный порыв ветра, увеличивающий угол атаки, могут привести к сваливанию из-за резкого уменьшения су
на закритических углах атаки.
Вычисляем для каждой высоты полета Мmin
и Vmin
, полученные значения Мmin
и Vmin
сведем в таблицу.
Таблица 5 – Минимальная скорость полета
| Н,м |
0 |
2000 |
4000 |
6000 |
8000 |
11000 |
| Мmin
|
0,31 |
0,35 |
0,4 |
0,45 |
0,52 |
0,65 |
| Vmin
|
104,9 |
115,7 |
128,3 |
142,9 |
160,1 |
192,2 |
1.3.2 Наивыгоднейшая скорость горизонтального установившегося полета
V
нв
(Мнв
)
Наивыгоднейшая скорость полета реализуется при Кmax
~ Рn
min
= m·g/Кmax
. В свою очередь Кmax
реализуется при полете с су
= су нВ
Наивыгоднейшую скорость полета определяем по графикам кривых потребных тяг (см. приложение А). Данные сводим в таблицу.
Таблица 6 – Наивыгоднейшая скорость полета
| Н,м |
0 |
2000 |
4000 |
6000 |
8000 |
11000 |
| Мнв
|
0,39 |
0,41 |
0,45 |
0,53 |
0,60 |
0,69 |
| Vнв
|
132,9 |
136,3 |
146,1 |
167,7 |
184,8 |
203,6 |
Эта характерная точка получается проведением прямой из начала координат касательной к кривой Рn
. Точка касания соответствует крейсерской скорости установившегося горизонтального полёта Vкр
.
Таблица 7 – Крейсерская скорость полета
| Н,м |
0 |
2000 |
4000 |
6000 |
8000 |
11000 |
| Мкр
|
0,62 |
0,65 |
0,67 |
0,71 |
0,74 |
0,82 |
Точки пересечения кривых потребной и располагаемой тяг будут соответствовать режиму максимальной скорости (см. приложение А).
Таблица 8 – Максимальная скорость полета
| Н,м |
0 |
2000 |
4000 |
6000 |
8000 |
11000 |
| Мmax
|
0,71 |
0,75 |
0,76 |
0,76 |
0,76 |
0,75 |
| Vmax
|
252,6 |
249,4 |
246,7 |
240,5 |
234,2 |
221,3 |
1.3.5 Вертикальная скорость самолета. Наивыгоднейшая скорость набора высоты. Время подъема
Между кривой, потребной для горизонтального полета тяги, и кривой располагаемой тяги находится область возможных режимов установившегося набора высоты (см. приложение А). Вертикальная составляющая скорость Vу
связана со скоростью по траектории V соотношением:
Vу
= (Р – Рn
) V/mg = ΔPV/mg, (1.14)
Для каждой из высот полета построим графики зависимостей Vу
от М. Все вычисления сведем в таблицу 9.
Графики кривых скороподъемности приведены в приложении Б.
Время набора высоты определяем графо-аналитическим путем. Для этого в диапазоне высот 0 < Н < 11000пр
строим график зависимости 1/ Vу
max
= f(H).
Площадь, ограниченная кривой 1/ Vу
max
, прямыми Н = 0, Н = Нпр
и осью Н, определяем время набора высоты Нпр.
Аналогично можно рассчитать и время снижения самолета, например, с крейсерской высоты полета.
Таблица 9 – Барограмма подъема
| Н,м |
0 |
2000 |
4000 |
6000 |
8000 |
11000 |
| Vу
max
(м/с) |
3,65 |
3,20 |
2,80 |
1,83 |
1,20 |
0,70 |
| 1/ Vу
max
|
0,27 |
0,31 |
0,36 |
0,55 |
0,83 |
1,43 |
| Δt (мин) |
0,0 |
9,0 |
11,2 |
15,2 |
23,0 |
37,7 |
| tнаб
(мин) |
0,0 |
9,0 |
20,2 |
35,4 |
58,4 |
96,1 |
Барограмма подъема приведена в приложении В.
2. Расчет характеристик устойчивости и управляемости самолета
Устойчивостью самолета называется его способность без вмешательства летчика сохранять заданный балансировочный режим полета и возвращаться к нему после прекращения действия внешних возмущений. Самолет статически устойчив, если при малом изменении углов атаки, скольжения и крена возникают силы и моменты, направленные на восстановление исходного режима полета. Динамическая устойчивость характеризуется затуханием переходных процессов возмущенного движения.
Управляемостью самолета называется его способность выполнять в ответ на целенаправленные действия летчика любой предусмотренный в процессе полета маневр при допустимых условиях. Балансировочными режимами называются режимы, при которых действующие на самолет силы и моменты уравновешены. Для достижения удовлетворительных показателей динамической устойчивости и управляемости требуется в первую очередь обеспечение статической устойчивости самолета.
САХ крыла является характерным отрезком хорды профиля крыла, от начала и в долях которого отсчитываются координаты центра масс и аэродинамического фокуса самолета. Величина САХ трапециевидного крыла определяется по формуле
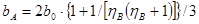 (2.1) (2.1)
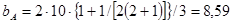 м м
Координаты носка САХ относительно носка центральной хорды вычисляется так
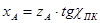 (2.2) (2.2)
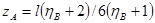 (2.3) (2.3)
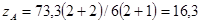 м м
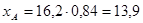 м м
Фокусом самолета называется точка на продольной оси самолета, относительно которой коэффициент продольного момента mz
не зависит от угла атаки. Другими словами, фокус является точкой приложения приращения аэродинамической силы при изменении угла атаки. Измеряется положение фокуса относительно САХ.
Расчет положения фокуса совместно с определением центра тяжести позволяет сделать вывод о продольной статической устойчивости самолета.
При малых значениях угла атаки (коэффициента су
) коэффициент mz
линейно зависит от угла атаки α и су
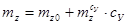 (2.4) (2.4)
где 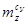 – степень продольной статической устойчивости, – степень продольной статической устойчивости,
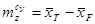 (2.5) (2.5)
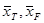 – координаты центра тяжести самолета и фокуса относительно носка САХ в долях bА
; – координаты центра тяжести самолета и фокуса относительно носка САХ в долях bА
; 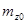 - нулевой момент самолета. - нулевой момент самолета.
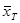 = 2,5; = 2,5; 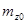 = – 0,02 = – 0,02
Для обеспечения продольной устойчивости необходимо, чтобы фокус самолета находился позади центра тяжести, т.е. 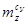 <0. <0.
Значение 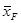 приближенно определяется соотношением приближенно определяется соотношением
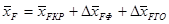 (2.6) (2.6)
где 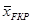 – координата фокуса крыла; – координата фокуса крыла;
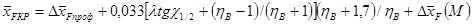 (2.7) (2.7)
Здесь 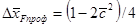 – фокус профиля со средней толщиной крыла; – фокус профиля со средней толщиной крыла;
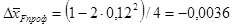 (2.8) (2.8)
 – изменение координаты фокуса от влияния сжимаемости воздуха в диапазоне чисел Маха М*
< М < 1,2 – изменение координаты фокуса от влияния сжимаемости воздуха в диапазоне чисел Маха М*
< М < 1,2
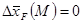 ; ;
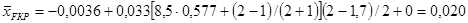
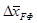 – сдвиг фокуса вследствие влияния фюзеляжа – сдвиг фокуса вследствие влияния фюзеляжа
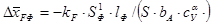 (2.9) (2.9)
Здесь kF
= – 1,6 – коэффициент, находится в зависимости от удлинения фюзеляжа λФ
и отношения хФ
/lФ
(хФ
– координата центра тяжести самолета относительно носка фюзеляжа определяется из расчета, что положение центра тяжести относительно САХ известно; SФ
– площадь проекции фюзеляжа в плане можно приближенно определить по формуле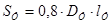 = 473,2; = 473,2; 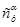 – производная су
по α для соответствующего режима полета, 1/град; – производная су
по α для соответствующего режима полета, 1/град;
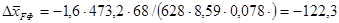
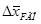 – сдвиг фокуса в долях bA
для самолета классической схемы с хвостом ГО находится по формуле – сдвиг фокуса в долях bA
для самолета классической схемы с хвостом ГО находится по формуле
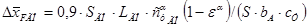 (2.10) (2.10)
Здесь LГО
– плечо ГО, отсчитываемое от фокуса без ГО, определяемого координатой (хF
кр
+ хF
Ф
), до четверти средней хорды ГО; 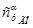 – производная сУ
ГО по углу атаки ; εα
– производная угла скоса потока у ГО по углу атаки крыла достигает значений 0,4 – 0,6 и рассчитывается по эмпирической формуле – производная сУ
ГО по углу атаки ; εα
– производная угла скоса потока у ГО по углу атаки крыла достигает значений 0,4 – 0,6 и рассчитывается по эмпирической формуле
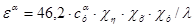 (2.11) (2.11)
Здесь χη
– коэффициент, учитывающий сужение крыла ηВ
, определяется из выражения 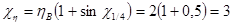 ; χх
, χу
– коэффициенты, учитывающие изменение скоса потока при удалении ГО от крыла, определяются в зависимости от безразмерных (в долях полуразмаха) величин ; χх
, χу
– коэффициенты, учитывающие изменение скоса потока при удалении ГО от крыла, определяются в зависимости от безразмерных (в долях полуразмаха) величин  ; ; 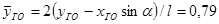 по формулам по формулам
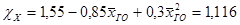 ; ; 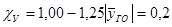
Здесь уГО
– вертикальная координата ГО относительно линии, проходящей через САХ крыла; α – угол атаки крыла, соответствующий крейсерскому режиму полета α = αкр
. = – 3,9
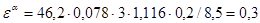
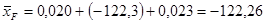
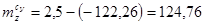
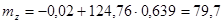
2.3 Расчет балансировочной кривой
Балансировочные кривые относятся к статическим характеристикам устойчивости и управляемости. Для расчета балансировочной кривой угла отклонения руля высоты в функции скорости (или числа М) используется упрощенное соотношение:
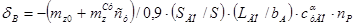 (2.12) (2.12)
где nP
– коэффициент эффективности руля высоты: 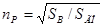 ; SВ
= 6 – площадь руля высоты. ; SВ
= 6 – площадь руля высоты.
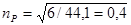
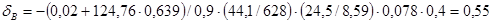
Список использованных источников
1 Мхитарян А.М. Аэродинамика. – М.: Машиностроение, 1976. – 448 с.
2 Шульженко М.Н. Конструкция самолетов. – М.: Машиностроение, 1971. – 416 с.
3 Расчет аэродинамических характеристик самолета: Учебно-методические указания по курсу «Аэродинамика» / Сост. В.В. Фролов. – Комсомольск-на-Амуре: ГОУВПО «КнАГТУ», 2004. – 39 с.
|