Реферат: Преобразования фигур

Малоязовская башкирская гимназия

Геометрия

Реферат

на тему:

“Преобразования фигур”

Выполнил: ученик 10 Б класса

Халиуллин А.Н.

Проверила: Исрафилова Р.Х.

Малояз 2003 год

План:

I . Преобразование.

II . Виды преобразований

1. Гомотетия

2. Подобие

3. Движение

III . Виды движения

1. Симметрия относительно точки

2. Симметрия относительно прямой

3. Симметрия относительно плоскости

4. Поворот

5. Параллельный перенос в пространстве

I . Преобразование - смещение каждой точки данной фигуры каким-нибудь образом, и получение новой фигуры.

II . Виды преобразования в пространстве : подобие, гомотетия, движение.

Подобие

Преобразование фигуры F называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз, т.е. для любых точек X и Y фигуры F и точек X’, Y’ фигуры F’, в которые он переходят, X’Y’ = k * XY.

Свойства подобия: 1. Подобие переводит прямые в прямые, полупрямые – в полупрямые, отрезки – в отрезки.

2. Подобие сохраняет углы между полупрямыми

3. Подобие переводит плоскости в плоскости.

Две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия.

Гомотетия

Гомотетия – простейшее преобразование относительно центра O с коэффициентом гомотетии k. Это преобразование, которое переводит произвольную точку X’ луча OX, такую, что OX’ = k*OX.

Свойство гомотетии: 1. Преобразованием гомотетии переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость (или в себя при k =1).

Доказательство. Действительно, пусть O – центр гомотетии и a - любая плоскость, не проходящая через точку O. Возьмем любую прямую AB в плоскости a. Преобразование гомотетии переводит точку A в точку A’ на луче OA, а точку B в точку B’ на луче OB, причем OA’/OA = k, OB’/OB = k, где k – коэффициент гомотетии. Отсюда следует подобие треугольников AOB и A’OB’. Из подобия треугольников следует равенство соответственных углов OAB и OA’B’, а значит, параллельность прямых AB и A’B’. Возьмем теперь другую прямую AC в плоскости a. Она при гомотетии перейдет а параллельную прямую A’C’. При рассматриваемой гомотетии плоскость aперейдет в плоскость a’, проходящую через прямые A’B’, A’C’. Так как A’B’||AB и A’C’||AC, то по теореме о двух пересекающихся прямых одной плоскости соответственно параллельными с пересекающимися прямыми другой плоскости, плоскости a и a’ параллельны, что и требовалось доказать.

Движение

Движением - преобразование одной фигуры в другую если оно сохраняет расстояние между точками, т.е. переводит любые две точки X и Y одной фигуры в точки X , Y другой фигуры так, что XY = XY

Свойства движения: 1. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения. Это значит, что если A, B, C, лежащие на прямой, переходят в точки A₁ ,B₁ ,C₁ . То эти точки также лежат на прямой; если точка B лежит между точками A и C, то точка B₁ лежит между точками A₁ и C_1.

Доказательство. Пусть точка B прямой AC лежит между точками A и C. Докажем, что точки A₁ ,B₁ ,C₁ лежат на одной прямой.

Если точка A₁ ,B₁ ,C₁ не лежат на прямой, то они являются вершинами треугольника. Поэтому A₁ C₁ < A₁ B₁ + B₁ C₁ . По определению движения отсюда следует, что AC<AB+BC. Однако по свойству измерения отрезков AC=AB+BC.

Мы пришли к противоречию. Значит, точка B₁ лежит на прямой A₁ C₁ . Первое утверждение теоремы доказано.

Покажем теперь, что точка B₁ лежит между A₁ и C₁ . Допустим, что точка A₁ лежит между точками B₁ и C₁ . Тогда A₁ B₁ + A₁ C₁ = B₁ C₁ , и, следовательно, AB+AC=BC. Но это противоречит неравенству AB+BC=AC. Таким образом, точка A₁ не может лежать между точками B₁ и C₁ .

Аналогично доказываем, что точка C₁ не может лежать между точками A₁ и B₁ .

Так как из трех точек A₁ ,B₁ ,C₁ одна лежит между двумя другими, то этой точкой может быть только B₁ . Теорема доказана полностью.

2. При движении прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки

3. При движении сохраняются углы между полупрямыми.

Доказательство. Пусть AB и AC – две полупрямые, исходящие из точки A, не лежащие на оной прямой. При движении эти полупрямые переходят в некоторые полупрямые A₁ B₁ и A₁ C₁ . Так как движение сохраняет расстояние, то треугольники ABC и A₁ B₁ C₁ равны по третьему признаку равенства треугольников. Из равенства треугольников следует равенство углов BAC и B₁ A₁ C₁ , что и требовалось доказать.

4. Движение переводит плоскость в плоскость.

Докажем это свойство. Пусть a - произвольная плоскость. Отметим на ней любые три точки A, B, C, не лежащие на одной прямой. Проведем через них плоскость a'.

Докажем, что при рассматриваемом движении плоскость a переходит в плоскость a'.

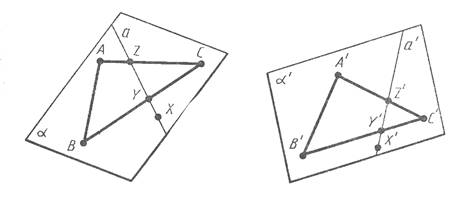Пусть X - произвольная точка плоскости a. проведем через нее какую-нибудь прямую a в плоскости a, пересекающую треугольник ABXC в двух точках Y и Z. Прямая а перейдет при движении в некоторую прямую a'. Точки Y и Z прямой a перейдут в точки Y' и Z', принадлежащие треугольнику A'B'C', а значит, плоскости a'.

Итак прямая a' лежит в плоскости a'. Точка X при движении переходит в точку X' прямой a', а значит, и плоскости a', что и требовалось доказать.

В пространстве, так же как и на плоскости, две фигуры называются равными , если они совмещаются движением.

III . Виды движения: симметрия относительно точки, симметрия относительно прямой, симметрия относительно плоскости, поворот, движение, параллельный перенос.

Симметрия относительно точки

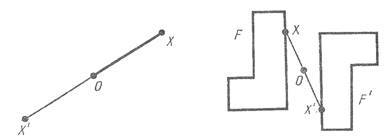Пусть О - фиксированная точка и X - произвольная точка плоскости. Отложим на продолжении отрезка OX за точку O отрезок OX', равный OX. Точка X' называется симметричной точке Xотносительно точки O. Точка, симметричная точке O, есть сама точка O. Очевидно, что точка, симметричная точке X', есть точка X.

Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точке O, называется преобразованием симметрии относительно точки O. При этом фигуры F и F' называются симметричными относительно точки O.

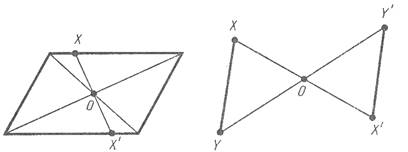Если преобразование симметрии относительно точки O переводит фигуру F в себя, то она называется центрально-симметричной , а точка O называется центром симметрии .

Например, параллелограмм является центрально-симметричной фигурой. Его центром симметрии является точка пересечения диагоналей.

Теорема: Преобразование симметрии относительно точки является движением.

Доказательство. Пусть X и Y - две произвольные точки фигуры F. Преобразование симметрии относительно точки O переводит их в точки X' и Y'. Рассмотрим треугольники XOY и X'OY'. Эти треугольники равны по первому признаку равенства треугольника. У них углы при вершине O равны как вертикальные, а OX=OX', OY=OY' по определению симметрии относительно точки O. Из равенства треугольников следует равенство сторон: XY=X'Y'. А значит, что симметрия относительно точки O есть движение. Теорема доказана.

Симметрия относительно прямой

Пусть g - фиксированная прямая. Возьмем произвольную точку X и опустим перпендикуляр AX н прямую g. На продолжении перпендикуляра за точку A отложим отрезок AX', равный отрезку AX. Точка X' называется симметричной точке Xотносительно прямой g. Если точка X лежит на прямой g, то симметричная ей точка есть сама точка X. Очевидно, что точка, симметричная точке X', есть точка X.

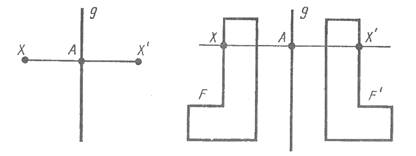Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F' называются симметричными относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.

Например, прямые, проходящие через точку пересечения диагоналей прямоугольника параллельно его сторонам, является осями симметрии прямоугольника. Прямые на которых лежат диагонали ромба, является его осями симметрии.

Теорема: Преобразование симметрии относительно прямой является движением.

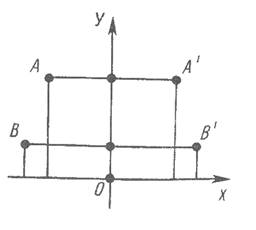Доказательство. Примем данную прямую за ось у декартовой системы координат. Пусть произвольная точка A (x;y) фигуры F переходит в точку A' (x';y') фигуры F'. Из определения симметрии относительно прямой следует, что у точек A и A' равные ординаты, а абсциссы отличаются только знаком: x' = -x.

Возьмем две произвольные точки A (x;y) и B (x;y). Они перейдут в точки A' (-x;y) и B' (-x;y).

Имеем:

AB² =(x₂ -x₁ )² +(y₂ -y₁ )²

A'B'² =(-x₂ + x₁ ) ² +(y₂ -y₁ )²

Отсюда видно, что AB=A'B'. А значит, что преобразование симметрии относительно прямой есть движение. Теорема доказана.

Симметрия относительно плоскости

Пусть a - произвольная фиксированная плоскость. Из точки X фигуры опускаем перпендикуляр XA на плоскость a и на его продолжении за точку Aоткладываем отрезок AX', равный XA. Точка X' называется симметричной точке X относительно плоскости a, а преобразование, которое переводит X в симметричную ей точку X', называется преобразованием симметрии относительно плоскости a.

Если точка X лежит в плоскости a, то считается, что точка X переходит в себя. Если преобразование симметрии относительно плоскости a переводит фигуру в себя, то фигура называется симметричной относительно плоскости a, а плоскость a называется плоскостью симметрии этой фигуры.

Поворот

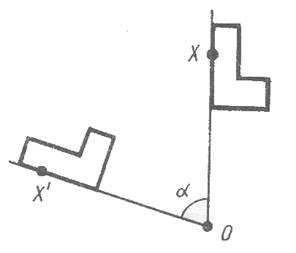Поворот плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из точки, поворачивается на один и тот же угол в одном и том же направлении.
Это значит, что если при поворот около точки O точка переходит в точку X', то лучи OX и OX' образуют один и тот же угол, какова бы ни была точка X. Этот угол называется углом поворота . Преобразование фигур при повороте плоскости также называется поворотом .

Параллельный перенос в пространстве

Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a,b,c одни и те же для всех точек (x; y; z). Параллельный переносов пространстве задается формулами

x'=x+a, y'=y+b, z'=z+c,

выражающими координаты x', y', z' точки, в которую переходит точка (x; y; z) при параллельном переносе. Так же, как и на плоскости, доказываются следующие свойства параллельного переноса:

1. Параллельные перенос есть движение.

2. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3. При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4. Каковы бы ни были точки A и A', существует единственный параллельный перенос, при котором точка A переходит в точку A'.

Новым для параллельного переноса в пространстве является следующее свойство:

5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную её плоскость.

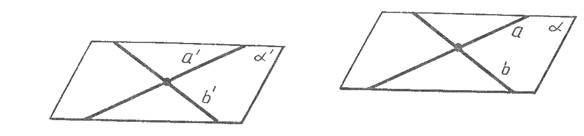
Действительно, пусть a - произвольная плоскость, проведем в этой плоскости две пересекающиеся прямые a и b. При параллельном переносе прямые a и b переходят либо в себя, либо в параллельные прямые a' и b'. Плоскость a переходит в некоторую плоскость a', проходящую через прямые a' и b'. Если плоскость a' не совпадает с a, то по теореме о двух пересекающихся прямых одной плоскости соответственно параллельными с пересекающимися прямыми другой плоскости, она параллельна a, что и требовалось доказать.

Список использованной литературы:

1. Учебник Геометрии 7-11 классы. А.В. Погорелов

2. Учебник Геометрии 10-11 классы. А.Д. Александров.