Рассматривается определение поля, примеры и простейшие свойства полей, определения подполя, простого поля и поля рациональных чисел.
п.1. Определение поля.
Определение. Пусть 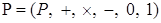 - кольцо с единицей 1. Элемент - кольцо с единицей 1. Элемент 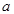 из множества из множества 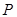 называется обратным в кольце называется обратным в кольце 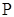 , если , если 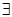 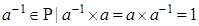 . . 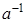 называется обратным к называется обратным к 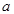 . .
Примеры.
Рассмотрим кольцо целых чисел, то есть кольцо 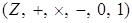 , элемент 2 необратим в этом кольце, так как , элемент 2 необратим в этом кольце, так как 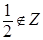 , элемент 5 необратим в кольце целых чисел. , элемент 5 необратим в кольце целых чисел. 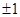 - обратимые элементы в кольце целых чисел - обратимые элементы в кольце целых чисел
Рассмотрим кольцо рациональных чисел 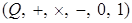 , обратимыми являются все элементы кроме , обратимыми являются все элементы кроме  . .
Рассмотрим кольцо действительных чисел, то есть кольцо 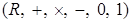 , обратимыми являются все элементы кроме , обратимыми являются все элементы кроме  . .
Определение. Поле – это кольцо 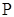 , если: , если:
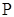 - коммутативное кольцо (операция - коммутативное кольцо (операция 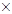 коммутативна) коммутативна)
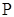 - кольцо с единицей 1, единица - кольцо с единицей 1, единица 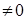 . .
Всякий ненулевой элемент кольца 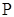 обратим. обратим.
Примеры полей.
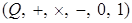 - поле рациональных чисел. - поле рациональных чисел.
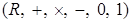 - поле действительных чисел. - поле действительных чисел.
Это поля с бесконечным числом элементов. Рассмотрим поле с конечным числом элементов.
Поле Галуа 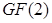 - галуафилд. - галуафилд. 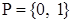 ; ; 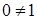 . Определим . Определим
операции сложения и умножения:
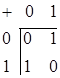 И И 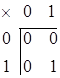 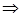 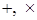 - бинарные операции, - бинарные операции, 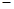 - унарная - унарная
Из этой таблицы видно, что операция 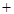 - коммутативна, - коммутативна, 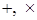 -бинарные операции, -бинарные операции, 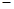 - унарная операция, т.к. - унарная операция, т.к. 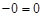 , , 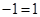 . .
п.2. Простейшие свойства поля.
Пусть 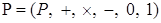 - поле. Обозначение: - поле. Обозначение: 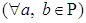 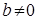 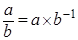 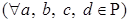 . .
Если 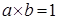 , то , то 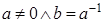 . .
Доказательство. Пусть 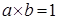 , докажем, что , докажем, что 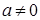 , то есть , то есть 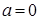 , тогда , тогда 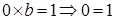 противоречие с аксиомой поля противоречие с аксиомой поля 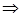 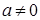 . Если . Если 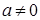 , то по аксиоме полей , то по аксиоме полей 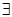 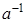 | | 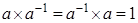 , , 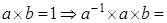 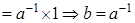 . .
Если 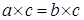 , , 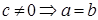 . . 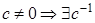 умножим равенство умножим равенство 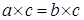 справа на справа на 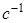 , то есть , то есть 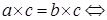 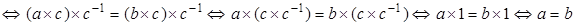 . .
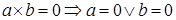 . .
Доказательство. Если 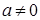 , то , то 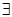 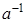 , умножая обе части равенства , умножая обе части равенства 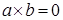 на на 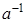 слева, слева, 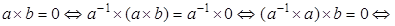 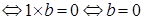 . .
В поле нет делителей 0.
Доказательство. Следует из свойства 3, применяя законы контрапозиции: 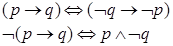 , , 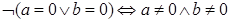 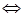 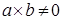 , значит нет делителей нуля. , значит нет делителей нуля.
Каждое поле является областью целостности.
Доказательство. Следует из определения поля и области целостности.
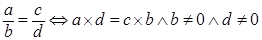 . .
Доказательство.  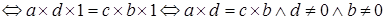 . Умножим обе части равенства справа на . Умножим обе части равенства справа на 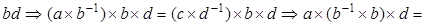 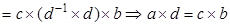 , где , где 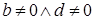 . .
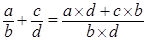 , где , где 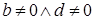 . .
Доказательство. Выпишем правую часть 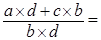 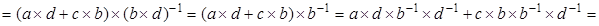 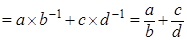 равна левой части. равна левой части.
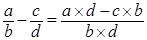 , где , где 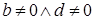 . .
Доказательство. Правая часть 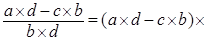 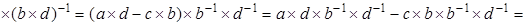 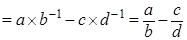 равна левой части. равна левой части.
 , , 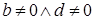 . .
Доказательство. Правая часть 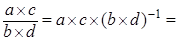 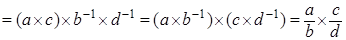 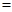 левая часть. левая часть.
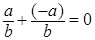 , , 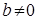 . .
Доказательство. Левая часть 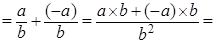 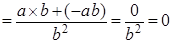 . .
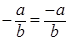 , , 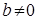 . .
Если 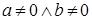 , то , то 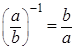 . .
Доказательство. Вычислим произведение 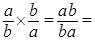 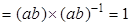 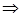 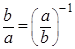 то есть то есть 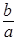 обратный элемент к обратный элемент к 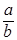 . .
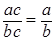 , где , где 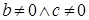 . .
Доказательство. Левая часть равна 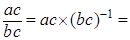 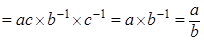 равна правой части. равна правой части.
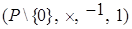 - коммутативная группа, которая называется мультипликативной группой не равных 0 элементов. - коммутативная группа, которая называется мультипликативной группой не равных 0 элементов.
Реклама

Доказательство. Следует из свойств поля: 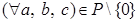
1. 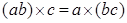 , так как поле. , так как поле.
2. 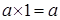
3. 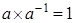
4. 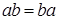 , так как поле , так как поле
Так как поле – это кольцо определённого вида, то под гомоморфизмами полей понимаются гомоморфизмы полей. Аналогично для изоморфизмов.
п.3. Подполе.
Определение. Подполем поля 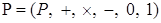 называется подкольцом с единицей поля называется подкольцом с единицей поля 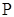 , в котором всякий ненулевой элемент обратим. Всякое подполе является полем. Подполе поля , в котором всякий ненулевой элемент обратим. Всякое подполе является полем. Подполе поля 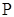 , отличное от , отличное от 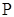 называется собственным полем. называется собственным полем.
Определение. Поле называется простым, если оно не имеет собственных подполей.
Пример. Рассмотрим поле действительных чисел, то есть поле 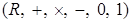 . Для того, чтобы найти подполе надо найти подмножества замкнутые относительно операции . Для того, чтобы найти подполе надо найти подмножества замкнутые относительно операции 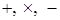 и и 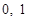 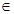 подмножеству. Например, поле рациональных чисел является подполем поля действительных чисел. подмножеству. Например, поле рациональных чисел является подполем поля действительных чисел.
п.4. Поле рациональных чисел.
Алгебраическая система 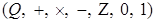 называется системой рациональных чисел, если: называется системой рациональных чисел, если:
Алгебра 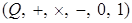 - это поле с единицей 1. - это поле с единицей 1.
Множество 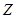 замкнуто относительно операции замкнуто относительно операции 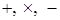 и и 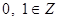
Аксиома минимальности, если 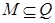 такое, что: такое, что:
а) 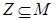
б) 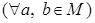 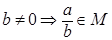 , тогда , тогда 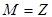 . .
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001
|