Рассматриваются бинарные и n-местные операции, виды бинарных операций, вводятся понятия алгебры, подалгебры, алгебраической системы, приводятся примеры.
п.1. Бинарные и n-местные операции.
Пусть 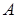 - непустое множество, то есть - непустое множество, то есть 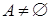 . .
Определение. Бинарной операцией на множестве 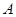 называется отображение прямого произведения называется отображение прямого произведения 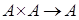 . .
Другими словами: если каждой упорядоченной паре элементов множества 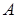 поставлен в соответствие единственный элемент из поставлен в соответствие единственный элемент из 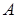 , то говорят, что задана бинарная операция на множестве , то говорят, что задана бинарная операция на множестве 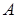 . .
Пример.
Пусть  - произвольные высказывания - произвольные высказывания
 : : 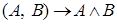 - бинарная операция на множестве высказываний. - бинарная операция на множестве высказываний.
Пусть  - произвольные множества - произвольные множества
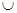 : : 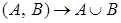 - бинарная операция на множестве множеств. - бинарная операция на множестве множеств.
Пусть 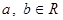
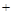 : : 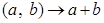 - бинарная операция на множестве действительных чисел. - бинарная операция на множестве действительных чисел.
 : : 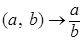 - не является бинарной операцией на множестве - не является бинарной операцией на множестве 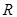 , так как , так как 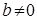 . .
Если 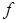 - произвольная бинарная операция на множестве - произвольная бинарная операция на множестве 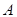 и паре и паре 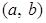 ставится в соответствие элемент ставится в соответствие элемент 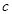 (то есть (то есть 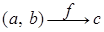 ), то вместо записи ), то вместо записи 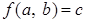 пишут пишут 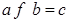 , то есть имеем , то есть имеем 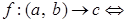 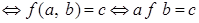 . Элемент . Элемент 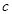 называется композицией элементов называется композицией элементов 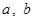 . .
Определение. Пусть 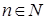 . Отображение . Отображение 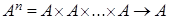 называется называется 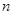 - местной операцией на множестве - местной операцией на множестве 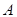 . Число . Число 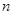 - ранг операции. - ранг операции.
Определение. Нульместной операцией на множестве 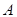 называется выделение (фиксация) какого-нибудь элемента множества называется выделение (фиксация) какого-нибудь элемента множества 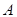 . Число . Число  называется рангом нульместной операции. называется рангом нульместной операции.
Определение. Одноместные операции называются унарными операциями. Другими словами: унарная операция каждому элементу из множества 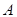 ставит в соответствие элемент из множества ставит в соответствие элемент из множества 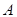 , то есть унарная операция – это отображение множества , то есть унарная операция – это отображение множества 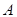 во множество во множество 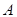 . .
Унарную операцию называют оператором.
Пример.
Пусть 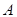 - множество натуральных чисел - множество натуральных чисел
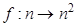 - унарная операция - унарная операция
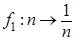 - не является унарной операцией - не является унарной операцией
На множестве высказываний операция 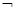 : : 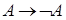 - унарная операция - унарная операция
На множестве подмножеств универсального множества операция дополнения – унарная операция.
Определение. Отображение из множества 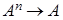 называется частичной называется частичной 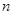 - местной операцией на множестве - местной операцией на множестве 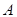 , если область определения отображения не совпадает с , если область определения отображения не совпадает с 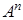 . .
Виды бинарных операций
Пусть 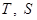 - бинарные операции на множестве - бинарные операции на множестве 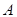 . .
Операция 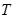 - коммутативна на множестве - коммутативна на множестве 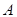 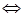 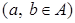 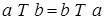 . .
Операция 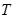 - ассоциативна на множестве - ассоциативна на множестве 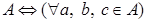 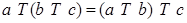 . .
Операция 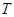 - дистрибутивна слева относительно операции - дистрибутивна слева относительно операции 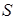 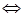 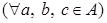 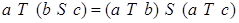 . .
Операция 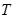 дистрибутивна справа относительно операции дистрибутивна справа относительно операции 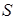 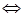 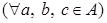 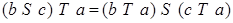 . .
Пример.
Операция 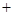 на множестве на множестве 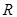 - коммутативна, ассоциативна. - коммутативна, ассоциативна.
Операция 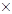 на множестве на множестве 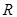 - коммутативна, ассоциативна. - коммутативна, ассоциативна.
Реклама

На множестве множеств операции 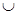 и и 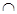 дистрибутивны относительно друг друга. дистрибутивны относительно друг друга.
На множестве функций композиция функций - ассоциативная операция, не является коммутативной операцией.
п.2. Понятие алгебры.
Определение. Алгебра 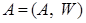 , где , где 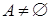 , , 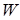 - множество операций на - множество операций на 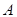 . .
Другими словами: если мы говорим об алгебре, то считаем, что задано множество и заданы операции.
Пример.
Пусть 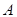 - множество высказываний - множество высказываний
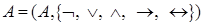 - алгебра логики высказываний. - алгебра логики высказываний.
Пусть 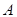 - множество натуральных чисел - множество натуральных чисел
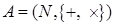 - алгебра натуральных чисел относительно операций - алгебра натуральных чисел относительно операций 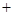 и и 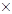 . .
Определение. Алгебра 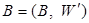 называется подалгеброй алгебры называется подалгеброй алгебры 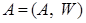 , если множество , если множество 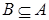 ; ; 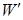 - ограничение операции - ограничение операции 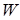 . .
Определение. Алгебраическая система 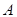 - это упорядоченная тройка - это упорядоченная тройка 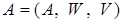 , где , где 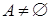 , , 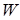 - множество операций на - множество операций на 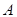 ; ; 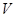 - множество отношений на - множество отношений на 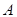 . .
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001
|