Реализовать графический метод решения задач линейного программирования.
1. Теоретические сведения
Наиболее простым и наглядным методом линейного программирования (ЛП) является графический метод. Он применяется для решения задач ЛП с двумя переменными.
Рассмотрим задачу ЛП в стандартной форме записи:
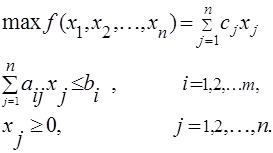
Положим n=2
, т.е. рассмотрим эту задачу на плоскости. Пусть система неравенств совместна (имеет хотя бы одно решение).
Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой ai1
x1
+ ai2
x2
= b
i
, i=1,2,… m
. Условия неотрицательности определяют полуплоскости, соответственно, с граничными прямыми x1=0, x2 =0. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.
Таким образом, геометрически задача линейного программирования (ЗЛП) представляет собой отыскание такой точки многоугольника решений, координаты которой доставляют линейной функции цели максимальное (минимальное) значение, причем допустимыми решениями являются все точки многоугольника решений.
Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости. Определим, какую часть плоскости описывает неравенство 2х1
+3х2
£
12.
Во-первых, построим прямую 2х1
+3х2
=12
. Эта прямая проходит через точки (6, 0) и (0, 4). Для того чтобы определить, какая полуплоскость удовлетворяет неравенству необходимо выбрать любую точку на графике, не принадлежащую прямой, и подставить ее координаты в неравенство. Если неравенство будет выполняться, то данная точка является допустимым решением и полуплоскость, содержащая точку, удовлетворяет неравенству. Удобной для использования при подстановке в неравенство является начало координат. Подставим х1
=х2
=0 в неравенство 2х1
+3х2
£
12
. Получим 2´0+3´0£12. Данное утверждение является верным, следовательно, неравенству 2х1
+3х2
£12 соответствует нижняя полуплоскость, содержащая точку (0.0). Это отражено на графике, изображенном на. 1.
Рис. 1. Неравенству 2х1
+3х2
£12 соответствует нижняя полуплоскость.
Аналогично можно изобразить графически каждое ограничение задачи линейного программирования.
Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений или областью определения. Необходимо помнить, что область допустимых решений удовлетворяет условиям неотрицательности (xj
³0, j=1,…, n). Координаты любой точки, принадлежащей области определения являются допустимым решением задачи.
Для нахождения экстремального значения целевой функции при графическом решении задач ЛП используют вектор–градиент, координаты которого являются частными производными целевой функции, т.е.
 .
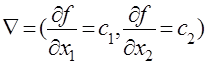Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая 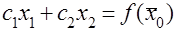 , состоит в том, что при параллельном смещении линии в одну сторону уровень перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине «a».
Меняя значение «a»
, получим семейство параллельных прямых, каждая из которых является линией уровня.
Важное свойство линии уровня линейной функции только возрастает, а при смещении в другую сторону – убывает.
С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.
Графический метод решения ЗЛП состоит из следующих этапов:
1. Строится многоугольная область допустимых решений ЗЛП – ОДР,
2. Строится вектор-градиент ЦФ в какой-нибудь точке Х0
принадлежащей ОДР –
 .
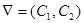3. Линия уровня C1
x1
+C2
x2
= а (а
–постоянная величина) – прямая, перпендикулярная вектору – градиенту 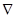 – передвигается в направлении этого вектора в случае максимизации f(x1,
x2
)
до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,
x2
).
4. Для нахождения ее координат достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x1,
x2
),
найденное в получаемой точке, является максимальным.
При минимизации f(x1,
x2
) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то соответствующий максимум или минимум f(x1,
x2
)
не существует.
Если линия уровня параллельна какому-либо функциональному ограничению задачи, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.
Интерфейс программы, реализующей графический метод решения задач линейного программирования:
программирование графический интерфейс линейный
Альтернативным является вариант организации интерфейса, когда основные области: область ввода данных для реализации метода и область построения расположены в одной рабочей области. Предложенный альтернативный вариант является оптимальным с точки зрения минимизации временных интервалов, так как при таком расположении основных областей, пользователь не будет вынужден совершать лишние перемещения мыши между указанными областями и лишние клики по рабочей области, однако, существующий интерфейс является более компактным, позволяет отображать область построения графиков в большем масштабе, поэтому данная реализация интерфейса является наиболее предпочтительной. Таким образом, реорганизация анализируемого интерфейса не целесообразна.
Спроектированный интерфейс является оптимальным, лаконичным и простым в использовании.
3.
Листинг
public class Line {
public float a, b, c;
public Line() {
}
public Line (float a, float b, float c) {
this.a = a;
this.b = b;
this.c = c;
}
Line (Point p1, Point p2) {
this (p1.y – p2.y, p2.x – p1.x, p1.x*p2.y – p2.x*p1.y);
}
Line (float A, float B, Point point) {
this (new Point (point.x + B, point.y – A), point);
}
public boolean isParalellWithLine (Line line) {
float k = a * line.b – line.a * b;
return MathUtil.isEqualWithEplsilon (k, 0);
}
public Point getIntersection (Line line) {
if (isParalellWithLine(line))
return null;
float znam = 1 / (a * line.b – line.a * b);
float x = (b * line.c – line.b * c) * znam;
float y = (c * line.a – line.c * a) * znam;
return new Point (x, y);
}
public double getDistanceToPoint (Point p) {
return (a * p.x + b * p.y + c) / Math.sqrt (a*a + b*b);
}
public float getA() {
return – a;
}
public void setA (float a) {
this.a = – a;
}
public float getB() {
return – b;
}
public void setB (float b) {
this.b = – b;
}
public float getC() {
return c;
}
public void setC (float c) {
this.c = c;
}
public String getView() {
return (a < 0? – a: a) + «* x1 +» + (b < 0? – b: b) + «* x2 <=» + c;
}
}
public class Polygon {
private ArrayList<Point> points = new ArrayList<Point>();
private ArrayList<Boolean> infinity = new ArrayList<Boolean>();
private ArrayList<Float> values = new ArrayList<Float>();
private Rect viewBox;
public Rect getViewBox() {
return viewBox;
}
public ArrayList<Point> getPoints() {
return points;
}
public Point getPoint (int i) {
return points.get(i);
}
public boolean getInfinity (int i) {
return infinity.get(i);
}
public float getValue (int i) {
return values.get(i);
}
private void clear() {
points.clear();
infinity.clear();
values.clear();
viewBox = null;
}
private void addPoint (Point p, boolean inf) {
points.add(p);
values.add (0.0f);
infinity.add(inf);
}
public Polygon() {
}
private Polygon (BoundingBox bb, boolean b) {
Point h = bb.getHigh();
Point l = bb.getLow();
addPoint (new Point(h), b);
addPoint (new Point (l.x, h.y), b);
addPoint (new Point(l), b);
addPoint (new Point (h.x, l.y), b);
}
public Polygon (ArrayList<Line> lines) {
// this.lines = lines;
BoundingBox bb = new BoundingBox();
for (Line li: lines) {
for (Line lj: lines) {
Point p = li.getIntersection(lj);
if (p == null)
continue;
boolean PointIn = true;
for (Line l: lines) {
if (l!= li && l!= lj && l.getDistanceToPoint(p) < 0) {
PointIn = false;
break;
}
}
if(PointIn) {
bb.addPoint(p);
}
}
}
if (! bb.isEmpty()) {
bb.extend (1.0f);
viewBox = new Rect(bb);
}
cutPolygonWithLines (new Polygon (bb, true), lines);
}
private void cutPolygonWithLines (Polygon p, ArrayList<Line> lines) {
points = p.points;
infinity = p.infinity;
values = p.values;
for (Line l: lines) {
cutWithLine(l);
}
}
public List<Point> getBoundingPoints (Rect viewRec) {
return points;
}
private void cutWithLine (Line l) {
Polygon p = new Polygon();
Point crossingPt = null;
for (int i = 0; i < points.size(); i++) {
int next = nextPointIndex(i);
boolean orgIsInside = (l.getDistanceToPoint (points.get(i)) > 0);
boolean destIsInside = (l.getDistanceToPoint (points.get(next)) > 0);
boolean infEdge = infinity.get(i);
if (orgIsInside!= destIsInside) {
crossingPt = l.getIntersection (new Line (points.get(i), points.get(next)));
}
if (orgIsInside && destIsInside) {
p.addPoint (points.get(i), infinity.get(i));
} else if (! orgIsInside && destIsInside) {
if (! MathUtil.isEqualWithEplsilon (points.get(i), crossingPt)) {
p.addPoint (crossingPt, infEdge);
}
} else if (! orgIsInside &&! destIsInside) {
} else {
if (! MathUtil.isEqualWithEplsilon (points.get(i), crossingPt)) {
p.addPoint (points.get(i), infinity.get(i));
}
p.addPoint (crossingPt, false);
}
}
this.points = p.points;
this.infinity = p.infinity;
this.values = p.values;
}
public int nextPointIndex (int i) {
if (i == points.size() – 1) {
return 0;
} else {
return i+1;
}
}
public int prevPointIndex (int i) {
if (i == 0) {
return points.size() – 1;
} else {
return i-1;
}
}
void setTargetLine (float A, float B, boolean max) {
if (points.isEmpty()) {
extremums = null;
}
for (int i = 0; i < points.size(); i++) {
infinity.get(i);
Point p = points.get(i);
float value = p.x * A + p.y * B;
values.set (i, value);
}
LinkedList<Integer> extrList = new LinkedList<Integer>();
extrList.add(0);
for (int i = 1; i < values.size(); i++) {
if(max) {
float extr = values.get (extrList.getLast());
if (MathUtil.isEqualWithEplsilon (extr, values.get(i))) {
if (values.get(i) > extr) {
extrList.add(i);
} else {
extrList.addFirst(i);
}
} else if (extr < values.get(i)) {
extrList.clear();
extrList.add(i);
}
} else {
float extr = values.get (extrList.getLast());
if (MathUtil.isEqualWithEplsilon (extr, values.get(i))) {
if (values.get(i) < extr) {
extrList.add(i);
} else {
extrList.addFirst(i);
}
} else if (extr > values.get(i)) {
extrList.clear();
extrList.add(i);
}
}
}
extremums = extrList;
}
private LinkedList<Integer> extremums;
LinkedList<Integer> getExtremums() {
return extremums;
}
}
Заключение
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно.
Графический метод, несмотря на свою очевидность и применимость лишь в случае малой размерности задачи, позволяет понять качественные особенности задачи линейного программирования, характерные для любой размерности пространства переменных и лежащие в основе численных методов ее решения.
|
