Федеральное агентство по образованию ГОУ ВПО
Филиал Уральского государственного экономического университета в г. Березники
Кафедра математики и естественных наук
Контрольная работа № 1
по дисциплине: "Математика"
Выполнил:
Студентка I курса,
группы ЭКПС-091
Лоскутова Ирина Петровна
Проверил:
к. ф-м. н., профессор
Кобзев Виктор Николаевич
Березники
2009
Задача 1.1 Вычислить определитель 4-го порядка
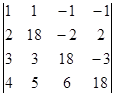
Решение. Так как элемент 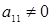 , то 1-ую строку нужно умножить на (– 2) и прибавить ко 2-ой строке; 1-ую строку умножаем на (– 3) и прибавляем к 3-ей строке; 1-ую строку умножаем на (– 4) и прибавляем к 4-ой строке, получаем матрицу: , то 1-ую строку нужно умножить на (– 2) и прибавить ко 2-ой строке; 1-ую строку умножаем на (– 3) и прибавляем к 3-ей строке; 1-ую строку умножаем на (– 4) и прибавляем к 4-ой строке, получаем матрицу:
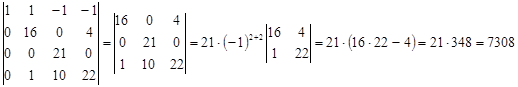
Ответ: 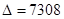 . .
Задача 1.2 Решить систему матричным способом
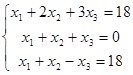
Решение. В матричной форме система имеет вид: 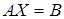 (1), где (1), где
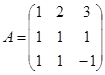 ; ; 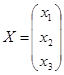 ; ; 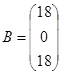 . .
Найдем определитель матрицы А:
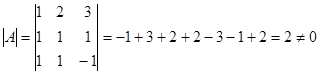 . .
Так как 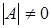 , то матрица А невырожденная и обратная матрица , то матрица А невырожденная и обратная матрица 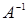 существует. существует.
Найдем матрицу 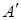 , транспонированную к А: , транспонированную к А:
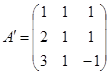 . .
Найдем алгебраические дополнения к матрице 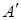 : :
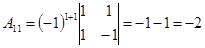 ; ;
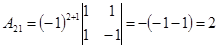 ; ;
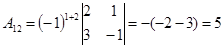 ; ;
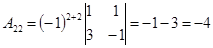 ; ;
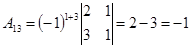 ; ;
 ; ;
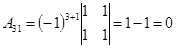 ; ;
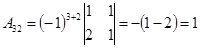
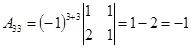 . .
Из алгебраических дополнений элементов матрицы 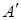 составим присоединенную матрицу составим присоединенную матрицу 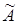 : :
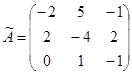 . .
Вычислим обратную матрицу 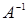 : :
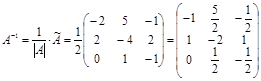 . .
Проверим правильность вычисления обратной матрицы:
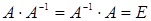
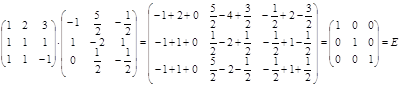
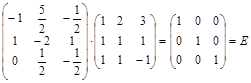
По формуле (1) вычислим:
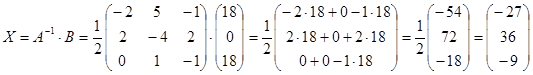
Ответ: 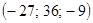
Проверка:
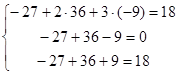
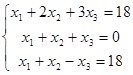 Þ Þ
Þ Система решена верно.
Задача 1.3 Решить систему методом Крамера
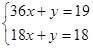
Решение. Найдем определитель системы
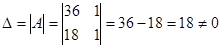
Так как 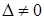 , то по теореме Крамера система имеет единственное решение. , то по теореме Крамера система имеет единственное решение.
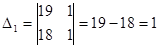 ; ;
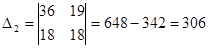 . .
математический матрица невырожденный транспонированный
По формулам Крамера:
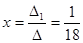 ; ;
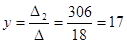
Ответ: решение системы 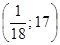 . .
Задача 1.4 Найти общее решение системы, используя метод Гаусса
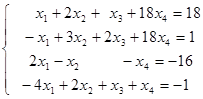
Решение. Расширенная матрица система имеет вид:
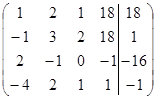
Так как элемент 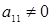 , то 1-ую строку прибавляем ко 2-ой строке, 1-ую строку умножаем на (– 2) и прибавляем к 3-ей строке, 1-ую строку умножаем на 4 и прибавляем к 4ой строке, исключим элемент , то 1-ую строку прибавляем ко 2-ой строке, 1-ую строку умножаем на (– 2) и прибавляем к 3-ей строке, 1-ую строку умножаем на 4 и прибавляем к 4ой строке, исключим элемент 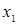 из всех строк, начиная со второй. Результаты запишем в матрицу: из всех строк, начиная со второй. Результаты запишем в матрицу:
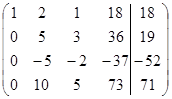
Так как элемент 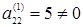 , то, прибавляем 2-ую строку к 3-ей, умножаем 2-ую строку на (– 2) и прибавляем к 4-ой строке, исключим элемент , то, прибавляем 2-ую строку к 3-ей, умножаем 2-ую строку на (– 2) и прибавляем к 4-ой строке, исключим элемент 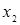 из 3-ей и 4ой строк. Результаты запишем в матрицу: из 3-ей и 4ой строк. Результаты запишем в матрицу:
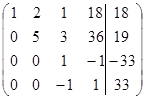
Так как элемент 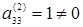 , то, умножаем 3-ю строку на (– 1) и прибавляем к 4-ой строке, исключим элемент , то, умножаем 3-ю строку на (– 1) и прибавляем к 4-ой строке, исключим элемент 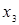 из 4-ой строки. Результаты запишем в матрицу: из 4-ой строки. Результаты запишем в матрицу:
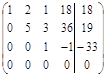
Система уравнений примет вид:
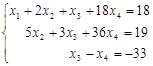 , ,
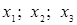 – связные элементы, – связные элементы, 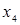 – свободная, – свободная, 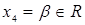
Реклама

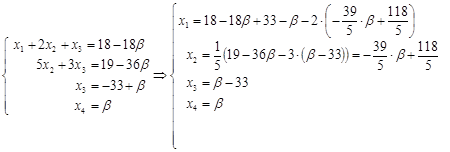
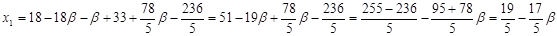
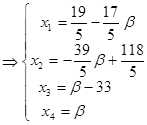
Ответ:
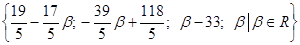
Проверка. Подставим все значения в первое уравнение системы.
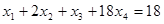
Получим:
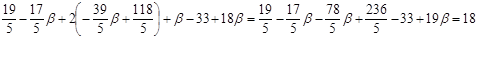
Þ система решена верно.
Задача 1.5
Даны векторы
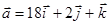 , , 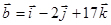 . .
Найти: 1) 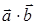 , 2) , 2) 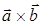 , 3) , 3) 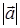 , 4) , 4) 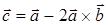 , 5) , 5) 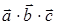 . .
Решение
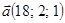 , , 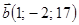 . .
1) 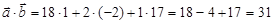 . .
2) 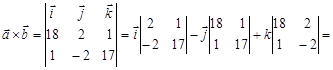
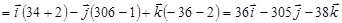 . .
3) 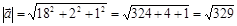 . .
4) 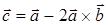
Т.к. 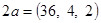 , то , то
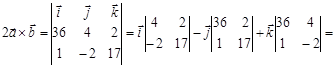
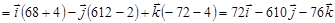
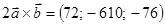
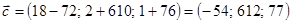
5) 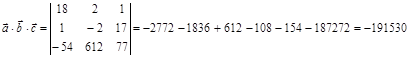 . .
Ответ:
1) 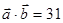 , ,
2) 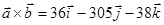 , ,
3) 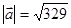 , ,
4) 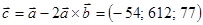 , ,
5) 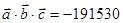 . .
|