РАССЕЯНИЕ ЭЛЕКТРОННОЙ ПЛОТНОСТИ
В МЕТАЛЛАХ И ИОННЫХ КРИСТАЛЛАХ
ПО РЕНТГЕНОГРАФИЧЕСКИМ
ДАННЫМ
Содержание
Введение
Глава 1.
Свойства исследуемых объектов и методы измерения электронной плотности по упругому рассеянию
1.1 Свойства исследуемых объектов
1.2 Методы измерения электронной плотности по упругому рассеянию
Глава 2.
Неупругое рассеяние рентгеновских лучей веществом
2.1 Импульсная аппроксимация
2.2Экспериментальные методы исследования комптоновского рассеяния
2.3 Атомно - рассеивающий фактор и распределение радиальной электронной плотности в литии по комптоновским профилям
Глава 3.
Методика измерений и обработки результатов
3.1. Подготовка образцов и методика измерений
3.2 Методика обработки дифракционных максимумов
3.3 Анализ результатов эксперимента
Заключение
Список используемой литературы
Введение
Экспериментальные исследования распределения электронных плотностей в кристаллах по данным рентгено - и нейтронографических измерений в последние годы значительно расширились. Этому способствует, во-первых, то обстоятельство, что получаемые карты распределения электронных плотностей в кристаллах дают возможность не только качественно судить о характере связи, но и количественно определять ряд физических свойств кристаллов. Метод определения физических свойств кристаллов по рентгенографическим данным распределения электронных плотностей в кристаллах, предположенный и развитый институтом физики твердого тела и полупроводников Академии наук Беларуси, находит широкое признание и используется во многих исследовательских центрах. Во-вторых, успешному развитию исследований природы химической связи рентгено - и нейронографическими методами в последнее время способствует значительное повышение точности абсолютных измерений интенсивности дифракционных рефлексов и определение кривых атомнорассеивающих факторов.
Очевидно, что функция распределения электронной плотности в кристалле – не только важнейшая характеристика особенности химической связи, но и непосредственно количественно связана с волновой функцией, являясь квадратом ее модуля. Поэтому определение распределения электронной плотности различными способами – по данным рассеяния рентгеновских лучей и электронов, методами ядерного гамма-резонанса, по комптоновским профилям и другими методами – важнейшая задача экспериментального исследования химической связи и представляет собой экспериментальную основу квантовой химии.
Реклама

Проблема восстановления волновой функции, достаточно точно описывающей действительное распределение электронов в кристалле и, следовательно, особенности межатомной химической связи, до сих пор не может считаться полностью решенной. Наиболее прямые методы нахождения функции распределения электронной плотности в кристаллах по рассеянию рентгеновских лучей, электронов и нейронов приводят к достаточно надежным результатам лишь для кристаллов, для которых первые бреговские рефлексы лежат при сравнительно малых значениях вектора обратной решетки. Для кристаллов этого типа интенсивности первых рефлексов в значительной мере определяются самой внешней частью электронных орбиталей. Однако к данному типу относится скорее меньшинство, чем большинство кристаллов.
Для восстановления и уточнения волновых функций, характеризующих истинное распределение внешней части электронов, в ряде случаев удобно и целесообразно использование косвенных методов, непосредственно характеризующих не функции распределения внешних электронов, а функции распределения момента количества движения, энергии ионизации, плотности состояния по энергиям.
В первую очередь к числу подобных методов следует отнести изучение комптоновских профилей. Открытый Комптоном эффект, как показал ряд исследований, в особенности работы Вейсса и его сотрудников, - весьма удобный и мощный метод изучения проблем химической связи. Существенными факторами, ограничивающими возможности исследования комптоновских профилей для изучения особенностей межатомной химической связи, являются чрезвычайно малая их интенсивность, сложность исследования элементов с большим порядковым номером, большая поглощающая способность и др.
Использование данных измерений комптоновских профилей позволяет найти функцию распределения плотности моментов и электронной плотности кристаллов во внешних частях орбиталей атомов. Измерения рассеяния рентгеновских лучей, электронов и нейронов дают возможность определять распределение электронной плотности во внешних и в особенности в средних частях электронных оболочек.
Объектами
исследования в настоящей работе являлись литий с ОЦК и
алюминий с ГЦК кубическими решетками, а также бинарное соединение фторид лития со структурой хлорида натрия, предметом
– интегральная интенсивность брегговских рефлексов, структурный множитель, функция атомного рассеяния, карты распределения электронной плотности для каждого объекта исследования при комнатной температуре.
Реклама

Цель исследования –
выяснить характер распределения электронной плотности в металлических и ионных кристаллах. Определить зависимость распределения электронной плотности от типа кристаллической решетки с металлической связью.
В соответствии с намеченной целью были поставлены следующие задачи исследования:
1. Систематизировать опыт исследований распределения электронной плотности и потенциала.
2. Рассмотреть методику определения интегральной интенсивности рефлекса исследуемых образцов.
3. Вычислить значения структурного и атомно-рассеивающего факторов лития, алюминия и фторида лития.
4. На основе экспериментальных данных построить карты распределения электронных плотностей лития, алюминия и фторида лития.
Новизна исследования:
Существующая модель металла, где ионы погружены в электронную «жидкость», не отражает химическую связь атомов друг с другом. В модели ионных кристаллов недостаточно ясно распределение электронной плотности между ионами.
В связи с этим исследование распределения электронной плотности рентгенографическим методом является актуальной проблемой, требующей ее решения.
Объем и структура диссертации:
Работа состоит из введения, литературного обзора, экспериментальной части, заключения, списка литературы и приложения. Работа изложена на 61 странице, включает в себя 32 рисунка, 8 таблиц, список литературы содержит 37 источников.
Положения, выносимые на защиту
:
- Методика и результаты расчета электронной плотности в металлах с различными типами решетки.
- Методика и результаты разделения атомно – рассеивающих факторов разных сортов атомов в бинарном соединении.
- Построение карт электронной плотности и их анализ.
Глава 1. Свойства исследуемых объектов и методы измерения электронной плотности по упругому рассеянию
1.1
Свойства исследуемых объектов
Литий.
При обычной температуре литий кристаллизуется в кубической объемно-центрированной решетке, а
= 3,5098 Å, в элементарной ячейке которой 2 атома с координатами (0,0,0) и (1/2,1/2,1/2). Литий - самый легкий металл; плотность 0,534 г/см3
(20°С); tпл
180,5°С, tкип
. 1317°С. Удельная теплоемкость (при 0-100°С) 3,31·103
Дж/(кг·К), термический коэффициент линейного расширения 5,6·10-5
. Удельное электрическое сопротивление (20°С) 9,29·10-4
Ом·м (9,29 мкОм·см); температурный коэффициент электрического сопротивления (0-100°С) 4,50·10-3
. Металл весьма пластичен и вязок, хорошо обрабатывается прессованием и прокаткой, легко протягивается в проволоку. Твердость по Моосу 0,6 (тверже, чем Na и К), легко режется ножом. Модуль упругости 5 Гн/м2
(500 кгс/мм2
), предел прочности при растяжении 116 Мн/м2
(11,8 кгс/мм2
), относительное удлинение 50-70% . Пары лития окрашивают пламя в карминово-красный цвет. [1]
Литий является модельным образцом, поскольку он имеет всего лишь 3 электрона с электронной конфигурацией 1s
2
2s
1
. Это обстоятельство позволяет достаточно просто найти волновую функцию, описывающую состояние атома.
Литий (Li) - щелочной металл. В компактном состоянии серебристо-белого цвета. Получил название от греческого lithos (камень). Открыт шведским химиком А. Арфведсоном в 1817 г. в минерале петалите (алюмосиликата лития). Металлический литий впервые выделен английским ученым Дэви в 1818 г. электролизом оксида лития. В 1885 г. в значительных количествах металлический литий получен независимо друг от друга Бунзеном (Германия) и Матиссеном (Англия) путем электролиза (электролитом служил хлорид лития). Содержание лития в земной коре 0,0065 % (по массе). В свободном состоянии литий не встречается из-за большой химической активности.
В промышленности металлический литий получают путем электролиза расплавленного хлорида лития или смеси расплавленных хлорида лития и хлорида калия с применением графитированного анода и стального катода. Литий высокой чистоты (99,95%), почти свободный от примесей щелочных и щелочноземельных металлов, получают электролизом насыщенного раствора LiCl в пиридине, разложением соединения NH3
Li в вакууме при 50-60 °С и восстановлением окиси лития алюминием в вакууме (примерно 10-1
Па) при 950-1000°С.
Физические свойства
Атомный номер 3, атомная масса 6,941 а. е. м., атомный объем  м3
/моль. Потенциалы ионизации атомов (эВ): 5,39; 75,61; 122,42. Из щелочных металлов Li обладает наименьшим атомным радиусом - 0,157 нм, а следовательно, наибольшим ионизационным потенциалом = 5,39 эВ, поэтому литий химически менее активен по сравнению с другими щелочными металлами. Ионный радиус Li+
равен 0,068 нм. Благодаря малому атомному радиусу литий обладает наиболее прочной кристаллической решеткой по сравнению с остальными щелочными металлами. Это обусловливает наиболее высокие температуры плавления и кипения лития по сравнению с его аналогами. При нормальной температуре литий имеет ОЦК решетку, период решетки 0,35023 нм, координационное число 8, межатомное расстояние 0,30331 нм. Ниже - 195 °С литий кристаллизуется в г. п. у. решетку с а = 0,3111 им и с = 0,5093 нм. Энергия кристаллической решетки 155,2 мкДж/кмоль. [2] м3
/моль. Потенциалы ионизации атомов (эВ): 5,39; 75,61; 122,42. Из щелочных металлов Li обладает наименьшим атомным радиусом - 0,157 нм, а следовательно, наибольшим ионизационным потенциалом = 5,39 эВ, поэтому литий химически менее активен по сравнению с другими щелочными металлами. Ионный радиус Li+
равен 0,068 нм. Благодаря малому атомному радиусу литий обладает наиболее прочной кристаллической решеткой по сравнению с остальными щелочными металлами. Это обусловливает наиболее высокие температуры плавления и кипения лития по сравнению с его аналогами. При нормальной температуре литий имеет ОЦК решетку, период решетки 0,35023 нм, координационное число 8, межатомное расстояние 0,30331 нм. Ниже - 195 °С литий кристаллизуется в г. п. у. решетку с а = 0,3111 им и с = 0,5093 нм. Энергия кристаллической решетки 155,2 мкДж/кмоль. [2]
Технологические свойства
Литий обладает очень высокой пластичностью и может легко деформироваться при комнатной температуре прессованием, прокаткой и волочением. При этом не происходит упрочнения, так как температура рекристаллизации лития лежит ниже 20 0
С. В холодном состоянии литий легко режется ножом.
Области применения
Важнейшей областью применения лития и его соединений является ядерная энергетика. Дейтерид лития используется в качестве твердого горючего в водородных бомбах, жидкий 7
Li - в качестве теплоносителя в ядерных реакторах. Ряд соединений лития применяют в военной технике, а также как топливо для ракет космических кораблей, управляемых снарядов подводных лодок, сверхскоростной авиации и т. д. Широко применяются соединения лития при получении керамики, эмали, специальных стекол, при сварке алюминиевых и магниевых сплавов, в химической промышленности, в холодильной технике, в радиоэлектронике и т. д. В металлургии литий, его соединения и литий содержащие сплавы используют для раскисления, дегазации и десульфурации расплавов различных металлов и сплавов. Литий используют для повышения прочности и пластичности сплавов, снижения их плотности, повышения коррозионной стойкости. Добавки лития к магнию позволяют получать сверхлегкие сплавы, плотность которых на 15-25 % ниже плотности стандартных магниевых сплавов. Легирование алюминия литием снижает плотность алюминиевых сплавов на 10-12 %. Литий улучшает антифрикционные и механические свойства подшипниковых сплавов, в частности в свинцовокальциевые баббиты вводят для этой цели 0,04 % Li. Литий улучшает литейные свойства чугуна. Некоторые соединения лития в последние годы находят применение в медицине.
Алюминий.
(лат. Aluminium), Al, химический элемент III группы периодической системы Менделеева; атомный номер 13, атомная масса 26,9815, серебристо - белый легкий металл. Состоит из одного стабильного изотопа 27
Al.
Наиболее характерными физическими свойствами алюминия является его малая относительная плотность, равная 2700 кг/м3
а также сравнительно высокие тепло- и электропроводность. При 0°C удельная электропроводность алюминия, т.е. электропроводность алюминиевой проволоки сечением 1 мм и длиной 1 м равна 37,1 Ом.
Температура плавления алюминия невысокая, она равна приблизительно 660o
C. Однако скрытая теплота плавления его очень большая – около 100 кал/ г.
Кристаллическая решетка алюминия представляет собой гранецентрированный куб, имеющий при 20ºC параметр решетки 4,04Å. Элементарная ячейка содержит в себе 4 атома с координатами (0,0,0); (1/2,1/2,0); (1/2,0,1/2) и (0,1/2,1/2). [3]
Историческая справка
Название алюминий происходит от лат. alumen - так еще за 500 лет до н. э. назывались алюминиевые квасцы, которые применялись как протрава при крашении тканей и для дубления кожи. Датский ученый X. К. Эрстед в 1825, действуя амальгамой калия на безводный АlСl3
и затем, отгоняя ртуть, получил относительно чистый алюминий. Первый промышленного способ производства алюминия предложил в 1854 французский химик А. Э. Сент-Клер Девиль: способ заключался в восстановлении двойного хлорида алюминия и натрия Na3
AlCl6
металлическим натрием.
Физические свойства алюминия
Алюминий сочетает весьма ценный комплекс свойств: малую плотность, высокую теплопроводность и электрическую проводимость, высокую пластичность и хорошую коррозионную стойкость. Он легко поддается ковке, штамповке, прокатке, волочению. Алюминий хорошо сваривается газовой, контактной и других видами сварки. Свойства алюминий, как и всех металлов, в значит, степени зависят от его чистоты. Алюминий обладает невысокой прочностью (предел прочности 50-60 Мн/м2
), твердостью (170 Мн/м2
по Бринеллю) и высокой пластичностью (до 50%). Обладая большим сродством к кислороду, алюминий на воздухе покрывается тонкой, но очень прочной пленкой оксида Al2
О3
, защищающей металл от дальнейшего окисления и обусловливающей его высокие антикоррозионные свойства.
Применение алюминия
Сочетание физических, механических и химических свойств алюминия определяет его широкое применение практически во всех областях техники, особенно в виде его сплавов с других металлами. В электротехнике алюминий успешно заменяет медь, особенно в производстве массивных проводников, например, в воздушных линиях, высоковольтных кабелях, шинах распределительных устройств, трансформаторах (электрическая проводимость алюминия достигает 65,5% электрической проводимости меди, и он более чем в три раза легче меди; при поперечном сечении, обеспечивающем одну и ту же проводимость, масса проводов из алюминия вдвое меньше медных). Сверхчистый алюминий употребляют в производстве электрических конденсаторов и выпрямителей, действие которых основано на способности оксидной пленки алюминия пропускать электрический ток только в одном направлении. Обладая относительно низким сечением поглощения нейтронов, алюминий применяется как конструкционный материал в ядерных реакторах.
В алюминиевых резервуарах большой емкости хранят и транспортируют жидкие газы (метан, кислород, водород и т. д.), азотную и уксусную кислоты, чистую воду, перекись водорода и пищевые масла. Алюминий широко применяют в оборудовании и аппаратах пищевой промышленности, для упаковки пищевых продуктов (в виде фольги), для производства разного рода бытовых изделий. Резко возросло потребление алюминий для отделки зданий, архитектурных, транспортных и спортивных сооружений.
Фторид лития
- химическое соединение лития и фтора с формулой LiF. При нормальных условиях - белый порошок или прозрачный бесцветный кристалл, негигроскопичный, почти не растворим в воде. Растворяется в азотной и плавиковой кислоте. Образует ионный кристалл с кубической решеткой.
Фторид лития обладает очень высокой прозрачностью от ультрафиолетовой до инфракрасной области спектра (0,12...6 мкм), поэтому он используется в ультрафиолетовой и инфракрасной оптике. Кроме того, он используется для измерения доз облучения методом термолюминесцентной дозиметрии. Монокристаллы фторида лития используются для изготовления высокоэффективных (КПД 80 %) лазеров на центрах свободной окраски. Проявляет слабые сцинтилляционные свойства. Диэлектрик; характеризуется высоким удельным электрическим сопротивлением вследствие большой ширины запрещенной зоны.
Высокая теплота плавления (1044 кДж/кг) позволяет использовать фторид лития как материал для хранения тепловой энергии. При плавлении увеличивает свой объём на 22%. Жидкий фторид лития вызывает быструю коррозию металлов. Фторид лития применяют для растворения соединений урана и тория непосредственно в реакторах.
LiF применяется как флюс при плавке металлов, сварке магния и алюминия, при электролизе алюминия, для производства специальных оптических стекол, керамических глазурей и кислотостойких эмалей. Получается действием фтористоводородной кислоты на Li2
СО3
или взаимодействием растворимых солей лития с фторидами калия или аммония.
Физические свойства
Бесцветный кристалл, растворим в воде 0,27 г/100 г (18°). В присутствии NH3
и, особенно, NH4
F растворимость в воде падает. Не растворяется в большинстве органических растворителей (в отличие от других галогенидов лития).
1.2 Методы измерения электронной плотности по упругому рассеянию
В настоящей работе рассматривается распределение электронной плотности в металлических и ионных кубических кристаллах. Поэтому для наилучшего понимания результатов эксперимента, необходимо было выяснить принципы химической связи в кристаллах.
Химическая связь между атомами в кристаллах возникает за счёт взаимодействия внешних валентных электронов атомов, тогда как внутренние электронные оболочки практически остаются неизменными. На рис. 1.2.1 показаны типичные кривые потенциальной энергии и(r
)межатомного взаимодействия. Равновесное расстояние r
р
между атомами обычно составляет 0,15-0,40 нм. При сближении атомов на расстояния меньшие, чем равновесное, возникает резкое их отталкивание. Это позволяет в первом приближении приписать атомам для того или иного типа связи определенные "размеры", т. е. некоторые постоянные радиусы, и тем самым перейти от физической модели кристалла к его геометрической модели как системе несжимающихся шариков.
По характеру химической связи кристаллы делятся на четыре основные группы: - ионные кристаллы (напр. NaCl), ковалентные (напр., алмаз, кремний), металлические (металлыи интерметаллические соединения) и молекулярные кристаллы (напр., нафталин).
электронный плотность комптоновский рассеяние

Рис. 1.2.
1Кривые энергии межатомного взаимодействия: I
-для сильной (ионной, ковалентной, металлической) связи, II
-для слабой (ван-дер-ваальсовой) связи.
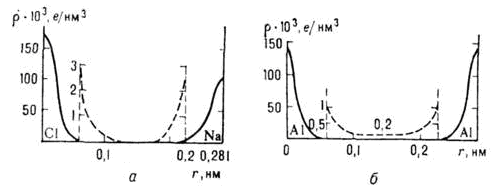
Рис. 1.2.2 Распределение электронной плотности на линии связи между атомами в кристаллах: а- ионная связь (NaCl), пунктирная линия - область внешних электронных орбит; б - металлическая связь (А1), пунктирная линия - плотность электронов в межатомном пространстве.
В ионных кристаллах внешние валентные электроны переходят от атомов металлов, которые становятся положительными ионами (катионами), к атомам неметаллов, которые становятся отрицательными ионами (анионами), что приводит к электростатическому притяжению между ними (рис. 1.2.2). Взаимодействие ионов является кулоновским, но при их соприкосновении начинают играть роль силы отталкивания между электронными оболочками; потенциальная энергия их взаимодействия описывается формулой

где r -
расстояние между центрами ионов; b
и п -
параметры, которые могут быть найдены из сжимаемости кристаллов; n
=(6-9). В межатомном пространстве в ионных кристаллах электронная плотность r (r
)близка к нулю рис. 1.2.2, а.
Потенциальная энергия взаимодействия рассчитывается по формуле:

где m
=4, а,
α, С -
константы, более точно u
ков
получают из решения методами квантовой химии уравнения Шрёдингера.
Природа металлической связи та же, что и ковалентной, т. е. обобществление внешних валентных электронов атомов, однако характер локализации этих электронов иной - они приблизительно равномерно заполняют всё межатомное пространство, образуя общий электронный "газ", который и осуществляет коллективное взаимодействие с заряженными положительно атомами металла (рис. 1.2.2, б)
В молекулярных кристаллах атомы внутри молекул объединены прочными ковалентными связями, а атомы соседних молекул взаимодействуют за счёт более слабых ван-дер-ваальсовых сил, имеющих дипольное и дисперсионное происхождение.
Расстояние между атомами соседних молекул 0,35-0,4 нм.
В работе о распределении электронной плотности и потенциала в решетке селенида марганца описывается разностный метод расчета электронной плотности.[4] В качестве исследуемого вещества выбран селенид марганца. По измеренным значениям интенсивностей подсчитывались абсолютные значения структурных амплитуд. При этом вводились поправки на дисперсию и температурный фактор.[5]
Измеренные структурные амплитуды (
F
)
для селенида марганца представлены на рис. 1.2.3, а,
где сплошными линиями нанесены теоретические значения F
,
рассчитанные по Хартри - Фоку для нейтральных атомов [6]. Как видно из рисунка, экспериментальные значения структурных амплитуд определяющиеся разностью fSe
– fMn
, при малых значениях 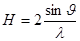 лежат выше теоретических. лежат выше теоретических.
Подсчитанные по структурным амплитудам функции атомного рассеяния (рис. 1.2.3, б)
при малых значениях H, также отличались от теоретических, причем для селена экспериментальные значения лежат выше теоретических, а для марганца ниже теоретических. Таким образом, полученные данные показали, что в решетке селенида марганца

Рис. 1.2.3 Структурные амплитуды (а) и функции атомного рассеяния ионов (б)
ионы марганцаимеют положительный заряд, а ионы селена отрицательный. Для оценки величины заряда ионов был выполнен разностный синтез трехмерного ряда Фурье
 (1.2.1) (1.2.1)
для направлений [100], [110] и [111], результаты которого показали, что электронная плотность в области иона марганца уменьшается ( отрицательно), а в области иона селена увеличивается. Численный расчет показал, что величина заряда ионов в селениде марганца составляет примерно 1,2 ±0,2 эл.
По полученным данным f-функций подсчитывалась электронная плотность в решетке MnSe между ионами марганца и селена с использованием разностного метода синтеза трехмерного ряда Фурье: [7] отрицательно), а в области иона селена увеличивается. Численный расчет показал, что величина заряда ионов в селениде марганца составляет примерно 1,2 ±0,2 эл.
По полученным данным f-функций подсчитывалась электронная плотность в решетке MnSe между ионами марганца и селена с использованием разностного метода синтеза трехмерного ряда Фурье: [7]
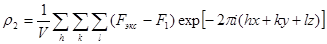 (1.2.2) (1.2.2)
где F
1
—структурная амплитуда преимущественно внутренних электронов, функция рассеяния которых аппроксимировалась в виде
 (1.2.3) (1.2.3)
Коэффициенты Zj
и  определялись по данным привязки к f - функции при больших порядках отражения с использованием теоретических значений. определялись по данным привязки к f - функции при больших порядках отражения с использованием теоретических значений.
Расчеты электронной плотности показали (рис, 1.2.4), что в направлении [100] между ближайшими ионами Mn-Se минимальное значение плотности электронов составляет примерно 0,15 эл/А3
и в направлении [110] между ионами Мn-Мn оно падает практически до нуля.
Для соединения МnО плотность между ближайшими ионами Мn - О в несколько раз больше, чем в MnSe, и составляет примерно 0,55 эл/А3
, Это обстоятельство указывает на то, что в селениде марганца ковалентная составляющая связи значительно меньше, чём в закиси марганца, и MnSe является близким к чисто ионным кристаллам. [8]
Из измеренных экспериментальных функций атомного рассеяния ионов, входящих в состав соединения селенида марганца, было рассчитано распределение потенциала в решетке данного соединения. Распределение потенциала в решетке выражалось трехмерным рядом Фурье
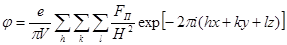 ,
(1.2.4) ,
(1.2.4)
где структурная амплитуда
 . .
Как видно из соотношения (1.2.4), распределение потенциала подсчитывалось непосредственно по экспериментальным значениям f - функций, полученным из данных интенсивности рентгеновских дифракционных спектров.
Расчеты показали, что если f - кривая какого-либо иона аппроксимируется выражением вида
 , ,
то электронная плотность и потенциал этого иона будутописываться выражением
 , ,
 , ,
где 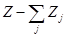 определяет степень ионизации рассматриваемогоиона. определяет степень ионизации рассматриваемогоиона.
Таким образом, чтобы подсчитать значение потенциала в какой-либо точке решетки, необходимо просуммировать значения потенциалов в данной точке от всех окружающих ионов. Наибольший вклад вносили ионы, расположённые на первой и второй координационных сферах, так как от более удаленных ионов вклады уменьшаются как за счет расстояния, так и за счет взаимной компенсации ионов противоположного знака.
В работе[9] рассматривается распределение валентной электронной плотности в преимущественно ионных кристаллах с различающимися подрешетками Браве. Выяснилось, что в случае кристаллов с различающимися подрешетками Браве анионная подрешетка представляла собой ковалентно связанный каркас, в который помещалась подрешетка металла.
В качестве величины, характеризующей связь подрешеток, использовалась разностная плотность, полученная как результат вычитания из кристаллической электронной плотности плотностей отдельных подрешеток. Разностная плотность исследованных кристаллов оказывалась на порядок меньше кристаллической и подрешеточных, что свидетельствовало о слабой гибридизации подрешеток и преимущественно ионном характере связи между ними.
В работе [10] рассматривается перераспределения электронной плотности в области точечных дефектов в алюминии методом функционала электронной плотности.
Для правильного определения механизмов диффузии говорится о необходимости использования новых, более точных и корректных методов моделирования точечных дефектов и их комплексов в металлах и сплавах.
Одной из важнейших характеристик твердого тела является распределение электронной плотности. Особенно сильно влияет перераспределение электронной плотности на характеристики точечных дефектов, следовательно, его знание и учет являются ключевыми моментами в определении истинных диффузионных механизмов в металлах и сплавах.
В настоящее время наиболее перспективным и точным методом расчета характеристик точечных дефектов в металлах является метод функционала электронной плотности. Это единственный метод, который позволяет учитывать перераспределение электронной плотности в области точечных дефектов. Также к преимуществам данного метода следует отнести тот факт, что для расчетов он не требует экспериментальных данных и подгоночных констант, а основан исключительно на фундаментальных константах, таких как заряд ядра и электронное строение атома. К недостаткам данного метода следует отнести невозможность расчета систем размером более сотен атомов и необходимость использовать достаточно мощные вычислительные системы.
В основу теории функционала электронной плотности положена теорема Хоэнберга и Кона, согласно которой все свойства основного состояния неоднородного взаимодействующего электронного газа могут быть описаны с помощью введения некоторых функционалов от электронной плотности  .
Вместо обычного гамильтониана системы вводится функционал следующей структуры: .
Вместо обычного гамильтониана системы вводится функционал следующей структуры:

где vext
(
r
)
- внешнее поле, в которое входит поле ядер; функционал G
[
p
]
является универсальным и не зависит от внешнего поля. [11]
С помощью метода функционала электронной плотности, было проведено моделирование моновакансии в чистом алюминии. Моделирование проводилось для ячейки 4x4x4 (256 атомов).
Для бездефектного алюминия был определен параметр решетки, который равен аА!
= 4,0468 Ǻ, что хорошо согласуется как с другими работами по моделированию , так и с экспериментальными данными.
Для алюминия содержащего моновакансию, была определена ее энергия образования, которая равна 0,66 эВ, что хорошо согласуется с работами, сделанными ранее, а также проведен расчет перераспределения электронной плотности при образовании вакансии (разность функций распределения электронной плотности в бездефектном алюминии и алюминии с вакансией). [12,13]
В работе [14] рассматривается расчет распределения электронной плотности и потенциала в алмазе по рентгенографическим данным. Распределение электронной плотности задается рядом Фурье
 , (1.2.5) , (1.2.5)
где Fhkl
-
экспериментально измеренные величины структурных амплитуд, H
–
вектор обратной решетки, абсолютная величина которого дается соотношением
 , ,
R
–радиус-вектор точки с координатами (x
,y
,z
), для которой определяется электронная плотность, V
– объем элементарной ячейки.
Зная интегральные интенсивности дифракционных максимумов Ihkl
, может быть определена следующего соотношения структурная амплитуда Fhkl
:
 , ,
где I
0
– интенсивность первичного рентгеновского пучка, падающего на исследуемый образец, А*
- произведение всех коэффициентов, входящих в выражение для интенсивности брегговского рефлекса.
Ряд (1.2.5) оказывается слабо сходящимся и его вычисление для известных значений структурных амплитуд может привести к непредсказуемым погрешностям. С другой стороны, распределение плотности заряда, как во всем кристалле, так и в его элементарной ячейке может быть описано уравнением Пуассона:
 (1.2.6) (1.2.6)
где j
- электростатический потенциал.
Представим электростатический потенциал j
рядом Фурье вида (1.2.5)
 (1.2.7) (1.2.7)
Подставляя (1.2.7) в уравнение (1.2.6) и сравнивая с (1.2.5), приходим к соотношению, выражающему  через структурные амплитуды Fhkl
: через структурные амплитуды Fhkl
:
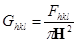 (1.2.8) (1.2.8)
С учетом (1.2.8), ряд (1.2.7) принимает вид
 (1.2.9) (1.2.9)
Полученный ряд (1.2.9) сходится существенно быстрее, чем ряд (1.2.5).
Представим ряд (1.2.9) в интегральной форме. Будем использовать функцию Эвальда
 (1.2.10) (1.2.10)
Тогда выражение для потенциала j
(x
,
y
,
z
) =j
(R
) примет следующий вид:
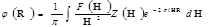 (1.2.11) (1.2.11)
где F(Н
)– функция, достаточно хорошо сглаживающая значения структурных амплитуд в точках Н
= H
hkl
. Правая часть равенства (1.2.11) представляет собой преобразование Фурье произведения двух функций F
(
H
)/
H
2
и Z
(H
). Применяя к выражению (1.2.11) теорему о свертке функций, получим
 , (1.2.12) , (1.2.12)
где функции f
(
R
)
и g
(
R
)
находятся Фурье-преобразованием функций F
(
H
)/
H
2
и Z
(H
).
Чтобы использовать выражение (1.2.12) для расчетов φ
(x
,у
,z
),необходимо знать аналитический вид функции F
(H
), которая на практике определена только в дискретных точках, где она имеет значение Fhkl
. Для нахождения F
(H
) воспользуемся методом аппроксимации. В качестве аппроксимирующей функции удобно взять следующее выражение:
 , (1.2.13) , (1.2.13)
где zi
– число электронов на i
-ой оболочке в атоме;
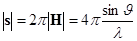 (1.2.14) (1.2.14)
Для функции F
(H
), данной выражением (1.2.13), может быть найдена функция f
(R
), входящая в выражение для φ
(х
,у
,z
) согласно (1.2.12). Эта функция находится Фурье-преобразованием выражения F
(Н
)/Н
2
. В случае кубических решеток Фурье-преобразование может быть сведено к синус-преобразованию, тогда для f
(R
) получим следующее выражение:
 (1.2.15) (1.2.15)
Функция g
(R
) является решеточной и находится Фурье-преобразованием Z
(H
). В зависимости от количества атомов в элементарной ячейке производится вычисление g(R
), для лития она имеет вид:
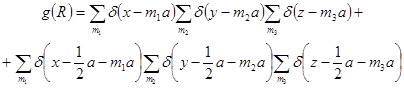 (1.2.16) (1.2.16)
где а
— постоянная решетки; m
1
, m
2
, m
3
— целые числа, начиная с нуля; δ
(x
-m
1
a
), δ
(y
-m
2
a
), δ
(z
-m
3
a
) — δ
-функции.
Совершив необходимые вычисления в (1.2.12), получаем следующее выражение для функции распределения потенциала:
 , (1.2.17) , (1.2.17)
Здесь через A
1
, А
2
обозначены следующие выражения:
 , (1.2.18) , (1.2.18)

  Значение электростатического потенциала, созданного электронами, получается умножением φ
(R
) на заряд электрона -е
. Потенциал ядер в произвольной точке ячейки V
находится суммированием кулоновских потенциалов отдельных ядер. Выражение для потенциала ядер имеет следующий вид: Значение электростатического потенциала, созданного электронами, получается умножением φ
(R
) на заряд электрона -е
. Потенциал ядер в произвольной точке ячейки V
находится суммированием кулоновских потенциалов отдельных ядер. Выражение для потенциала ядер имеет следующий вид:
 (1.2.19) (1.2.19)
где A
1
, А
2
даются выражениями (1.2.18). Полный потенциал решетки находится суммированием eφ
(R
) и V
(R
), т. е.
 (1.2.20) (1.2.20)
Используя формулы (1.2.19), а также значения zi
и найденные значения αi
2
, для потенциала кристаллической решетки получают следующее выражение:
 (1.2.21) (1.2.21)
где Аj
даются выражениями (1.2.18)
Аналогичные вычисления для электронной плотности дают следующее выражение:
 (1.2.22) (1.2.22)
Глава 2. Неупругое рассеяние рентгеновских лучей веществом
2.1 Импульсная аппроксимация
Комптон-эффект исследовался многими учеными в практическом и теоретическом плане. КЭ занимались Дю-Монд, Купер, Вейс, Филипс. В их работах было рассмотрено рассеяние на не покоящихся электронах.
Рассеяние монохроматического излучения на покоящихся электронах должно приводить, очевидно, к δ-образному комптоновскому спектру. В дальнейшем, однако, было обнаружено, что спектральная линия КЭ шире, чем этого следовало ожидать из учета немонохроматичности и расходимости основного излучения, как показано на рисунке (2.1.1).
Джансей и более строго Дю-Монд объяснили это расхождение влиянием не учитываемого ранее начального распределения электронов по импульсам. [15]
Пусть ω1
, k
1
и ω2
, k
2
- соответственно частота и волновой вектор падающего и рассеянного излучений; тогда величины ω = ω1
- ω2
и k
= k
1
- k
2
определяют энергию и импульс, передаваемые среде в единичном акте рассеяния. А законы сохранения в нерелятивистском приближении (ħν << mc2
) выглядят следующим образом.
 (2.1.1) (2.1.1)
где р
1
и р
2
- импульсы электрона до и после рассеяния. Согласно (2.1.1)
 (2.1.2) (2.1.2)
Энергетическое смещение комптоновской линии задается первым членом в (2.1.2), а второе слагаемое описывает доплеровское уширение линии, определяемое проекцией q импульса р
1
па ось k
. Так как k
1
= ω1
/c = 2π/λ1
и k
= 2k
1
sin( /2), то из (2.1.2) следует известное соотношение Комптона для положения центра линии КЭ на свободных не взаимодействующих электронах: /2), то из (2.1.2) следует известное соотношение Комптона для положения центра линии КЭ на свободных не взаимодействующих электронах:
 (2.1.3) (2.1.3)
где  - угол рассеяния (угол между направлениями k
2
и k
1
). - угол рассеяния (угол между направлениями k
2
и k
1
).
Тем самым было показано, что частотный комптоновский профиль несет информацию о функции одномерного (в проекции на k
) распределения электронов по импульсам. Именно это обстоятельство и определяет важность изучения КЭ, так как из импульсного распределения с помощью фурье-преобразования можно получить функцию распределения электронной плотности |ψi
(r
)|2
. Уже ранние работы Дю-Монда с сотрудниками продемонстрировали перспективность этого метода для изучения электронного импульсного распределения, который к настоящему времени значительно усовершенствован и доведен до рабочего во многих исследовательских центрах. [16]
Основным приближением в теории КЭ является так называемая импульсная аппроксимация.
Проекция импульса
 (2.1.4) (2.1.4)
характеризует отклонение l
= λ2
- λ20
длины волны сигнала λ2
от центра комптоновской линии λ20
= λ1
+ 2λс
sin2
( /2), λс
– комптоновская длина волны. /2), λс
– комптоновская длина волны.
Выражение для импульсной аппроксимации имеет вид
 (2.1.5) (2.1.5)
где χi
(p) - фурье-компонента волновой функции основного состояния ψi
(r
). Функция J(q) называется комптоновским профилем (КП) и (2.1.5) является основным соотношением теории ИА.
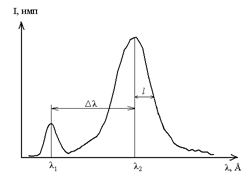
Рис 2.1.2. Схематическая диаграмма КП в типичном эксперименте.
Обычно же на практике используется обратная процедура, т. е. вначале выбирается система волновых функций ψi
, находится теоретическое значение J(q) и сравнивается с экспериментальным профилем. В случае значительного расхождения берется другая система функций и процедура повторяется, т.е. если подобрать χi
(p), то можно найти распределение импульсов в кристалле. В свою очередь распределение импульсов в кристалле связано через Фурье-преобразование с распределением электронной плотности в кристалле. По распределению электронной плотности в кристалле можно судить о внешних валентных электронах, а по ним судить о химической связи вещества, т. к. внешние валентные электроны отвечают за химическую связь.
В комптоновский профиль дают вклады как внешние, так и внутриатомные электроны. Волновые функции внешних электронов в твердом теле сильно отличаются от ψ-функций свободных атомов, а для сильно связанных электронов перекрытием с соседними атомами можно пренебречь. Это приводит к тому, что вклад в КП за счет локализованных атомных электронов можно вычислить с большой точностью. Отсюда, зная полный экспериментальный профиль, простым вычитанием легко выделить вклад внешних электронов. Это является одной из основных причин исследования КП.
Для металлов и вообще веществ с большой концентрацией электронов ИА можно получить на основе идеализированной модели поведения электронов в металле, т. е. на основе теории электронного газа Ферми – Дирака и модели свободных атомов.
Для вырожденного электронного газа |χ(p ≤ pF
)|2
= 3/4πpF
3
и |χ(p)|2
= 0 при р > pF
, где pF
= ħkF
импульс Ферми
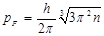 (2.1.6) (2.1.6)
где n – атомная концентрация.
Из (2.1.4) следует, что комптоновский профиль электронов проводимости имеет вид «перевернутой» параболы:
 (2.1.7) (2.1.7)
В модели свободных атомов с волновой функцией K-электрона ψK
= (πa3
)-1/2
* exp(-r/a), где а = a0
/Z и а0
= ħ2
/mc2
боровский радиус:
 (2.1.8) (2.1.8)
где величина qK
= ħ/a определяет ширину КП K-электронов.
На рисунке (2.1.3) приведен результат Филлипса и Вейсса по наблюдению рассеяния излучения MoKα
в Li под углом 117° (верхняя кривая с точками). [17] Нижняя сплошная кривая проведена для компоненты Kα1
с поправкой на фон и поглощение, пунктирные кривые 1 (обратная парабола) и 2 рассчитаны соответственно для свободных электронов проводимости и 1s2
-электронов в приближении Хартри – Фока.
Обычно величина проекции импульса на ось Z находится от середины до линии КП, не учитывая ширину спектральной линии падающего излучения. Для MoKα
1
излучения с длинной волны λ = 0,70926 Å полуширина спектральной линии Δλ составляет 0,00029 Å. С учетом этого, для электронов с нулевым импульсом профиль будет иметь δ-образную форму, как показано на рис.(2.1.1). Если определить импульс не от середины КП, а от δ-образного пика, то появится поправка порядка ~ 1%. Однако, если учесть что КП рассчитывается с точностью до долей процента, то указанная поправка существенна. [18]
2.2 Экспериментальные методы исследования комптоновского рассеяния
Особенности экспериментального исследования Комптон эффекта
Исследование комптоновского рассеяния связано с рядом особенностей и трудностей. Одна из этих трудностей заключается в том, что интенсивность некогерентного излучения очень мала. Это в основном связано с необходимостью применения кристалла – анализатора для отделения некогерентного излучения от остального фона. Отсюда вытекает необходимость либо увеличивать мощность рентгеновских трубок, либо увеличивать время экспозиции, либо совершенствовать экспериментальные установки.
Существует несколько методов исследования комптоновского рассеяния с помощью рентгеновского излучения.
Первый метод основывается на использовании монохроматического излучения, например MoKa
, с последующим отделением комптоновской составляющей при помощи кристалла-анализатора. Большим недостатком данного метода является то, что интенсивность комптоновской составляющей очень мала и она плохо различима над уровнем фона. Применение данного метода требует использование рентгеновского излучения большой мощности.
Второй метод заключается в определении полного диффузного рассеяния без применения кристалла анализатора. Здесь предполагается, что полное диффузное рассеяние состоит только из теплового диффузного рассеяния и комптоновского рассеяния. Отделение теплового диффузного рассеяния производилось путем проведения эксперимента при низких температурах или его теоретической оценкой. Применение данного метода не позволяет установить распределение импульсов электронов.
Третий метод заключается в том, что на рассеивающее вещество направляется весь полихроматический луч, а рассеянное излучение анализируется при помощи кристалла анализатора. Впервые данный метод предложил Чипмэн и в дальнейшем он широко использовался.
Одним из методов повышения интенсивности рассеянного излучения является применение фокусировки вторичного излучения.
Метод фокусировки по Бреггу – Брентано широко применяется для решения ряда задач рентгеноструктурного анализа, в которых необходимо точное измерение ширины линий на рентгенограммах, т.к. при недостаточно четкой центровке расширения линий может происходить за счет несоблюдения геометрии съемки. Кроме того, применение фокусировки позволяет увеличить интенсивность рассеянного излучения. [19]
Другой проблемой является отсутствие серийно выпускаемой рентгеновской аппаратуры для их исследований, а использование не специализированной аппаратуры может сказаться на результатах эксперимента.
Точность определения комптоновского профиля в свою очередь зависит от многих факторов, например, таких как соблюдение геометрии хода лучей, точности определения угла кристалла-анализатора, его отражающей и разрешающей способности, времени экспозиции, угла некогерентного рассеяния рентгеновских лучей, методов сглаживания профиля по экспериментальным данным и разделения дублета Кa
. [20]
Методика получения комптоновских профилей
Поскольку комптоновское излучение имеет очень малую интенсивность. Это является основной причиной того, что эксперимент по определению комптоновского профиля занимает продолжительное время.
Использование автоматизированной рентгеновской установки ДРОН-3 при получении комптоновских профилей позволило полностью освободить экспериментатора от постоянного контроля за ходом эксперимента, проводить непрерывный эксперимент длительное время без внешнего вмешательства (время снятия комптоновского профиля одного исследуемого образца с шагом сканирования 0.050
и экспозицией в каждой экспериментальной точке 2000 с составляет в среднем 36 часов), значительно облегчить обработку экспериментальных результатов, обрабатывать промежуточные результаты без остановки эксперимента. [21]
Для исследования комптоновского рассеяния использовалась рентгенооптическая схема с фокусировкой кристалла-анализатора по Бреггу-Брентано, приведенная на рисунке 2.2.1.
Источником рентгеновских лучей служила трубка БСВ-23 с молибденовым анодом, для которого длина волны рентгеновского излучения K
a
1
=
0,70926 Å, K
a
2
=
0,71354 Å, K
b
=
0,63225 Å. Приемником рентгеновского излучения служил сцинтилляционный детектор БДС NaJ
(
Tl
)
с дискриминатором импульсов кристаллом. [22]
Рентгеновский пучок первичного излучения формировался щелью шириной 2 мм, а вторичного (рассеянного) излучения вертикальной щелью шириной 0.5 мм и горизонтальной щелью высотой 6 мм. Перед детектором устанавливалась щель шириной 0.25 мм. Система щелей Соллера, а также фильтр для отсеивания K
b
излучения не использовались.
Использование полихроматического излучения позволило повысить интенсивность вторичного излучения. Но его основным недостатком является присутствие в полученных экспериментальных данных дополнительных неиспользуемых линий.
Измерения интенсивности комптоновского рассеяния проводились при установленном на рентгеновской трубке токе 25 мА и напряжении 36 кВ. Выбор данного режима работы рентгеновской трубки связан с наибольшей стабильностью излучения и минимальным дрейфом режимов в течении длительного времени.
2.3 Атомо-рассеивающий фактор и распределение
радиальной электронной плотности в литии по комптоновским профилям
Волновая функция, описывающая основное состояние лития – 1s
2
2s
2
в первом приближении может быть представлена в виде простого произведения по методу Хартри
 (2.3.9) (2.3.9)
где 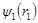 и и  - волновые функции основного состояния 1s водородоподобного атома, зависящую только от радиальных координат, - волновые функции основного состояния 1s водородоподобного атома, зависящую только от радиальных координат,  волновая функция, описывающая основное состояние 2s водородоподобного атома, также зависящую только от радиальной координаты. волновая функция, описывающая основное состояние 2s водородоподобного атома, также зависящую только от радиальной координаты.
Функция аппроксимирующая КП лития рассчитывается по формуле:
 , (2.3.10) , (2.3.10)
где μ1
, μ2
, μ3
вариационные параметры.
На рисунке (2.3.3) показан экспериментально полученный КП лития (точки) и аппроксимирующая кривая (сплошная линия), полученная по формуле (2.3.10) с вариационными параметрами μ1
= 0,44, μ2
= 0,9, μ3
= 100.
Радиальная электронной плотность будет описываться уравнением с полученными значениями вариационных параметров
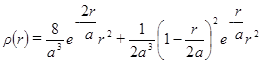
На рисунке (2.3.4) приведён график радиальной электронной плотности лития и водорода.
Выражение для атомно-рассеивающего фактора будет иметь вид:
 , ,
где 
Как видно из рисунка (2.3.4) ,максимальное значение электронной плотности лития значительно превышает это значение для алмаза на малых расстояниях от ядра (порядка 0,01Å). [23]
На рисунке (2.3.5) приведены графики атомно-рассеивающего фактора лития, пунктирная линия – теоретически рассчитанная для уединённого атома и сплошная линия – экспериментально полученная численными методами для структурированного состояния из КП.

Рис. 2.3.5. Экспериментально полученные значения атомно-рассеивающего фактора от поликристаллического лития (1). теоретически рассчитанные данные для уединенного атома лития (2) [32],.
Из рисунка 2.3.5 видно существенное различие атомно – рассеивающего фактора для структурированного состояния и уединённого атома лития.
Глава 3. Методика измерений и обработки результатов
3.1 Подготовка образцов и методика измерений
Для исследований образец лития приготавливался следующим образом. Литий марки ЛЭ-2 плавили в тигле из нержавеющей стали в среде аргона при температуре 200ºС с последующим резким охлаждением. После прессования таблетки для снятия механических напряжений литий отжигался при температуре 150ºС также с последующим резким охлаждением. Таблетка Li, диаметром 20 мм и толщиной 3 мм, помещалась во фторопластовую кювету. Для защиты от окисления поверхность образца смазывалась машинным маслом и покрывалась тонкой фторопластовой пленкой.
Образец алюминия был изготовлен из алюминия марки А87 (содержание алюминия 99,87%) в виде таблетки толщиной 2,5 мм и диаметром 20 мм. Для снятия механических напряжений после формовки, образец был отожжен при температуре 600º С в аргоне с последующим резким охлаждением в жидком азоте. [24]
Монокристаллический LiF был измельчен в яшмовой ступке до среднего размера зерна 1,4 10-4 м. Далее порошковый препарат был запрессован в кювету.
Измерения проводились на рентгеновском дифрактометре ДРОН-3. Рентгеновская трубка питалась напряжение 36 кВ с силой тока 25 мА. Такие параметры питающего напряжения и тока были выбраны с одной стороны для получения достаточно интенсивных максимумов и с другой стороны они обеспечивают достаточно стабильную работу аппарата. [25]
Образец крепился на приставке ГП-3, которая устанавливалась на поворотной оси гониометра и обеспечивала вращение образца в его плоскости. Такое вращение исключало влияние текстуры исследуемого образца (преимущественной ориентации кристаллографических плоскостей), что позволило увеличить точность измерений.[26]
После установки образца в приставку гониометр юстировался по методике, описанной в [21]. Снятие экспериментальных данных проводилось по точкам. Шаг детектора при сканировании был выбран 0,02°. Первоначально определялись границы максимумов. Время экспозиции для каждого максимума подбиралось с учетом его интенсивности, таким образом, чтобы суммарная интенсивность с учетом фона для сильных и слабых линий была примерно одинакова. Экспозиция в измеряемых точках профиля дифракционных максимумов составила от 2 то 250 секунд.
По экспериментальным данным интенсивностей строились общие рентгенограммы для каждого вещества. На рисунке (3.1.1) приведена обзорная рентгенограмма поликристаллического лития, которая была получена на Кα
излучении трубки с медным анодом (λ
= 1,5405 Å). В связи с разной интенсивностью дифракционных максимумов рентгенограмма снималась с различной экспозицией (для каждого профиля). Экспозиция варьировалась от 3 до 250 секунд.

Рис. 3.1.1. Обзорная рентгенограмма поликристаллического лития
На рисунке (3.1.2) приведена рентгенограмма поликристаллического алюминия. Рентгенограмма была получена на Кα
излучении трубки с кобальтовым анодом (λ
= 1,7889Å). В связи с разной интенсивностью дифракционных максимумов рентгенограмма снималась с различной экспозицией (для каждого профиля). Экспозиция варьировалась от 2 до 5 секунд.
Обзорная рентгенограмма LiF представлена на рисунке 3.1.3
Измерение интенсивности дифракционных максимумов производилось на излучении трубки с молибденовым анодом (λ = 0,7063 Å). В зависимости от интенсивности рефлекса экспозиция выбиралась от 2 до 10 секунд.
3.2 Методика обработки максимумов
Одной из главных проблем при определении распределения электронной плотности является нахождение атомно-рассеивающего фактора f(s), связанный со структурным фактором  и, соответственно, интегральной интенсивностью дифракционных максимумов и интенсивностью первичного пучка. [28] и, соответственно, интегральной интенсивностью дифракционных максимумов и интенсивностью первичного пучка. [28]
Экспериментальное значение структурного фактора определялось из выражения:
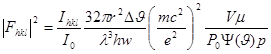 (3.2.1) (3.2.1)
где I
0
– интенсивность первичного пучка, l
– длина волны рентгеновского излучения, h
– высота приемной щели, w
– ширина приемной щели, r
– расстояние от образца до детектора, m
– линейный коэффициент поглощения исследуемого вещества, P
o
– поляризационный фактор, Р
0
=0.5(1+cos2
2J), р
– фактор повторяемости, V
– объем элементарной ячейки, J
– угол брегговского рассеяния, DJ =J2
-J1
, 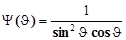 - геометрический множитель, I
hkl
– интегральная интенсивность рефлекса, которая находилась по методике описанной в. [29] - геометрический множитель, I
hkl
– интегральная интенсивность рефлекса, которая находилась по методике описанной в. [29]
Методика расчета интенсивности первичного пучка
Интенсивность первичного пучка I
0
в сотни раз превышает предел измерения детектора. Для измерения интенсивности первичного пучка, падающего на образец, использовалась стопка тонких пластин-поглотителей СП, которая размещалась между столиком и детектором, как показано на рис.3.2.1. При этом материал, из которого изготовлены пластины соответствовал материалу анода трубки.
Исходя из закона поглощения рентгеновского излучения веществом
 (3.2.2) (3.2.2)
Интенсивности прошедшего и падающего рентгеновских пучков.
Для набора из N пластин одинаковой толщины d0
можно записать:
 (3.2.3) (3.2.3)
где In
– интенсивность рентгеновского пучка, прошедшего n
пластин поглощающего вещества, In
-1
– интенсивность рентгеновского пучка, прошедшего n
-1 пластину поглощающего вещества. Исходя из выражений (3.2.2), (3.2.3) интенсивность I
0
будет равна:
 (3.2.4) (3.2.4)
где 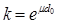 – коэффициент поглощения рентгеновского излучения одной пластиной. [30] – коэффициент поглощения рентгеновского излучения одной пластиной. [30]
Для повышения точности вычисления I
0
были проведены измерения In
для стопки, содержащей от 16 до 4 пластин. Для каждого измерения был вычислен коэффициент поглощения рентгеновского излучения kn
,
n
-1
. На основании этих данных был вычислен средний коэффициент поглощения k
.
В качестве поглощающего вещества использовались молибденовые пластины толщиной 0,075 мм. [31] Интенсивности In
определялись, как среднее значение интенсивности за 600 сек. Среднее значение k
в эксперименте получилось равным 1,75. На рисунке 3.2.2 приведен график зависимости измеряемой интенсивности от количества пластин. Значение интенсивности на промежутке от 0 до 4 получены экстраполяцией кривой, построенной по экспериментально измеренным значениям интенсивности проходящего пучка при 4 – 16-х пластинах. Интенсивность первичного пучка составила  имп./сек. имп./сек.
После нахождения интенсивности первичного пучка определялась интегральная интенсивность каждого дифракционного максимума.

Рис.3.2.3 Дифракционный максимум поликристаллического лития
Интенсивность в i-й точке равна  , ,  , где d – ширина щели, h – высота щели, n – количество квантов, ti
– время экспозиции. Интегральная интенсивность рефлекса , где d – ширина щели, h – высота щели, n – количество квантов, ti
– время экспозиции. Интегральная интенсивность рефлекса  . В свою очередь интенсивность первичного пучка . В свою очередь интенсивность первичного пучка 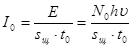 . При расчете структурного фактора (3.2.1) площадь щели sщ
и энергия фотона . При расчете структурного фактора (3.2.1) площадь щели sщ
и энергия фотона 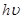 сокращаются, поэтому интегральной интенсивность рассчитывалась по формуле: сокращаются, поэтому интегральной интенсивность рассчитывалась по формуле:
 (3.2.5) (3.2.5)
где Iобщ
– сумма интенсивностей всех точек дифракционного максимума,
t – время экспозиции, Т – общее время экспозиции.
3.3 Анализ результатов эксперимента
В таблице 3.3.1 приведены параметры исследованных дифракционных максимумов для лития.
Таблица
3
.3.1.
| № |
Угловая
ширина, º
|
Угловое
положение пика,º
|
Время экспозиции, с |
Интегральная интенсивность, имп/с |
| 1 |
34 - 37,2 |
35,74 |
3 |
243,96 |
| 2 |
49,8 - 54 |
51,54 |
5 |
489,89 |
| 3 |
62 - 66 |
64,48 |
15 |
115,29 |
| 4 |
86 - 89,2 |
87,52 |
30 |
23,28 |
| 5 |
97,5 - 100,3 |
98,54 |
60 |
9,21 |
| 6 |
108,5 - 115,5 |
110,12 |
200 |
10,78 |
| 7 |
121,5 - 124,5 |
122,4 |
250 |
8,45 |
В таблице 3.3.2 приведены значения межплоскостных расстояний d
, фактор повторяемости Р
и структурного множителя для разрешенных hkl
.
Таблица
3
.3.2
| № |
hkl |
d, Å |
P |
Структурный множитель |
| 1 |
110 |
3,15 |
12 |
4 |
| 2 |
200 |
2,21 |
6 |
4 |
| 3 |
211 |
1,8 |
24 |
4 |
| 4 |
220 |
1,56 |
12 |
4 |
| 5 |
311 |
1,4 |
24 |
4 |
| 6 |
222 |
1,18 |
8 |
4 |
| 7 |
321 |
1,01 |
48 |
4 |
В таблице 3.3.3 приведены экспериментально полученные значения структурного множителя и атомно-рассеивающего фактора.
Таблица 3.3.3.
| № |
|F|2
|
fэксп.
|
fтеор.
|
 |
| 1 |
26,412 |
2,580 |
2,473 |
0,199 |
| 2 |
11,296 |
2,300 |
2,102 |
0,282 |
| 3 |
1,10 |
1,530 |
1,825 |
0,346 |
| 4 |
0,383 |
1,380 |
1,441 |
0,449 |
| 5 |
0,064 |
1,200 |
1,305 |
0,492 |
| 6 |
0,056 |
1,120 |
1,191 |
0,532 |
| 7 |
0,007 |
1,060 |
1,096 |
0,569 |
На рисунке (3.3.1) показана кривая атомно-рассеивающего фактора лития.
 Рис. 3.3.1 Атомно-рассеивающий фактор лития.
Рис. 3.3.1 Атомно-рассеивающий фактор лития. 1 – сглаженные экспериментальные значения, полученные по выражению 3.3.1. 2 – теоретические значения,
полученные по методу Хартри-Фока. [32]
Для расчета атомно - рассеивающего фактора использовалась аппроксимирующая функция, поддающаяся Фурье-преобразованию вида:
 , (3.3.1) , (3.3.1)
где a
1
=0,7581, a
2
=2,4649, a
3
=0,07. На графике она показана сплошной линией. Пунктирной линией показана f-кривая, полученная методом Хартри-Фока [32].
Для расчета потенциала кристаллической решетки использовалось следующее выражение:

Вычисление электронной плотности производилось следующим образом:

Распределение электронной плотности и потенциала в основных кристаллографических направлениях рассчитывались на ЭВМ по написанной программе (см. компакт - диск) с учетом параметра кристаллической решетки, координат атомов и экспериментальных значений атомно-рассеивающего фактора лития.
Распределение электронной плотности и потенциала в основных кристаллографических направлениях для лития приведены на рисунках (3.3.2) – (3.3.4).

Рис. 3.3.2. Распределение электронной плотности и потенциала в кристалле лития в направлении [100]

Рис. 3.3.3. Распределение электронной плотности и потенциала в кристалле лития в направлении [110]
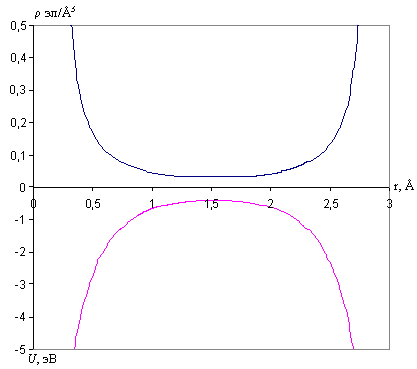
Рис. 3.3.4. Распределение электронной плотности и потенциала в кристалле лития в направлении [111]
Как видно из приведенных рисунков электронная плотность и потенциал ни в одном из направлений в ноль не обращается. Минимальное значение электронной плотности в направлении [100] составило ρ
= 0,023 эл/А3
, в направлении [110] ρ
= 0,026 эл/А3
, в направлении [111] ρ
= 0,03 эл/А3
. Минимальные значения потенциала в направлениях [100], [110] и [111] равны соответственно U
= -0,28814, U
= -0,28382 и U
= -0,38184 эВ. [33]
Для оценки эффективной формы атома, были построены изоэлектронные уровни распределения по минимальному значению электронной плотности вдоль кристаллографического направления [111]
На рисунке(3.3.5). приведена диаграмма электронной плотности эффективной поверхности атома лития.

 Рис. 3.3.5. Диаграмма распределения электронной плотности в кристалле лития. Линия 1 соответствует минимальному значению электронной плотности (ρ
=0,024 эл/Å3
) в направлении [111], линия 2 соответствует значению электронной плотности на расстоянии 0,3 Å от центра атома (ρ
=0,485 эл/Å3
)
Наглядно представить картину распределения электронной плотности в литии в основных кристаллографических плоскостях можно посредством карт распределения электронной плотности, которые представлены на рисунке 3.3.6.
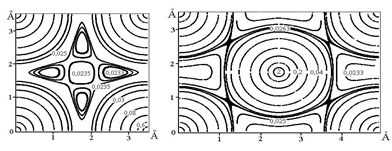
Рис. 3.3.6. Карты распределения электронной плотности в кристалле лития: а – плоскость (100), б – плоскость (110)
В таблице 3.3.4 приведены параметры исследованных дифракционных максимумов для алюминия.
Таблица
3
.3.4
| № |
Угловая ширина, º |
Угловое положение, º |
Время измерения, с |
Интегральная
интенсивность, имп/сек
|
| 1 |
2 |
44,98 |
200 |
1444 |
| 2 |
2,1 |
52,42 |
210 |
1190 |
| 3 |
2,3 |
77,28 |
230 |
511 |
| 4 |
2 |
94,16 |
300 |
586 |
| 5 |
2,5 |
99,8 |
625 |
94 |
| 6 |
3,5 |
124,08 |
875 |
129 |
| 7 |
5 |
148,54 |
1250 |
255 |
В таблице 3.3.5 приведены значения межплоскостных расстояний d
, фактор повторяемости Р
и структурного множителя для разрешенных hkl
.
Таблица
3
.3.5
| № |
hkl |
d, Å |
Р |
Структурный множитель F |
| 1 |
111 |
2,33 |
8 |
16 |
| 2 |
200 |
2,02 |
6 |
16 |
| 3 |
220 |
1,12 |
12 |
16 |
| 4 |
311 |
1,21 |
24 |
16 |
| 5 |
222 |
1,16 |
8 |
16 |
| 6 |
400 |
1,01 |
6 |
16 |
| 7 |
331 |
0,92 |
24 |
16 |
В таблице 3.3.6 приведены экспериментально полученные значения структурного множителя и атомно-рассеивающего фактора.
Таблица
3
.3.6
| № |
|F|2
|
fэксп
|
fтеор
|
sinθ/λ |
| 1 |
2,73 |
6,26 |
6,04 |
0,21 |
| 2 |
4,25 |
6,19 |
5,98 |
0,25 |
| 3 |
2,08 |
4,28 |
4,14 |
0,35 |
| 4 |
1,49 |
3,32 |
3,96 |
0,41 |
| 5 |
0,31 |
2,29 |
3,26 |
0,43 |
| 6 |
1,00 |
2,20 |
3,13 |
0,49 |
| 7 |
0,26 |
1,31 |
2,62 |
0,54 |
На рисунке (3.3.7) показана кривая атомно-рассеивающего фактора лития. Для дальнейших расчетов использовалась аппроксимирующая функция, поддающейся Фурье-преобразованию вида:
 , (3.3.2) , (3.3.2)
которая на графике показана сплошной линией. Пунктирной линией показана f
-кривая, полученная методом Хартри-Фока [34]. Значение коэффициентов составили a
1
=0,022, a
2
=0,022, a
3
=0,37.

Рис. 3.3.7 Атомно-рассеивающий фактор алюминия.
1 – теоретические значения [32], 2 – экспериментальные значения
Из экспериментальных значений атомно-рассеивающего фактора были рассчитаны значения потенциала и электронной плотности в основных кристаллографических направлениях по следующим формулам соответственно:

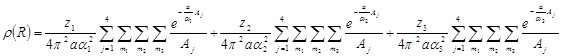
Распределение электронной плотности и потенциала в основных кристаллографических направлениях рассчитывались на ЭВМ по написанной программе (см. компакт - диск) с учетом параметра кристаллической решетки, координат атомов и экспериментальных значений атомно-рассеивающего фактора алюминия.
Распределение электронной плотности и потенциала для алюминия приведены на рисунках (3.3.8) – (3.3.10).
Из графиков видно, что ни в одном из направлений электронная плотность и потенциал в ноль не обращаются. Минимальное значение плотности в направлении [100] составляет ρ
= 0,08 эл/Å3
, в направлении [110] ρ
= 0,086 эл/Å3
, для направления [111] ρ
= 0,096 эл/Å3
. Минимальные значения потенциала составляют: в направлении [100] U
= -0,06153 эВ, в направлении [110] U
= 0,1523 эВ и в направлении [111] U
= -0,06154 эВ.
 |
 ,ГПа ,ГПа |
 , , |
| Li |
100 |
3,2 |
0,023 |
| 110 |
8,93 |
0,026 |
| 111 |
22,8 |
0,03 |
| Al |
100 |
62,5 |
0,08 |
| 110 |
71,4 |
0,086 |
| 111 |
75,1 |
0,096 |
Для кристаллов лития и алюминия наибольшая электронная плотность наблюдается в направлении [111], а наименьшая - [100], что соответствует значениям модуля растяжения E в указанных кристаллографических направлениях.

Рис. 3.3.8Распределение электронной плотности и потенциала алюминия в направлении [100]

Рис. 3.3.9. Распределение электронной плотности и потенциала алюминия в направлении [110]

Рис. 3.3.10. Распределение электронной плотности и потенциала алюминия в направлении [111]
На рисунке (3.3.11) показана изоэлектронная линия эффективной формы атома алюминия.

Рис. 3.3.11. Диаграмма распределения электронной плотности в кристалле алюминия. Внешняя линия соответствует минимальному значению электронной плотности в направлении [110], внутренняя линия соответствует значению электронной плотности на расстоянии 0,3 Å от центра атома.

Рис. 3.3.12.Карты распределения электронной плотности в кристалле алюминия: а – плоскость (100), б – плоскость (110)
На рисунке (3.3.12) показаны изоэлектронные уровни распределения электронной плотности в алюминии.
В таблице (3.3.7) приведены параметры исследованных дифракционных максимумов.
Таблица
3
.3.7.
| № |
hkl |
Угловая ширина, ° |
Положение, ° |
Интегральная интенсивность, имп/сек |
Экспозиция, сек |
d, Å |
| 1 |
111 |
2,2 |
17,3 |
128263 |
2 |
2,32 |
| 2 |
200 |
2 |
20,13 |
202526 |
2 |
2,01 |
| 3 |
220 |
2,3 |
28,85 |
94641 |
2 |
1,42 |
| 4 |
311 |
2,4 |
33,82 |
55060 |
5 |
1,21 |
| 5 |
222 |
2,2 |
35,3 |
45781 |
5 |
1,16 |
| 6 |
400 |
2,9 |
41,08 |
45859 |
5 |
1,02 |
| 7 |
420 |
2 |
46,2 |
33633 |
10 |
0,90 |
| 8 |
422 |
2,3 |
50,88 |
31095 |
10 |
0,82 |
При расчете электронной плотности в ионном кристалле LiF, содержащего два сорта атомов, из экспериментальных данных интегральных интенсивностей определялись значения атомно – рассеивающих факторов f1
и f2
для каждого элемента в отдельности. В таблице 3.3.8 представлены соотношения между структурным множителем F и атомно – рассеивающими факторами f1
и f2
разрешенных рефлексов фтористого лития. [35]
Таблица
3.3.8.
Значения фактора повторяемости р, структурного множителя F и экспериментально полученного структурного фактора  для разрешенных рефлексов hkl кристалла LiF. для разрешенных рефлексов hkl кристалла LiF.
| hkl |
p |
F |

|
| 111 |
8 |
16(f1
- f2
)2
|
26,85 |
| 200 |
6 |
16(f1
+ f2
)2
|
33,57 |
| 220 |
12 |
16(f1
+ f2
)2
|
30,28 |
| 311 |
24 |
16(f1
- f2
)2
|
11,59 |
| 222 |
8 |
16(f1
+ f2
)2
|
13,84 |
| 400 |
6 |
16(f1
+ f2
)2
|
19,21 |
| 331 |
24 |
16(f1
- f2
)2
|
9,42 |
| 420 |
24 |
16(f1
+ f2
)2
|
7,47 |
Как видно из таблицы структурный множитель, в зависимости от hkl, принимает значения 16(f1
-f2
)2
или 16(f1
+f2
)2
. Из экспериментально полученных значений структурного фактора  были построены зависимости (f1
+f2
), (f1
-f2
) от sinθ/λ как показано на рис. 3.3.13. были построены зависимости (f1
+f2
), (f1
-f2
) от sinθ/λ как показано на рис. 3.3.13.

Рис.3.3.13 Рис.3.3.14
Кривые аппроксимировались полиномом второй степени. Атомно – рассеивающий фактор для Li и F определялись по формулам:
 , ,  , ,
где значения (f1
+ f2
) и (f1
- f2
) брались из сглаженных кривых. Графики зависимостей 1- fF
(sinθ/λ) и 2 - fLi
(sinθ/λ) приведены на рис. 3.3.14.
Построение карты РЭП в LiF производилось следующим образом. Используя коэффициенты α1
, α2
, α3
аппроксимирующих выражений атомно – рассеивающих факторов для Li и F,
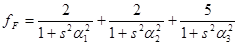 , , 
с помощью ЭВМ строились РЭП в отдельности для каждого сорта атомов, а затем они накладывались друг на друга.
Границы атомов выбирались из условия равенства минимальных значений электронных плотностей для первого и второго сорта атомов. На рис. 3.3.15 показано распределение электронной плотности в кристалле LiF в плоскости (100). На изоэлектронных линиях указаны её значения в единицах эл/Å3
. [36]

Рис.3.3.15. Карта распределения электронной плотности в кристалле LiF в плоскости (100)  F - , Li - F - , Li -
Как видно из карты, оболочки ионов фтора перекрываются между собой при значении электронной плотности равной 0,15 эл/Å3
, у катионов лития такого перекрытия не наблюдается. Определенные по карте радиусы атомов составляют для F - 1,18 Å, Li – 0,27Å. В кристаллах с металлической связью (cм. рис.3.3.6 и 3.3.12 ) наблюдается перекрытие электронных оболочек с электронной плотностью для Li – 0,0263 эл/Å3
, а Al – 0,04 эл/Å3
. Их атомные радиусы составили соответственно 1,35 Å, 1,5 Å. [37]
Заключение
В первой главе настоящей работы рассмотрены свойства исследуемых объектов, а также методы расчета электронной плотности. Проведен анализ литературы, посвященной данной проблеме. Выяснилось, что по экспериментальным методам исследования распределения электронной плотности существует небольшое количество источников литературы.
Во второй главе анализируется неупругое рассеяние рентгеновских лучей веществом, экспериментальные методы исследования комптоновского рассеяния. Рассчитывается атомно – рассеивающий фактор и распределение электронной плотности в литии по комптоновским профилям.
В третьей главе описывается методика по измерению интегральной интенсивности брегговских рефлексов для лития, алюминия и фторида лития, определение интенсивности первичного пучка, приводятся данные расчета структурного фактора |F|2
, атомно – рассеивающего фактора f. Представлены обзорные рентгенограммы, таблицы, карты распределения электронной плотности и потенциала исследуемых объектов.
Основные результаты выполнения работы.
При выполнении работы были исследованы интегральные интенсивности брегговских рефлексов соединений. По их значениям строились атомно – рассеивающие факторы, карты распределения электронной плотности и потенциала. Выяснилось, что в основных кристаллографических направлениях электронная плотность не уменьшается до нуля, а формы атомов не являются строго шарообразными.
Были получены значения атомных факторов при неупругом и упругом рассеянии. Анализ результатов показал некоторое отличие значений друг от друга.
При рассмотрении карты электронной плотности фторида лития, обнаружились довольно интересные особенности. Между атомами фтора наблюдались «электронные мостики», образующие «электронный каркас», в который помещались атомы лития.
Литература
1. В.М. Ажажа, И.Л. Гнедая Щелочные металлы – получение, свойства, применение. Национальный научный центр «Харьковский физико-технический институт»,г. Харьков, Украина. ВАНТ №1 2006, 184-194.
2. Кэй Дж., Лэби Т. Таблицы физических и химических постоянных. – М.: Государственное издательство физмат литературы, 1962. – 247 с.
3. Справочник. Свойства элементов. Часть 1. Физические свойства. Под редакцией Г.В. Самсонова, - с.85.
4. Н.Н. Сирота, Э.А. Васильев. Химическая связь в полупроводниках и термодинамика., Минск, 1969. с. 59.
5. С.Н. Dauben, D. Templeton. Acta Cryst., 12, 341, 1955.
6. International tables for X-ray crystall. Birmingham, 1962.
7. H.H. Сирота, Е.М. Гололобов, А.У. Шелег, Н.М. Олехнович. Изв АН СССР, серия «Неорганические материалы», 1, 1673, 1965.
8. Н.М. Олехнович, Н.Н. Сирота. В кн.: «Химическая связь в полупроводниках и твердых телах». Минск, изд-во «Наука и техника», 1965.
9. Распределение валентной электронной плотности в преимущественно ионных кристаллах с различающимися подрешетками Браве //
Ю.Н. Журавлев, А.С. Поплавной
10. В.В. Никитин, изучение перераспределения электронной плотности в области точечных дефектов в алюминии методом функцонала электронной плотности//Московский инженерно-физический институт.
11. Немошкаленко Физика твердого тела. Зонная теория металлов. Киев: Науковадумка, 1985.-408 с.
12. Mikhin A.G., Diego N. D. Interionic potential model for the Al-Li system. Philosophical Magazine A, 1999, Vol. 79, No. 5, 1233-1246.
13.Turner D.E.,Zhu Z.Z., Chan C.T. and Ho K.M. Energetics of vacancy and substitutional impurities in aluminum bulk and clusters. 1997, Phys. Rev. B, 55.
14. Артемов М.И., Беховская К.С., Матюта А.А., Сидоров А.А/ Расчет распределения электронной плотности и потенциала в алмазе по рентгенографическим данным/Сборник студенческих научных работ . Вып. 7 – Брянск: РИО БГУ, 2008.-с. 127-132.
15. В.А. Бушуев, Р.Н. Кузьмин. Неупругое рассеяние рентгеновского и синхротронного излучения в кристаллах, когерентные эффекты в неупругом рассеянии. Журнал «Успехи физических наук». М.: Наука, том 122, вып. 1(500), 1977.
16. Яворский Б.М., Пинский А.А. Основы физики. Т. II. – М.: Наука, 1981.
17. W.C. Phillips, R. J. Weiss, ibid. 171, 790, 1968
18. Вейсс В. Физика твердого тела. – М.: Атомиздат, 1968
19. М.А. Блохин. Методы рентгеноспектральных исследований. –М.:Физматгиз, 1959 г.
20. Бахтияров А.В., Чернобережская С.А. Аппаратура и методы рентгеновского анализа. –М.: Машиностроение, 1972, вып. 11, с. 200.
21. Сидоров А.А., Бавкунов М.А., Исследование неупругого рентгеновского излучения на дифрактометре ДРОН-3, ВНКСФ 12. Новосибирск 2006, с.86-87
22. Малофеев С.Е./ Комптоновские профили кремния и германия на рентгеновском дифрактометре ДРОН - 3: дис. На соискание степени магистра/ С.Е. Малофеев. – Брянск, 2001. – 75 с
23. Горелик С.С. Рентгеновский и электроннооптический анализ. – М.: Наука,1987. – 870 с.
24. Б.Ф. Ормонт/ Введение в физическую химию и кристаллохимию полупроводников. – М.: Высшая школа,1982 г.
25. Куликов Е.Т., Штауберг И.Ф. Определение содержания молибдена в вольфрамовом покрытии локальным рентгенофлуоресцентным методом /Аппаратура и методы рентгеновского анализа: выпуск 21. – Л.: Машиностроение, -1978. с. 20.
26. Linder P. Theoretical Momentum Densities. // Physica Scripta. Vol. 15, 112-118, 1977.
27. Уманский Я.С. Рентгенография металлов. – М.: Металлургия, 1967. – 235с.
28. М.А. Блохин, И.Г. Швейцер/ Рентгеноспектральный справочник. – М.: Наука,1982. - 376 с.
29. Кульченков Е.А./ Структурный множитель и атомно-рассеивающий фактор кремния: дис. На соискание степени магистра/ Е.А. Кульченков. – Брянск, 2001. – 76 с
30. Г.С. Жданов. Основы рентгеновского структурного анализа. – М.:Гостехиздат, 1958 г.
31. Ковальский А.Е., Пивоваров Л.Х. Кристаллография, 1960, с. 280.
32. Л.И. Миркин/ Справочник по рентгеноструктурному анализу поликристаллов. – М.: Физматгиз, 1961г.
33. Я.С. Уманский. Рентгенография металлов. – М.: Металлургия,
1967 г.
34. Г.Б. Бокий. Кристаллохимия, второе издание. – М.: МГУ, 1960 г.
35. Киттель Ч. Введение в физику твердого тела. – М.: Наука, 1978. – 792 с.
36. Векилов Ю.Х. Межатомное взаимодействие и электронная структура твердых тел// Соровский образовательный журнал, №11, 1996 г.
37. Кацнельсон А.А., Кринчик Г.С. Структура твердого тела и магнитные явления. – М.: МГУ, 1982 г.
|