Приклади рішення задач з оптичної фізики
Задача 1
Об'єкт знаходиться на відстані  від збиральної лінзи з фокусною відстанню f=12см . Визначити відстань від лінзи до зображення. від збиральної лінзи з фокусною відстанню f=12см . Визначити відстань від лінзи до зображення.
Дано:  , ,  . .
Знайти: 
Рішення. Використовуючи формулу лінзи
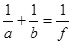 , ,
визначимо
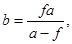
 . .
Відповідь. 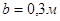
Задача 2
Пучок світла, що сходиться, падає на розсіювальну лінзу з фокусною відстанню f=18см. Якщо пучок сходиться на відстані 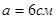 за лінзою (мал.1), визначити положення зображення. за лінзою (мал.1), визначити положення зображення.
Дано: 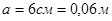 , , 
Знайти: 

Мал.1
Рішення. Оскільки лінза розсіювальна і джерело світла уявне (утворене променями, що сходяться), то формула лінзи перетвориться до наступного виду
 , ,
Відкіля
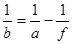 , ,
 , ,
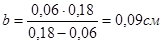 . .
Відповідь.  . .
Задача 3
оптичний лінза фокусний
Об'єкт розташований на відстані 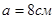 від лінзи, що створює уявне зображення предмета зі збільшенням від лінзи, що створює уявне зображення предмета зі збільшенням  . Визначити фокусну відстань лінзи і відстань від лінзи до зображення. . Визначити фокусну відстань лінзи і відстань від лінзи до зображення.
Дано: 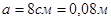 , , 
Знайти:
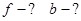
Рішення. Оскільки отримано збільшене зображення, то лінза є збиральною. Збільшення, що дається лінзою
 , ,
де  розмір зображення, розмір зображення,  розмір об'єкта. розмір об'єкта.
Формула лінзи в цьому випадку має вид
 . .
З останніх двох співвідношень одержуємо
 , ,
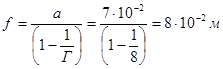 . .
Відстань від зображення до лінзи дорівнює

 . .
Відповідь. 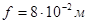 , ,  . .
Задача 4
На якій відстані від збиральної лінзи з фокусною відстанню f=20см, треба помістити предмет, щоб збільшення, що дається лінзою дорівнювало а) 1; б) 4.
Дано:  , ,  . .
Знайти: 
Рішення. Збільшення рівне одиниці можна одержати тільки у випадку дійсного зображення. У цьому випадку формула лінзи має вид
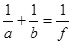 . .
Перепишемо формулу, з урахуванням вираження для збільшення лінзи
 , ,
Відкіля
 , ,
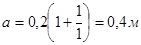 . .
Якщо збільшення дорівнює чотирьом, то зображення може бути як дійсним, так і уявним.
У випадку дійсного зображення
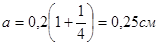 . .
Для уявного зображення формула лінзи має вид

 , ,

Відповідь. 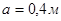 , ,  , ,  . .
Задача 5
Яка найменша можлива відстань  між предметом і його дійсним зображенням, створюваним збиральною лінзою з головною фокусною відстанню f=12см ? між предметом і його дійсним зображенням, створюваним збиральною лінзою з головною фокусною відстанню f=12см ?
Дано: 
Знайти: 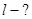
Рішення.
Відстань між об'єктом і зображення дорівнює 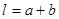 . Оскільки зображення дійсне, то формула лінзи має вид . Оскільки зображення дійсне, то формула лінзи має вид
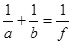 . .
Перетворимо останнє вираження
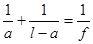 , ,
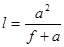 . .
Продиференціюємо останнє вираження

 . .
З останнього виразу одержуємо
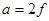 . .
Визначимо відстань від лінзи до зображення
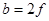 . .
Таким чином, найменша відстань між предметом і його дійсним зображенням дорівнює
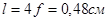 . .
Відповідь. 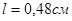
Реклама

Задача 6
Коли предмет знаходився в точці А, лінза давала збільшення  , а коли предмет перемістили в точку В, збільшення стало рівним , а коли предмет перемістили в точку В, збільшення стало рівним  . Яким буде збільшення, якщо предмет буде знаходитися в середині відрізка АВ? (мал.2 ) . Яким буде збільшення, якщо предмет буде знаходитися в середині відрізка АВ? (мал.2 )

Мал.2
Дано:  , ,  . .
Знайти: 
Рішення.
Застосовуючи формулу лінзи
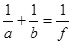
і формулу, що визначає збільшення об'єкта
 . .
Одержимо наступні співвідношення
 , ,
де  відстані від об'єкта до лінзи у випадку, коли об'єкт знаходився в точці А і В, відповідно. відстані від об'єкта до лінзи у випадку, коли об'єкт знаходився в точці А і В, відповідно.
Збільшення, що буде отримане, коли об'єкт знаходиться в середині відрізка АВ, дорівнює
 . .
Вирішуючи отримані рівняння спільно, одержимо
 . .
Відповідь.  . .
Задача 7
Відношення радіусів кривизни поверхні лінзи дорівнює  . При якому радіусі кривизни опуклої поверхні оптична сила лінзи дорівнює 10дптр. . При якому радіусі кривизни опуклої поверхні оптична сила лінзи дорівнює 10дптр.
Дано:  , , 
Знайти: 
Рішення. Оптична сила лінзи дорівнює
 , ,
де  показник заломлення матеріалу лінзи, показник заломлення матеріалу лінзи,
 показник заломлення матеріалу середовища, показник заломлення матеріалу середовища,
 радіуси кривизни поверхні лінзи. радіуси кривизни поверхні лінзи.
Оскільки лінза виготовлена зі скла, то  , показник заломлення середовища приймемо рівним одиниці. , показник заломлення середовища приймемо рівним одиниці.
За умовою задачі  , тоді , тоді
 , ,
 . .
Відповідь.  . .
Задача 8
Зі скляної пластинки були виготовлені три лінзи (мал.1.37). При цьому виявилося, що оптична сила системи (1,2) дорівнює -2дптр, а оптична сила системи (2,3) дорівнює -3дптр. Знайти оптичну силу всіх лінз.
Дано: 
Знайти: 
Рішення.

Мал.4
Оскільки лінзи утворять плоско-паралельну пластинку, паралельні промені, що падають на неї, також виходять паралельним пучком.
Отже, оптична сила плоско-паралельної пластинки дорівнює нулю
 . .
За умовою задачі:
 . .
Вирішуючи отримані рівняння спільно, визначимо оптичну силу кожної лінзи
 . .
Відповідь.  . .
Задача 9
Плоско-опукла лінза з радіусом кривизни 50см має оптичну силу  . Як зміниться ця величина, якщо посріблити плоску поверхню лінзи? сферичну поверхню? . Як зміниться ця величина, якщо посріблити плоску поверхню лінзи? сферичну поверхню?
Дано:  , , 

Рішення. 1) Якщо посріблити плоску поверхню, то світло, що падає на лінзу, пройде через неї, відіб'ється від плоскої поверхні і знову пройде через лінзу. Тому результуюча оптична сила система буде дорівнює
 , ,
де  - оптична сила лінзи, - оптична сила лінзи,  оптична сила плоского дзеркала. Оптична сила плоского дзеркала дорівнює оптична сила плоского дзеркала. Оптична сила плоского дзеркала дорівнює
 , ,
де 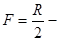 фокусна відстань дзеркала. Для плоского дзеркала фокусна відстань дзеркала. Для плоского дзеркала 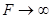 , тому , тому 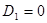 . .
Отже, результуюча оптична сила дорівнює
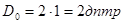 . .
2) Якщо посріблити сферичну поверхню, те результуюча оптична сила
 , ,
де  - оптична сила лінзи. Оптична сила увігнутого дзеркала в цьому випадку буде дорівнювати - оптична сила лінзи. Оптична сила увігнутого дзеркала в цьому випадку буде дорівнювати
 . .
Отже, результуюча оптична сила системи дорівнює
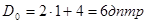 . .
Відповідь.  , , 
Задача 10
За допомогою товстої лінзи на екрані отримане зображення світної точки у вигляді світлої цятки - результат сферичної аберації. Щоб зменшити аберацію, застосована кругла діафрагма. а) Куди треба перемістити екран, щоб одержати різке зображення крапки? б) Куди треба перемістити екран, якщо буде закрита центральна частина лінзи?
Реклама

Відповідь.
а) При сферичній аберації промені, що падають від краю лінзи, заломлюються сильніше, ніж центральні промені. Якщо для корекції зображення застосована кругла діафрагма, що залишає тільки центральні промені, то екран треба відсунути далі від лінзи.
б) Якщо буде закрита центральна частина отвору (центральні промені), то буде відбуватися фокусування бічних променів і тому екран треба присунути до лінзи.
Задача 11
Дальня і ближня точки найкращого зору для короткозорої людини складають відповідно 200см і 15см.
Лінзу з якою фокусною відстанню треба помістити на відстані 2см від очей людини, щоб її око було акомодованим на нескінченність? Як зміниться при цьому ближня точка найкращого зору?
Дано: 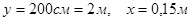 , , 
Знайти:

Рішення. Для поліпшення зору короткозорої людини варто помістити перед її очима розсіювальну лінзу. Уявне зображення, що сформоване на відстані 2м від ока, повинне бути сформоване на нескінченності. Відстань між лінзою і уявним зображенням дорівнює
 . .
Застосуємо формулу лінзи
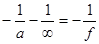
з урахуванням того, що зображення сформоване на нескінченності.
Тоді
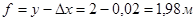
Оскільки лінза розсіювальна, то оптична сила лінзи дорівнює
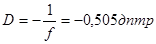 . .
Ближня точка найкращого зору була розташована на відстані  . Нове положення ближньої точки таке, що об'єкт, розташований у цій позиції, дає уявне зображення на відстані . Нове положення ближньої точки таке, що об'єкт, розташований у цій позиції, дає уявне зображення на відстані  від лінзи. Використовуючи формули лінзи, одержимо від лінзи. Використовуючи формули лінзи, одержимо
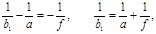
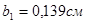 . .
Отже, ближня точка найкращого зору дорівнює
 , ,
 . .
Відповідь.  , , 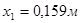 . .
Задача 12
Визначити оптичну силу окулярів для далекозорої людини, щоб вона бачила так само, як людина з нормальним зором. Відстань найкращого зору людини, що бачить нормально, складає 25см, далекозорої - 1 м.
Дано:  , ,  . .
Знайти: 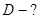
Рішення. Зображення предмета (уявне пряме), що дається окулярами зі збиральними лінзами, дозволяє розглядати його на відстані найкращого зору для далекозорої людини. При цьому сам предмет повинний знаходиться на відстані найкращого зору людини з нормальним зором. Для очей в окулярах «предметом» є вже не сам об'єкт, а створене лінзою уявне зображення цього об'єкта, розташоване на відстані найкращого зору для далекозорої людини 1м.
У цьому випадку формула лінзи має вид
 , ,
відкіля
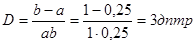 . .
Відповідь.  . .
|