Проверка гипотезы о нормальности закона распределения экспериментальных данных
1. Цель работы
Смоделировать работу генератора случайных двоичных чисел, имеющего закон распределения, заданного с помощью модели Гильберта; ограниченной последовательности 0 и 1.
2. Основная часть
В качестве входной последовательности выбрали следующую:
2) 1100101010111100001000010000001010101111000010010000100111100100
Моделирование случайной последовательности проводилась средствами языка С++ (среда BorlandBuilderC++ )
Текст программы
генератор двоичный число гильберт
//---------------------------------------------------------------------------
#include <stdlib.h>
#include <stdio.h>
#include <time.h>
#include <math.h>
//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include "systemsimulation.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TMainForm *MainForm;
//---------------------------------------------------------------------------
__fastcall TMainForm::TMainForm(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------------------------------------------------
//Вывод в поле RichEdit с заданием цвета выводимого текста
//REditAddColor(RichEdit1, "Test", clRed);
void __fastcall TMainForm::REditAddColor(TRichEdit *RichEditX, AnsiString Text, TColor Color)
{
//HideCaret(RichEditX->Handle);
RichEditX->SelAttributes->Color = Color; //задаёмцветтекста
RichEditX->Lines->Add(Text);//выводимтекст
RichEditX->Perform(EM_LINEINDEX, RichEditX->Lines->Count-1, 0);//устанавливаемпозициюкаретки
RichEditX->Perform(EM_SCROLLCARET, 0, 0);//прокручиваем поле к позиции каретки
}
//---------------------------------------------------------------------------
//Основываясь на входной последовательности формируем закон распределения
void __fastcall TMainForm::ZakonRaspr(AnsiString InSequence, double *P)
{
//P0 //P1 //P00 //P01 //P10 //P11
P[0] = 0; P[1] = 0; P[2] = 0; P[3] = 0; P[4] = 0; P[5] = 0;
int i;
//по определённому алгоритму формируем закон распределения
for(i = 1; i <= InSequence.Length(); i += 2)
Реклама

{
switch(((AnsiString)InSequence[i]+(AnsiString)InSequence[i+1]).ToInt())
{
case 00:
{
P[0] += 2;//P0
P[2] ++; //P00
} break;
case 01:
{
P[0] ++;//P0
P[1] ++;//P1
P[3] ++;//P01
} break;
case 10:
{
P[1] ++;//P1
P[0] ++;//P0
P[4] ++;//P10
} break;
case 11:
{
P[1] += 2;//P1
P[5] ++; //P11
} break;
}
}
P[2] /= InSequence.Length()/2;// P00/(длина входной последовательности разделённая на 2)
P[3] /= InSequence.Length()/2;// P01/(длина входной последовательности разделённая на 2)
P[4] /= InSequence.Length()/2;// P10/(длина входной последовательности разделённая на 2)
P[5] /= InSequence.Length()/2;// P11/(длина входной последовательности разделённая на 2)
P[0] /= InSequence.Length(); // P0/(длина входной последовательности)
P[1] /= InSequence.Length(); // P1/(длина входной последовательности)
}
//---------------------------------------------------------------------------
//генерирует случайное число с плавающей запятой в заданном диапазоне
double __fastcall TMainForm::Randouble(double min, double max)
{return (double)rand()/(double)RAND_MAX*(max-min)+min;
}
//---------------------------------------------------------------------------
//генерируем последовательность из случайных чисел
AnsiString GenSequence;
AnsiString __fastcall TMainForm::GenModel(double *P, int Count)
{
double Pi1, Pi2, Pi3, Pi4;
GenSequence = "";
Pi1 = P[2];
Pi2 = P[2] + P[3];
Pi3 = P[2] + P[3] + P[4];
Pi4 = P[2] + P[3] + P[4] + P[5];
double rnd;
for (int i = 0; i < Count; i+=2)
{
rnd = Randouble(0.0, 1.0);
if (rnd < Pi1) { GenSequence += "00"; }
if ((rnd >= Pi1) && (rnd < Pi2)) { GenSequence += "01"; }
if ((rnd >= Pi2) && (rnd < Pi3)) { GenSequence += "10"; }
if ((rnd >= Pi3) && (rnd < Pi4)) { GenSequence += "11"; }}
return GenSequence;}
//---------------------------------------------------------------------------
//моделирование случайной последовательности двоичных чисел
void __fastcall TMainForm::ModelSlPosl(double *P, int Count, bool Prn)
{
double **experiment = new double*[3];
for (int i = 0; i < 3; i++)
{experiment[i] = new double[6];
ZakonRaspr(GenModel(P, Count), experiment[i]);
}
REditAddColor(RichEdit1, "|---------------------------------------------------------------------------------------------------------|", clBlue);
REditAddColor(RichEdit1, "| Длина| | Номеропыта | Среднее | Теоретическое | |", clBlue);
Реклама

REditAddColor(RichEdit1, "|последовательности|Параметры| 1 | 2 | 3 | значение| значение|Ошибка|", clBlue);
REditAddColor(RichEdit1, "|---------------------------|---------------|-----|------|------|-------------|--------------------|---------|", clBlue);
AnsiString PrnScr;
double SrZnach, Err;
AnsiString Prametru[6] = {"P0","P1","P00","P01","P10","P11"};
for(int i = 0; i <= 5; i ++)
{SrZnach = (experiment[0][i] + experiment[1][i] + experiment[2][i])/3;
Err = fabs(P[i] - (experiment[0][i] + experiment[1][i] + experiment[2][i])/3);
PrnScr.sprintf("|%18d|%9s|%5.3lf|%5.3lf|%5.3lf|%9.3lf|%15.3lf|%6.3lf|", Count, Prametru[i], experiment[0][i], experiment[1][i], experiment[2][i], SrZnach, P[i], Err); REditAddColor(RichEdit1, PrnScr, clBlue);
switch(i)
{case 0:
{LineP0->Add(SrZnach, "при N = " + (AnsiString)Count, clRed);
if(Prn)LineP0->Add(P[i], "Теорет.", clRed);
} break;
case 1:
{
LineP1->Add(SrZnach, "при N = " + (AnsiString)Count, clGreen);
if(Prn)LineP1->Add(P[i], "Теорет.", clGreen);
} break;
}
}
for (int i = 0; i < 3; i++) { delete [] experiment[i]; }
delete [] experiment;
}
//---------------------------------------------------------------------------
void __fastcall TMainForm::StartSimulationClick(TObject *Sender)
{LineP0->Clear();
LineP1->Clear();
RichEdit1->Lines->Clear();
StartSimulation->Enabled = false;
double P[6];
//формируем закон распределения
ZakonRaspr(InSequence->Lines->Strings[0], P);
//проводим моделирование случайной последовательности двоичных чисел
//для различных длин последовательностей
ModelSlPosl(P, 100);
ModelSlPosl(P, 1000);
ModelSlPosl(P, 10000, true);
StartSimulation->Enabled = true;}
//---------------------------------------------------------------------------
При моделировании использовался генератор случайных чисел с равномерным распределением: при моделировании события А, наступающего с вероятностью Р, берется случайное число х из равномерного распределения на интервале (0, 1) и сравнивается с Р. Если х≤Р, то считается, что событие А наступило, в противном случае наступило событие Ā.
Моделирование случайной последовательности двоичных чисел проводилось для различных длин последовательностей (N=100, N=1000, N=10000), результаты которого представлены на рис. 1, 2

Рис. 1
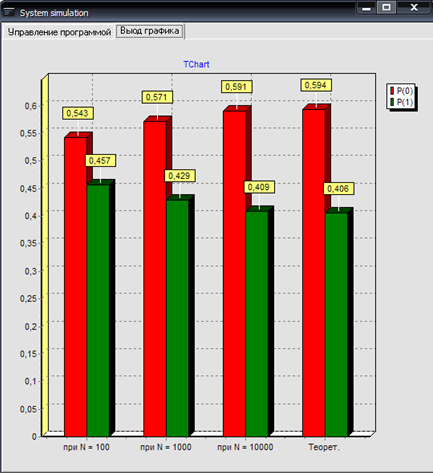
Рис. 2
3. Вывод
При моделировании
В ходе выполнения задания смоделировали работу генератора случайных двоичных чисел, подчиняющегося равномерному закону распределения, заданного с помощью модели Гильберта; ограниченной последовательности 0 и 1. Мы представили законы распределения случайных чисел, заданных в неявном виде, в виде гистограмм, а далее с помощью языка программирования С++ обеспечили процедуру генерирования случайных чисел, с различными длительностями их последовательности, соответствующих вышеуказанному закону распределения.Из рис.1,2 видно, что при увеличении длины последовательности экспериментально полученные данные приближаются к теоретическим данным.
|