Содержание
Занятие 1 - Определение инерционных характеристик главного вала горячештамповочного автомата
Занятие 2 - Обработка эксперимента по определению приведенного модуля объемной упругости жидкости
Занятие 3 - Расчет коэффициентов математической модели на примере исследования операции вырубки листовых образцов
Занятие 4 - Исследование операции вытяжки цилиндрического стакана из плоской заготовки
Занятие 5 - Обработка данных экстремальных экспериментов на примере исследования операции вытяжки листовых образцов
Занятие 6 - Исследование операции обжима
Занятие 7 - Оптимизация раскроя листового материала
Занятие 8 - Обработка данных экспериментов с несколькими выходными переменными
Цели работы:
· познакомиться с основными понятиями электронной таблицы
· освоить основные приемы заполнения и редактирования таблицы
· научиться сохранять и загружать таблицы
Постановка задачи:
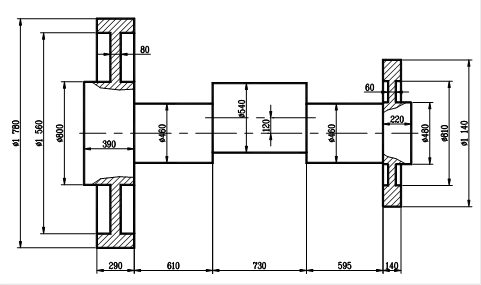
Определить массу и момент инерции главного вала горячештамповочного автомата:
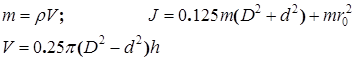
m
- масса цилиндра; J
- момент инерции цилиндра
r
=7850кг/м3
- плотность
V
- объем; D
- наружный диаметр; d
- внутренний диаметр; h
- высота
r0
- расстояние от оси цилиндра до оси вращения
Последовательность выполнения
1. Запустить EXCEL
2. Развернуть окно EXCEL во весь экран и рассмотреть его
(Используйте стандартные кнопки управления окном, расположенные в правом верхнем углу окна)
2.1. Основные элементы окна:
· верхняя строка - заголовок окна с кнопками управления
· вторая строка - меню EXCEL
· третья и четвертая строки - панели инструментов Стандартная и Форматирование
· пятая строка - строка редактирования формул
· строки между пятой и предпоследней - рабочее поле таблицы, состоящее из пронумерованных ячеек
· вторая снизу - ярлыки листов (для переключения между рабочими листами) и полоса прокрутки
· последняя строка - строка состояния
2.2. прочитать назначение кнопок панели Стандартная и Форматирование, медлено перемещая курсор по кнопкам.
3. Произвести настройку экрана
3.1. В меню Вид, установить флажки b (если их нет) щелчком мыши в следующих элементах: Строка формул, Строка состояния
3.2. В меню Вид выбрать команду Панелиинструментов4, в открывшемся подменю установить флажки b в следующих элементах: Стандартная, Форматирование.
Реклама

3.3. Вменю Сервис, выбрать команду Параметры… и раскрыть вкладку Вид,
3.4. Проверить установку флажков и переключателей
В группе Отображать - Строкаформул, строкасостояния
В группе Примечания - Только индикатор
В группе Объекты - Отображать.
В группе Параметры окна - всекроме Авторазбиение на страницы, Формулы
Раскрыть вкладку Общие и проверить установку переключателя Защита от макровирусов, установить Листов в новой книге - 3.
Нажать кнопку ОК
4. Основные понятия электронных таблиц
4.1. Рабочее
поле
- 16384строки, 256столбцов. Каждое пересечение строки и столбца образует ячейку, в которую можно вводить данные (текст, число или формулу)
4.2. Номер
строки (числа на левой границе рабочего поля), буква
столбца на верхней границе рабочего поля (A-Z,AA-AZ,BA-BZ…)
4.3. Ячейка
- пересечение строки и столбца - может содержать текст, число, формулу, имеет уникальный адрес
, состоящий из буквы столбца и номера строки (например B3)
4.4. Указатель
ячейки - жирный черный прямоугольник, с точкой в правом нижнем углу, определяющий текущую ячейку. Может перемещаться мышью (щелчок левой клавишей мыши по ячейке) и клавишами управления курсором (на клавиатуре)
· Выделите ячейку D4 - мышью, а затем вернитесь в ячейку A1 с помощью клавиш управления курсором.
4.5. Блок
- прямоугольная область смежных ячеек, Адрес
блока состоит из координат противоположных углов, разделенных двоеточием (B13: C19)
4.6. Книга
- программа на EXCEL, состоит из (по умолчанию) рабочих листов (по умолчанию - 3 для Excel97 и 16 для Excel7), переход от одного листа к другому - щелчком по ярлыку
· перейти к Лист3, вернуться к Лист1
5. Выделение основных элементов
5.1. мышью
строки (столбца
) - щелкнуть мышью по цифре (букве) - имени строки (столбца)
нескольких смежных строк (столбцов) -
щелкнуть по цифре (букве) первой строки (столбца) и не отпуская кнопку мыши протащить курсор до последней строки (столбца)
блок
- щелкнуть мышью по угловой ячейке блока (например, левый верхний угол) и не отпуская кнопки протащить курсор до противоположной угловой ячейки (например, правый нижний угол), либо щелкнуть по первой угловой ячейке блока, а затем с нажатой клавишей Shiftпо противоположной угловой ячейке блока.
несмежные ячейки (блоки) -
выделить первый блок (ячейку, столбец, строку), а затем выделить последующие с нажатой клавишей CTRL
· выделить блок B2: E12 - первым способом, D3: F14 - вторым,
Реклама

· выделить строки, столбцы 3, F, 1: 5, J: M
· выделить несмежные блоки (A2: B5; D3: E8), (8: 12; D: E)
5.2. клавиатурой: выделение блока-
перейти в ячейку, занимающую угол блока,
нажать SHIFT и раздвигать область клавишами управления курсором
· выделить блок C4: F10
5.3. весь лист - нажать на пустую кнопку в левом верхнем углу на пересечении номеров и строк
6. Основные приемы заполнения таблиц данными (текст, число, дата, время, формула) - общий принцип - переместиться в нужную ячейку, набрать данные (не более 240 символов), нажать ENTER, или перейти в другую ячейку мышью или клавишами
6.1. Текст - если первый символ - буква, то EXCEL автоматически считает данные - текстом, если текст начинается с цифры, то нужно сначала ввести символ апостроф ‘ (в латинском режиме). По умолчанию текст прижимается к левой границе. При вводе данных в правую ячейку изображение текста будет обрезано, но сам он сохранится
· ввести в ячейку A1 текст:
· Расчет массы и момента инерции главного вала автомата AO339 (в дальнейшем подобные задания будут записаны как:
· A1 ® Расчет массы и момента инерции главного вала автомата AO339)
· A2 ® Выполнен
6.2. Числа - начинаются со знака или без него. Если число очень большое (или маленькое) то EXCEL отображает его в экспоненциальной форме (3Е10 - означает 3´1010
). Если необходимо ввести десятичное число - то в качестве разделителя используется либо десятичная точка, либо десятичная запятая (в зависимости от настройки Windows). По умолчанию число прижимается к правому краю.
Занесите в ячейки данные, необходимые для расчета инерционных параметров венца зубчатого колеса
· A4®1.780 (с точкой!) (это будет наружный диаметр участка (в метрах))
· B4®1,560 (с запятой!) (это - внутренний диаметр)
Проверьте в какой ячейке введено десятичное чисто (оно будет прижато к правому краю), исправьте число в ячейке, в которой десятичный разделитель был введен неправильно. Для правильного ввода десятичного разделителя, независимо от настройки, следует пользоваться точкой справа на дополнительной клавиатуре.
Исправления можно выполнять либо непосредственно в ячейке, предварительно указав на нее курсором и выполнив двойной щелчок правой клавишей мыши, либо в строке формул, для чего необходимо сначала одинарным щелчком выделить нужную ячейку, а затем перевести курсор в строку формул, щелкнув правой клавишей мыши в позиции редактирования.
· С4 ® 0,29 (это - высота участка)
· D4 ® 0 (это - расстояние до оси вращения)
6.3. Дата - через дробь дд/мм/гг, дд-мм-гг, (либо месяц буквами, в зависимости от настройки английским или русскими) - после фиксации в качестве разделителя используется точка.
6.4. EXCEL преобразует дату в число равное количеству прошедших суток от 1 января 1990 г
· B2 ® текущая дата (например для 12 марта: 12-04)
6.5. Формула - арифметическое выражение, состоящее из последовательности чисел, ссылок на ячейки и функций, соединенных арифметическими знаками и начинающихся со знака =. Завершение ввода формулы - нажатие клавиши ENTER, либо щелчок мышью по кнопке b (зеленого цвета) в строке формул. В ячейке после этого появляется результат. Формула отображается в строке формул.
Можно вводить ссылки на ячейки вручную, а можно путем указания на соответствующую ячейку мышью.
Например для ввода в ячейку Е4 формулы для определения массы зубчатого венца =3,14*7850* (A4^2-B4^2) *C4/4 необходимо выполнить следующую последовательность действий:
установить курсор в ячейку Е4
набрать =3,14*7850* (
с клавиатуры щелкнуть по ячейке A4
набрать ^2-
щелкнуть по ячейке B4
набрать ^2) *
щелкнуть по ячейке C4
набрать /4
щелкнуть по кнопкеb (зеленого цвета) в строке формул
6.6. Попробуйте заменить какие-нибудь числа в ячейках A4: C4 и убедитесь, что значения в ячейке E4 также изменяются. Проверьте на калькуляторе правильность записанной формулы.
6.7. Число p=3.14¼можно заменить его точным значением, использовав встроенную функцию ПИ (). Для этого необходимо двойным щелчком выделить число 3,14 и на этом месте ввести с клавиатуры ПИ (), либо воспользоваться мастером функций, выполнив следующую последовательность действий:
щелкнуть по кнопке fx
на панели - Стандартная
в открывшемся окне в группе Категория
выбрать - Математические
в группе Функции
выбрать функцию ПИ
нажать на кнопку ОК
в нижней части окна
щелкнуть по кнопкеb (зеленого цвета) в строке формул
7. Заполните ячейки A5¼D12 значениями размеров соответствующих участков вала, разбив его на цилиндрические участки и поместив в столбец Aзначения наружного диаметра, в столбец B - внутреннего, C - высоты цилиндра.
8. Основные приемы редактирования таблиц
8.1. Операции с ячейками, строками, столбцами, блоками.
Прежде, чем произвести какие-либо действия с элементом его надо выделить
.
Действия по перемещению, копированию, удалению и очистке блока можно производить несколькими способами:
-с помощью кнопок панели инструментов (Вырезать, Копировать, Вставить)
-через меню (в меню Правка команды Вырезать, Копировать, Вставить, Удалить, Очистить, Заполнить)
-с помощью мыши, методом DragandDrop (перетащи и брось) -
-с помощью контекстно-зависимого меню (меню правой кнопки мыши при щелчке по выделенному элементу)
8.2. Копирование
-методом DragandDrop
выделить ЧТО (диапазон ячеек которые копируются),
перевести указатель мыши на границу выделенного диапазона так, чтобы указатель превратился в стрелку, направленную влево под углом
нажать левую клавишу мыши и удерживать клавишу CTRL на клавиатуре. Рядом с указателем появится маленький знак + признак операции копирования.
мышью выделенный диапазон перетащить в необходимый диапазон книги. В процессе перетаскивания границы копируемого диапазона будут отображаться на экране, что облегчает позиционирование копируемого диапазона на новое место.
после позиционирования копируемого диапазона на новом месте следует сначала отпустить левую клавишу мыши, а затем клавишу CTRLна клавиатуре.
-кнопками панели инструментов - выделить ЧТО, кнопка Копировать, выделить КУДА, кнопка Вставить
· скопировать A1 ® в A14 методом Drag and Drop
· скопировать A4: E4 в A15: E15 с помощью кнопок панели инструментов. Обратить внимание на изменение формулы в ячейке E15 - ссылки на ячейки с исходными данными автоматически изменились. При выполнении операции копирования, в том случае, если в ячейке записана формула, то ссылки на ячейки в формуле изменяются в соответствии с расстоянием (по столбцам и строкам) на которое был перемещен диапазон.
8.3. Очистка - выделить необходимы диапазон и нажать DEL
· очистить ячейки в 14 и 15 строках
8.4. Перемещение выполняется аналогично копированию, только в методе DragandDropне надо держать нажатой клавишу CTRL, а при использовании кнопок панели инструментов вместо кнопки Копировать следует использовать кнопку Вырезать.
· переместить A4: E12 на один столбец вправо.
8.5. Заполнение - выделенные ячейки копируются несколько раз за одно действие. Методика заполнения: Выделить блок, навести курсор на маркер заполнения (жирный квадрат в нижнем правом углу выделенного блока или ячейки), маркер заполнения должен превратиться в крестик, затем раздвигать выделенную область
· E4 ® E4: E12 (весь столбец должен автоматически заполниться нулями)
· F4 ® F4: F12 (ячейки должны заполниться значениями, вычисленными по скопированным формулам)
· Занесите в ячейку G4 формулу для вычисления момента инерции =F4* (B4^2+C4^2) /8+F4*E4^2 и заполните ею диапазон G4: G12.
· В строчке, соответствующей участку шейки кривошипа занесите в ячейку столбца D значение эксцентриситета. Убедитесь, что значение момента инерции автоматически пересчиталось.
8.6. Удаление - в отличие от очистки удаленные ячейки схлопываются - т.е. другие ячейки занимают место удаленных. Осуществляется через меню Правка, Удалить (или контекстное меню - щелчок правой кнопкой мыши по нужной ячейке и из предложенных действий выбрать нужное).
8.7. Примечание: Если Вы случайно совершили неправильное действие (например удалили лишнюю ячейку), с помощью кнопки Отменить на панели инструментов или команды Отменить меню Правка можно отменить последнее действие (для EXCEL5,7) или несколько последних действий (для EXCEL97)
· Удалить строку 2 через меню Правка
· удалить ячейку A1 через контекстно-зависимое меню
· отменить удаление
8.8. Автозаполнение - позволяет быстро создавать различные типовые последовательности. Работает также, как и обыкновенное заполнение. EXCEL анализирует выделенные ячейки и если находит зависимость, то интерполирует ее на другие ячейки
-Арифметическая прогрессия
· A4® 1; A5 ® 2; выделить A4: A5; маркер заполнения протащить до A12
-Дни недели
· A17® Понедельник, Заполнить до H17
-Месяцы
· A18® Январь, Заполнить до K18
-Даты
· A19® Скопировать дату из ячейки B2, Заполнить до H19
· Удалить строки 17: 19
8.9. Изменение ширины столбцов и высоты строк.
С помощью мыши
- Плавное изменение (подвести указатель к правой границе столбца, указатель изменил вид, зацепился - потащил, отпустил) и подбор минимального значения (подвести указатель к правой границе столбца, указатель изменил вид, дважды щелкнуть левой клавишей мыши).
С помощью меню
- Формат, Строка, Высота (Автоподпор высоты) или Столбец, Ширина (Автоподбор ширины)
· Подберите мышью ширину столбцов таблицы в соответствии со своим вкусом
· Строка 9 ®высота 30, а затем обратно® 12.75 (через меню Формат)
9. Абсолютная относительная и смешанная адресация ячеек и блоков.
Использовавшаяся до сих пор адресация - относительная. При ее использовании EXCEL запоминает расположение относительно текущей ячейки и при копировании автоматически меняет адрес.
Иногда при копировании необходимо сохранить ссылку на конкретную ячейку (столбец, строку) - абсолютная адресация. Перед буквой столбца и номером строки следует вставить символ $ (можно после вставки относительного адреса нажать F4 тогда символы $ вставятся автоматически) - такая адресация называется абсолютной
Иногда при копировании необходимо изменять только один параметр адреса. Тогда символ $ ставится только там, где он необходим (только перед буквой столбца или номером строки) - такая адресация называется смешанной.
-В нашем примере при определении массы в формулу вставляли конкретное значение плотности материала 7850кг/м3
. В том случае, если бы вал сделали из материала, имеющего другую плотность, нам нужно было бы менять каждую формулу для определения массы. Попытаемся обобщить таблицу на случай произвольного материала
· В ячейку A2 ввести текст Плотность материала
· В ячейку B2 внести значение 7850
· Выделить ячейку F3. В строке формул появится формула для вычисления массы.
· Выделить в формуле число 7850 двойным щелчком левой клавиши мыши, затем щелкнуть по ячейке B2 (в формуле значение 7850 должно замениться на B2) и нажать на клавишу F4 в верхнем ряду клавиатуры (B2 должно измениться на $B$2). После этого щелкнуть по кнопкеb (зеленого цвета) в строке формул.
· Заполнить формулой в ячейке F4 диапазон F4: F12 и убедиться что в каждой формуле есть ссылка $B$2 на адрес ячейки со значением плотности.
· Изменить плотность материала и убедиться, что произведен пересчет во всех ячейках одновременно.
· Переместить диапазон A3: G12 на одну строчку вниз и убедиться, что абсолютная адресация в формулах при перемещении и копировании сохраняется, в отличии от относительной.
10.Определим массу и момент инерции вала. Для этого необходимо просуммировать значения, стоящие в соответственно в столбцах Fи G. Для суммирования столбца Fнеобходимо выделить ячейку F13, нажать кнопку Автосуммирование (S) на панели инструментов, убедиться, что диапазон суммирования выбран программой правильно и нажать клавишу Enter на клавиатуре. В ячейке F13 появится значение суммы масс по участкам.
· Просуммировать значения в столбце G
11.Добавьте заголовки к столбцам таблицы и заголовок для строки с результатами суммирования
12.Операции с таблицей в целом - сохранить, сохранить как, открыть, создать. Выполняются либо из меню Файл, либо используя соответствующие кнопки панели инструментов.
· сохранить work1. xls в своем каталоге
13.Завершить работу
14.Запустить EXCEL, вернуться к документу work1. xls и предъявить его преподавателю.
15.Итоги. Проверьте
15.1. знаете ли Вы, что такое: строка, столбец, ячейка, лист, книга, контекстно-зависимое меню, панель инструментов, абсолютная, относительная и смешанная адресация
15.2. умеете ли Вы: вводить текст, редактировать данные, изменять размеры ячеек, перемещать, копировать, заполнять, удалять, сохранять
16.Предъявить преподавателю краткий конспект занятия.
Цели работы:
· закрепление основных приемов заполнения и редактирования таблицы
· освоение основных приемов форматирования таблицы (внешнего вида)
· освоение методов построения точечных графиков
· получение начальных сведений для построения регрессионных зависимостей
Постановка задачи:
Создать электронную таблицу для обработки данных эксперимента по определению приведенного модуля объемной упругости жидкости.
Последовательность выполнения опыта:
1. Аккумулятор винтового пресса-молота заряжается до начального давления 25 МПА.
2. Открывается вентиль, через который жидкость (минеральное масло) начинает вытекать в мерный объем (мензурку)
3. Фиксируется объем вытекшего масла через определенные промежутки текущего давления в аккумуляторе.
4. Опыт повторяется 3 раза
Модуль объемной упругости жидкости определяли путем обработки результатов эксперимента по следующему алгоритму:
1. Определяется объем вытекшего масла на каждом интервале замеров давления:
2. i=1
¼9
число точек фиксации объема вытекшего масла pi
=20,15,10,5,4,3,2,1,0
[МПа] - давления, при которых фиксируется объем масла Vi
-
объем вытекшего масла, соответствующийi-
мудавлению в аккумуляторе D
Vi
=
Vi
+1
-
Vi
, (
1) приi=1
¼8,
D
V9
=0
3. Вычисления по п1 выполняют для каждого из трех опытов
4. Вычисляют среднее значение изменения объема на каждом интервале:
5. D
Vср
i
= (
D
V1, i
+
D
V2, i
+
D
V3, i
) /3,
(2) где индексы 1, i 2, i 3, i
соответствуют номеру опыта и номеру интервала
6. Вычисляют среднее значение объема масла в точках фиксации давления по результатам трех опытов:
7. Vср
i
=
Vср
i+1
+
D
Vi
(
3) приi=8
¼1,
Vср9
=0
8. Строится график P=
f (
Vср)
и визуально определяют точку n
перехода от нелинейного начального к линейному конечному участку графика
9. Результаты соответствующие точкам i=1
¼
n
аппроксимируют прямой p=
b0+
b1*
Vср
(4)
10. Определяют приведенный модуль объемной упругости жидкости по формуле:
11. k=
V0
*
dp/
dVср
(5) гдеV0
=1,1577*104
см3
-
объем аккумулятораdp/
dVср
=
tana=
b1,
a -
угол наклона прямой, аппроксимирующей линейный участок зависимостиP=
f (
Vср)
Последовательность выполнения
1. Запустить EXCEL
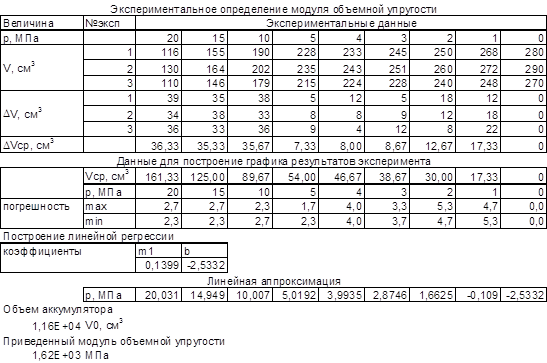
2. Создать таблицу с исходными данными эксперимента и поясняющими надписями в соответствие с прилагаемой ниже таблицей. Обратить внимание, что текст, целиком не помещающийся в ячейку вводится в ячейку, номер которой соответствует началу текста. Например, весь текст "Экспериментальное определение модуля объемной упругости" вводится в ячейку А1
При заполнении, там где это целесообразно, пользуйтесь методами автозаполнения и копирования, изученными на предыдущем занятии
Символы DVв тексте пояснений в таблице заменяют символы в D
V
формулах
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
| 1 |
Экспериментальное определение модуля объемной упругости |
| 2 |
Величина |
№эксп |
Экспериментальные данные |
| 3 |
p, МПа |
20 |
15 |
10 |
5 |
4 |
3 |
2 |
1 |
0 |
| 4 |
1 |
116 |
155 |
190 |
228 |
233 |
245 |
250 |
268 |
280 |
| 5 |
DV, см3 |
2 |
130 |
164 |
202 |
235 |
243 |
251 |
260 |
272 |
290 |
| 6 |
3 |
110 |
146 |
179 |
215 |
224 |
228 |
240 |
248 |
270 |
| 7 |
1 |
0 |
| 8 |
DV, см3 |
2 |
0 |
| 9 |
3 |
0 |
| 10 |
DVср, см3 |
0 |
| 11 |
Данные для построение графика результатов эксперимента |
| 12 |
Vср, см3 |
0 |
| 13 |
p, МПа |
20 |
15 |
10 |
5 |
4 |
3 |
2 |
1 |
0 |
| 14 |
погрешность |
max |
| 15 |
min |
| 16 |
Построение линейной регрессии |
| 17 |
коэффициенты |
m1 |
b |
| 18 |
| 19 |
Линейная аппроксимация |
| 20 |
p, МПа |
| 21 |
Объем аккумулятора |
| 22 |
1,1577E4 |
V0, см3 |
| 23 |
Приведенный модуль объемной упругости |
| 24 |
МПа |
3. Занести в ячейку С7 формулу (1), которая будет иметь вид =D4-C4 и распространить ее на диапазон C7: J9.
4. Занести в ячейку С10 формулу для определения среднего значения изменения объема D
Vср
i
Для этого можно воспользоваться встроенной функцией СРЗНАЧ. Рассмотрим порядок ввода формул с использованием встроенных функций на этом примере:
-установить курсор в ячейку C10
-нажать на кнопку 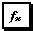 (
Мастер функции или Вставить функцию) на стандартной панели инструментов (
Мастер функции или Вставить функцию) на стандартной панели инструментов
-в открывшемся окне выбрать Категория: Математические, Функция: СРЗНАЧ и щелкните по кнопке ОК (для Excel97) или Шаг> (для Excel5.0,7.0)
-в открывшемся окне диалога в пункте Число1 вместо предложенного мастером функций диапазона занесите диапазон ячеек, для которых вы вычисляете среднее значение C7: C9 и щелкните по экранной кнопке OK (Закончить) Ввод диапазона можно осуществлять как вручную (обратите внимание на то, что клавиатура должна находиться в латинском регистре), так и мышью - что более предпочтительно.
-Для ввода диапазона с помощью мыши необходимо просто выделить мышью нужный вам диапазон в таблице (если нужный диапазон закрыт окном диалога, то окно можно передвинуть в другое место экрана методом DragandDrop)
5. Распространить формулу в ячейке С10 на диапазон
6. Для того, чтобы увидеть точное значение вычисленных величин (если Excelокруглил их до целых), выделите диапазон С10: J10 и несколько раз нажмите кнопку 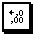 (Увеличить разрядность) на панели инструментов Форматирование. (Увеличить разрядность) на панели инструментов Форматирование.
7. В ячейку J12 внести формулу (3), которая будет иметь вид=K12+J10 и распространить ее на диапазон J12: C12. Если это необходимо, то увеличьте разрядность отображения величин.
8. В ячейки C14 и C15 занесите формулы для определения максимальной и минимальной погрешности вычисления объема, которые будут иметь вид:
microsoft excel электронная таблица
9. для C14: =МАКС (С7: C9) - C10 для C15: =C10-МИН (C7: C9) Функции МИН и МАКС находятся в категории Статистические мастера функций.
10.Распространите формулы из диапазона C13: C14 на диапазон C13: K14
11.
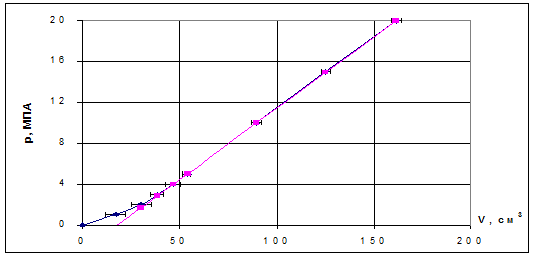
Построить график зависимости P=
f (
Vср):
-выделите диапазон ячеек B12: K13, на основании которого вы будете строить диаграмму.
-щелкните по кнопке Мастер диаграмм стандартной панели инструментов (в зависимости от версии Excel она имеет различный внешний вид, поэтому найдите ее сами с помощью всплывающих подсказок) либо воспользуйтесь командой меню Вставка-Диаграмма.
-следуйте указаниям Мастера диаграмм в каждом диалоговом окне, возникающим последовательно после нажатия экранных кнопок Далее> (или Шаг> для ранних версий). Ниже приведена последовательность действий для Excel97 (для ранних версий Excel последовательность и содержание окон несколько другое, но получаемый результат будет идентичен). Если Вас что-то не устраивает в построенной диаграмме, то в последующем ее можно изменить:
- Шаг1: Щелчком мыши выберите тип диаграммы Точечная, а вид - со значениями, соединенными сглаживающими линиями. Нажмите кнопку Далее.
- Шаг2: Если диапазон данных в окне ввода Диапазон указан верно, а вид диаграммы тот, который вы ожидаете, нажмите кнопку Далее. В противном случае в окне Диапазон введите нужный диапазон данных
- Шаг3: В окно Название диаграммы сотрите содержащиеся там данные; в окне Ось X введите: V, см3; в окне Ось Y введите: p, МПа. Нажмите кнопку Далее.
- Шаг4: В окне Поместить диаграмму на листе выберите пункт Имеющемся, рядом с которым выберите в открывающемся списке пункт Лист2. Нажмите кнопку Готово.
12.Как правило, вид созданной диаграммы мастером диаграмм бывает неудовлетворительным, поэтому диаграмму следует отформатировать. Выполните форматирование диаграммы в соответствие со следующими указаниями:
-Щелкните мышью по области диаграммы. Область диаграммы выделится черной рамкой, по углам которой и в середине сторон имеются черные квадратики - размерные маркеры. Кроме того в меню Excelдобавится пункт Диаграмма Для изменения размеров диаграммы необходимо буксировать размерные маркеры. Перед буксировкой необходимо навести указатель мыши на один из размерных маркеров. Указатель мыши при этом примет вид двунаправленной стрелки. После чего необходимо нажать левую клавишу мыши и перемещать (буксировать) маркер. Буксировка маркера, расположенного в середине стороны, позволяет изменять горизонтальные и вертикальные размеры диаграммы. Буксировка углового маркера позволяет изменять одновременно вертикальные и горизонтальные размеры.
-Для перемещения диаграммы необходимо навести указатель мыши на область диаграммы (указатель примет вид белой стрелки, направленной под углом влево-вверх) и отбуксировать ее на новое место
-Отбуксируйте диаграмму в левый верхний угол листа, а затем измените ее размеры так, чтобы она занимала примерно ¾ пространства листа.
-Диаграмма состоит из нескольких элементов. К ним, в частности, относятся:
- область диаграммы (весь чертеж)
- область построения диаграммы
- легенда
- ряды данных
- названия осей и т.п.
Для редактирования элемента его необходимо выделить. Это можно сделать нажатием стрелок перемещения курсора ↑ ↓ на клавиатуре, либо одиночным щелчком левой клавиши мыши по соответствующему элементу. При выделении в поле имени (крайнее левое поле в строке формул) появляется название элемента. Выделенный элемент отмечается размерными маркерами.
Редактирование выделенного элемент осуществляется через меню Формат, в котором появляется пункт для редактирования соответствующего элемента, либо нажатием клавиатурной комбинации Ctrl-1, которая позволяет произвести форматирование текущей ячейки, диапазона, элемента диаграммы или объекта.
Выделенный элемент можно перемещать, менять его размеры методом буксировки, а также удалять, нажав клавишу Del.
-Выделите диаграмму, щелкнув по области диаграммы
-Последовательно нажимая клавишу ↑ на клавиатуре обратите внимание на элементы диаграммы, присутствующие в построенной вами диаграмме.
-Удалите легенду
-Отбуксируйте название оси X (категорий) в правый нижний угол области диаграммы
-Измените размеры области построения диаграммы так, чтобы она занимала максимальный размер внутри области диаграммы. Выберите подходящий цвет заливки области построения (по нашему мнению для черно-белых принтеров наиболее целесообразно применять прозрачную заливку).
-Отобразите на диаграмме погрешности вычисления. Для этого выделите кривую (она имеет название Ряд "p, МПа"), нажмите клавиатурную комбинацию Ctrl-1. Затем в окне Формат ряда данных выберите вкладку X-погрешности, в который выберите вид показа - обе планки погрешностей, величина погрешностей - пользовательская, в графе "+" введите диапазон положительной погрешности, вычисленной Вами =Лист1! $C$14: $K$14 (это можно сделать и мышью, выделяя соответствующий диапазон в таблице), а в графе "-"=Лист1! $C$15: $K$15
-Добавьте (если их нет) линии сетки для значений по оси X. Для этого в меню Диаграмма выберите пункт Параметры диаграммы и на вкладке Линии сетки щелкните по пункту ОсьX - основные линии, после чего нажмите кнопку OK
-Отформатируйте осьYтак, чтобы график занимал всю область построения диаграммы. Для этого после выделения оси и перехода в окно редактирования одним из указанных выше способов (например с помощью клавиатурной комбинации Ctrl-1) выберите вкладку Шкала и в графе Максимальное значение поставьте максимальное значение давления в исходной таблице - 20. Посмотрите другие вкладки в окне форматирования оси. Возможно Вы захотите изменить и другие параметры и внешний вид элементов оси.
-Измените название оси категорий так, чтобы размерность объема была поставлена правильно: не см3, а см3
. Для это выделите название оси, затем выделите цифру 3 в размерности, нажмите клавиатурную комбинацию Ctrl-1 и в открывшемся окне форматирования шрифта щелкните мышью по пункту Верхний индекс раздела Эффекты.
13.Проанализируйте, начиная с какой точки график изменения объема становится линейным. По-видимому это будет точка, соответствующая давлению 4 МПа. Определите параметры прямой, которой можно аппроксимировать кривую изменения давления на линейном участке. Для этого следует воспользоваться встроенной функцией ЛИНЕЙН, позволяющей построить функцию вида y=b+m1*x1+¼+mi*xiна основе некоторого массива исходных данных методом наименьших квадратов. Функция ЛИНЕЙН относится к категории статистических. В данном случае воспользуемся "ручным" набором, без использования мастера функций.
Синтаксис функции
ЛИНЕЙН (известные_значения_y; известные_значения_x; константа; статистика)
- Константа - это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если константа имеет значение ИСТИНА (1), то b вычисляется обычным образом.
- Статистика - это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если статистика имеет значение ЛОЖЬ (0), то функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
14.Выделите диапазон ячеек C18: D18, затем в строке формул наберите следующую формулу =ЛИНЕЙН (C13: G13; C12: G12; 1; 0) и нажмите клавиатурную комбинацию Ctrl-Shift-Enter (по этой клавиатурной комбинации вводится единая формула для всего массива). Обратите внимание, что после ввода клавиатурной комбинации Ctrl-Shift-Enterнабранная формула заключается в фигурные скобки, что означает, что это формула массива, а не одной ячейки, а в ячейках C18: D18 появляются значения.
15.Постройте прямую, аппроксимирующую график на линейном участке, на той же диаграмме. Для этого сначала необходимо сформировать массив данных, а затем изменить диаграмму.
- В ячейку C20 введите формулу =$D$18+$C$18*C12 (вспомните, что для превращения относительной ссылки в абсолютную не обязательно вручную вводить знаки $ - достаточно нажать клавишу F4)
- Распространите формулу из ячейки C20 на диапазон C20: K20
- Выделите диаграмму на Листе2, затем в меню Диаграмма выберите пункт Добавить данные
- Для ввода в окно Диапазон нового ряда данных щелкните по закладке Лист1, в нем курсором мыши выделите диапазон C20: J20 и нажмите кнопку OK - на диаграмме появится график прямой.
16.Вычислите приведенный модуль объемной упругости рабочей жидкости, для чего в ячейку A24 введите формулу (5), которая будет иметь вид =A22*C18
17.Отформатируйте таблицу.
- Расположите заголовке по центру диапазона столбцов. Для этого выделите нужный диапазон столбцов и нажмите кнопку  (Центрировать по выделению) на панели инструментов Форматирование. Проделайте это для диапазонов A1: K1; C2: K2; A11: K11; A19: K19 (Центрировать по выделению) на панели инструментов Форматирование. Проделайте это для диапазонов A1: K1; C2: K2; A11: K11; A19: K19
- В необходимых местах добавьте линии границ ячеек. Выделите ячейки A2: K10, нажмите клавиатурную комбинацию Ctrl-1, выберите вкладку Границы, отметьте Все внешние и внутренние границы. Для ячеек K5,K8 уберите верхнюю и нижнюю границу (выделите ячейки, Ctrl-1, убрать границы). Аналогично оформите таблицы в диапазонах A12: K15; A17: D18; B20: K20.
-Измените формат показателей степени в размерностях см3. Для это нужной ячейке выделите цифру 3 в размерности, нажмите клавиатурную комбинацию Ctrl-1 и в открывшемся окне форматирования шрифта щелкните мышью по пункту Верхний индекс раздела Эффекты. Повторите это для ячеек A5, A8, B12, B22.
-В ячейках A8, A10 измените символы DVна DV. Для этого выделите Dв соответствующих ячейках, нажмите клавиатурную комбинацию Ctrl-1 и в открывшемся окне форматирования шрифта выберите шрифт Symbolв окне Шрифт
18.Посмотрите, поместится ли созданная Вами таблица на один лист при печати. Для этого нажмите кнопку  (Предварительный просмотр) на стандартной панели инструментов. Измените ширину столбцов A-Kтаким образом, чтобы все столбцы поместились на одной странице, и при этом все данные и надписи в столбцах были бы видны. Для плавного изменения ширины столбца достаточно щелкнуть по букве столбца мышью (выделить весь столбец), навести указатель курсора на границу столбца (указатель примет вид двунаправленной стрелки) и отбуксировать границу в нужное место. (Предварительный просмотр) на стандартной панели инструментов. Измените ширину столбцов A-Kтаким образом, чтобы все столбцы поместились на одной странице, и при этом все данные и надписи в столбцах были бы видны. Для плавного изменения ширины столбца достаточно щелкнуть по букве столбца мышью (выделить весь столбец), навести указатель курсора на границу столбца (указатель примет вид двунаправленной стрелки) и отбуксировать границу в нужное место.
19.Проверьте себя: приблизительный внешний вид таблиц и диаграммы приведен в приложении
20.Завершить работу, сохранив ее в файле work2. xls.
21.Запустить EXCEL, вернуться к документу work2. xls и предъявить его преподавателю.
22.Предъявить преподавателю краткий конспект занятия.
Цели работы:
- закрепление основных приемов создания и форматирования таблицы
- закрепление методов построения точечных графиков
- освоение основных методов обработки многофакторных экспериментов
Постановка задачи [1]
:
Исследуется влияние величины зазора Z между пуансоном и матрицей на качество среза и силу P, необходимую для вырубки листовых образцов.
Заготовки после вырубки осматривают и оценивают качество среза по 3-х бальной шкале. Наилучшим срезом, оцениваемым в 3 бала, считается состоящий из трех зон (I - зона скругления, II - блестящий поясок, III - зона скола) При этом зона Iдолжна иметь незначительный размер. Если эта зона возрастает по сравнению с наименьшей, полученной при вырубке заготовки из данного материала, или вырубленный образец имеет заметный прогиб, то качеству среза присваивают оценку 2 бала. Если же поверхность рваная, с дополнительными поясками, то качеству среза присваивают оценку 1 балл.
Вырубаются кружки из стали 45 и меди в матрице диаметром 25 мм. Толщина заготовок 7 мм. Уровни варьирования зазора, по отношению к толщине заготовки составляют 0.03, 0.05 и 0.1.
По результатам опыта необходимо построить зависимость качества реза и силы вырубки от зазора между пуансоном и матрицей для каждого из используемых материалов и определить оптимальные величины зазоров.
Методы решения с использованием Excel:
При использовании методов планирования эксперимента изучаемый объект представляют в виде некоторого "черного ящика", выходные параметры которого зависят от входных параметров. Математическая модель, отражающая связь между выходными и контролируемыми входными параметрами записывают в виде полинома следующего вида:
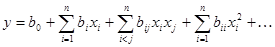 (1) (1)
Задачей обработки эксперимента является определение значений коэффициентов регрессионной модели. Расчет коэффициентов производят на основе метода наименьших квадратов, путем минимизации суммы квадратов разностей между экспериментальными и рассчитанными по модели значениями. Естественно, что количество опытов в эксперименте должно быть не меньше количества неизвестных коэффициентов в модели.
Для нахождения коэффициентов моделей типа (1) в Excelприменяют встроенную функцию ЛИНЕЙН. Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Уравнение для прямой линии имеет следующий вид:
y=
b+
m1
d1
+
m2
d2
+. (
2)
где зависимое значение y
является функцией независимых значений d
i
. Значения m
i
- это коэффициенты, соответствующие каждой независимой переменной d
i
, а b
- это постоянная.
Сравнение формул (1) и (4) показывает, что если в качестве переменных di
использовать значения переменных xi
, а также различные функции от xi
, то коэффициент b
в формуле (2) имеет смысл коэффициента b0
в формуле (1), а коэффициенты mi
- соответственно коэффициентов bi
,
bij
,
bii
Функция ЛИНЕЙН возвращает массив значений коэффициентов в обратном порядке {mn
; mn‑1
;.; m1
; b}. ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Синтаксис функции: ЛИНЕЙН (Y; D; K; C)
Здесь: Y - множество (обычно столбец) известных значений y
D - множество (обычно диапазон) известных значений d
. Если множество Y - столбец, то диапазон Dдолжен иметь столько же строк, сколько столбец значений Y. Количество столбцов диапазона Dопределяет количество n
неизвестных коэффициентов mi
регрессионной модели
K - логическое значение, которое указывает, требуется ли, чтобы константа b
была равна 0. Если K=1 (имеет значение ИСТИНА), то b
вычисляется обычным образом. Если K=0 (имеет значение ЛОЖЬ), то b
полагается равным 0.
С - логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если С=1 (ИСТИНА), то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику (дополнительную информацию о регрессионной статистике можно получить воспользовавшись справкой Excel). Если С=0 (ЛОЖЬ) то функция ЛИНЕЙН возвращает только коэффициенты m
и постоянную b
.
В настоящей работе математическая модель качества среза y1 и силы вырубки y2 записывают в виде полинома следующего вида:
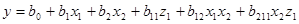 (3) (3)
Здесь x1
- значение зазора в кодовом масштабе, x2
- код материала, z1
- квадратичная функция от x1
.
В натуральном масштабе матрица плана эксперимента выглядит следующим образом:
| Номер опыта |
X1
|
X2
|
Качество среза, y1
|
Сила вырубки [кН], y2
|
| 1 |
0,03 |
0 |
2 |
197 |
| 2 |
0,05 |
0 |
1 |
195 |
| 3 |
0,1 |
0 |
1 |
192 |
| 4 |
0,03 |
1 |
3 |
100 |
| 5 |
0,05 |
1 |
2 |
98 |
| 6 |
0,1 |
1 |
1 |
96 |
Для обработки данных эксперимента переходят к кодированному масштабу. В данной задаче по методике, изложенной в [1] получены следующие формулы для перехода от натурального к кодированному масштабу:
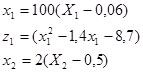 (4) (4)
Оптимизацию полученных регрессионных моделей можно осуществить двумя способами: либо визуально, построив графики, либо используя методы оптимизации, реализованные в Excel.
Последовательность выполнения
1. Запустить EXCEL
2. Переименуйте листы книги следующим образом: Лист1 - Модель, Лист2 - Сталь, Лист3 - Медь. Для этого необходимо щелкнуть правой клавишей мыши по ярлычку листа и в открывшемся контекстном меню выбрать пункт Переименовать.
3. На листе Модель создать таблицу с исходными данными эксперимента и поясняющими надписями по следующему образцу (при заполнении таблиц пользуйтесь способами копирования и автозаполнения):
| A |
B |
C |
D |
E |
F |
G |
H |
| 1 |
Исследование операции вырубки листовых образцов |
| 2 |
Матрица плана в натуральном масштабе |
| 3 |
N опыта |
X1 |
X2 |
| 4 |
1 |
0,03 |
0 |
| 5 |
2 |
0,05 |
0 |
| 6 |
3 |
0,1 |
0 |
| 7 |
4 |
0,03 |
1 |
| 8 |
5 |
0,05 |
1 |
| 9 |
6 |
0,1 |
1 |
| 10 |
Матрица плана в кодированном масштабе |
| 11 |
N опыта |
x1 |
x2 |
z1 |
x1x2 |
x2z1 |
y1 |
y2, кН |
| 12 |
d1 |
d2 |
d3 |
d4 |
d5 |
| 13 |
1 |
2 |
197 |
| 14 |
2 |
1 |
195 |
| 15 |
3 |
1 |
192 |
| 16 |
4 |
3 |
100 |
| 17 |
5 |
2 |
98 |
| 18 |
6 |
1 |
96 |
| 19 |
Коэффициенты регрессионных моделей вида |
| 20 |
y=b+m1*d1+m2*d2+m3*d3+m4*d4+m5*d5 |
| 21 |
m5 |
m4 |
m3 |
m2 |
m1 |
b |
| 22 |
y1 |
| 23 |
y2 |
4. На листе Сталь и Медь
| A |
B |
C |
D |
E |
F |
G |
H |
| 1 |
Варьирование зазором |
| 2 |
X1 |
x1 |
x2 |
z1 |
x1x2 |
x2z1 |
y1 |
y2, кН |
| 3 |
0,1 |
| 4 |
0,09 |
| 5 |
0,08 |
| 6 |
0,07 |
| 7 |
0,06 |
| 8 |
0,05 |
| 9 |
0,04 |
| 10 |
0,03 |
| 11 |
Поиск оптимального зазора |
| 12 |
X1 |
x1 |
x2 |
z1 |
x1x2 |
x2z1 |
y1 |
y2, кН |
5. Заполните диапазон B13: D18 формулами (4) для перехода от натурального масштаба к кодированному. Для ячейки B13 формула будет выглядеть следующим образом: =100* (B4‑0,06)
6. Заполните диапазон E13: F18 формулами для подсчета произведений x1
x2
и x2
z1
7. В диапазон B22: G22 введите формулу для определения коэффициентов регрессии для модели качества среза (y1) с помощью мастера функций. Последовательность действий приведена ниже:
- Выделить B22: G22
- Меню Вставка-Функция (или кнопка Вставка функции)
- Категория - Статистические, Функция - ЛИНЕЙН, Кнопка OK
- Окно Изв_знач_y - G13: G18 (мышью или с клавиатуры)
- Окно Изв_знач_x - B13: F18 (мышью или с клавиатуры)
- Окно Константа - 1
- Окно Стат - 0
- Нажать клавиатурную комбинацию Ctrl-Shift-Enter
- Формула массива вставится в выделенный диапазон и в нем появятся значения коэффициентов
8. Аналогично введите формулу для определения коэффициентов модели для силы вырубки (y2) в диапазон B23: G23. В качестве диапазона известных значений yиспользуйте столбец со значениями y2 в матрице плана в кодированном масштабе.
9. Постройте графики изменения качества реза и силы деформирования для стали на основании полученной модели. Для этого сначала необходимо заполнить таблицу данных на Листе Сталь. Используйте следующую последовательность действий:
- В ячейку Сталь! B3 занесите формулу =100* (A3-0,06) для перехода в кодированный масштаб
- В диапазон Сталь! С3: C10 занесите значение - 1 (минус 1), соответствующее коду стали в кодированном масштабе.
- Скопируйте формулы из диапазона Модель! D13: Модель! F13 в диапазон Сталь! D3: Сталь! F3, для чего:
- Выделите диапазон D13: F13 на листе Модель и нажмите кнопку Копировать
- Выделите ячейку D3 на листе Сталь и нажмите кнопку Вставить
- Распространите формулы диапазона B3: F3 на диапазон B3: F10
- Занесите в ячейку G3 на листе Сталь формулу для определения качества реза:
- =Модель! $G$22+Модель! $F$22*B3+Модель! $E$22*C3+Модель! $D$22*D3+ Модель! $C$22*E3+Модель! $B$22*F3
- Аналогично занесите в ячейку H3 на листе Сталь формулу для определения силы вырубки (вид формулы продумайте сами)
- Распространите формулы из диапазона G3: H3 на диапазон G3: H10
- Проверьте себя: для строк со значениями x1=4,-1,3 величины y1 и y2 должны точно совпадать с исходными данными
10. Постройте точечные графики y1=f (X1), y2=f (X1) на различных диаграммах и расположите их на том же листе Сталь и отформатируйте так, как показано в приложении. Область диаграммы y1=f (X1) должна занимать диапазон A15: D28, а y2=f (X1) - диапазон E15: H28. Указание: Прежде чем начать строить диаграммы с помощью мастера диаграмм выделите сначала диапазон значений аргумента A3: A10, а затем держа нажатой клавишу Ctrlна клавиатуре - диапазон значений аргумента (соответственно G3: G10 для y1 и H3: H10 для y2). Выделение с нажатой клавишей Ctrlпозволяет выделить несмежные диапазоны данных.
11. Проанализируйте график качества среза. Очевидно, что наилучшее качество достигается при минимальном зазоре 0.03. Значение оптимального зазора можно было найти не прибегая к построению графика, воспользовавшись встроенными в Excelсредствами поиска оптимальных решений.
- Скопируйте формулы из диапазона B3: H3 в диапазон B13: H13
- Выполните команду меню Сервис-Поиск решения
- В открывшемся окне Поиск решения занесите в окошки ввода следующие величины (мышью или с клавиатуры):
- Установить целевую - $G$13
- Равной - максимальному значению
- Изменяя ячейки - $A$13
- Ограничения - $A$13>=0.03; $A$13<=0.1 (Воспользуйтесь кнопкой Добавить справа от окна Ограничения. При вводе десятичной точки строго пользуйтесь точкой на основной клавиатуре)
- Нажмите кнопку Выполнить
- Excelвыполнит поиск оптимального решения с заданными ограничениями, после чего появится окно Результаты поиска решений, в котором следует нажать кнопку OK. Убедитесь, что Excelсамостоятельно нашел правильное решение.
- Попытайтесь найти самостоятельно зазор, обеспечивающий наихудшее качество
12. Постройте графики для Меди повторив пункты 9-11 на листе Медь (столбец x2 должен иметь значение 1, соответствующее коду меди). Пункт 12 можно выполнить проще. Если догадаетесь как - то сэкономите себе время.
13. Отформатируйте таблицы и графики так, как это показано в приложении. Если сможете - сделайте внешний вид полученных таблиц более привлекательным.
14. Завершить работу, сохранив ее в файле work3. xls.
15. Запустить EXCEL, вернуться к документу work3. xls и предъявить его преподавателю.
16. Предъявить преподавателю краткий конспект занятия.
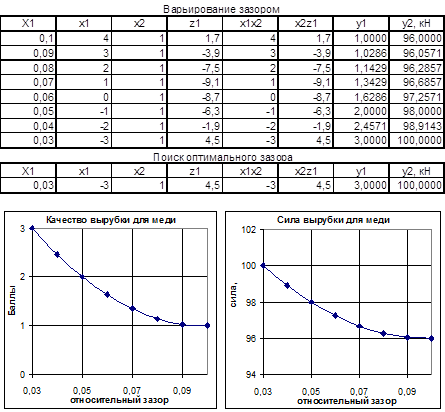
Приложение
Лист Модель:

Лист Сталь:

Лист Медь:
Цели работы:
- закрепление основных приемов создания и форматирования таблицы
- освоение методов построения пространственных графиков и графиков с областями
- освоение основных методов поиска решений средствами Excel
- исследование влияния силы прижима, радиуса матрицы и толщины заготовки на напряжение в опасном сечении.
Постановка задачи [2]
:
Исследуется влияние силы прижима, радиуса матрицы и толщины заготовки на напряжение в опасном сечении на основании классических формул, полученных Е.А. Поповым.
Максимальную величину растягивающего напряжения sr
max
, действующую на границе пластически деформируемой части заготовки, без учета упрочнения материала можно определить по формуле
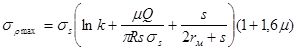 (1) (1)
Здесь s
s
- напряжение текучести, k=R/r - коэффициент вытяжки, R - радиус заготовки, r=0,5 (dп
+s) - радиус вытягиваемого стакана, dп
- диаметр пуансона, s - толщина заготовки, Q - сила прижима, rм
- радиус кромки матрицы, m - коэффициент трения.
Первое слагаемое в скобках отражает влияние напряженно-деформированного состояния во фланце заготовки, второе - влияние сил трения на фланце заготовки от силы прижима, третье - влияние изгиба-спрямления на кромке матрицы. Дополнительный множитель 1+1,6mучитывает силы трения на кромке матрицы.
Сила прижима Qпрепятствует потере устойчивости заготовки во фланце (складкообразование) одновременно увеличивая напряжения в опасном сечении.
Различные исследователи предлагают различные эмпирические формулы для определения рациональной силы прижима. Так, например, И.А. Норицыным предложена простая оценка рациональной силы прижима[3]
, как ¼ от силы вытяжки.
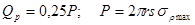 (2) (2)
С учетом упрочнения формула (1) принимает следующий вид[4]
:
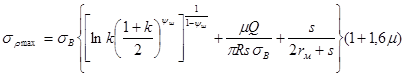 (3) (3)
Здесь sВ
- предел прочности материала, yш
-
относительное уменьшение площади поперечного сечения к моменту образования шейки.
При проведении занятия необходимо средствами Excelрешить следующие задачи:
1. Для заданных геометрических параметров заготовки, матрицы и пуансона, а также свойств материала определить, исходя из формулы (1) максимальную силу прижима, при которой отсутствует разрушение, а также, исходя из формул (1) и (2) - рациональную силу прижима.
2. Проанализировать вклад различных составляющих формулы (1), отражающих влияние напряженно-деформированного состояния во фланце, сил трения во фланце и изгиба-спрямления на кромке матриц, при изменении силы прижима от »Qр
до »Qmax
с шагом 10000 Н
3. Определить максимальный коэффициент вытяжки для заданных условий по формуле (3)
4. Построить пространственный график взаимного влияния толщины заготовки и радиуса матрицы на величину максимального напряжения в опасном сечении при рациональном значении силы прижима.
Методы решения с использованием Excel:
Для поиска решений в Excelприменяются два основных средства, доступных из меню Сервис: Подбор параметра… и Поиск решения….
Средство Подбор параметра используют в том случае, когда необходимо найти определенный числовой результат в какой-либо ячейке путем подбора значения другой ячейки. Типичный пример - решение алгебраических уравнений: необходимо подобрать такое значение неизвестного, при котором правая и левая часть уравнения равны между собой. В нашем случае это средство в наилучшей степени подходит для решения задачи определения максимальной и рациональной силы прижима.
При выборе этого средства раскрывается диалоговое окно, имеющее несколько полей:
- В поле Установить в ячейке
введите ссылку на ячейку, содержащую необходимую формулу.
- В поле Значение
введите искомый результат.
- В поле Изменяя значение ячейки
введите ссылку на ячейку, содержащую подбираемое значение.
Средство Поиск решения имеет более общее назначение. Процедуру поиска решения можно использовать для определения значений влияющих ячеек, которое соответствует экстремуму зависимой ячейки (например, максимальный коэффициент вытяжки). Влияющие и целевая ячейки должны быть связаны формулой на одном листе, иначе при изменении значения одной не будет изменяться другая. Надстройка Поиск решения позволяет задавать большое количество ограничений как на зависимую, так и на влияющие ячейки, что делает его мощным орудием анализа данный в Excel.
При выборе пункта Поиск решения из меню Сервис открывается диалоговое окно следующего вида:
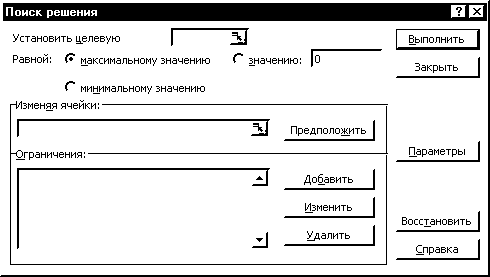
В поле Установить целевую необходимо занести ссылку на зависимую ячейку - т.е. на ту ячейку, значение которой будет подбираться путем изменения значений во влияющих ячейках - их адреса заносятся в поле Изменяя ячейки. Можно осуществить поиск значений влияющих ячеек сообщающих целевой ячейке максимальное, минимальное значения, либо значения, равные конкретному числу (аналог Подбора параметра). Для этого необходимо выбрать нужный пункт в группе радиокнопок Равной. В поле Ограничения следует записать ограничения на влияющие и целевую ячейки. Добавление новых ограничений осуществляется после нажатия на экранную кнопку Добавить. Открывающееся диалоговое окно позволяет накладывать ограничения в виде равенств и неравенств на значения в ячейках, а также требовать их целочисленности. После заполнения всех полей следует нажать экранную кнопку Выполнить.
При оформлении таблиц в заголовках часто приходится использовать греческие символы. К сожалению, в Excelотсутствует команда меню Вставить…Символ, как в Word. Поэтому рационально использовать следующую методику:
- Вместо греческих символов ввести латинский эквивалент (наиболее распространенные греческие символы на латинской клавиатуре имеют следующий эквивалент:
- a - a
; b - b
; d - d
; D - D
; e - e
; h - h
; g - g
; l - l
; m - m
; n - n
; w - w
; j - j
; p -p
;
- y - y
; r - r
; s - s
; t - t
; q - q
; x - x
).
- Выделить набранный символ и воспользовавшись полем Шрифт панели инструментов Форматирование изменить для этого символа тип шрифта на Simbol
Для создания верхних и нижних индексов следует воспользоваться аналогичной методикой. Сначала набрать символы, помещаемые в индексы, затем выделить их в строке формул, нажать клавиатурную комбинацию Ctrl-1 (либо выполнить команду меню Формат - Ячейки) и в открывшемся диалоговом окне щелкнуть мышью по флажку нижний индекс
в группе Эффекты, после чего нажать экранную кнопку OK.
Последовательность выполнения
17. Запустить EXCEL
18. На листе 1 создать таблицу с исходными данными эксперимента и поясняющими надписями по следующему образцу (при заполнении таблиц пользуйтесь способами копирования и автозаполнения):
| A |
B |
C |
D |
E |
F |
G |
H |
I |
| 1 |
Исследование операции вытяжки |
| 2 |
Исходные данные |
| 3 |
ss
, МПа |
200 |
sв
, МПа |
250 |
yш
|
0,35 |
| 4 |
D, мм |
62 |
s, мм |
2 |
| 5 |
dп
, мм |
37 |
rм
, мм |
3 |
m |
0,15 |
| 6 |
Результаты расчета |
| 7 |
d |
k |
1+1,6*m |
| 8 |
Qmax, Н |
sф
|
sп
|
sм
|
sr
max
|
| 9 |
| 10 |
Qрац, Н |
sф
|
sп
|
sм
|
sr
max
|
P, Н |
0.25*P |
d |
| 11 |
| 12 |
Q, Н |
sф
|
sп
|
sм
|
sr
max
|
фланец% |
прижим% |
матрица% |
| 13 |
20000 |
| 14 |
30000 |
| 15 |
40000 |
| 16 |
50000 |
| 17 |
60000 |
| 18 |
70000 |
| 19 |
80000 |
| 20 |
k |
Qрац, Н |
sф
|
sп
|
sм
|
sr
max
|
P, Н |
0.25*P |
d |
19. Занести в следующие ячейки формулы для определения диаметра стаканчика и коэффициента вытяжки
20. Занести в ячейку F7 формулу для определения коэффициента 1+1,6*m, в выражениях (1) и (3).
21. В следующие ячейки занести формулы для определения составляющих максимального напряжения в опасном сечении по формуле (1) (предварительно внесите в ячейку A9 значение 10000, которое будет являться начальным для подбора максимальной силы прижима)
| Ячейка |
Формула |
Вид формулы в Excel |
Значение в ячейке (для контроля правильности ввода) |
| B9 |
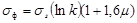 |
=$B$3*LN ($D$7) *$F$7 |
114,966 |
| C9 |
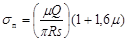 |
=$F$5*A9*2/ (ПИ () *$B$4 *$D$4) *$F$7 |
9,549 |
| D9 |
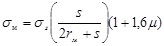 |
продумать самостоятельно |
22. В ячейку Е9 занести формулу для вычисления максимального напряжения в опасном сечении как сумму значений в ячейках B9: D9
23. Подобрать значение Qmax, воспользовавшись командой Сервис-Подбор параметра. В открывшемся диалоговом окне заполнить поля следующим образом

24. Значение 250 соответствует пределу прочности материала, что определяет предельное состояние в опасном сечении. Нажать экранную кнопку ОК. После подбора параметра в окне Результаты подбора параметра также нажать экранную кнопку ОК
25. Подобрать рациональное значение силы прижима, для чего предварительно выполнить следующие действия:
25.1. Скопировать формулы и значения из диапазона A9: E9 в диапазон A11: E11.
25.2. Занести в ячейку F11 формулу =ПИ () *$B$4*$D$4*E11 для определения максимальной силы вытяжки по формуле (2)
25.3. Занести в ячейку G11 формулу для определения силы прижима как ¼ от силы вытяжки.
25.4. Занести в ячейку H11 формулу для определения ошибки, как разницы между предположенным значением силы прижима в ячейке A11 и полученным значением рациональной силы прижима в ячейке G11.
25.5. С помощью Сервис - Подбор параметра определить величину рациональной силы прижима, поставив задачу следующим образом: "Изменяя значение предположенной величины силы прижима в ячейке A11 добиться того, чтобы ошибка вычисления силы была равна 0"
26. В ячейках A13: H19 подготовить данные для построения графика степени влияния различных слагаемых в формуле (1) на величину максимального напряжения в опасном сечении при изменении силы прижима в диапазона 10000…80000 Н с шагом 10000Н. Указания:
- для заполнения ячеек B13: E19 воспользуйтесь уже готовыми формулами в ячейках A11: E11;
- для быстроты заполнения ячеек F13: H19 воспользуйтесь смешанной адресацией введя в ячейку F13 следующую формулу для вычисления относительного влияния фланца =B13/$E13;
- распространите формулу в ячейке F13 на диапазон F13: H19;
- задайте в диапазоне F13: H19 процентный формат представления числа, воспользовавшись кнопкой % на панели Форматирование.
27. Отобразите графически результаты, представленные в ячейках F13: H19, воспользовавшись следующей последовательностью операций:
27.1. Выделите диапазон F12: H19 и нажмите экранную кнопку Мастер диаграмм на Основной панели инструментов.
27.2. В открывшемся диалоговом окне выберите Тип диаграммы: С областями, Вид: Нормированная диаграмма (третья слева в верхнем ряду), нажмите кнопку Далее.
27.3. На вкладке Ряд (Шаг 2 мастера диаграмм) в поле Подписи оси Х внесите диапазон: =Лист1! $A$13: $A$19, нажмите кнопку Далее;
27.4. На вкладке Подписи данных (Шаг 3 мастера диаграмм) щелкните мышью в пункте категория группы Подписи значений; на вкладке Легенда уберите флажок в пункте Добавить легенду; на вкладке Заголовки в поле Ось Х наберите: Q, Н, нажмите экранную кнопку Готово
27.5. Переместите полученную диаграмму в диапазон A22: F39, изменив размеры с помощью размерных маркеров.
27.6. Измените цвет заливки областей так, чтобы были хорошо видны надписи внутри. Для этого сначала необходимо щелкнуть мышью по области так, чтобы она выделилась, а затем использовать кнопку Цвет заливки на панели инструментов Форматирование. Примерный вид получившейся диаграммы приведен ниже:
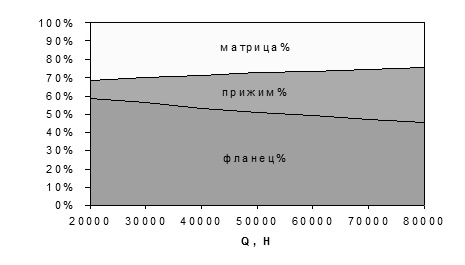
28. Определите максимальное значение коэффициента вытяжки для заданных значений параметров материала, параметров заготовки и матрицы, используя формулу (3). Для этого выполните следующую последовательность действий:
28.1. В ячейки A21 и B21 занесите начальные значения коэффициента вытяжки и величины силы прижима (соответственно 1,5 и 10000).
28.2. В ячейки С21: E21 занесите следующие формулы:
| Ячейка |
Формула |
Вид формулы в Excel |
Значение в ячейке (для контроля правильности ввода) |
| C21 |
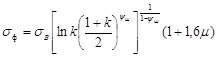 |
=$D$3* (LN ($A$21) * ( (1+$A$21) /2) ^$F$3) ^ (1/ (1-$F$3)) *$F$7 |
87,17572 |
| D21 |
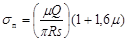 |
продумать самостоятельно |
9,549297 |
| E21 |
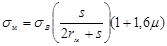 |
продумать самостоятельно |
77,5 |
28.3. Ввести в ячейки F21: I21 формулы аналогично ячейкам E11: H11. Результаты в ячейках должны получиться следующими:
| sr
max
|
P, Н |
0.25*P |
d |
| 174,225 |
67870,66 |
16967,66 |
-6967,66 |
28.4. Воспользоваться надстройкой Поиск решения. В диалоговом окне Поиск решения внести следующие данные:
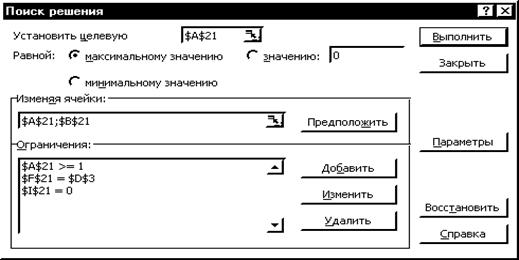
28.5. Нажать кнопку Выполнить и после окончания процесса поиска решения, который может продлиться несколько секунд, нажать кнопку ОК в окне Результаты поиска решения.
29. Построить пространственный график влияния толщины заготовки и радиуса кромки матрицы на величину напряжения в опасном сечении, для чего выполнить следующие подготовительные действия:
29.1. Скопировать данные и формулы из диапазона A1: H11 листа 1 в тот же диапазон на листе 2 (воспользуйтесь кнопками Копировать и Вставить на панели инструментов Основная). Все дальнейшие действия производить на листе 2
29.2. Удалите строки с 8 по 9
29.3. Перенесите (не копировать!) содержимое следующих ячеек: из C5 в I8; из D5 в I9
29.4. В формуле, содержащейся в ячейке D9 замените абсолютный адрес ячейки $I$9 на смешанный $I9 (это позволит в дальнейшем воспользоваться приемом автозаполнения).
29.5. В ячейки I9: I13 занесите варьируемые значения радиуса скругления кромки матрицы 3; 5; 7; 9; 11
29.6. Используя прием автозаполнения, распространите формулы и значения из диапазона A9: H9 на диапазон A9: H13.
29.7. Убедитесь в том, что значения силы прижима для радиусов матрицы отличных от 3 нерациональны (ошибка ¹0). Для построения требуемых зависимостей следует подобрать рациональное значение силы прижима для всех радиусов матрицы, в противном случае результаты будет трудно сравнивать. Для подбора рациональных значений силы прижима можно воспользоваться средством Подбор параметра, как это было сделано выше. Однако быстрее результат будет получен, если использовать Поиск решения:
29.7.1. Занесите в ячейку H14 формулу суммарной ошибки определения силы прижима для всех 5-и значений радиусов матриц
29.7.2. Сформулируйте задачу поиска решения так, как это показано ниже и выполните поиск. Убедитесь в том, что нужное решение было найдено сразу для всех значений радиусов матриц.

29.8. Создайте в ячейках A15: G21 следующую вспомогательную таблицу
| A |
B |
C |
D |
E |
F |
G |
| 15 |
1 |
2 |
3 |
4 |
5 |
s, мм |
| 16 |
3 |
| 17 |
5 |
| 18 |
7 |
| 19 |
9 |
| 20 |
11 |
| 21 |
rм
, мм |
29.9. Скопируйте значения (а не формулы!) из диапазона E9: E13 в диапазон C16: C20 (поскольку значения максимального напряжения в опасном сечении были получены для толщины заготовки 2 мм - см. значение в ячейке D4). Для копирования значений пользуются следующим приемом:
29.9.1. Выделите копируемый диапазон E9: E13 и нажмите кнопку копировать
29.9.2. Перейдите в ячейку C16 (начальная ячейка диапазона куда копируют) и выполните команду меню Правка-Специальная вставка
29.9.3. В открывшемся диалоговом окне щелкнуть мышью в пункте Значения группы Вставить и нажать экранную кнопку ОК.
29.10. Меняя последовательно значения толщины заготовки в ячейке D4 на 1, 3,4,5 выполните подбор силы прижима в соответствие с п.12.7.2 и скопируйте полученные значения напряжений в соответствующий столбец таблицы п12.8 по методике 12.9.
30. Отобразите графически результаты, представленные в ячейках B16: F20, воспользовавшись следующей последовательностью операций:
30.1. Выделите диапазон A15: F20 и нажмите экранную кнопку Мастер диаграмм на Основной панели инструментов.
30.2. В открывшемся диалоговом окне выберите Тип диаграммы: Поверхность, Вид: Поверхность (пиктограмма в верхнем левом углу группы вид), нажмите кнопку Далее.
30.3. Ничего не меняя на Шаге 2 мастера диаграмм, нажмите кнопку Далее;
30.4. На вкладке Заголовки (Шаг 3 мастера диаграмм) в поле Ось Х наберите: s, мм, в поле Ось Y - r, мм и нажмите экранную кнопку Готово
30.5. Переместите полученную диаграмму в диапазон A22: F39, изменив размеры с помощью размерных маркеров.
30.6. Выполните форматирование полученной диаграммы:
30.6.1. Измените диапазон изменения по оси Z. Щелкните мышью по оси так, чтобы она выделилась
30.6.2. Выполните команду меню Формат - Выделенная ось.
30.6.3. В открывшемся диалоговом окне на вкладке Шкала в поле Минимальное значение введите 140, в поле максимальное значение - 240, в поле цена основных делений - 20. Нажмите экранную кнопку OK.
30.6.4. Щелкните правой клавишей мыши по пустому полю диаграммы вблизи правого верхнего угла. В открывшемся контекстном меню выберите пункт Объемный вид…
30.6.5. Изменяя значения в полях Возвышение, Перспектива и Поворот (это можно сделать с помощью экранных кнопок с соответствующими пиктограммами) добейтесь наиболее информативного вида диаграммы. Результаты изменения объемного вида можно просмотреть не закрывая диалогового окна, нажав на экранную кнопку применить. По нашему мнению неплохой вид диаграмма получит при значениях Возвышение=15, Перспектива=30, Поворот=160. Примерный вид диаграммы приведен ниже
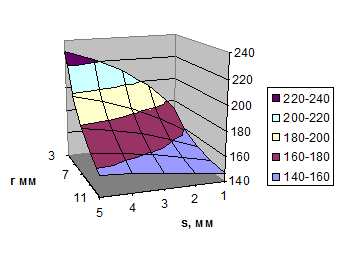
30.6.6. Попытайтесь поэкспериментировать с другими возможностями форматирования объемной диаграммы, не забывая, что прежний вид всегда можно вернуть, нажав на экранную кнопку Отменить (не более 3-х шагов назад)
31. Завершить работу, сохранив ее в файле work3. xls.
32. Запустить EXCEL, вернуться к документу work3. xls и предъявить его преподавателю.
33. Предъявить преподавателю краткий конспект занятия.
Цели работы:
- закрепление основных приемов создания и форматирования таблицы
- освоение методов поиска решений с помощью встроенных средств Excel
Постановка задачи [5]
:
Рассматривается задача отыскания максимального коэффициента вытяжки цилиндрического стаканчика из листовой заготовки с использованием метода крутого восхождения Бокса-Уилсона.
Напомним, что коэффициентом вытяжки k=D/d, где D - диаметр исходной заготовки, d - диаметр вытянутого из этой заготовки стаканчика. Предельная величина коэффициента вытяжки за один переход ограничена величиной максимальных напряжения sr
max
во фланце заготовки. Разрушение заготовки произойдет тогда, когда sr
max
достигнет предела прочности материала sВ
. При этом значение коэффициента вытяжки является максимальным. На величину предельного коэффициента вытяжки, помимо других факторов, влияет радиус скругления кромки матрицы (rм
) и скорость деформирования (V
).
Идея экстремальных экспериментов заключается в линейной аппроксимации гиперповерхности отклика, оценке составляющих градиента и проведении серии "мысленных" опытов (т.е. без выполнения реального эксперимента) в направлении оптимума.
Метод планирования эксперимента Бокса-Уилсона включает в себя построение линейной модели исследуемого объекта в виде y=
b0
+
b1
x1
+
b2
x2
+
¼+
bn
xn
, где n
- количество факторов. В этом случае оценками составляющих вектора градиента являются коэффициенты полинома. Для движения по градиенту необходимо менять факторы пропорционально величинам коэффициентов. Такая процедура называется крутым восхождением. При движении по градиенту факторы изменяют с определенным шагом. Шаги изменения рассчитывают в натуральном масштабе.
Таким образом процедура решения задачи сводится к следующей последовательности шагов:
- проведение натурного эксперимента, для получения линейной модели y=
b0
+
b1
x1
+
b2
x2
+
b3
x3
(1), где y=
sr
max
; x1
,
x2
,
x3
- факторы k,
rм
,
V
в кодовом масштабе (результаты натурного эксперимента заданы в качестве исходных данных);
- определению коэффициентов bi
линейной модели;
- определению составляющих градиента в натуральном масштабе;
- осуществлении крутого восхождения - т.е. подбора такого шага в направлении градиента из центра плана, при котором в формуле (1) y=
sВ
.
Предел прочности материала, используемого в опытах 310 МПа
Методы решения с использованием Excel:
Для определения коэффициентов линейной модели (1) достаточно провести 4 опыта. Интервалы варьирования факторов D
Xi
относительно центра плана Xi
0
в проведенном натурном эксперименте приведены в таблице 1. Матрица плана исходного натурного эксперимента в кодированном масштабе приведена в таблице 2. Кодированные значения факторов связаны с натуральными соотношениями вида:
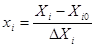 (2) (2)
Таблица 1. Уровни варьирования факторов
| Факторы |
1 |
2 |
3 |
| k
|
rм
, мм
|
V, мм/с
|
| Xi0
|
1,3 |
3 |
0,5 |
| D
Xi
|
0,1 |
1 |
0,2 |
Таблица 2. Матрица плана исходного эксперимента
| № опыта |
x1
|
x2
|
x3
|
y
(
sr
max
, МПа)
|
| 1 |
-1 |
-1 |
-1 |
189 |
| 2 |
1 |
-1 |
1 |
236 |
| 3 |
-1 |
1 |
1 |
167 |
| 4 |
1 |
1 |
-1 |
223 |
Коэффициенты регрессионной модели (1) определяют с помощью уже известной вам функции ЛИНЕЙН. Если вы забыли синтаксис функции ЛИНЕЙН, воспользуйтесь встроенной справкой Excel.
Исходная точка для крутого восхождения - центр плана с координатами в натуральном масштабе:
X1о
=1.3,
X2о
=3,
X3о
=0.5
(3)
Составляющие градиента вычисляются по формуле
gi
=
bi
D
Xi
(
4)
Шаг крутого восхождения в натуральном масштабе по каждой из координат
Xi
=
Xi
0
+
gi
*
S
(5)
Подбор такой кратности шагов S, одинаковой для всех координат, при котором y=
sВ
осуществляют с помощью команды меню Excel "Сервис-Подбор параметра".
Последовательность выполнения
34. Запустить EXCEL
35. Переименуйте Лист1 книги в "Крутое восхождение". Остальные листы книги удалите. Для этого необходимо щелкнуть правой клавишей мыши по ярлычку листа и в открывшемся контекстном меню выбрать пункт Удалить.
36. На листе Крутое восхождение создать таблицу с исходными данными эксперимента и поясняющими надписями по следующему образцу (при заполнении таблиц пользуйтесь способами копирования и автозаполнения):
| A |
B |
C |
D |
E |
F |
G |
H |
| 1 |
Определение максимального коэффициента вытяжки |
| 2 |
Уровни варьирования факторов |
| 3 |
1 |
2 |
3 |
| 4 |
Xi0
|
1,3 |
3 |
0,5 |
| 5 |
DXi
|
0,1 |
1 |
0,2 |
| 6 |
Матрица плана исходного эксперимента в кодированном масштабе |
| 7 |
№ опыта |
x1
|
x2
|
x3
|
sr
max
,
МПа |
| 8 |
1 |
-1 |
-1 |
-1 |
189 |
| 9 |
2 |
1 |
-1 |
1 |
236 |
| 10 |
3 |
-1 |
1 |
1 |
167 |
| 11 |
4 |
1 |
1 |
-1 |
223 |
| 12 |
Коэффициенты регрессионной модели |
| 13 |
b3
|
b2
|
b1
|
b0
|
| 14 |
| 15 |
Составляющие градиента |
| 16 |
g1
|
g2
|
g3
|
| 17 |
| 18 |
С учетом направления восхождения |
| 19 |
g1
|
g2
|
g3
|
| 20 |
| 21 |
Крутое восхождение (с помощью "Сервис-Подбор параметра. ") |
| 22 |
Xi=Xi0
+S*gi
|
xi
= (Xi
-Xi0
) /
DXi
|
| 23 |
S
|
X1
|
X2
|
X3
|
x1
|
x2
|
x3
|
sr
max
|
| 24 |
37. В диапазон A14: D14 введите формулу для определения коэффициентов регрессии для модели напряжений sr
max
, используя функцию ЛИНЕЙН и мастер функций. Последовательность действий приведена ниже:
- Выделить A14: D14
- Меню Вставка-Функция (или кнопка Вставка функции)
- Категория - Статистические, Функция - ЛИНЕЙН, Кнопка OK
- Окно Изв_знач_y - диапазон известных значений sr
max
- Окно Изв_знач_x - диапазон значений xi
в опытах
- Окно Константа - 1
- Окно Стат - 0
- Нажать клавиатурную комбинацию Ctrl-Shift-Enter
- Формула массива вставится в выделенный диапазон и в нем появятся значения коэффициентов
38. Введите в диапазон A17: C17 формулы (4) для определения составляющих градиента. Обратите внимание, что порядок следования составляющих градиента gi
в диапазоне A17: C17 и порядок следования коэффициентов bi
в диапазоне A14: С14 не совпадают.
39. Обратите внимание, что полученные значения составляющих градиента для факторов 2 и 3 имеют отрицательные значения. Это означает, что шаги в этом направлении приведут к уменьшению sr
max
. Поэтому мы должны двигаться в направлении антиградиента по этим факторам (напомним, что направление градиента - это направление увеличения функции). Таким образом в ячейки A20: C20 следует внести следующие формулы:
- A20 - =A17
- B20 - = - C17
- C20 - = - C17
40. Занесите в ячейку A24 значение 1, являющееся начальным значением кратности шагов S
41. Занесите в диапазон B24: D24 формулы (5) для определения значений варьируемых факторов в натуральном масштабе. Составляющие градиента расположены в ячейках A20: C20. Значения центра плана Xi
0
- в ячейках B4: D4. Для использования автозаполнения в формулах следует вводить абсолютный адрес ячейки $A$24
42. В ячейки E24: G24 внесите формулы (2) для перехода от натурального масштаба к кодированному.
43. В ячейку H24 введите формулу для определения sr
max
по значениям факторов xi
в ячейках E24: G24 в соответствии с моделью (1). Коэффициенты модели bi
были определены вами ранее в ячейках A14: D14. При вводе формулы обратите внимание на обратный порядок значений коэффициентов bi
в диапазоне A14: D14. Обратите внимание, что величина напряжения получилась значительно большей, чем максимально возможное значение 310 МПа.
44. Меняя значение в ячейке A24 попытайтесь вручную подобрать такую кратность шагов S, при которой значение напряжения в ячейке H24 было бы равно 310 МПа.
45. Верните в ячейку A24 значение 1 и подберите точное значение с помощью встроенных в Excelсредств автоматического подбора значений. Для этого:
- Выполните команду меню Сервис-Подбор параметра
- В открывшемся окне Подбор параметра введите следующие значения, используя мышь или клавиатуру:
- в поле Установить в ячейке: $H$24
- в поле Значение: 310
- в поле Изменяя значение ячейки: $A$24
- Нажмите кнопку OK. Убедитесь, что решение найдено.
46. Решение поставленной задачи можно сформулировать так: "Может быть достигнут коэффициент вытяжки, равный значению в ячейке B24, при использовании матрицы, радиус скругления которой в мм приведен в ячейке C24 и проведении вытяжки со скоростью деформирования, значение которой в мм/с приведено в ячейке C24".
47. Отформатируйте таблицы и графики так, как это показано в приложении. Если сможете - сделайте внешний вид полученных таблиц более привлекательным.
48. Завершить работу, сохранив ее в файле work5. xls.
49. Запустить EXCEL, вернуться к документу work4. xls и предъявить его преподавателю.
50. Предъявить преподавателю краткий конспект занятия.
Приложение:

Занятие
6 - Исследование операции обжима
Цели работы:
- закрепление основных приемов создания и форматирования таблицы, построения графиков различного вида и поиска решений в Excel
- создание модуля для автоматизации обработки результатов эксперимента по исследованию операции обжима.
Постановка задачи:
В ходе настоящей работы необходимо создать электронную таблицу, позволяющую автоматизировать результаты обработки экспериментальных данных по исследованию операции обжима и используя теоретические зависимости исследовать влияние отдельных параметров на напряжение в опасном сечении. Схема операции обжима с образованием цилиндрической части приведена ниже.
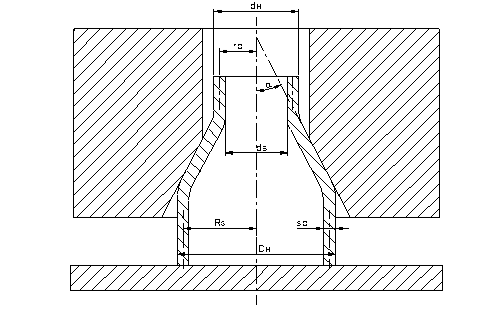
Максимальную величину сжимающих напряжений sr
max
, действующих в недеформируемых стенках заготовки, без учета упрочнения материала можно определить по формуле
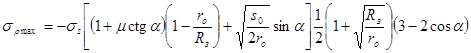 (1) (1)
Максимальная сила деформирования
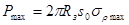 (2) (2)
Здесь s
s
- напряжение текучести, m - коэффициент трения,
r0
=0,25 (dн
+dв
), (
3), Rз
=0,5 (Dн
+s0
). (
4)
При проведении эксперимента по обжиму трубы Dн=28 мм, s0
=2 мм были получены следующие результаты
| a, градусы |
dн
, мм |
dв
, мм |
Pmax
, Н |
| 10 |
22,8 |
18 |
27800 |
| 15 |
22,4 |
17,4 |
30000 |
| 20 |
22,5 |
17,8 |
29000 |
| 25 |
22 |
17 |
35900 |
| 30 |
21,6 |
16,4 |
41000 |
При проведении занятия необходимо средствами Excelрешить следующие задачи:
5. Используя формулу (2) определить экспериментальное значение для различных углов конусности матрицы sr
max
.
6. Используя формулу (1) для s
s
=250 МПа, m=найти расчетные значения sr
max
7. Определить ошибку расчета по сравнению с экспериментом.
8. Построить графики изменения максимального напряжения от угла конусности по результатам расчета и эксперимента
9. Определить оптимальное значение угла конусности для значения r0
=10 мм исходя из минимального значения напряжений по формуле (1)
10. Построить пространственный график взаимного влияния толщины заготовки и радиуса обжима r0
на величину максимального напряжения при найденном оптимальном значении угла конусности.
Методы решения с использованием Excel:
Методы решения поставленных задач с использованием Excelописаны в предыдущих работах. В настоящей работе все действия по созданию и форматированию таблицы производятся с самостоятельно
Последовательность выполнения
51. Запустить EXCEL
52. На лист 1 занести заголовок, исходные данные для расчета (см. приложение).
53. Определить радиус заготовкиRз по формуле (4)
54. Занести в таблицу результаты эксперимента (см. приложение)
55. Для a=10°определить
55.1. r0
по формуле (3)
55.2. sr
max
экспериментальное по формуле (2)
55.3. sr
max
расчетное по формуле (1) (обратить внимание на необходимость применения как абсолютной, так и относительной адресации, в противном случае будет невозможно пользоваться методом автозаполнения)
55.4. определить относительную ошибку расчета eв %
56. Распространить формулы, записанные в строке для a=10° на строки с остальными значениями углов. Прежде, чем двигаться дальше, сравните Ваши результаты с данными преподавателя, и исправьте ошибки, если они есть.
57. На основании полученных данных постройте графики изменения максимальных напряжений в зависимости от угла конусности матрицы по результатам расчета и эксперимента. (см. приложение).
58. Используя команду Сервис-Поиск решения определите оптимальный угол конусности для r0
=10 по формуле (1).
59. Создайте вспомогательную таблицу для построения пространственного графика зависимости максимального напряжения от толщины заготовки s0
=1,2,3,4,5 мм и радиуса обжима r0
=8,9,10,11,12 мм. Внешний вид такой таблицы приведен в приложении.
60. Заполните вспомогательную таблицу. Это можно сделать записав в одной из ячеек общую формулу с использованием абсолютных, относительных и смешанных адресов, а затем распространив эту формулу на всю таблицу. Сравните полученные результаты с данными преподавателя и исправьте ошибки если они есть.
61. Постройте пространственный график по данным таблицы
62. Отформатируйте таблицу и графики так, как это показано в приложении.
63. Завершить работу, сохранив ее в файле work6. xls.
64. Запустить EXCEL, вернуться к документу work6. xls и предъявить его преподавателю.
65. Предъявить преподавателю краткий конспект занятия.
Приложение: Пример форматирования итоговой таблицы и графиков (результаты в таблицах не показаны).
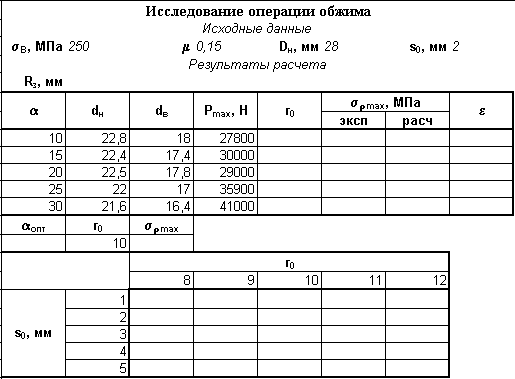
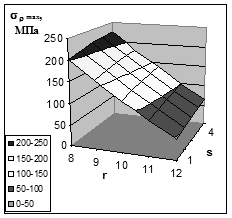 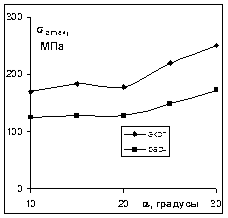
Занятие
7 - Оптимизация раскроя листового материала
Цели работы:
- освоение методов решения задач оптимизации с использованием Excel
Постановка задачи:
В ходе настоящей работы необходимо создать электронную таблицу, позволяющую произвести оптимизацию раскроя листа для вырубки круглых заготовок. Схема, поясняющая постановку задачи приведена ниже.
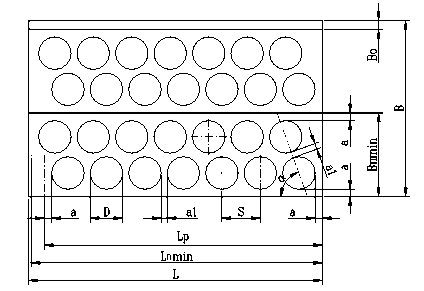
Необходимо выбрать наилучшие размеры и найти наилучший вариант раскроя листа шириной Bи длиной L. Диапазон возможного изменения длин листа: L=2000…3000 мм с шагом 100 мм, диапазон возможного изменения ширины листа: В=600…1100 мм с шагом 50 мм. Предварительно выбрана схема двухрядного косого раскроя, что определяется размерами штампового пространства используемого прессового оборудования.
Наилучший вариант раскроя обеспечивает наибольший коэффициент использования металла, который может быть рассчитан следующим образом:
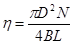
Здесь N - количество заготовок, помещающихся на листе.
Для сравнения вариантов, одинаковых по величине коэффициента использования металла, можно использовать дополнительный показатель - площадь концевого отхода, остающегося при раскрое полосы. Можно ожидать, что чем больше эта площадь, тем с большей эффективностью можно использовать концевой отход для других производственных нужд. Для приведения этого критерия к безразмерному виду можно отнести величину площади концевого отхода к максимальной площади листа, который может быть использован. Как следует из изложенного выше, максимальная площадь листа составляет Bmax
´Lmax
=1100´3000 мм2
. Тогда критерий площади концевого отхода может быть рассчитан как:
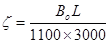
В качестве обобщенной целевой функции F
(критерия качества), может быть использована аддитивная функция, в которой критерий площади концевого отхода z
взят с весовым коэффициентом 0.1, как менее важный, по сравнению с критерием использования материала h
.
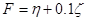
В такой постановке целевая функция зависит от ширины и длины исходного листа, которые могут изменяться с определенным шагом и угла косого раскроя a, который может изменяться в общем случае в пределах от 0 до 90 градусов непрерывно.
Таким образом, задача оптимизации сформулирована следующим образом (см. курс "Основы автоматизированного проектирования"):
- Целевая функция: F®max
- Вектор управляемых параметров: B, L, a
- Ограничения на управляемые параметры: B=600…1100 с шагом 50, L=2000…3000 с шагом 100, 0£a£90
Ниже приведен возможный алгоритм вычисления целевой функции в рамках поставленной задачи. Для определенности варьируемым (управляемым) параметрам заданы начальные значения. Величина ширины перемычек aи a1 (см. чертеж) приняты постоянными для диаметров детали в пределах 100…200 мм.
| Наименование |
Формула (пояснение) |
| 1 |
Кратность по ширине *
|
iB
=5 (варьируемый параметр iB
=0…10) |
| 2 |
Кратность по длине * |
iL
=5 (варьируемый параметр iL
=0…10) |
| 3 |
Угол косого раскроя |
a=60 (варьируемый параметр 0£a£90) |
| 4 |
Ширина листа |
B=600+50i
B
,
|
| 5 |
Длина листа |
L=2000+100i
L
,
|
| 6 |
Диаметр детали |
D=141
|
| 7 |
Ширина перемычек |
a1=2
|
| 8 |
a=2,5
|
| 9 |
Мин. ширина полосы |
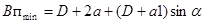 |
| 10 |
Количество полос |
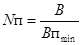 , округлить до меньшего целого , округлить до меньшего целого |
| 11 |
Шаг между заготовками в ряду **
|
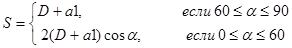 |
| 12 |
Количество заготовок в ряду |
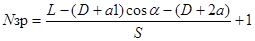 , округлить до меньшего целого , округлить до меньшего целого |
| 13 |
Длина ряда |
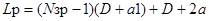 |
| 14 |
Наличие дополнительной заготовки в ряду ***
|
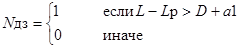 |
| 15 |
Количество заготовок в полосе |
N
зп=2N
зр+N
дз |
| 16 |
Количество заготовок в листе |
N
=N
пN
зп |
| 17 |
Коэффициент использования металла |
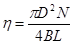 |
| 18 |
Ширина концевого отхода |
B
o=B
-N
пB
пmin
|
| 19 |
Целевая функция |
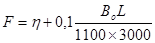 |
Пояснения к алгоритму:
*
Поскольку ширина и длина листа могут изменяться не непрерывно, а с определенным шагом, то алгоритмически проще варьировать количеством таких шагов (их кратностью) несколько преобразовав формулу для определения соответственно ширины и длины шага (см. пп4,5)
**
Шаг между заготовками в ряду при углах косого раскроя менее 60° увеличивается за счет того, что заготовки из соседних рядов при величине перемычки равной a1 начинают накладываться друг на друга.
***
Дополнительную заготовку можно разместить в нижнем ряду в том случае, если длина ряда окажется меньше длины полосы на величину диаметра с учетом перемычки
При проведении занятия необходимо средствами Excelрешить следующие задачи:
11. Используя алгоритм, приведенный выше, составить электронную таблицу, позволяющую рассчитать целевую функцию для произвольного диаметра Dварьируя размерами листа и углом косого раскроя.
12. Проанализировать влияние угла раскроя на величину коэффициента использования металла, ширину концевого отхода и обобщенную целевую функцию при значения диаметра заготовки D=141 мм и D=120 мм, построив соответствующие графики.
13. Используя методы поиска решений в Excel определить все параметры для нахождения оптимального значения варьируемых параметров (угол раскроя и размеры листа)
14. Найти оптимальный раскрой листа для значения диаметра заготовки, заданного преподавателем.
Методы решения с использованием Excel:
Для решения задач оптимизации в Excelиспользуют уже изученную нами надстройку Поиск решения, диалоговое окно которой вызывается по команде Сервис-Поиск решения (см. работу 3). Здесь мы поясним дополнительные возможности настройки алгоритма поиска решения. Окно настройки вызывают нажатием экранной клавиши Параметры диалогового окна Поиск решения.
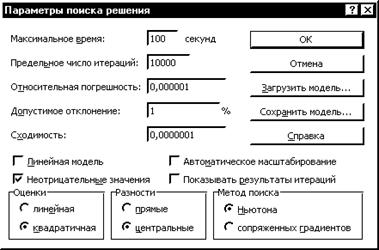
Диалоговое окно "Параметры поиска решения" служит для изменения условия и вариантов поиска решения для линейных и нелинейных задач, а также для загрузки и сохранения оптимизируемых моделей. Значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач.
Максимальное время - Служит для ограничения времени, отпускаемого на поиск решения задачи. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства простых задач.
Итерации - Служит для управления временем решения задачи, путем ограничения числа промежуточных вычислений. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства простых задач.
Точность - Служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 (нуля) до 1. Чем меньше введенное число, тем меньше точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Допустимое отклонение - Служит для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большего допуска поиск решения заканчивается быстрее.
Сходимость - Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 (нуля) до 1. Лучшую сходимость характеризует большее количество десятичных знаков ѕ например, 0,0001 ѕ это меньшее относительное изменение, чем 0,01. Лучшая сходимость требует больше времени на поиск оптимального решения.
Линейная модель - Служит для ускорения поиска решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи.
Показывать результаты итераций - Служит для приостановки поиска решения для просмотра результатов отдельных итераций.
Автоматическое масштабирование - Служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
Значения не отрицательны - Позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение.
Оценка - Служит для указания метода экстраполяции (линейная или квадратичная) используемого для получения исходных оценок значений переменных в каждом одномерном поиске.
Линейная - Служит для использования линейной экстраполяции вдоль касательного вектора.
Квадратичная - Служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.
Производные - Служит для указания метода численного дифференцирования (прямые или центральные производные) который используется для вычисления частных производных целевых и ограничивающих функций.
Прямые - Используется для гладких непрерывных функций.
Центральные - Используется для функций, имеющих разрывную производную. Не смотря на то, что данный способ требует больше вычислений, он может помочь при получении итогового сообщения о том, что процедура поиска решения не может улучшить текущий набор влияющих ячеек.
Метод - Служит для выбора алгоритма оптимизации (метод Ньютона или сопряженных градиентов) для указания направление поиска.
Ньютона - Служит для реализации квазиньютоновского метода (метод второго порядка), в котором запрашивается больше памяти, но выполняется меньше итераций, чем в методе сопряженных градиентов.
Сопряженных градиентов - Служит для реализации метода сопряженных градиентов (метод первого порядка), в котором запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.
Загрузить модель - Служит для отображения на экране диалогового окна Загрузить модель, в котором можно задать ссылку на область ячеек, содержащих загружаемую модель.
Сохранить модель - Служит для отображения на экране диалогового окна Сохранить модель, в котором можно задать ссылку на область ячеек, предназначенную для хранения модели оптимизации. Данный вариант предусмотрен для хранения на листе более одной модели оптимизации (первая модель сохраняется автоматически).
Дополнительно, к использованным ранее тригонометрическим функциям, функции ПИ () и функции РАДИАНЫ (), в данной задаче будут полезны следующие функции:
ЦЕЛОЕ (число
): округляет число
вниз до ближайшего целого.
Аргумент число
, может быть числом, для которого вы хотите найти следующее наименьшее целое, либо ссылкой на ячейку, в которой вычисляется округляемое число, либо формулой, в результате которой будет получено округляемое число.
ЕСЛИ (логическое_выражение
; значение_если_истина
; значение_если_ложь
): служит для получения в ячейке результата, зависящего от некоторых условий.
Аргумент логическое_выражение
служит для записи условия, в котором сравниваются числа, функции, формулы. Любое логическое выражение должно содержать по крайней мере один оператор сравнения, который определяет отношение между элементами логического выражения. Такими операторами могут быть: > (больше), < (меньше), = (равно), <= (меньше либо равно), >= (больше либо равно),<> (не равно). В качестве аргументов логического выражения можно использовать числа, ссылки не другие ячейки, другие функции, а также формулы.
Аргументы значение_если_истина
и значение_если_ложь
представляют собой числа или формулы для вычисления чисел, которые должны использоваться для расчета значений в ячейке если значение логического выражения является соответственно истиной, либо ложью.
Последовательность выполнения
66. Запустить EXCEL
67. На листе 1 создать таблицу для вычисления целевой функции в соответствии с алгоритмом. Внешний вид таблицы вместе с исходными данными и результатами (для справки) приведен в приложении.
68. Создать рядом с основной таблицу для варьирования величиной угла раскроя в пределах от 55 до 90 градусов с шагом в 5 градусов.
69. Определить значения коэффициента использования металла, целевой функции и ширины концевого отхода в зависимости то угла раскроя для D=141 при iВ
=iL
=5. Результаты поместить во вспомогательную таблицу на Лист2 (копируйте значения, а не формулы).
70. Повторить вычисления для D=120 при iВ
=iL
=5. Результаты также поместить на Лист2.
71. Построить графики изменения полученных величин. Вид графиков, которые должны получиться приведены в приложении 2.
72. Задать необходимые параметры для поиска оптимального решения. Целевая ячейка - в которой вычисляется F. Изменяемые ячейки - те в которых помещены значения, iB
, iL
,a. Ограничения: 0£a£90, 0£iВ
£10, 0£iL
£10, iB
, iL
- целые. Рекомендуемы параметры окна настройки поиска решения приведены на рисунке выше.
73. Найти оптимальное решение для D=141 и D=120 мм. При поиске решения следует иметь ввиду, что целевая функция является многоэкстремальной. Для таких функций невозможно гарантировать получение глобального экстремума из любой начальной точки. Поэтому используется метод пробных начальных точек. Выбирают несколько начальных точек в различных областях пространства управляемых параметров. Производят оптимизацию из каждой начальной точки и за глобальный оптимум принимают наилучшее из полученных решений. В качестве начальных пробных точек в данной задаче рекомендуется использовать следующие:
| Номер начальной точки |
1 |
2 |
3 |
4 |
5 |
| a |
70 |
70 |
70 |
70 |
70 |
| iВ
|
1 |
10 |
5 |
10 |
10 |
| iL
|
1 |
10 |
5 |
1 |
1 |
74. Найти оптимальное решение для значения диаметра, предложенное преподавателем.
75. Построить для найденных оптимальных размеров листа графики изменения коэффициента использования металла, целевой функции и ширины концевого отхода на листе 3.
76. Завершить работу, сохранив ее в файле work7. xls.
77. Запустить EXCEL, вернуться к документу work5. xls и предъявить его преподавателю.
Приложение 1: Внешний вид таблицы и результаты вычислений (для справки)
| Кратность по ширине |
iB
|
2 |
| Кратность по длине |
iL
|
2 |
| Угол косого раскроя |
a |
60 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
| Ширина листа |
B |
700 |
| Длина листа |
L |
2200 |
| Диаметр детали |
D |
141 |
| Ширина перемычек |
a1 |
2 |
| a |
2,5 |
` |
| Мин. ширина полосы |
Bmin |
269,8416 |
| Коичество полос |
Nп |
2 |
| Шаг в ряду |
S |
143,0000 |
| Количество заготовок в ряду |
Nзр |
14 |
| Длина ряда |
Lр |
2005 |
| Наличие дополнительной заготовки в ряду |
Nдз |
1 |
| Количество заготовк в полосе |
Nзп |
29 |
| Количество заготовок в листе |
N |
58 |
| Коэффициент использования металла |
h |
0,5881 |
| Ширина концевого отхода |
Bо |
160,3167 |
| Целевая функция |
F |
0,5988 |
Приложение 2:
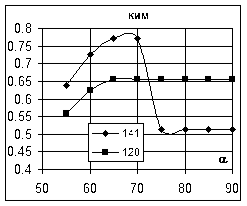 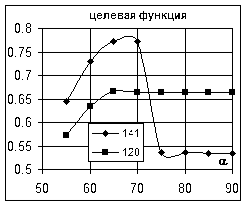
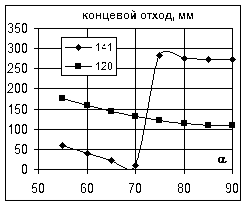
Цели работы:
- освоение методов обработки сложных экспериментов с помощью средств Excel
- освоение методов построения пространственных диаграмм в Excel
Постановка задачи [6]
:
Рассматривается задача отыскания методов обработки бронзы А10Ж3Мц1,5 (температуры и скорости деформирования), которые бы обеспечивали наилучший комплекс механических свойств (предела текучести s
, предела прочности s
, относительного удлинения d
, относительного сужения Ψ
).
Для оптимизации комплекса свойств следует рассмотреть обобщенную функцию желательности, которая в нашем случае имеет вид:
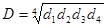 (1) (1)
где di
- частные функции желательности по каждому из показателей комплекса свойств.
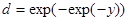 (2) (2)
Здесь y
-
условная шкала, имеющая линейную связь со значениями показателей комплекса свойств s
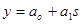 (3) (3)
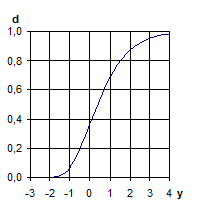
Коэффициенты a0
,
a1
определяют по двум "реперным" точкам, в которых исследователь задает соответствие истинным значениям комплекса свойств определенное с его точки зрения значение функции желательности. Шкала функции желательности выглядит следующим образом: d=0…0,368 (y= - ∞…0) -
недопустимый уровень качества; d=0,368…0,63 (y=0…0,77) -
допустимый уровень качества; d=0,63…0,8 (
y=0,77…1,5) -
хороший уровень качества; d=0,8…1 (
y=1,5…∞) -
превосходный уровень качества. Зависимость d=
f (
y)
приведена на рисунке.
Очевидны следующие соотношения:
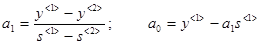 (4) (4)
Здесь. y<
i>
,s<
i>
- пары реперных точек. В нашем случае предлагается следующие значения реперных точек:
| Характеристика |
sT
|
sB
|
d
|
Y
|
| Значение, s |
25 |
21,5 |
44 |
29,6 |
23 |
26,2 |
45 |
60 |
| Функция желательности, d |
0,368 |
0,63 |
0,368 |
0,8 |
0,368 |
0,8 |
0,368 |
0,95 |
| Условная шкала, y |
0 |
0,77 |
0 |
1,5 |
0 |
1,5 |
0 |
3 |
Для обобщенной желательности строится в кодированном масштабе математическая модель вида
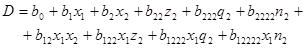 (5) (5)
где z2
,
q2
,
n2
-
следующие функции от x2
:
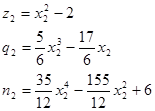 (6) (6)
Уравнения связи между факторами в натуральном и кодированном масштабах
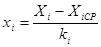 (7) (7)
Фактор X1
-
скорость растяжения мм/с, X2
- температура нагрева о
С испытываемого на растяжение образца. X1ср
=27,5;. k1
=22,5 мм/с; X2ср
=350; k2
=100 о
С.
Матрица плана эксперимента и результаты в натуральном масштабе приведена в таблице:
№
опыта
|
скорость,
мм/с
|
температура,
о
С
|
sT
|
sB
|
d
|
|
| 1 |
5 |
150 |
29,3 |
61,5 |
21,9 |
36,1 |
| 2 |
5 |
250 |
35,1 |
58,1 |
20,5 |
45,2 |
| 3 |
5 |
350 |
34,7 |
54,4 |
20,2 |
37 |
| 4 |
5 |
450 |
29,2 |
34,5 |
27,6 |
47,5 |
| 5 |
5 |
550 |
14,3 |
17 |
25,5 |
57,3 |
| 6 |
50 |
150 |
28,5 |
61,2 |
21,7 |
37,6 |
| 7 |
50 |
250 |
39,6 |
58,7 |
19,7 |
48,3 |
| 8 |
50 |
350 |
36 |
54,7 |
19,9 |
43,8 |
| 9 |
50 |
450 |
32 |
43,5 |
22,4 |
42,7 |
| 10 |
50 |
550 |
20,8 |
24,6 |
24,7 |
52,9 |
Методы решения с использованием Excel:
Решение задачи разбивается на несколько шагов с созданием соответствующих таблиц:
1. Определение коэффициентов соответствия механических свойств условной шкале в формуле (3) по зависимостям (4) с учетом данных таблицы 1.
2. Построения матрицы плана эксперимента в кодовом масштабе по формулам (7) (6)
3. Определение значений условной шкалы для результатов каждого опыта по формулам (3), частных функций желательности по формуле (2), а затем обобщенной функции желательности по формуле (1).
4. Определение значений коэффициентов b
в модели (5) с использованием функции ЛИНЕЙН.
5. Построение графика изменения функции желательности Dпо уравнению (5) в зависимости от двух варьируемых параметров - скорости и температуры и определения области допустимых режимов обработки.
Последовательность выполнения
78. Запустить EXCEL
79. На листе1 создать таблицы с исходными данными эксперимента и поясняющими надписями по следующему образцу (при заполнении таблиц пользуйтесь способами копирования и автозаполнения):
| A |
B |
C |
D |
E |
F |
G |
H |
I |
| 1 |
Определение оптимального интервала штамповки |
| 2 |
Определение коэффициентов перехода к условной шкале |
| 3 |
Характеристика |
sT
|
sB
|
d
|
|
| 4 |
Значение, s |
25 |
21,5 |
44 |
29,6 |
23 |
26,2 |
45 |
60 |
| 5 |
Условная шкала, y |
0 |
0,77 |
0 |
1,5 |
0 |
1,5 |
0 |
3 |
| 6 |
Коэффициенты перехода |
a0
|
a1
|
a0
|
a1
|
a0
|
a1
|
a0
|
a1
|
| 7 |
| 8 |
Варьируемые параметры |
| 9 |
ki
|
Xiср
|
| 10 |
Скорость растяжения, мм/с |
X1
|
22,5 |
27,5 |
| 11 |
Температура нагрева, o
C |
X2
|
100 |
350 |
80. На листе 2 создать таблицы с исходными данными эксперимента и поясняющими надписями по следующему образцу (при заполнении таблиц пользуйтесь способами копирования и автозаполнения).
Таблица.
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
| 1 |
Матрица плана эксперимента |
| 2 |
N оп |
Натуральн |
Кодовый масштаб |
| 3 |
X1
|
X2
|
x1
|
x2
|
z2
|
q2
|
n2
|
x1
*x2
|
x1
*z2
|
x1
*q2
|
x1
*n2
|
| 4 |
1 |
5 |
150 |
| 5 |
2 |
5 |
250 |
| 6 |
3 |
5 |
350 |
| 7 |
4 |
5 |
450 |
| 8 |
5 |
5 |
550 |
| 9 |
6 |
50 |
150 |
| 10 |
7 |
50 |
250 |
| 11 |
8 |
50 |
350 |
| 12 |
9 |
50 |
450 |
| 13 |
10 |
50 |
550 |
| 14 |
Результаты опытов |
| 15 |
sT
|
sB
|
d |
|
ysT
|
ys
B
|
yd
|
y
|
ds
T
|
ds
B
|
dd
|
d
|
D |
| 16 |
1 |
29,3 |
61,5 |
21,9 |
36,1 |
| 17 |
2 |
35,1 |
58,1 |
20,5 |
45,2 |
| 18 |
3 |
34,7 |
54,4 |
20,2 |
37 |
| 19 |
4 |
29,2 |
34,5 |
27,6 |
47,5 |
| 20 |
5 |
14,3 |
17 |
25,5 |
57,3 |
| 21 |
6 |
28,5 |
61,2 |
21,7 |
37,6 |
| 22 |
7 |
39,6 |
58,7 |
19,7 |
48,3 |
| 23 |
8 |
36 |
54,7 |
19,9 |
43,8 |
| 24 |
9 |
32 |
43,5 |
22,4 |
42,7 |
| 25 |
10 |
20,8 |
24,6 |
24,7 |
52,9 |
| 26 |
Коэффициенты регрессионной модели |
| 27 |
b12222
|
b1222
|
b122
|
b12
|
b2222
|
b222
|
b22
|
b2
|
b1
|
b0
|
| 28 |
| 29 |
Построение графика линий уровней обобщенной функции желательности |
| 30 |
x1
|
| 31 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
X1
|
| 32 |
-2 |
2 |
-1 |
1 |
150 |
| 33 |
-1,5 |
0,25 |
1,44 |
-8,3 |
200 |
| 34 |
-1 |
-1 |
2 |
-4 |
250 |
| 35 |
-0,5 |
-1,75 |
1,31 |
2,95 |
300 |
| 36 |
0 |
-2 |
0 |
6 |
350 |
| 37 |
0,5 |
-1,75 |
-1,31 |
2,95 |
400 |
| 387 |
1 |
-1 |
-2 |
-4 |
450 |
| 39 |
1,5 |
0,25 |
-1,44 |
-8,3 |
500 |
| 40 |
2 |
2 |
1 |
1 |
550 |
| 41 |
x2
|
z2
|
q2
|
n2
|
X2
|
81. На Листе1 в ячейки B7 и C7 введите формулы (4) для определения коэффициентов соответствия механических свойств условной шкале в формуле (3): C7 -= (B5-C5) / (B4-C4)
- B7 - составьте выражение самостоятельно
и скопируйте их в диапазоны D7: E7; F7: G7; H7: I7
82. На Листе2 в ячейки D4 и E4 введите формулы (7) для перехода от натурального масштаба к кодированному:
- D4 - = (B4-Лист1! $D$10) /Лист1! $C$10
- E4 - составьте выражение самостоятельно
83. На Листе2 в ячейки F4: H4 введите формулы (6) для вычисления функций z2
,
q2
,
n2
Например, G4 - (5/6) *E4^3- (17/6) *E4
84. На Листе2 в ячейки I4: L4 введите формулы для определения произведения соответствующих функций
85. Распространите формулы диапазона D4: L4 на диапазон D4: L13
86. На Листе2 в ячейки F13: I13 введите формулы (3) для перехода от истинных значений механических свойств к условной шкале Например, G16 - =Лист1! D$7+Лист1! E$7*C16
87. На Листе2 в ячейку J16 введите формулу для определения функции желательности =EXP (-EXP (-F16)) и распространите ее на диапазон J16: M16
88. На Листе2 в ячейку N16 введите формулу для определения обобщенной функции желательности = (J16*K16*L16*M16) ^ (0,25)
89. Распространите формулы диапазона F16: N16 на диапазон F16: N25
90. В диапазон A28: J28 введите формулу для определения коэффициентов регрессии для модели обобщенной функции желательности, используя функцию ЛИНЕЙН и мастер функций. Последовательность действий приведена ниже:
- Выделить A28: J28
- Меню Вставка-Функция (или кнопка Вставка функции)
- Категория - Статистические, Функция - ЛИНЕЙН, Кнопка OK
- Окно Изв_знач_y - диапазон известных значений D
- Окно Изв_знач_x - диапазон значений xi
и производных от них функций в опытах
- Окно Константа - 1
- Окно Стат - 0
- Нажать клавиатурную комбинацию Ctrl-Shift-Enter
- Формула массива вставится в выделенный диапазон и в нем появятся значения коэффициентов
91. Присвойте ячейкам диапазона A28: J28 имена, соответствующие названиям коэффициенты, используя вместо латинских букв "b" русские "в", например ячейке C28 присвойте имя "в122". Присвоение имени ячейкам осуществляется следующим образом:
- выделите нужную ячейку
- выполните команду меню Вставка-Имя-Присвоить
- в окне Присвоение имени в поле Имя внесите необходимое название ячейки, а в поле Формула - ссылку на соответствующий адрес ячейки.
- нажмите кнопку Добавить
92. В диапазоне F32: O40 создайте массив данных для построения графика изменения функции желательности в зависимости от скорости (X1
) и температуры (X2
). Excelпозволяет точно строить пространственные диаграммы только при пропорциональном изменении данных вдоль каждой строки и столбца. Поэтому мы заранее ввели значения X1
и X2
, изменяющиеся с некоторым шагом. Для облегчения ввода формул в диапазон F32: O40 следует сначала создать вспомогательные диапазоны изменения факторов в кодированном масштабе.
93. В ячейку F30 введите формулу = (F31-Лист1! $D$10) /Лист1! $C$10 для перехода от X1
к x1
и распространите ее на диапазон F30: O30
94. В ячейку A32 введите формулу = (E32-Лист1! $D$11) /Лист1! $C$11 для перехода от X2
к x2
95. В диапазон B32: D32 скопируйте формулы из диапазона F4: H4
96. Распространите формулы диапазона A32: D32 на диапазон A32: D40
97. Введите в ячейку F32 формулу для определения функции желательности по полученной регрессионной модели =в0+в1*F$30+в2*$A32+в22*$B32+в222*$C32+в2222*$D32+в12*F$30*$A32+в122*F$30*$B32+в1222*F$30*$C32+в12222*F$30*$D32 обратите внимание на использование имен коэффициентов и смешанной адресации (знак $ стоит только перед именем столбца или номером строки). Смешанная адресация позволяет распространить формулу из ячейки на весь диапазон
98. Распространите формулу из ячейки F32 на диапазон F32: O40
99. Постройте диаграмму изменения функции желательности в зависимости от скорости (X1
) и температуры (X2
). Для этого:
- Выделите диапазон E31: O40
- Воспользуйтесь командой меню Вставка-Диаграмма
- Выберите тип диаграммы: Поверхность, Вид диаграммы - Цветная контурная (в виде цветных сечений поверхностей уровня)
- Следуйте указаниям мастера диаграмм, ориентируясь на получение диаграммы, приведенной в приложении.
- Если внешний вид диаграммы не соответствует приведенной в приложении - отформатируйте ее.
100. Перенесите полученную диаграмму с листа 2 на лист 1
101. Проанализируйте по полученной диаграмме области возможных режимов обработки материала, памятуя, что допустимый уровень функции желательности D=0,368
102. Отформатируйте таблицы и графики так, как это показано в приложении. Завершить работу, сохранив ее в файле work8. xls.
103. Запустить EXCEL, вернуться к документу work8. xls и предъявить его преподавателю.
104. Предъявить преподавателю краткий конспект занятия.
Приложение:
Лист 1
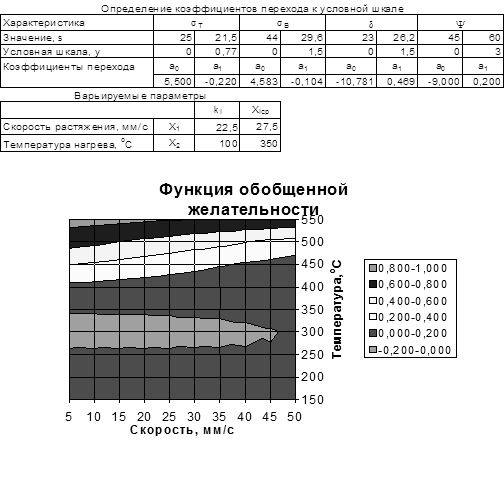
Лист 2
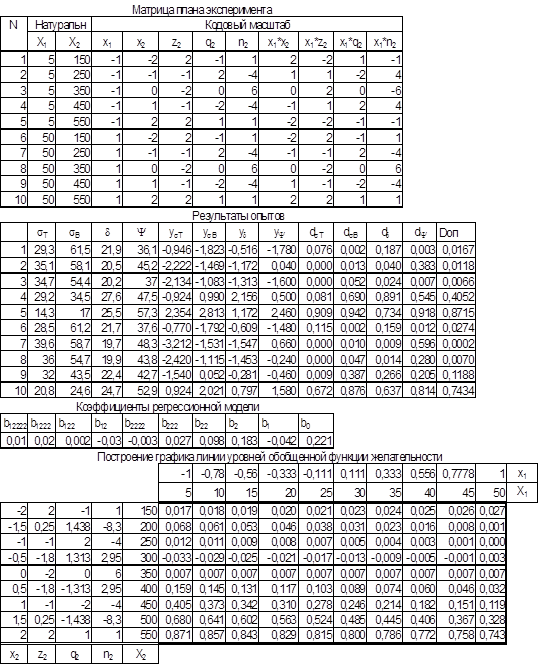
[1]
Дмитриев А.М., Коробова Н.В., Ступников В.П. Методы факторного планирования эксперимента в обработке давлением: Учебное пособие для вузов. - М.: МГТУ им. Н.Э. Баумана, 1999. - 105 с.
[2]
Попов Е.А. Основы теории листовой штамповки. - М.: Машиностроение, 1968. - 283 с.
[3]
Зубцов М.Е. Листовая штамповка. - Л: Машиностроение, 1967. - 504 с.
[4]
Теория ковки и штамповки // Под ред. Е.П. Унксова и А.Г. Овчинникова. - М.: Машиностроение, 1992. - 720 с.
[5]
Дмитриев А.М., Коробова Н.В., Ступников В.П. Методы факторного планирования эксперимента в обработке давлением: Учебное пособие для вузов. - М.: МГТУ им. Н.Э. Баумана, 1999. - 105 с.
[6]
Дмитриев А.М., Коробова Н.В., Ступников В.П. Методы факторного планирования эксперимента в обработке давлением: Учебное пособие для вузов. - М.: МГТУ им. Н.Э. Баумана, 1999. - 105 с.
|