Тема 1.
Вопросы:
1. Какие явления изучает статистика?
Статистика изучает массовые социально-экономические явления и процессы, выступающие как множества отдельных фактов, обладающих как индивидуальными, так и общими признаками.
2. Что понимается под статистической закономерностью?
Статистическая закономерность – это форма проявления причинной связи, выражающаяся в последовательности, регулярности, повторяемости событий с достаточно высокой степенью вероятности, если причины (условия), порождающие события, не изменяются или изменяются незначительно.
3. На какие науки опирается и в каких науках используется статистика?
Статистика во многом опирается на математику и теорию вероятностей. Используется статистика в таких науках как математическая статистика, экономическая статистика, прикладная статистика, разнообразные отраслевые статистики, демография и др.
4. Как организована государственная статистика Российской Федерации, в каких изданиях публикуются статистические данные?
Структура органов государственной статистики соответствует административно-территориальному делению страны. В двух городах – Москве и Санкт-Петербурге имеются местные комитеты по статистике, то же – в автономных республиках. В краях и областях также работают комитеты статистики. Низовым звеном являются районные инспектуры государственной статистики, которые имеются в административных районах краев и областей, крупных городов.
Статистические данные публикуют журналы «Коммерсант»,»Вопросы статистики», «Статистическое обозрение», газеты «Деловой мир», «Финансовая газета», статистический ежегодник «Российская федерация в 20.. году», региональные статистические сборники и др.
Задание 1
1. Статистика исследует не отдельные факты, а массовые социально-экономические явления и процессы, выступающие как множества отдельных фактов, обладающих как индивидуальными, так и общими признаками.
2. Статистика изучает, прежде всего, количественную сторону общественных явлений и процессов в конкретных условиях места и времени.
3. статистика характеризует структуру общественных явлений.
4. Статистика исследует изменение уровня и структуры явления в динамике.
Реклама

5. статистика выявляет взаимосвязь явлений.
Задание 2
Производительность сельскохозяйственных предприятий. Изучая это явление, можно выявить наиболее и наименее доходные предприятия, выявить территориальное расположение крупнейших предприятий.
Распределение жителей страны по росту, окружности головы, длине стопы и другим физическим признакам. Эти данные необходимы для предприятий, изготавливающих одежду и обувь.
Задание 3
Совокупность студентов второго курса. Интерес для статистки могут представлять средний возраст студентов и их средний балл.
Совокупность преподавателей. Интерес для статистики могут представлять процент занятости преподавателей (ставка) и структура их ученых званий (доцент, кандидат наук, профессор).
Тема 3.
Вопросы:
1. Из каких этапов состоит статистическое исследование, и какие задачи решает каждый этап?
К этапам статистического исследования относятся:
- Статистическое наблюдение – массовый научно организованный сбор первичной информации об отдельных единицах изучаемого явления;
- Группировка и сводка материала – обобщение данных наблюдения для получения абсолютных величин (учетно-оценочных показателей) явления;
- Обработка статистических данных и анализ результатов для получения обоснованных выводов о состоянии изучаемого явления и закономерности его развития.
2. Какие формы статистического наблюдения используются, и в каких случаях они применяются?
Статистические наблюдения можно разбить на группы по следующим признакам:
1. Времени регистрации фактов
- Текущее. Изменения в отношении изучаемых явлений фиксируются по мере их наступления. Проводится с целью изучения динамики явления.
- Периодическое. Данные, отражающие изменения объекта, собираются в ходе нескольких исследований. Цель и программа схожи с предыдущим методом.
- Единовременное. Дает сведения о количественных характеристиках явления или процесса в момент его исследования.
2. Охвату единиц совокупности
- Сплошное. Получение информации о всех единицах исследуемой совокупности.
- Несплошное. Получение информации в более короткие сроки, чем при сплошном.
- Выборочное. Характеристики всей совокупности фактов дается по некоторой их части, отобранной в случайном порядке.
- Метод основного массива. Наблюдение ведется за наиболее крупными единицами совокупности, в которых сосредоточена значительная часть всех подлежащих изучению фактов.
- Монографическое. Проводится с целью выявления имеющихся или намечающихся тенденций в развитии нового явления.
Реклама

3. Что такое абсолютные и средние величины статистической сводки?
Абсолютными величинами в статистике называются показатели, выражающие численность единиц совокупности и суммы изучаемых признаков в соответствующих единицах меры по признакам и вцелом по совокупности. Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.
Задание 4
Результаты экзамена по статистике в группе из 20 человек заданы в следующей строчке: 5, 4, 4, 5, 3, 3, 2, 4, 5, 3, 4, 4, 4, 5, 3, 2, 2, 4, 4, 5.
| Оценка |
Частота |
| 2 |
3 |
| 3 |
4 |
| 4 |
8 |
| 5 |
5 |
| Всего |
20 |
Средняя оценка:

Тема 5
статистика закономерность показатель
Вопросы:
1. Как связаны относительные и абсолютные показатели?
Относительный показатель представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений.
2. Какие виды относительных показателей используются в статистике?
В статистике используются относительные показатели:
- Динамики;
- Плана;
- Реализации плана;
- Структуры;
- Координации;
- Интенсивности и уровня экономического развития;
- Сравнения.
3. Как определяются средняя величина и чем отличаются простые и взвешенные средние?
Определить среднюю во многих случаях можно через исходное соотношение средней или ее логическую формулу:

Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность.
4. Какие виды средних величин используются в статистике?
В статистике используют следующие виды средних величин:
- Средняя арифметическая;
- Средняя гармоническая;
- Средняя геометрическая;
- Средняя квадратическая, кубическая и т.д.
5. Что такое структурные средние?
В качестве статистических характеристик вариационных рядов распределения рассчитываются структурные средние – мода и медиана.
Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.
Медианой называется значение признака, приходящееся на середину ранжированной совокупности.
Задание 1
Объем продаж в магазине в 199г. Составил (в тыс. руб.)
| Месяц |
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
| Объем продаж |
92 |
88 |
103 |
98 |
102 |
96 |
Относительные показатели динамики:


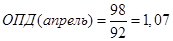
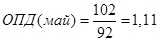

Цепные показатели динамики:




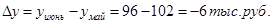
Среднемесячный объем продаж:

Средний цепной показатель динамики:
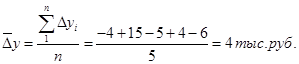
Медианное значение объема продаж:
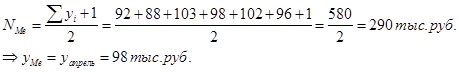
Задание 2
Сведения о заработной плате промышленных предприятий города N даны в таблице
| Предприятие |
Месячный фонд заработной платы (тыс. руб.) |
Средняя заработная плата (руб.) |
| Цементный завод |
586 |
1125 |
| Молокозавод |
375 |
820 |
| Мебельный комбинат |
521 |
1012 |
Относительные показатели структуры и координации:
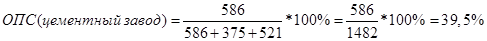

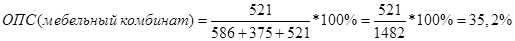
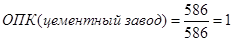
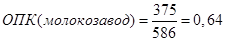
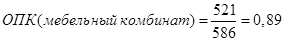
Отображение табличных данных на диаграммах:
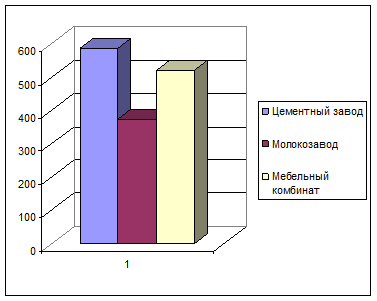
Месячный фонд заработной платы (тыс. руб.)
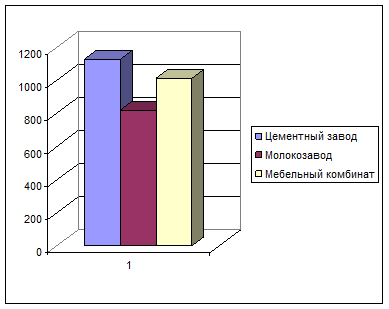
Средняя заработная плата (руб.)
Средняя заработная плата:
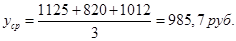
Значение моды для заработной платы:
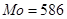
Задание 3
Данные о стоимости жилья приведены в таблице
Цена 1  (в $) (в $) |
Общая площадь (в тыс.  ) ) |
| 100-200 |
31,1 |
| 200-300 |
21,5 |
| 300-400 |
8,4 |
| 400-500 |
8 |
| 500-600 |
14 |
Относительные показатели структуры:
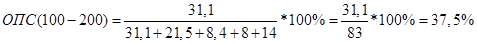
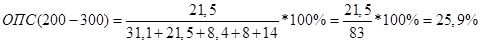
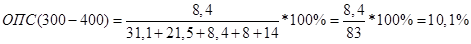

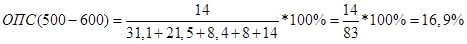
Значения моды и медианы:
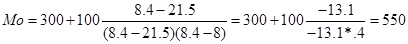
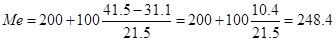
Гистограмма и кумулята:
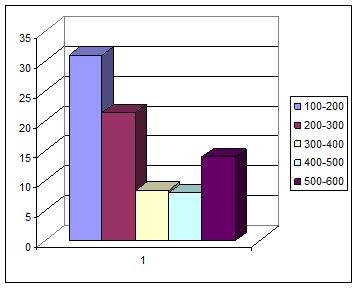
Гистограмма
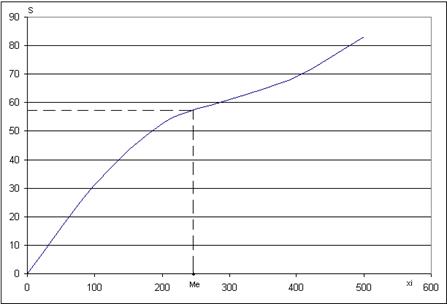
Кумулята
Средняя цена за 1 
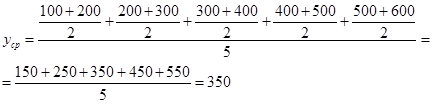
Значение первой квартили
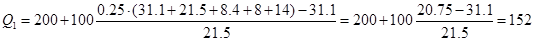
Тема 7.
Вопросы:
1. Что такое генеральная и выборочная совокупности?
Совокупность отобранных для обследования единиц в статистике принято называть выборочной, а совокупность единиц, из которых производится отбор – генеральной.
2. Какие виды выборок используются?
Виды выборок:
- Собственно-случайная;
- Механическая;
- Типическая;
- Серийная;
- Комбинированная.
3. Что такое доверительная вероятность и предельная ошибка выборки?
Доверительная вероятность – вероятность того, что значение параметра генеральной совокупности находится в построенном для него доверительном интервале.
Предельная ошибка выборки дает возможность оценить, в каких пределах находится величина генеральной средней.
4. Как сравниваются результаты нескольких выборок?
На основании сравнения двух выборочных средних делается вывод о случайности или существовании зависимости их расхождений. Для этого абсолютная разность показателей 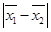 сопоставляется со средней ошибкой разности. Если при сопоставляется со средней ошибкой разности. Если при 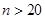 результат этого соотношения результат этого соотношения 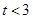 , то делается вывод о случайности расхождения. Если , то делается вывод о случайности расхождения. Если 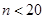 , то полученное значение , то полученное значение 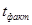 сравнивают с табличным, определяемым по таблицам t-распределения Стьюдента при заданном числе степеней свободы и уровне значимости. И если сравнивают с табличным, определяемым по таблицам t-распределения Стьюдента при заданном числе степеней свободы и уровне значимости. И если  , расхождение можно считать случайным. , расхождение можно считать случайным.
5. Как рассчитывается необходимая численность выборки?
Для определения необходимой численности выборки исследователь должен задать уровень точности выборочной совокупности с определенной вероятностью.
Задание 1
Для определения среднего уровня зарплаты в деревообрабатывающей промышленности были установлены зарплаты 625 рабочих, отобранных методом случайной выборки. При этом средний уровень зарплаты по выборке равен 1134 руб., среднеквадратичное отклонение 111 руб. Найти 95% доверительный интервал для значения средней зарплаты рабочих в промышленности.
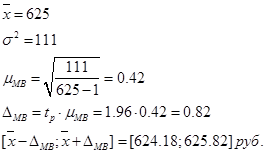
Задание 2
Для определения среднего возраста студентов вуза с числом студентов 1250 был зафиксирован возраст 100 студентов.
| Возраст |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
| Число студентов |
11 |
13 |
17 |
20 |
15 |
11 |
7 |
6 |
Средний возраст студентов выборки:
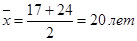
Среднеквадратическое отклонение студентов выборки:
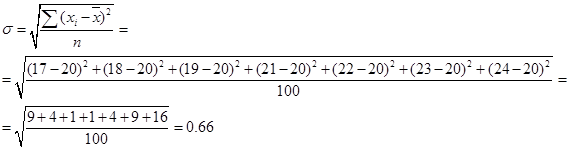
99% доверительный интервал для среднего возраста студентов вуза:
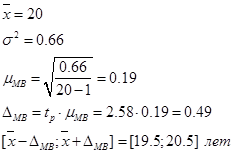
Задание 3
В городе проводится обследование семей с целью выявления доли расходов семейных бюджетов на оплату жилья. Предыдущее аналогичное исследование дало результаты в 9,6%. Сколько нужно обследовать семей, чтобы с вероятностью 0,99 и точностью не менее 0,5% определить эту долю?
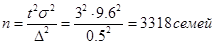
Задание 4
В городе исследуются затраты времени жителей на ведение домашнего хозяйства. Опрошено 101 мужчина и 199 женщин. При этом выяснилось, что мужчины тратят на домашние работы в среднем 2,5 часа при среднеквадратичном отклонении 20 мин., а женщины – 3,5 часа при среднеквадратичном отклонении 10 мин. Найти 99% доверительный интервал для разности значений среднего времени, затрачиваемого женщинами и мужчинами на домашние работы.
Можно ли по приведенным данным утверждать, что женщины, проживающие в этом городе, в среднем затрачивают больше времени на домашние работы, чем мужчины?
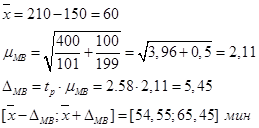
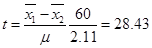
Так как t=28.43 >3, то можно утверждать, что женщины затрачивают больше времени на домашние работы.
Тема 9
Вопросы:
1. Какие виды связей существуют?
В статистике выделяют следующие виды связей:
- Статистическая;
- Корреляционная;
- Стохастическая;
- Функциональная;
- Прямая;
- Обратная;
- Прямолинейная;
- Нелинейная.
2. Что такое корреляция?
Корреляция – это статистическая зависимость между случайными величинами, не имеющими строгого функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
3. Как строится уравнение регрессии?
Уравнение регрессии имеет вид:
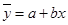
где 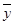 - среднее значение результативного признака при определенном значении факторного признака х, - среднее значение результативного признака при определенном значении факторного признака х,
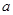 - свободный член уравнения, - свободный член уравнения,
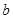 - коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака у от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения – вариация у, приходящаяся на единицу вариации х. - коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака у от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения – вариация у, приходящаяся на единицу вариации х.
4. Что такое значимость параметров уравнения взаимосвязи и как она оценивается?
Значимость параметров уравнения взаимосвязи – соответствие оценок корреляции и регрессии истинным параметрам взаимосвязи. Ее можно оценить с помощью ошибки коэффициента корреляции.
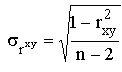
В первом приближении нужно, чтобы 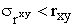 . Значимость rxy проверяется его сопоставлением с . Значимость rxy проверяется его сопоставлением с 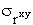 , при этом получают , при этом получают
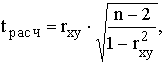
где tрасч – так называемое расчетное значение t-критерия.
Если tрасч больше теоретического (табличного) значения критерия Стьюдента (tтабл) для заданного уровня вероятности и (n-2) степеней свободы, то можно утверждать, что rxy значимо.
5. Какие существуют непараметрические методы оценки связей?
- Распределение единиц совокупности в форма таблиц взаимной сопряженности;
- Вычисление коэффициента взаимной сопряженности;
- Вычисление ранговых коэффициентов корреляции.
Задание 1
По восьми предприятиям района имеются следующие данные об объеме реализованной продукции и полученной прибыли.
| № предприятия |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Объем реализованной продукции (млн. руб.) |
92 |
83 |
82 |
79 |
77 |
75 |
74 |
60 |
| Прибыль (млн. руб.) |
14,4 |
13,2 |
7,2 |
7,3 |
6 |
8 |
10,1 |
5 |
Уравнение парной линейной регрессии:
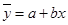 - уравнение парной регрессии. Коэффициенты - уравнение парной регрессии. Коэффициенты 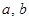 найдем из системы нормальных уравнений: найдем из системы нормальных уравнений:
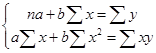
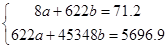
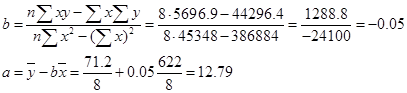
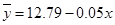 - уравнение регрессии - уравнение регрессии
| x |
y |
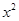 |
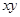 |
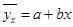 |
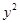 |
| 92 |
14,4 |
8464,00 |
1324,80 |
7,87 |
207,36 |
| 83 |
13,2 |
6889,00 |
1095,60 |
8,35 |
174,24 |
| 82 |
7,2 |
6724,00 |
590,40 |
8,40 |
51,84 |
| 79 |
7,3 |
6241,00 |
576,70 |
8,56 |
53,29 |
| 77 |
6 |
5929,00 |
462,00 |
8,67 |
36,00 |
| 75 |
8 |
5625,00 |
600,00 |
8,78 |
64,00 |
| 74 |
10.1 |
5476,00 |
747,40 |
8,83 |
102,01 |
| 60 |
5 |
3600,00 |
300,00 |
9,58 |
25,00 |
| 622 |
71,2 |
45348,00 |
5696,90 |
69,04 |
713,74 |
Уравнение обратной линейной зависимости (гиперболы):
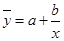 - уравнение гиперболы (в общем виде). - уравнение гиперболы (в общем виде).
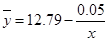 - уравнение гиперболы. - уравнение гиперболы.
Оценка тесноты связи:
Для оценки тесноты связи применим формулу:
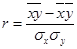
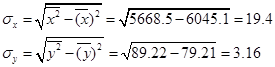
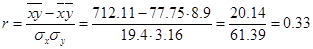
Отображение результатов на графиках:
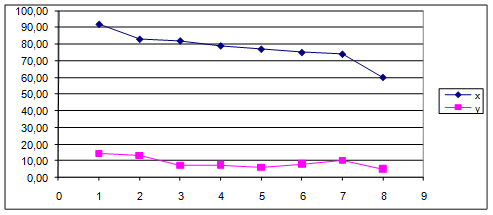
Выводы об объеме реализованной продукции и прибыли:
Прибыль и объем реализованной продукции слабо связаны друг с другом, т. к.  . .
Задание 2
С помощью коэффициента корреляции рангов Спирмена установите тесноту связи между ценой спроса и предложения на девять различных товаров
| № товара |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| Цена спроса |
140 |
145 |
149 |
149 |
184 |
189 |
200 |
220 |
220 |
| Цена предложения |
131 |
136 |
181 |
172 |
196 |
202 |
200 |
211 |
264 |
Для расчета коэффициента Спирмена вначале ранжируем значения признаков в каждом ряду. Затем находим разности рангов, возводим их в квадрат и подставляем в формулу:

| x |
y |
 |
 |
 |
 |
| 140 |
131 |
1 |
1 |
0 |
0 |
| 145 |
136 |
2 |
2 |
0 |
0 |
| 149 |
181 |
3 |
4 |
-1 |
1 |
| 149 |
172 |
4 |
3 |
1 |
1 |
| 184 |
196 |
5 |
5 |
0 |
0 |
| 189 |
202 |
6 |
7 |
-1 |
1 |
| 200 |
200 |
7 |
6 |
1 |
1 |
| 220 |
211 |
8 |
8 |
0 |
0 |
| 220 |
264 |
9 |
9 |
0 |
0 |
| 4 |

Судя по значению полученного коэффициента, связь между x и y довольно большая.
|