РЕФРАКТОМЕТРИЧЕСКИЙ МЕТОД АНАЛИЗА В ХИМИИ
Оглавление
Введение
1. Некоторые понятия физической оптики
1.1 Распространение света
1.2 Показатель преломления света (показатель рефракции)
1.3 Дисперсия света
1.4 Полное внутреннее отражение
2. Дипольные моменты и рефракция
2.1 Поляризуемость и дипольный момент
2.1.1 Молярная поляризуемость
2.2 Молярная рефракция
3. Рефракция и структура молекул
3.1 Аддитивность рефракции
3.2 Оптическая экзальтация
3.3 Дисперсия молекулярной рефракции
3.4 Рефракция и размеры молекул
4. Рефрактометрия растворов
4.1 Анализ двухкомпонентных растворов
4.2 Анализ трёхкомпонентных растворов
5. Рефрактометрия полимеров
Заключение
Список используемой литературы
Введение
Рефрактометрический метод имеет многолетнюю историю применения в химии.
Рефрактометрия (от латинского refraktus – преломлённый и греческого metréō – мерю, измеряю) – это раздел прикладной оптики, в котором рассматриваются методы измерения показателя преломления света (n) при переходе из одной фазы в другую, или, иными словами, показатель преломления n – это отношение скоростей света в граничащих средах.
Применительно к химии рефракция имеет более широкое смысловое значение. Рефракция R (от латинского refractio – преломление) есть мера электронной поляризуемости атомов, молекул, ионов.
Поляризация электронных облаков в молекулах отчётливо проявляется в инфракрасном (ИК) и ультрафиолетовом (УФ) поглощении веществ, но в ещё большей степени она ответственна за явление, которое количественно характеризуется молекулярной рефракцией.
Когда свет как электромагнитное излучение проходит через вещество, то даже в отсутствие прямого поглощения он может взаимодействовать с электронными облаками молекул или ионов, вызывая их поляризацию. Взаимодействие электромагнитных полей светового пучка и электронного поля атома приводит к изменению поляризации молекулы и скорости светового потока. По мере возрастания поляризуемости среды возрастает и n – показатель, величина которого связана с молекулярной рефракцией. Указанное явление используется наряду с методом дипольных моментов для изучения структуры и свойств неорганических, органических и элементоорганических соединений.
Реклама

Рефрактометрия широко применяется также для определения строения координационных соединений (комплексов молекулярного и хелатного типа), изучения водородной связи, идентификации химических соединений, количественного и структурного анализа, определения физико–химических параметров веществ.
В производственной практике показатель преломления света n используется для контроля степени чистоты и качества веществ; в аналитических целях – для идентификации химических соединений и их количественного определения. Таким образом, рефрактометрия – это метод исследования веществ, основанный на определении показателя преломления (коэффициента рефракции) и некоторых его функций. Из функций n, используемых в химии, наибольшее значение имеют: функция Лоренца – Ленца, производная n по концентрации растворённых веществ (инкремент n) и дисперсионные формулы, включающие разности показателей преломления для двух длин волн. Инкременты n используют в жидкостной хроматографии и при определении молекулярной массы полимеров методом рассеяния света. Для рефрактометрического анализа растворов в широких диапазонах концентраций пользуются таблицами или эмпирическими формулами, важнейшие из которых (для растворов сахарозы, этилового спирта и др.) утверждаются международными соглашениями и лежат в основе построения шкал специализированных рефрактометров для анализа промышленной и сельскохозяйственной продукции. Разработаны способы анализа трехкомпонентных растворов, основанных на одновременном определении n и плотности или вязкости, либо на осуществлении химических превращений с измерением n исходных и конечных растворов; эти способы применяют при контроле нефтепродуктов, фармацевтических препаратов и др. Идентификация органических соединений, минералов, лекарственных веществ осуществляется по таблицам n, приводимым в справочных изданиях. Преимуществами рефрактометрического метода являются его простота и относительно невысокая стоимость приборов для определения коэффициента преломления света.
1. Некоторые понятия физической оптики
1.1 Распространение света
рефракция поляризуемость преломление химический
Первая гипотеза – эмиссионная или корпускулярная, утверждала, что свет представляет собой поток мельчайших частиц – корпускул, испускаемых нагретым светящимся телом. Достигая глаза, эти частицы отражают зрительные ощущения. Ударяясь о преграду, частицы отражаются от её поверхности или проникают внутрь в зависимости от свойств материала тела.
Реклама

Легко объясняя законы отражения света, эта гипотеза не могла объяснить некоторые особенности преломления света и вовсе не объясняла интерференцию света.
Вторая гипотеза – волновая, утверждала, что частицы, испускаемые светящимся телом, находятся в состоянии чрезвычайно быстрых колебаний, генерирующих волны, которые распространяются во все стороны и, достигая глаза, вызывают зрительные ощущения. Волновая теория хорошо объясняла интерференцию света и другие явления, недоступные корпускулярной гипотезе, но была не в состоянии объяснить, каким образом распространяются волны в вакууме. Впоследствии эта неясность была устранена признанием за световыми волнами электромагнитного характера. Таким образом, свет по этой гипотезе представляет собой быстро меняющееся электромагнитное поле.
В дальнейшем с накоплением экспериментальных данных и их теоретической интерпретации, удалось установить особый, двойственный, характер световых явлений и свести обе, казалось, взаимоисключающие гипотезы в одну стройную, свободную от внутренних противоречий теорию. В соответствии с этой теорией свет равноправно может рассматриваться и как волновое движение электромагнитной природы, и как поток частиц, излучаемых источником света в виде отдельных порций света – квантов или фотонов.
Вместе с тем световые явления могут рассматриваться также и с позиции геометрической или лучевой оптики, представляющей собой применение геометрических построений и теорем.
Фундаментом для сближения геометрии с учением о свете и развития лучевой оптики явились представления о прямолинейности распространения света. Лучевая оптика и в настоящее время сохраняет ведущую роль во всех оптических и светотехнических расчётах, благодаря их простоте и наглядности, и показывает обычно полное соответствие вычисленных и экспериментальных данных.
Лучевая оптика базируется на трёх основных приложениях:
- прямолинейности распространения света в однородной среде;
- поведении света на границе раздела двух сред при условии, что такая граница представляет собой идеально гладкую поверхность;
- независимости распространения света.
Указанные положения установлены эмпирически, т. е. опытным путём посредством сравнения геометрических соотношений без учёта особенностей, связанных со сложной природой света.
Чтобы оперировать только наглядными геометрическими элементами, в лучевой оптике введены два условных понятия о луче и о светящейся точке.
Под лучом понимают направление, по которому распространяется свет. Экспериментально установлено, что в вакууме и в однородной (газовой, жидкой или твёрдой) прозрачной среде (например, в воздухе при постоянном давлении, в воде или стекле) свет распространяется прямолинейно, и луч представляет собой прямую линию, началом которой является источник света.
Под светящейся точкой понимают источник света, незначительными размерами которого можно пренебречь. Физически любой источник света обладает определёнными размерами, однако, если сравнить эти размеры с теми расстояниями, на которые распространяется действие света, то условно (без существенной погрешности) источник света принимают за точку.
От светящейся точки света расходится во все стороны в виде пучка бесконечное число лучей, заполняющих всё окружающее пространство. Такой пучок называется неограниченным. Однако, если на пути такого пучка поместить диафрагму – непрозрачный экран с отверстием, то за диафрагмой свет будет распространяться уже как ограниченный пучок.
Уменьшая отверстие диафрагмы, можно выделять всё более и более тонкие пучки. Казалось бы, это должно привести к столь тонкому пучку, что его можно считать "отдельным лучом". Однако опыт не подтверждает это предположение. При уменьшении диаметра отверстия лучи теряют прямолинейность и начинают огибать его края, и тем больше, чем меньше становится отверстие.
Явление огибания световыми (звуковыми и т. д.) волнами встречающихся на пути препятствий называется дифракцией света и обусловлено его волновой природой. По этой причине нельзя выделить отдельный луч и в действительности существуют только пучки лучей.
1.2 Показатель преломления света (показатель рефракции)
Если на пути светового пучка, распространяющегося в прозрачной однородной среде (например, в воздухе), встречается другая прозрачная однородная среда (например, стекло), то на границе раздела сред пучок света разделяется на два луча, из которых один луч входит в новую среду, изменяя своё направление (преломляется), а другой, отражаясь от поверхности раздела и изменяя своё направление, продолжает распространяться в первой среде. Луч при распространении в однородных средах, изменяя свою однонаправленность, сохраняет прямолинейность распространения и до, и после границы раздела (рис.1).
Таким образом, преломление и отражение не противоречат прямолинейности распространения света в однородных средах.

Рис. 1. Поведение луча на поверхности раздела
Линия ММ на рис. 1 изображает поверхность (границу) раздела между воздухом и стеклом. Падающий луч монохроматического света (света, условно одной длины волны) составляет с нормалью О\О’
к поверхности раздела сред угол АВО = α. Этот угол называется углом падения луча. В другой среде луч составляет с нормалью угол преломления О’
ВС = β.
Если изменять угол падения луча α, то будет изменяться и угол преломления луча β, но при этом всегда будет сохраняться неизменным отношение синуса угла падения луча к синусу угла преломления:
 (1) (1)
Если заменять стекло на другие однородные прозрачные среды (например, воду, другой сорт стекла), то в любом случае n будет оставаться величиной постоянной, но значения её будут другими. Причём, чем больше значение n, тем больше оптическая плотность второй среды.
Если луч входит в какую-либо однородную прозрачную среду не из другой прозрачной среды, а из вакуума, то такой показатель преломления называется абсолютным показателем преломления среды (N).
Поскольку значение n зависит от длины волны света (λ) и от температуры, то её измерение проводят при монохроматическом свете и постоянной температуре.
Законы преломления света формулируются следующим образом:
- падающий и преломлённый лучи находятся в одной плоскости с нормалью к поверхности раздела, но расположены на противоположных сторонах от неё;
- отношение синуса угла падения луча к синусу угла преломления для двух соприкасающихся однородных сред постоянно и не зависит от угла падения;
- падающий и преломленный лучи взаимно обратимы, т.е., если луч, входя из одной среды в другую, идет по направлению АВС, то, выходя из второй среды в первую, он пойдет по направлению СВА.
Очевидно, при переходе из более плотной среды (стекло, рис. 1) в менее плотную (воздух) луч удалится от нормали, а показатель преломления примет обратное соотношение:
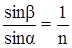 (2) (2)
Показатель преломления как постоянная величина является характеристикой вещества (подобно температуре плавления).
Свет как электромагнитное излучение при прохождении через однородную прозрачную среду, и взаимодействуя с её частицами (молекулами, атомами, ионами), изменяет свою скорость. Наибольшая скорость распространения света достигается в вакууме ( С0
= 3·1010
м/с). В воздухе скорость света (Св
) уменьшается, и значение абсолютного показателя преломления воздуха (Nв
) составляет:
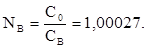 (3) (3)
Относительный показатель преломления определённой среды nс
– это отношение скорости света в воздухе к скорости света в исследуемой среде (Сс
):
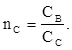 (4) (4)
Таким образом, абсолютный и относительный показатели преломления воздуха связаны между собой соотношением:
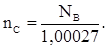 (5) (5)
Для жидких и твердых тел n определяют, как правило, относительно воздуха, а для газов – относительно вакуума.
1.3 Дисперсия света
В то время как для любого монохроматического луча углы падения равны углам отражения, показатель преломления в одной и той же среде разный для каждой длины волны λ. Поэтому, если на поверхность раздела сред будет падать не монохроматический, а "белый" свет, то после преломления отдельные его составляющие будут отклоняться по-разному и иметь разные углы преломления при одном и том же угле падения. Наибольшее отклонение происходит у самых коротковолновых (фиолетовых) лучей, а наименьшее – у самых длинноволновых (красных) лучей, т. е. "белый" свет, переходя в более плотную прозрачную однородную среду, рассеивается или диспергирует.
Причиной дисперсии света является неодинаковая скорость распространения электромагнитного излучения различных длин волн в прозрачной однородной среде. Мерой дисперсии света служит разность между значениями показателя преломления, измеренным при различных длинах волн (например, ΔnFC
; табл.1).
Показатель преломления в зависимости от условий его определения дополняется латинской буковой n с подстрочным и надстрочным индексами (напрмер, 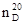 , ,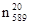 ). Верхний индекс показывает температуру (в 0
С), а нижний индекс – линии или длину волны (в нм), при которых производилось измерение. Обычно n определяют при указанных в табл. 1 длинах волн. ). Верхний индекс показывает температуру (в 0
С), а нижний индекс – линии или длину волны (в нм), при которых производилось измерение. Обычно n определяют при указанных в табл. 1 длинах волн.
Обозначение показателя преломления от условий его определения
Таблица 1
| Линия спектра водорода |
Индекс линии |
λ, нм |
Обозначение показателя преломления |
| жёлтая |
D |
589,3 |
nD
|
| красная |
C |
656,3 |
nC
|
| синяя |
F |
486,1 |
nF
|
| фиолетовая |
G |
434,0 |
nG
|
В рефрактометрии часто используется показатель n∞
, значение которого определяют экстраполяцией зависимости n = f(λ) до бесконечно больших длин волн. Такая экстраполяция осуществляется обычно по формуле Коши:
n = n∞
+ b/λ. (6)
Константы n∞
и b определяют, измерив n при разных λ (например λF
и λС
– линий спектра водорода). В большинстве случаев определяют не n∞
, а nD
желтой линии спектра натрия (D-линии).
На практике используются три способа выражения дисперсии света.
1. Средняя дисперсия:
ΔnFC
= (nF
− nC
)∙104
.(7)
2. Коэффициент дисперсии или число Аббе:
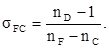 (8) (8)
3. Удельная дисперсия:
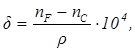 (9) (9)
где ρ – плотность вещества.
Средняя дисперсия, nF
– nC
, частные дисперсии 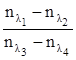 и число Аббе служат важнейшими характеристиками оптических материалов. Относительная дисперсия и число Аббе служат важнейшими характеристиками оптических материалов. Относительная дисперсия 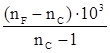 и родственные ей функции применяют для групповой идентификации углеводородов и анализа нефтяных фракций. и родственные ей функции применяют для групповой идентификации углеводородов и анализа нефтяных фракций.
Поскольку показатель преломления изменяется с изменением температуры и длины волны света (который, безусловно, не должен поглощаться веществом), то первое условие должно быть, строго говоря, оговорено, но на самом деле изменение величины R в зависимости от температуры вполне укладывается в рамки ошибок эксперимента, и поэтому температуру указывать не обязательно.
Наиболее часто используемыми длинами волн являются Нα
-линии при 653,3 нм, Нβ
-линия при 486,1 нм и D-линия натрия на 589,3, и значения R вполне чётко зависят от того, какая линия выбрана.
Если нужно определить молекулярную рефракцию твёрдого вещества, то прибегают к модифицированному уравнению, учитывающему изменение показателя преломления с концентрацией раствора.
1.4 Полное внутреннее отражение
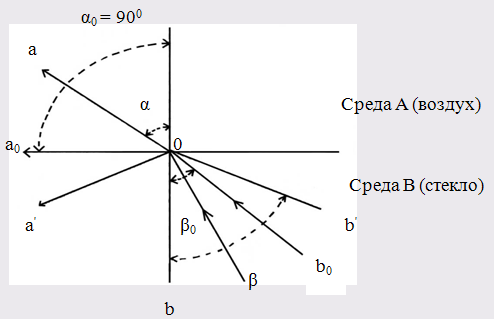
Рис.2. Схема направления распространения лучей при полном внутреннем отражении
b0
Oa0
– распространение луча при предельном угле;
b′Oa′ - распространение лучей при полном внутреннем отражении
Если луч света распространяется из более плотной среды В в менее плотную среду А (рис.2), то при некотором угле β = β0
угол преломления α достигнет максимального значения α0
= 900
. Далее луч будет распростра-няться вдоль поверхности раздела сред и выражение (2) примет следующий вид:
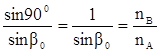 . .
Если направить луч в среду В (рис. 2) под углом β > β0
, то он вообще не попадёт в среду А, отразившись от поверхности раздела (рис. 2). Это явление называется полным внутренним отражением, а угол β0
– предельным углом.
На измерении предельного угла основан принцип работы рефрактометров.
2. Дипольные моменты и рефракция
Коэффициент преломления, как уже отмечалось, зависит от поляризуемости атомов, молекул и ионов. Поэтому исследование электрических характеристик вещества даёт важную информацию о распределении зарядов в молекуле и позволяет установить некоторые свойства вещества, обусловленные его электрической асимметрией.
Рассмотрим некоторые вопросы, касающиеся природы возникновения дипольного момента в молекуле.
2.1 Поляризуемость и дипольный момент
Любая молекула представляет собой совокупность положительно заряженных ядер и отрицательно заряженных электронов. При суммарном заряде, равном +е, заряд всех электронов будет равен –е .
Если распределение ядер и электронов в пространстве таково, что центры "тяжести" положительных и отрицательных зарядов не совпадают, то молекула обладает постоянным дипольным моментом:
μ =е∙l, (10)
где l – расстояние между центрами электрических зарядов.
Такая молекула является полярной. Мерой полярности молекулы служит величина дипольного момента, которую выражают в дебаях (D):
D = 3,33564·10−30
Кл·м
Дипольный момент – величина векторная. Направление вектора "→"выбирается от отрицательного полюса к положительному. В химической литературе, однако, традиционно принимается противоположное направление, т. е. от "+" к "−".
Если в двухатомных молекулах простых веществ, т. е. состоящих из одинаковых атомов, и в многоатомных молекулах сложных веществ, обладающих высокой симметрией, центры "тяжести" разноимённых электрических зарядов совпадают (l = 0), то такие молекулы не обладают постоянным моментом (μ = 0) и являются неполярными.
Если любую неполярную молекулу поместить в постоянное электрическое поле, создаваемое, например, конденсатором, то происходит её поляризация, выражающаяся в разнонаправленном смещении зарядов (деформационная поляризация). Тяжёлые ядра атомов будут несколько смещаться в сторону отрицательного полюса, а электроны незначительной массой будут легко смещаться в сторону положительного полюса. В результате центры "тяжести" положительных и отрицательных зарядов совпадать не будут, и в молекуле будет возникать индуцированный (наведённый) диполь, момент которого пропорционален напряжённости электрического поля:
μинд
= αD
∙Е, (11)
где Е – напряжённость внутреннего электрического поля в молекуле [эл. ст. ед./см2
; Кл/см2
]
αD
– коэффициент пропорциональности, который показывает, какой дипольный момент создается при напряжённости электрического поля равной единице. Чем больше αD
, тем легче поляризуется молекула. Коэффициент αD
, называемый деформационной поляризуемостью, равен сумме электронной αD
и атомной поляризуемостей αат
:
αD
= αэл
+ αат
(12)
Чем дальше удалены внешние (более подвижные) валентные электроны от атомных ядер, тем выше электронная поляризуемость молекулы. Так как смещение атомных ядер незначительно (αат
составляет 5 – 10 % от αэл
) и им можно пренебречь, то приближённо будет αD
= αэл
.
Таким образом, в электрическом поле образуется диполь с наведённым или как его называют индуцированным дипольным моментом.
Если любую полярную молекулу поместить в электрическое поле, то будут происходить два процесса. Во-первых, молекула будет ориентироваться вдоль поля, и, во-вторых, расстояние между центрами "тяжести зарядов будет увеличиваться, увеличивая дипольный момент молекулы".
Таким образом, полярные молекулы в электрическом поле так же, как и неполярные испытывают деформационную поляризацию. Кроме того, под влиянием электрического поля они ориентируются вдоль его силовых линий, стремясь принять устойчивое положение, отвечающее минимуму потенциальной энергии. Это явление, называемое ориентационной поляризацией, даёт эффект, эквивалентный увеличению поляризуемости молекулы на величину αор
, называемую ориентационной поляризуемостью:
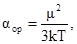 (13) (13)
где k – постоянная Больцмана (1,380662(44)∙10−23
Дж/К);
Т – абсолютная температура, К.
Таким образом, полная поляризуемость молекулы α складывается из трёх величин:
α = αэл
+ αат
+ αор
или α = αD
+ αор
(14)
Из уравнений (11) и (12) следует, что полная поляризуемость α будет иметь размерность объёма [см3
или Å3
].
2.1.1 Молярная поляризуемость
В электрическом (электромагнитном) поле молекулы поляризуются и возникает состояние напряжённости, характеризуемое величиной диэлектрической проницаемости (ε) вещества, которая входит в уравнение закона Кулона и может быть определена экспериментально.
Измеряя диэлектрическую проницаемость, характеризующую вещество в целом, можно определить по теории поляризации диэлектриков электрооптические параметры его молекул, связанные с ε формулой Клаузиуса-Моссотти:
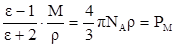 , (15) , (15)
где NA
– число Авогадро;
М – молекулярная масса вещества;
Ρ – плотность вещества, г/мл.
РМ
– молярная поляризация – величина, характеризующая меру индуцированного момента в объёме, который занимает 1 моль вещества.
Молярная поляризация, дипольный момент и общая поляризуемость молекулы связаны друг с другом уравнением Дебая, которое выводится из уравнений (12) – (14):
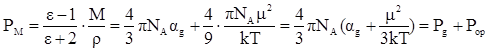 (16) (16)
По уравнению Дебая можно вычислить значения α и μ по известным величинам ε, М и ρ.
Поляризация молекул веществ, имеющих сравнительно большие значения ε и Р (например Н2
О, HCN, HCl), зависит от температуры, уменьшаясь при её повышении. Молекулы таких веществ, не имея центра симметрии зарядов, являются постоянными диполями. Для них молярная поляризация в уравнении Дебая выражается линейной функцией от 1/Т:
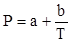 , (17) , (17)
Где
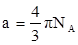 и и 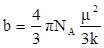 . .
Вещества с μ = 0 состоят из симметричных молекул (например О2
, СО2
, СS2
, молекулы многих углеводородов). В электрическом поле в таких молекулах возникает индуцированный дипольный момент. Поляризация молекул этого типа не зависит от температуры (рис. 3).
Для случая молекул постоянных диполей (прямая а; рис. 3) отрезок ординаты ОА = а определяет величину поляризуемости α, а tgβ = b – величину дипольного момента μ
Полная поляризация молекул может наблюдаться или в статическом электрическом поле, или в электромагнитном поле низкой частоты, но не в поле высокой частоты, где диполи не успевают ориентироваться. Поэтому, например, в поле низкочастотного инфракрасного излучения происходит и электронная, и атомная поляризация, а в более высокочастотном поле видимого света – только электронная поляризация (Рэл
= 4/3πNА
αэл
), т.к. при высокочастотных колебаниях успевают смещаться только очень лёгкие частицы – электроны. Для неполярных веществ: РОР
= 0 и Р = РД
≈ РЭЛ
.
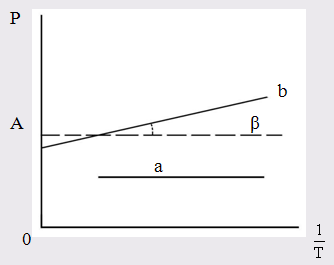
Рис. 3. Зависимость молярной поляризации
от обратной температуры
а – для молекулы, постоянных диполей;
b – для неполярных молекул.
2.2 Молярная рефракция
Из электромагнитной теории света Максвелла следует, что для длин волн, значительно удалённых от области их поглощения молекулами вещества, справедливо равенство:
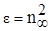 , (18) , (18)
где n∞
- показатель преломления света для определённых длин волн.
С учётом этого уравнение Клаузиуса-Мосотти (15) принимает следующий вид:
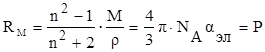 [ см3
/(г·моль)] (19) [ см3
/(г·моль)] (19)
Из полученного выражения видно, что показатель RМ
, называемый молярной рефракцией, имеет размерность объёма молекул, содержащихся в 1 моль вещества.
Уравнение (15), которое носит название уравнения Лорентца - Лоренца, выведено в 1880 г. независимо друг от друга Х. Лорентцем и Л. Лоренцем.
На практике часто пользуются показателем удельной рефракции r, то есть рефракцией одного грамма вещества. Удельная и молярная рефракции связаны соотношением: R = r∙M, где М молярная масса.
Поскольку в уравнении (19) N пропорционально плотности, то его можно представить в следующем виде:
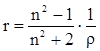 [ см3
/г] (20) [ см3
/г] (20)
Х. Лорентц и Л. Лоренц вскрыли физический смысл понятия рефракции – как меры электронной поляризуемости и подвели под учение о рефракции прочный теоретический фундамент.
Величина удельной рефракции практически не зависит от температуры, давления и агрегатного состояния вещества.
В исследовательской практике кроме молярной и удельной рефракции RМ
и r используют и другие производные от показателей преломления n(табл. 2).
Показатель преломления неполярных веществ практически не зависит от частоты волн света и поэтому уравнение (19) справедливо при всех частотах. Например, для бензола n2
= 2,29 (длина волны 289,3 нм), тогда как ε = 2,27. поэтому, если для приближённых расчётов рефракции достаточно пользоваться показателем преломления видимого спектра, то для точных расчётов необходимо производить экстраполяцию по формуле Коши:
nλ
= n∞
+ a/λ2
, (21)
где nλ
– показатель преломления при длине волны λ;
а – эмпирический коэффициент.
Таблица 2 Рефрактометрические константы
| N |
Наименование |
Обозначение |
Область применения |
| 1 |
Показатель преломления |
n |
Характеристика чистоты веществ. Анализ двойных систем веществ |
| 2 |
Удельная рефракция |
r |
Характеристика чистоты веществ. Определение концентрации веществ |
| 3 |
Молекулярная рефракция |
R |
Определение значений некоторых атомных и молекулярных констант. Определение строения органических молекул |
| 4 |
Относительная дисперсия |
σ |
Анализ сложных смесей. Определение строения органических молекул |
Для полярных веществ ε > n2
. Для воды, например, n2
= 1,78 (λ = 589,3 нм), а ε = 78. Более того, в этих случаях нельзя непосредственно экстраполировать nλ
по формуле Коши вследствие того, что показатель преломления полярных веществ часто аномально изменяется с частотой. Однако обычно нет необходимости производить такую экстраполяцию, так как рефракция является величиной аддитивной и сохраняется, если показатели преломления всех веществ измерять при определённой длине волны. За такую стандартную длину волны выбрана жёлтая линия в спектре натрия (λD
= 589,3). В справочных таблицах приводятся данные именно для этой длины волны. Таким образом, для расчёта молекулярной рефракции (в см3
/моль) пользуются формулой, в которой n∞
заменён на nD
:
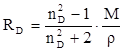 . (22) . (22)
Обычно индекс D опускают и формулу записывают как уравнение (19).
3. Рефракция и структура молекул
3.1 Аддитивность рефракции
Рефракция, является аддитивной величиной. Использование рефрактометрии в науке было начато в середине XIX века, когда обнаружили, что между молекулярными рефракциями соседних членов гомологического ряда органических соединений выполняется простое соотношение:
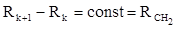 .(23) .(23)
Согласно этому соотношению молекулярную рефракцию k-го члена гомологического ряда можно представить в виде суммы молекулярных рефракций первого члена ряда и k−1 группы СН2
:
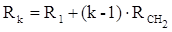 .(24) .(24)
Впоследствии было обнаружено, что ряд изомеров также имеют одинаковые молекулярные рефракции. Это обстоятельство позволило предположить, что молекулярная рефракция вещества зависит только от природы и числа атомов в молекуле и может быть вычислена простым суммированием характерных для каждого элемента атомных рефракций:
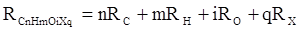 ,(25) ,(25)
где 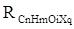 – молекулярная рефракция органического соединения состава Сn
Hm
Oi
Xq
; – молекулярная рефракция органического соединения состава Сn
Hm
Oi
Xq
;
RC
, RH
и др. – соответственно рефракции атомов углерода, водорода и других элементов (табл. 3).
Было установлено и то, что молекулярная рефракция большого числа органических соединений может весьма отличаться от суммы составных рефракций. К простейшим соединениям такого типа относятся этиленовые углеводороды и их алкилпроизводные. Этот класс соединений всё же был включён в аддитивную схему путём учёта того обстоятельства, что в этих соединениях имеются двойные связи типа С=С, аналогично был произведён учёт наличия тройных связей С≡С, которыми характеризуются ацетиленовые соединения.
Таким образом, рассчитывая рефракцию молекулы через рефракции составляющих её атомов и фрагментов, следует учитывать валентные состояния атомов – инкременты (вклады) рефракций двойных и тройных связей, а также поправки на особое положение отдельных атомов и атомных групп в молекулах:
R = ∑RA
+ ∑R1
, (26)
где RА
и R1
– соответственно атомные рефракции и инкременты связей (табл. 3, 4).
Поляризуемость ионов. В органической химии большое значение имеет поляризуемость анионов. Существует несколько наборов рефракций ионов. Определяемых либо в растворах, либо в твёрдом или газообразном состоянии.
1. Рефракции и, следовательно, поляризуемости увеличиваются с увеличением размера иона в пределах одной группы периодической системы химических элементов.
Например: F¯ < Cl¯ < J¯ (табл. 3); ОН¯ < SH¯ (табл. 4).
2. Анионы легче поляризуются, чем соответствующие нейтральные молекулы.
Например: SH¯ > H2
S; OH¯ > H2
O.
3. Анионы с большим зарядом легче поляризуются, чем с меньшим.
Например: S2–
> SH¯.
Наличие координационной (донорно-акцепторной, семиполярной) связи в молекуле вызывает уменьшение рефракции по сравнению с суммой рефракций индивидуальных молекул, образующих эту связь.
Например: величины R для (СН3
)3
N+
–B¯F3
и (C2
H5
)2
O+
−B¯F3
примерно на 3,5 и 2,0 см3
меньше суммы величин R для этих компонент [(CH3
)3
N – триметиламина, (С2
Н5
)2
О – диэтилового эфира и BF3
– трёхфтористого бора].
Молекулярная рефракция обычно рассматривается как аддитивно конститутивное свойство. Конститутивный характер этого свойства следует из происхождения этого явления. Однако аддитивный характер совсем не так легко продемонстрировать, поскольку, хотя по определению следует, что рефракция молекул должна равняться сумме рефракций отдельных её частей, не вполне ясно, каким образом выделять эти части. Существуют три различные схемы для определения основных констант. Это система атомных рефракций, рефракций групп и связей. Так, согласно первой, R = ∑rA
, где ∑r выражает сумму индивидуальных атомных рефракций.
Например, для этилового спирта СН3
СН2
ОН или диметилового эфира СН3
ОСН3
она равна 2r + 5rH
+ r0
.
Согласно второй схеме, величина R для этилового спирта определяется как сумма рефракций групп (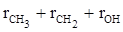 ), в то время как для диметилового эфира эта величина будет равна ( ), в то время как для диметилового эфира эта величина будет равна (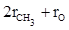 ). ).
Согласно третьей схеме, величина R для этилового спирта будет определяться суммой (5rC
−
H
+ rC
−
C
+ rO
−
H
), а для диметилового эфира (6rC
−
H
+ 2rC
−
O
).
Эти схемы не дают идентичных значений для одного и того же соединения, а также ни одна из них не даёт строго аддитивных значений.
Схема рефракции связей является наилучшей из всех трёх для определения рефракции органических молекул. Наиболее важное её преимущество перед другими связано с тем, что эта схема облегчает прямой подход к концепции анизотропии поляризации, причём этот термин означает, что поляризуемость орбитали, ориентация которых совпадает с направлением поля, отличается от их поляризуемости при иной ориентации. Само по себе не кажется очевидным, что поляризуемость почти сферических атомов должна изменяться при изменении ориентации молекулы в поле: более очевидным является то, что поляризуемость связей должна изменяться в соответствии с тем - колинеарны они полю или перпендикулярны ему, и удалось добиться некоторых положительных результатов при анализе рефракций связей, представляя их как совокупность продольных, поперечных и вертикальных параметров.
Одна из главных трудностей, с которыми приходится сталкиваться, – это решение вопроса о вкладе в общую поляризуемость, вносимом несвязанными парами электронов гетероатомов таких групп, как С–Х, С–О, С–N.
Величина R прямо пропорциональна электронной поляризуемости молекул и обладает свойством аддитивности, так что её можно вычислить суммированием ряда постоянных слагаемых Ri
, приписываемых содержащимся в молекуле атомам, группам атомов, связям или некоторым особенностям структуры (кратным связям, кольцам) и называемых соответственно атомными, групповыми, связевыми рефракциями и структурными инкрементами:
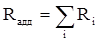 . .
Так, например, молекулярная рефракция нафтеновых углеводородов (алициклов) Сn
H2
n
может быть вычислена как сумма атомных рефракций углерода RC
и водорода RH
:
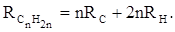 (27) (27)
Поскольку основной вклад в общую поляризуемость молекул дают легко поляризуемые внешние (валентные) электроны, 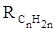 можно рассматривать и как сумму связевых рефракций: можно рассматривать и как сумму связевых рефракций:
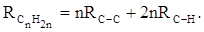 (28) (28)
Однако молекулярная рефракция изомерных нафтенов олефинов, содержащая очень легко поляризуемые π-связи, заметно больше. В системе атомных рефракций повышенный вклад С=С-связи учитывается добавлением постоянного слагаемого – инкремента двойной связи.
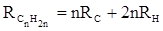 (29) (29)
В системе связевых рефракций сумма содержит иные слагаемые:
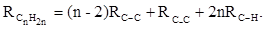 (30) (30)
Тройная углерод-углеродная связь имеет ещё бóльшую поляризуемость, чем двойная, и характеризуется бóльшими величинами инкремента молекулярной рефракции и связевой рефракции RС≡С
, с помощью которых вычисляются рефракции ацетиленов:
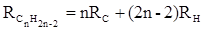
или
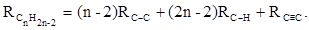 (31) (31)
Весьма важно, что изомерные ацетиленовые соединения с двумя двойными связями имеют иные (ещё больше) значения молекулярной рефракции, а именно – в системе атомных рефракций и инкрементов:
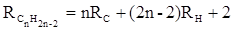
или в системе связевых рефракций:
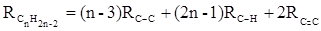 .(32) .(32)
При этом только диены с изолированными и кумулированными (алленовыми  двойными связями обнаруживают согласие с расчётами по (7,9) или (7,10), а у диенов с сопряженными двойными связями двойными связями обнаруживают согласие с расчётами по (7,9) или (7,10), а у диенов с сопряженными двойными связями 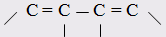 молекулярная рефракция оказывается большей, чем вычисленная по правилам аддитивности. Таким образом, открывается возможность определения по величинам молекулярной рефракции не только числа и природы содержащихся в молекуле (двойных и тройных) связей, но и их относительного расположения.Расхождение между экспериментальной и аддитивной (вычисленной с учётом инкрементов кратных связей) величинами R называется экзальтацией молекулярной рефракции ЕМ: молекулярная рефракция оказывается большей, чем вычисленная по правилам аддитивности. Таким образом, открывается возможность определения по величинам молекулярной рефракции не только числа и природы содержащихся в молекуле (двойных и тройных) связей, но и их относительного расположения.Расхождение между экспериментальной и аддитивной (вычисленной с учётом инкрементов кратных связей) величинами R называется экзальтацией молекулярной рефракции ЕМ:
ЕМ = R – Rадд
.
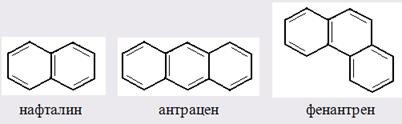
Главной причиной экзальтации является π–π-сопряжение простых связей, и величина экзальтации быстро возрастает с увеличением длины сопряженных систем. Однако частичное или полное включение сопряжённой системы в цикл, а также образование простейших ароматических структур приводит к снижению экзальтации, так что углеводороды ряда бензола и большинство их производных не обнаруживают экзальтации при расчёте аддитивных значений по формуле кекуле. Правилу аддитивости подчиняются не только ароматические соединения с несколькими изолированными бензольными кольцами, но соединения с конденсированными кольцами (нафталины, антрацены, фенантрены) и сопряженными (непосредственно соединенными) кольцами. Эти соединения так же проявляют эффект экзальтации.
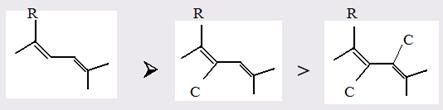
Для структурного анализа имеет значение также тот факт, что величина экзальтации существенно зависит от разветвлённости углеродного скелета в месте расположения сопряжённой системы: появление боковых цепей у центральных С-атомов сопряжённых связей влечёт за собой снижение экзальтации, так что в группах изомеров. В пределах одного гомологического ряда с данной сопряжённой системой экзальтация зачастую возрастает пропорционально массе.
Для характеристики сопряжённых систем предлагалось использовать экзальтации, приведённые к молекулярной массе 100 а.е.м. – так называемые удельные экзальтации (Е∑):
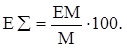 (33) (33)
р-π-сопряжение неподелённых электронных пар (галогенов, азота, кислорода) с π-электронами соседних кратных связей проявляется в разных структурах весьма различно.
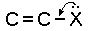
У непредельных галогенпроизводных эти эффекты столь невелики, что при расчётах по классической аддитивной схеме вообще не учитываются, а у галогенангидридов карбоновых кислот, RCOGal, амидов RCONH2
и ароматических аминов ArNH2
они по сложившейся традиции учитываются введением особых (повышенных) значений атомных или связевых рефракций галогенов и азота в таких структурах и, следовательно, формально не рассматриваются как экзальтации. Понятие "экзальтация рефракции" является, таким образом, весьма условным, связанным с примитивностью самой классической аддитивной схемы и её историей, но всё же полезным для выявления и классификации, содержащихся в исследуемом веществе сопряжённых систем. В современных, более детализированных аддитивных системах, учитывающих состояние гибридизации соседних атомов и влияние непосредственно не связанных атомов, понятие "экзальтация" вообще не используется. Однако такие схемы, разработанные для расчёта свойств органических соединений, требуют установления большого числа исходных аддитивных констант, предъявляют повышенные требования к чистоте исследуемых веществ и в повседневной практике структурного анализа не используются. Возможности структурного анализа по молекулярной рефракции, основанного на классической аддитивной схеме расчёта, ограничиваются информацией о числе и природе кратных связей и об эффектах сопряжения. В рамках выявления этих особенностей структуры обе разновидности классической аддитивной схемы (атомная и связевая) практически равноценны по точности и границам применимости.
Более старая система атомных констант сохранила следы своего исторического развития: структурные эффекты учитываются в ней разными способами – различными значениями атомных рефракций данного элемента в разных группировках, специальными структурными инкрементами и групповыми рефракциями, используемыми наряду с атомными. Несмотря на разнородность расчетных констант, система атомных рефракций удобна при структурном анализе неизвестных веществ, так как позволяет производить вычисление Rадд
, исходя непосредственно из брутто-формулы, без подсчёта числа различных связей в предположительных структурных формулах.
Атомные и групповые рефракции для D - линии спектра натрия
Таблица 3
| Атом или связь |
Rк
, мл/моль |
Атом или связь |
Rк
, мл/моль |
| H |
1,100 |
третичных |
2,840 |
| F |
0,997 |
N в нитрилах |
3,118 |
| Cl |
5,967 |
С=С |
1,733 |
| Br |
8,885 |
С≡С |
2,398 |
| I |
13,900 |
| C |
2,418 |
С в спиртах |
1,660 |
N в аминах:
первичных
|
2,322 |
С в простых эфирах или оксидах |
1,643 |
| вторичных |
2,502 |
С в карбониле |
2,211 |
Молярную рефракцию атомов, построенных из ионов, рассчитывают как сумму ионных рефракций (табл. 4).
Приступая к установлению строения вещества по молекулярной рефракции, следует, прежде всего, обеспечить необходимую точность исходных данных. Экспериментальные величины показателя преломления и плотности должны иметь погрешность до нескольких единиц четвёртого десятичного знака, легко достижимую на обычных лабораторных рефрактометрах предельного угла и при работе с пикнометрами объёмом более 1 – 2 мл с термостатированием до  0,10
С. Абсолютное значение температуры несущественно, но обе величины (n и ρ) обязательно должны быть измерены при одной и той же температуре. В расчётную формулу необходимо вставлять величину плотности ρ 0,10
С. Абсолютное значение температуры несущественно, но обе величины (n и ρ) обязательно должны быть измерены при одной и той же температуре. В расчётную формулу необходимо вставлять величину плотности ρ : отношение весов равных объёмов вещества и воды при температуре t пересчитывают в плотность по формуле: : отношение весов равных объёмов вещества и воды при температуре t пересчитывают в плотность по формуле:
ρ = ρ = ρ + ( ρ + ( ρ )воды
. )воды
.
При вычислениях надо употреблять точное значение М согласно установленной или предполагаемой брутто-формуле, а не непосредственно результат приближённого экспериментального определения, так как погрешности большинства обычных физико-химических методов определения молекулярной массы достигают нескольких процентов и сопоставимы с величиной самих структурных влияний на молекулярную рефракцию.
Уравнение (26) выражает правило аддитивности молярной рефракции.
Физически более обоснован способ расчёта рефракции как суммы рефракций не атомов, а связей (табл. 5).
Таблица 4 Ионные рефракции
| Ион |
RD
, газ. |
RD
, раств. |
RD
, крист. |
Ион |
RD
, газ. |
RD
, раств. |
RD
, крист. |
| Li+
|
0,08 |
0,32 |
0,20 |
NH+
|
4,13 |
4,13 |
3,87 |
| Na+
|
0,47 |
0,20 |
0,47 |
NH3
|
5,63 |
5,33 |
– |
| K+
|
2,25 |
2,25 |
2,25 |
NO3
‾ |
11,01 |
11,01 |
10,69 |
| Rb+
|
3,79 |
3,79 |
3,79 |
CN‾ |
8,68 |
8,68 |
8,36 |
| Cs+
|
6,53 |
6,53 |
6,53 |
CNS‾ |
17,78 |
17,78 |
16,49 |
| Ca+
|
1,40 |
0,71 |
1,40 |
S2
‾ |
22,70 |
– |
13,40 |
| Sr+
|
2,58 |
1,89 |
2,58 |
SO4
2
‾ |
14,72 |
14,72 |
14,60 |
| Ba+
|
4,73 |
4,37 |
4,73 |
F‾ |
2,44 |
2,60 |
3,37 |
| H+
|
0 |
-0,61 |
0 |
Cl‾ |
9,06 |
9,06 |
8,68 |
| H2
O |
3,76 |
3,71 |
3,70 |
Br‾ |
12,66 |
12,66 |
11,86 |
| HO‾ |
4,76 |
5,15 |
4,44 |
J‾ |
19,22 |
19,22 |
17,70 |
| O2
‾ |
6,95 |
6,28 |
Правило аддитивности молярной рефракции используют для установления строения молекул, сравнивая R, найденную экспериментально, с рассчитанной по уравнению (26) для предлагаемой структуры молекулы. Близость значений Rэксп.
и Rвыч.
служит подтверждением строения молекулы (табл. 6). Расхождения до 0,3 – 0,4 мл/моль обусловлены возможными ошибками эксперимента и неточностью собственно аддитивных констант, а для ионных соединений отклонения от аддитивности дополнительно связаны с взаимной поляризацией ионов.
Закономерности рефракций связей.
1. Константы связей какого-либо элемента с атомами других элементов, принадлежащих к одной и той же группе периодической системы, увеличиваются с увеличением размера атома.
Например: C–F < C–Cl < C–Br < C–J.
Наиболее легко поляризуемые орбитали, то есть наружные орбитали атомов большого размера, менее прочно удерживаются связанными ядрами, чем аналогичные орбитали атомов меньшего размера.
2. Несмотря на повышенную электроотрицательность гетероатома, константы связей С–О и С–N имеют большие значения, чем С–С - связи. Это связано с наличием несвязанных электронов на гетероатоме.
3. Величины констант для кратных связей больше, чем для одинарных связей между теми же элементами.
Например: С≡С > C=C > C−C (табл. 3)
Причем двойная связь имеет величину, более чем вдвое превышающую величину для одинарной связи (rC
=
C
> 2rC
−
C
). Это показывает, что π-электроны гораздо легче поляризуются, чем σ-электроны. Исключением из этого правила является, по-видимому, двойная связь N=O.
4. Для констант связей С=С, C=N и С=О обнаруживается характерная связь с положением элементов в группах и периодах периодической системы, и эти константы уменьшаются по мере роста электроотрицательностей неодинаковых атомов в соответствии с данным порядком перечисления, а константы для связей C=S и С=О уменьшаются в приведённом порядке. Значительное различие между величиной констант для С=О и C=S ( гораздо больше, чем различие между С−О и C−S) связано с тем, что атом серы не склонен к образованию двойной связи с углеродом и поэтому проявляет, находясь в этом состоянии, сильный М-эффект.
Учитывая указанные тенденции, следует иметь в виду, что точные величины рефракции связей довольно сильно меняются при изменении молекулярного окружения связей, и поэтому будет наблюдаться большее или меньшее отклонение наблюдаемых молекулярных рефракций от величин, рассчитанных на основании стандартных или средних значений.
Например, значения молекулярных рефракций для изомеров бутина
СH3
−CH2
−C≡CH и СН3
−С≡С−СН3
будут различны, поскольку различны величины рефракций для концевой и неконцевой С≡С - связи (табл. 5).
Таблица 5 Рефракции связей для D-линии спектра натрия при 20 0
С
| Тип связи |
Rк
, мл/моль |
Тип связи |
Rк
, мл/моль |
| Н−Н |
2,08 |
N−N |
1,99 |
| С−Н |
1,676 |
C−N в аминах |
1,57 |
| N−H |
1,76 |
C−O в простых эфирах |
1,54 |
| O−H |
1,66 |
C=O |
3,32 |
| C−C в циклопропане |
1,49 |
C−F |
1,60 |
| С−С в циклобутане |
1,37 |
C−Cl |
6,51 |
| С−С в ароматич. кольце |
2,688 |
C−Br |
9,39 |
| C=C |
4,17 |
C−J |
14,61 |
| C≡C концевая |
5,87 |
C−S |
4,61 |
| C≡C неконцевая |
6,26 |
N−O |
1,95 |
| C=N |
3,76 |
N→O |
1,78 |
| C≡N |
4,82 |
N=O |
4,00 |
| O−O |
1,80 |
C=S |
11,91 |
| S−H |
4,80 |
N=N |
4,12 |
| S−S |
8,11 |
Для соединений с одинаковой эмпирической формулой, но с разным химическим строением рефракция различна. Поэтому, экспериментально определяя рефракцию и сравнивая её с вычисленным значением, можно установить химическое строение исследуемого органического соединения.
Примеры структурного анализа по молекулярной рефракции
Необходимой предпосылкой успешного проведения структурного анализа по молекулярной рефракции является полное использование информации, содержащейся в самой брутто-формуле. Её следует сопоставить с формулами предельных соединений с тем же числом углеродных атомов, и по разнице в содержании водорода сделать заключение о степени непредельности анализируемого вещества и возможном содержании в нём кратных связей и циклов.
Пример:
Формула С8
Н11
Сl2
Br, где общее число атомов одновалентных элементов nI
= 11 + 2 + 1 = 14 – на 4 атома меньше, чем в предельном соединении с nIV
= 8 (2∙8 + 2 = 18), должна отвечать либо ациклическим структурам, содержащим две двойные связи или одну тройную, либо моноциклической структуре с одной двойной связью, либо же бициклической - без кратных связей. Эти альтернативные типы структур и должны быть положены в основу подсчёта RАДД
по формуле (17). Сравнение экспериментального значения R с RАДД
даёт возможность отвергнуть некоторые из предполагаемых альтернативных вариантов структур, подтвердить другие и сделать более детальные заключения о строении, основываясь на следующих соображениях:
1. Совпадение R и RАДД
с погрешностью в несколько десятых долей миллилитров в моле подтверждает вероятность, как предполагаемой брутто-формулы, так и структуры. При этом расхождения до 0,3 – 0,4 относятся за счёт приближённого характера самих аддитивных констант, возможных ошибок измерений и влияния примесей. Если при расчёте предполагалось наличие двух и более кратных связей, то совпадение с экспериментальной величиной свидетельствует о том, что кратные связи изолированы друг от друга, кумулированы или образуют простейшие ароматические структуры (бензольное кольцо, некоторые гетероциклы). Окончательные формулировки выводов, как правило, должны учитывать вероятность нескольких структур, неразличимых по молекулярной рефракции в указанных пределах погрешности расчётов.
2. Расхождение R и RАДД
более чем на 0,3 – 0,4 мл/моль указывает на ошибочность сделанных при подсчёте RАДД
предположений о строении и составе органического соединения или свидетельствует об особенностях структуры, вызывающих экзальтации молекулярной рефракции. В этом случае необходимо рассмотреть другие возможные при данной брутто-формуле значения RАДД
для иного числа и природы кратных связей или напряжённых колец, а также иных функциональных групп. Превышение экспериментальной величины R над аддитивной, вычисленной для структур с двумя и более кратными связями, может быть экзальтацией молекулярной рефракции, вызванной сопряжением. Сопоставление величины экзальтации с литературными (табличными) данными для хорошо изученных сопряжённых систем может дать дополнительную информацию о характере сопряжённой системы и разветвлённости углеродного скелета в месте её расположения.
Депрессия молекулярной рефракции (случай, когда R < RАДД
) наблюдается только у некоторых ароматических гетероциклических соединений. За исключением этого специального случая отрицательные величины R−RАДД
свидетельствуют о несоответствии состава и строения органического соединения предполагаемым. Другие возможные причины отрицательных разностей R−RАДД
– ошибки, допущенные в расчётах и измерениях.
Рефрактометрия была первым из физических методов, широко применявшихся для определения структуры органических соединений и в течение многих десятилетий (до начала применения ИК – спектроскопии в сороковых годах ХХ века) играла ведущую роль. В настоящее время она применяется в качестве легко доступного источника предварительной информации, дополняющей данные других методов.
3.2 Оптическая экзальтация
Отклонение рассчитанных величин R от экспериментальных примерно до 1 %, обусловлено тем, что средние величины рефракций связей не дают в сумме строго аддитивно молярную рефракцию. Значительно большие отклонения (до 10 %) могут встречаться в случае молекул, содержащих сопряжённые кратные связи. Поскольку наблюдаемая величина R больше рассчитанной, то это явление называется оптической экзальтацией и обозначается как ER. Экзальтация указывает на наличие в молекуле сопряжённых кратных связей, например:
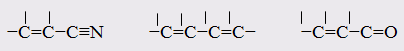
В молекулах с подобными фрагментами π-электронное облако делокализовано по всем атомам, образующим систему сопряжённых связей, и может свободно перемещаться вдоль этой системы, то есть обладает высокой подвижностью. Такое электронное облако легко смещается под действием электрического поля, благодаря чему молекула проявляет повышенную поляризуемость, и наблюдается оптическая экзальтация.
Степень экзальтации, возрастая с увеличением длины цепи сопряжения, указывает на повышение подвижности электронов, их поляризуемость, например, в системах:

Оптическая экзальтация встречается и в случае замещённых бензолов. Заместители, обладающие положительным электромерным эффектом (+Е – эффектом), обуславливают экзальтацию, которая уменьшается в ряду
NR2
> NH2
> OR > OH > галогены. Это объясняется увеличением поляризуемости молекулы, возникающей за счёт сопряжения свободной пары электронов с π-электронным секстетом бензольного кольца, которое дополнительно облегчается в случае групп NR2
и öR наличием электронодонарных алкилов. Способность −Е – групп, таких как NO2
, C=O, C≡N, увеличивать подвижность π-электронов бензольного кольца проявляется в экзальтации, наблюдаемой для нитробензола С6
Н5
NO2
, ацетофенона С6
Н5
СОСН3
, бензонитрила С6
Н5
С≡N и др. Алкильные группы также увеличивают молекулярную рефракцию за счёт +Е – эффекта.
Таким образом, в области видимого света поляризуемость молекул практически полностью обусловлена смещением π-электронов, и поэтому для органических соединений она равна сумме эффективных смещений отдельных электронов. Последнее обстоятельство придаёт молекулярной рефракции свойство аддитивности для составляющих фрагментов молекулы, что находит широкое применение при определении состава и строения молекул.
3.3 Дисперсия молекулярной рефракции
Дисперсией рефракции называется зависимость рефракции или показателя преломления света от длины волны. При нормальной дисперсии показатель преломления n возрастает с уменьшением длины волны. Дисперсию можно охарактеризовать, как разность значений рефракции одного и того же соединения при двух различных длинах волн α и β (Rα
– Rβ
). Однако обычно в качестве меры дисперсии используют безразмерную величину – относительную дисперсию:
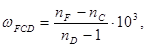 (34) (34)
где nF
, nC
, nD
– показатели преломления, измеренные для F – C – линий спектра водорода. F (λ = 486,1 нм), С (λ = 656,3 нм) и D спектра натрия (λ = 589,3 нм), (см. табл. 1).
Относительная дисперсия весьма чувствительна к наличию и положению кратных связей в молекуле. Например, для алифатических парафинов ωFCD
≈ 17−18
, а для бензола ωFCD
= 33,3. Это позволяет по величине дисперсии и показателю преломления определить принадлежность углеводорода к тому или иному классу соединений и предположить его возможное строение.
3.4 Рефракция и размеры молекул
Рефракцию можно использовать для вычисления не только электронной поляризуемости молекулы или иона (по уравнению 19), но и для расчёта эффективного радиуса частицы (атома, иона). Поскольку рефракция имеет размерность объёма, отнесённого к определённому количеству вещества (удельная – к одному грамму, молярная – к одному молю), то можно (условно) рассматривать молекулу как сферу с радиусом rм
и проводящей поверхностью. В этом случае:
αэл
= rМ.
Тогда из уравнения (19) получим:
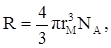 (35) (35)
откуда:
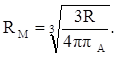 (36) (36)
4. Рефрактометрия растворов
Аддитивность рефракции характерна и для жидких смесей (растворов). Рефракция смеси равна сумме рефракций компонентов, отнесённых к их долям в смеси.
Молярную и удельную рефракции двухкомпонентной смеси можно соответственно представить в виде следующих уравнений:
R = N1
R1
+ (1 – N1
) R2
(37)
r = w1
r1
+ (1 – w1
) r2
, (38)
где N1
, N2
и w1
, w2
– соответственно мольная и массовая доли первого и второго компонентов.
Уравнения (37) и (38) используются для определения состава смеси и рефракции её компонентов.
Рефрактометрия достаточно широко применяется для идентификации веществ, а также для оценки степени их чистоты. При идентификации, а также определении чистоты веществ критерием служит совпадение показателей преломления исследуемого образца и заведомо известного чистого соединения. Важно, чтобы все измерения n выполнялись при одинаковой температуре и при одних и тех же длинах волн.
Если образец загрязнён, то его можно рассматривать как разбавленный раствор примесей в исследуемом соединении. При этом в случае незначительного содержания примесей их концентрацию Сх
можно определить, воспользовавшись линейным соотношением:
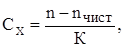 (39) (39)
где n и nчист.
– показатели преломления образца и чистого вещества;
К – коэффициент, определяемый экспериментально.
Для ориентировочной оценки величину Сх
можно определить, исходя из аддитивности показателей преломления. Чувствительность этого метода тем выше, чем сильнее различаются показатели преломления примесей и чистого органического соединения. Рефрактометрический метод иногда применяется для контроля за процессом очистки вновь синтезированных органических соединений, показатели преломления которых ещё не известны. Если при очистке образца различными способами показатель преломления от одной очистки к другой продолжает изменяться, то органическое соединение не считают чистым (индивидуальным), и процесс очистки продолжают.
4.1 Анализ двухкомпонентных растворов
По значению показателя преломления бинарного раствора можно определить его концентрацию. Для этого необходимо, чтобы была известна зависимость показателя преломления от состава раствора. Для ряда растворов (например, сахарозы, некоторых спиртов, кислот, оснований, солей) зависимости показателей преломления установлены и сведены в таблицы, которыми и пользуются при количественном анализе. Если таких таблиц нет, то используют градуировочные графики, которые строят по результатам измерений эталонных растворов.
Кривые зависимостей показателя преломления от состава бинарных растворов существенно изменяются с изменением природы раствора. Эти кривые подразделяют на три типа:
I тип – изотермы, имеющие незначительную положительную или отрицательную кривизну, когда изменение n от состава отличается от линейного хода по величине не более, чем на 0,0075-0,008 (рис. 4а);
II тип – изотермы, имеющие заметную кривизну, когда Δn > 0,008 (рис. 4б);
III тип – изотермы с сингулярной точкой (рис. 4в).
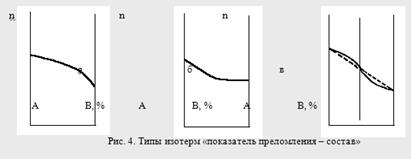
Большинству бинарных растворов соответствуют кривые I-го типа. Сюда относятся нормальные растворы и растворы с ассоциированными компонентами, а также растворы с химическим взаимодействием компонентов и растворы, в которых по каким-либо причинам такое взаимодействие не проявляется отчётливо на изотерме "показатель преломления – состав".
К растворам типа II и III относятся растворы с сильно выраженным химическим взаимодействием компонентов и с образованием частично диссоциированных соединений. В некоторых случаях по положению сингулярной точки на кривой III-го типа удаётся определить стехиометрический состав образовавшегося соединения.
Таким образом, в рефрактометрии двухкомпонентных систем, используется помимо количественного физико-химический метод анализа, который позволяет обнаружить достаточно выраженное взаимодействие компонентов. При отсутствии межмолекулярного взаимодействия, приводящего к ассоциации компонентов, справедливо свойство аддитивности рефракции. В этом случае молярная рефракция раствора RР
равна сумме произведений рефракций его компонентов и их мольных долей в этом растворе:
Rp
= N1
∙R1
+ N2
∙R2
,
где R1
и R2
– молярные рефракции соответственно растворителя и растворённого вещества; N1
и N2
– мольные доли растворителя и растворённого вещества.
Для расчёта RР
с использованием экспериментальных данных по уравнению (15) необходимо знать величины "среднемолекулярной массы" раствора, которая определяется соотношением:
Мср
= N1
∙M1
+ N2
∙M2
,
где M1
и М2
– молекулярные массы компонентов раствора, N1
и N2
- мольные доли компонентов раствора.
Свойством аддитивности, подобно молекулярной рефракции, обладает и удельная рефракция:
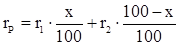 (40) (40)
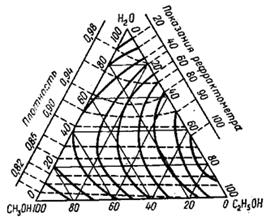
Рис. 5. Треугольная диаграмма для рефрактометрического анализа тройной системы: этиловый спирт - метиловый спирт - вода
4.2 Анализ трёхкомпонентных растворов
Для анализа тройных систем необходимо знать два каких-либо независимых, характеризующих состав системы, параметра. Одним из таких параметров обычно служит показатель преломления, а вторым – как правило, плотность раствора. Состав смеси по значениям этих параметров можно определить графически. Для этого сначала готовят трёхкомпонентные смеси известного состава и строят зависимость "состав – свойство". Зависимость значений показателя преломления и плотности раствора от состава системы представлена на рис. 5. посредством, так называемой тройной диаграммы (треугольник Гиббса – Розебома). Осями координат служат стороны равностороннего треугольника, на каждой из которых откладывается массовая доля бинарной системы, вершины треугольника соответствует 100 % компонентам, а любая точка внутри треугольника определяет состав трехкомпонентной системы. Определив ρ и n стандартных растворов, наносят на диаграмму изоденсы по точкам, соответствующим составам и имеющим одну и ту же плотность, и изорефракты – по точкам, определяющим состав равнопреломляющих смесей. Из окончаний изоденс и изорефракт опускают перпендикуляры на дополнительные шкалы (линии, проведённые параллельно боковым сторонам треугольника), плотности и показатели преломления соответствующие значениям этих величин.
При проведении анализа измеряют плотность и показатель преломления исследуемого образца и определяют точку, отвечающую составу, на пересечении изорефракты изоденсы. Из этой точки проводят линии, параллельные сторонам треугольника, и по отсечённым этими линиями отрезкам определяют состав анализируемой смеси.
Подробно методика построения тройных диаграмм описана в методических указаниях по физической химии "Изучение взаимной растворимости жидкостей в трёхкомпонентных системах" [14].
5. Рефрактометрия полимеров
Рефрактометрический метод достаточно часто применяют при анализе высокомолекулярных соединений. Этот метод впервые был предложен и впоследствии нашёл широкое применение для количественного определения стирола в продуктах его сополимеризации с дивинилом (1,3-бутадиен). Методика [9] позволяет с погрешностью до 5 % установить число содержащихся в сополимерах звеньев дивинила, присоединённых в положения 1-2, а также температуру стеклования таких полимеров с погрешностью до 3–4 0
С.
Рефрактометрический метод применяется и для исследования кристаллизуемости хлоропреновых каучуков. При помощи этого метода можно определить степень кристалличности образцов полихлоропрена, закристаллизованных при разных температурах [8].
При переходе от одного углеводородного полимера к другому поляризуемость молекулы существенно не меняется, однако замена атомов водорода на атомы галогенов приводит к изменению поляризуемости полимеров и соответственно к изменению их показателя преломления
Рефрактометрия является простым и удобным методом исследования процессов кристаллизации и плавления полимеров, подвергшихся кристаллизации в различных температурных условиях.
Таблица 6 Показатели преломления полимеров
| Полимер |
N |
| Политетрафторэтилен (тефлон) |
1,35 – 1,38 |
| Полихлорфторэтилен |
1,39 – 1,43 |
| Ацетат целлюлозы |
1,46 – 1,50 |
| Поливинилацетат целлюлозы |
1,47 – 1,49 |
| Полиметилметакрилат |
1,48 – 1,49 |
| Полипропилен |
1,49 |
| Поливиниловый спирт |
1,49 – 1,53 |
| Фенолформальдегидный полимер |
1,50 – 1,70 |
| Полиизобутилен |
1,51 |
| Полиэтилен |
1,51 |
| Натуральный каучук (полиизопрен) |
1,519 |
| Синтетический каучук (полиизопрен) |
1,522 |
| Полибутадиен |
1,520 |
| Полиамид |
1,54 |
| Поливинилхлорид (ПВХ) |
1,54 – 1,56 |
| Полистирол |
1,59 – 1,60 |
| Поливинилиденхлорид |
1,60 – 1,63 |
В табл. 7 приведены значения коэффициентов аморфной (nам
) и кристаллической (nкр
) фаз хлоропренового каучука в зависимости от температуры для образца, закристаллизованного при комнатной температуре (20 0
С).
Таблица 7 Значения коэффициентов nам
и nкр
в зависимости от температура образца
| Т, 0
С |
nам
|
nкр
|
Т, 0
С |
nам
|
nкр
|
| −15 |
1,5698 |
1,6510 |
10 |
1,5623 |
1,6510 |
| −10 |
1,5678 |
1,6510 |
15 |
1,5587 |
1,6508 |
| −5 |
1,5659 |
1,6510 |
20 |
1,5571 |
1,6485 |
| 0 |
1,5641 |
1,6510 |
25 |
1,5550 |
1,6435 |
| 5 |
1,5623 |
1,6510 |
30 |
1,5533 |
1,6321 |
На основании представленных данных можно вычислить степень кристаллизации (φ) хлоропренового каучука по уравнению:
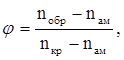 (41) (41)
где nобр
показатель преломления образца при определённой температуре.
Заключение
Рефрактометрия - метод исследования веществ, основанный на определении показателя преломления (коэффициента рефракции) и некоторых его функций. Этот метод применяется для идентификации химических соединений, количественного и структурного анализа, определения физико-химических параметров веществ. Показатель преломления – это отношение скоростей света в граничащих средах. Для жидкостей и твердых тел показатель преломления определяют, как правило, относительно воздуха, для газов - относительно вакуума. Значения показателя преломления зависят от длины волны света и температуры. Например, показатель преломления при 20 °С для D-линии спектра натрия (589 нм). Часто используют также линии С и F спектра водорода (соответственно 656 и 486 нм). В случае газов необходимо учитывать зависимость показателя преломления от давления (указывать его или приводить данные к нормальному давлению). Анизотропные тела, одно- и двухосные кристаллы характеризуются соответственно двумя экстремальными или тремя значениями показателя преломления. Все задачи, поставленные вначале исследования, решены. Цель курсовой работы достигнута.
Список использованной литературы
1. Минкин В.И., Осипов О.А., Жданов Ю.А. Дипольные моменты в органической химии: М.: Химия, 1968. – 246 с.
2. Боровиков Ю.А. Диюэлектрометрия в органической химии: Киев: Наукова думка, 1987. – 215 с.
3. Бацанов С.С. Структурная рефрактометрия: Изд-во Московского ун-та, 1959. – 223 с.
4. Шишловский А.А. Прикладная физическая оптика,. ФизматГИЗ, 1970. – 822 с.
5. Ляликов Ю.С. Физико–химические методы анализа, М.: Химия, 1964.
6. Барановский В.Ф., Горелкин С.М., Городенцева В.А. Физико – химические методы анализа: М.: Высшая школа, 1972.
7. Рабек Я. Экспериментальные методы в химии полимеров: М.: Мир, 1983. Ч. 1. – 382 с.
8. Новикова Г.Е., Трапезникова О.Н. // Каучук и резина, 1968. – № 8.
9. Пиотровский К.Б., Стерензат Д.Е. // Каучук и резина, 1957. – № 11.
10. Пилипенко А.Т., Пятницкий И.В. Аналитическая химия; М.: Химия, 1990.
11. Практикум по физической химии под ред. Н.К. Воробьева; М.: Химия, 1975. – 367 с.
12. Иоффе Б.В. Рефрактометрические методы анализа в химии; Л.: Химия
13. Уитли П. Определение молекулярной структуры; М.: Мир, 1970.
14. Методические указания. Рефрактометрия. Лабораторная работа № 1. Волгоград. Изд-во ВПИ, 1983. – 14 с.
15. Краткий справочник физико–химических величин под редакцией К.П Мищенко: М.: Химия, 1967.
|