Задание
Дано:
· Универсум 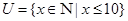
· Множества 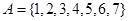 , , 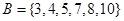 , , 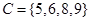
· Бинарные отношения
· Функция 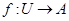
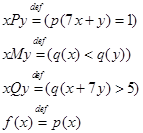
Требуется:
1. Найти
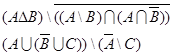
2. Решить уравнение 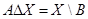
3. Построить графы и матрицы отношений P и Q, указать 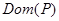 , , 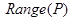 , , 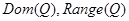
4. Исследовать отношение Р на наличие стандартных свойств (рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность).
5. Построить граф и матрицу отношения 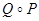 , указать , указать 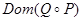 , , 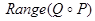 . .
6. Построить граф и матрицу отношения 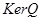 , указать , указать 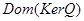 , , 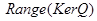 . .
7. Построить графы и матрицы замыканий отношения Р:
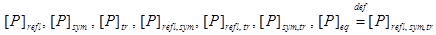 . Для каждого из замыканий указать . Для каждого из замыканий указать 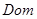 и и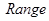 . .
8. Найти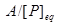 , построить естественную проекцию , построить естественную проекцию 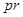 : :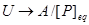 . .
9. Построить таблицу значений, граф и матрицу функции f.
Указать 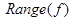 . .
10. Построить граф и матрицу отношения 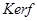 . .
11. Найти 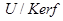 , построить индуцированное отображение , построить индуцированное отображение 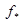 : : 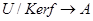 . .
12. Построить граф и матрицу отношения М
. Указать 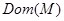 , , 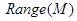 . .
13. Доказать, что отношение М есть отношение строгого порядка в А.
14. Исследовать М на линейность (полноту).
15. Интерпретируя отношение М как «меньше», найти в множестве А относительно М минимальные и максимальные, наименьшие и наибольшие элементы (если таковые существуют).
Решение
1. Найти
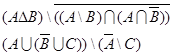

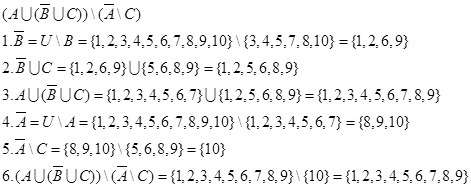
2. Решить уравнение 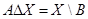
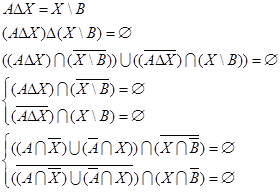
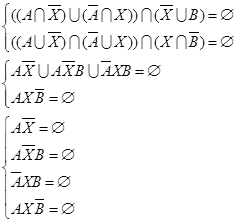
3. Построить графы и матрицы отношений P и Q, указать 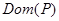 , , 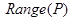 , , 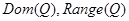
рефлексивность симметричность граф матрица
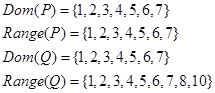
4. Исследовать отношение Р на наличие стандартных свойств (рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность).
По матрице отношения Р определяем его свойства:
1. Не рефлексивно, т.к. на главной диагонали имеются нули.
2. Не антисимметрично, т.к. на главной диагонали имеются единицы.
3. Не симметрично
4. Не антисимметрично
5. Для определения является ли отношение транзитивным, возведем его матрицу в квадрат:
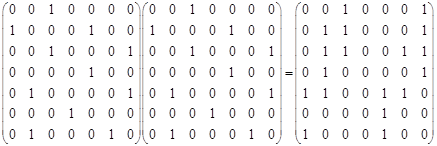
По полученной матрице видно, что отношение Р не транзитивно.
5. Построить граф и матрицу отношения 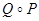 , указать , указать 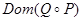 , , 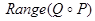 . .
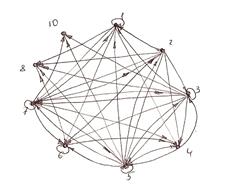
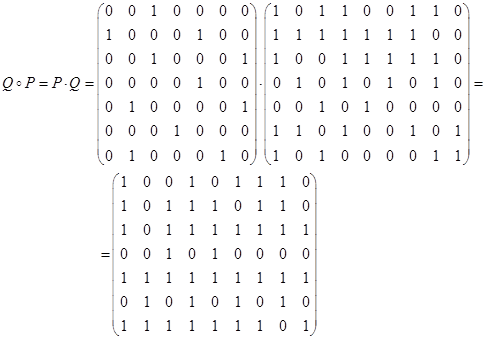
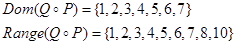
6. Построить граф и матрицу отношения 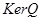 , указать , указать 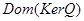 , , 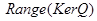 . .
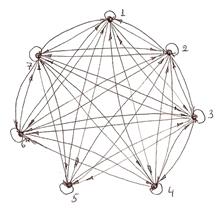
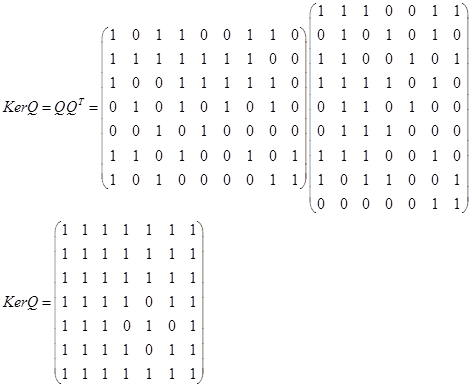
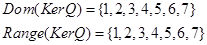
7. Построить графы и матрицы замыканий отношения Р: 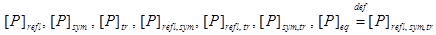 . Для каждого из замыканий указать . Для каждого из замыканий указать 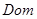 и и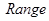 . .
8. Найти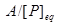 , построить естественную проекцию , построить естественную проекцию 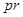 : :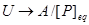 . .
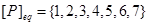
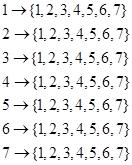
9. Построить таблицу значений, граф и матрицу функции f.
Указать 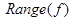 . .
| x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| f(x) |
5 |
7 |
1 |
2 |
2 |
4 |
3 |
2 |
1 |
1 |
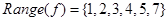
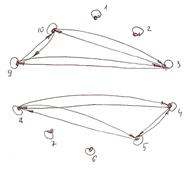
10. Построить граф и матрицу отношения 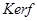 . .
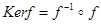 или в матричной форме или в матричной форме 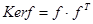
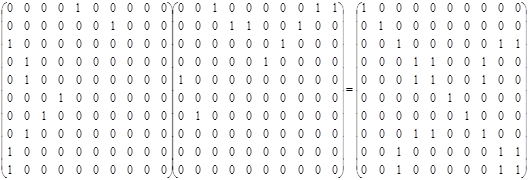
11. Найти 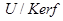 , построить индуцированное отображение , построить индуцированное отображение 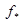 : : 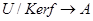 . .
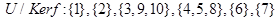
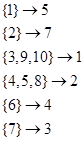
12. Построить граф и матрицу отношения М
. Указать 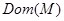 , , 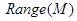 . .
Реклама

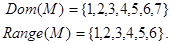
13. Доказать, что отношение М есть отношение строгого порядка в А.
Отношение называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно. По матрице отношении М:
1. Отношение антирефлексивно, т.к. на главной диагонали нет 1.
2. Отношение антисимметрично, т. к. при aRb
иbRa
a=
b.
3. Для проверки на транзитивность возведем матрицу отношения в квадрат:
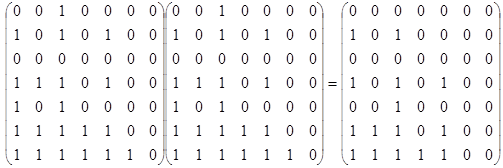
Сравнивая полученную матрицу с исходной видим, что отношение транзитивно.
Следовательно, отношение М является отношением строгого порядка.
14. Исследовать М на линейность (полноту).
Рассмотрим отношения связности:
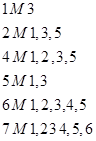
На основе этого строим ранжированный граф:
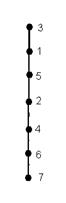
Граф представляет собой прямую линию, т.е. в нем нет параллельных вершин, следовательно, отношение М линейно.
15. Интерпретируя отношение М как «меньше», найти в множестве А относительно М минимальные и максимальные, наименьшие и наибольшие элементы (если таковые существуют).
Рассмотрим ранжированный граф.
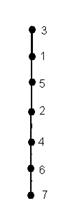
В графе нет параллельных вершин, поэтому минимальный элемент является наименьшим, а максимальный – наибольшим. Наименьший элемент – 3, наибольший элемент – 7.
|