|
В последние годы, в связи с применением многогранников Вороного и симплексов Делоне в самых различных науках, появляется интерес к истории возникновения этих геометрических построений. В ходе нашей работы мы рассмотрим математическую сторону метода Делоне, обсудим идеи и основные результаты. Как известно, Борис Николаевич был одним из учеников известного математика Г.Ф. Вороного. И поэтому результаты работ Делоне очень тесно связаны с методами Вороного.
Существует довольно много областей наук, где используются методы этих двух замечательных математиков. Кроме физики, математики и химии можно отметить наиболее известные: астрономию (изучение структуры Вселенной), экономику (методы оптимизации), картографию, экологию и компьютерную графику. Но все же главным полем применения методов в наше время являются математические науки.
Следует рассказать об одной простой, но важной теории, которую Борис Николаевич начал еще в начале 1920-х годов, — о так называемом методе пустого шара и связанном с ним разбиении пространства на специальные многогранники. Где-то в 1980-е годы, уже после смерти Б. Н. Делоне, эти разбиения получили название «триангуляции Делоне».
В нашей работе мы исследовали один из его методов – построение круга Делоне для трех многоугольников, а также вычисление радиуса и центра круга.
Борис Николаевич Делоне прожил долгую и плодотворную жизнь, внеся свой вклад в теорию чисел, алгебру и геометрию, а также воспитав многих выдающихся учеников. Делоне был чрезвычайно одаренным человеком, неутомимым альпинистом, талантливым педагогом. Заслуга Делоне еще в том, что он мог изложить фундаментальные математические результаты, как свои, так и других авторов, простым и наглядным языком, понятным не только математикам.
Работы Делоне тесно связаны с результатами работ Вороного. Классические результаты Вороного и Делоне получены для систем точек (центров). Объектом нашего исследования является система точек, произвольно расположенных в пространстве. Наши точки обособлены одна от другой, и в системе точек нет бесконечно больших пустот. Делоне сформулировал это следующим образом:
a) Можно указать некоторый конечный радиус (пусть даже очень маленький), такой, что внутри сферы этого радиуса, построенной вокруг любой точки системы, нет других точек, принадлежащих данной системе.
b) Можно указать другой конечный радиус (пусть даже очень большой), такой, что внутри сферы этого радиуса, расположенной в любом месте нашей системы, всегда найдется хотя бы одна точка системы.
Никаких других ограничений нет. Точки могут располагаться как упорядоченно, так и случайно. Будем обозначать такую систему как {А}, поскольку наши точки обычно являются центрами атомов.
Реклама

2.1 Метод пустого шара Делоне. Симплекс Делоне
Воспользуемся пустым шаром, который мы будем перемещать, изменяя его размер так, чтобы он мог касаться точек системы {А}, но всегда оставался пустым.
Итак, поместим в систему точек {А} пустой шар Делоне. Это всегда возможно, если выбрать шар достаточно малым. Начнем увеличивать его радиус, оставляя центр шара на месте. В какой-то момент поверхность шара встретит некоторую точку i системы {А}. Это обязательно произойдет, ибо в нашей системе нет неограниченно больших пустот. Будем продолжать увеличивать радиус пустого шара так, чтобы точка i оставалась на его поверхности. Для этого придется двигать центр шара от точки i. Рано или поздно шар достигнет своей поверхностью другой точки системы {А}.

Рисунок 2.1 – Разбиение Делоне двумерной системы точек
Симплексы Делоне заполняют пространство без щелей и наложений.
Описанная сфера любого симплекса не содержит внутри себя других точек системы.
Пусть это будет точка j. Продолжим увеличивать радиус нашего шара, сохраняя уже обе точки на его поверхности. Увеличиваясь, шар достигнет какой-то третьей точки системы, точки k. В двумерном случае наш «пустой круг» в этот момент зафиксируется, т.е. станет невозможным дальнейшее увеличение его радиуса при сохранении круга пустым. При этом мы выявляем элементарную двумерную конфигурацию трех точек (i,j,k), определяющую некий треугольник, особенностью которого является то, что внутри его описанной окружности нет других точек системы {А}. В трехмерном пространстве шар не определяется тремя точками. Продолжим увеличивать его радиус, сохраняя все три найденные точки на его поверхности. Это будет возможно до тех пор, пока поверхность шара не встретится с четвертой точкой l системы. После этого движение и рост пустого шара станут невозможными. Найденные четыре точки (i,j,k,l) определяют вершины тетраэдра, который характерен тем, что внутри его описанной сферы нет других точек системы {А}. Такой тетраэдр называется симплексом Делоне.
Симплексом в математике называют простейшую фигуру в пространстве данной размерности: тетраэдр – в трехмерном пространстве; треугольник – в двумерном. Произвольная тройка (четверка) точек системы, не лежащих в одной плоскости, всегда определяет некий симплекс. Однако он будет симплексом Делоне только с том случае, если его описанная сфера пуста. Другими словами, симплексы Делоне определяются особым выбором троек (четверок) точек в системе {А}.
Реклама

Мы построили один симплекс Делоне, однако, помещая пустой шар в различные места и повторяя ту же процедуру, можно определить и другие. Утверждается, что совокупность всех симплексов Делоне системы {А} заполняет пространство без наложений и щелей, т.е. реализует разбиение пространства, но на этот раз на тетраэдры. Это разбиение называется разбиением Делоне (рисунок 1).
Мы ограничились тем фактом, что ровно четыре точки в пространстве фиксируют пустой шар. В общем случае возможно, чтоб на его поверхности оказалось больше, чем четыре точки системы. Например, если имеется октаэдрическая конфигурация точек, то на поверхности вписанного шара будет лежать шесть точек – вершин октаэдра, а если кубическая, то восемь. Можно представить произвольную конфигурацию любого числа точек, лежащих на одной сфере. Все такие конфигурации, если они имеются в системе, будут выявляться с помощью пустого шара Делоне. Если мы наткнулись поверхностью шара сразу на несколько точек системы {А}, то при дальнейшем увеличении радиуса будем сохранять их всех на его поверхности. Рано или поздно мы упремся в последнюю точку (или точки), которая остановит движение нашего пустого шара.
Итак, если на поверхности пустого шара оказалось более четырех точек, будем их рассматривать как вершины некоего несимплициального многогранника. Будем называть такой многогранник несимплициальным полиэдром Делоне. Любой несимплициальный полиэдр Делоне может быть разбит на симплексы Делоне. Однако сделать это можно различными способами. В двумерном случае для многоугольника с N вершинами может реализоваться 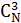 (число сочетаний из N по три) различных симплексов. Каждое конкретное разбиение содержит всегда N-2 симплекса. В трехмерном пространстве можно построить (число сочетаний из N по три) различных симплексов. Каждое конкретное разбиение содержит всегда N-2 симплекса. В трехмерном пространстве можно построить 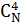 различных симплексов (рисунок 2). Однако, в отличии от двумерного случая, здесь в разных конкретных разбиениях может быть различное число симплексов. различных симплексов (рисунок 2). Однако, в отличии от двумерного случая, здесь в разных конкретных разбиениях может быть различное число симплексов.
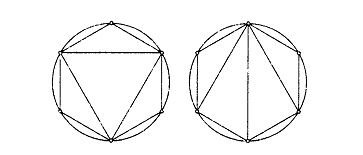
Рисунок 2 – Различные разложения двумерного несимплициального полиэдра на симплексы
Любой Х-угольник разбивается всегда на N-2 симплекса
Систему {A} будем называть вырожденной, если в ней имеется хотя бы один несимплициальный полиэдр Делоне, т.е. хотя бы один раз на поверхности пустого шара оказывается более четырех точек системы. Если нет ни одной такой конфигурации, то система называется невырожденной.
3 Теорема о разбиении Делоне
Теорема: Полиэдры Делоне системы {A} не входят друг в друга и заполняют все пространство, будучи смежными по целым граням. Разбиение пространства на полиэдры Делоне однозначно определяется системой {A} и, обратно, однозначно ее определяет.
Покажем, что полиэдры Делоне не входят друг в друга. Возьмем какие-либо два полиэдра Делоне системы {A}, обозначим их как D1 и D2, а описанные вокруг них сферы S1 и S2. Если S1 и S2 не пересекаются, то полиэдры D1 и D2 также не имеют общих точек и поэтому не входят друг в друга. Если же S1 и S2 пересекаются, то все вершины полиэдра D1 всегда лежат на той «шапочке» сферы S1, которая расположена вне сферы S2, поскольку по условию сфера S2 пуста (рисунок 3). Точно так же рассуждая, приходим к тому, что вершины полиэдра D2 лежат на той «шапочке» сферы S2, которая располагается вне сферы S1. Следовательно, вершины полиэдров D1 и D2 всегда лежат по разные стороны от хордальной плоскости этих сфер или, возможно, частично на ней самой. Это означает, что все точки полиэдров D1 и D2 должны лежать по разные стороны от этой плоскости, ибо все полиэдры Делоне – выпуклые многогранники. Отсюда следует, что никакие из них не входят друг в друга, но, возможно, касаются своими поверхностями.
Нужно убедиться, что полиэдры Делоне могут соприкасаться только по целым граням. Возьмем произвольную грань некоторого полиэдра D. Станем двигать центр описанной вокруг него сферы по направлению из полиэдра перпендикулярно этой грани.
разбиение симплекс делоне круг
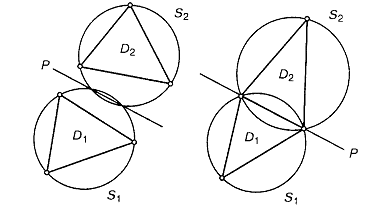
Рисунок 3 – К доказательству теоремы
Если пустые сферы двух полиэдров Делоне пересекаются, то их вершины всегда лежат по разные стороны от плоскости пересечения этих сфер (плоскость Р) или, может быть, на этой плоскости (иначе сферы не были бы пусты). Поэтому любые два полиэдра Делоне никогда не входят друг в друга.
При этом будем так менять радиус сферы, чтобы вершины выбранной грани оставались на ее поверхности. Сфера сразу покинет все остальные вершины D и, в конце концов, наткнется на некоторую точку (или точки) системы {A}, лежащую вне этого полиэдра. Отсюда мы найдем новый полиэдр Делоне, который является смежным полиэдру D по целой грани (грань полностью определяется своими тремя вершинами, а мы их не меняли). Это означает, что для произвольной грани любого полиэдра Делоне всегда существует смежный по целой грани другой полиэдр Делоне этой же системы {A}.
Отсюда следует, что в системе полиэдров Делоне нет пустот. Иначе существовали бы грани, являющиеся стенками таких пустот, не покрытые другими полиэдрами систем {A}.
Если бы разбиение пространства на полиэдры Делоне было неоднозначным, то это означало бы, что в системе нашлось два нетождественных полиэдра Делоне, имеющих общие внутренние точки. Но такого не может быть, ибо как было показано, никакие полиэдры Делоне одной системы {A} не входят друг в друга.
Обратное утверждение о том, что система дискретных точек {A} однозначно определяется разбиением Делоне, следует из того, что система {A} совпадает с множеством вершин полиэдров Делоне заданного разбиения. Итак, теорема доказана.
3.1 Симплициальное разбиение (триангуляция)
Следуя первоначальной логике Б.Н. Делоне, разбиением Делоне является разбиение системы {A} на полиэдры Делоне, т.е. допускаются вырожденные конфигурации точек. Однако во всех приложениях обычно предпочитают иметь дело только с симплексами. Каких-либо общих критериев разложения вырожденной конфигурации на симплициальные не существует. Но проблемы здесь нет. Всегда можно произвести достаточно малые смещения точек вырожденной конфигурации. В результате несимплициальный полиэдр распадется на конкретные симплексы Делоне. В дальнейшем будем предполагать, что наша система {A} невырождена, т.е. разбиение Делоне однозначно представлено симплексами Делоне.
Разбиение системы точек на симплексы иногда называют триангуляцией системы. В двумерном случае это разложение системы на треугольники. В общем случае мы будем называть такое разбиение симплициальным, или просто разбиением Делоне.
Отметим, что центр описанной сферы может служить точкой, «обозначающей» соответствующий симплекс Делоне. Множество всех таких центров будем называть системой {D}. Из теоремы о разбиении Делоне следует, что система {A} однозначно определяет систему {D} и наоборот, имея {D}, можно однозначно восстановить {A}.
3.2 Особенности взаимного расположения симплексов Делоне
Симплексы Делоне могут быть произвольной формы. Однако их взаимное расположение в составе разбиения Делоне подчиняется определенным требованиям. Отметим, что центр описанной сферы симплекса Делоне может располагаться как внутри, так и вне симплекса, хотя на первый взгляд кажется, что центр всегда должен быть внутри симплекса. Будем называть симплекс закрытым, если центр его описанной сферы лежит внутри симплекса (рисунок 4,а). Если центр вне симплекса , то такой симплекс назовем открытым (рисунок 4,а). Возможна ситуация, когда центр описанной сферы лежит точно на поверхности симплекса, в частности, на грани или ребре. Такие симплексы называются полуоткрытыми (рисунок 4,а). Заметим, что все вершины открытых и полуоткрытых симплексов лежат на одной полусфере. Грань симплекса назовем закрытой, если центр описанной сферы лежит по ту же сторону от плоскости этой грани, что и сам симплекс. Аналогично грань симплекса назовем открытой, если центр описанной сферы симплекса лежит по другую сторону от плоскости этой грани, чем сам симплекс. Открытый симплекс всегда имеет открытую грань.
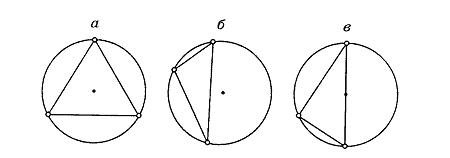
Рисунок 4 – Центр описанной сферы симплекса может располагаться: а внутри; б – вне; в – на границе симплекса
Соответствующие симплексы называются закрытыми, открытыми и полуоткрытыми. Вне вершины открытых и полуоткрытых симплексов лежат на одной полусфере описанной сферы.
Найдём пересечение трёх окружностей (одну точку), центры которых совпадают с данными, а радиусы увеличены на одинаковую величину
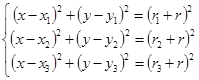
Перенесём начало координат в центр первой окружности
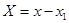 ; ; 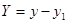 ; ; 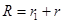
 , где , где
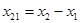 ; ; 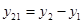 ; ; 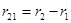
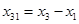 ; ; 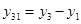 ; ;  . .
Отнимем от 2-го и 3-го уравнения 1-ое
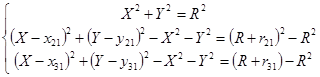
Раскроем скобки, удалив при этом квадраты
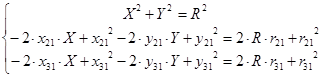
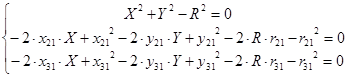
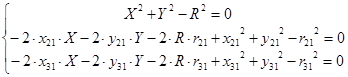
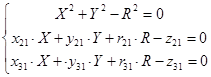 , где , где
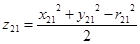 ; ; 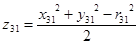 . .
Найдём 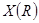 и и 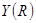 , умножив на соответствующие коэффициенты и найдя разницу уравнений , умножив на соответствующие коэффициенты и найдя разницу уравнений
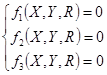
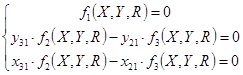
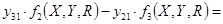
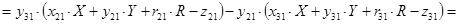
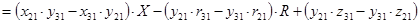
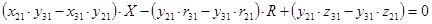
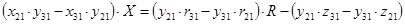
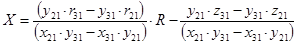
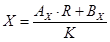
где 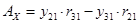 , , 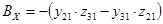 , , 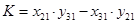 . .
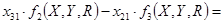
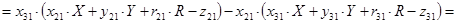
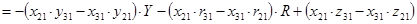
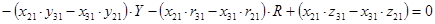
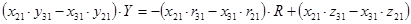
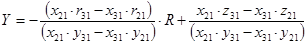
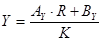
где 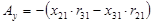 , , 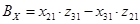 , , 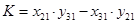 . .
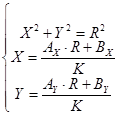
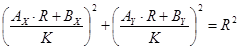
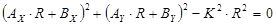
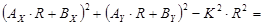
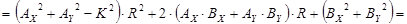
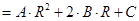 , где , где 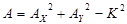 , , 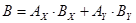 , , 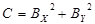 . .
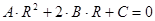
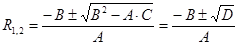 , где , где 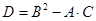 . .
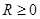
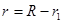
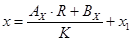
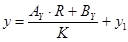
Последовательный расчёт
+ * 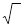 if if
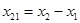 ; 1 0 0 0 ; 1 0 0 0
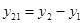 ; 1 0 0 0 ; 1 0 0 0
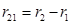 ; 1 0 0 0 ; 1 0 0 0
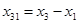 ; 1 0 0 0 ; 1 0 0 0
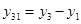 . 1 0 0 0 . 1 0 0 0
 . 1 0 0 0 . 1 0 0 0
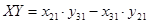 ; 1 2 0 0 ; 1 2 0 0
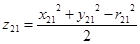 ; 2 4 0 0 ; 2 4 0 0
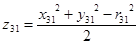 ; 2 4 0 0 ; 2 4 0 0
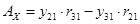 ; 1 2 0 0 ; 1 2 0 0
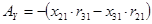 ; 1 2 0 0 ; 1 2 0 0
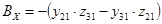 ; 1 2 0 0 ; 1 2 0 0
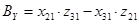 ; 1 2 0 0 ; 1 2 0 0
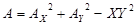 ; ;  2 3 0 1 2 3 0 1
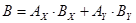 ; 1 2 0 0 ; 1 2 0 0
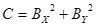 ; 1 2 0 0 ; 1 2 0 0
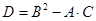 , , 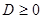 ; 1 2 0 1 ; 1 2 0 1
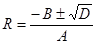 , , 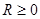 ; 1 1 1 1 ; 1 1 1 1
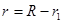 1 0 0 0 1 0 0 0
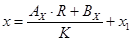 ; 2 2 0 0 ; 2 2 0 0
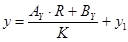 . 2 2 0 0 . 2 2 0 0
26 32 1 3
+ * 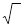 if if
5
Описание работы программы
Создаем в оболочке WPF три круга которые можно передвигать при помощи нажатия левой кнопки мыши с1, с2, с3. И два круга которые будут прорисовываться в результате вычисления формул с4 и с5.
<Window x:Class="DeloneCircleWPF.MainWindow"
xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Title="MainWindow" Height="350" Width="525" KeyDown="Window_KeyDown" xmlns:chartingToolkit="clr-namespace:System.Windows.Controls.DataVisualization.Charting;assembly=System.Windows.Controls.DataVisualization.Toolkit" MouseWheel="Window_MouseWheel">
<Canvas>
<Ellipse Name="c1" Width="100" Height="100" Canvas.Left="100" Canvas.Top="100" Fill="#E0FF0000" MouseLeftButtonDown="Ellipse_MouseLeftButtonDown" MouseLeftButtonUp="Ellipse_MouseLeftButtonUp" MouseMove="Ellipse_MouseMove"/>
<Ellipse Name="c2" Width="100" Height="100" Canvas.Left="200" Canvas.Top="100" Fill="#E000FF00" MouseLeftButtonDown="Ellipse_MouseLeftButtonDown" MouseLeftButtonUp="Ellipse_MouseLeftButtonUp" MouseMove="Ellipse_MouseMove"/>
<Ellipse Name="c3" Width="100" Height="100" Canvas.Left="150" Canvas.Top="200" Fill="#E00000FF" MouseLeftButtonDown="Ellipse_MouseLeftButtonDown" MouseLeftButtonUp="Ellipse_MouseLeftButtonUp" MouseMove="Ellipse_MouseMove"/>
<Ellipse Name="c4" Width="0" Height="0" Canvas.Left="0" Canvas.Top="0" Fill="Black"
Stroke="Black"/>
<Ellipse Name="c5" Width="0" Height="0" Canvas.Left="0" Canvas.Top="0" Stroke="Silver"/>
</Canvas>
</Window>
Создаем переменные для начальных координат Х и У, для события если мышь нажата, и для выгибания круга.
double beginX = 0;
double beginY = 0;
bool isMouseDown = false;
Shape shape;
Несколько функций для подкрепления рисунка с работой мыши.
private void Ellipse_MouseLeftButtonDown(object sender, MouseButtonEventArgs e)
{
shape = (Shape)sender;
Ellipse b = sender as Ellipse;
beginX = e.GetPosition(this).X;
beginY = e.GetPosition(this).Y;
isMouseDown = true;
b.Opacity = 0.5;
b.SetValue(Canvas.ZIndexProperty, 1);
b.CaptureMouse();
}
private void Ellipse_MouseLeftButtonUp(object sender, MouseButtonEventArgs e)
{
Ellipse b = sender as Ellipse;
isMouseDown = false;
b.Opacity = 1.0;
b.SetValue(Canvas.ZIndexProperty, 0);
b.ReleaseMouseCapture();
}
private void Ellipse_MouseMove(object sender, MouseEventArgs e)
{
if (isMouseDown)
{
Ellipse b = sender as Ellipse;
double currX = e.GetPosition(this).X;
double currY = e.GetPosition(this).Y;
double left = (double)b.GetValue(Canvas.LeftProperty);
double top = (double)b.GetValue(Canvas.TopProperty);
b.SetValue(Canvas.LeftProperty, left + currX - beginX);
b.SetValue(Canvas.TopProperty, top + currY - beginY);
beginX = currX;
beginY = currY;
ReCalclateDeloneCircle();
}
}
private void Window_KeyDown(object sender, KeyEventArgs e)
{
switch (e.Key)
{
case Key.Left:
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) - 1);
break;
case Key.Right:
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) + 1);
break;
case Key.Up:
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) - 1);
break;
case Key.Down:
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) + 1);
break;
case Key.PageUp:
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) - 1);
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) - 1);
shape.Width += 2;
shape.Height += 2;
break;
case Key.PageDown:
if (shape.Width - 2 >= 0)
{
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) + 1);
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) + 1);
shape.Width -= 2;
shape.Height -= 2;
}
break;
case Key.Tab:
if (shape == c1)
shape = c2;
else
if (shape == c2)
shape = c3;
else
shape = c1;
break;
case Key.Escape:
Close();
break;
}
ReCalclateDeloneCircle();
}
private void Window_MouseWheel(object sender, MouseWheelEventArgs e)
{
int k = Math.Abs(e.Delta) / e.Delta;
if (shape.Width + 2 * k >= 0)
{
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) - k);
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) - k);
shape.Width += 2 * k;
shape.Height += 2 * k;
}
ReCalclateDeloneCircle();
}
Функции для определения радиусов кругов Делоне, и для переопределения по мере передвижения кругов по рабочему окну.
private void ReCalclateDeloneCircle()
{
double r1 = c1.Width / 2;
double x1 = (double)c1.GetValue(Canvas.LeftProperty) + r1;
double y1 = (double)c1.GetValue(Canvas.TopProperty) + r1;
double r2 = c2.Width / 2;
double x2 = (double)c2.GetValue(Canvas.LeftProperty) + r2;
double y2 = (double)c2.GetValue(Canvas.TopProperty) + r2;
double r3 = c3.Width / 2;
double x3 = (double)c3.GetValue(Canvas.LeftProperty) + r3;
double y3 = (double)c3.GetValue(Canvas.TopProperty) + r3;
double x4, y4, r4, x5, y5, r5;
CalclateDeloneCircle(x1, y1, r1, x2, y2, r2, x3, y3, r3, out x4, out y4, out r4, out x5, out y5, out r5);
r4 = Math.Abs(r4);
if (!double.IsInfinity(r4))
{
c4.SetValue(Canvas.LeftProperty, x4 - r4);
c4.SetValue(Canvas.TopProperty, y4 - r4);
c4.Width = 2 * r4;
c4.Height = 2 * r4;
}
r5 = Math.Abs(r5);
if (!double.IsInfinity(r4))
{
c5.SetValue(Canvas.LeftProperty, x5 - r5);
c5.SetValue(Canvas.TopProperty, y5 - r5);
c5.Width = 2 * r5;
c5.Height = 2 * r5;
}
}
private void CalclateDeloneCircle(
double x1, double y1, double r1,
double x2, double y2, double r2,
double x3, double y3, double r3,
out double x4, out double y4, out double r4,
out double x5, out double y5, out double r5)
{
double x21 = x2 - x1;
double y21 = y2 - y1;
double r21 = r2 - r1;
double x31 = x3 - x1;
double y31 = y3 - y1;
double r31 = r3 - r1;
double XY = x21 * y31 - x31 * y21;
if (XY == 0)
{
x4 = double.NaN;
y4 = double.NaN;
r4 = double.NaN;
x5 = double.NaN;
y5 = double.NaN;
r5 = double.NaN;
return;
}
double z21 = (x21 * x21 + y21 * y21 - r21 * r21) / 2;
double z31 = (x31 * x31 + y31 * y31 - r31 * r31) / 2;
double Ax = y21 * r31 - y31 * r21;
double Ay = -(x21 * r31 - x31 * r21);
double Bx = -(y21 * z31 - y31 * z21);
double By = x21 * z31 - x31 * z21;
double A = Ax * Ax + Ay * Ay - XY * XY;
double B = Ax * Bx + Ay * By;
double C = Bx * Bx + By * By;
double D = B * B - A * C;
if (D < 0)
{
x4 = double.NaN;
y4 = double.NaN;
r4 = double.NaN;
x5 = double.NaN;
y5 = double.NaN;
r5 = double.NaN;
return;
}
double R;
R = (-B - Math.Sqrt(D)) / A;
r4 = R - r1;
y4 = (Ay * R + By) / XY + y1;
x4 = (Ax * R + Bx) / XY + x1;
R = (-B + Math.Sqrt(D)) / A;
r5 = R - r1;
y5 = (Ay * R + By) / XY + y1;
x5 = (Ax * R + Bx) / XY + x1;
}
6. Вид рабочего приложения

Рис. 6.1
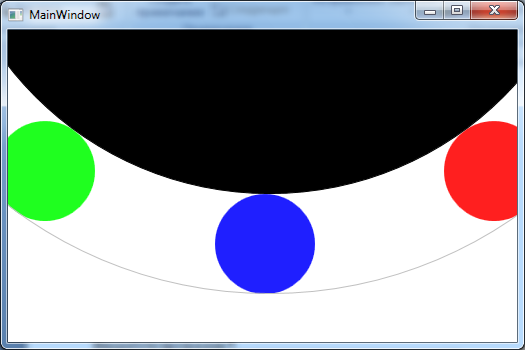
Раис 6.2
ВЫВОДЫ
Данная программа демонстрирует возможности программирования с помощью технологии Microsoft Windows Presentation Foundation. В этой программе наглядно показано новшества, которые WPF внесло в программирование Windows приложений, а именно: новое визуальное оформление, новая философия настройки элементов, новые графические средства и новый программный интерфейс.WPF состоит из двух взаимосвязанных программных интерфейсов. Программы WPF могут быть полностью написаны на C# или любом другом языке программирования, компилируемом в соответствии с правилами .NET CLS(Common Language Specification). Кроме того, WPF содержит новый язык разметки на базе XML, называемый XAML( eXtensible Application Markup Language).В отдельных случая на XAML можно написать целую программу, однако это приложение построено как из программного кода, так и из кода разметки. В этой программе XAML используется для определения пользовательского интерфейса, а программный код – для обработки событий. Подводя итоги можно сказать, что данная программа показывает преимущества технологии WPF над технологией Windows Forms.
1. Медведев Н.Н. Метод Вороного – Делоне в исследовании структуры некристаллических систем / РАН, Сиб. отд-ние, РФФИ, Институт химической кинетики и горения СО РАН. Новосибирск: НИЦ ОИГГМ СО РАН, Издательство СО РАН, 2000, 214 с.
|