Модели оптимального размещения файлов в вычислительной сети со звездообразной топологией
Задача1
Вычислительная сеть состоит из трех узлов, среди которых следует распределить семь файлов.
Обозначения:
qsr - вероятность того, что запрос, инициированный в узле Кs, использует для своего обслуживания файл, находящийся в локальной БД узла Кr.
Для определения общей средней задержки при выполнении запроса в сети введем следующие величины:
li
- средняя интенсивность запросов, инициированных в узле Ki
;
lik
- средняя интенсивность поступления запросов k
-того типа во входную сеть узла Ki
.
Wik
– среднее время обработки запросов k
-того типа на узле Ki
;
W2
ik
– дисперсия времени обработки запроса k
-того типа на узле Ki
;
l - средняя интенсивность входного потока сообщений в коммутаторе данных;
m - средняя скорость обслуживания сообщений в коммутаторе данных;
Т
i
– среднее время обслуживания запроса, инициированного на узле Ki
;
Т
– общее среднее время ответа на запрос по всей вычислительной системе.
Вероятности pij
(i
= 1,2,3; j
= 1,2, … , 7):
| P
|
F1
|
F2
|
F3
|
F4
|
F5
|
F6
|
F7
|
| K1
|
0,05 |
0,3 |
0,15 |
0,25 |
0,1 |
0,06 |
0,09 |
| K2
|
0,4 |
0,1 |
0,05 |
0,08 |
0,12 |
0,1 |
0,15 |
| K3
|
0,15 |
0,07 |
0,4 |
0,03 |
0,1 |
0,15 |
0,1 |
Распределение фалов по узлам вычислительной сети задано ниже:
| X |
K1
|
K2
|
K3
|
| F1
|
0 |
1 |
0 |
| F2
|
1 |
0 |
0 |
| F3
|
0 |
0 |
1 |
| F4
|
1 |
0 |
0 |
| F5
|
1 |
0 |
0 |
| F6
|
0 |
1 |
0 |
| F7
|
0 |
1 |
0 |
Таблица значений qsr будет иметь вид:
| q |
K1
|
K2
|
K3
|
| K1
|
0,65 |
0,2 |
0,15 |
| K2
|
0,3 |
0,65 |
0,05 |
| K3
|
0,2 |
0,4 |
0,4 |
Задали самостоятельно li
- среднюю интенсивность запросов, инициированных в узле Ki:
| λ |
Значение |
| λ1 |
2 |
| λ2 |
3 |
| λ3 |
2 |
Выполняем расчет средней интенсивности поступления запросов k-того типа во входную сеть узла Ki и средней интенсивности входного потока сообщений в коммутаторе данных по следующим формулам:
li
1
= 2li
(1 – qii
)
li
2
= 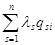
l = 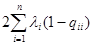 . .
Результаты расчетов приведены ниже:
| λi |
λi1 |
λi2 |
| 1 |
1,4 |
2,6 |
| 2 |
2,1 |
3,15 |
| 3 |
2,4 |
1,25 |
λ |
5,9 |
Среднее время обработки запросов k
-того типа на узле Ki
и дисперсия времени обработки запроса k
-того типа на узле Ki
приведены в таблицах:
| W |
Wi1 |
Wi2 |
| 1 |
0,3 |
0,17 |
| 2 |
0,25 |
0,13 |
| 3 |
0,35 |
0,1 |
|
| W2 |
Wi1 |
Wi2 |
| 1 |
0,14 |
0,075 |
| 2 |
0,115 |
0,055 |
| 3 |
0,165 |
0,04 |
|
Средняя скорость обслуживания сообщений в коммутаторе данных равна m=6.
Выполняем расчет значений Qi
1
и Ri
1,
Qi
2
и Ri
2
- времени ожидания и обслуживания заявок определенного типа и Q и R – время ожидания и обслуживания на коммутаторе по приведенным ниже формулам:
Qi1
= 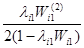
Ri1
= 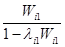
Qi2
= 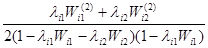
Ri2
= 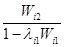
Q = 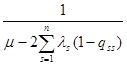
R = 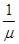
Результаты расчетов приведены таблицах:
| Qi |
Qi1 |
Qi2 |
Q |
| 1 |
0,05684 |
0,015648 |
10 |
| 2 |
0,057356 |
0,006452 |
| 3 |
0,03168 |
0,001249 |
|
| Ri |
Ri1 |
Ri2 |
R |
| 1 |
0,517241 |
0,293103 |
0,166667 |
| 2 |
0,
42105
|
0,273684 |
| 3 |
2,1875 |
0,625 |
|
Выполняем подсчет суммы li
по формуле:
S
= 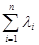 = 7 = 7
На основании полученных данных выполняем расчет среднего времени обслуживания запроса соответствующего типа, инициированного на узле Ki
и общее среднее время ответа на запрос по всей вычислительной системе с помощью формул приведенных ниже:
Реклама

Тil
= 2Qi
1
+ 2Ri
1
+ 2Q + 2R + Qj
2
+ Rj
2
Тi
2
= Qi
2
+ Ri
2
Т
= 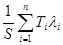
Результаты расчетов приведены ниже:
| Ti |
Ti1 |
Ti2 |
Т |
| 1 |
21,63146 |
0,308751 |
22,07032 |
| 2 |
21,6949 |
0,280136 |
| 3 |
21,84405 |
0,626249 |
Задача2
Обозначения:
n
- число узлов вычислительной сети;
m
- число независимых файлов РБД;
Fj
- j
-й файл РБД;
Ki
- i
-й узел сети;
λi
- средняя интенсивность запросов, инициированных в узле Ki
;
Wik
- среднее время обработки запроса k
-го (k
=1,2) типа в узле Ki
;
pik
- вероятность того, что для обслуживания, запроса, инициированного в узле Ki
,
необходим файл Fj
.
qsr
- вероятность того, что запрос, инициированный в узле Ks
использует для своего
обслуживания файл, находящийся в локальной базе данных узла Kr
;
λik
- средняя интенсивность поступления запросов k
-го (k
=1,2) типа во входную очередь
узла Ki
.
Вычислительная сеть состоит из трех узлов K
1
, K
2
, K
3
, а РБД содержит семь файлов F
1
, F
2
, …,
F
7
. А λi
(i
= 1, 2, 3) имеют значения: λ
1
= 2, λ
2
= 3, λ
3
= 2, а величины pij
(i
= 1, 2, 3; j
= 1, 2,..., 8) и Wik
(i
= 1, 2, 3; k = 1, 2) приведены в таблицах 1 и 2 соответственно:
табл.1
| P |
F1
|
F2
|
F3
|
F4
|
F5
|
F6
|
F7
|
| K1
|
0,05 |
0,3 |
0,15 |
0,25 |
0,1 |
0,06 |
0,09 |
| K2
|
0,4 |
0,1 |
0,05 |
0,08 |
0,12 |
0,1 |
0,15 |
| K3
|
0,15 |
0,07 |
0,4 |
0,03 |
0,1 |
0,15 |
0,1 |
табл.2
| Wi |
W1 |
W2 |
| 1 |
0,001 |
0,6 |
| 2 |
0,21 |
0,18 |
| 3 |
0,28 |
0,2 |
Найдем оптимальное распределение файлов по узлам вычислительной сети.
Используя формулу Qjs
= 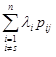 , находим Qjs
(j
=1, 2,..., 8; s
= 1, 2, 3). Эти величины имеют значения: , находим Qjs
(j
=1, 2,..., 8; s
= 1, 2, 3). Эти величины имеют значения:
вычислительная сеть размещение файл
| Q |
K1 |
K2 |
K3 |
MIN |
| F1 |
1,5 |
0,4 |
1,3 |
0,4 |
| F2 |
0,44 |
0,74 |
0,9 |
0,44 |
| F3 |
0,93 |
1,08 |
0,45 |
0,45 |
| F4 |
0,3 |
0,56 |
0,74 |
0,3 |
| F5 |
0,58 |
0,42 |
0,56 |
0,42 |
| F6 |
0,6 |
0,42 |
0,42 |
0,42 |
| F7 |
0,65 |
0,38 |
0,63 |
0,38 |
В соответствии с выбранными 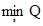 начальное распределение будет иметь вид: начальное распределение будет иметь вид:
| K1
|
K2
|
K3
|
| F1
|
0 |
1 |
0 |
| F2
|
1 |
0 |
0 |
| F3
|
0 |
0 |
1 |
| F4
|
0 |
1 |
0 |
| F5
|
0 |
1 |
0 |
| F6
|
0 |
0 |
1 |
| F7
|
0 |
1 |
0 |
Полученное начальное распределение является оптимальным. Оптимальное значение линейной функции L
равно
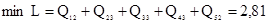 . .
МОДЕЛИ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ФАЙЛОВ В ВЫЧИСЛИТЕЛЬНОЙ СЕТИ С КОЛЬЦЕВОЙ ТОПОЛОГИЕЙ
Обозначения:
n – число узлов сети;
m – число независимых файлов РБД;Kj
– j-й узел сети;
Fi
– i-йфайлРБД;
Li
– объем i-го файла;
bj
– объем памяти узла Kj
, предназначенной для размещения файлов;
dsj
– расстояние между узлами Ks
и Kj
(dss
=0, s=1,2,…,n);
lij
– интенсивность запросов к файлу Fi
, инициированных в узле Kj
;
aij
– объем запроса к файлу Fi
, инициированного на терминале узла Kj
;
bij
– объем запрашиваемых данных при выполнении запроса к файлу Fi
, поступившего на терминал узла Kj
;
Задача 1
Вычислительная сеть состоит из трех узлов, среди которых следует распределить пять файлов.
Размеры файлов:
Реклама

| Li |
Значение |
| 1 |
50 |
| 2 |
10 |
| 3 |
48 |
| 4 |
70 |
| 5 |
33 |
Расстояние между узлами:
| dsj |
K1 |
K2 |
K3 |
| K1 |
0 |
1 |
1 |
| K2 |
1 |
0 |
1 |
| K3 |
1 |
1 |
0 |
Интенсивности запросов к файлу Fi
, инициированных в узле Kj
:
| λij |
K1 |
K2 |
K3 |
| F1 |
5 |
2 |
1 |
| F2 |
2 |
3 |
1 |
| F3 |
3 |
7 |
8 |
| F4 |
4 |
2 |
9 |
| F5 |
9 |
1 |
6 |
Объем памяти узла Kj
, предназначенной для размещения файлов:
Объемы запроса к файлу Fi
, инициированного на терминале узла Kj
:
| aij |
K1 |
K2 |
K3 |
| F1 |
5 |
6 |
1 |
| F2 |
8 |
1 |
3 |
| F3 |
3 |
8 |
2 |
| F4 |
1 |
5 |
7 |
| F5 |
8 |
9 |
2 |
Объемы запрашиваемых данных при выполнении запроса к файлу Fi
, поступившего на терминал узла Kj
:
| bij |
K1 |
K2 |
K3 |
| F1 |
40 |
15 |
23 |
| F2 |
10 |
8 |
6 |
| F3 |
42 |
40 |
30 |
| F4 |
53 |
49 |
20 |
| F5 |
25 |
30 |
8 |
Сумма произведений объемов данных, пересылаемых из узла Кs
и в этот же узел при функционировании системы в течение единицы времени, на расстояния, на которые эти данные пересылаются, в случае хранения файла Fi
в узле Ks
рассчитывается по формуле 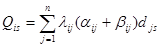 . Результаты расчетов представлены в таблице 1: . Результаты расчетов представлены в таблице 1:
табл. 1
| Qij |
K1 |
K2 |
K3 |
МИН |
| F1 |
66 |
249 |
267 |
66 |
| F2 |
36 |
45 |
63 |
36 |
| F3 |
592 |
391 |
471 |
391 |
| F4 |
351 |
459 |
324 |
324 |
| F5 |
99 |
357 |
336 |
99 |
Находим распределение файлов, т.е. определяем матрицу Х={xij
}m
,
n
хij
(i=1,2, …, m; j=1,2,…,n) – величины, определяемые по формуле
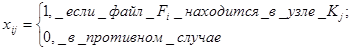 . .
Результаты расчетов:
| X |
K1 |
K2 |
K3 |
| F1 |
1 |
0 |
0 |
| F2 |
1 |
0 |
0 |
| F3 |
0 |
1 |
0 |
| F4 |
0 |
0 |
1 |
| F5 |
1 |
0 |
0 |
Выполняем проверку, достаточно ли памяти на узлах для размещения файлов. Результаты проверки приведены ниже:
| X*Li |
K1 |
K2 |
K3 |
| F1 |
50 |
0 |
0 |
| F2 |
10 |
0 |
0 |
| F3 |
0 |
48 |
0 |
| F4 |
0 |
0 |
70 |
| F5 |
33 |
0 |
0 |
| СУММА |
93 |
48 |
70 |
Полученное размещение является оптимальным.
Задача 2
Вычислительная сеть состоит из трех узлов, среди которых следует распределить пять файлов.
Размеры файлов:
| Li |
Значение |
| 1 |
50 |
| 2 |
10 |
| 3 |
48 |
| 4 |
70 |
| 5 |
33 |
Расстояние между узлами:
| dsj |
K1 |
K2 |
K3 |
К4 |
| K1 |
0 |
1 |
1 |
2 |
| K2 |
1 |
0 |
1 |
2 |
| K3 |
1 |
1 |
0 |
1 |
| К4 |
2 |
2 |
1 |
0 |
Интенсивности запросов к файлу Fi
, инициированных в узле Kj
:
| λij |
K1 |
K2 |
K3 |
К4 |
| F1 |
4 |
2 |
1 |
5 |
| F2 |
2 |
5 |
1 |
4 |
| F3 |
3 |
7 |
8 |
3 |
| F4 |
4 |
2 |
9 |
7 |
| F5 |
9 |
1 |
6 |
1 |
Объем памяти узла Kj
, предназначенной для размещения файлов:
| Bj |
1 |
2 |
3 |
4 |
| 812 |
564 |
702 |
250 |
Объемы запроса к файлу Fi
, инициированного на терминале узла Kj
:
| aij |
K1 |
K2 |
K3 |
К4 |
| F1 |
5 |
6 |
1 |
2 |
| F2 |
8 |
1 |
3 |
7 |
| F3 |
3 |
8 |
2 |
6 |
| F4 |
1 |
5 |
7 |
3 |
| F5 |
8 |
9 |
2 |
5 |
Объемы запрашиваемых данных при выполнении запроса к файлу Fi
, поступившего на терминал узла Kj
:
| bij |
K1 |
K2 |
K3 |
К4 |
| F1 |
40 |
15 |
23 |
48 |
| F2 |
10 |
9 |
6 |
2 |
| F3 |
42 |
40 |
30 |
44 |
| F4 |
53 |
33 |
10 |
68 |
| F5 |
25 |
30 |
8 |
21 |
Сумма произведений объемов данных, пересылаемых из узла Кs
и в этот же узел при функционировании системы в течение единицы времени, на расстояния, на которые эти данные пересылаются, в случае хранения файла Fi
в узле Ks
рассчитывается по формуле 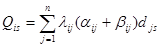 . Результаты расчетов: . Результаты расчетов:
| Qij |
K1 |
K2 |
K3 |
К4 |
МИН |
| F1 |
566 |
704 |
472 |
468 |
468 |
| F2 |
131 |
117 |
122 |
181 |
117 |
| F3 |
892 |
691 |
621 |
1198 |
621 |
| F4 |
1223 |
1363 |
789 |
737 |
737 |
| F5 |
151 |
409 |
362 |
732 |
151 |
Находим распределение файлов, т.е. определяем матрицу Х={xij
}m
,
n
хij
(i=1,2, …, m; j=1,2,…,n) – величины, определяемые по формуле
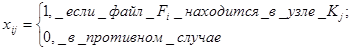 . .
Результаты расчетов:
| X |
K1 |
K2 |
K3 |
К4 |
| F1 |
0 |
0 |
0 |
1 |
| F2 |
0 |
1 |
0 |
0 |
| F3 |
0 |
0 |
1 |
0 |
| F4 |
0 |
0 |
0 |
1 |
| F5 |
1 |
0 |
0 |
0 |
Выполняем проверку, достаточно ли памяти на узлах для размещения файлов. Результаты проверки приведены в таблице 9:
| X*Li |
K1 |
K2 |
K3 |
К4 |
| F1 |
0 |
0 |
0 |
50 |
| F2 |
0 |
10 |
0 |
0 |
| F3 |
0 |
0 |
48 |
0 |
| F4 |
0 |
0 |
0 |
70 |
| F5 |
33 |
0 |
0 |
0 |
| СУММА |
33 |
10 |
48 |
120 |
Полученное размещение является оптимальным.
МОДЕЛИ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ФАЙЛОВ В ВЫЧИСЛИТЕЛЬНОЙ СЕТИ С ПРОИЗВОЛЬНОЙ ТОПОЛОГИЕЙ
Задача1
Вычислительная сеть состоит из трех узлов, среди которых следует распределить пять файлов.
Размеры файлов:
| Li |
Значение |
| 1 |
50 |
| 2 |
10 |
| 3 |
48 |
| 4 |
70 |
| 5 |
33 |
Расстояние между узлами:
табл. 2
| dsj |
K1 |
K2 |
K3 |
К4 |
| K1 |
0 |
1 |
1 |
2 |
| K2 |
1 |
0 |
1 |
2 |
| K3 |
1 |
1 |
0 |
1 |
| К4 |
2 |
2 |
1 |
0 |
Интенсивности запросов к файлу Fi
, инициированных в узле Kj
:
| λij |
K1 |
K2 |
K3 |
К4 |
| F1 |
4 |
2 |
1 |
5 |
| F2 |
2 |
5 |
1 |
4 |
| F3 |
3 |
7 |
8 |
3 |
| F4 |
4 |
2 |
9 |
7 |
| F5 |
9 |
1 |
6 |
1 |
Интенсивность корректирующих сообщений к файлу Fi
из узла Kj
:
| λ'ij |
K1 |
K2 |
K3 |
К4 |
| F1 |
1 |
3 |
6 |
1 |
| F2 |
5 |
1 |
2 |
1 |
| F3 |
2 |
4 |
3 |
2 |
| F4 |
7 |
2 |
2 |
3 |
| F5 |
1 |
1 |
3 |
2 |
Объем памяти узла Kj
, предназначенной для размещения файлов:
| Bj |
1 |
2 |
3 |
4 |
| 812 |
564 |
702 |
250 |
Объемы запроса к файлу Fi
, инициированного на терминале узла Kj
:
| aij |
K1 |
K2 |
K3 |
К4 |
| F1 |
5 |
6 |
1 |
2 |
| F2 |
8 |
1 |
3 |
7 |
| F3 |
3 |
8 |
2 |
6 |
| F4 |
1 |
5 |
7 |
3 |
| F5 |
8 |
9 |
2 |
5 |
Объемы запрашиваемых данных при выполнении запроса к файлу Fi
, поступившего на терминал узла Kj
:
bij
|
K1 |
K2 |
K3 |
К4 |
| F1 |
40 |
15 |
23 |
48 |
| F2 |
10 |
9 |
6 |
2 |
| F3 |
42 |
40 |
30 |
44 |
| F4 |
53 |
33 |
10 |
68 |
| F5 |
25 |
30 |
8 |
21 |
Объемы корректирующих сообщений к файлу Fi
из узла Kj
:
| Tij |
K1 |
K2 |
K3 |
К4 |
| F1 |
20 |
15 |
8 |
10 |
| F2 |
2 |
4 |
7 |
5 |
| F3 |
18 |
10 |
25 |
12 |
| F4 |
40 |
30 |
24 |
27 |
| F5 |
10 |
15 |
8 |
10 |
Средний объем данных, необходимых для пересылки при выполнении запроса в системе вычисляется по формуле 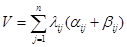 . Результаты расчетов представлены ниже: . Результаты расчетов представлены ниже:
| V |
K1 |
K2 |
K3 |
К4 |
| F1 |
180 |
42 |
24 |
250 |
| F2 |
36 |
50 |
9 |
36 |
| F3 |
135 |
336 |
256 |
150 |
| F4 |
216 |
76 |
153 |
497 |
| F5 |
297 |
39 |
60 |
26 |
Средний объем данных, необходимых для пересылки при обработке корректирующего сообщения в системе вычисляется по формуле 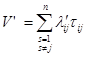 . Результаты расчетов представлены ниже: . Результаты расчетов представлены ниже:
| V' |
K1 |
K2 |
K3 |
К4 |
| F1 |
20 |
45 |
48 |
10 |
| F2 |
10 |
4 |
14 |
5 |
| F3 |
36 |
40 |
75 |
24 |
| F4 |
280 |
60 |
48 |
81 |
| F5 |
10 |
15 |
24 |
20 |
Находим распределение файлов, т.е. определяем матрицу Х={xij
}m
,
n
хij
(i=1,2, …, m; j=1,2,…,n) – величины, определяемые по формуле
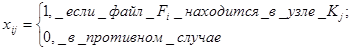 . .
Результаты расчетов представлены ниже:
| X |
K1 |
K2 |
K3 |
К4 |
| F1 |
0 |
1 |
1 |
0 |
| F2 |
0 |
0 |
1 |
1 |
| F3 |
1 |
0 |
0 |
1 |
| F4 |
0 |
1 |
1 |
0 |
| F5 |
0 |
1 |
0 |
1 |
Выполняем проверку, достаточно ли памяти на узлах для размещения файлов. Результаты проверки:
| X*Li |
K1 |
K2 |
K3 |
К4 |
| F1 |
0 |
50 |
50 |
0 |
| F2 |
0 |
0 |
10 |
10 |
| F3 |
48 |
0 |
0 |
48 |
| F4 |
0 |
70 |
70 |
0 |
| F5 |
0 |
33 |
0 |
33 |
| СУММА |
48 |
153 |
130 |
91 |
Полученное размещение является оптимальным.
|