1. Механизмы переноса
Можно выделить три механизма, общие для переноса перечисленных выше субстанции: молекулярный, конвективный
и турбулентный.
1.1 Молекулярный механизм
Молекулярный механизм переноса субстанции обусловлен тепловым движением молекул или иных микроскопических частиц (ионов в электролитах и кристаллах, электронов в металлах). Взаимодействие между молекулами грубо можно представить как "жесткое" отталкивание на малых расстояниях между их центрами (
l
)
и "мягкое" притяжение на больших.
Кинетическая энергия молекул, определяющая среднюю квадратичную скорость их движения в условиях термодинамического равновесия, связана с температурой системы
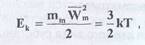
откуда может быть найдена средняя квадратичная скорость молекул:
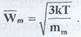
Как видно, она зависит только от температуры системы и массы молекулы. Так, для молекул кислорода при нормальных условиях (Т = 273 К) Wm=461 м/с = 1660 км/ч. С такими средними скоростями осуществляется тепловое движение молекул.
В зависимости от фазового состояния вещества характер молекулярного движения различен. В газах молекулы движутся хаотически. Вследствие малой плотности системы большую долю времени составляет "свободный пробег", т.е. движение молекул практически без взаимодействия друг с другом. При понижении температуры системы уменьшается кинетическая энергия молекул. Они теряют возможность преодолевать силы межмолекулярного притяжения, и система, конденсируясь, переходит из газового состояния в жидкое. Хаотический характер молекулярного движения при этом в основном сохраняется. Однако в связи со значительным увеличением плотности возрастает роль межмолекулярного взаимодействия, большая доля объема системы становится занятой самими молекулами. Затрудняется выход молекул из своего ближайшего окружения.
При дальнейшем понижении температуры большинство систем переходит в кристаллическое состояние. Кинетической энергии молекулы уже недостаточно для выхода из ячейки, образованной окружающими ее молекулами. Формируется наиболее выгодная с энергетической точки зрения структура кристаллической решетки. Перемещение молекул из одного узла в другой возможно лишь за счет нарушений регулярности структуры - наличия дислокаций, "дырок". Преобладающим является тепловое движение молекул внутри ячейки.
Реклама

Процедуры осреднения скорости молекул быть различными. Можно проводить осреднение по времени, т.е., выбрав какую-то молекулу, следить за ней и замерять ее скорость в различные моменты времени, а затем сложить все эти значения и поделить на количество измерений n:
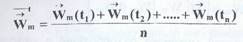
Вследствие хаотичности теплового движения молекул, направления вектора скорости в различные моменты времени были бы различны и при достаточно большом промежутке времени по сравнению со временем "свободного пробега" молекул средняя по времени скорость молекулы для равновесной неподвижной системы была бы равна нулю. Поэтому в качестве характеристики теплового движения используют среднюю квадратичную скорость, величина которой отлична от нуля
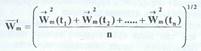
Можно проводить осреднение не по времени, а по объему, т.е. в фиксированный момент времени замерить скорости всех N молекул в выделенном объеме и найти среднее значение скорости:
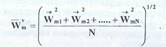
Для равновесных систем обе эти процедуры осреднения дадут одинаковые результаты. Разумеется, непосредственное осуществление описанных выше процедур невозможно, так как требует измерения скоростей отдельных молекул, характерный размер которых ~ 10-10 – 10-9. Инженерная практика оперирует макроскопическими величинами, которые описываются непрерывными или кусочно-непрерывными функциями пространственных координат и времени. Абстрагируясь от молекулярного микроскопического представления вещества, на макроуровне рассматривают среду в качестве сплошной. Однако свойства макроскопических объектов обусловлены их микроскопическим поведением. Связать макроскопические непрерывные величины с микроскопическими дискретными позволяет статистическая механика. Оперируя такими понятиями, как функции распределения случайной величины, она дает возможность проводить процедуру осреднения и находить наблюдаемые макроскопические величины, например,
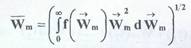
В статистической механике разработаны и методы определения функций распределения. Так, в условиях равновесия f (Wm) является известной функцией распределения молекул по скоростям Максвелла. Она характеризует плотность вероятности, с которой молекула может двигаться с тем или иным значением скорости. Неравновесная статистическая механика, или, как ее еще называют, кинетическая теория, позволяет определять неравновесные функции распределения и на их основе описывать явления переноса.
Реклама

Молекула, перемещаясь из одной точки пространства в другую, переносит все три вида субстанции - массу, импульс и энергию. В условиях равновесия, когда система покоится, а концентрации компонентов и температура во всех точках одинаковы, видимого макроскопического переноса субстанций не наблюдается, так как перенос молекул в любом направлении равновероятен. В отсутствие равновесия появляется преобладающая вероятность молекулярного переноса массы в направлении от больших значений концентрации к меньшим, импульса - от больших значений скоростей к меньшим и энергии - от больших температур к меньшим. Это приводит к наблюдаемым макроскопическим явлениям переноса.
Следует обратить внимание на различные составляющие молекулярного механизма переноса для различных субстанций. Так, перенос массы может осуществляться только за счет поступательного переноса, т.е. непосредственного перемещения молекулы из одной точки пространства в другую. Перенос импульса и энергии может происходить как за счет поступательного переноса, так и за счет взаимодействия молекул. Наиболее простой моделью взаимодействия молекул является рассмотрение их как сталкивающихся твердых шаров. Для качественного описания процессов переноса такая модель вполне приемлема. При столкновении молекул происходит изменение их скоростей, что приводит к так называемому столкновительному переносу импульса и энергии.
В разреженных и умеренно плотных газах основную долю в переносе импульса и энергии составляет поступательный перенос. В плотных газах и конденсированных системах увеличивается доля столкновительного переноса, и она становится преобладающей.
1.2 Конвективный механизм
Конвективный механизм переноса субстанции обусловлен движением макроскопических объемов среды как целого. Как уже отмечалось, характерные масштабы инженерных задач позволяют оперировать макроскопическими величинами, которые могут задаваться в каждой точке пространства путем усреднения микроскопических величин. Совокупность значений физической величины, однозначно определенных в каждой точке некоторой части пространства, называется полем данной величины (поле плотности, концентраций, давления, скорости, температуры и т.д.). Выбор дискретной микроскопической или сплошной макроскопической модели для описания явления зависит от масштаба рассматриваемой задачи. Исследуя или проектируя промышленный аппарат, по-видимому, можно с достаточной степенью точности рассматривать в качестве минимальной цены деления пространственных координат 1 мм и временных координат 1 с. Понятию "точки" пространства при такой шкале будет соответствовать объем в 1 мм3. Но в 1 мм3 содержится от 1016 молекул в умеренно плотном газе и до 1019 молекул жидкости. За "момент" времени в 1с произойдет 109-1012 столкновений для каждой молекулы. Проведя осреднение случайных значений молекулярных микроскопических характеристик в системе, состоящей из такого большого числа частиц и претерпевающей значительную по микроскопическим масштабам эволюцию, можно получить с большой степенью вероятности вполне определенное значение макроскопической величины.
В общем случае минимальная цена деления макроскопического масштаба пространственной ∆lили временной ∆t координаты должна быть достаточно малой, чтобы пренебречь изменением макроскопических физических величин в пределах ∆l или ∆t, и достаточно большой, чтобы пренебречь флуктуациями (случайными отклонениями от среднего значения) макроскопических величин, полученных осреднением микроскопических величин по времени ∆t или элементу пространства (∆l)3. Выбор минимальной цены деления макроскопического масштаба определяется характером решаемой задачи.
Так, при любом из рассмотренных выше способов осреднения скорости можно получить ее макроскопическое значение для каждой "точки" пространства в любой момент времени. Такую скорость назовем конвективной и обозначим W(x,y,z,t). Если система находится в равновесии и неподвижна относительно выбранной нами системы отсчета, обычно связанной с аппаратом, то любая процедура осреднения даст нулевые значения скорости. В неравновесных условиях при движении среды относительно аппарата средние скорости молекул в каждой точке пространства будут отличны от нуля. На практике конвективную скорость определяют экспериментально или рассчитывают, применяя макроскопические уравнения гидродинамики.
Движение макроскопических объемов среды приводит к переносу массы ρ, импульса 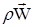 и энергии ρЕ’ единичного объема (р - плотность или масса единичного объема, и энергии ρЕ’ единичного объема (р - плотность или масса единичного объема, 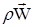 - импульс единичного объема, рЕ' - энергия единичного объема). - импульс единичного объема, рЕ' - энергия единичного объема).
В зависимости от причин, вызывающих конвективное движение, различают свободную и вынужденную конвекцию. Свободная конвекция обусловлена естественными причинами и происходит, под действием силы тяжести, а вынужденная вызывается искусственно, с использованием насосов, компрессорных машин, перемешивания и т.д.
1.3 Турбулентный механизм
Турбулентный механизм переноса занимает промежуточное место между молекулярным и конвективным механизмами с точки зрения пространственно-временного масштаба. Для создания турбулентного движения необходимо выполнение наибольшего количества условий. Так, молекулярное тепловое движение происходит в любой, в том числе и равновесной, системе, температура которой отличается от абсолютного нуля, т.е. практически всегда. Конвективное движение наблюдается только в неравновесных системах при перемещении макроскопических объемов среды. Турбулентное движение возникает лишь при определенных условиях конвективного движения: достаточные удаленность от границы раздела фаз и неоднородность поля конвективной скорости.
При малых конвективных скоростях движения среды (газа или жидкости) относительно границы раздела фаз ее макроскопические слои движутся регулярно, параллельно друг другу. Такое движение называется ламинарным. Возникающие в реальных условиях случайные или искусственные малые возмущения, изменяющие регулярность движения (шероховатость поверхности, ограничивающей поток, и т.д.), не развиваются с течением времени, а, наоборот, затухают. Однако если и неоднородность скорости, и удаленность от границы раздела фаз превышают определенные значения, устойчивость движения по отношению к малым возмущениям нарушается. Происходит развитие нерегулярного хаотического движения отдельных объемов среды (вихрей). Такое движение называется турбулентным.
Первые исследования режимов движения осуществил в 1883 г. английский физик О. Рейнольдс, изучавший движение воды в трубе с введением в основной поток подкрашенной тонкой струйки. При ламинарном движении тонкая подкрашенная струйка не смешивалась с основной массой движущейся жидкости и имела прямолинейную траекторию. При увеличении скорости потока или диаметра трубы струйка приобретала волнообразное движение, что свидетельствует о возникновении возмущений. При дальнейшем увеличении вышеназванных параметров струйка смешивалась с основной массой жидкости, и окрашенный индикатор размывался по всему поперечному сечению трубы. Отсутствие видимого смешения индикатора при ламинарном движении объясняется малой интенсивностью молекулярного механизма переноса массы в жидкости. Поскольку увеличение конвективной скорости или диаметра трубы не влияет на молекулярный перенос, а интенсивность перемешивания в направлении, перпендикулярном конвективной скорости, существенно возрастает, опыт Рейнольдса свидетельствует о возникновении дополнительного механизма переноса при турбулентном режиме движения, интенсивность которого к тому же выше молекулярного.
Подобно тому, как характеристиками молекулярного движения являются средняя квадратичная скорость молекул и их размер, вводятся аналогичные величины, характеризующие турбулентное движение. Используется понятие масштаба турбулентности, определяющего размер вихрей. В отличие, например, от молекул вихри не являются устойчивыми, четко ограниченными в пространстве образованиями. Онизарождаются, распадаются на более мелкие вихри, затухают с переходом энергии в тепловую (диссипация энергии). Поэтому масштаб турбулентности является осредненной статистической величиной. В литературе известны различные определения этой величины. Наиболее употребительные основаны на статистической одномоментной корреляции (связи) скоростей в различных точках пространства. Можно ввести понятие скорости вихря 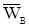 и рассмотреть ее в лабораторной системе отсчета, т.е. связанной с аппаратом. Однако, поскольку турбулентное движение развивается лишь на фоне конвективного, обычно используют пульсационную скорость и рассмотреть ее в лабораторной системе отсчета, т.е. связанной с аппаратом. Однако, поскольку турбулентное движение развивается лишь на фоне конвективного, обычно используют пульсационную скорость
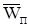 , являющуюся скоростью вихря в системе отсчета, движущейся с конвективной скоростью W: , являющуюся скоростью вихря в системе отсчета, движущейся с конвективной скоростью W:
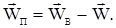
Пульсационная скорость изменяется хаотически по направлению и величине с частотой обратно пропорциональной масштабу вихря. Сложность описания турбулентного движения заключается в широком спектре значений масштаба турбулентности. Наибольшие вихри соизмеримы с масштабом аппарата, а мелкомасштабные имеют размер до 10"6м. В связи с этим возможны различные подходы к описанию турбулентного движения, определяющиеся выбором минимальной цены деления макроскопического масштаба.
Первыйподход состоит в выборе ∆lи ∆t меньших, чем характерные масштабы турбулентного движения. Допустим, ∆l =10-7м, ∆t =10-7с, тогда любые вихри будут рассматриваться как макроскопические объемы, и их движение будет являться конвективным. В этом случае нет необходимости вводить понятие "турбулентный механизм переноса". Недостатком такого подхода является необходимость задания начальных и граничных условий для турбулентно движущейся среды, что практически невозможно, учитывая неоднородность поля скорости, обусловленную огромным количеством мелкомасштабных вихрей.
Второй подход состоит в выборе промежуточных значений ∆lи ∆t. Допустим ∆l =10-3м, ∆t=1с. В этом случае перенос субстанций крупномасштабными вихрями будет рассматриваться как конвективный - детерминированный, а мелкомасштабными - как турбулентный - случайный.
Однако на практике в основном используется третий подход. Он применим для стационарных или достаточно медленно протекающих процессов. Заключается этот подход во временном осреднении значений физических величин (скорости, концентраций, температуры) на интервалах, значительно превышающих характерные периоды пульсаций даже крупномасштабных вихрей (для стационарных процессов интервал временного осреднения может быть сколь угодно большим). Осредненные по большим интервалам времени величины могут быть описаны непрерывными функциями, т.е. удовлетворять условиям, накладываемым на макроскопические поля. В этом случае перенос субстанции за счет пульсационной составляющей турбулентного движения рассматривается как особый турбулентный механизм переноса.
Осреднение по значительному промежутку времени, соответствующему выбранной минимальной цене деления макроскопического масштаба ∆t, в данном случае неравнозначно осреднению по пространству (∆l)э, так как последнее не обеспечивает отсутствие значительных флуктуации осредненных по (∆l)3 величин, вследствие соизмеримости ∆lс масштабом турбулентности.
Осредненные по времени макроскопические величины иногда употребляются в литературе с символами осреднения 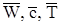 и т.д. Применяя временное осреднение к скорости вихря в лабораторной системе отсчета и к пульсационной скорости, получим и т.д. Применяя временное осреднение к скорости вихря в лабораторной системе отсчета и к пульсационной скорости, получим
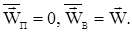
По аналогии со средней квадратичной молекулярной скоростью можно ввести среднюю квадратичную пульсационную скорость:
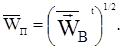
Отношение этой величины к конвективной скорости называется интенсивностью турбулентности:
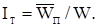
Если составляющие средней квадратичной пульсационной скорости одинаковы по всем направлениям, то такая турбулентность называется изотропной. Подобно тому, как за счет хаотического движения молекул осуществляется перенос массы, импульса и энергии, турбулентные вихри также осуществляют эти виды переноса. Отличие от молекулярного механизма заключается в масштабе вихрей и отсутствии столкновительного переноса субстанции, так как при столкновении вихрей происходит их смешение, а не упругое взаимодействие.
турбулентный конвективный молекула энергия перенос
2. Уравнения переноса
2.1 Перенос массы
2.1.1 Конвективный механизм
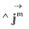 Поток массы в лабораторной системе отсчета за за счет конвективного механизма для любой точки системы может быть связан с конвективной скоростью: Поток массы в лабораторной системе отсчета за за счет конвективного механизма для любой точки системы может быть связан с конвективной скоростью:
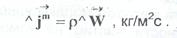
В случае многокомпонентной среды можно рассмотреть поток массы каждого компонента
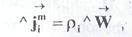
где i - номер компонента, ρi - плотность компонента i.
Зачастую удобнее использовать поток вещества, а не массы
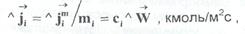
где mi, - мольная масса компонента i, кг/кмоль, сi, - мольная концентрация, кмоль/мэ. Отметим, что конвективная скорость и потоки рассматривались в лабораторной системе отсчета, т.е, относительно системы отсчета, связанной с аппаратом. В условиях гидромеханического равновесия конвективная скорость относительно аппарата является не просто постоянной, а нулевой величиной.
2.1.2 Молекулярный механизм
Собственно молекулярный механизм переноса массы можно наблюдать в термодинамически равновесной системе при наличии лишь градиентов концентрации меченых частиц сорта i(
I’-
изотопы молекул сорта i)
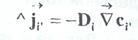
Знак минус свидетельствует о противоположной направленности векторов потока вещества и градиента концентрации. Градиент концентрации направлен в сторону максимального 'увеличения концентрации, а поток вещества - в сторону ее уменьшения, выравнивания неоднородности. Эйнштейном было показано, что коэффициенты пропорциональности в этом соотношении характеризуют средний квадрат смещения молекул за единицу времени вследствие хаотического теплового движения:
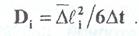
Эти величины называют эйнштейновскими коэффициентами диффузии.
Они экспериментально определяются с помощью методов меченых атомов или ядерного магнитного резонанса, а также на основе численного эксперимента методом молекулярной динамики (моделирование движения совокупности частиц на компьютере). Di
зависят от динамических характеристик молекул (масса, потенциал взаимодействия), а также от давления и температуры системы. Поскольку Di
характеризуют подвижность молекул, они существенно зависят от фазового состояния системы.
В соответствии с подходом независимой диффузии предполагается, что в неравновесных условиях собственно диффузионные потоки можно описать эйнштейновскими коэффициентами. Тогда для изотермической системы в отсутствие турбулентности поток компонента i складывается из диффузионного и конвективного:
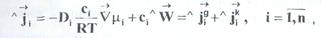
где n - число компонентов в системе. Следует иметь в виду, что в неравновесных условиях конвективная скорость может появляться и за счет самой диффузии. Например, рассмотрим аппарат, в одной части которого находится компонент 1, а в другой - компонент 2, отделенные друг от друга перегородкой. Давление и температура в обеих частях аппарата одинаковы. Если убрать перегородку, то за счет молекулярной диффузии возникнут противоположно направленные потоки компонентов. Однако величины потоков будут различны вследствие отличия динамических характеристик молекул компонентов и, следовательно, эйнштейновских коэффициентов диффузии Di. Допустим D1 > D2, тогда диффузионный поток первого компонента будет больше второго. Молекулярный механизм вызовет суммарный перенос вещества из первой чаоти аппарата во вторую, что приведет к возникновению в закрытом аппарате градиента плотности числа частиц и, соответственно, давления (р2 >р1). Это вызовет противоположно направленный конвективный поток, выравнивающий градиент давления
Таким образом, в неравновесных условиях наблюдать и изучать в чистом виде молекулярный перенос массы затруднительно, так как это требует искусственного поддержания' постоянства давления в системе. Сложность представляет экспериментальное определение величин Di, и конвективной скорости 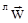 . Даже измерив в лабораторной системе отсчета потоки всех компонентов . Даже измерив в лабораторной системе отсчета потоки всех компонентов 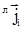 , и поля концентраций сi,
нельзя разрешить последнюю систему n уравнений, поскольку она содержит n+1 неизвестную величину (Di, , и поля концентраций сi,
нельзя разрешить последнюю систему n уравнений, поскольку она содержит n+1 неизвестную величину (Di, 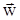 ). Поэтому обычно диффузионные потоки определяют в системе отсчета, скорость движения которой относительно лабораторной устанавливается достаточно просто. Как правило, используют среднемассовую или среднеобъемную системы отсчета. Система отсчета задается условием равенства нулю суммарного потока соответствующего признака (обозначим его zi ) в данной системе отсчета: ). Поэтому обычно диффузионные потоки определяют в системе отсчета, скорость движения которой относительно лабораторной устанавливается достаточно просто. Как правило, используют среднемассовую или среднеобъемную системы отсчета. Система отсчета задается условием равенства нулю суммарного потока соответствующего признака (обозначим его zi ) в данной системе отсчета:
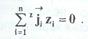
В среднемассовой системе отсчета zi=mi (мольная масса компонента), а в среднеобъемной zi=Vi (парциальный мольный объем компонента Vi м3/кмоль).
Используя последнее уравнение, можно выразить 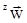 через Di, μi, cii=1,n и представить потоки в виде через Di, μi, cii=1,n и представить потоки в виде
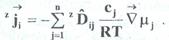
На практике удобнее использовать коэффициенты диффузии, связывающие потоки не с градиентами химических потенциалов, а с градиентами концентрации. Выражая химические потенциалы через мольные концентрации и используя соотношение
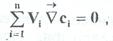
позволяющее сократить на единицу число независимых переменных, можно записать
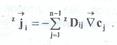
Таким образом, макроскопический поток каждого компонента в системе отсчета z зависит от градиентов концентраций всех компонентов, а коэффициенты пропорциональности носят название матрицы коэффициентов многокомпонентной диффузии и определяются как свойствами компонентов среды, так и выбором системы отсчета. Экспериментальное нахождение коэффициентов диффузии осуществляется, как правило, в замкнутом приборе. В этих условиях суммарный поток объема равен нулю, т.е. лабораторная система отсчета совпадает со среднеобъемной. Поэтому экспериментальные данные по коэффициентам диффузии обычно приводятся для среднеобъемной системы отсчета. В частном случае двухкомпонентной системы матрица 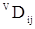 вырождается в единственный коэффициент бинарной (взаимной)
диффузии вырождается в единственный коэффициент бинарной (взаимной)
диффузии
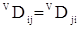
Это соотношение называется первым законом Фика.
2.1.3 Турбулентный механизм
Турбулентный перенос массы можно рассматривать по аналогии с молекулярным как следствие хаотического перемещениявихрей. Вводится коэффициент турбулентной диффузии
DT, зависящий как от свойств среды, так и от неоднородности скорости и удаленности от межфазной поверхности. При турбулентном движении, суммарный поток вещества относительно лабораторной системы, отсчета может быть записан
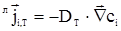
Поскольку объемы среды, участвующие в турбулентных пульсациях, значительно превышают молекулярные размеры, интенсивность турбулентного переноса массы может быть существенно выше молекулярного. Отношение коэффициентов турбулентной и молекулярной диффузии в пристенной области достигает DT/Di ~ 102 - 105.
2.2 Перенос энергии
Энергию системы можно подразделить на микроскопическую и макроскопическую. Микроскопическая, являющаяся мерой внутренней энергии самих молекул, их теплового движения и взаимодействия, называется внутренней энергией системы (U). Макроскопическая складывается из кинетической энергии (Ек), обусловленной конвективным движением среды, и потенциальной энергии системы в поле внешних сил (Еп). Таким образом, полную энергию системы, приходящуюся на единицу массы, можно представить как
Е' = U' + Е'п + Е'к , Дж/кг
Штрихами отмечены величины, отнесенные к единице массы.
Энергия может передаваться в форме теплоты или работы. Теплота
- форма передачи энергии на микроскопическом уровне, работа
- форма передачи энергии на макроскопическом уровне. Рассмотрим выражения для потока энергии за счет различных механизмов переноса.
2.2.1 Конвективный механизм
Поток энергии, переносимый конвективным механизмом в лабораторной системе отсчета, имеет вид
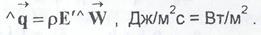
Это количество энергии, переносимое движущимся макроскопическим "объемом за единицу времени через единицу поверхности.
2.2.2 Молекулярный механизм
Молекулярным механизмом осуществляется перенос энергии на микроскопическом уровне, т.е. в форме тепла. Поток тепла за счет молекулярного механизма в условиях механического и концентрационного равновесия может быть представлен в виде
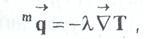
где λ
- коэффициент молекулярной теплопроводности,
Вт/м К. Это уравнение носит название закона Фурье.
В разреженных одноатомных газах допустимо пренебречь потенциальной энергией взаимодействия молекул и считать внутреннюю энергию равной средней кинетической энергии поступательного движения молекул pU'=3NkT/2V. В этом случае поток
тепла будет определяться потоком кинетической энергии молекул:
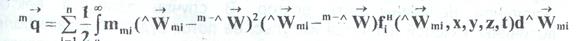
В плотных газах и конденсированных средах при определении внутренней энергии необходимо учесть энергию потенциального взаимодействия. В этомслучае поток тепла будет определяться поступательным переносом кинетической и потенциальной энергии молекул, а также и столкновительным переносом. Таким образом, коэффициент молекулярной теплопроводности складывается из трех составляющих:
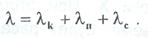
Этим объясняется тот факт, что в отличие от коэффициента молекулярной диффузии, уменьшающегося с увеличением плотности системы, коэффициент молекулярной теплопроводности возрастает с увеличением плотности, несмотря на затруднения в подвижности молекул. Величина коэффициента молекулярной теплопроводности составляет для газов λ
~
10-2 Вт/(м К), для жидкостей λ
~
10-1 Вт/(м К), для металлов λ~
102 Вт/(м К).
2.2.3 Турбулентный механизм
Турбулентный перенос энергии можно рассмотреть по аналогии с молекулярным, вводя коэффициент турбулентной теплопроводности
λТ:
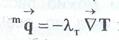
Как и коэффициент турбулентной диффузии, λТбудет определяться свойствами системы и режимом движения. Суммарный поток энергии в лабораторной системе отсчета может быть записан как
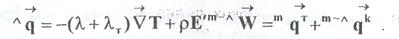
2.3 Перенос импульса
Врассмотренных выше явлениях переноса массы и энергии переносимые субстанции являлись скалярными величинами, поток скалярной величины есть вектор. В случае переноса векторной величины, каковой является импульс, ее поток будет обладать большей размерностью, а именно, представлять собой тензор второго ранга, для задания которого требуется уже 9 чисел (скаляр задается одним, вектор - тремя).
2.3.1 Конвективный перенос
В простейшем случае, когда среда движется с некоторой конвективной скоростью 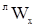 относительно лабораторной системы отсчета в направлении оси X. При этом импульс, или количество движения единичного объема, будет равен относительно лабораторной системы отсчета в направлении оси X. При этом импульс, или количество движения единичного объема, будет равен 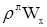 . Тогда количество движения . Тогда количество движения 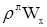 , переносимого за счет конвективного механизма в направлении оси X за единицу времени через единицу поверхности, будет равно , переносимого за счет конвективного механизма в направлении оси X за единицу времени через единицу поверхности, будет равно

Если представить теперь, что эта система или ее часть совершает дополнительно конвективное движение в направлении оси Y. Тогда импульс ρWx будет переноситься и в направлении оси Y. Количество движения, направленного вдоль оси X, переносимое за единицу времени через единичную поверхность в направлении оси Y, будет равно
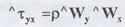
Аналогичным образом можно рассмотреть перенос импульса в лабораторной системе отсчета по всем направлениям, что даст 9 компонентов тензора конвективного потока импульса,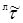 : :
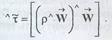
Запись в квадратных скобках является тензорным произведением двух векторов.
2.3.2 Молекулярный перенос
Рассмотрим движение среды в направлении оси X (рис. 1). При этом скорость 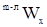 изменяется по величине в направлении оси Y. За счет теплового движения молекулы будут хаотически перемещаться во всех направлениях, в том числе и в направлении оси Y. Переходя из области с большими значениями скорости изменяется по величине в направлении оси Y. За счет теплового движения молекулы будут хаотически перемещаться во всех направлениях, в том числе и в направлении оси Y. Переходя из области с большими значениями скорости 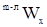 в область с меньшими значениями в область с меньшими значениями 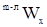 молекулы будут переносить импульс, ускоряющий движение в направлении оси X, и, наоборот, переход молекул из области с меньшими скоростями в область с большими скоростями будет замедлять движение быстрых слоев в направлении оси X. молекулы будут переносить импульс, ускоряющий движение в направлении оси X, и, наоборот, переход молекул из области с меньшими скоростями в область с большими скоростями будет замедлять движение быстрых слоев в направлении оси X.
Рис. 1
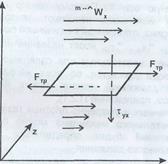
Это приведет к уменьшению неоднородности поля скорости 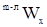 . .
Количество движения, направленного вдоль оси X (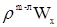 ), переносимое вдоль оси Y за единицу времени через единицу поверхности за счет молекулярного механизма, можно представить как ), переносимое вдоль оси Y за единицу времени через единицу поверхности за счет молекулярного механизма, можно представить как
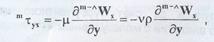
где μ [Па.С] и ν [м2/с] - коэффициенты динамической
и кинематической молекулярной вязкости
соответственно. Это уравнение носит название закона вязкости Ньютона. В случае если коэффициенты вязкости не зависят от величины производной д т-л
Wx/ д
y, т.е. зависимость 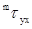 от д т-л
Wx/ д
y линейна, такие среды называются ньютоновскими.
Если же это условие не выполняется, то среды называются неньютоновскими.
К последним относятся полимеры, пасты, суспензии и ряд других, используемых в промышленности материалов. от д т-л
Wx/ д
y линейна, такие среды называются ньютоновскими.
Если же это условие не выполняется, то среды называются неньютоновскими.
К последним относятся полимеры, пасты, суспензии и ряд других, используемых в промышленности материалов.
Можно рассмотреть и иную трактовку закона вязкости Ньютона. Как известно из механики, в соответствии со вторым законом Ньютона изменение импульса за единицу времени есть сила. Перенос импульса между слоями среды, движущимися с различными скоростями, можно трактовать как проявление силы трения. С этой точки зрения 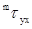 есть сила, действующая в направлении оси X на единичную площадку, перпендикулярную оси Y. Поэтому тензор потока импульса за счет молекулярного механизма называют тензором вязких напряжений (напряжение - сила, отнесенная к единичной поверхности). Диагональные элементы есть сила, действующая в направлении оси X на единичную площадку, перпендикулярную оси Y. Поэтому тензор потока импульса за счет молекулярного механизма называют тензором вязких напряжений (напряжение - сила, отнесенная к единичной поверхности). Диагональные элементы 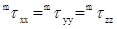 носят название нормальных напряжений, а носят название нормальных напряжений, а
недиагональные - касательных или сдвиговых. В общем случае, когда сжимаемая среда движется во всех направлениях (например, при вращательном движении), тензор вязких напряжений имеет более сложный вид.
2.3.3 Турбулентный перенос
Перенос импульса за счет турбулентного механизма может рассматриваться по аналогии с молекулярным:
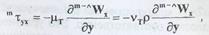
где где μт и νт - динамический
и кинематический коэффициенты турбулентной вязкости,
определяющиеся свойствами среды и режимом движения νт ≈ DТ.
Остальные 8 элементов тензора могут быть найдены аналогично.
Суммарный поток импульса в лабораторной системе отсчета можно записать как
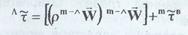
где 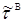 - тензор вязких напряжений,
элементы которого включают как молекулярный, так и турбулентный перенос импульса: - тензор вязких напряжений,
элементы которого включают как молекулярный, так и турбулентный перенос импульса:
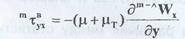 . .
В умеренно плотных газах коэффициенты молекулярного переноса с достаточной степенью точности могут рассчитываться по соотношениям кинетической теории на основе динамических характеристик молекул. Статистико-механическое описание переноса в плотных средах затруднено вследствие многочастичности межмолекулярного взаимодействия, что предопределяет использование на практике экспериментальных данных или полуэмпирических формул. Следует отметить, что при одновременном наличии в системе нескольких движущих сил, например, градиентов температуры и концентрации, возникают так называемые, "перекрестные эффекты", т.е. градиент температуры вызывает поток массы, а градиенты концентраций - поток тепла (явление термодиффузии). Вследствие относительной малости этих эффектов в практике инженерных расчетов типовых процессов и аппаратов химической технологии ими обычно пренебрегают. При наличии диффузионных потоков компонентов за скорость конвективного переноса энергии и импульса обычно принимается среднемассовая скорость 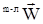 как наиболее просто поддающаяся определению. Для нахождения коэффициентов турбулентного переноса применяют, как правило, эмпирические и полуэмпирические корреляции. как наиболее просто поддающаяся определению. Для нахождения коэффициентов турбулентного переноса применяют, как правило, эмпирические и полуэмпирические корреляции.
Список использованной литературы
1. Дытнерский Ю.И. Процессы и аппараты химической технологии: Учебник для вузов. Изд. 3-е. В 2-х кн.: Часть 1. Теоретические основы процессов химической технологии. Гидромеханические и тепловые процессы и аппараты. М.: Химия, 2002. - 400с.: ил.
2. Разинов А.И. Явления переноса: Учеб. пособие / А.И. Разинов, Г.С. Дьяконов.: Казан. гос. технол. ун-т. - Казань, 2002. – 136 с.
3. Берд Р. Явления переноса: Пер. с англ. / Р. Берд, В. Стюарт Е. Лайфут. – М.: Химия, 1974. – 688 с.
|