Элементы биомеханики
План
1. Деформация и её виды
2. Основные характеристики деформации. Закон Гука для упругой деформации
3. Реологическое моделирование биотканей
4. Механические свойства биотканей
4.1Механические свойства костной ткани
4.2 Механические свойства ткани кровеносных сосудов
1. Деформация и её виды
деформация биоткань механический костный сосуд
Деформацией называется изменение взаимного расположения точек тела, которое сопровождается изменением его форм и размеров, обусловленное действием внешних сил на тело.
Виды деформации:
1. Упругая – полностью исчезает после прекращения действия внешних сил.
2. Пластическая (остаточная) – остается после прекращения действия внешних сил.
3. Упруго-пластическая – неполное исчезновение деформации.
4. Вязко-упругая – сочетание вязкого течения и эластичности.
В свою очередь упругие деформации бывают следующих видов:
а) деформация растяжения или сжатия происходит под действием сил, действующих в направлении оси тела:

2. Основные характеристики деформации
Деформация растяжения (сжатия) возникает в теле при действии силы, направленной вдоль его оси.

где l0
– исходный линейный размер тела.
Δl – удлинение тела
[l] - м
Деформация ε (относительное удлинение) определяется по формуле
 ε – безразмерная величина. ε – безразмерная величина.
Мерой сил, стремящихся вернуть атомы или ионы в первоначальное положение является механическое напряжение σ. При деформации растяжения напряжение σ можно определить отношением внешней силы к площади поперечного сечения тела:
 
Упругая деформация подчиняется закону Гука:

где Е – модуль нормальной упругости (модуль Юнга – это механическое
напряжение, которое возникает в материале при увеличении
первоначальной длины тела в два раза).

Если живые ткани мало деформируется, то в них целесообразно определять не модуль Юнга, а коэффициент жесткости. Жесткость характеризует способность физической среды сопротивляться образованию деформаций.
Представим экспериментальную кривую растяжения:

ОА – упругая деформация, подчиняющася закону Гука. Точка В – это предел упругости т.е. максимальное напряжение при котором ещё не имеет место деформация, остающаяся в теле после снятия напряжения. ВД – текучесть (напряжение, начиная с которого деформация возрастает без увеличения напряжения).
Реклама

Упругость, свойственную полимерам называют эластичностью.
Всякий обрзец, подвергнутый сжатию или растяжению вдоль его оси, деформируется так же и в перпендикулярном направлении.
Абсолютное значение отношения поперечной деформации  к продольной деформации к продольной деформации  образца называется коэффициентом поперечной деформации или коэффициентом Пуассона и обозначается: образца называется коэффициентом поперечной деформации или коэффициентом Пуассона и обозначается:
 (безразмерная величина) (безразмерная величина)
Для несжимаемых материалов (вязкотекучие пасты; резины) μ=0,5; для большинства металлов μ≈0,3.
Величина коэффициента Пуассона при растяжении и сжатии одна и та же. Таким образом, определяя коэффициент Пуассона можно судить о сжимаемости материала.
3. Реологическое моделирование биотканей
Реология – это наука о деформациях и текучести вещества.
Упругие и вязкие свойства тел легко моделируются.
Представим некоторые реологические модели.
а) Модель упругого тела – это упругая пружина.

Напряжение, возникающее в пружине, определяется законом Гука:

Если упругие свойства материала одинаковы во всех направлениях, то он называется изотропным, если эти свойства неодинаковы – анизотропным.
б) Модель вязкой жидкости - это жидкость, находящаяся в цилиндре с поршнем, неплотно прилегающим к его стенкам или: - это поршень с отверстиями, который движется в цилиндре с жидкостью.

Для этой модели характерна прямо пропорциональная зависимость между возникающим напряжением σ и скоростью деформации 

где η – коэффициент динамической вязкости.
в) Реологическая модель Максвелла представляет собой последовательно соединенные упругий и вязкий элементы.

Работа отдельных элементов зависит от скорости нагрузки общего элемента.
Для упругой деформации выполняется закон Гука:

Откуда

Скорость упругой деформации будет:
 (1) (1)
Для вязкой деформации:

тогда скорость вязкой деформации будет:
 (2) (2)
Общая скорость вязко-упругой деформации равна сумме скоростей упругой и вязкой деформаций.
 (3) (3)
Это есть дифференциальное уравнение модели Максвелла.
Вывод уравнения ползучести биоткани. Если к модели приложить силу, то пружина мгновенно удлиняется, а поршень движется с постоянной скоростью. Таким образом, на данный модели реализуется явление ползучести. Если F=const, то возникающее напряжение σ=const, т.е.  тогда из уравнения (3) получим: тогда из уравнения (3) получим:
 , отсюда , отсюда 


- уравнение ползучести биоткани.
Представим график ползучести:

Вывод уравнения релаксации напряжения в биотканях.
Реклама

Если модель Максвелла растянуть и закрепить, то пружина начнет сокращаться. Со временем будет происходить релаксация, т.е. уменьшение напряжения. Если ε=const, то  тогда уравнение (3) примет вид: тогда уравнение (3) примет вид:

Решаем дифференциальное уравнение:



где σ0
– начальное напряжение.

Потенцируем:

Откуда

- уравнение релаксации напряжения
Представим график релаксации напряжения.

г) Модель Фойгта представляет собой параллельно соединенные упругий и вязкий элементы. Эта модель характерна для полимеров.


4. Механические свойства биотканей
Под механическими свойствами биотканей понимают две разновидности:
Первая (активная) связана с процессами биологической подвижности: сокращение мышц, рост клеток, движение хромосом в клетках, их деления и т.д. Эти процессы обусловлены химическими процессами и энергетически обеспечиваются АТФ. Другая разновидность - пассивные механические свойства биосистем обусловленные внешними воздействиями.
Биологическая ткань – композиционный материал, образованный объемным сочетанием химически разнородных элементов и обладающий реологическими свойствами, отличающимися от свойств отдельных компонентов биоткани. Основу биотканей составляют коллаген, эластин и связующее вещество.
Механические воздействие на биоткани вызывают в них деформации и напряжения, появляется механическое движение, распространяются волны. Физиологическая реакция на эти факторы зависит от механических свойств биотканей. Знать, как меняются эти реакции и свойства тканей очень важно для профилактики, защиты организма, для применения искусственных тканей и органов, а также для понимания их физиологии и патологии.
В биомеханике все ткани человека подразделяются по плотности и типу пространственной структуры на твердые (кость, эмаль и дентин зубов), мягкие (мышцы, эпителий, эндотелий, соединительная ткань, паренхима), жидкие (кровь, лимфа, ликвор, слюна, сперма).
4.1 Механические свойства костной ткани
Костная ткань – основной материал опорно-двигательной системы. Прочность костной ткани зависит от химического состава, общей структуры, системы внутреннего армирования, количества и прочности компонентов, ориентации основных компонентов по отношению к продольной оси кости, возраста, плотности, индивидуальных условий роста и.т.д.
Компактная костная ткань представляет собой среду с пятью структурными уровнями.
Строение компактной костной ткани по Кнетсу.
| № уровня |
Состав уровня |
| 1 |
Биополимерная молекула трипоколлагена и неорагнические кристаллы (гидроксилопатит 3Са3
(РО4
)2
Са(ОН)2
) |
| 2 |
Микрофибриллы коллагена (образованы пятью молекулами трипоколлагена) |
| 3 |
Волокно (армирующий компонент) состоит из большого количества микрофибрилл и связанные с ними микрокристаллы. |
| 4 |
Ламеллы (наименьший самостоятельный конструкционный элемент) – это тонкие изогнутые пластинки, состоящие из коллагенно-минеральных веществ, объединённых при помощи вяжущего вещества. |
| 5 |
Остеоны – образуются вокруг кровеносных сосудов, включающихся в объем кости. Состоят из концентрически расположенных костных ламелл. |
Плотность костной ткани »2,4 г/см3
. Минеральные компоненты кости составляют »70 % массы кости, а белковые »20 %.
С увеличением возраста в костной ткани протекает ряд изменений. Изменяется химический состав и внутренняя структура, возникает множество вторичных остеонов, образующих новую внутреннюю конструктивную систему. При старении биологическая активность уменьшается, меняется степень минерализации, а также порядок расположения минеральных кристаллов и остенов, уменьшается количество связующего вещества, некоторая чать ткани исчезает и появляются поры.
Обновление костной ткани происходит дискретно – в определенных местах, на ограниченных участках. В течение жизни человека один и тот же участок кости обновляется неоднократно. К 35 годам процесс костеобразования замедляется. Костная масса у вегетарианцев больше, т.к. в растительной пище много солей. Курение и алкоголь уменьшают костную массу. Недостаточное содержание кальция уменьшает прочность костной ткани, что приводит к остеопорозу.
Волокна костной ткани деформируются преимущественно упругим образом, а матрица (остальная часть) – пластически и разрушаются хрупким образом.
Зависимость напряжения от деформации: s=f(e) компактной костной ткани имеет следующий вид (эта зависимость аналогична для твердого тела):
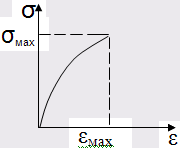
Напряжение σмах
при котором материал разрывается, называется пределом прочности.
Представим предел прочности костной ткани и её компонентов при сжатии и растяжении:
| Вид ткани |
Сжатие |
Растяжение |
| Прочность [МПа] |
Модуль Юнга [МПа] |
Прочность [МПа] |
Модуль Юнга [МПа] |
Компактная кость
Минеральный компонент
Белковый компонент
|
147
44
0,1
|
10200
6400
10
|
98
5
7
|
22 400
16600
20
|
Анализ таблицы: Минеральный и белковый компоненты по отдельности слабые, но в сочетании дают высокую прочность, сравнимую с прочностью металлов. В науке остаётся вопрос: почему имеется различные свойств на растяжение и сжатие.
Реологическая модель Зингера компактной костной ткани и средняя кривая ползучести.
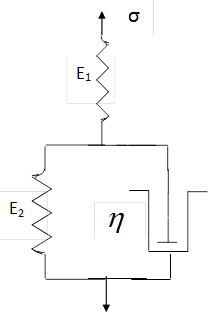
Дифференциальное уравнение, описывающее данную модель имеет вид:
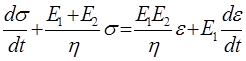
Средняя кривая деформации компактной костной ткани.
Максимальное растяжение, которое может выдержать костной материал составляет »0,01% что соответствует изменению длины кости »1 %.
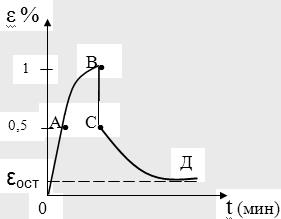
ОА – мгновенная деформация в продольном направлении (действует постоянная нагрузка мгновенно растягивается пружина 1) АВ – ползучесть (вытягивается поршень). Точка В – прекращение нагрузки. ВС – быстрая деформация (быстрое сжатие пружины 1) СД – обратная ползучесть (пружина 2 втягивает поршень в обратное положение) Точка Д – соответствует остаточной деформации (модель этого не учитывает).
При деформации костной ткани в ней возникает пьезоэлектрический эффект. Если вырезать из кости полоску, закрепить её с одной стороны и подвергнуть деформации изгиба, то на выпуклой стороне появляется "+" заряд, на вогнутой "-" заряд, т.е. появляется разность потенциалов.
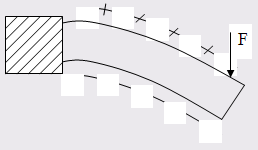
Есть основания считать, что генерация пьезоэлектричества имеем место при механических нагрузках костей в организме и возникающие электрические токи могут стимулировать новообразование или рассасывание костной ткани.
4.2 Механические свойства ткани кровеносных сосудов
Прочностные и деформационные свойства стенок кровеносных сосудов и изменение этих свойств (с возрастом) имеет большое значение для медицины.
Кровеносные сосуды состоять из трех концентрических слоёв:
внутренний – интима; средний – средняя сосудистая оболочка; наружный – внешняя сосудистая оболочка.
Механические свойства кровеносных сосудов обуславливаются, главным образом, свойствами средней сосудистой оболочки, состоящий из коллагена, эластина и гладких мышечных волокон. Представим допускаемые деформации этих элементов:
| Элемент |
Деформация ε в % |
Модуль Юнга (МПа) |
Эластин
Коллаген
Мышечное волокно (при сокращении)
Кровеносный сосуд
|
200-300
до 10
20
5-50
|
0,1 – 0,6
10 – 100
0,01 – 0,1
0,06 – 0,7
|
Следует отметить, что гладкие мышечные клетки могут менять свою длину (сокращаться) под действием нервных или химических стимуляторов. Гладкая мышца осуществляет активное поведение кровеносных сосудов, так как в результате её сокращения меняется диаметр кровеносного сосуда и механические свойства сосудистой стенки в целом.
Таким образом, достигается оптимальное распределение и регулирование кровяного потока.
Содержание трёх основных компонентов сосудистой ткани меняется для различных мест стенки. Отношение эластина к коллагену в сосудах ближе к сердцу равно 2:1, но оно убывает с удалением от него и в бедренной артерии оно равно 1:2. С удалением от сердца увеличивается содержание гладких мышечных волокон, и уже в артериоллах они становятся основной составляющей сосудистой ткани.
Установлено, что сосудистая ткань является практически несжимаемой. Кровеносные сосуды обладают криволинейной ортотропией (т.е. их механические свойства в радиальном, осевом и кольцевом направлениях существенно различны).
Механическое поведение сосудов усложняется ещё и тем, что в организме они находятся под влиянием окружающих тканей, растянуты в продольном направлении и их деформации в этом направлении ограничены. В сосудах наблюдаются значительные отклонения механических характеристик для отдельных индивидов от установленных средних значений.
Напряжение, возникающее при деформации в стенке кровеносного сосуда определяется уравнением Ламе.
Вывод уравнения Ламе.
Возьмём часть кровеносного сосуда длиной l и толщиной стенки h.
Представим стенки сосуда вдоль и поперёк:
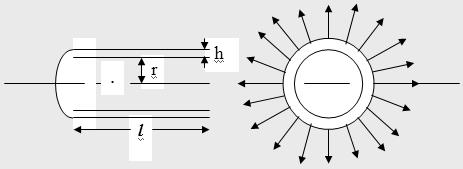
Две половины цилиндрического сосуда взаимодействуют между собой по сечениям стенок сосуда. Общая площадь сечения взаимодействия будет: 2hl, тогда сила взаимодействия двух половинок:
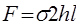
Эта сила уравновешивается силами давления крови изнутри:
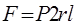
Таким образом, имеем: 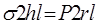 , откуда , откуда
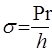 - уравнение Ламе - уравнение Ламе
Таким образом, напряжение, возникающее в стенках кровеносных сосудов зависит от величины давления крови, внутреннего радиуса и от толщины стенок сосуда.
|