ГОУ ВПО
Уфимский Государственный Авиационный Технический Университет
Кафедра вычислительной математики и кибернетики
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе
по теории вероятности
на тему:
Интервальный анализ дохода трамвайного парка в очередные сутки с применением доверительной вероятности
Исходные данные
– суточный доход трамвайного парка (млн. руб.):
12,56; 12,41; 12,52; 12,80; 12,98; 12,70.
Актуальные вопросы
: Каков практический максимум суточного дохода трамвайного парка? В каких пределах практически будет находиться доход трамвайного парка в очередные сутки?
Сформулировать эти вопросы на языке теории вероятностей и дать на них ответы.
Высказать предположение (с обоснованием) о законе распределения суточного дохода трамвайного парка, найти оценки и построить доверительные интервалы для математического ожидания и дисперсии суточного дохода.
Решение
Исходный материал – данные наблюдений над суточным доходом трамвайного парка (млн. руб):
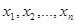
По условию известно:
х1
=12,56; х2
=12,41; х 3
=12,52; х 4
=12,80; х 5
=12,98;х 6
=12,70;n
=
6.
Под X
будем понимать случайную величину - доход, который получит трамвайный парк в будущий день. Данная величина дискретна, так как получить доход , например, 89,623 руб нельзя, существуют определенные стандарты. Но для решения этой задачи мы перейдем к идеализации и допустим, что π, е
и др.– все это возможные значения X
.
Тогда X
–
непрерывная случайная величина.
Исчерпывающей характеристикой случайной величины является закон распределения, который зависит от условий проведения опыта. В нашем случае, опыт – это завтрашняя работа трамвайного парка. Учесть все условия невозможно. Может быть на следующий день резко возрастут цены на проезд в автобусах, и люди предпочтут пользоваться трамваями. А может это будет выходной, и людям просто захочется остаться дома. Так как же проанализировать условия?
1. В трамвайном парке работает множество трамваев. Пусть число трамваев – s
.
2. Доход каждого трамвая завтра зависит от случая. Занумеруем трамваи:
3. Общий доход, который получат трамваи завтра:
X
=
 + +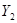 + + +…+ +…+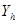
Т.е. X
можно представить в виде суммы большого числа слагаемых. В силу центральной предельной теоремы мы можем ожидать, что закон распределения X
близок к нормальному.
Реклама

Пусть с
– доход, который будет получен трамвайным парком в очередные сутки.
Событие  является желательным событием. Найдем его вероятность. является желательным событием. Найдем его вероятность.
Нам известно, что вероятность того, что X
не превысит величины с
, согласно нормальному закону распределения, зависит от с
следующим образом:
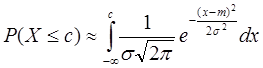
где m
=M
(
X
)
– математическое ожидание X
,  =D
(Х)
– дисперсия, а =D
(Х)
– дисперсия, а  - стандартное отклонение X
. Эти константы можно оценить, используя формулы: - стандартное отклонение X
. Эти константы можно оценить, используя формулы:
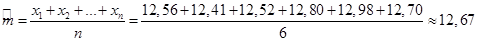 (млн.руб) (млн.руб)
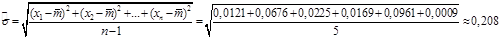
Следует отметить, что оценки  и и 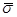 зависят от данных наблюдений, которые зависят от случая, когда m
и зависят от данных наблюдений, которые зависят от случая, когда m
и  от случая не зависят. от случая не зависят.
Зная оценки  и и 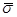 , можно приближенно ответить на вопрос: «Какой доход (величина с
) получит трамвайный парк в очередной день, т.е. чтобы вероятность события , можно приближенно ответить на вопрос: «Какой доход (величина с
) получит трамвайный парк в очередной день, т.е. чтобы вероятность события 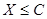 была достаточно велика, например, равна была достаточно велика, например, равна  ?» Величину с
найдем из уравнения: ?» Величину с
найдем из уравнения:
 . .
Сделаем подстановку 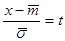 , тогда: , тогда:
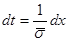 , , 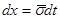 ; при ; при 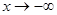 , , 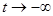 ; при ; при 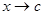 , ,  . .
Получим уравнение:
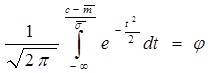 . .
Выберем вероятность  равной 0,95 (т.е. чтобы получить практический максимум суточного дохода трамвайного парка) и решим уравнение с помощью таблицы значений нормальной функции распределения. Получим: равной 0,95 (т.е. чтобы получить практический максимум суточного дохода трамвайного парка) и решим уравнение с помощью таблицы значений нормальной функции распределения. Получим:
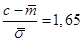 ; ; 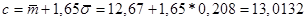 (млн.руб) (млн.руб)
Таким образом, мы получили, что в очередные сутки практическим максимумом суточного дохода трамвайного парка будет являться 13,0132 млн. руб. Ответим на вопрос: «В каких пределах практически будет находиться доход трамвайного парка в очередные сутки?»
Общая формула:
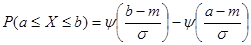 , где , где 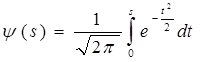
функция Лапласа, а a
и b
– концевые точки.
Пусть a
и b
расположены симметрично относительно m
: a
=m
-
s
* ; b
=m
+
s
* ; b
=m
+
s
* . Тогда: . Тогда:
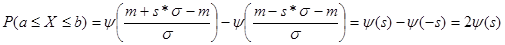 , ,
т.к. функция нечетная. По таблицам найдем, что если s
=1,96, то 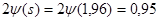 . .
Таким образом, нам известно, что с вероятностью 0,95 Х
будет находиться в пределах 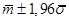 . .
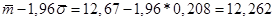

Т.е. доход трамвайного парка будет практически находиться в пределах от 12,262 до 13,077 млн. руб.
Как уже отмечалось, оценки  и и 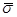 зависят от случая, в то время как m
и зависят от случая, в то время как m
и  от случая не зависят. О местоположении этих констант на числовой оси дают представление доверительные интервалы, т.е. такие интервалы, для которых до проведения наблюдений известна вероятность того, что они в итоге наблюдений накроют константу. от случая не зависят. О местоположении этих констант на числовой оси дают представление доверительные интервалы, т.е. такие интервалы, для которых до проведения наблюдений известна вероятность того, что они в итоге наблюдений накроют константу.
В нашем случае концевые точки доверительного интервала для m
находятся по формулам:  , ,  , где , где
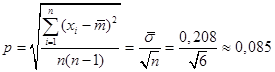 , ,
а коэффициент 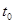 зависит от устраивающей нас вероятности накрывания интервалом константы m
: зависит от устраивающей нас вероятности накрывания интервалом константы m
:
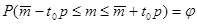 . .
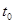 можно найти из таблицы: при можно найти из таблицы: при  =0,95 и k
=5(где k
=(n
-1) – число степеней свободы) =0,95 и k
=5(где k
=(n
-1) – число степеней свободы) 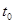 =2,57. =2,57.
Реклама

Доверительный интервал для m
:
(12,45; 12,89) с вероятностью покрытия 0,95.
Концевые точки доверительного интервала для  находятся по формулам: находятся по формулам:
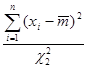 , , 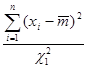 . .
Вероятность того, что такой интервал накроет  , обозначим: , обозначим:

Она зависит от чисел  и и 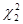 . Выберем вероятность накрывания дисперсии, например, . Выберем вероятность накрывания дисперсии, например, 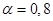 и воспользуемся таблицами для вычисления и воспользуемся таблицами для вычисления  и и 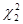 . Для этого вычислим: . Для этого вычислим:
(1-α)/2=0,1 – погрешность слева; (1+α)/2=0,6 – погрешность справа, k
=n
-1=5 – число степеней свободы.
Значит  =1,610; =1,610; 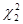 =9,24. =9,24.
Интервал: (0,113; 0,646) – доверительный интервал для дисперсии с вероятностью покрытия 0,8.
В продолжение задания 1. Существенно ли изменились условия проведения опыта, если очередная серия наблюдений привела к следующим данным? Поставить этот вопрос на языке теории вероятностей и получить ответ.
11,84; 12,50; 11,70; 11,72; 11,81; 11,78; 11,70.
Решение
Новые суточные доходы трамвайного парка: 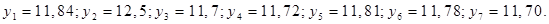 п2
=7. п2
=7.
Перед нами стоит вопрос: «Существенно ли изменились условия проведения опыта, если очередная серия наблюдений привела к следующим данным, т.е. изменились ли математическое ожидание и дисперсия в новой серии наблюдений?»
Предполагается, что над случайной величиной X
проведены 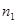 независимых испытаний, а над Y
- независимых испытаний, а над Y
-
 независимых испытаний. независимых испытаний.
Пусть случайные величины X
и Y
независимы и каждая подчиняется одному и тому же нормальному закону распределения.
Нормальный закон распределения определяется функцией распределения или плотностью вероятностей, которые зависят только от двух констант - m
и  . Пусть дисперсии X
и Y
одинаковы. Тогда если математические ожидания X
и Y
одинаковы, то условия проведения опыта полностью совпадают. . Пусть дисперсии X
и Y
одинаковы. Тогда если математические ожидания X
и Y
одинаковы, то условия проведения опыта полностью совпадают.
Найдем оценки 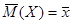 и и  : :
 (млн.руб); (млн.руб);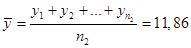 (млн.руб). (млн.руб).
Если действовать согласно интуиции, то можно прийти к такому выводу: если в результате наблюдений случайная величина  примет значение, сильно отличающееся от нуля, то следует, что математические ожидания X
и Y
неодинаковы. Но как понять, что значит «сильно отличаться от нуля», а что – «не сильно»? Для этого нам необходимо найти границу. примет значение, сильно отличающееся от нуля, то следует, что математические ожидания X
и Y
неодинаковы. Но как понять, что значит «сильно отличаться от нуля», а что – «не сильно»? Для этого нам необходимо найти границу.
Рассмотрим случайную величину:
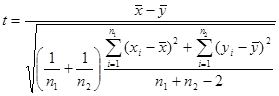
Возьмем какое-либо число 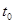 , которое назовем пороговым числом, т.е. границей между значениями t
, достаточно сильно отличающимися от 0 и не сильно. Тогда: , которое назовем пороговым числом, т.е. границей между значениями t
, достаточно сильно отличающимися от 0 и не сильно. Тогда:
1) если |t
|>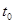 , то проверяемая гипотеза отвергается; , то проверяемая гипотеза отвергается;
2) если |t
|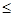 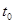 , то отвергать гипотезу не будем. , то отвергать гипотезу не будем.
Но данные наблюдений всегда зависят от случая, поэтому мы можем отвергнуть справедливую гипотезу и допустить ошибку. Выберем устраивающую нас достаточно малую вероятность такой ошибки β.
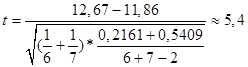 . .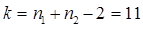 . .
Пусть β=0,05. Нужно использовать таблицу для погрешностей, но т.к. ее нет, найдем φ=1- β=0,95.
По таблицам Стьюдента 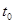 =2,20. =2,20.
Сравним t
и 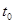 : | 5,4 |>2,20 : | 5,4 |>2,20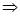 гипотеза отвергается, и M
(
X
) гипотеза отвергается, и M
(
X
)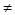 M
(
Y
)
.
M
(
Y
)
.
Таким образом, с вероятностью ошибки 0,05 можно считать, что условия проведения опыта существенно изменились.
Задание 3
Условие
В продолжение задания 1. Можно ли утверждать, что указанные в задании 1 данные говорят о существенном изменении условий проведения опыта, если известно, что для проведения этих наблюдений математическое ожидание рассматривающейся случайной величины составляло 12,42?
Решение
У нас имеется случайная величина X
, закон распределения которой близок к нормальному закону. Нам нужно ответить на вопрос: «Справедливо ли, что математическое ожидание X
равно заданной константе m
,
где m
=
12,42?» Если нет, то условия проведения нашего опыта существенно изменились. Предполагается, что над случайной величиной проведены n
независимых испытаний.
Введем оценку математического ожидания для X
:

Интуитивно мы можем сделать вывод по такому правилу: если после наблюдений случайная величина 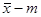 примет значение, сильно отличающееся от нуля, то условия проведения опыта существенно изменились. Но, опять же, нужно найти данную границу. Рассмотрим случайную величину: примет значение, сильно отличающееся от нуля, то условия проведения опыта существенно изменились. Но, опять же, нужно найти данную границу. Рассмотрим случайную величину:
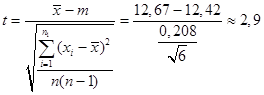 . .
Если |t
|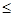 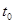 , то условия проведения опыта существенно не изменились, если |t
|> , то условия проведения опыта существенно не изменились, если |t
|>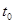 , то условия изменились. Но, как и в задаче 2, это может привести к ошибке. Выберем малую вероятность такой ошибки: β=0,05. , то условия изменились. Но, как и в задаче 2, это может привести к ошибке. Выберем малую вероятность такой ошибки: β=0,05.
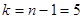 . .
С помощью таблицы Стьюдента найдем 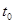 : : 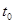 =2,57. =2,57.
Сравним t
и 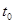 : | 2,9 |>2,57 : | 2,9 |>2,57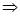 М(Х) М(Х) 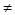 m
.
m
.
Таким образом, условия проведения опыта существенно изменились с вероятностью ошибки 0,05.
математическое ожидание дисперсия
1.Рудерман С.Ю. Законы в мире случая. Том 1. Уфа, 2005
2.Рудерман С.Ю. Законы в мире случая. Том 2. Уфа: РИО БашГУ, 2005
3.Вентцель Е.С. Теория вероятностей. М.: Высшая школа, 1999
4.Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ-ДАНА, 2002
|