Содержание
Введение
1. Теорема о неподвижной точке
2.1 Неподвижная точка и отношения эквивалентности
2.2 Системный трюк: ещё одно доказательство
2.3 Несколько замечаний
3. Практическая часть
Заключение
Список литературы
Введение
Рекурсивные функции (от позднелатинского recursio - возвращение), название, закрепившееся за одним из наиболее распространённых вариантов уточнения общего понятия арифметического алгоритма, т.е. такого алгоритма, допустимые исходные данные которого представляют собой системы натуральных чисел, а возможные результаты применения являются натуральными числами. Рекурсивные функции были введены в 30-х гг. 20 в. С.К. Клини, в свою очередь основывавшимся на исследованиях К. Гёделя, Ж. Эрбрана и др. математиков.
Теорема (Клини) о неподвижной точке является основным инструментом исследования в теории рекурсивных функций. Это глубокий результат в том смысле, что он даёт изящный и экономичный метод обращения с конструкциями, что в ином случае потребовало бы долгих и сложных рассуждений.
Эта теорема может быть приведена в нескольких формах и может рассматриваться с нескольких точек зрения. В определённом смысле теорема суммирует некоторый класс диагональных методов, включая метод, используемый для построения рекурсивно-перечислимых, но не рекурсивных множеств. С другой стороны, эта теорема устанавливает некоторый результат о неподвижной точке и, подобно теоремам о неподвижной точке из математического анализа, может быть использована для доказательства существования многих неявно заданных функций.
1. ТЕОРЕМА О НЕПОДВИЖНОЙ ТОЧКЕ
1.1 Неподвижная точка и отношения эквивалентности
Теорема 1. Пусть U — главная вычислимая универсальная функция для класса вычислимых функций одного аргумента, a h — произвольная всюду определённая вычислимая функция одного аргумента. Тогда существует такое число n, что Un = Uh(n), то есть n и h(n) — номера одной функции.
Другими словами, нельзя найти алгоритма, преобразующего программы, который бы по каждой программе давал другую (не эквивалентную ей). Эту теорему называют теоремой Клини о неподвижной точке или теоремой о рекурсии.
Рассмотрим произвольное отношение эквивалентности (которое мы будем обозначать x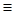 у) на множестве натуральных чисел. Мы покажем, что следующие два свойства этого отношения не могут выполняться одновременно: у) на множестве натуральных чисел. Мы покажем, что следующие два свойства этого отношения не могут выполняться одновременно:
Реклама

Для всякой вычислимой функции f существует всюду определённая вычислимая функция g, являющаяся её  -продолжением (это означает, что если f(x) определено при некотором x, то g(х) -продолжением (это означает, что если f(x) определено при некотором x, то g(х)  f(x)). f(x)).
Существует всюду определённая вычислимая функция h, не имеющая 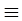 -неподвижной точки. -неподвижной точки.
Если x 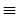 у — отношение равенства (x = у), то второе свойство выполнено (положим, например, h(n) = n + 1), поэтому не выполнено первое. Теорема о неподвижной точке получится, если x = у понимать как Ux = Uy (x и y — номера одной и той же функции). В этом случае выполнено первое свойство, как мы сейчас убедимся, и потому не выполнено второе. у — отношение равенства (x = у), то второе свойство выполнено (положим, например, h(n) = n + 1), поэтому не выполнено первое. Теорема о неподвижной точке получится, если x = у понимать как Ux = Uy (x и y — номера одной и той же функции). В этом случае выполнено первое свойство, как мы сейчас убедимся, и потому не выполнено второе.
Почему выполнено первое свойство? Пусть f — произвольная вычислимая функция одного аргумента. Рассмотрим функцию V(n, x) = U(f(n), x). Поскольку U является главной универсальной функцией, найдётся всюду определённая функция s, для которой V(n, x) = U(s(n),x) при всех n и х. Эта функция и будет искомым 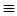 -продолжением. В самом деле, если f(n) определено, то s(n) будет другим номером той же функции, что и f(n). (Отметим, что если f(n) не определено, то s(n) будет одним из номеров нигде не определённой функции.) -продолжением. В самом деле, если f(n) определено, то s(n) будет другим номером той же функции, что и f(n). (Отметим, что если f(n) не определено, то s(n) будет одним из номеров нигде не определённой функции.)
Для завершения доказательства теоремы о неподвижной точке осталось проверить, что указанные два свойства отношения эквивалентности несовместны. Возьмём вычислимую функцию f, от которой никакая вычислимая функция не может отличаться всюду (например, диагональную функцию х → U(x, х) для некоторой вычислимой универсальной функции U). По предположению существует всюду определённое вычислимое 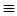 -продолжение g функции f. Рассмотрим функцию t(x) = h(g(x)), где h — вычислимая всюду определённая функция, не имеющая -продолжение g функции f. Рассмотрим функцию t(x) = h(g(x)), где h — вычислимая всюду определённая функция, не имеющая 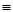 -неподвижной точки. Тогда t будет всюду отличаться от f. В самом деле, если f(x) определено, то f(x) -неподвижной точки. Тогда t будет всюду отличаться от f. В самом деле, если f(x) определено, то f(x)  g(х) g(х) 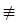 h(g(x)) = t(x), и потому f(x) h(g(x)) = t(x), и потому f(x) 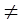 t(x). Если же f(x) не определено, то этот факт сам по себе уже отличает f(x) и t(x). t(x). Если же f(x) не определено, то этот факт сам по себе уже отличает f(x) и t(x).
Теорему о неподвижной точке можно переформулировать и так:
Теорема 2. Пусть U(n, x) — главная вычислимая универсальная функция для класса вычислимых функций одного аргумента. Пусть V(n, x) — произвольная вычислимая функция. Тогда функции U и V совпадают на некотором сечении: найдётся такое р, что Up = Vp, то есть U(p, n) = V(p, n) для любого n.
Так как функция U является главной, найдём такую всюду определённую вычислимую функцию h, что V(n,x) = U(h(n),x) при всех n и x. Осталось взять в качестве р неподвижную точку функции h.
Реклама

(Пример следствия из этой теоремы: как бы ни старались разработчики, для любых двух версий компилятора существует программа, которая одинаково работает в обеих версиях — например, зацикливается и там, и там. Впрочем, это всё же не наверняка, а только если компилятор задаёт главную универсальную функцию — но надо очень постараться, чтобы это было не так!)
Поучительно развернуть цепочку приведённых рассуждений и проследить, как строится неподвижная точка. Для наглядности вместо U(n,x) мы будем писать [n](x) и читать это «результат применения программы n к входу x»;
Рассуждение начинается с рассмотрения «диагональной» функции U(x,x), которую теперь можно записать как [x](x) (результат применения программы x к себе). Далее мы строим её всюду определённое  -продолжение. Это делается так. Выражение [[x] (x)] (у) вычислимо зависит от двух аргументов. Мы вспоминаем, что U есть главная универсальная функция, и находим такую программу g, что [[g](x)](y) = [[x] (x)] (у) при всех x и у. При этом [g](x) определено для всех x. Пусть мы хотим найти неподвижную точку программы h. Мы рассматриваем композицию [h]([g](x)). Это выражение вычислимо зависит от x, и потому существует программа t, для которой [t](x) = [h](g(x)) при всех x. Эта программа применима ко всем x, поскольку таковы h и g. Теперь неподвижной точкой будет [g](t). Чтобы убедиться в этом, мы должны проверить, что [[g](t)](x) = [h ([g](t))] (x) для всех x. В самом деле, по свойству g имеем [[g](t)](x) = [[t](t)](x). Вспоминая определение t, это выражение можно переписать как [[h] ([g](t))] (x) — что как раз и требовалось. -продолжение. Это делается так. Выражение [[x] (x)] (у) вычислимо зависит от двух аргументов. Мы вспоминаем, что U есть главная универсальная функция, и находим такую программу g, что [[g](x)](y) = [[x] (x)] (у) при всех x и у. При этом [g](x) определено для всех x. Пусть мы хотим найти неподвижную точку программы h. Мы рассматриваем композицию [h]([g](x)). Это выражение вычислимо зависит от x, и потому существует программа t, для которой [t](x) = [h](g(x)) при всех x. Эта программа применима ко всем x, поскольку таковы h и g. Теперь неподвижной точкой будет [g](t). Чтобы убедиться в этом, мы должны проверить, что [[g](t)](x) = [h ([g](t))] (x) для всех x. В самом деле, по свойству g имеем [[g](t)](x) = [[t](t)](x). Вспоминая определение t, это выражение можно переписать как [[h] ([g](t))] (x) — что как раз и требовалось.
1.2 Системный трюк: ещё одно доказательство
Если попросить любителей разных языков программирования написать на своём любимом языке по возможности короткую программу, которая бы печатала свой исходный текст, то чемпионом, скорее всего, окажется короткая программа на бейсике:
10 LIST
Дело в том, что в бейсике есть команда LIST, которая печатает текст программы и может быть запущена изнутри программы.
Прежде всего, это хорошая шутка. Но можно отнестись к ней неожиданно серьёзно и использовать эту идею в ещё одном доказательстве теоремы о неподвижной точке (точнее, в ещё одном варианте того же доказательства).
Прежде всего заметим, что теорему достаточно доказать для какой-то одной главной нумерации. В самом деле, пусть для какой-то другой главной нумерации существует функция без неподвижной точки, то есть имеется способ преобразовывать программы в заведомо неэквивалентные. Тогда с помощью трансляции туда и обратно такой способ
можно найти и для первой нумерации (для которой мы теорему считаем доказанной).
Теперь рассмотрим язык программирования, в котором помимо обычных возможностей есть встроенная процедура
GetProgramText (var s: string)
Эта процедура помещает текст исходной программы в строку s. Несмотря на некоторую необычность этой идеи, вполне можно представить себе интерпретатор этого языка — и интерпретация этой процедуры не представляет труда, так как интерпретатору, разумеется, доступен текст программы. Сделаем ещё один шаг и представим себе, что в этом языке есть также процедура
ExecuteProgram(s: string)
Эта процедура передаёт управление программе, текст которой находится в строке s, считая входом этой программы вход исходной программы (как сказал бы настоящий программист, «передавая программе s дескриптор входного потока»). И в этом случае понятно, как должен действовать интерпретатор языка: он должен рекурсивно вызвать себя на содержимом строки s и входных данных.
Наш обогащенный язык программирования, разумеется, допускает трансляцию с него в обычные языки (поскольку имеет интерпретатор) и наоборот (так как можно не пользоваться новыми конструкциями). Поэтому задаваемая им нумерация вычислимых функций является главной. Пусть h — всюду определённая вычислимая функция, у которой мы хотим найти неподвижную точку. Запишем вычисляющий её алгоритм в виде процедуры нашего языка:
function Compute_h (x: string) : string; begin
end;
(При этом нам даже не нужны новые возможности.) Теперь напишем программу, являющуюся неподвижной точкой функции А:
program fixed_point; var s: string;
function Compute_h (x:string) : string; begin
end; begin
GetProgramText (s);
s := Compute_h (s);
ExecuteProgram (s); end.
Выполнение этой программы сразу же сводится к выполнению программы, получающейся применением к ней функции А, так что она будет неподвижной точкой по построению.
Мы только что объяснили, как с помощью языка с дополнительной процедурой «получить текст программы» можно доказать теорему о неподвижной точке. Но можно рассуждать и в обратном направлении и объяснить, почему применение теоремы о неподвижной точке заменяет такую дополнительную процедуру.
В самом деле, пусть мы имеем программу р, в которой есть строка GetProgramText (s). Заменим эту строку на оператор присваивания s : = t, где t — некоторая строковая константа. Получится новая программа, зависящая от t. Назовём её p(t). Согласно теореме о неподвижной точке, существует такое значение t, при котором программы t и p{t) эквивалентны. При этом t выполнение программы t эквивалентно выполнению её текста, в котором в момент вызова процедуры GetProgramText(s) в строку s помещается текст программы t — чего мы и хотели.
Теперь становится понятнее, почему теорема о неподвижной точке называется ещё теоремой о рекурсии. В самом деле, рекурсия состоит в том, что мы вызываем программу изнутри её самой. Здесь происходит даже больше: мы не только имеем право вызвать программу, но и можем получить доступ к её тексту! Обычный вызов действительно является частным случаем доступа к тексту, так как мы можем вызвать процедуру интерпретации на этом тексте. (Конечно, при этом нам понадобится включить в состав программы текст интерпретатора нашего языка программирования, записанный на этом языке.)
1.3 Несколько замечаний
Бесконечное множество неподвижных точек
Теорема 4. (о неподвижной точке) утверждает существование хотя бы одной неподвижной точки. Легко понять, что на самом деле их бесконечно много: в обозначениях этой теоремы существует бесконечно много чисел n, при которых U = U = U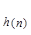 . .
Это можно объяснить, например, так: если бы неподвижных точек было бы конечное число, то можно было бы изменить функцию h в этих точках так, чтобы неподвижных точек не осталось. Недостаток этого рассуждения в том, что оно не позволяет эффективно перечислять неподвижные точки (указать для данной функции h бесконечное перечислимое множество, состоящее из её неподвижных точек).
Неподвижная точка с параметром
Если преобразователь программ вычислимо зависит от некоторого параметра, то и неподвижную точку можно выбрать вычислимо зависящей от этого параметра. Точный смысл этого утверждения таков:
Теорема 5. Пусть U — главная универсальная функция для класса вычислимых функций одного аргумента, а h — всюду определённая вычислимая функция двух аргументов. Тогда существует всюду определённая вычислимая функция n одного аргумента, которая по любому р указывает неподвижную точку для функции h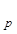 , так что , так что 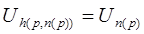 , или, другими словами, U(h(p,n(p)),x) = U(n(p),x) при всех р и х (как обычно, обе части могут быть одновременно не определены). , или, другими словами, U(h(p,n(p)),x) = U(n(p),x) при всех р и х (как обычно, обе части могут быть одновременно не определены).
Мы видели, что неподвижная точка строится конструктивно. Поэтому если мы ищем неподвижную точку для функции h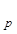 , вычислимо зависящей от параметра р, то и результат нашего построения будет вычислимо зависеть от параметра р. , вычислимо зависящей от параметра р, то и результат нашего построения будет вычислимо зависеть от параметра р.
Конечно, можно было бы формально записать рассуждение, реализующее этот план, но оно довольно громоздко (и вряд ли от этого доказательство станет более понятным).
В этой теореме мы предполагали, что семейство функций h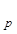 состоит из всюду определённых функций. На самом деле это не обязательно: для произвольного вычислимого семейства вычислимых функций h состоит из всюду определённых функций. На самом деле это не обязательно: для произвольного вычислимого семейства вычислимых функций h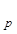 (другими словами, для произвольной вычислимой функции h двух аргументов) существует всюду определённая вычислимая функция n одного аргумента с таким свойством: при каждом р либо функция h (другими словами, для произвольной вычислимой функции h двух аргументов) существует всюду определённая вычислимая функция n одного аргумента с таким свойством: при каждом р либо функция h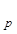 не определена в точке n(р), либо n(р) является неподвижной точкой функции h не определена в точке n(р), либо n(р) является неподвижной точкой функции h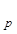 . .
Неподвижная точка для перечислимых множеств
Всё сказанное почти без изменений переносится на главные нумерации перечислимых множеств (если W — главное универсальное перечислимое множество, то всякая вычислимая всюду определённая функция h имеет неподвижную точку n, для которой 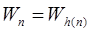 ). ).
В самом деле, если W — главное универсальное перечислимое множество, то к отношению эквивалентности
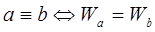
применимо рассуждение из доказательства теоремы 4, поскольку любая вычислимая функция f имеет вычислимое всюду определённое 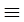 -продолжение. -продолжение.
Проверим это. Для этого рассмотрим множество
V = {(р,х) / f(р) определено и (f(р), x) 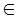 W}. W}.
Легко понять, что это множество перечислимо (например, оно есть область определения вычислимой функции (р, x) → w(f(р),x), где w — вычислимая функция с областью определения W). При этом  ), если f(р) определено, и ), если f(р) определено, и 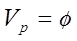 , если f(р) не определено. Вспоминая, что W является главным универсальным множеством, мы находим всюду определённую функцию s, для которой , если f(р) не определено. Вспоминая, что W является главным универсальным множеством, мы находим всюду определённую функцию s, для которой  . Таким образом, . Таким образом, 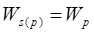 ) для тех р, для которых f(р) определено, что и требовалось. ) для тех р, для которых f(р) определено, что и требовалось.
3. Практическая часть
Классическим примером применения теоремы о неподвижной точке является такое её следствие: существует программа, печатающая (на любом входе) свой собственный текст. В самом деле, если бы такой программы не было, то преобразование
р → (программа, которая на любом входе печатает р) не имело бы неподвижной точки.
Формально говоря, это следствие можно выразить так:
Теорема 3. Пусть U(n,х) — главная вычислимая универсальная функция для класса всех вычислимых функций одного аргумента. Тогда существует такое число р, что U(p, х) = р для любого х.
В программистских терминах: пусть U(p, x) — результат применения паскаль-программы р к стандартному входу х. (Уточнения: (1) мы отождествляем числа и последовательности байтов; (2) если программа не завершает работы, мы считаем, что результат не определён, даже если на стандартный выход что-то послано.) Ясно, что функция U будет главной универсальной функцией. Поэтому к ней можно применить сформулированное только что утверждение; получим программу р, которая при любом входе на выходе даёт р.
Ясно, что это рассуждение применимо для любого языка программирования; то, что мы упомянули язык паскаль, роли не играет.
Выпишем явно программу на паскале, печатающую свой текст. (Это — хорошая задача для любителей программирования.) Для начала напишем неформальную инструкцию на русском языке: напечатать два раза, второй раз в кавычках, такой текст: «напечатать два раза, второй раз в кавычках, такой текст:»
Чтобы написать что-то похожее на паскале, понадобятся некоторые дополнительные хитрости, но идея ясна: строковая константа используется два раза. Вотодинизвозможныхвариантов:
program selfprint;
var a:array[1..100]of string;i:integer; begin
a[1]:=’ program selfprint ;';
a[2]:=’ var a:array[1..100]of string;i:integer;’;
a[3]:=’begin’;
a[4]:=’for i:=1 to 3 do writeln(a[i]);’;
a[5]:=’ ’for i:=1 to 11 do begin’;
a[6]:=’ write(chr(97),chr(91),i);';
a[7]:=’write(chr(93),chr(58),chr(61));';
a[8]:=’writeln(chr(39),a[i],chr(39),chr(59));';
a[9]:= 'end;';
a[10]:='for i:=4 to 11 do writeln(a[i]);';
a[11]:='end.';
for i:=1 to 3 do writeln(a[i]); for i:=1 to 11 do begin write(chr(97),chr(91),i); write(chr(93),chr(58),chr(61)); writeln(chr(39),a[i],chr(39),chr(59)) ; end;
for i:=4 to 11 do writeln(a[i]); end.
Читая эту программу, полезно иметь в виду соответствие между символами и их кодами:
а [ ] : = ' ;
97 91 93 58 61 39 59
Видно, что эту программу легко модифицировать, чтобы она, скажем, печатала свой текст задом наперёд — вместо команд write и writeln, печатающих текст, надо написать команды, записывающие его в файл (или в массив байтов), а потом команды, печатающие этот файл или массив в обратном порядке.
Сделав ещё один шаг, можно получить и доказательство теоремы о неподвижной точке. Пусть h — некоторое преобразование паскаль-программ, у которого мы хотим найти неподвижную точку. Тогда напишем программу наподобие только что приведённой, которая будет записывать свой текст в строку р, затем применять h к р, получая некоторую другую строку q, а затем запускать интерпретатор Паскаля на строке q (используя в качестве входа программы q вход исходной программы). Конечно, эта программа уже не будет такой короткой, так как будет включать в себя (и даже два раза — первый раз просто так, а второй раз в кавычках) интерпретатор паскаля, написанный на паскале.
Ясно, что такая программа будет неподвижной точкой преобразования h, так как её выполнение начинается ровно с того, что вычисляется значение функции h на её тексте, после чего это значение воспринимается как программа и применяется к входу.
клини неподвижный точка программирование
Заключение
В курсовой работе были рассмотрены следующие вопросы:
· Дана теорема о неподвижной точке и её доказательство.
· Рассмотрен способ доказательства теоремы с помощью языка с дополнительной процедурой «получить текст программы»
· Приведён классический пример применения теоремы о неподвижной точке.
В практической части было показано, как с помощью теоремы о неподвижной точке можно показать, что в любом языке программирования обязательно найдётся программа, которая не получает ничего на вход, но печатает свой текст. Также с помощью теоремы можно доказать алгоритмическую невычислимость (т.к. если мы узнаем, что у какой-то функции нет неподвижной точки, то она невычислима).
Список литературы
1. Н.К. Верещагин, А. Шень. Лекции по математической логике и теории алгоритмов. Часть3. Вычислимые функции. Москва, 1999 МЦНМО.
2. Х. Роджерс. Теория вычислимых функций и эффективная вычислимость. Издательство «МИР» Москва, 1972г.
3. http://wikipedia.ru
|