Расчетно-графическая работа
по теории алгоритмов
На тему
«Решение задачи коммивояжера методом ветвей и границ»
План
1. Вступление
2. Постановка задачи
3. Математическая модель задачи коммивояжера
4. Алгоритм решения
5. Выводы
6. Список использованной литературы
1. Вступление
В 1859 г. Сэр Вильям Гамильтон, знаменитый математик, давший миру теорию комплексного числа и кватерниона, предложил детскую головоломку, в которой предлагалось совершить «круговое путешествие» по 20 городам, расположенных в различных частях земного шара. Каждый город соединялся дорогами с тремя соседними так, что дорожная сеть образовывала 30 ребер додекаэдра, в вершинах которого находились города a, b, … t. Обязательным условием являлось требование: каждый город за исключением первого можно посетить один раз.
Гамильтонова задача о путешественнике нередко преобразуется в задачу о коммивояжере. Коммивояжер – не свободно путешествующий турист, а деловой человек, ограниченный временными, денежными или какими-либо другими ресурсами. Гамильтонова задача может стать задачей о коммивояжере, если каждое из ребер снабдить числовой характеристикой. Это может быть километраж, время на дорогу, стоимость билета, расход горючего и т.д. Таким образом, условные характеристики дадут числовой ряд, элементы которого могут быть распределены между ребрами как угодно.
2. Постановка задачи
Рассмотрим задачу о коммивояжере.
Имеются n городов, расстояния (стоимость проезда, расход горючего на дорогу и т.д.) между которыми известны. Коммивояжер должен пройти все n городов по одному разу, вернувшись в тот город, с которого начал. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние (стоимость проезда и т.д.) будет минимальным.
Очевидно, что задача коммивояжера – это задача отыскания кратчайшего гамильтонова цикла в полном графе.
Можно предложить следующую простую схему решения задачи коммивояжера: сгенерировать все n! возможных перестановок вершин полного графа, подсчитать для каждой перестановки длину маршрута и выбрать кратчайший. Однако, n! с ростом nрастет быстрее, чем любой полином от n, и даже быстрее, чем 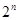 . Таким образом, решение задачи коммивояжера методом полного перебора оказывается практически неосуществимым, даже при достаточно небольших n. . Таким образом, решение задачи коммивояжера методом полного перебора оказывается практически неосуществимым, даже при достаточно небольших n.
Реклама

Решить задачу коммивояжера также можно с помощью алгоритма Крускала и «деревянного» алгоритма. Эти методы ускоряют разработку алгоритма по сравнению с методом полного перебора, однако не всегда дают оптимальное решение.
Существует метод решения задачи коммивояжера, который дает оптимальное решение. Этот метод называется методом ветвей и границ. Решение задачи коммивояжера методом ветвей и границ по-другому называют алгоритмом Литтла.
Если считать города вершинами графа, а коммуникации (i,j) – его дугами, то требование нахождения минимального пути, проходящего один и только один раз через каждый город, и возвращения обратно, можно рассматривать как нахождение на графе гамильтонова контура минимальной длины.
Для практической реализации идеи метода ветвей и границ применительно к задаче коммивояжера нужно найти метод определения нижних границ подмножества и разбиения множества гамильтоновых контуров на подмножества (ветвление).
Определение нижних границ базируется на том утверждении, что если ко всем элементам i-й строки или j-го столбца матрицы C прибавить или отнять число 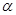 , то задача останется эквивалентной прежней, то есть оптимальность маршрута коммивояжера не изменится, а длина любого гамильтонова контура изменится на данную величину , то задача останется эквивалентной прежней, то есть оптимальность маршрута коммивояжера не изменится, а длина любого гамильтонова контура изменится на данную величину 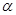 . .
Опишем алгоритм Литтла для нахождения минимального гамильтонова контура для графа с n вершинами. Граф представляют в виде матрицы его дуг. Если между вершинами Xi
и Xj
нет дуги, то ставится символ «∞».
Алгоритм Литтла для решения задачи коммивояжера можно сформулировать в виде следующих правил:
1. Находим в каждой строке матрицы 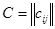 минимальный элемент минимальный элемент 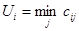 и вычитаем его из всех элементов соответствующей строки. Получим матрицу, приведенную по строкам, с элементами и вычитаем его из всех элементов соответствующей строки. Получим матрицу, приведенную по строкам, с элементами
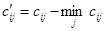
2. Если в матрице 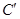 , приведенной по строкам, окажутся столбцы, не содержащие нуля, то приводим ее по столбцам. Для этого в каждом столбце матрицы , приведенной по строкам, окажутся столбцы, не содержащие нуля, то приводим ее по столбцам. Для этого в каждом столбце матрицы 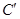 выбираем минимальный элемент выбираем минимальный элемент 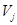 , , 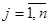 и вычитаем его из всех элементов соответствующего столбца. Получим матрицу и вычитаем его из всех элементов соответствующего столбца. Получим матрицу
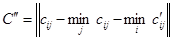
каждая строка и столбец, которой содержит хотя бы один нуль. Такая матрица называется приведенной по строкам и столбцам.
3. Суммируем элементы 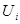 и и 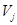 , получим константу приведения , получим константу приведения
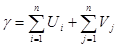
которая будет нижней границей множества всех допустимых гамильтоновых контуров, то есть
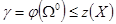
4. Находим степени нулей для приведенной по строкам и столбцам матрицы. Для этого мысленно нули в матице заменяем на знак «∞» и находим сумму минимальных элементов строки и столбца, соответствующих этому нулю. Записываем ее в правом верхнем углу клетки
Реклама

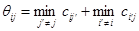
5. Выбираем дугу 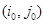 , для которой степень нулевого элемента достигает максимального значения , для которой степень нулевого элемента достигает максимального значения
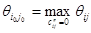
6. Разбиваем множество всех гамильтоновых контуров 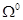 на два подмножества на два подмножества 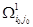 и и 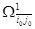 . Подмножество . Подмножество 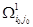 гамильтоновых контуров содержит дугу гамильтоновых контуров содержит дугу 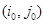 , , 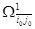 - ее не содержит. Для получения матрицы контуров - ее не содержит. Для получения матрицы контуров 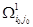 , включающих дугу , включающих дугу 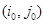 , вычеркиваем в матрице , вычеркиваем в матрице 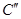 строку строку 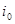 и столбец и столбец 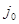 . Чтобы не допустить образования негамильтонова контура, заменим симметричный элемент . Чтобы не допустить образования негамильтонова контура, заменим симметричный элемент 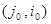 на знак «∞». на знак «∞».
7. Приводим матрицу гамильтоновых контуров 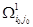 . Пусть . Пусть 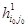 - константа ее приведения. Тогда нижняя граница множества - константа ее приведения. Тогда нижняя граница множества 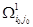 определится так определится так
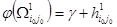
8. Находим множество гамильтоновых контуров 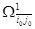 , не включающих дугу , не включающих дугу 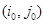 . Исключение дуги . Исключение дуги 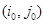 достигается заменой элемента достигается заменой элемента 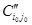 в матрице в матрице 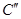 на ∞. на ∞.
9. Делаем приведение матрицы гамильтоновых контуров 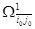 . Пусть . Пусть 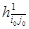 - константа ее приведения. Нижняя граница множества - константа ее приведения. Нижняя граница множества 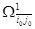 определится так определится так
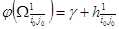
10. Сравниваем нижние границы подмножества гамильтоновых контуров 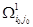 и и 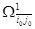 . Если . Если 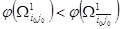 , то дальнейшему ветвлению в первую очередь подлежит множество , то дальнейшему ветвлению в первую очередь подлежит множество 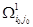 . Если же . Если же 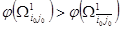 , то разбиению подлежит множество , то разбиению подлежит множество 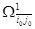 . .
Процесс разбиения множеств на подмножества сопровождается построением дерева ветвлений.
11. Если в результате ветвлений получаем матрицу 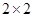 , то определяем полученный ветвлением гамильтонов контур и его длину. , то определяем полученный ветвлением гамильтонов контур и его длину.
12. Сравниваем длину гамильтонова контура с нижними границами оборванных ветвей. Если длина контура не превышает их нижних границ, то задача решена. В противном случае развиваем ветви подмножеств с нижней границей, меньшей полученного контура, до тех пор, пока не получим маршрут с меньшей длиной или не убедимся, что такого не существует.
3. Математическая модель задачи коммивояжера
Задача коммивояжера может быть сформулирована как целочисленная введением булевых переменных 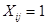 , если маршрут включает переезд из города i непосредственно в город j и , если маршрут включает переезд из города i непосредственно в город j и 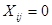 в противном случае. Тогда можно задать математическую модель задачи, то есть записать целевую функцию и систему ограничений в противном случае. Тогда можно задать математическую модель задачи, то есть записать целевую функцию и систему ограничений
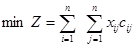 (1) (1)
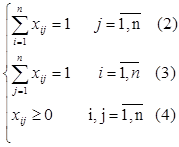
Условия (2) – (4) в совокупности обеспечивают, что каждая переменная 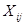 равна или нулю, или единице. При этом ограничения (2), (3) выражают условия, что коммивояжер побывает в каждом городе один раз в него прибыв (ограничение (2)), и один раз из него выехав (ограничение (3)). равна или нулю, или единице. При этом ограничения (2), (3) выражают условия, что коммивояжер побывает в каждом городе один раз в него прибыв (ограничение (2)), и один раз из него выехав (ограничение (3)).
Однако этих ограничений не достаточно для постановки задачи коммивояжера, так как они не исключают решения, где вместо простого цикла, проходящего через n вершин, отыскиваются 2 и более отдельных цикла (подцикла), проходящего через меньшее число вершин. Поэтому задача, описанная уравнениями (2) – (4) должна быть дополнена ограничениями, обеспечивающими связность искомого цикла.
Для того, чтобы исключить при постановке задачи все возможные подциклы в систему ограничений задачи включают следующее ограничение:
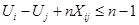 , где , где 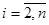 , , 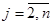 и и 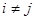 . .
4. Алгоритм решения
Дана матрица расстояний, представленная в таблице 1. Необходимо с помощью алгоритма Литтла решить задачу коммивояжера.
Табл.1
j
i
|
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
∞ |
7 |
16 |
21 |
2 |
17 |
| 2 |
13 |
∞ |
21 |
15 |
43 |
23 |
| 3 |
25 |
3 |
∞ |
31 |
17 |
9 |
| 4 |
13 |
10 |
27 |
∞ |
33 |
12 |
| 5 |
9 |
2 |
19 |
14 |
∞ |
51 |
| 6 |
42 |
17 |
5 |
9 |
23 |
∞ |
1) Справа к таблице присоединяем столбец Ui
, в котором записываем минимальные элементы соответствующих строк. Вычитаем элементы Ui
из соответствующих элементов строки матрицы.
j
i
|
1 |
2 |
3 |
4 |
5 |
6 |
Ui
|
| 1 |
∞ |
7 |
16 |
21 |
2 |
17 |
2 |
| 2 |
13 |
∞ |
21 |
15 |
43 |
23 |
13 |
| 3 |
25 |
3 |
∞ |
31 |
17 |
9 |
3 |
| 4 |
13 |
10 |
27 |
∞ |
33 |
12 |
10 |
| 5 |
9 |
2 |
19 |
14 |
∞ |
51 |
2 |
| 6 |
42 |
17 |
5 |
9 |
23 |
∞ |
5 |
2) Внизу полученной матрицы присоединяем строку Vj
, в которой записываем минимальные элементы столбцов. Вычитаем элементы Vj
из соответствующих столбцов матрицы.
j
i
|
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
∞ |
5 |
14 |
19 |
0 |
15 |
| 2 |
0 |
∞ |
8 |
2 |
30 |
10 |
| 3 |
22 |
0 |
∞ |
28 |
14 |
6 |
| 4 |
3 |
0 |
17 |
∞ |
23 |
2 |
| 5 |
7 |
0 |
17 |
12 |
∞ |
49 |
| 6 |
37 |
12 |
0 |
4 |
18 |
∞ |
| Vj
|
0 |
0 |
0 |
2 |
0 |
2 |
3) В результате вычислений получаем матрицу, приведенную по строкам и столбцам, которая изображена в виде таблицы 2.
Табл.2
j
i
|
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
∞ |
5 |
14 |
17 |
019
|
13 |
| 2 |
03
|
∞ |
8 |
02
|
30 |
8 |
| 3 |
22 |
04
|
∞ |
26 |
14 |
4 |
| 4 |
3 |
00
|
17 |
∞ |
23 |
04
|
| 5 |
7 |
07
|
17 |
10 |
∞ |
47 |
| 6 |
37 |
12 |
08
|
2 |
18 |
∞ |
4) Находим константу приведения
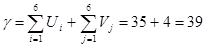
Таким образом, нижней границей множества всех гамильтоновых контуров будет число
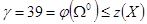
5) Находим степени нулей полностью приведенной матрицы. Для этого как бы заменяем в ней все нули на знак «∞» и устанавливаем сумму минимальных элементов соответствующей строки и столбца. Степени нулей записаны в правых верхних углах клеток, для которых 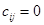 . .
6) Определяем максимальную степень нуля. Она равна 19 и соответствует клетке (1;5). Таким образом, претендентом на включение в гамильтонов контур является дуга (1;5).
7) Разбиваем множество всех гамильтоновых контуров 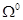 на два: на два: 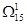 и и 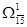 . Матрицу . Матрицу 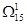 с дугой (1;5) получаем табл.2 путем вычеркивания строки 1 и столбца 5. Чтобы не допускать образования негамильтонова контура, заменяем элемент (5;1) на знак «∞». с дугой (1;5) получаем табл.2 путем вычеркивания строки 1 и столбца 5. Чтобы не допускать образования негамильтонова контура, заменяем элемент (5;1) на знак «∞».
j
i
|
1 |
2 |
3 |
4 |
6 |
| 2 |
0 |
∞ |
8 |
0 |
8 |
| 3 |
22 |
0 |
∞ |
26 |
4 |
| 4 |
3 |
0 |
17 |
∞ |
0 |
| 5 |
∞ |
0 |
17 |
10 |
47 |
| 6 |
37 |
12 |
0 |
2 |
∞ |
8) Матрицу гамильтоновых контуров 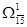 получим из таблицы 2 путем замены элемента (1;5) на знак «∞». получим из таблицы 2 путем замены элемента (1;5) на знак «∞».
j
i
|
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
∞ |
5 |
14 |
17 |
∞ |
13 |
5 |
| 2 |
0 |
∞ |
8 |
0 |
30 |
8 |
| 3 |
22 |
0 |
∞ |
26 |
14 |
4 |
| 4 |
3 |
0 |
17 |
∞ |
23 |
0 |
| 5 |
7 |
0 |
17 |
10 |
∞ |
47 |
| 6 |
37 |
12 |
0 |
2 |
18 |
∞ |
| 14 |
9) Делаем дополнительное приведение матрицы контуров 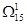 : :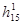 = 0. Нижняя граница множества = 0. Нижняя граница множества 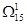 равна равна 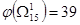 . .
10) Находим константу приведения для множества контуров
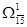 : :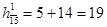
Следовательно, нижняя граница множества 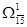 равна равна
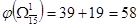
11) Сравниваем нижние границы подмножеств 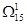 и и 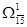 . Так как . Так как
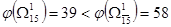
то дальнейшему ветвлению подвергаем множество 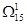 . .
На рис.1 представлено ветвление по дуге (1;5).
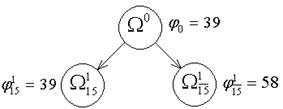
Рис.1
Переходим к ветвлению подмножества 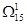 . Его приведенная матрица представлена в таблице ниже. . Его приведенная матрица представлена в таблице ниже.
j
i
|
1 |
2 |
3 |
4 |
6 |
| 2 |
03
|
∞ |
8 |
02
|
8 |
| 3 |
22 |
04
|
∞ |
26 |
4 |
| 4 |
3 |
00
|
17 |
∞ |
04
|
| 5 |
∞ |
010
|
17 |
10 |
47 |
| 6 |
37 |
12 |
010
|
2 |
∞ |
12) Узнаем степени нулей матрицы. Претендентами на включение в гамильтонов контур будут несколько дуг (5;2) и (6;3). Для дальнейших расчетов выберем дугу (6;3). Разбиваем множество 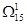 на два подмножества: на два подмножества: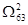 и и 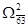 (табл. 3 и 4). Чтобы не допустить образования негамильтонова контура, в таблице 3 заменяем элемент (3;6) на знак «∞» (табл. 3 и 4). Чтобы не допустить образования негамильтонова контура, в таблице 3 заменяем элемент (3;6) на знак «∞»
Табл.3
j
i
|
1 |
2 |
4 |
6 |
| 2 |
0 |
∞ |
0 |
8 |
| 3 |
22 |
0 |
26 |
∞ |
| 4 |
3 |
0 |
∞ |
0 |
| 5 |
∞ |
0 |
10 |
47 |
Табл.4
j
i
|
1 |
2 |
3 |
4 |
6 |
| 2 |
0 |
∞ |
8 |
0 |
8 |
| 3 |
22 |
0 |
∞ |
26 |
4 |
| 4 |
3 |
0 |
17 |
∞ |
0 |
| 5 |
∞ |
0 |
17 |
10 |
47 |
| 6 |
37 |
12 |
∞ |
2 |
∞ |
2 |
| 8 |
Определим константы приведения для этих матриц
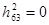 , , 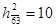
Следовательно
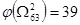 , , 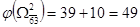
Так как 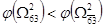 , то дальнейшему ветвлению подлежит подмножество , то дальнейшему ветвлению подлежит подмножество 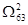 . Находим степени нулей матрицы. . Находим степени нулей матрицы.
j
i
|
1 |
2 |
4 |
6 |
| 2 |
03
|
∞ |
02
|
8 |
| 3 |
22 |
022
|
26 |
∞ |
| 4 |
3 |
00
|
∞ |
08
|
| 5 |
∞ |
010
|
10 |
47 |
Претендентом к включению в гамильтонов контур станет дуга (3;2). Разбиваем множество 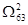 на два на два 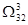 и и 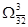 . .
j
i
|
1 |
4 |
6 |
| 2 |
0 |
0 |
8 |
| 4 |
3 |
∞ |
0 |
| 5 |
∞ |
10 |
47 |
10 |
j
i
|
1 |
2 |
4 |
6 |
| 2 |
0 |
∞ |
0 |
8 |
| 3 |
22 |
∞ |
26 |
∞ |
22 |
| 4 |
3 |
0 |
∞ |
0 |
| 5 |
∞ |
0 |
10 |
47 |
Очевидно
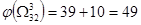 , , 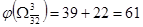
Следовательно, очередному ветвлению нужно подвергнуть подмножество 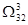 . .
Переходим к ветвлению подмножества 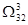 . Определяем степени нулей. Претендентом на включение в гамильтонов контур является дуга (5;4). Разбиваем множество . Определяем степени нулей. Претендентом на включение в гамильтонов контур является дуга (5;4). Разбиваем множество 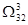 на два подмножества: на два подмножества: 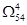 и и 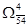 . .
Находим нижние границы
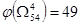 , , 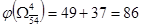
Следовательно, очередному ветвлению нужно подвергнуть подмножество 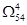 . Но его матрица имеет размерность . Но его матрица имеет размерность 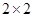 . Поэтому в гамильтонов контур следует включить дуги, соответствующие в матрице . Поэтому в гамильтонов контур следует включить дуги, соответствующие в матрице 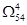 нулевым элементам. нулевым элементам.
Определим полученный гамильтонов контур. В него вошли дуги
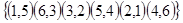
Длина контура равна
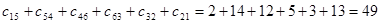
Так как границы оборванных ветвей больше длины контура 1 – 5 – 4 – 6 – 3 – 2 – 1, то этот контура имеет наименьшую длину.
алгоритм крускал коммивояжер

Рис.25
Выводы
Задача коммивояжера является частичным случаем гамильтоновой задачи о путешественнике. Суть задачи коммивояжера состоит в нахождении суммарной минимальной характеристики (расстояния, стоимости проезда и т.д.), при этом коммивояжер должен пройти все n городов по одному разу, вернувшись в тот город, с которого начал.
Существуют несколько методов решения задачи коммивояжера: метод полного перебора, с помощью метода ветвей и границ (алгоритм Литтла), алгоритма Крускала, «деревянного» алгоритма и т.д. Однако только метод ветвей и границ дает нам в итоге самое оптимальное решение.
Основная идея метода Литтла состоит в том, что вначале строят нижнюю границу длин маршрутов для всего множества гамильтоновых контуров 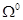 . Затем все множество контуров . Затем все множество контуров 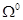 разбивают на два подмножества таким образом, чтобы первое подмножество разбивают на два подмножества таким образом, чтобы первое подмножество 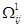 состояло из гамильтоновых контуров, содержащих некоторую дугу (i,j), а другое подмножество состояло из гамильтоновых контуров, содержащих некоторую дугу (i,j), а другое подмножество 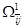 не содержало этой дуги. не содержало этой дуги.
Для практической реализации идеи метода ветвей и границ применительно к задаче коммивояжера нужно найти метод определения нижних границ подмножества и разбиения множества гамильтоновых контуров на подмножества (ветвление). Такое определение нижних границ базируется на том утверждении, что если ко всем элементам i-й строки или j-го столбца матрицы C прибавить или отнять число 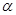 , то задача останется эквивалентной прежней, то есть оптимальность маршрута коммивояжера не изменится, а длина любого гамильтонова контура изменится на данную величину , то задача останется эквивалентной прежней, то есть оптимальность маршрута коммивояжера не изменится, а длина любого гамильтонова контура изменится на данную величину 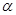 . .
Используя ЭВМ, методом ветвей и границ можно решить задачи коммивояжера для 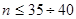 . .
6. Список использованной литературы
1. О. Е. Акимов «Дискретная математика. Логика, группы, графы», Москва, 2003, 376 с., ил., изд. дом «Лаборатория базовых знаний».
2. Ф. А. Новиков «Дискретная математика для программистов» С.-Петербург, 2002 г. 304 с., ил., изд. дом «Питер».
3. В. М. Бондарев «Основы программирования» 1998 г., 368 с. изд. дом «Феникс»
|