Введение
Тема контрольной работы «Построение экспериментального графика» по дисциплине «Информатика».
Цель работы: Научиться строить график на основе табличных данных, анализировать данные с использованием метода наименьших квадратов.
Современные ПК могут успешно использоваться при решении самых разных научно-технических и инженерных задач. Дисциплины механического цикла составляют важную часть обучения в высших технических заведениях. Решение задач теоретической механики, сопротивления материалов, прикладной механики требуют проведения большой и подчас монотонной вычислительной работы. Использование ПК позволяет не только автоматизировать вычисления, но и дает возможности оптимизировать выбор наилучшего варианта конструкции или детали машин. Совокупность знаний и навыков в области вычислительной техники может помочь студенту при выполнении лабораторных работ (обработка результатов наблюдений), курсовых и контрольных работ. Приобретенные навыки будущий специалист должен использовать и в своей профессиональной деятельности.
1. Формулировка задачи
При изучении зависимости электрического сопротивления r
некоторого медного стержня от температуры t
была получена следующая таблица:
Таблица 1
| t
|
20,1 |
24,5 |
30,1 |
35,0 |
39,6 |
45,1 |
50,0 |
| r
|
73,10 |
74,90 |
77,90 |
80,10 |
81,30 |
83,50 |
84,60 |
2. Постановка задачи
Дано:
Результаты эксперимента представлены в табличной форме (Таблица 1)
Требуется:
1. Построить график функции на основе таблицы
2. Отформатировать график.
3. Выбрать две подходящие линии тренда, определить линию тренда, наиболее удачно аппроксимирующую табличные данные
4. Определить значение r (электрического сопротивления) при значении температуры t
=
33.50
3. Выполнение работы
1. Загрузить
программу
Excel
(Пуск
-
Программы
-
Microsoft
Excel
и сохранить в собственной
папке
под именем
Практическая работа №3 фамилия
2. Ввести в ячейку A
1
- Практическая работа №3
3. Ввести в ячейку A
3
- Тему контрольной работы
4. Создать таблицу, согласно исходных данных (Таблица 1)
Таблица 2
| A |
B |
C |
D |
E |
F |
G |
H |
| 1 |
Контрольная работа №3 |
| 2 |
| 3 |
Тема: построение экспериментального графика |
| 4 |
| 5 |
| 6 |
t
|
20,1 |
24,5 |
30,1 |
35,0 |
39,6 |
45,1 |
50,0 |
| 7 |
r
|
73,10 |
74,90 |
77,90 |
80,10 |
81,30 |
83,50 |
84,60 |
5. Построение графика
5.1. Выделить диапазон A
6:
H
7
5.2. Щелкнуть на значке  Мастер диаграмм
(появится окно). Мастер диаграмм построит диаграмму за 4 шага. Мастер диаграмм
(появится окно). Мастер диаграмм построит диаграмму за 4 шага.
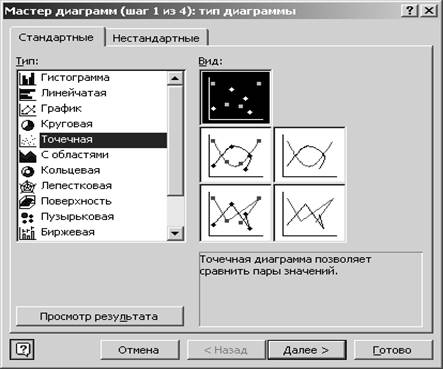
Рис. 1
В списке Тип
(в окне диалога) выберите пункт Точечная
. В палитре Вид
выберите первый пункт. Щелкните по кнопке Далее
Реклама

5.3. Так как диапазон ячеек был выбран заранее, то Мастер диаграмм
автоматически определяет расположение рядов данных.
Щелкните по кнопке Далее
5.4. Появится окно (шаг 3 из 4
)
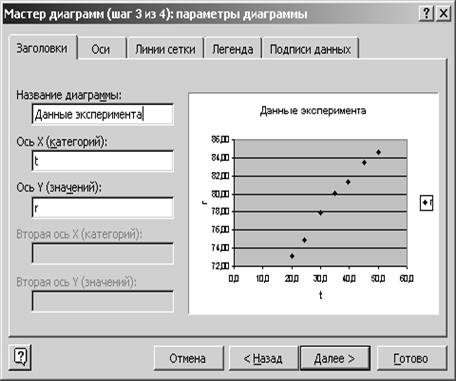
Рис. 2
На вкладке Заголовки:
5.4. Вводим в полеНазвание диаграммыДанные эксперимента
5.5.В полеОсь категорийt
5.6.В полеОсь значенийr
и Щелкните по кнопкеДалее
5.7. В следующем окне Мастера диаграмм (шаг 4 из 4) щелкнуть на кнопке Готово
Появится диаграмма:
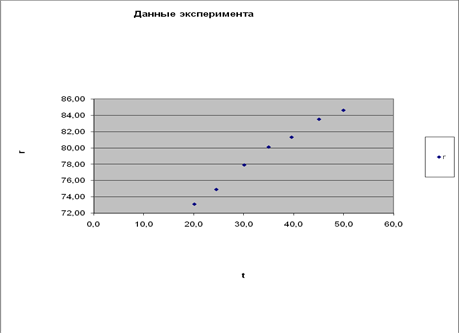
Рис. 3
Готовую диаграмму можно:
– перемещать
– так же, как и объекты в Word,
– изменять
.
Диаграмма состоит из набора элементов
:
ряды данных,
легенда,
ось категорий,
ось значений,
заголовок диаграммы,
названия осей и т.д.
Эти элементы можно выбирать и изменять.
При наведении указателя мыши на элемент диаграммы, автоматически появляется название этого элемента.
При щелчке правой
кнопки мыши на элементе появляется контекстное меню
, из которого выбирают пункт Формат
.
После чего появляется диалоговое окно для форматирования выбранного элемента диаграммы.
Отформатируем диаграмму, чтобы она приняла вид, соответствующий Рис. 4
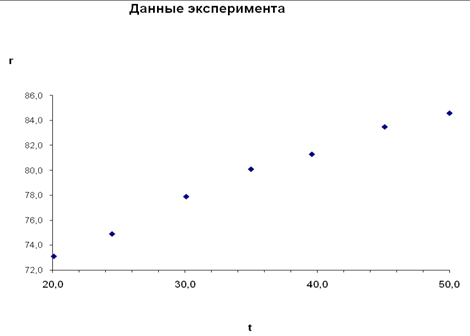
Рис. 4
график квадрат наименьший тренд
Анализ данных с использованием метода наименьших квадратов.
Недостаток табличного представления функции состоит в том, что невозможно задать функцию полностью. Например, таблица не позволяет ответить на вопрос о том, каково сопротивление стержня при температуре 33.5о
.
MS
Excel
предоставляет такую возможность – использование линий тренда.
Линия тренда – это линия регрессии, которая аппроксимирует точки данных в виде линий (логарифмической, показательной, степенной, прямой).
Линии тренда позволяют графически отображать тенденции данных и прогнозировать данные. Подобный анализ называется также регрессионный анализ.
Использование линии тренда того или иного вида определяется типом данных.
Надежность линии тренда.
Наиболее надежна линия тренда, для которой значение R-квадрат
равно или близко к 1.
При подборе линии тренда к данным Excel автоматически рассчитывает значение R2
.
Чтобы дополнить ряд данных линией тренда:
6.1. Подвести указатель мыши к из точек на графике и из появившегося меню выбрать команду Добавить
линию тренда.
6.1.1. В появившемся окне выбирают тип линии тренда (т.е. выбирают такую линию тренда, которая более всего походит для данных, представленных на графике). Выберем Линейная
и нажимаем кнопку OK.
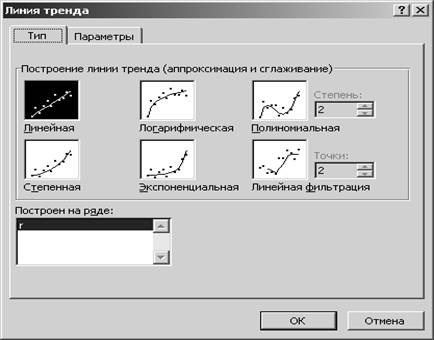
Рис. 5
В этом окне на Вкладке
Параметры
устанавливают флажкиПоказать
уравнение на диаграмме
и Поместить на диаграмму величину достоверности
аппроксимации
R
2
.
Реклама

6.2. Выполнить еще раз все действия, описанные в пункте 6.1., выбрав линию тренда Логарифмическая
.
Окончательно принимаем линию, достоверность которой R
2
, ближе
к единице, т.е. в нашем случае Логарифмическую
– R2
=0,9958>0,9863
Уравнение этой линии y
= 12.999*Ln(x
) + 33.735
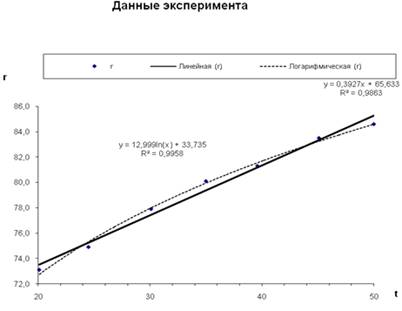
Рис. 6
7. Определение электрического сопротивления при t=33.5o
7.1. В ячейку С36
ввести текст t
7.2. В ячейку D36
введем текст r
7.3. В ячейку С37
ввести значение температуры 33,5
7.4. В ячейку D37
ввести формулу =12.999*LN(C37)+33.735
7.5. В ячейке D37
результат вычисления
r
Если изменить содержимое
ячейки C
37,
то автоматически произойдет и пересчет ячейки D37.
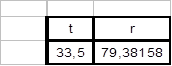
Рис. 7
Л
итература
1. Воробьев В.В. MicrosoftExcel 2000: Пособие для начинающих – К.: 2000, 36 с.
2. Симонович С., Евсеев Г. Практическая информатика: универсальный курс. – М.: АСТ-ПРЕСС; Инфорком-Пресс, 2009,480 с.
3. Симонович С., Евсеев Г., Алексеев А. Специальная информатика: универсальный курс. – М.: АСТ-ПРЕСС; Инфорком-Пресс, 2009,480 с.
4. Симонович С. Информатика: базовый курс. – СПб.: Питер, 2009, 640 с.
5. Рычков В. Самоучитель Excel 2000. – СПб.: Питер, 2009, 512 с.
|