Введение
Для успешного изучения материальной части техники войск РХБ защиты необходимы глубокие знания общетехнических дисциплин. Многие детали машин в процессе эксплуатации подвергаются циклическим напряжениям. Поэтому курсанты должны иметь представление о параметрах и видах циклов напряжений, явлении и пределе выносливости.
Поэтому материал данной лекции имеет большое значение. Цель данной лекции дать курсантам основные термины и определения, связанные с циклическими напряжениями, изучить вопрос расчета элементов конструкций на прочность при данном виде нагружения.
1. Понятие о циклических напряжениях. Параметры и виды циклов напряжений
К динамическим нагрузкам, несмотря на отсутствие значительных инерционных сил, можно отнести периодические многократно повторяющиеся (циклические) нагрузки, действующие на элементы конструкции. Такого рода нагружения характерны для большинства машиностроительных конструкций, таких, как оси, валы, штоки, пружины, шатуны и т.д.
Прочность материалов при повторно-переменном нагружении во многом зависит от характера изменения напряжений во времени.
Периодическая нагрузка
– переменная нагрузка с установившимся во времени характером изменения, значения которой повторяются через определенный промежуток (период) времени.
Цикл напряжений
– совокупность всех значений переменных напряжений за время одного периода изменения нагрузки.
Обычно цикл напряжений характеризуется двумя основными параметрами цикла:  и и  - максимальным и минимальным напряжениями цикла. - максимальным и минимальным напряжениями цикла.
Среднее напряжение цикла 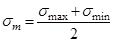 . .
Амплитудное напряжение цикла 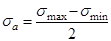 . .
Коэффициент асимметрии цикла напряжений  . .
В зависимости от величины перечисленных характеристик циклы напряжений могут быть подразделены на следующие основные виды:
Симметричный цикл
– максимальное и минимальное напряжения равны по абсолютной величине и противоположны по знаку  , R
= -1. , R
= -1.
Асимметричный цикл
– максимальное и минимальное напряжения не равны по абсолютной величине  , при этом асимметричный цикл может быть знакопеременным или знакопостоянным. , при этом асимметричный цикл может быть знакопеременным или знакопостоянным.
Знакопеременный цикл
– максимальное и минимальное напряжения не равны по абсолютной величине и противоположны по знаку  , ,  , ,  . .
Реклама

Знакопостоянный цикл
– максимальное и минимальное напряжения не равны по абсолютной величине и имеют одинаковый знак  , , 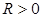 , ,  . .
Отнулевой (пульсирующий) цикл
– максимальное или минимальное напряжения равны нулю  или или  , , 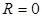 или или  . .
2. Явление усталости. Кривая усталости. Предел выносливости
Как показывает практика, нагрузки, циклически изменяющиеся во времени по величине или по величине и по знаку, могут привести к разрушению конструкции при напряжениях, существенно меньших, чем предел текучести (или предел прочности). Такое разрушение принято называть «усталостным». Материал как бы «устает» под действием многократных периодических нагрузок.
Усталостное разрушение
– разрушение материала под действием повторно-переменных напряжений.
Усталость материала
– постепенное накопление повреждений в материале под действием переменных напряжений, приводящих к образованию трещин в материале и разрушению.
Выносливость
– способность материала сопротивляться усталостному разрушению.
Физические причины усталостного разрушения материалов достаточно сложны и еще не до конца изучены. Одной из основных причин усталостного разрушения принято считать образование и развитие трещин.
Механизм усталостного разрушения во многом связан с неоднородностью реальной структуры материалов (различие размеров, очертаний, ориентации соседних зерен металла; наличие различных включений – шлаков, примесей; дефекты кристаллической решетки, дефекты поверхности материала – царапины, коррозия и т. д.). В связи с указанной неоднородностью при переменных напряжениях на границах отдельных включений и вблизи микроскопических пустот и различных дефектов возникает концентрация напряжений, которая приводитк микропластическим деформациям сдвига некоторых зерен металла, при этом на поверхности зерен могут появляться полосы скольжения,и накоплению сдвигов, которое на некоторых материалах проявляется в виде микроскопических бугорков и впадинок – экструзий и интрузий. Затем происходит развитие сдвигов в микротрещины, их рост и слияние; на последнем этапе появляется одна или несколько макротрещин, которая достаточно интенсивно развивается (растет). Края трещины под действием переменной нагрузки притираются друг об друга, и поэтому зона роста трещины отличается гладкой (полированной) поверхностью. По мере роста трещины поперечное сечение детали все больше ослабляется, и, наконец, происходит внезапное хрупкое разрушение детали, при этом зона хрупкого долома имеет грубозернистую кристаллическую структуру, как при хрупком разрушении.
Реклама

Кривая усталости (кривая Веллера) строится на основании результатов усталостных испытаний при симметричном цикле. Она показывает, что с увеличением числа цикла максимальное напряжение, при котором происходит разрушение материала, значительно уменьшается. При этом для многих материалов, например углеродистой стали, можно установить такое наибольшее напряжение цикла, при котором образец не разрушается после любого числа циклов (горизонтальный участок диаграммы), называемое пределом выносливости (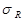 ). ).
Предел выносливости (усталости)
– наибольшее (предельное) напряжение цикла, при котором не происходит усталостного разрушения образца после произвольно большого числа циклов.
Так как испытания нельзя проводить бесконечно большое время, то число циклов ограничивают некоторым пределом, который называют базовым числом циклов. В этом случае, если образец выдерживает базовое число циклов (для черных металлов – N
= 107
), то считается, что напряжение в нем не выше предела выносливости.
Кривые усталости для цветных металлов не имеют горизонтальных участков, поэтому для них за базовое число циклов увеличивается до N
= 108
и устанавливается предел ограниченной выносливости.
В реальных конструкциях подавляющее число деталей работает при ассиметричном нагружении.
Диаграмма предельных напряжений (диаграмма Смита) строится, как минимум, по трем режимам нагружения (по трем точкам), для каждого из которых определяют предел выносливости.
Первый режим (точка 1) – обычный симметричный цикл нагружения ( , , 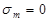 , ,  , ,  ). ).
Второй режим (точка 2) – асимметричный цикл нагружения, как правило, отнулевой (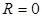 , , 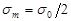 , ,  , ,  ). ).
Третий режим (точка 3) – простое статическое растяжение ( , ,  ). ).
Полученные точки соединяют плавной линией, ординаты точек которой соответствуют пределам выносливости материала при различных значениях коэффициента асимметрии цикла.
Луч, проходящий под углом  через начало координат диаграммы предельных напряжений, характеризует циклы с одинаковым коэффициентом асимметрии R
: через начало координат диаграммы предельных напряжений, характеризует циклы с одинаковым коэффициентом асимметрии R
:
 . .
Диаграмма предельных амплитуд (диаграмма Хейга) строится в координатах: среднее напряжение цикла – амплитуда цикла (рисунок 7). При этом для ее построения необходимо провести усталостные испытания так же как минимум для трех режимов: 1 – симметричный цикл; 2 – отнулевой цикл; 3 – статическое растяжение.
Соединяя полученные точки плавной кривой, получают график, характеризующий зависимость между значениями предельных амплитуд и значениями предельных средних напряжений в цикле.
Кроме свойств материала, на усталостную прочность оказывают влияние следующие факторы: 1) наличие концентраторов напряжений; 2) масштабный фактор, то есть влияние абсолютных размеров детали (чем больше размеры детали, тем ниже усталостная прочность); 3) качество обработки поверхности (с уменьшением шероховатости поверхности детали растет усталостная прочность); 4) эксплуатационные факторы (температура, коррозия, частота нагружения, радиационное облучение и т.д.); 5) наличие поверхностного слоя, упрочненного различными технологическими методами.
напряжение усталость кривая прочность
3. Расчет на прочность при циклических напряжениях
Расчет на прочность при циклических напряжениях начинают с построения диаграммы усталостной прочности (часто, для простоты рассуждений предельную линию представляют в виде прямой) и показывают на ней рабочую точку М
цикла в случае, если рассматриваемый элемент испытывает только простое растяжение и сжатие.
Рассмотрим все те циклы, рабочие точки которых лежат на одной прямой, и для которых справедливо выражение sà
=sm
∙tga. Тогда  . .
Значит, можно сделать вывод о том, что все подобные циклы лежат на одной прямой. Тогда, под запасом усталостной прочности будем понимать отношение отрезка ON
к отрезку OM
:  , где точка M
соответствует действующему циклу, а точка N
получается вследствие пересечения предельной прямой и продолжения отрезка OM
. , где точка M
соответствует действующему циклу, а точка N
получается вследствие пересечения предельной прямой и продолжения отрезка OM
.
Для определения 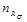 (т.е. в ситуации, когда действуют лишь нормальные напряжения) в инженерной практике применяются как графический, так и аналитический способы. При графическом способе строго по масштабу строится диаграмма предельных напряжений в системе координат. Далее, на этой диаграмме наносится рабочая точка и определяется отношение величин отрезков ON
и OM
. Для определения расчетных зависимостей для (т.е. в ситуации, когда действуют лишь нормальные напряжения) в инженерной практике применяются как графический, так и аналитический способы. При графическом способе строго по масштабу строится диаграмма предельных напряжений в системе координат. Далее, на этой диаграмме наносится рабочая точка и определяется отношение величин отрезков ON
и OM
. Для определения расчетных зависимостей для 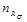 воспользуемся условием подобия треугольников OND
и OMK
и получим: воспользуемся условием подобия треугольников OND
и OMK
и получим:
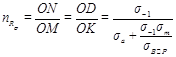 . .
Полученный коэффициент запаса соответствует идеальному образцу. Реальная же его величина зависит, как отмечалось выше, от геометрии, размеров и состояния поверхности образца, учитываемых коэффициентами К
1
, соответственно. Для этого необходимо предел усталости при симметричном нагружении уменьшить в 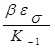 раз, или, что тоже самое, амплитудное напряжение цикла увеличить в раз, или, что тоже самое, амплитудное напряжение цикла увеличить в 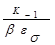 раз. Тогда раз. Тогда
 , ,
где  . .
Аналогичным образом могут быть получены соотношения усталостной прочности и при чистом сдвиге. Эксперименты показывают, что диаграмма усталостной прочности для сдвига заметно отличается от прямой линии, свойственной простому растяжению (сжатию), и имеет вид кривой. В первом приближении эту кривую в координатных осях a
, m
можно представить в виде двух наклонных, как это изображено на рисунке 9. Причем, если одна из них (ближняя к оси ординат) соответствует разрушению образца вследствие усталостных явлений, то другая по причине наступления пластического состояния.
В данном случае расчетная формула для  записывается в виде записывается в виде
 , ,
где  эмпирическая величина, определенная на основе обработки экспериментальных данных. эмпирическая величина, определенная на основе обработки экспериментальных данных.
При сложном напряженном состоянии, т.е. если в рабочей точке при действии внешних нагрузок одновременно возникают как нормальные, так и касательные напряжения, для вычисления nR
применяется следующая приближенная формула:
 , ,
где nR
искомый коэффициент запаса усталостной прочности;
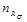 коэффициент запаса усталостной прочности в предположении, что касательные напряжения в рабочей точке отсутствуют; коэффициент запаса усталостной прочности в предположении, что касательные напряжения в рабочей точке отсутствуют;
 коэффициент запаса прочности по усталости при предположении, что в рабочей точке нормальные напряжения отсутствуют. коэффициент запаса прочности по усталости при предположении, что в рабочей точке нормальные напряжения отсутствуют.
Резюмируя, заметим, что физические основы теории твердого деформируемого тела недостаточно развиты, многие предпосылки современной теории усталостной прочности базируются на эмпирической основе. Отсутствие твердых предпосылок в теории выносливости в современном виде лишает ее нужной строгости. Так как полученные эмпирические зависимости не являются универсальными, сами результаты расчетов являются достаточно приближенными. Однако указанные приближения оказываются допустимыми для решения инженерных задач.
|