Расчёт рекуперативного теплообменного аппарата
Иваново 2010
1. Расчётная часть
Определим внутренний диаметр корпуса теплообменника.
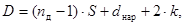
Исходя из того, что нам задано общее число трубок в теплообменном аппарате n=130, выбираем из таблицы 1 [1] при расположении трубок по концентрическим окружностям число трубок – 130. Тогда число труб по диагонали 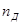 = 13. = 13.
Наружный диаметр трубок задан и равняется dнар
=22 мм.
Шаг труб выбираем из соотношения S=(1,3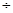 1,5) dнар
=28.6 1,5) dнар
=28.6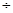 33, принимаем S=30 мм. 33, принимаем S=30 мм.
k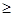 6 мм – кольцевой зазор между трубами и корпусом, принимаем k=10 мм. 6 мм – кольцевой зазор между трубами и корпусом, принимаем k=10 мм.
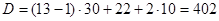 мм. мм.
Задаём температуру холодного теплоносителя на выходе из теплообменника.
Температура насыщенного сухого водяного пара при Рн
=0.6 бар:
 0
С. 0
С.
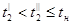 . .
Примем 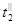 =32.44 0
С. =32.44 0
С.
Определяем расход холодного теплоносителя G2 из уравнения неразрывности.
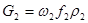 ; ;
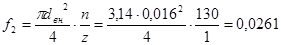 м2
; м2
;
Средняя температура холодного теплоносителя:
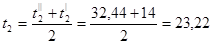 0
С; 0
С;
Из таблицы 8 [2] выписываем параметры холодного теплоносителя:
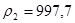 кг/м3
; кг/м3
;
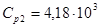 Дж/кгК; Дж/кгК;
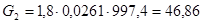 кг/с. кг/с.
Из уравнения теплового баланса находим тепловую мощность аппарата Q.
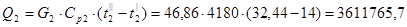 Вт. Вт.
Строим график изменения температур теплоносителя вдоль поверхности нагрева t=f(F) и рассчитываем среднюю температуру теплоносителей 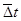 . .
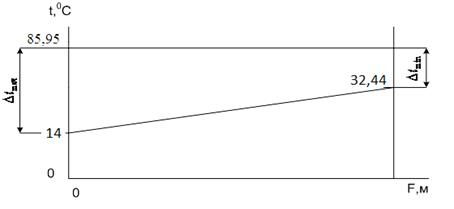
График изменения температуры теплоносителя вдоль поверхности нагрева
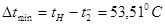 ; ;
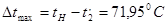 ; ;
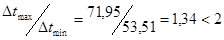 , значит , значит 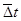 определяется как среднее арифметическое: определяется как среднее арифметическое:
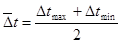 ; ;
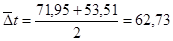 0
С. 0
С.
Определение коэффициента теплопередачи k.
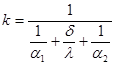 ; ;
Теплофизические свойства материала трубок таблица 6 [3] (Сталь 2Х13): 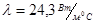 ; ;
Толщина стенки δ=0,5 (dнар
-dвн
)=0,5 (22–16)=3 мм
Определение 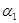 и и 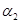 . .
Задаёмся
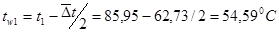 , , 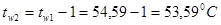
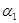 – коэффициент теплоотдачи при конденсации водяного пара на одиночной горизонтальной трубе. – коэффициент теплоотдачи при конденсации водяного пара на одиночной горизонтальной трубе.
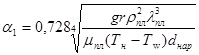 , ,
где из таблиц 8 и 9 [2]
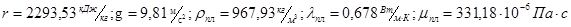
при Топр = Тнас = 85,95 0
C.
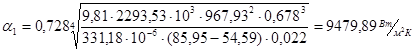
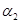 – коэффициент теплопередачи при вынужденном движении текучей среды в прямых гладких трубах. – коэффициент теплопередачи при вынужденном движении текучей среды в прямых гладких трубах.
Определяем критерий Рейнольдса.
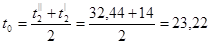 0
С; 0
С;
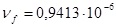 м2
/с; м2
/с;
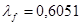 Вт/мК. Вт/мК.
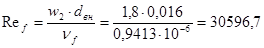 >104
режим турбулентный. >104
режим турбулентный.
Значит, средняя теплоотдача рассчитывается по формуле Михеева:
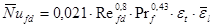 , ,
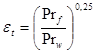 -поправка, учитывающая изменение физических свойств среды от температуры. -поправка, учитывающая изменение физических свойств среды от температуры.
Из таблицы 8 [2]:
По t0 = 23,22 0
С находим Prf= 6,5048
По tw2 = 53,59 0
С находим Prw=3,321
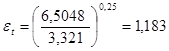
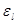 – поправка на изменение коэффициента теплоотдачи на начальном участке гидродинамической стабилизации. – поправка на изменение коэффициента теплоотдачи на начальном участке гидродинамической стабилизации.
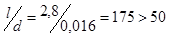 , значит , значит 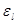 =1. =1.
Тогда, 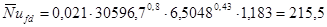 . .
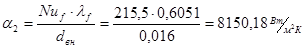 . .
Определяем k:
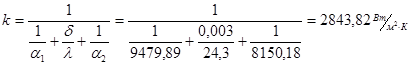
Т.к. при расчетах температуры стенок были заданы приближенно, то их необходимо уточнить. Для этого определим удельный тепловой поток исходя из температур теплоносителей:
Реклама

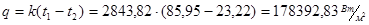 . .
Температуры стенок могут быть найдены из выражений:
 , ,
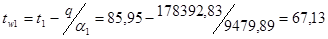 0
С, 0
С,
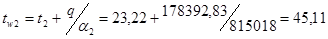 0
С. 0
С.
Пересчитаем α1
и α2
:
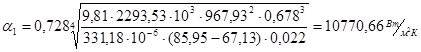
При 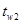 =45,11 0
С найдём значения Prw
: =45,11 0
С найдём значения Prw
:
Prw
=3,917,
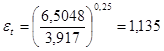 . .
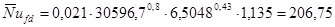 . .
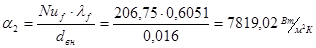 . .
Уточним коэффициент теплопередачи:
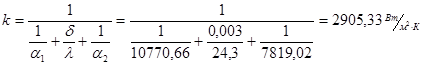
Ещё раз определим значения температур стенок:
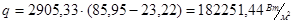 , ,
 0
С, 0
С,
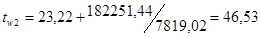 0
С. 0
С.
Пересчитаем α1 и α2:
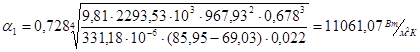
При 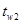 =46,53 0
С найдём значения Prw
: =46,53 0
С найдём значения Prw
:
Prw
=3,807,
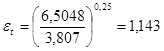 . .
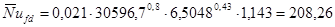 . .
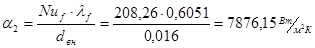 . .
Уточним коэффициент теплопередачи:
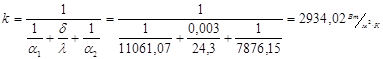
Ещё раз определим значения температур стенок:
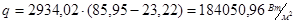 , ,
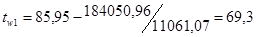 0
С, 0
С,
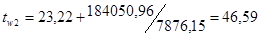 0
С. 0
С.
Т.к. расхождение с предыдущими температурами менее 1%, то полученную в последнем приближении величину k=2934,02 Вт/м2
К будем считать окончательной.
2. Площадь поверхности теплообмена Fрасч из уравнения теплопередачи
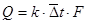 , ,
теплообменник корпус уравнение нагрев
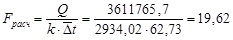 м2
, м2
,
Сравниваем 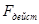 и и 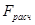 . .
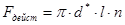 – действительная площадь поверхности теплообмена. – действительная площадь поверхности теплообмена.
Т.к. коэффициенты теплопередачи имеют разные порядки, то в качестве 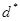 берём диаметр, равный берём диаметр, равный 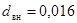 м, т. к. м, т. к. 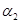 < <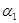 . .
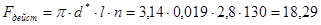 м2
. м2
.
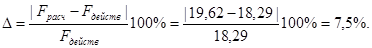
Т.к. 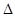 >5% то перезадаём значение t2
, и производим расчёт заново с пункта 1. >5% то перезадаём значение t2
, и производим расчёт заново с пункта 1.
Задаём температуру холодного теплоносителя на выходе из теплообменника. Используя формулу эффективности для конденсации, найдем 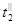 . .
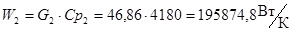
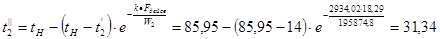 0
С. 0
С.
Определяем расход холодного теплоносителя G2 из уравнения неразрывности.
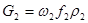 ; ;
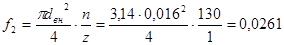 м2
; м2
;
Средняя температура холодного теплоносителя:
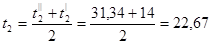 0
С; 0
С;
Из таблицы 8 [4] выписываем параметры холодного теплоносителя:
 кг/м3
; кг/м3
;
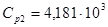 Дж/кгК; Дж/кгК;
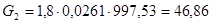 кг/с. кг/с.
Из уравнения теплового баланса находим тепловую мощность аппарата Q.
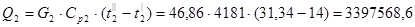 Вт. Вт.
Строим график изменения температур теплоносителя вдоль поверхности нагрева t=f(F) и рассчитываем среднюю температуру теплоносителей 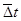 . .
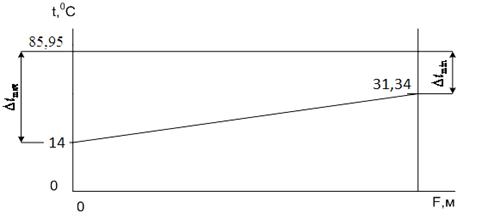
График изменения температуры теплоносителя вдоль поверхности нагрева
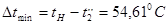 ; ;
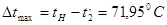 ; ;
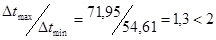 , значит , значит 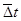 определяется как среднее арифметическое: определяется как среднее арифметическое:
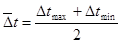 ; ;
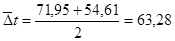 0
С. 0
С.
Определение коэффициента теплопередачи k.
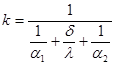 ; ;
Теплофизические свойства материала трубок таблица 6 (Сталь 2х13): 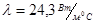 ; ;
Толщина стенки δ=0,5 (dнар
-dвн
)=0,5 (22–16)=3 мм
Определение 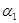 и и 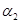 . .
Задаёмся 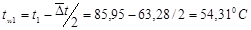 , ,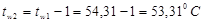
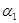 – коэффициент теплоотдачи при конденсации водяного пара на одиночной горизонтальной трубе. – коэффициент теплоотдачи при конденсации водяного пара на одиночной горизонтальной трубе.
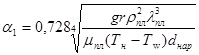 , ,
где из таблиц 8 и 9 [2] 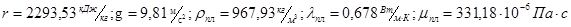
при Топр = Тнас = 85,95 0
C.
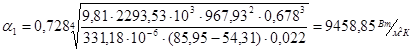
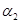 – коэффициент теплопередачи при вынужденном движении текучей среды в прямых гладких трубах. – коэффициент теплопередачи при вынужденном движении текучей среды в прямых гладких трубах.
Определяем критерий Рейнольдса.
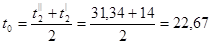 0
С; 0
С;
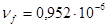 м2
/с; м2
/с;
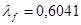 Вт/мК. Вт/мК.
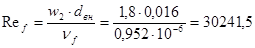 >104
режим турбулентный. >104
режим турбулентный.
Значит, средняя теплоотдача рассчитывается по формуле Михеева:
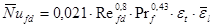 , ,
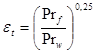 -поправка, учитывающая изменение физических свойств среды от температуры. -поправка, учитывающая изменение физических свойств среды от температуры.
Из таблицы 8 [2]:
По t0 = 22,670
С находим Prf= 6,5928
Реклама

По tw2 = 53,310
С находим Prw=3,381
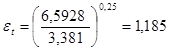
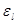 – поправка на изменение коэффициента теплоотдачи на начальном участке гидродинамической стабилизации. – поправка на изменение коэффициента теплоотдачи на начальном участке гидродинамической стабилизации.
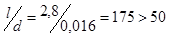 , значит , значит 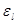 =1. =1.
Тогда, 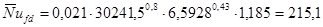 . .
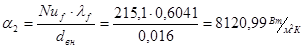 . .
Определяем k:
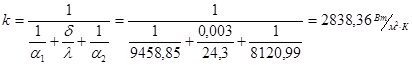
Т.к. при расчетах температуры стенок были заданы приближенно, то их необходимо уточнить. Для этого определим удельный тепловой поток исходя из температур теплоносителей:
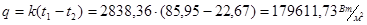 . .
Температуры стенок могут быть найдены из выражений:
 , ,
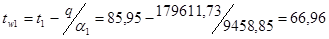 0
С, 0
С,
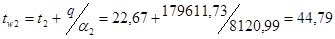 0
С. 0
С.
Пересчитаем α1
и α2
:
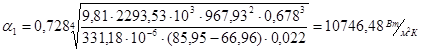
При 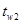 =44,79 0
С найдём значения Prw
: =44,79 0
С найдём значения Prw
:
Prw
=3,941,
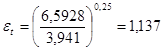 . .
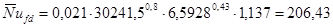 . .
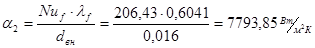 . .
Уточним коэффициент теплопередачи:
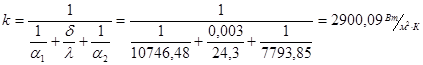
Ещё раз определим значения температур стенок:
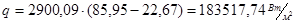 , ,
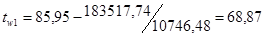 0
С, 0
С,
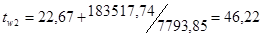 0
С. 0
С.
Пересчитаем α1
и α2
:
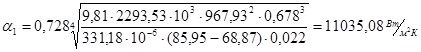
При 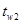 =46,22 0
С найдём значения Prw
: =46,22 0
С найдём значения Prw
:
Prw
=3,831,
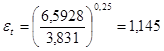 . .
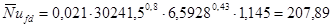 . .
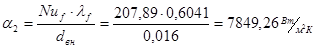 . .
Уточним коэффициент теплопередачи:
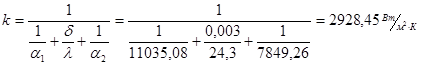
Ещё раз определим значения температур стенок:
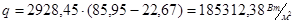 , ,
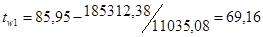 0
С, 0
С,
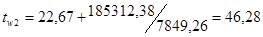 0
С. 0
С.
Т.к. расхождение с предыдущими температурами менее 1%, то полученную в последнем приближении величину k=2928,45 Вт/м2
К будем считать окончательной.
Находим площадь поверхности теплообмена Fрасч из уравнения теплопередачи.
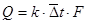 , ,
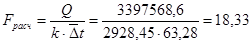 м2
, м2
,
Сравниваем 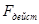 и и 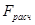 . .
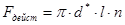 – действительная площадь поверхности теплообмена. – действительная площадь поверхности теплообмена.
Т.к. коэффициенты теплопередачи имеют разные порядки, то в качестве 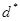 берём диаметр, равный берём диаметр, равный 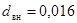 м, т.к. м, т.к. 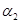 < <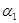 . .
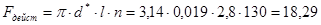 м2
. м2
.
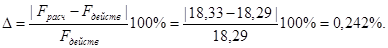
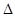 <5% <5%
Из уравнения теплового баланса находим расход горячего теплоносителя G1.
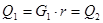 ; ;
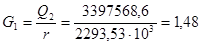 кг/с. кг/с.
Заключение
В результате расчета получили:
Температуры холодного теплоносителя на выходе – 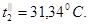
Расходы горячего и холодного теплоносителей:
G1 = 1,48 кг/с
G2 = 46,86 кг/с
Внутренний диаметр корпуса D = 0,402 м.
Тепловая мощность аппарата Q = 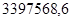 Вт Вт
Список литературы
1. Шипилов В.М., Бухмиров В.В., Чухин И.М. Пример расчета теплообменника: Методические указания к курсовой работе. – Иваново, 1988.
2. Бухмиров В.В. Расчет коэффициента конвективной теплоотдачи: Методические указания к выполнению практических и лабораторных занятий. – Иваново, 2007.
3. Краснощеков Е.А., Сукомел А.С. Задачник по теплопередаче. – М.: Энергия, 1980.
|