Содержание
1. Введение
2. Постановка задачи
3. Описание метода решения
4. Разработка модели
4.1 Логико-математическое описание моделируемой системы
4.2 Формализованная схема объекта моделирования
4.3 Временная диаграмма
4.4 Блок-схемы программных блоков и основной программы
5. Перевод алгоритма на язык программирования
6. Верификация: установление правильности машинной программы
7. Результаты эксперимента
8. Анализ результатов
9. Заключение
10. Список использованной литературы
1.
Введение
Имитационное моделирование применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек, руководящий операцией, может в зависимости от сложившейся обстановки, принимать те или иные решения. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки, в ответ на это решение и к каким последствиям оно приведет спустя некоторое время. Следующее текущее решение принимается уже с учетом реальной новой обстановки и т. д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучиваться принимать правильные решения – если не оптимальные, то почти оптимальные.
В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений. Статистические модели, по сравнению, с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории – неограниченно большое) число факторов. Но и у них – свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходятся искать «на ощупь», путем догадок и проб.
Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей. Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить как бы контур основных закономерностей. Любые уточнения могут быть получены с помощью статистических моделей.
Реклама

Имитационное моделирование основано на прямом описании моделируемого объекта. Существенной характеристикой таких моделей является структурное подобие объекта и модели. Это значит, каждому существенному с точки зрения решаемой задачи элементу объекта ставится в соответствие элемент модели. При построении имитационной модели описываются законы функционирования каждого элемента объекта и связи между ними. Работа с имитационной моделью заключается в проведении имитационного эксперимента. Процесс, протекающий в модели в ходе эксперимента, подобен процессу в реальном объекте. Поэтому исследование объекта на его имитационной модели сводится к изучению характеристик процесса, протекающего в ходе эксперимента.
Для формального представления информационной системы при имитационном моделировании обычно используется схема с дискретными событиями. При этом процесс функционирования системы во времени отождествляется с последовательностью событий, возникающих в системе в соответствии с закономерностями ее функционирования. И формальное понятие «событие» вкладывается конкретное смысловое содержание, определяемое целями моделирования. Ценным качеством имитации является возможность управлять масштабом времени. Динамический процесс в имитационной модели протекает в так называемом системном времени. Системное время имитирует реальное время. При этом пересчет системного времени в модели можно выполнять двумя способами. Первый заключается в «движении» по времени с некоторым постоянным шагом Δt, второй - в «движении» по времени от события к событию. Считается, что в промежутках времени между событиями в модели изменении не происходит. Кроме реального и системного времени существует ещё один тип времени - машинное, т.е. время, за которое реализуется имитационный эксперимент.
Цель курсовой работы по дисциплине «Имитационное моделирование экономических процессов» состоит в ознакомлении с современными концепциями построения моделирующих систем, с основными приемами имитационного моделирования, встраиваемыми в общую процедуру преобразования информации от структурирования и формализации составляющих предметных областей до интерпретации обработанных данных и приобретенных знаний, связанных с описанием экономических процессов.
Реклама

2. Постановка задачи
Фирма имеет в городе 1 точку розничной продажи. Спрос на товары (в единицах товара) в этих точках имеет пуассоновское распределение с математическим ожиданием 10 единиц в день. Торговая точка обслуживаются оптовым магазином. На передачу запроса торговой точки в магазин требуется 1 день. Товары по запросу поступают из оптового магазина в торговую точку в среднем через 5 дней после получения запроса. Эта величина имеет логнормальное распределение с дисперсией 1. Оптовый магазин каждые 14 дней размещает заказы на фабрике. Время, в течение которого магазин получает груз с фабрики, распределено нормально с ожиданием 90 дней, среднеквадратичным отклонением 10 дней; однако заказ при этом никогда не выполняется ранее 60 дней и позднее 120 дней. Проимитировать работу описанной системы с целью определения изменения уровня запаса при данной стратегииуправления розничной торговой точкой и оптовым магазином.
Задать следующие начальные условия моделирования: первый запрос поступает в нулевой момент времени; текущий запас товара в каждой торговой точке составляет 70 единиц, нормативный запас также 70 единиц; запас в магазине составляет 1920 единиц; с фабрики отправлены три груза, в каждом из которых находится по 1800 единиц товара, причем первый груз поступит в магазин на 30-й день, второй - на 60-й, а третий - на 90-й день.
3. Описание метода решения
В нашей курсовой работе мы использовали метод имитационного моделирования. Его основные достоинства
:
1. Имитационная модель позволяет описать моделируемый процесс с большой адекватностью, чем другие.
2. Имитационная модель обладает гибкостью варьирования, структуры алгоритмов и параметров системы.
3. Применение ЭВМ существенно сокращает продолжительность испытаний по сравнению с натуральным экспериментом, если он возможен, а также их стоимость.
Основные недостатки метода имитационного моделирования:
1. Решение, полученное на имитационной модели, всегда носит частный характер, т.к. оно соответствует фиксированным элементам структуры, алгоритмам поведения и значениям параметров системы.
2. Большие трудозатраты на создание модели и проведение экспериментов, а также обработку их результатов. Использование термина имитационное моделирование предполагает работу с такими математическими моделями, с помощью которых результаты исследуемой операции нельзя заранее вычислить или предсказать. Поэтому необходим эксперимент имитации на модели при заданных исходных данных. Сущность машинной имитации заключается в реализации численного метода проведения на ЭВМ экспериментов с математическими моделями, описывающими поведение сложной системы в течение заданного или формируемого периода времени.
Дискретно-событийный подход в имитационном моделировании
Суть дискретно-событийного подхода - моделирование системы с помощью описания изменений состояния системы, происходящих в дискретные моменты времени. Момент времени, в который может измениться: состояние системы, называется моментом наступления события, а соответствующая ему логическая процедура обработки "изменений состояния системы называется событием. Для построения дискретно-событийной модели системы необходимо определить события, при которых может изменяться состояние системы, а затем смоделировать процедуры, соответствующие каждому типу событий. Динамический портрет системы воспроизводится с помощью упорядоченной во времени последовательности событий, в каждом из которых, согласно логической процедуре, моделируются изменения состояния системы.
Состояние системы в дискретно-событийной модели, подобно состоянию в сетевой модели, определяется значениями переменных и атрибутов компонентов, принадлежащих различным классам. Начальное состояние системы устанавливается с помощью задания начальных значений переменных модели, генерации (при необходимости) начальных компонентов в системе, а также с помощью начального планирования событий в модели. В ходе имитации система «движется» от состояния к состоянию по мере того, как компоненты участвуют в действиях, изменяющих состояние системы. При дискретно-событийной имитации изменения состояния системы могут происходить только в начале действия, т. е. когда что-либо начинается, или в конце действия, т. е. когда что-либо завершается. Для моделирования начала и окончания действий используются события.
имитационное моделирование язык программирование

Рис. 1.1. Связь между понятиями «действие» и «событие».
Понятие события, происходящего мгновенно в определенный момент времени, в который начинается или заканчивается некоторое действие, является основополагающим. На рис. 1.1 показана связь между понятиями «действие» и «событие». Внутри события время не изменяется, а изменения состояния системы происходят только в моменты наступления событий. Поведение системы имитируется последовательностью изменений ее состояния, происходящих по мере наступления событий. Когда происходит событие, состояние системы может быть изменено четырьмя способами: 1) изменением значений одной или нескольких переменных модели; 2) изменением количества компонентов в системе; 3) изменением значении одного иди нескольких атрибутов одного компонента; 4) изменением взаимосвязей между компонентами с помощью средств оперирования с файлами. Отметим, что возможны и такие события, при которых состояние системы не меняется.
В ходе имитации осуществляется планирование наступления событий в заданные моменты времени. События имеют атрибуты и заносятся в файл в хронологическом порядке. Например, при планировании наступления события окончания обслуживания атрибуты обслуживаемого клиента являются частью этого события, поэтому они доступны в момент его обработки. Таким образом, если компонент проходят через некоторую последовательность действий, причем завершение каждого из них отображается в соответствующем событии, то по мере обработки событий атрибуты компонента передаются через всю систему.
Процесс имитационного моделирования
Процесс последовательной разработки имитационной модели наминается с создания простой модели, которая затем постепенно усложняется в соответствии с требованиями, предъявляемыми решаемой проблемой. В процессе имитационного моделирования можно выделить следующие основные этапы:
1. Формулирование проблемы: описание исследуемой проблемы и определение целей исследования.
2. Разработка модели: логико-математическое описание моделируемой системы в соответствии с формулировкой проблемы.
3. Подготовка данных: идентификация, спецификация и сбор данных.
4. Трансляция модели: перевод модели на язык, приемлемый для используемой ЭВМ
5. Верификация: установление правильности машинных программ.
6. Валидация: оценка требуемой точности и соответствия имитационной модели реальной системе.
7. Стратегическое и тактическое планирование: определение условий проведения машинного эксперимента с имитационной моделью.
8. Экспериментирование: прогон имитационной модели на ЭВМ для получения требуемой информации.
9. Анализ результатов имитационного эксперимента для подготовки выводов и рекомендаций по решению проблемы.
10. Реализация и документирование: реализация рекомендаций, полученных па основе имитации, и составление документации по модели и ее использованию.
Первой задачей имитационного исследования является точное определение проблемы и детальная формулировка целей исследования. Затем начинается этап построения модели исследуемой системы. Модель включает статистическое и динамическое описание системы. В статистическом описании определяются элементы системы и их характеристики, а в динамическом - взаимодействия элементов системы, в результате которых происходят изменения ее состояния во времени.
Модель должна быть простой для понимания и в то же время достаточно сложной, чтобы реалистично отображать характерные черты реальной системы. Наиболее важными являются принимаемые разработчиком решения относительно того, верны ли принятые упрощения и допущения, какие элементы и взаимодействия между ними должны быть включены в модель. Уровень детализации модели зависит от цели ее создания. Необходимо рассматривать только те элементы, которые имеют существенное значение для решения исследуемой проблемы. Как на этапе формулирования проблемы, так и на этапе моделирования необходимо тесное взаимодействие между разработчиками модели и ее пользователями.
На этапе разработки модели определяются требования к входным данным. Некоторые из этих данных могут уже быть в распоряжении разработчика модели, в то время как для сбора других потребуются время и усилия. Обычно значения таких входных данных задаются на основе некоторых гипотез или предварительного анализа. В некоторых случаях томные значения одного (и более) входных параметров оказывают небольшое влияние на результаты прогонов модели. Чувствительность получаемых результатов к изменению входных данных может быть оценена путем проведения серии имитационных прогонов для различных значений входных параметров. Имитационная модель, следовательно, может использоваться для уменьшения затрат времени и средств на уточнение входных данных.
Следующей задачей является перевод модели в форму, доступную для ЭВМ. Хотя для программирования имитационной модели может использоваться универсальный язык, применение специализированного имитационного языка имеет существенные преимущества. Помимо сокращения времени программирования использование имитационного языка упрощает разработку модели, так как язык содержит набор понятий для формализованного описания системы.
Условия проведения машинных прогонов модели определяются на этапах стратегического и тактического планирования. Задача стратегического планирования заключается в разработке эффективного плана эксперимента, в результате которого либо выясняется взаимосвязь между управляемыми переменными, либо находится комбинация значений управляемых переменных, минимизирующая пли максимизирующая отклик имитационной модели. В тактическом планировании в отличие от стратегического решается вопрос о том, как в рамках плана эксперимента провести каждый имитационный прогон, чтобы получать наибольшее количество информации из выходных данных. Важное место в тактическом планировании занимают определение начальных условий имитационных прогонов и методы снижения дисперсии среднего значения отклика модели.
Следующие этапы в процессе имитационного исследования - проведение машинного эксперимента и анализ результатов - включают прогон имитационной модели на компьютере и интерпретацию полученных выходных данных.
Последним этапом в процессе имитационного исследования являются реализация полученных решений и документирование имитационной модели и ее использования.
При имитационном моделировании реальных систем, как правило, стремятся «сжать» реальное время, т.е. продолжительность процессов в модели, измеряется машинным временем, значительно меньше продолжительности тех же процессов в реальном объекте. Это дает возможность изучать функционирование реальной системы на достаточно длительных интервалах времени. Таким образом, основное назначение имитационного моделирования состоит в следующем:
· выделить наиболее существенные переменные, оценить степень влияния их изменения на исследуемые параметры сети, а также определить «узкие места».
· изучить воздействие различных изменений на показатели надежности сети;
· оценить различные варианты технических решений при поиске оптимальной структуры информационной сети.
Имитационное моделирование реализуются программно с использованием различных языков, как универсальных – БЕЙСИК, РАСКАЛЬ, СИ, так и специализированных для построения имитационных моделей - СИМСКРИПТ. СТАМ/КЛАСС, GPSS, SLAM, Pilgrim.
Этапы процесса построения математической модели системы:
1. Формулируются основные вопросы о поведении системы, ответы на которые мы хотим получить с помощью модели.
2. Из множества законов, управляющих поведением системы, выбираются те, влияние которых существенно при поиске ответов на поставленные вопросы.
3. В пополнение к этим законам, если необходимо, для системы в целом или отдельных ее частей формулируются определенные гипотезы о функционировании.
Трудности при построении математической модели сложной системы:
- Если модель содержит много связей между элементами, разнообразные нелинейные ограничения, большое число параметров;
- Реальные системы зачастую подвержены влиянию случайных различных факторов, учет которых аналитическим путем представляет весьма большие трудности, зачастую непреодолимые при большом их числе;
- Возможность сопоставления модели и оригинала при таком подходе имеется лишь в начале.
Процесс последовательной разработки имитационной модели начинается с создания простой модели, которая затем постепенно усложняется в соответствии с требованиями, предъявляемыми решаемой проблемой. В процессе имитационного моделирования можно выделить следующие основные этапы:
1. Формулирование проблемы: описание исследуемой проблемы и определение целей исследования.
2. Разработка модели: логико-математическое описание моделируемой системы в соответствии с формулировкой проблемы.
3.Подготовка данных: идентификация, спецификация и сбор данных.
4.Трансляция модели: перевод модели на язык, приемлемый для используемой ЭВМ.
5.Верификация: установление правильности машинных программ.
6.Валидация: оценка требуемой точности и соответствия имитационной модели реальной системе.
7. Стратегическое и тактическое планирование: определение условий проведения машинного эксперимента с имитационной моделью.
8. Экспериментирование: прогон имитационной модели на ЭВМ для получения требуемой информации.
9. Анализ результатов: изучение результатов имитационного эксперимента для подготовки выводов и рекомендаций по решению проблемы.
10.Реализация и документирование: реализация рекомендаций, полученных на основе имитации, составление документации по модели и ее использованию.
Хотя некоторые из этих этапов уже обсуждались выше в связи с построением модели, мы, тем не менее, снова кратко рассмотрим основные этапы процесса имитационного моделирования.
Первой задачей имитационного исследования является точное определение проблемы и детальная формулировка целей исследования. Как правило, определение проблемы является непрерывным процессом, который обычно осуществляется в течение всего исследования. Оно пересматривается по мере более глубокого понимания исследуемой проблемы и возникновения новых ее аспектов.
Как только сформулировано начальное определение проблемы, начинаемся этап построения модели исследуемой системы. Модель включает статистическое и динамическое описание системы. В статистическом описании определяются элементы системы и их характеристики, а в динамическом - взаимодействия элементов системы, в результате которых происходят изменения ее состояния во времени.
Процесс формулирования модели во многом является искусством. Разработчик модели должен попять структуру системы, выявить правила ее функционирования и суметь выделить в них самое существенное, исключив ненужные детали. Модель должна быть простой для понимания и в то же время достаточно сложной, чтобы реалистично отображать характерные черты реальной системы. Наиболее важными являются принимаемые разработчиком решения относительно того, верны ли принятые упрощения и допущения, какие элементы и взаимодействия между ними должны быть включены в модель. Уровень детализации модели зависит от цели ее создания. Необходимо рассматривать только те элементы, которые имеют существенное значение для решения исследуемой проблемы. Как на этапе формулирования проблемы, так и на этапе моделирования необходимо тесное взаимодействие между разработчиками модели и ее пользователями. «Первый эскиз» модели должен быть построен, проанализирован и обсужден. Во многих случаях это требует от разработчиков большой ответственности и готовности продемонстрировать свое возможное незнание исследуемой системы. Однако эволюционный процесс моделирования позволяет быстрее обнаруживать допущенные разработчиками неточности и более эффективно их конкретизировать. Кроме того, тесное взаимодействие на этапах формулирования проблемы и разработки модели создает у пользователя уверенность в правильности модели и поэтому помогает обеспечить успешную реализацию результатов имитационного исследования.
На этапе разработки модели определяются требования к входным данным. Некоторые из этих данных могут уже быть в распоряжении разработчика модели, в то время как для сбора других потребуются время и усилия. Обычно значения таких входных данных задаются на основе некоторых гипотез или предварительного анализа. В некоторых случаях томные значения одного (и более) входных параметров оказывают небольшое влияние на результаты прогонов модели. Чувствительность получаемых результатов к изменению входных данных может быть оценена путем проведения серии имитационных прогонов для различных значений входных параметров. Имитационная модель, следовательно, может использоваться для уменьшения затрат времени и средств на уточнение входных данных.
После того как разработана модель и собраны начальные входные данные, следующей задачей является перевод модели в форму, доступную для ЭВМ. Хотя для программирования имитационной модели может использоваться универсальный язык, применение специализированного имитационного языка имеет существенные преимущества. Помимо сокращения времени программирования использование имитационного языка упрощает разработку модели, так как язык содержит набор понятий для формализованного описания системы.
Следующие этапы в процессе имитационного исследования - проведение машинного эксперимента и анализ результатов - включают прогон имитационной модели на компьютере и интерпретацию полученных выходных данных. При использовании результатов имитационных экспериментов для подготовки выводов или проверки гипотез о функционировании реальной системы применяются статистические методы.
Последним этапом в процессе имитационного исследования являются реализация полученных решений и документирование имитационной модели и ее использования. Ни один из имитационных проектов не должен считаться законченным до тех пор, пока их результаты не были использованы в процессе принятия решений. Успех реализации во многом зависит от того, насколько правильно разработчик модели выполнил все предыдущие этапы процессов имитационного исследования. Если разработчик и пользователь работали в тесном контакте и достигли взаимопонимания при разработке модели и ее исследовании, то результаты проекта, скорее всего, будут успешно внедряться. Если же между ними не было тесной взаимосвязи, то, несмотря на элегантность и адекватность имитационной модели, сложно будет разработать эффективные рекомендации.
Названные выше этапы имитационного исследования редко выполняются в строго заданной последовательности, начиная с определения проблемы и кончая документированием. В ходе имитационною исследования могут быть сбои в прогонах модели, ошибочные допущения, от которых в дальнейшем приходится отказываться, пере формулировки целей исследования, повторные оценки и перестройки модели. Такой итеративный процесс позволяет разработать имитационную модель, которая дает верную оценку альтернатив и облегчает процесс принятия решения.
4. Разработка модели
В данной курсовой работе применяются следующие распределения: равномерное, нормальное, логнормальное, пуассоновское распределение. Время ответа на запрос точки магазином имеет логнормальное распределение. Спрос на товары в точке за день имеет пуассоновское распределение. Время ответа на запрос магазина фабрикой распределено нормально, а для нахождения одного нормального числа нужно найти 12 равномерно распределенных чисел.
4.1 Логико-математическое описание моделируемой системы
Нормальное распределение
Функция плотности вероятности нормального закона имеет вид:
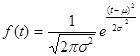
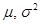 - параметры нормального закона, ( - параметры нормального закона, (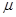 - среднее значение, - среднее значение, 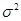 - дисперсия нормального распределения). - дисперсия нормального распределения).
Генератор нормально распределенной случайной величины X можно получить по формулам:

где Tj
(j=1,…,12) – значения независимых случайных величин, равномерно распределенных на интервале (0,1).
Равномерное распределение
Функция плотности вероятности равномерного распределения задает одинаковую вероятность для всех значений, лежащих между минимальным и максимальным значениями переменной. Другими словами, вероятность того, что значение попадает в указанный интервал, пропорциональна длине этого интервала. Применение равномерного распределения часто вызвано полным отсутствием информации о случайной величине, кроме ее предельных значений. Равномерное распределение называют также прямоугольным.
 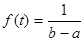 при при 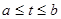 . .
Среднее значение распределения равно
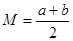 , ,
дисперсия равна
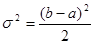 . .
Равномерно распределенная случайная величина X на отрезке [a,b] выражается через равномерно распределенную на отрезке [0,1] случайную величину R формулой
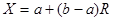 . .
Логнормальное распределение
Метод получения случайного выборочного значения Y=eX
, где X – нормальное распределение случайной величины с дисперсией 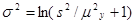 и средним значением и средним значением 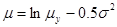
Распределение Пуассона
Для получения пуассоновски распределенной случайной величины Y можно воспользоваться следующим методом:
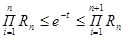 , ,
где Rn
– n-е псевдослучайное число.
4.2 Формализованная схема объекта моделирования
 обслуженный запрос выполненный заказ обслуженный запрос выполненный заказ
запрос заказ
Прибор обслуживания: торговая точка, оптовый магазин и фабрика. При окончании собственных товаров в торговой точке происходит их запрос от нее в оптовый магазин. Тот обслуживает запрос. Если и в магазине все запрашиваемые товары закончились, происходит их заказ на фабрику в целях пополнения запаса магазина. Фабрика производит в установленные сроки выполнение заказа.
4.3 Временная диаграмма
При нехватке товаров в торговой точке ежедневно поступает запрос на их определенное количество от нее в оптовый магазин. Спрос на товары в точке за день имеет пуассоновское распределение. Оптовый магазин каждые 14 дней размещает заказы на фабрике. Время ответа на запрос точки магазином имеет логнормальное распределение. Время ответа на запрос магазина фабрикой распределено нормально.
4.4 Блок-схемы программных блоков и основной программы
Принятые сокращения:
TTEK – текущее время;
KOLTOV – спрос на товары в торговой точке;
ZAKTOV –заказанное магазином количество товаров у фабрики;
Z – заказанное торговой точкой количество товаров у магазина;
KOLTEK – текущее количество запасов торговой точке
SHOP[i] – массив с данными о текущем времени и числом товаров в магазине;
TOVMAG –число товаров в оптовом магазине.
time – текущее время при обращении в оптовый магазин.
Рис. 1. Блок-схема равномерного распределения.

Рис. 2. Блок-схема нормального распределения
Рис. 4. Блок-схема логнормального распределения.

Нет да
Рис.3. Блок-схема распределения Пуассона.

нет
нет
нет
нет
нет
нет

Рис. 4. Блок-схема функции «Оптовый магазин».
Ввод KOLTEK
нет
Вывод KOLTOV, TTEK, ZAKTOV,Z,SHOP
Рис.5. Блок-схема основной программы.
5. Перевод алгоритма на язык программирования
Структурное программирование – это технология создания программ, позволяющая путем соблюдения определенных правил уменьшить время разработки и количество ошибок, а также облегчить возможность модификации программы.
Разные типы процессоров имеют разный набор команд. Если язык программирования ориентирован на конкретный тип процессора и учитывает его особенности, то он называется языком программирования низкого уровня. Языком самого низкого уровня является язык ассемблера, который просто представляет каждую команду машинного кода в виде специальных символьных обозначений, которые называются мнемониками. С помощью языков низкого уровня создаются очень эффективные и компактные программы, т.к. разработчик получает доступ ко всем возможностям процессора. Т.к. наборы инструкций для разных моделей процессоров тоже разные, то каждой модели процессора соответствует свой язык ассемблера, и написанная на нем программа может быть использована только в этой среде. Подобные языки применяют для написания небольших системных приложений, драйверов устройств и т. п.
С помощью языка программирования создается текст, описывающий ранее составленный алгоритм. Чтобы получить работающую программу, надо этот текст перевести в последовательность команд процессора, что выполняется при помощи специальных программ, которые называются трансляторами. Трансляторы бывают двух видов: компиляторы и интерпретаторы. Компилятор транслирует текст исходного модуля в машинный код, который называется объектным модулем за один непрерывный процесс. При этом сначала он просматривает исходный текст программы в поисках синтаксических ошибок. Интерпретатор выполняет исходный модуль программы в режиме оператор за оператором, по ходу работы, переводя каждый оператор на машинный язык.
Языки программирования высокого уровня не учитывают особенности конкретных компьютерных архитектур, поэтому создаваемые программы на уровне исходных текстов легко переносятся на другие платформы, если для них созданы соответствующие трансляторы. Разработка программ на языках высокого уровня гораздо проще, чем на машинных языках.
Си – был создан в 70- е годы первоначально не рассматривался как массовый язык программирования. Он планировался для замены ассемблера, чтобы иметь возможность создавать такие же эффективные и короткие программы, но не зависеть от конкретного процессора. Он во многом похож на Паскаль и имеет дополнительные возможности для работы с памятью. На нем написано много прикладных и системных программ, а также операционная система Unix. Си++ - объектно-ориентированное расширение языка Си, созданное Бьорном Страуструпом в 1980г.
Программа
:
#include<iostream.h>
#include<math.h>
#include<conio.h>
#include<stdlib.h>
#include<stdio.h>
float ravnom(float d11, float d21)
{
randomize();
float R;
R=d11+(d21-d11)*random(100)/100.0;
return R;
}
float normal(float b1, float b2)
{
randomize();
float X=0;
int i;
float R,d1,d2;
d1=(b1-sqrt(3*b2*12))/12;
d2=(b1+sqrt(3*b2*12))/12;
for(i=1;i<=12;i++)
X=X+ravnom(d1,d2);
return X;
}
float lognorm(float Ay, float By)
{
randomize();
float X,Y,a,b;
b=log(By/pow(Ay,2)+1);
a=log(Ay-0.5*b);
X=normal(a,b);
Y=exp(X);
return Y;
}
int puasson(float t)
{
randomize();
int n;
int R, R11;
do
{ R*=random(100)/100.0;
R11=R;
R*=random(100)/100.0;
n++; }
while(exp(-t)>=R11&&exp(-t)<R);
return (n-1);
}
float optmag(float &TTEK, int ZZ)
{
int Tzak,a=90,b=10;
static int TOVMAG;
if(ZZ<=1920){
TOVMAG=1920-ZZ;
TTEK=TTEK+lognorm(5,1);
}
if(TTEK==30) TOVMAG+=1800;
if(TTEK==60) TOVMAG+=1800;
if(TTEK==90) TOVMAG+=1800;
if(TOVMAG<=0)
Tzak=normal(a,b);
if(Tzak>=60&&Tzak<=120)
{
TOVMAG=1920-TOVMAG;
TTEK+=Tzak;
}
return (TOVMAG);
}
main()
{
clrscr();
int Z,SHOP,KOLTEK,KOLTOV;
float TTEK;
cout<<"Vvedite tekushee kolichestvo tovarov v torgovoj tochke:\n";
cin>>KOLTEK;
cout<<"\n\n";
TTEK=0;
KOLTOV=puasson(TTEK);
if (KOLTOV<=KOLTEK)
KOLTEK=KOLTEK-KOLTOV;
TTEK++;
Z=KOLTOV-KOLTEK;
SHOP=optmag(TTEK,Z);
cout<<"Tekushee vremya="<<TTEK<<"\n";
cout<<"Spros na tovari v torg. tochke="<<KOLTOV<<"\n";
cout<<"Zakazannoe magazinom kol-vo tovarov y fabriki="<<SHOP<<"\n";
cout<<"Zakazannoe torg. tochkoj kol-vo tovarov y magazina="<<Z<<"\n";
cout<<"Normativnij zapas tivarov v magazine = 70"<<"\n";
getch();
return 0;
}
6. Верификация: установление правильности машинной программы
На этапах верификации и валидации осуществляется оценка функционирования имитационной модели. На этапе верификации определяется, соответствует ли запрограммированная для ЭВМ модель замыслу разработчика. Это обычно осуществляется путем ручной проверки вычислений, а также может быть использован и ряд статистических методов. Написанная программа полностью отвечает требованиям курсовой работы. В ходе выполнения были найдены некоторые ошибки, которые были устранены при выполнении программы.
7. Результаты эксперимента
При запуске программы со следующими входными параметрами:
Vvedite tekushee kolichestvo tovarov v torgovoj tochke:
70
Получим следующие результаты:
Tekushee vremya=98
Spros na tovari v torg. tochke=2730
Zakazannoe magazinom kol-vo tovarov y fabriki=1920
Zakazannoe torg. tochkoj kol-vo tovarov y magazina=2660
Normativnij zapas tоvarov v magazine = 70
8. Анализ результатов

9. Заключение
Программа выдает на экран вероятностные и статистические характеристики объекта моделирования. Она имитирует работу описанной системы с целью определения изменения уровня запаса при заданной стратегииуправления розничной торговой точкой и оптовым магазином.
На основании проделанной работы, можно сделать следующие выводы:
1. Созданная математическая модель адекватна реальному объекту;
2. Проведенные исследования показали эффективность модели и способов “приведения её в действие” при определении необходимых нам параметров по сравнению с ручным способом моделирования и расчетов параметров;
3. Созданная модель имеет достаточную, для таких моделей, степень универсальности, т.к. диапазон входных параметров системы можно легко и быстро изменить.
10. Список использованной литературы
1. Клейнрок Л.«Теория массового обслуживания.»-М.: Машиностроение, 1979.-432 с.
2. Прицкер А. «Введение в имитационное моделирование» -М.: Мир, 1987.-644с.
3. Емельянов А.А., Власова Е.А., «Имитационное моделирование экономических процессов» - М. Финансы и статистика,2002.
6. Вентцель Е. С. Теория вероятностей. - М.: Наука, 1969. - 564 с.
7.Пугачев В. С. Теория вероятностей и математическая статистика. - М: Наука, 1979. -327 с.
8.Бусленко Н.П. Моделирование сложных систем. - М.: Наука, 1978. 399 с.
9.Шрайбер Т. Дж. Моделирование на GPSS. -W.: Машиностроение, 1979. - 287 с,
10. Варфоломеев В.И. Алгоритмическое моделирование элементов экономических систем. - М.: Финансы и статистика, 2000. -208 с.
|