Министерство образования Республики Башкортостан
Стерлитамакский колледж строительства, экономики и права
КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ
«МАТЕМАТИЧЕСКИЕ МЕТОДЫ»
На тему: «Методы решения задач линейного программирования с
n
-переменными»
Выполнила: студентка гр. ПО-32
Талант Людмила Владимировна
Руководитель: Шалаева И.И.
г. Стерлитамак 2011
Введение
Постановка основной задачи линейного программирования с n-переменными
Графический метод решения задач линейного программирования с n-переменными
Симплекс-метод решения задач линейного программирования с n-переменными
Математическая модель
Решение задачи в MS Excel
Решение задачи графическим методом
Решение задачи симплекс-методом
Аналитическая часть
Заключение
Список используемой литературы
В
ведение
Цель курсового проектирования — закрепить, систематизировать и комплексно обобщить знания по методам решения задач линейного программирования с n-переменными и развить навыки самостоятельной творческой работы; научиться практически применять полученные теоретические знания при решении конкретных вопросов; научиться пользоваться справочной литературой, стандартами, другими нормативно-техническими документами и средствами вычислительной техники. Объектом исследования будет конкретная задача, описанная ниже. В курсовой работе рассмотрим графический и симплекс-методы линейного программирования с n-переменными и найдем оптимальный план производства товаров, обеспечивающего предприятию максимальную прибыль.
Актуальность подобных задач в настоящее время сомнений, как правило, ни у кого не вызывает, т.к. проблема оптимального планирования производства сейчас, в постиндустриальный век, является, наверное, второй по степени важности после проблемы наилучшей организации передачи и хранения информации, а в России, скорее всего, главной, если говорить исключительно о развитии научного прогресса в нашей стране.
Постановка
основной задачи линейного программирования с n-переменными
Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств. Называется программированием условно, не имея ничего общего с написанием машинного кода.
Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.
Реклама

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.
Термин «программирование» нужно понимать в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, ещё до того, как компьютеры были использованы для решения линейных задач оптимизации.
В линейном программировании изучаются свойства решений линейных
систем уравнений и неравенств с n-переменными следующего вида:
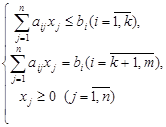 (1.1)
(1.1)
В системах (1.1) коэффициенты aij
и правые части bi
являются числами.
Системы (1.1) называются системами ограничений.
Точка в n - мерном пространстве
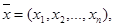 (1.2) (1.2)
удовлетворяющая системе (1.1), называется допустимым планом.
Основной задачей линейного программирования (ОЗЛП) с n-переменными называется задача о нахождении такого допустимого плана, который доставляет максимум функции
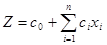 (1.3) (1.3)
Функция Z, определенная соотношением (1.3), называется функцией прибыли (целевой функцией).
Допустимый план, доставляющий максимум функции (1.3), называется оптимальным планом.
Иногда в задачах линейного программирования вместо нахождения максимума функции прибыли Z требуется найти минимум функции затрат
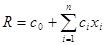 (1.4) (1.4)
В этом случае с помощью введения функции Z = − R задача о нахождении минимума функции затрат R сводится к задаче о нахождении максимума функции прибыли Z.
Задача линейного программирования для n-переменных
Рассмотрим задачу формирования плана производства.
Некоторое предприятие может выпускать определённый набор продукции. Нормы затрат известны. Требуется построить производственный план, учитывающий ограниченность ресурсов.
Формализация
n - число различных видов продукции.
m - число различных ресурсов.
Таблица №1
| Вид продукции |
Норма расхода ресурса на единицу продукции |
Прибыль на единицу продукции |
| 1 |
2 |
3 |
... |
i |
… |
m |
| 1 |
a11
|
c21
|
a31
|
… |
ai1
|
… |
am1
|
c1
|
| 2 |
a12
|
c22
|
a32
|
… |
ai2
|
… |
am2
|
c2
|
| 3 |
a13
|
c23
|
a33
|
… |
ai3
|
… |
am3
|
c3
|
| … |
… |
… |
… |
… |
… |
… |
… |
… |
| j |
a1j
|
c2j
|
a3j
|
… |
aij
|
… |
amj
|
cj
|
| … |
… |
… |
… |
… |
… |
… |
… |
… |
| n |
a1n
|
a2n
|
a3n
|
… |
ain
|
… |
amn
|
cn
|
| Ограничения на ресурсы |
b1
|
b2
|
b3
|
… |
bi
|
… |
bm
|
aij
- объём i-того ресурса, который расходуется на производство одной единицы j-того вида продукции i=1..m, j=1..n.
xj
- объем (количество единиц) j-того вида продукции в производственном плане предприятия (j от 1 до n).
Необходимо определить нормы выпуска каждого вида продукции, чтобы прибыль от её реализации была максимальной.
Построение экономико-математической модели
Прибыль обозначим F, тогда F=c1
x1
+c2
x2
+...+cn
xn
g max
Составим ограничения для первого ресурса:
а11
- объем первого ресурса, который расходуется на производство одной единицы первого вида продукции;
а11
x1
- объём первого ресурса, который требуется на изготовление x1
единиц первого вида продукции;
Реклама

а12
x2
- объём первого ресурса, который требуется на изготовление x2
единиц второго вида продукции;
а1n
xn
- объём первого ресурса, который требуется на изготовление xn
единиц n-ого вида продукции;
а11
x1
+a12
x2
+...+a1n
xn
- объём первого ресурса, который требуется на изготовление продукции, следовательно, мы имеем следующее ограничение:
а11
x1
+а12
+...+а1n
xn
<=b1
Аналогично для остальных ресурсов:
а21
x1+а22
+...+а2n
xn
<=b2
а31
x1+а32
+...+а3n
xn
<=b3
...
аm1
x1
+аm2
+...+amn
xn
<=bm
Кроме того, количество выпущенной продукции не может быть отрицательной, следовательно, x1
>= 0, x2
>=0, ...,xn
>=0.
Таким образом, получаем следующую экономико-математическую модель задачи линейного программирования:
 (2.1) (2.1)
Задачу линейного программирования для N (любое целое число) переменных можно представить в следующем виде:

Решения, удовлетворяющие системе ограничений условий задачи и требованиям неотрицательности, называются допустимыми, а решения, удовлетворяющие одновременно и требованиям минимизации (максимализации) целевой функции, — оптимальными .
С помощью графического метода может быть решена задача линейного программирования, система ограничений которой содержит n неизвестных и m линейно независимых уравнений, если N и M связаны соотношением N – M = 2.
Действительно, пусть поставлена задача линейного программирования.
Найти максимальное значение линейной функции
Z = c1
х1
+c2
х2
+... +cN
xN
при ограничениях
a11
x1
+ a22
x2
+ ... + a1N
ХN
= b1
a21
x1
+ a22
x2
+ ... + a2N
ХN
= b2
. . . . . . . . . . . . . . .
aМ
1
x1
+ aМ
2
x2
+ ... + aМ
N
ХN
= bМ
xj
≥ 0 (j = 1, 2, ..., N)
где все уравнения линейно независимы и выполняется соотношение N - M = 2.
Используя метод Жордана-Гаусса, производим M исключений, в результате которых базисными неизвестными оказались, например, M первых неизвестных х1
, х2
, ..., хM
, а свободными — два последних: хМ+1
, и хN
, т. е. система ограничений приняла вид:
x1
+ a1,М+1
xМ+1
+ a1N
ХN
= b1
x2
+ a2,М+1
xМ+1
+ a2N
ХN
= b2
. . . . . . . . . . . .
xМ
+ aМ, М+1
x2
+ aМN
ХN
= bМ
xj
≥ 0 (j = 1, 2, ..., N)
С помощью уравнений преобразованной системы выражаем линейную функцию только через свободные неизвестные и, учитывая, что все базисные неизвестные — неотрицательные: хj
≥ 0 (j = 1, 2, ..., M), отбрасываем их, переходя к системе ограничений, выраженных в виде неравенств.
Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.
Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь — система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные x1
, x2
, ..., xr
. Тогда наша система уравнений может быть записана как
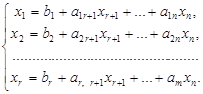 (3.1) (3.1)
К такому виду можно привести любую совместную систему, например, методом Гаусса. Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными.
Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные x1
, x2
, ..., xr
, то решение {b1
, b2
,..., br
, 0, ..., 0} будет опорным при условии, что b1
, b2
,..., br
≥ 0.
Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.
Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем.
Имея систему ограничений, приведенную к общему виду, то есть к системе m-линейных уравнений с n-переменными (m < n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще.
Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то, осуществляется переход к другому, обязательно допустимому базисному решению.
Симплексный метод гарантирует, что при этом новом решении линейная форма, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.
Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.
Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения.
При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода.
Приведенная схема симплексного метода явно выражает его алгоритмический характер (характер четкого предписания о выполнении последовательных операций), что позволяет успешно программировать и реализовать этот метод на ЭВМ. Задачи же с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.
Практическая часть
Постановка задачи
Торговое предприятие планирует организовать продажу 4 видов товара A, B, C, D, учитывая при этом только два вида ресурсов: рабочее время продавцов в количестве 970 часов и площадь товарного зала 290 м2
. Плановые нормативы затрат ресурсов в расчете на единицу товара каждого наименования и прибыль от их продажи заданы в таблице.
| Показатели |
Товары |
Общее кол-во ресурсов |
| A |
B |
C |
D |
| Расход рабочего времени на единицу товара, ч |
0,62 |
0,81 |
0,71 |
0,43 |
970 |
| Использование площади торгового зала на единицу товара, м2 |
0,13 |
0,22 |
0,45 |
0,22 |
290 |
| Прибыль от продажи единицы товара, руб |
30 |
50 |
62 |
40 |
Требуется определить оптимальную структуру товарооборота, обеспечивающую торговому предприятию максимум прибыли.
Математическая модель
Пусть x – количество товара, продажу которого планирует организовать торговое предприятие. Тогда x1
– товар вида A, x2
– товар вида B, x3
– товар вида C и x4
– товар вида D.
0,62x1
+0,81x2
+0,71x3
+0,43x4
– расход рабочего времени на изготовление товара. Так как этот ресурс ограничен, имеем следующее ограничение: 0,62x1
+0,81x2
+0,71x3
+0,43x4
£970.
0,13x1
+0,22x2
+0,45x3
+0,22x4
– использование торгового зала на изготовление товара. Так как этот ресурс ограничен, имеем следующее ограничение: 0,13x1
+0,22x2
+0,45x3
+0,22x4
£290.
Кроме того, количество выпущенной продукции не может быть отрицательной, следовательно, x1
³0, x2
³0, x3
³0, x4
³0.
Задача состоит том, чтобы найти значения x1
, x2
, x3
и x4
при которых полученная прибыль будет наибольшей. Прибыль обозначим F, тогда
F=30x1
+50x2
+62x3
+40x4
Þmax
Таким образом, получаем следующую экономико-математическую модель задачи линейного программирования:
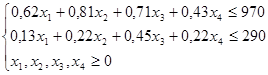
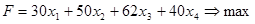
В качестве значений переменных x1
, x2
, x3
, x4
будем использовать ячейки $B$12:$B$15. Для значения целевой функции будем использовать ячейку $C$16.
В целевую ячейку $C$16 впишем формулу: B5*B12+C5*B13+D5*B14+E5*B15.
В ячейку $C$12 впишем формулу прибыли от товара A: B5*B12.
В ячейку $C$13 впишем формулу прибыли от товара B: C5*B13.
В ячейку $C$14 впишем формулу прибыли от товара C: D5*B14.
В ячейку $C$15 впишем формулу прибыли от товара D: E5*B15.
В ячейку $G$3 впишем формулу ограничения расхода рабочего времени: B3*B12+C3*B13+D3*B14+E3*B15.
В ячейку $G$4 впишем формулу ограничения использования площади торгового зала: B4*B12+C4*B13+D4*B14+E4*B15.

Рис. 1 Компьютерная модель задачи
Далее выбираем пункт меню Сервис/Поиск решения:
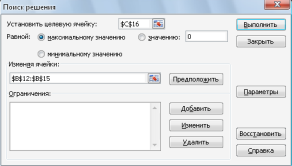
Рис. 2 Окно поиска решения
Перед нами открывается диалоговое окно Поиск решения. В нём указываем, что нам необходимо установить ячейку $
C
$16
максимальному значению, изменяя ячейки $
B
$12:$
B
$15
. Далее нажимаем кнопку Добавить для добавления ограничений. И добавляем следующие ограничения:

Рис. 3 Добавление ограничений
Ограничения по расходу рабочего времени на единицу товара.
После ввода каждого ограничения нажимаем кнопку Добавить. После ввода последнего ограничения нажимаем кнопку OK. И диалоговое окно Поиск решения принимает следующий вид:
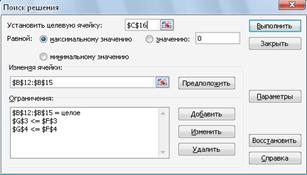
Рис. 4 Окно поиска решения, после ввода ограничений
Задаем параметры поиска решения:
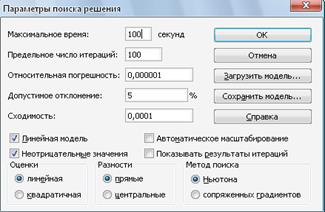
Рис. 5 Измененеие параметров поиска решения
Нажимаем кнопку Выполнить. И перед нами открывается диалоговое окно Результаты поиска решения:
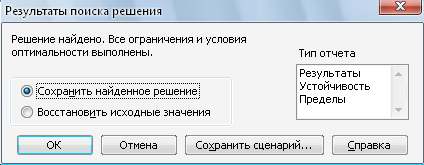
Рис. 6 Выбираем отчет по результатам
Выбираем создание отчёта по результатам. Отчеты по устойчивости и пределам не создаются при использовании целочисленных ограничений на переменные. После нажатия кнопки OK в рабочей книге появляется новый лист с названием Отчет по результатам, содержащий отчёт по результатам, и получаем следующие результаты:
| Товар |
Кол-во |
Прибыль |
| A |
0 |
0 |
| B |
1061 |
53050 |
| C |
0 |
0 |
| D |
257 |
10280 |
| Стоимость продукции |
63330 |
Рис. 7 Результат выполнения поиска решения
Отчет по результатам
| Microsoft Excel 11.0 Отчет по результатам |
| Рабочий лист: [Лююю.xls]Лист1 |
| Отчет создан: 15.02.2011 11:47:21 |
| Целевая ячейка (Максимум) |
| Ячейка |
Имя |
Исходное значение |
Результат |
| $C$16 |
Стоимость продукции Прибыль |
63337,32057 |
63330 |
| Изменяемые ячейки |
| Ячейка |
Имя |
Исходное значение |
Результат |
| $B$12 |
A Кол-во |
0 |
0 |
| $B$13 |
B Кол-во |
1061,004785 |
1061 |
| $B$14 |
C Кол-во |
0 |
0 |
| $B$15 |
D Кол-во |
257,1770335 |
257 |
| Ограничения |
| Ячейка |
Имя |
Значение |
Формула |
Статус |
Разница |
| $A$20 |
Расход рабочего времени на единицу товара, ч |
969,92 |
$A$20<=$F$3 |
не связан. |
0,08 |
| $B$20 |
Использование площади торгового зала на единицу товара, м2 |
289,96 |
$B$20<=$F$4 |
не связан. |
0,04 |
| $B$15 |
D Кол-во |
257 |
$B$15>=0 |
не связан. |
257 |
| $B$14 |
C Кол-во |
0 |
$B$14>=0 |
связанное |
0 |
| $B$12 |
A Кол-во |
0 |
$B$12>=0 |
связанное |
0 |
| $B$13 |
B Кол-во |
1061 |
$B$13>=0 |
не связан. |
1061 |
| $B$12 |
A Кол-во |
0 |
$B$12=целое |
связанное |
0 |
| $B$13 |
B Кол-во |
1061 |
$B$13=целое |
связанное |
0 |
| $B$14 |
C Кол-во |
0 |
$B$14=целое |
связанное |
0 |
| $B$15 |
D Кол-во |
257 |
$B$15=целое |
связанное |
0 |
Ответ: Чтобы прибыль максимальной – 63330 денежных единиц, предприятие должно выпустить 0 изделий товара A, 1061 изделий товара B, 0 изделий товара C и 257 изделий товара D.
линейное программирование прибыль товарооборот
Решение задачи графическим методом
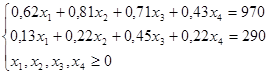
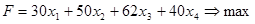
Задача решается графическим методом, если разность между количеством переменных и количеством ограничений равна двум.
n=4 (количество переменных)
m=2 (количество ограничений)
n
-m=4-2=2
Выразим две переменные:
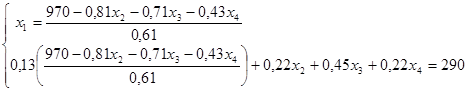
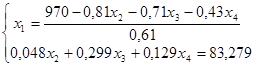
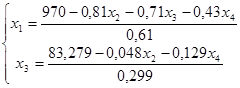
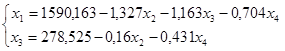
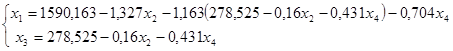
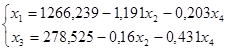
Подставим значения переменных в целевую функцию.
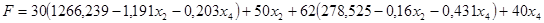
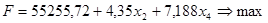
Найдем координаты прямых.
I. 1266,239-1,191x2
-0,203x4
=0
1,191x2
+0,203x4
=1266,239
x2
=1063,172-0,17x4
II. 278,525-0,16x2
-0,431x4
=0
0,16x2
+0,431x4
=278,525
x4
=646,229-0,371x2
III. 55255,72+4,35x2
+7,188x4
=0
-4,35x2
-7,188x4
=55255,72
x2
= -12702,464-1,652x4
Построим область допустимых решений задачи, ограниченную прямыми:
x2
=1063,172-0,17x4
(I)
x4
=646,229-0,371x2
(II)
x2
= -12702,464-1,652x4
(III)
Найдем max:
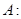 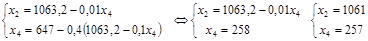
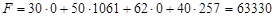

Рис. 1 График функции
Построим линию уровня 55255,72+4,35x2
+7,188x4
=0 и вектор градиента (4,35; 7,188). Будем передвигать линию уровня, пока не выйдем из многоугольника, что произойдет в точке A с координатами (1061; 257). В этой точке функция принимает максимальное значение 63330.
Ответ: Чтобы достичь максимальной прибыли предприятие должно выпустить 1061 изделий товара B и 257 изделий товара D.
Решение задачи симплекс-методом
Решим прямую задачу линейного программирования симплекс-методом. Определим максимальное значение целевой функции F(X) = 30x1
+50x2
+62x3
+40x4
при следующих условиях:
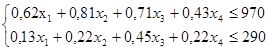
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
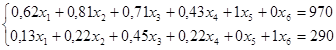
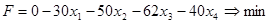
Выразим базисные переменные x5
и x6
через небазисные.
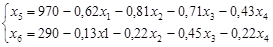
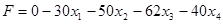
Переходим к основному алгоритму симплекс-метода.
Поскольку задача решается на максимум, то переменную для включения в текущий план выбирают по максимальному положительному числу в уравнении для x0
.
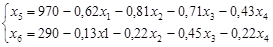
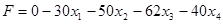
В качестве новой переменной выбираем x3
.
Вычислим значения D3
по всем уравнениям для этой переменной
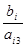 и выберем из них наименьшее: и выберем из них наименьшее:
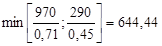
Вместо переменной x6
в план войдет переменная x3
.
Выразим переменную x3
через x6
и подставим во все выражения.
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
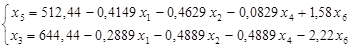
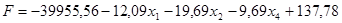
Полагая небазисные переменные x5
и x3
равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (-12.09, -19.69, 0, -9.69, 0, 137.78), x0
= 39955.5556
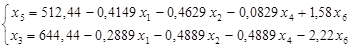
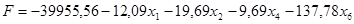
В качестве новой переменной выбираем x2
.
Вычислим значения D2
по всем уравнениям для этой переменной.
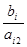 и выберем из них наименьшее: и выберем из них наименьшее:
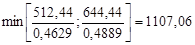
Вместо переменной x5
в план войдет переменная x2
.
Выразим переменную x2
через x5
и подставим во все выражения.
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
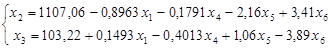
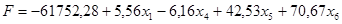
Полагая небазисные переменные x2
и x3
равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (5.56, 0, 0, -6.16, 42.53, 70.67), x0
= 61752.2804
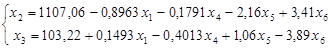
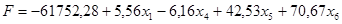
В качестве новой переменной выбираем x4
.
Вычислим значения D4
по всем уравнениям для этой переменной.
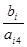 и выберем из них наименьшее: и выберем из них наименьшее:
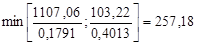
Вместо переменной x3
в план войдет переменная x4
.
Выразим переменную x4
через x3
и подставим во все выражения.
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
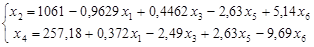
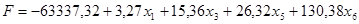
Полагая небазисные переменные x2
и x4
равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (3.27, 0, 15.36, 0, 26.32, 130.38), x0
= 63337.3206
Выражение для x0
не содержит положительных элементов. Найден оптимальный план.
Окончательный вариант системы уравнений:
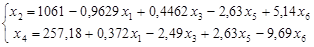
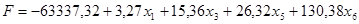
Оптимальный план можно записать так:
x2
= 1061
x4
= 257.18
Так как необходимо определить плановые нормативы затрат ресурсов в расчете на единицу товара каждого наименования, обеспечивающие торговому предприятию максимум прибыли, то оптимальный план запишем так:
x2
= 1061
x4
= 257
Максимальная прибыль предприятия:
F(x) = 50*1061 + 40*257= 63330
Ответ: Чтобы прибыль максимальной – 63330 денежных единиц, предприятие должно выпустить 1061 изделий товара B и 257 изделий товара D.
Линейное программирование – это раздел исследования операций, в котором изучаются линейные оптимизационные модели, т.е. задачи поиска минимума затрат при условии выполнения необходимого объема работ или максимума прибыли при линейных ограничениях на ресурсы.
Ценность решения задач линейного программирования объясняется возможностью на основании итогового отчёта принимать важные управленческие решения и моделировать реальную производственную ситуацию. Это особенно ценно сейчас, в век широкого применения информационных технологий при решении реальных задач.
Математическая модель отражает проблему в абстрактной форме и позволяет учесть большое число разнообразных характеристик, от которых зависит эта проблема. Анализ и расчет математической модели позволяют выбрать оптимальные решения поставленной задачи и обосновать этот выбор.
В ходе исследования вопроса о решении задачи максимизации методами линейного математического программирования, мною было установлено, что наилучшим алгоритмом решения подобного рода задач является симплекс-метод.
Для убеждения в том, что решение выполнено правильно, поставленная задача была решена несколькими методами и проверена в MSExcel.
Мною было заключено, что решения выполнены верно, так как они совпали друг с другом.
Для наглядности в проекте приводятся скриншоты решения поставленной задачи в MSExcel и подробно расписано решение графического и симплекс-метода.
Решение определило следующий оптимальный план производства товаров:
Для максимизации прибыли, которая составляет 63330 денежных единиц, предприятие должно выпустить 0 изделий товара A, 1061 изделий товара B, 0 изделий товара C и 257 изделий товара D.
По моему мнению, наилучшим методом максимизации, т.е. решения конкретной поставленной передо мной задачи, является симплекс метод решения задач линейного программирования, которого достаточно подробно освещается в основной части теоретического раздела.
В ходе работы над данным курсовым проектом, были раскрыты методы линейного программирования с n- переменными, в частности, графический метод и симплекс-метод и построена экономико-математическая модель задачи линейного программирования с её подробным описанием, получен исчерпывающий отчёт о результатах решения задачи, а также получено графическое и симплекс-решение.
Была решена конкретная поставленная передо мною практическая задача. Полученные решения различными методами совпали, что свидетельствует о правильном выполнении задания. Я получила оптимальное решение выпуска товара при максимальной прибыли в 63330 денежных единиц. Были выполнены все необходимые ограничения и выявлено в каком количестве стоит производить различные товары.
Выполняя данный курсовой проект, я лучше усвоила знания, в особенности симплекс-метод. Выполняя практическое задание, была использована дополнительная литература, которую я брала в библиотеке и на сайтах.
Таким образом, было наглядно представлено и прокомментированы полученные решения задач и нахождение оптимального плана выпуска товара, где достигалась максимальная прибыль и ресурсы использовались наиболее полно.
С
писок используемой литературы
1. Ашманов С.А. Линейное программирование. М.: Наука, 2001.
2. Калихман И.Л. Линейная алгебра и программирование. - М.: Высшая школа, 1987
3. http://revolution./emodel/00188498_0.html
4. Лунгу К.К. Линейное программирование. Руководство к решению задач. – М.: ФИЗМАТЛИТ, 2005.
|