Министерство образования и науки РФ
Череповецкий государственный университет
Институт информационных технологий
Кафедра прикладной математики
Дисциплина: Геометрия и алгебра
Курсовая работа
на тему «Некоторые замечательные кривые»
г. Череповец
2010-2011 уч.г.
Содержание
Введение
1. Строфоида
1.1 Определение
1.2 Исторические сведения
1.3 Стереометрическое образование
1.4 Особенности формы
1.5 Задача
2. Циссоида Диокла
2.1 Определение и построение
2.2 Исторические сведения
2.3 Площадь S полосы
2.4 Объем V тела вращения
2.5 Задача
3. Декартов лист
3.1 Исторические сведения
3.2 Построение
3.3 Особенности формы
3.4 Задача
4. Улитка Паскаля
4.1 Определение и построение
4.2 Исторические сведения
4.3 Особенности формы
4.4 Свойства нормали
4.5 Построение касательной
4.5 Задача
5. Лемниската Бернулли
5.1 Определение
5.2 Исторические сведения
5.3 Построение
5.4 Особенности формы
5.5 Свойства нормали
5.6 Построение касательной
5.7 Задача
Заключение
Используемая литература
Введение
В данной работе мы рассмотрим некоторые замечательные кривые и их особенности.
В параграфе 1 будет рассмотрена строфоида, особенности её формы, стереометрическое образование и исторические сведения.
Во 2-м параграфе мы изучим циссоиду Диокла и некоторые формулы, связанные с ней.
В параграфе 3 узнаем метод построения, особенности формы и исторические сведения о кривой, называемой «Декартов лист».
В 4-м параграфе рассмотрим улитку Паскаля. Её определение, построение, особенности формы, свойства нормали и построение касательной. плоский кривой лемниската бернули строфоида
В параграфе 5 будет изучена лемниската Бернулли: определение, построение, исторические сведения, особенности формы, свойства нормали и построение касательной.
А также при помощи задач узнаем формулы кривых в прямоугольной декартовой и полярной системах координат.
1. Строфоида
1.1 Определение.
Прямая строфоида
, или просто строфоида
, определяется так: берём взаимно-перпендикулярные прямые AB, CD (рис.1) и на одной из них точку A; через неё проводим произвольую прямую AL, пересекающую CD в точке P. На AL откладываем отрезки PM1,
, PM2
равные PO (O – точка пересечения AB и CD). Строфоида (прямая) есть геометрическое место точек M1
,M2
.
Реклама

Косая строфоида
(рис.2) строится аналогично с той разницей, что AB и CD пересекаются косоугольно.
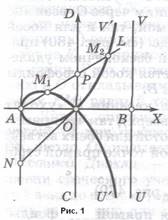 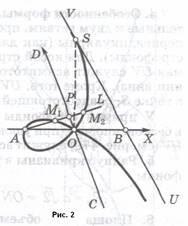
1.2 История вопроса
Строфоида была рассмотрена (вероятно, впервые) Ж. Робервалем в 1645 г. под именем птероиды. Нынешнее название введено Миди в 1849 г.
1.3 Стереометрическое образование
Представим себе цилиндрическую поверхность с осью CD (см. рис.1) и радиусом AO. Через точку A проведем перпендикулярную плоскости чертежа произвольную плоскость K (прямая AL – след этой плоскости). В сечении получим эллипс; его фокусы M1
, M2
описывают прямую строфоиду.
Косая строфоида строится аналогично с той лишь разницей, что цилиндрическая поверхность заменяется конической: ось конуса (OS на рис.2) проходит через O перпендикулярно AB; прямая UV, проходящая через B параллельно CD, – одна из образующих. Точки M1
, M2
– фокусы соответствующего конического сечения; косая строфоида расположена на обеих полостях конической поверхности и проходит через вершину S последней.
1.4 Особенности формы
Точка O – узловая; касательные к ветвям, проходящим через O, взаимно перпендикулярны (как для прямой, так и для косой строфоиды). Для косой строфоиды (рис.2) прямая UV служит асимптотой (при бесконечном удалении вниз). Кроме того, UV касается косой строфоиды в точке S, равноотстоящей от A и B.
У прямой строфоиды точка касания S «уходит в бесконечность» (при удалении вверх), так что прямая UV (см. рис.1) служит асимптотой для обеих ветвей.
1.5 Задача
Написать уравнение строфоиды в прямоугольной декартовой системе координат, осями которой являются прямые AB и CD, а направление оси OX определяется направлением оси строфоиды.
Решение:
Пусть O – начало координат; ось OX направлена по лучу OB; AO=a, 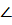 AOD=α; когда строфоида – косая, система координат – косоугольная, ось OY направлена по лучу OD: AOD=α; когда строфоида – косая, система координат – косоугольная, ось OY направлена по лучу OD:
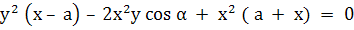 (1) (1)
Для прямой строфоиды уравнение (1) приводится к виду
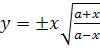 . .
2. Циссоида Диокла
2.1 Определение и построение
На отрезке OA = 2a, как на диаметре, строим окружность C (рис.3) и проводим через A касательную UV. Через O проводим произвольную прямую OF, пересекающую UV в точке F; эта прямая пересечет (вторично) окружность C в точке E. На прямой OF от точки F по направлению к O откладываем отрезок FM, равный хорде OE.
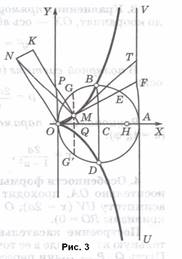
Линия, описываемая точкой M при вращении OF около O, называется циссоидой Диокла – по имени греческого ученого 2 века до н.э., который ввел эту линию для графического решения задачи об удвоении куба.
Реклама

Особенности формы.
Циссоида симметрична относительно OA, проходит через точки B, D и имеет асимптоту UV (x = 2a); O – точка возврата (радиус кривизны RO = O).
Построение касательной.
Чтобы построить касательную к циссоиде в ее точке M, проводим MP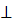 OM. Пусть Q, P – точки пересечения MP с прямыми OX, OY. От точки P на продолжении отрезка QP откладываем отрезок PK = PQ. Строим KN OM. Пусть Q, P – точки пересечения MP с прямыми OX, OY. От точки P на продолжении отрезка QP откладываем отрезок PK = PQ. Строим KN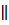 MO и ON MO и ON QP. Точку N пересечения KN и ON соединяем с M. Прямая MN – нормаль к циссоиде. Искомая касательная MT перпендикулярна MN. QP. Точку N пересечения KN и ON соединяем с M. Прямая MN – нормаль к циссоиде. Искомая касательная MT перпендикулярна MN.
2.2 Исторические сведения
Диокл определял циссоиду с помощью другого построения. Он проводил диаметр BD, перпендикулярный OA; точка M получалась в пересечении хорды
OE с прямой GG̕
 BD, проведенной через точку G, симметричную с E относительно BD. Поэтому линия Диокла располагалась целиком внутри круга C. Она состояла из дуг OB и OD. Если замкнуть линию BOD полуокружностью BAD, описанной точкой E, получается фигура, напоминающая лист плюща. Отсюда название «циссоида». BD, проведенной через точку G, симметричную с E относительно BD. Поэтому линия Диокла располагалась целиком внутри круга C. Она состояла из дуг OB и OD. Если замкнуть линию BOD полуокружностью BAD, описанной точкой E, получается фигура, напоминающая лист плюща. Отсюда название «циссоида».
Примерно в 1640 г. Роберваль, а позднее Р.
де Слюз заметили, что циссоида неограниченно продолжается и за пределы окружности, если точка E описывает и другую полуокружность BOD; тогда M лежит на продолжении хорды OE. Однако наименование «циссоида Слюза», предложенное Гюйгенсом, не утвердилось в литературе.
2.3 Площадь
S
полосы
заключенной между циссоидой и ее асимптотой (эта полоса простирается в бесконечность), конечна; она втрое больше площади производящего круга C:
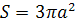 . .
2.4 Объем
V
тела вращения
вышеупомянутой полосы около асимптоты UV равен объему V̕ тела вращения круга C около той же оси (Слюз):
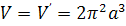 . .
При вращении той же полосы около оси симметрии получается тело бесконечного объема.
2.5 Задача
Дана циссоида Диокла с полюсом в точке O, осью OA и параметром 2a. Приняв точку O за полюс, а ось кривой за ось полярной системы, вывести уравнение кривой в полярных координатах. Записать уравнение кривой в прямоугольной декартовой системе координат.
Решение:
Пусть O – начало координат, OX – ось абсцисс. Тогда уравнение в прямоугольной системе координат:
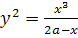 . .
Если O – полюс и OX – полярная ось, то уравнение в полярных координаты будет иметь вид:
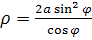 . .
3. Декартов лист
3.1 Исторические сведения
В 1638 г. Р. Декарт, чтобы опровергнуть (неверно им понятое) правило П. Ферма для нахождения касательных, предложил Ферма найти касательную к линии 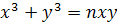 . При обычном для нас толковании отрицательных координат эта линия, которую в 18 веке стали называть декартовым листом, состоит из петли OBAC (рис.4) и двух бесконечных ветвей (OI, OL). . При обычном для нас толковании отрицательных координат эта линия, которую в 18 веке стали называть декартовым листом, состоит из петли OBAC (рис.4) и двух бесконечных ветвей (OI, OL).
Но в таком виде ее представил впервые Х. Гюйгенс (в 1692 г.). До этого линию 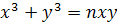 представляли в виде четырех лепестков (один из них OBAC), симметрично расположенных в четырех координатных углах. Поэтому ее называли «цветком жасмина». представляли в виде четырех лепестков (один из них OBAC), симметрично расположенных в четырех координатных углах. Поэтому ее называли «цветком жасмина».
3.2 Построение
Чтобы построить декартов лист с диаметром петли 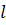 проведем окружность A радиуса проведем окружность A радиуса 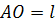 и какую-либо прямую GH, параллельную AO. Далее проведем прямые AA̕
и OE, перпендикулярные AO, и отметим точки A̕
, E их пересечения с GH. Наконец, отложим на луче OA отрезок OF = 3OA и проведем прямую FE. Теперь искомая линия строится по точкам следующим образом. и какую-либо прямую GH, параллельную AO. Далее проведем прямые AA̕
и OE, перпендикулярные AO, и отметим точки A̕
, E их пересечения с GH. Наконец, отложим на луче OA отрезок OF = 3OA и проведем прямую FE. Теперь искомая линия строится по точкам следующим образом.
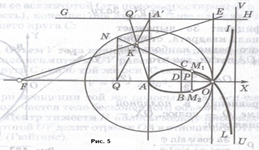
Через O проводим любую прямую ON и через точку N, где эта прямая пересекает (вторично) окружность, проводим NQ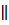 AA̕
. Точку Q, где NQ пересекает прямую OF соединяем с A̕
и отмечаем точку K, где QA̕
пересекает FE. Проводим прямую AK до пересечения с прямой GH в точке Q̕
. Наконец, откладываем на прямой OA отрезок OP, равный и равнонаправленный с отрезком A̕
Q̕
. Прямая M1
M2
, проведенная через P параллельно AA̕
, пересечет прямую ON в точке M1
. Эта точка (а также точка M2
, симметричная ей относительно AO), принадлежит искомой линии. AA̕
. Точку Q, где NQ пересекает прямую OF соединяем с A̕
и отмечаем точку K, где QA̕
пересекает FE. Проводим прямую AK до пересечения с прямой GH в точке Q̕
. Наконец, откладываем на прямой OA отрезок OP, равный и равнонаправленный с отрезком A̕
Q̕
. Прямая M1
M2
, проведенная через P параллельно AA̕
, пересечет прямую ON в точке M1
. Эта точка (а также точка M2
, симметричная ей относительно AO), принадлежит искомой линии.
Когда точка N, исходя из O, описывает окружность A против часовой стрелки, точка M1
описывает траекторию LOCABOI.
3.3 Особенности формы
Точка O – узловая. Касательные, проходящие через O, совпадают с осями координат. Прямая OA (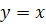 ) есть ось симметрии. Точка ) есть ось симметрии. Точка 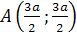 , наиболее удаленная от узловой точки, называется вершиной (коэффициент , наиболее удаленная от узловой точки, называется вершиной (коэффициент 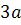 выражает диагональ квадрата, сторона которого равна наибольшей хорде OA петли, так что выражает диагональ квадрата, сторона которого равна наибольшей хорде OA петли, так что 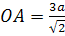 ). Прямая UV ( ). Прямая UV (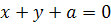 ) – асимптота обеих бесконечных ветвей. ) – асимптота обеих бесконечных ветвей.
3.4 Задача
Написать уравнение декартова листа в прямоугольной системе координат и, приняв точку O за полюс, в полярной системе координат.
Решение:
Уравнение в прямоугольной системе:
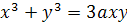 . .
Уравнение в полярной системе (OX – полярная ось):
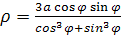 . .
4. Улитка Паскаля
4.1 Определение и построение
Даны: Точка O (полюс
), окружность K диаметра OB=a (рис.6), проходящая через полюс (основная окружность
; она показана на чертеже пунктиром), и отрезок 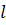 . Из полюса O проводим произвольную прямую OP. От точки P, где прямая OP вторично пересекает окружность, откладываем в обе стороны от P отрезки . Из полюса O проводим произвольную прямую OP. От точки P, где прямая OP вторично пересекает окружность, откладываем в обе стороны от P отрезки 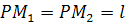 . Геометрическое место точек M1
, M2
(жирная линия на рис.6) называется улиткой Паскаля
– в честь Этьена Паскаля
(1588 – 1651), отца знаменитого французского ученого Блеза Паскаля (1623 – 1662). . Геометрическое место точек M1
, M2
(жирная линия на рис.6) называется улиткой Паскаля
– в честь Этьена Паскаля
(1588 – 1651), отца знаменитого французского ученого Блеза Паскаля (1623 – 1662).
4.2 Исторические сведения
Термин «улитка Паскаля» предложен Ж. Робервалем
, современником и другом Паскаля. Роберваль рассматривал эту линию как один из видов обобщенной конхоиды.

4.3 Особенности формы
Улитка Паскаля симметрична относительно прямой OB. Эта прямая (ось улитки) пересекает улитку: 1) в точке O (если последняя принадлежит улитке); 2) в двух точках A, C (вершины
). Форма линии зависит от соотношения между отрезками 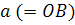 и и 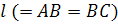 . .
1) Когда  (линия 1 жирная; для неё (линия 1 жирная; для неё 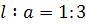 ) улитка Паскаля пересекает сама себя в узловой точке O ) улитка Паскаля пересекает сама себя в узловой точке O
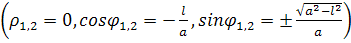 , ,
Образуя две петли: внешнюю OHA1
GO и внутреннюю OH'
C1
G'
O. Угловой коэффициент касательных OD, OE в узловой точке:
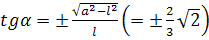 . .
Для построения касательных достаточно провести хорд OD, OE длины l в окружности K. Наиболее удаленным от оси точкам G, H внешней петли отвечает значение
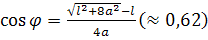 ; ;
Наиболее удаленным точкам G'
, H'
внутренней петли – значение
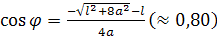 . .
Соответствующее полярное значение полярного радиуса:
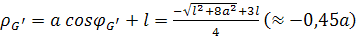 . .
2) Когда 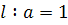 (линия 2 на рис.6), внутренняя петля стягивается к полюсу и превращается в точку возврата, где движение по направлению луча OX сменяется движением в противоположном направлении. Наиболее удаленным от оси точкам L, M отвечают значения (линия 2 на рис.6), внутренняя петля стягивается к полюсу и превращается в точку возврата, где движение по направлению луча OX сменяется движением в противоположном направлении. Наиболее удаленным от оси точкам L, M отвечают значения
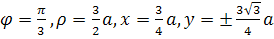 . .
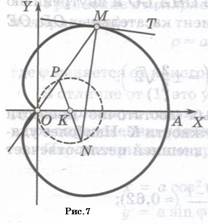
Линия 2 называется кардиоидой
, т.е. «сердцеобразной» (термин введен Кастиллоном в 1741г.). Она изображена отдельно на рис.7
3) Когда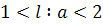 (линия 3; для неё (линия 3; для неё 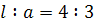 ), улитка Паскаля – замкнутая линия без самопересечения; оторвавшись от полюса, она заключает его внутри себя. Наиболее удаленным от оси точкам L'
, N'
отвечает значение ), улитка Паскаля – замкнутая линия без самопересечения; оторвавшись от полюса, она заключает его внутри себя. Наиболее удаленным от оси точкам L'
, N'
отвечает значение 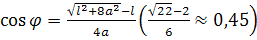 . Лишившись точки возврата, улитка приобретает взамен точки перегиба R, Q, которым отвечает значение . Лишившись точки возврата, улитка приобретает взамен точки перегиба R, Q, которым отвечает значение 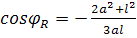 . Угол ROQ . Угол ROQ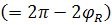 , под которым отрезок RQ виден из полюса, по мере возрастания , под которым отрезок RQ виден из полюса, по мере возрастания 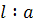 сначала возрастает от нуля до сначала возрастает от нуля до 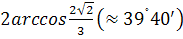 ; этому значению соответствует ; этому значению соответствует 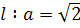 . При дальнейшем увеличении . При дальнейшем увеличении 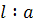 угол ROQ убывает, стремясь к нулю при угол ROQ убывает, стремясь к нулю при 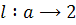 . .
4) При 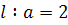 точки перегиба, сливаясь с вершиной C пропадают (причем кривизна в точке C становится равной нулю). Улитка приобретает овальную форму и сохраняет ее при всех значениях точки перегиба, сливаясь с вершиной C пропадают (причем кривизна в точке C становится равной нулю). Улитка приобретает овальную форму и сохраняет ее при всех значениях 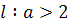
(линия 4; для нее 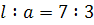 ). Наиболее удаленным от оси точкам L''
, N''
отвечает значение ). Наиболее удаленным от оси точкам L''
, N''
отвечает значение
 . .
4.4 Свойства нормали
Нормаль улитки Паскаля в ее точке M (рис.7) проходит через точку N основной окружности K, диаметрально противоположную той точке P, где OM пересекается с основной окружностью.
4.5 Построение касательной
Чтобы провести касательную к улитке Паскаля в ее точке M, соежиняем последнюю с полюсом O. Точку N основной окрудности K, диаметрально противополжную точке P, соединяем с M. Прямая MN будет нормалью к улитке. Проводя MT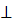 MN, получим искомую касательную. MN, получим искомую касательную.
4.6 Задача
Дана улитка Паскаля с полюсом в точке O. Написать уравнения в прямоугольной и полярной системах координат.
Решение:
Пусть начало координат – в полюсе O, ось OX направлена по лучу OB. Тогда уравнение в прямоугольной системе координат будет иметь вид:
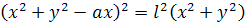 . (1) . (1)
Строго говоря, это уравнение представляет фигуру, состоящую из улитки Паскаля и полюса O, который может и не принадлежать определенному выше геометрическому месту (такой случай имеет место для линий 3 и 4 на рис.6).
Уравнение в полярной системе (O – полюс, OX – полярная ось):
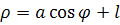 ,
(2) ,
(2)
где 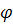 меняется от какого-либо значения меняется от какого-либо значения 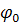 до до 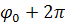 . .
5. Лемниската Бернулли
5.1 Определение
Лемниската есть геометрическое место точке, для которых произведение расстояний от них до концов данно отрещка 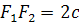 равно равно 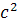 . Точки F1
, F2
называются фокусами
лемнискаты; прямая F1
F2
– ее осью. . Точки F1
, F2
называются фокусами
лемнискаты; прямая F1
F2
– ее осью.
5.2 Исторические сведения
В 1694 г. Якоб Бернули
в работе, посвященной теории приливов и отливов, использовал в качестве вспомогательного средства линию, которую он задает уравнением 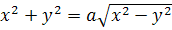 . Он отмечает сходство этой линии (рис.8) с цифрой 8 и узлообразной повязкой, которую он именует «лемниском». Отсюда называние лемниската. Лемниската получила широкую ивестность в 1718 г., когда итальянский математик Джулио Карло Фаньяно
(1682 – 1766) установил, что интеграл, представляющий длину дуги лемнискаты, не выражается через элементарные функции, и тем не менее лемнискату можно разделить (с помощью линейки и циркуля) на n равных дуг при условии, что . Он отмечает сходство этой линии (рис.8) с цифрой 8 и узлообразной повязкой, которую он именует «лемниском». Отсюда называние лемниската. Лемниската получила широкую ивестность в 1718 г., когда итальянский математик Джулио Карло Фаньяно
(1682 – 1766) установил, что интеграл, представляющий длину дуги лемнискаты, не выражается через элементарные функции, и тем не менее лемнискату можно разделить (с помощью линейки и циркуля) на n равных дуг при условии, что 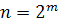 или или 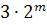 или или 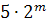 , где m – любое целое положительное число. , где m – любое целое положительное число.
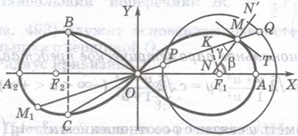
Лемниската есть частный вид линии Кассини. Однако, хотя линии Кассини получили всеобщую известность с 1749 г., тождественность «восьмерки Кассини» с лемнискатой Бернули была уставновлена лишь в 1806 г. (итальянским математиком Саладини
).
5.3 Построение
Можно применять общий способ построя линия Кассини, но нижеизложенный способ (К. Маклорена
) и проще и лучше. Строим (см. рис.) окружность радиуса 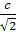 с центром в точке F1
(или F2
). Проводим произвольную секущую OPQ и откладываем на этой прямой в обе стороны от точки O отрезки OM и OM1
, равные хорде PQ. Точка M опишет одну из петель лемнискаты, точка M1
– другую. с центром в точке F1
(или F2
). Проводим произвольную секущую OPQ и откладываем на этой прямой в обе стороны от точки O отрезки OM и OM1
, равные хорде PQ. Точка M опишет одну из петель лемнискаты, точка M1
– другую.
5.4 Особенности формы
Лемниската имеет две оси симметрии: прямую F1
F2
(OX) и прямую OY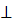 OX. Точка O – узловая; обе ветви имеют здесь перегиб. Касательные в этой точке составляют с осью OX углы OX. Точка O – узловая; обе ветви имеют здесь перегиб. Касательные в этой точке составляют с осью OX углы 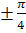 . Точки A1
,A2
лемнискаты, наиболее удаленные от узла O (вершины
лемнискаты), лежат на оси F1
F2
на расстоянии . Точки A1
,A2
лемнискаты, наиболее удаленные от узла O (вершины
лемнискаты), лежат на оси F1
F2
на расстоянии  от узла. от узла.
5.5 Свойства нормали.
Подяоный радиус OM лемнискаты образует с нормалью MN угол 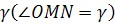 , вдвое больше полярного угла , вдвое больше полярного угла 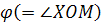 : :
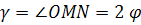 . .
Другими словами: угол 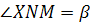 между осью OX и вектором NN'
внешней нормали лемнискаты в точке M равен утроенному полярному углу точки M: между осью OX и вектором NN'
внешней нормали лемнискаты в точке M равен утроенному полярному углу точки M:
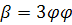 . .
5.6 Построение касательной
Чтобы построить касательную к лемнискате в ее точке M, проводим полярный радиус OM и строим 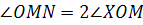 . Перпендикуляр MT к прямой MN есть искомая касательная. . Перпендикуляр MT к прямой MN есть искомая касательная.
5.7 Задача
Написать уравнение лемнискаты Бернулли в прямоугольной системе координат (O – серидина отрезка F1
F2
) и в полярной системе координат (O – полюс).
Решение:
Пусть точка O – начало координат ; ось OX направлена по F1
F2
. Тогда Уравнение в прямоугольной системе координат:
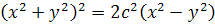 . .
Если O – полюс, OX – полярная ось, то уравнение в полярной системе:
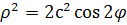 . .
Угол 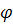 изменяется в промежутках изменяется в промежутках 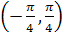 и и 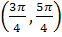 . .
Заключение
В данной работе мы рассмотрели некоторые замечательные кривые, изучили их способы построения, особенности формы и задачи, связанные с этими кривыми.
В параграфе 1 была рассмотрена строфоида, особенности её формы, стереометрическое образование и исторические сведения.
Во 2-м параграфе мы изучили циссоиду Диокла и некоторые формулы, связанные с ней.
В параграфе 3 узнали метод построения, особенности формы и исторические сведения о кривой, называемой «Декартов лист».
В 4-м параграфе рассмотрели улитку Паскаля. Её определение, построение, особенности формы, свойства нормали и построение касательной.
В параграфе 5 была изучена лемниската Бернулли: определение, построение, исторические сведения, особенности формы, свойства нормали и построение касательной.
А также при помощи задач узнали формулы кривых в прямоугольной декартовой и полярной системах координат.
Используемая литература:
1. Маркушевич А.И., Замечательные кривые, М., 1978 г., 48 стр. с ил.
2. Выгодский М.Я., Справочник по высшей математике, М.: АСТ: Астрель, 2008, 991 стр. с ил.
3. Атанасян Л.С. и Атанасян В.А., Сборник задач по геометрии. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. Ч. I, М., "Просвещение", 1973, 256 с.
4. Гурова А.Э. Замечательные кривые вокруг нас. М, 1989
5. Маркушевич А.И. Замечательные кривые. - М, 1978
6. http://ru.wikipedia.org/wiki/Строфоида
7. http://ru.wikipedia.org/wiki/Лемниската_Бернулли
8. http://ru.wikipedia.org/wiki/Улитка_Паскаля
|