Курсовая работа
На тему:
«Решение математических задач с использованием программного пакета
MathCad
»
Екатеринбург 2010
1.
Краткие теоретические сведения
Дифференциальными уравнениями называются уравнения, в которых неизвестными являются функции одного или нескольких переменных, причем в уравнения входят не только сами функции, но и их производные. Рассмотрим обыкновенное дифференциальное уравнение n-го порядка:
y(
n
)
= f (x, y, y’
, y’’
… y(
n
-1)
)
Общее решение этого уравнения зависит от n-произвольных постоянных.
Точное решение дифференциального уравнения может быть найдено вручную, либо операторным методом в пакете MathCad. Также есть приближенные методы решения: решение с помощью рядов, численные методы и др.Каждый из этих методов определяет один или несколько бесконечных процессов, с помощью которых при выполнении определённых условий можно получить точное решение задачи. Для получения приближенного решения останавливаются на некотором шаге процесса.
Принцип операторного метода состоит в том, что при переводе функции дифференциального уравнения y(
n
)
= f (x, y, y’
, y’’
… y(
n
-1)
) в пространство Лапласа мы получаем изображение F(s), которое зависит только от одной переменной s. Отсюда, по теореме о единственности мы можем найти точное решение дифференциального уравнения.
Если решение ищется в виде бесконечного ряда, то за приближенное решение принимают конечный отрезок ряда. Например, пусть требуется найти решение дифференциального уравнения y' = f (x, у), удовлетворяющее начальным условиям у (х0
) = y0
, причём известно, что f (x, у) – аналитическая функция х, у в некоторой окрестности точки (х0
, y0
). Тогда решение можно искать в виде степенного ряда:
y (x) – y (x0
) = 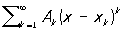
Коэффициенты Ak
ряда могут быть найдены либо последовательным дифференцированием, либо с помощью метода неопределенных коэффициентов, который применяется в курсовой работе. Метод рядов позволяет находить решение лишь при малых значениях величины х – х0
.
К численным методам относятся методы, позволяющие находить приближенное решение при некоторых значениях аргумента (т.е. получать таблицу приближённых значений искомого решения), пользуясь известными значениями решения в одной или нескольких точках. Такими методами являются, например, метод Эйлера, метод Рунге и целый ряд разностных методов (метод Рунге-Кутты).
Реклама

Если a – точное решение, то абсолютной погрешностью приближенного значения a*
называют величину Д(а*
), которая определяется следующим образом:
|a*
-a| ≤ Д(a*
)
Относительной погрешностью Дa приближенного значения называют некоторую величину, которая определяется следующим образом:
|(a*
-a)/ a*
| ≤ д(a*
)
Таким образом, эти две погрешности связаны между собой:
д(a*
) = Д(a*
) / |a*
|
Относительную погрешность часто выражают в процентах. Числа a*
и Дa принято записывать с одинаковым количеством знаков после запятой.
Получить точное решение дифференциального уравнения вручную, операторным методом, приближенное решение с помощью рядов (до 5 элемента ряда) на интервале [0,1], численное решение методами Эйлера и Рунге-Кутты, представить совместное графическое решение ДУ всеми способами. Рассчитать локальную погрешность методов Эйлера и Рунге-Кутты. Рассчитать относительную и абсолютную погрешность всех методов с использованием точного решения.
Дано:
2x''+5x'=29cost
x(0)= -1
x'(0)=0
Пусть X(s) изображение, а х(t) оригинал.
Продифференцируем левую часть уравнения:
2x''+5x'=5*(s2
*X-s*x(0) – x'(0))+5*(s*X-x(0))
Подставим данные значения x(0) и x'(0) в уравнение и получим:
x''-3x'+2x= 2*(s2
*X+s)+5*(s*X+1)=X*(2s2
+5s)+s*2+5
Преобразуем правую часть уравнения в пространство Лапласа

Найдем значение изображения:
Given
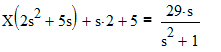 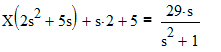
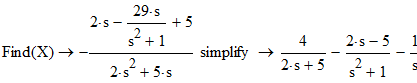
Сопоставим изображению оригинал:
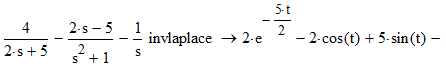
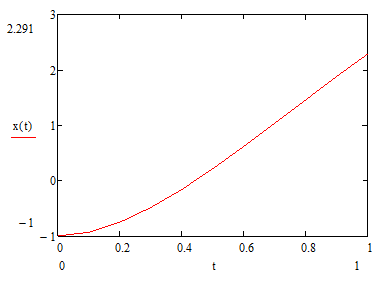
Найдем значения функции, построим её график:
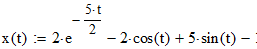 
 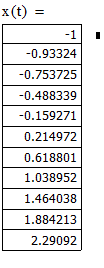
дифференциальный уравнение эйлер операторный
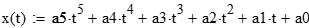
Запишем функцию в виде ряда:
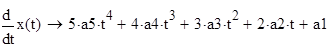
Найдем производные первого и второго порядков от этой функции:
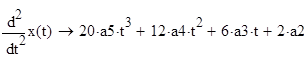
Разложим в ряд правую часть уравнения:
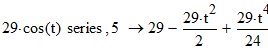
Полученные ряды подставим в исходное уравнение:
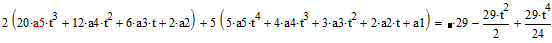
Найдем значения коэффициентов
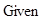
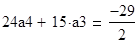
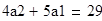
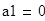
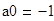
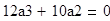 
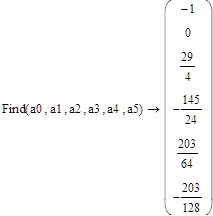
Подставим найденные значения в разложение функции в ряд и построим график функции:
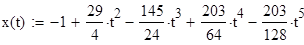
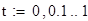
Перепишем условие следующим образом:
x'=z
z'+ 5z=29cos t
z'=29cos t – 5z
Задаём начальные данные:
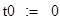
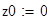
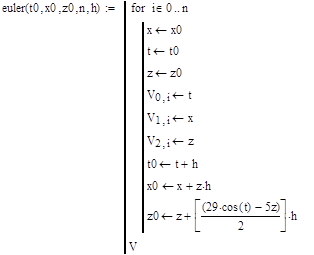
Находим значение x и x'
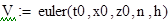

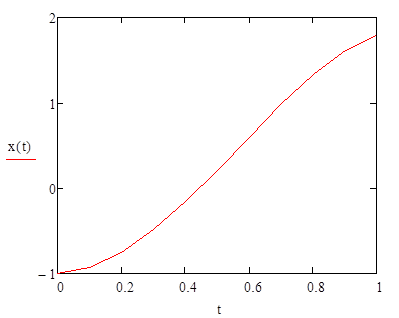
Для сравнения решим это дифференциальное уравнение с шагом 0,01. Построим график.
Определяем функцию D, задающую производные и находим значения функции. Строим график функции:
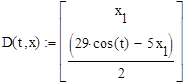
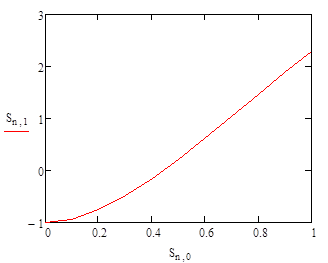
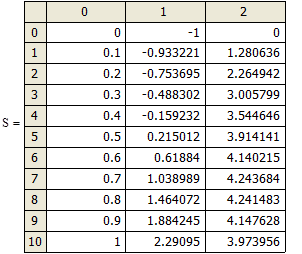
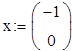
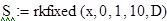
Таблица 1 – Значения функции
| Заданный интервал |
Точное решение |
Приближенное с помощью рядов |
Метод Эйлера (шаг 0,1) |
Метод Эйлера (шаг 0,01) |
Метод Рунге Кутты |
| 0 |
-1,000000 |
-1,000000 |
-1,000000 |
-1,000000 |
-1,000000 |
| 0,1 |
-0,933240 |
-0,933240 |
-1,000000 |
-0,938953 |
-0,933221 |
| 0,2 |
-0,753725 |
-0,753766 |
-0,855000 |
-0,762488 |
-0,753695 |
| 0,3 |
-0,488339 |
-0,488787 |
-0,601974 |
-0,498255 |
-0,488302 |
| 0,4 |
-0,159271 |
-0,161707 |
-0,270096 |
-0,168991 |
-0,159232 |
| 0,5 |
0,214972 |
0,205973 |
0,117337 |
0,206412 |
0,215012 |
| 0,6 |
0,618801 |
0,592753 |
0,541466 |
0,612091 |
0,618840 |
| 0,7 |
1,038952 |
0,975227 |
0,986812 |
1,034588 |
1,038989 |
| 0,8 |
1,464038 |
1,326187 |
1,440495 |
1,462384 |
1,464072 |
| 0,9 |
1,884213 |
1,612712 |
1,891659 |
1,885536 |
1,884245 |
| 1 |
2,290920 |
1,794271 |
2,331055 |
2,295416 |
2,290950 |
Таблица 2 – Локальная, абсолютная и относительная погрешность
| Абсолютная погрешность |
Относительная погрешность |
| Решения с помощью рядов |
метода Эйлера (шаг 0,1) |
метода Эйлера (шаг 0,01) |
метода Рунге Кутты |
Решения с помощью рядов |
метода Эйлера (шаг 0,1) |
метода Эйлера (шаг 0,01) |
метода Рунге Кутты |
| Локальная погрешность |
0,000000 |
0,000000 |
0,000000 |
0,000000 |
0,0 |
0,0 |
0,0 |
0,000 |
| 0,000000 |
0,066760 |
0,005713 |
-0,000019 |
0,0 |
-6,7 |
-0,6 |
0,002 |
| 0,000041 |
0,101275 |
0,008763 |
-0,000030 |
0,0 |
-11,8 |
-1,1 |
0,004 |
| 0,000448 |
0,113635 |
0,009916 |
-0,000037 |
-0,1 |
-18,9 |
-2,0 |
0,008 |
| 0,002436 |
0,110825 |
0,009720 |
-0,000039 |
-1,5 |
-41,0 |
-5,8 |
0,024 |
| 0,008999 |
0,097635 |
0,008560 |
-0,000040 |
4,4 |
83,2 |
4,1 |
-0,019 |
| 0,026048 |
0,077335 |
0,006710 |
-0,000039 |
4,4 |
14,3 |
1,1 |
-0,006 |
| 0,063725 |
0,052140 |
0,004364 |
-0,000037 |
6,5 |
5,3 |
0,4 |
-0,004 |
| 0,137851 |
0,023543 |
0,001654 |
-0,000034 |
10,4 |
1,6 |
0,1 |
-0,002 |
| 0,271501 |
-0,007446 |
-0,001323 |
-0,000032 |
16,8 |
-0,4 |
-0,1 |
-0,002 |
| 0,496649 |
-0,040135 |
-0,004496 |
-0,000030 |
27,7 |
-1,7 |
-0,2 |
-0,001 |
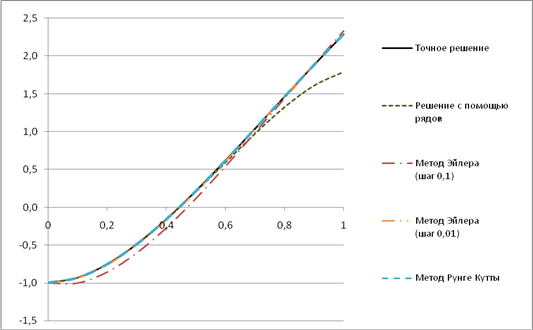
Рисунок 1 – Совместное графическое решение
Из всех методов наиболее точным оказался метод Рунге-Кутты, его максимальная относительная погрешность 0,024%, относительная погрешность приближенного метода составила 27,7%. Метод Эйлера с шагом 0,1 имеет наибольшую погрешность 83,2%, однако при уменьшении шага в до 0,01 его погрешность составляет всего 5,8%. Это подтверждает то, что погрешность метода Эйлера сильно зависит от принятого шага. Проанализировав графическое решение делаем вывод о том, что методы Эйлера и Рунге-Кутты повторяют форму кривой точного решения, а график приближенного решения с увеличением аргумента всё сильнее отклоняется от искомого графика – свидетельство того, что погрешность решения с помощью рядов зависит от количества членов ряда. Характер кривой также говорит о том, что точность приближенного решения с помощью рядов удовлетворительна только вблизи некоторой точки.
Реклама

Решить систему дифференциальных уравнений, получить точное решение вручную, операторным методом, приближенное решение с помощью рядов (до 5 элемента), численное решение методом Эйлера, Рунге-Кутты. Представить графическое совместное решение, рассчитать локальную, относительную и абсолютную погрешность решения.
Дано:
dx/dt=3x + y
dy/dt=5/2x – y + 2
x(0)=0
y(0)=1
Пусть X(s) изображение, для оригинала x(t), Y(s) изображение для оригинала y(t). Перейдем от оригинала к изображению:
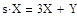
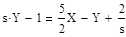
Найдем значения изображений:
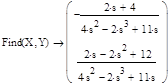
Найдем значения функции и построим её график:
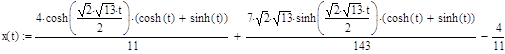
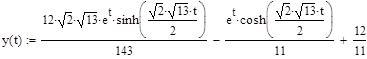
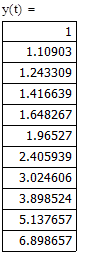 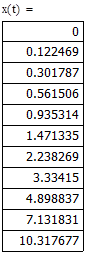
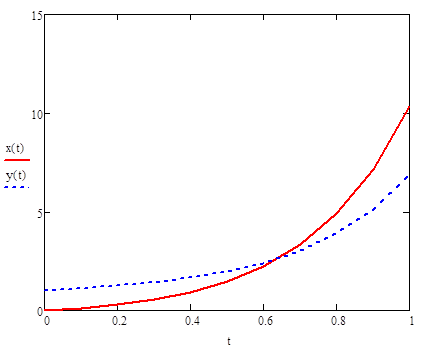
Преобразуем систему таким образом что, получим дифференциальное уравнение второго порядка, зависящее только от x:
x''-2x'-11/2x-2=0
Алгоритм решения такой же, как и при решении дифференциального уравнения с правой частью специального вида, но без необходимости раскладывать правую часть.
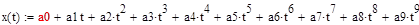
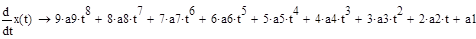
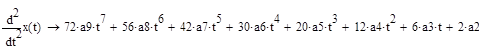
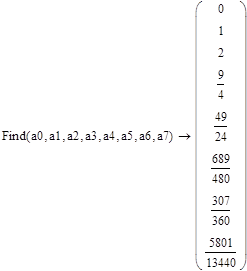
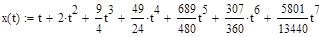
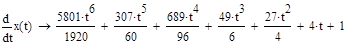
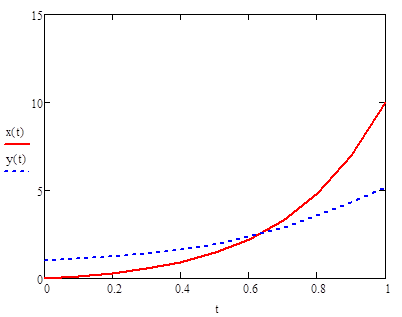
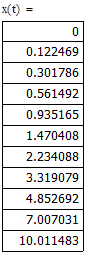 
Наименьшую погрешность имеет метод Рунге-Кутты четвертого порядка – для функции x(t) относительная погрешность на десятом шаге составляет 0,036%, для функции y(t) 0,0297%. Наибольшая погрешность у метода Эйлера с шагом 0,1 – для функции x(t) 70,8%, для функции y(t) 51,4%. При изменении шага до 0,01 погрешность существенно уменьшается до 6,6% и 5,3% соответственно. Вывод о влиянии шага на погрешность в методе Эйлера совпадает с выводами решения дифференциального уравнения – большую роль в точности этого метода играет шаг. Можно еще раз подтвердить вывод о том, что точность приближенного метода решения сильно зависит от того, на сколько членов будет разложена дифференциальная функция.
|